A novel microfluidic concept for bioanalysis using freely moving beads trapped in recirculating flows

Abstract

There are only a few examples in which beads are employed for heterogeneous assays on microfluidic devices, because of the difficulties associated with packing and handling these in etched microstructures. This contribution describes a microfluidic device that allows the capture, preconcentration, and controlled manipulation of small beads (<6 μm) in etched microchannels using fluid flows only. The chips feature planar diverging and converging channel elements connected by a narrow microchannel. Creation of bi-directional liquid movement by opposing electro-osmotic and pressure-driven flows can lead to the generation of controlled recirculating flow at these elements. Small polymer beads can actually be captured in the controlled rotating flow patterns. The clusters of freely moving beads that result can be perfused sequentially with different solutions. A preliminary binding curve was determined for the reaction of streptavidin-coated beads and fluorescein-labelled biotin, demonstrating the potential of this bead-handling approach for bioanalysis.

---

Introduction

The potential benefits of microfluidic devices for many applications in the life sciences have been demonstrated, particularly with respect to fast analysis and high throughput. Most successful examples to date have employed structures based on microchannel networks formed in planar glass or plastic substrates, in which solutions are pumped using applied electric fields.^1–3 The mechanism underlying this pumping principle is electro-osmosis, a bulk flow which originates at the surface of charged substrates like glass, and requires no pumps, valves or other moving parts.⁴ An additional advantage of using electric fields is that species may also be separated electrophoretically as a function of their different charge-to-mass ratios.^1–5 Many chip-based applications therefore involve capillary electrophoresis (CE) in free solution. However, examples of microfluidic platforms for heterogeneous analysis, in which biospecific molecules are immobilized on a surface to capture the analyte of interest in solution, are still rare. This is due in part to the added development work involved if microchannel surfaces are to be reproducibly and effectively modified.^6–9 The use of bead-based materials could be a viable alternative, as they are ideal reagent delivery vehicles providing large reactive surface areas and have become omnipresent in biomedical applications like immunoassay.¹⁰ However, beads have not often been employed in flow systems, conventional or integrated, for heterogeneous assay.^11,12 This is especially true in microfluidic structures because of the difficulties associated with packing and handling beads in etched channels, despite possible benefits related to facilitated fluid handling and accelerated analysis. To date, the approach generally adopted for on-chip, bead-based chemistry has been to fabricate a retaining feature in the microchannel to confine beads to a specific location within the microfluidic network.^12–17 The resulting structures must fulfill the dual purpose of holding back particles while at the same time allowing solution to be delivered from a separate, particle-free compartment on the chip. Other approaches consist of using ultrasonic standing waves or magnetic fields to trap beads, but these require the integration of a transducer for wave or magnetic field generation.^18–21

We present here a new way of handling beads on chip that is not limited by a need for physical barriers and additional transducers. Our approach is to trap and manipulate beads using fluid flows only, in special channel geometries incorporating planar diverging and converging channel elements. (“Diverging channel” refers to a channel segment of expanding cross-section, whereas “converging channel” refers to a contracting cross-section. These elements are defined in this work in terms of the direction of pressure-driven flow.) Creation of a bi-directional flow in a microfluidic device with diverging and converging channel elements can result in the generation of controlled recirculating flow or vortices^22–24 (Fig. 1). Early visualization experiments revealed that small, fluorescent polymer beads (2.5 μm, Alignflow, Molecular Probes, The Netherlands) not only delineated the streamlines, but could actually be captured and preconcentrated in these rotating flow patterns as well.²³ Furthermore, clusters of freely moving beads could be held in place while being sequentially perfused by different solutions.²⁵ In this paper, we demonstrate the practical application of this phenomenon for facilitated bead handling in microfluidic devices with an analysis of fluorescein-labelled biotin at different concentrations using 2 μm streptavidin-coated beads (SC beads).

Fig. 1 (a) Schematic of a microchannel showing the velocity profiles of electro-osmotic flow and pressure-driven flow (left). Velocities are additive and can be combined to give rise to a bi-directional flow (right). (b) Top schematic view of the microfluidic vortex device. Streamlines in the plane halfway between the top and bottom of the channel (parallel to the page) are shown. EOF and PF conditions are such that v_ave is close to zero. In the large channels, streamlines of the flow follow EOF. A pair of symmetrical vortices is generated at each end of the trapping channel, and flow recirculates between the diverging and converging channel elements through this channel. θ_con: opening angle of the converging channel element; θ_div: opening angle of the diverging channel element; A₁: cross-sectional area of the narrow trapping channel; A₂: cross-sectional area of the wide channel segment after the diverging channel element.

Methods and material

Electro-osmotic flow (EOF) is a bulk flow of fluid which results when motion, generated in the diffuse double-layer at microchannel walls through application of an axial electric field, is transferred to adjacent fluid layers by viscous forces. Combining the flat, plug-like velocity flow profile of EOF and the parabolic profile of a counter, pressure-driven flow (PF) can give rise to bi-directional flow, in accordance with theory²⁶ (Fig. 1(a)). In a straight microchannel of uniform cross-section, two well-defined regions of laminar flow are generated in opposite directions as the average velocity, v_ave, approaches 0. In the core of the microchannel, PF is predominant. Close to channel walls, EOF determines the direction of flow. The introduction of a diverging channel or converging channel alters the equilibrium between these regions in a unique way, resulting in the generation of recirculating flow at the low flow rates commonly used for microfluidic applications. Under these conditions, streamlines are laminar and well-defined, and rotating flow behavior is not expected. However, application of a counter flow increases resistance to the flow. As v_ave approaches zero, PF entering a diverging channel divides and is deflected to the sides to give rise to a pair of vortices of predictable shape and velocity distribution (Fig. 1(b)). The situation at a converging channel element is reversed, with PF entering the converging channel and increasing the resistance to EOF. Flow separates from the walls as a result, creating controlled vortex motion similar to that at a diverging channel. Thus, vortices at diverging and converging channel elements situated at opposite ends of a narrow microchannel can combine with bi-directional flow in the channel itself to yield a well-defined, stable, recirculating flow pattern through the channel.

The streamlines shown schematically in Fig. 1 are substantiated by experiments performed with beads (diameter ranging between 1 and 6 μm), which reveal the generation of vortices at diverging and converging channel geometries. More intriguing, beads can be captured and preconcentrated in the narrow channel between the diverging and converging channel elements, to form clusters of freely moving beads at both these elements. This part of the microfluidic device is thus termed “the trapping channel” (Fig. 1).

The microfluidic devices, fabricated in our labs, were isotropically etched in Pyrex 7740 glass wafers (Guinchard SA, Yverdon, Switzerland) and required only one photolithographic step.⁶ Microchannels were 50 μm wide across the top and 20 μm deep. Diverging and converging channels were incorporated into the microfluidic devices by including two wider segments along a channel (Fig. 1(b)). These were designed so that ratios of cross-sectional areas of the wide to narrow segments (A₂/A₁) were kept constant, and only the opening angle, θ_div (for a diverging channel) or θ_con (for a converging channel), was varied. Wide and narrow segments had the same depth, and had the 90°-rotated D-shaped cross-sections produced by isotropic etching of Pyrex with hydrofluoric acid.

The chip was mounted onto an X–Y–Z translation stage. Voltage control was achieved using a computer-controlled system built in-house.⁶ The same buffer (10 mM sodium tetraborate (Sigma Chemicals, Buchs, Switzerland), pH 9) was used in all the measurements. Hydrostatic pressure was applied to a reservoir using a column of buffer to generate the PF. In general, a head ranging from 4 to 12 cm (4 to 12 mbar) was used, and a potential equivalent to an electric field ranging from 0 to 350 V cm⁻¹ was applied between reservoirs to induce EOF. An argon ion laser (488 nm, Ion Laser Technology, UT, USA) was used to achieve the detection of the labelled biotin by laser-induced fluorescence (LIF) using a confocal fluorescence detection set-up. The laser light was reflected by a dichroic filter (488 nm, ILEE, Urdorf, Switzerland) and focused in the channel by means of a microscope objective (25×; N.A.= 0.35; Leica AG, Glattbrugg, Switzerland). The fluorescence signal collected by the microscope objective was passed through the dichroic filter and a 1 mm pinhole before being detected with a photomultiplier tube (PMT) (Hamamatsu Photonics K.K., Schüpfen, Switzerland). For visual inspection, the PMT was replaced with a CCD camera (Digital ½ inch CCD, JVC).

Simulations (CoventorWare v2001.3, Coventor Technologies, Inc., USA) of flow velocity vector fields under experimentally employed boundary conditions confirmed flow patterns observed by visualization with beads.

Results and discussion

Video imaging such as that shown in Fig. 2 provides three important pieces of information, as discussed below.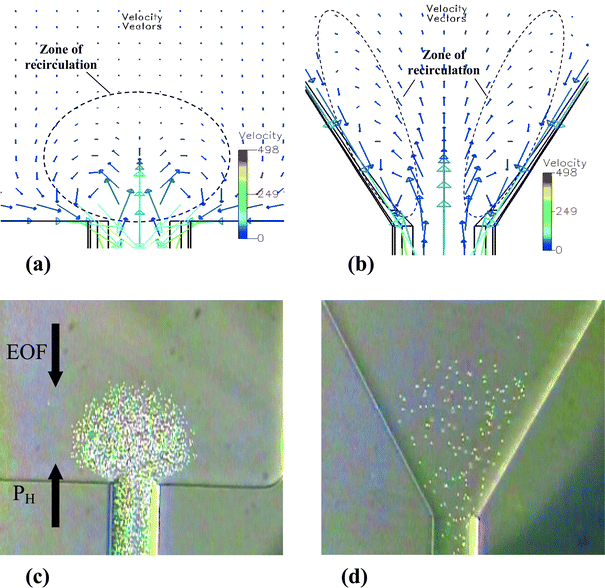

Fig. 2 Simulation of the velocity vector field of the flow (μm s⁻¹) of diverging channels with (a) θ_div = 180° and (b) θ_div = 60°, and the corresponding photos (c) and (d) showing bead clustering. Boundary conditions are the same for both diverging channels, that is, an average electric field of E = 200 V cm⁻¹, P_H = 7 mbar and A₂/A₁ = 7. Protein A-coated fluorescent beads (1 μm) were used to obtain these images.

Firstly, the recirculating flow is very reproducible and stable. Moreover, the length of the trapping channel, l_TC, and the lengths and widths of the two wider channel elements of the microfluidic device are important parameters for controlling this flow. Experience has shown that dimensions must be chosen such that EOF is stronger than PF over the whole cross-sectional area of the diverging element of the trapping channel. At the same time, PF must dominate at the converging channel. If both these criteria are satisfied, beads will be prevented from escaping from the trapping channel to any large extent, though a few beads will always be lost. For example, we have observed that about 5 beads will be lost every 2 s at the converging element and no beads lost at the diverging element for θ_div = θ_con = 90°. We found that for l_TC ≥ 3000 μm, A₂/A₁ = 7, 60° ≤ θ_div ≤ 180°, and 90° ≤ θ_con ≤ 120°, beads are well confined to the trapping channel. These values for the various geometric parameters are empirical, however, and could be optimized using simulation tools to better predict flow patterns.

Secondly, video images show that beads delineate flow patterns that are very similar to those simulated for the trapping channel (compare Fig. 2(a) with (c), and Fig. 2(b) with (d)). The size and velocity distribution of the recirculating flow patterns can be varied by modifying device geometry, or by simply tuning the applied potential at a given pressure or vice versa. Hence, modulation of bead cluster size and shape can also be accomplished by controlling geometric and/or pumping parameters, since bead motion is strongly dependent on flow streamlines.²⁴

Last but not least, video imaging and simulations indicate that flow considerations do not always reveal the whole story with respect to bead behavior. The electrokinetic mobility of the beads themselves has also proven to play a significant role in determining under which electric field and pressure conditions clusters are formed experimentally. This becomes increasingly true for beads with high, well-defined surface charge densities. Initial experiments with negatively charged, fluorescent, 2.5 μm polystyrene beads, whose mobility opposes the EOF, seemed to indicate that clusters form under conditions close to the point of zero net flow in the channel. This, however, proved not always to be the case. For instance, with negatively charged, 1 and 2 μm SC- or Protein A-coated beads, less pressure than predicted by theory^22,26 needed to be applied to form a bi-directional flow of beads in a channel of constant cross-section. Not unexpectedly, bead size also plays a role in particle mobility, with larger particles (>4 μm) apparently subject to higher frictional losses in the flow than smaller particles. Thus, it is difficult to predict the electric field and hydrostatic pressure conditions under which bead recirculation could be accomplished, without additional knowledge about the electrokinetic mobility of the particles themselves. Development of a theoretical model relating the electrokinetic mobility of beads to the optimum flow conditions for cluster formation is ongoing.

The ability to capture and preconcentrate beads locally in a microchannel network is fundamental to bead handling in these devices. Combining this with controlled bead transport from one point to another provides an added flexibility which is not possible in packed bed systems. The six video frames in Fig. 3 illustrate the controlled movement of clusters of 2.5 μm latex beads from one diverging channel to another. Simply by turning off the electric field and hence removing the EOF component of the flow, the bead cluster can be transported as a plug to the next diverging channel. Once there, re-application of the electric field leads to the immediate re-establishment of rotating flows with consequent trapping of beads and reformation of the clusters.

Fig. 3 Experiments illustrating the controlled transport of 2.5 μm latex beads from one diverging channel to another. The applied pressure was 10 mbar throughout the experiment. The layout resembled that shown in Fig. 1. Maximum width at the first diverging channel was 360 μm, and 260 μm at the second diverging channel. The trapping channel was 50 μm wide, 20 μm deep and 3 mm in length. At t = 0 s, beads were recirculating at the first diverging channel. When the potential was turned off, they were transported towards the second diverging channel by hydrostatically induced pressure flow. At t = 6 and 12 s, the beads delineated the parabolic profile typical of Poiseuille flow, before passing through the trapping channel (34 s < t < 61 s). Once the beads had reached the channel outlet, the potential was re-applied. About 30 s were required for beads to be recaptured in the trapping channel and the clusters to reform.

Recirculating flow in our devices is generated under conditions where a net flow still exists in the direction of the EOF. This means that it should be possible to retain clusters of freely moving beads in the trapping channel while sequentially pumping sample(s) and reagents from different reservoirs over them. (This assumes that conditions suitable for electrokinetic reagent delivery can be maintained upon switching from one solution to the next.) To demonstrate that this works, binding experiments were carried out in a microdevice, using 2 μm, SC beads (Polysciences, Germany) as reagent. As analyte, either biotin-4-fluorescein (B4F) or 5-((N-(5-(N-(6-(biotinoyl)amino)hexanol)amino)pentyl)thioureidyl)fluorescein (FLB) was used (both compounds were obtained from Molecular Probes Europe B.V., Leiden, The Netherlands). In B4F, the spacer length between fluorescein and biotin is 9 atoms long, whereas it is 21 atoms long in FLB. Hence, FLB is less prone to quenching than B4F. The original bead buffer was replaced before experimentation by 10 mM sodium tetraborate buffer (pH 9) through centrifugation. Visual inspection of bead handling was combined with quantitative measurement of fluorescence using a PMT-based confocal detection system. The streptavidin–biotin interaction was chosen for its large affinity constant and many applications in immunochemistry.²⁷

Fig. 4 shows a schematic of the device and the different stages for the biotin–streptavidin binding experiment. Hydrostatic pressure was kept constant during the whole experiment, with only the applied potential being switched between reservoirs. The binding experiment comprises four steps. (1) SC bead loading and trapping: SC beads (c_beads = 10⁷ beads mL⁻¹) are introduced from reservoir 3 using a flow induced by application of hydrostatic pressure (column of buffer: 9 cm high (9 mbar)). Once past the second diverging channel, 1.5 kV is applied between reservoirs 1 and 3, giving rise to an opposing EOF. The SC beads are driven back and held in the trapping channel (c_beads ≅ 10⁸ beads mL⁻¹). (2) Sample loading and binding: While the SC beads are recirculating, the potential is switched (≅ 50 ms) from between reservoirs 1 and 3 to between reservoirs 2 and 4 (U₂₄ = 1.5 kV). Labelled biotin is then loaded up to and through the trapping channel, and the freely moving SC beads are continuously perfused. (3) Flushing: After a certain incubation time, the potential is switched back again to reservoirs 1 and 4 to flush the excess sample away, while the newly bound labelled biotin–SC beads are still clustering. (4) Detection: Detection of fluorescently labelled biotin bound to SC beads is carried out at 20 μm from the second diverging channel entrance. Once an analysis is finished, the beads can be washed away by simply increasing the applied voltage, followed by collection in a waste reservoir (reservoir 4).

Fig. 4 Initial state: Schematic of the 2 × 4 cm device used for the biotin–streptavidin binding experiment. Reservoirs 1 and 4 are filled with sodium tetraborate (10 mM, pH 9, μ_EOF = 6.2 × 10⁻⁴ cm² V⁻¹ s⁻¹), reservoir 2 with labelled biotin (solutions ranging from 0.4 to 4 μM in sodium tetraborate buffer were used) and reservoir 3 with 2 μm SC beads (5 μL in sodium tetraborate, c_beads = 5 × 10⁷ beads mL⁻¹). The different stages of the binding experiment are described in more detail in the text.

Fig. 5(a) shows the fluorescence signal recorded by the PMT, located at the second diverging channel, as a function of time. The signal shown was acquired after excess labelled biotin had been flushed away with buffer, and thus is due to the newly bound, biotin–streptavidin-coated beads still recirculating in the trapping channel. The experiments yielding the results in Fig. 5(a) each used a sample perfusion or incubation time of 200 s, with a total cycle time of 400 s. The lowest concentration of B4F considered was 0.4 μM. Comparison of signal intensities recorded for beads with that for buffer alone indicates that binding did indeed take place. Moreover, the measured fluorescence increased as a function of B4F concentration, allowing a preliminary dose-response curve to be constructed by averaging the signal at each concentration over 50 s (Fig. 5(b)). This curve is very typical of analysis based on affinity binding, with available streptavidin sites more or less saturated in 200 s by B4F at a 4 μM concentration. Use of a similar microfluidic device yielded fluorescence as a function of incubation time for 1 μM FLB binding to SC beads (Fig. 5(c)). Signal was averaged over 20 s to obtain each of the data points in this figure. In this case, available streptavidin sites were more or less saturated in 400 s by 1 μM FLB, indicating that the detection of much lower concentrations should be possible in reasonable incubation times. In fact, the lowest FLB concentration considered with this system was 50 nM for an incubation time of 120 s (Fig. 5(d)). The signal-to-noise ratio in this particular case was 3.3.

Fig. 5 (a) Binding curves for biotin bound to SC beads after flushing away excess biotin. A significant difference in intensity is observed for B4F-bound beads with respect to pure buffer, indicating that binding did take place. The perfusion or incubation time was 200 s, for a total cycle time of 400 s for each analyte concentration. (b) A dose-response curve (fluorescence signal as a function of biotin concentration) was constructed from the data in (a). (c) Fluorescence signal as a function of incubation time obtained with 1 μM FLB. The curve is calculated using a 1^st-order binding model.⁶ (d) Graphic showing a complete analysis from incubation to flushing for 50 nM FLB.

Conclusion

Future studies will focus on the analytical aspects of the method, using the streptavidin/biotin model initially for optimisation of experimental parameters. The development of a theoretical model taking into account EOF, PF, channel geometry and bead mobilities in order to predict bead trapping is also underway. The influence of particle composition and size on trapping behavior will be considered. The significant variety of beads available, and the novel bead handling method presented in this paper, could enable new approaches for applications in drug discovery, combinatorial chemistry, and bioanalysis.

Acknowledgements

The authors thank the Centre Suisse d'Electronique et de Microtechnique (Neuchâtel, Switzerland) for financial support of this work.

References

1. D. J. Harrison, K. Fluri, K. Seiler, Z. H. Fan, C. S. Effenhauser and A. Manz, Science, 1993, 261, 895–897.
2. C. S. Effenhauser, A. Manz and H. M. Widmer, Anal. Chem., 1993, 65, 2637–2642.
3. S. C. Jacobson, R. Hergenröder, L. B. Koutny and J. M. Ramsey, Anal. Chem., 1994, 66, 1114–1118.
4. A. Manz, C. S. Effenhauser, N. Burggraf, D. J. Harrison, K. Seiler and K. Fluri, J. Micromech. Microeng., 1994, 4, 257–265.
5. S. C. Jakeway, A. J. de Mello and E. L. Russell, Fresenius J. Anal. Chem., 2000, 366, 525–539.
6. A. Dodge, K. Fluri, E. Verpoorte and N. F. de Rooij, Anal. Chem., 2001, 73, 3400–3409.
7. E. Eteshola and D. Leckband, Sens. Actuators B–Chem., 2001, 72, 129–133.
8. T. Yang, S.-y. Jung, H. Mao and P. S. Cremer, Anal. Chem., 2001, 73, 165–169.
9. V. Linder, E. Verpoorte, W. Thormann, N. F. de Rooij and H. Sigrist, Anal. Chem., 2001, 73, 4181–4189.
10. M. B. Meza, Drug Discovery Today, 2000, 1, 38–41.
11. B. Willumsen, G. D. Christian and J. Ruzicka, Anal. Chem., 1997, 69, 3482–3489.
12. K. Sato, M. Tokeshi, T. Odake, H. Kimura, T. Ooi, M. Nakao and T. Kitamori, Anal. Chem., 2000, 72, 1144–1147.
13. C. Wang, R. Oleschuk, F. Ouchen, J. Li, P. Thibault and D. J. Harrison, Rapid Commun. Mass Spectrom., 2000, 14, 1377–83.
14. A. B. Jemere, R. D. Oleschuk, F. Ouchen, F. Fajuyigbe and D. J. Harrison, Electrophoresis, 2002, 23, 3537–3544.
15. H. Andersson, W. van der Wijngaart, P. Enoksson and G. Stemme, Sensors and Actuators B, 2000, 67, 203–208.
16. H. Andersson, W. van der Wijngaart and G. Stemme, Electrophoresis, 2001, 22, 249–257.
17. R. D. Oleschuk, L. L. Shultz–Lockyear, Y. Ning and D. J. Harrison, Anal. Chem., 2000, 72, 585–590.
18. K. Yasuda, Sens. Actuators B, 2000, 64, 128–135.
19. J.-W. Choi, K. W. Oh, A. Han, C. A. Wijayawardhana, C. Lannes, S. Bhansali, K. T. Schlueter, W. R. Heineman, H. B. Halsall, J. H. Nevin, A. J. Helmicki, H. T. Henderson and C. H. Ahn, Biomed. Microdev., 2001, 3, 191–200.
20. Z. H. Fan, S. Mangru, R. Granzow, P. Heaney, W. Ho, Q. Dong and R. Kumar, Anal. Chem., 1999, 71, 4851–4859.
21. G. Jiang and D. J. Harrison, Analyst, 2000, 125, 2176–2179.
22. G. Boer, A. Dodge, K. Fluri, B. H. van der Schoot, E. Verpoorte and N. F. de Rooij, in Micro Total Analysis Systems ′98: Proceedings of the μTAS′98 Workshop, eds. D. J. Harrison and A. van den Berg, Kluwer Academic Publishers, Dordrecht, 1998, pp. 53–56.
23. G. Lettieri, A. Dodge, G. Boer, J. Lichtenberg, E. Verpoorte and N. F. de Rooij, in Micro Total Analysis Systems 2000: Proceedings of the μTAS 2000 Symposium, eds. A. van den Berg, W. Olthuis and P. Bergveld, Kluwer Academic Publishers, Dordrecht, The Netherlands, 2000, pp. 351–354.
24. G.-L. Lettieri, E. Verpoorte and N. F. de Rooij, in Transducers′01: The 11th International Conference on Solid–State Sensors and Actuators: Technical Digest, Springer-Verlag, Berlin, Heidelberg, New York, 2001, vol. 2, pp. 1510–1513.
25. G.-L. Lettieri, E. Verpoorte and N. F. de Rooij, in Micro Total Analysis Systems 2001: Proceedings of the μTAS 2001 Symposium, eds. J. M. Ramsey and A. van den Berg, Kluwer Academic Publishers, Dordrecht, The Netherlands, 2001, pp. 503–504.
26. C. L. Rice and R. Whitehead, J. Phys. Chem., 1965, 69, 4017–4024.
27. M. Haun and S. Wasi, Anal. Biochem., 1990, 191, 337–342.

---

Footnote

† Present address: Applied Optics Group, Institute of Microtechnology, University of Neuchâtel, Rue A.-L. Breguet 2, CH-2007 Neuchâtel, Switzerland.

---