Intercalation of tetraazamacrocycles into molybdenum disulfide†
Rabin Bissessur*a, Robert I. Haines*a and Ralf Brüningb
aDepartment of Chemistry, University of Prince Edward Island, Charlottetown, Prince Edward Island, Canada C1A 4P3. E-mail: rabissessur@upei.ca, rhaines@upei.ca
bDepartment of Physics, Mount Allison University, Sackville, New Brunswick, Canada E4L 1E6
First published on 21st November 2002
Abstract
A series of intercalation compounds of tetraazamacrocycles in molybdenum disulfide have been synthesized using the exfoliation and restacking properties of LiMoS2. The sandwiched compounds were characterized by powder X-ray diffraction, thermogravimetric analyses, differential scanning calorimetry, and four-probe electrical conductivity measurements. The interlayer spacing of the intercalation compound was found to be dependent on the size of the macrocyclic ligand, indicating that the intercalated macrocycles are co-planar with the MoS2 sheets.
Introduction
The synthesis and characterization of organic–inorganic nanocomposite materials achieved via the technique of intercalation chemistry continues to be an important field of research.1 The inorganic components may be 3-D materials such as zeolites2 and other inorganic network structures,3 2-D lamellar structures such as clays,4 graphite,5 graphite oxide,6 transition metal oxides,7 oxyhalides,3,8 and dichalcogenides,9 1-D polymeric chains,10 or zero-dimensional materials such as C60.11 On the other hand, the organic components may be small aromatic or aliphatic organic compounds,12 polymers,13 cryptands,14 or crown ethers.15 The resulting nanocomposites may exhibit properties synergistically derived from the two components, such as improved mechanical strength,16 higher electronic conductivity,17 increased ionic conductivity,18 and enhanced thermal stability.19Molybdenum disulfide (MoS2) is a layered structure that has generated a great deal of interest in recent years.20 It occurs naturally as the mineral molybdenite21 and hence is cheap and readily available. It is already an important material with several practical applications. For instance, it is extensively used as a catalyst for the hydrodesulfurization (HDS) process, i.e. removal of sulfur from organosulfur compounds such as thiophene and bithiophene in fossil fuels.22 Similar to graphite, MoS2 is also used as a solid lubricant23 because of its layered character. Lattice vibration frequencies have shown that the interlamellar van der Waals forces are weak.24 Furthermore, MoS2 may find use as a cathode material in high energy density lithium batteries.25 The electrochemical insertion of lithium into MoS2 is highly exothermic and the energy released can be harnessed to obtain a reversible battery system.
In spite of the tremendous importance of MoS2 in practical applications, its intercalation chemistry using conventional redox techniques has been limited to alkali and alkaline earth metals dissolved in liquid ammonia26 and organolithium reagents such as n-butyllithium.27 Treatment of MoS2 with organic molecules such as hydrazine, aniline, ammonia, or pyridine does not lead to intercalation, even if high temperatures are employed. In this respect, MoS2 distinguishes itself from other transition metal dichalcogenides.28 The resistance of MoS2 toward intercalation is due to the fact that the Mo is in the +4 oxidation state and is therefore very difficult to reduce. However, MoS2 has been shown to disperse readily into a colloidal suspension of single layers on reaction of the lithiated form of MoS2, i.e. LixMoS2 with water.29 Flocculation of the layers in the presence of organic molecules,30 clusters,31 metal ions,32 organometallics,33 and polymers13,34 results in the formation of intercalation compounds.
Recently, we utilized this exfoliation method to react single-layer MoS2 in water with a pendant-arm tetraazamacrocycle, namely, 5,5,7,12,12,14-hexamethyl-1,4,8,11-tetraazacyclotetradecane-1-acetic acid (L6), and intercalate it into MoS2.35 In this article, we report the intercalation of a series of tetraazamacrocycles to produce a family of tetraazamacrocycle–MoS2 nanocomposites. The macrocycles L1 to L8 are shown in Fig. 1.
 | ||
| Fig. 1 Structures of macrocycles L1–L8. | ||
Tetraazamacrocycles are an interesting class of compounds in their own right. Interest in these complexes has focussed on applications to catalysis and ion selection,36 and their use as radioimmunotherapy agents.37 Transition metal macrocycle complexes find utility as electrocatalysts in fuel cells38 or as catalysts for decomposition of environmentally important small molecules (NOx, SOx and CO2).39 Cobalt(III) macrocycles will bond sulfur directly to the metal,40 and these complexes, which are also extremely stable in aggressive environments, are excellent candidates for both fundamental and applied studies of hydrodesulfurization of fossil fuels. Thus, macrocycles may provide a portal to a completely unique class of intercalation compounds, which may prove to be robust, efficient HDS catalysts.
Experimental
Synthesis of tetraazamacrocycles, L
The macrocycles L1–L3 were purchased from Aldrich Chemical Co. and were used without further purification. L4 and L5 were prepared according to the literature.41 The acetato pendant-arm macrocycles (L6–L8) were prepared according to Xu and Ni.42The purity of all synthesized macrocycles was confirmed by 1H and 13C NMR, FTIR, and melting point (analytical data is provided as ESI).
Preparation of LixMoS2
LixMoS2 was prepared by reacting MoS2 (99%, Aldrich) with 3 equivalents of n-BuLi (2.5 M solution in hexane) in a dry box under N2, according to eqn. 1.| MoS2 + C4H9Li → LiMoS2 + 1/2C8H18 | (1) |
The concentration of n-BuLi was adjusted to 1 M by adding dry pentane and the reaction mixture was allowed to stir for at least 2 days at room temperature. The product was filtered off in the dry box, washed with pentane and then dried under suction. The product stoichiometry is known to be LiMoS2.13
Synthesis of intercalation compounds
Reaction of LiMoS2 with water results in the formation of single layers of MoS2, as shown in eqn. 2. In a typical reaction, 20 mL of water was added to 200 mg of LiMoS2 and the suspension sonicated for 2 h. This procedure results in complete exfoliation of the MoS2 layers.| LiMoS2 + H2O → (MoS2)single layers + LiOH + 1/2H2 | (2) |
In a typical experiment, an ethanolic or aqueous solution of the appropriate macrocycle (L) was added to the exfoliated MoS2 solution and the reaction mixture allowed to stir at room temperature for two days. The mixture was then filtered and the insoluble product washed thoroughly with water and ethanol to remove LiOH and excess L. This experimental procedure leads to the formation of an intercalation compound of L into MoS2, as shown in eqn. 3.
| (MoS2)single layers + xL → (L)xMoS2 | (3) |
Instrumentation
Powder X-ray diffraction (XRD) was carried out on a diffractometer equipped with a graphite monochromator and an analyzer crystal, along with a scintillation detector. Cu-Kα radiation (λ = 1.542 Å) was utilized and the data collection was carried out at 22 °C. Samples were analyzed under vacuum with a scan range of 3 to 100°. In order to minimize scattering from materials other than those under investigation, the powdered samples were placed on a single crystal silicon substrate with the surface cut parallel to the (510) plane (supplied by The Gem Dugout, State College, PA, USA).Thermogravimetric analyses (TGA) were performed on a Mettler Toledo Star system using a heating rate of 10 °C min−1. Differential scanning calorimetry (DSC) data were obtained with a TA DSC-Q1000 apparatus using a heating rate of 5 °C min−1.
Electrical conductivities were measured on pressed pellets of the samples by using the conventional four-probe technique. The diameters of the pellets were either 0.68 or 1.27 cm.
Results and discussion
Powder X-ray diffraction spectra of the products of reaction of exfoliated MoS2 with the series of macrocycles L1–L8 clearly show successful intercalation of the macrocycles into the host material. In all cases, the first few (00l) reflections were observed, indicative of a lamellar structure. The powder diffraction pattern for (L7)0.13MoS2 is shown in Fig. 2. Table 1 lists the interlayer spacings and expansions for the intercalation compounds (L1)MoS2–(L8)MoS2. The observed interlayer spacings of the intercalated compounds were between 14.49 and 10.28 Å, showing interlayer expansions in the range 8.34 to 4.13 Å relative to pristine MoS2, which has an interlayer spacing of 6.15 Å. These expansions are consistent with monolayers of the macrocycles lying virtually co-planar with the MoS2 sheets. | ||
| Fig. 2 Powder XRD pattern for (L7)0.13MoS2. | ||
| Macrocycle | Interlayer spacing/Å | Interlayer expansion/Å | Macrocycle dimensions | |
|---|---|---|---|---|
| Thickness/Å | Cross-sectional area/Å2 | |||
| L1 | 10.28 | 4.13 | 3.7 | 53 |
| L2 | 10.28 | 4.13 | 3.5 | 53 |
| L3 | 10.40 | 4.25 | 4.4 | 65 |
| L4 | 11.34 | 5.19 | 5.6 | 70 |
| L5 | 11.34 | 5.19 | 5.6 | 76 |
| L6 | 11.48 | 5.33 | 5.9 | 72 |
| L7 | 14.49 | 8.34 | 7.9 | 86 |
| L8 | 14.49 | 8.34 | 7.9 | 86 |
Included in Table 1 are the estimated thicknesses and cross-sectional areas of the macrocycles, determined from their geometry-optimized structures using HyperChem 6® (Hypercube Inc., Gainesville, FL, USA). It can be seen that the effective thickness of the macrocycles increases in the order L1, L2 < L3 < L4, L5 < L6 < L7, L8. L1 and L2 take up a chair conformation, presenting the thinnest profile. L3, with an extra methylene group in the backbone, is a little thicker than L1 and L2, due to some buckling of the ring. L4 and L5, while having the chair conformation for their backbones, present thicker profiles due to the presence of the six methyl groups attached to the ring carbons. The thickness of L6 is slightly greater still, due to the presence of the additional pendant acetato arm attached to the ring nitrogen. Finally, L7 and L8 present the greatest thickness, having two acetato pendant arms each.
From the XRD data for the last two cases, an interlayer spacing of 14.49 Å was observed, corresponding to an interlayer expansion of 8.34 Å. This value correlates very well with the calculated thickness of the macrocycles and suggests that the guest molecules are oriented within the gallery space such that they are co-planar with the disulfide sheets. Fig. 3 plots the measured interlayer expansion of the intercalation compounds versus the calculated macrocycle thicknesses for L1 to L8. Given the rather crude estimate of macrocycle thickness, there is a quite a good linear correlation between macrocycle thickness and interlayer expansion (regression slope = 0.93 ± 0.11; intercept = 0.35 ± 0.64; R2 = 0.924), suggesting that for all compounds the macrocycles are aligned in a similar fashion, i.e. the intercalation compounds comprise monolayers of the guest aligned co-planar with the disulfide sheets of the host. This alignment is depicted for L6 in Fig. 4.
 | ||
| Fig. 3 Plot of measured interlayer expansion versus macrocycle thickness. | ||
 | ||
| Fig. 4 Schematic illustration of the proposed structure of (L6)0.11MoS2. | ||
Similarly, intercalation compounds of L4 and L5 gave identical d-spacing, regardless of the stereochemistry of the substituents on the backbone of the macrocycles. However, the smaller interlayer spacing of 11.34 Å observed for L4 and L5 compared with L7 and L8 is consistent with the absence of pendant-arm acetato groups in the former pair. The effect of steric crowding is further demonstrated in the disulfide intercalation compounds of L1 and L2, which have an even smaller interlayer spacing of 10.28 Å. This is consistent with the total absence of substituents (both methyl and carboxylic acid groups) on the macrocycle.
The foregoing discussion assumes that the macrocycle loading in the intercalates represents a monolayer or less of macrocycle within each layer. From the crystallite size (below), we calculate that for a perfectly cubic crystallite, the cross-sectional area of each layer is 6400 Å2, with 13 layers per crystallite (and therefore 12 gallery spaces). For cyclam, with an estimated rectangular cross-section of 53 Å2, the stoichiometry of an intercalate that contains one full monolayer of macrocycle in each interlayer space would be (cyclam)0.33MoS2. This value stems from an estimated 1500 cyclam molecules per interlayer, and 355 MoS2 units per layer, based on the unit cell dimensions of MoS2.43 Similar calculations for macrocycles L2 to L8 give stoichiometries of 0.38, 0.42, 0.46, 0.43, 0.51, and 0.51 macrocycles per MoS2. Under practical conditions, perfect monolayer loading would not be achieved. Furthermore, re-stacking of layers in the intercalate is far from perfect, resulting in stepped, fragmented, and/or non-coplanar layers. It is clear that the measured stoichiometries of the intercalates correspond to loadings of less than a full monolayer of macrocycle per interlayer. That the interlayer expansions correlate well with the macrocycle thicknesses suggests that the guest molecules may act as (short) pillars, this may give rise to microporous materials.
The crystallite sizes of the intercalation compounds were estimated from their powder X-ray diffraction patterns by using the Scherrer formula.44 A simplified version of the formula is shown in eqn. 4,
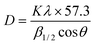 | (4) |
The intercalation compounds were characterized by thermogravimetric analysis. This technique was used to determine the thermal stabilities of the materials under both oxygen and nitrogen flow. All the materials showed good thermal stabilities under both conditions, being stable to at least 200 °C or higher in all cases (Table 2). In addition, TGA under oxygen flow was used to determine the stoichiometry of the intercalated materials. This method has been previously shown to give reliable results that agree closely with elemental analyses.45 For example, examination of the thermogram of the intercalated phase of L6 in MoS2 shows that the material is stable up to 308 °C. Thereafter, a major weight loss is observed up to 450 °C, followed by the formation of MoO3, which is stable up to 650 °C. The identity of the MoO3 phase was confirmed by FTIR spectroscopy and XRD. The TGA data in air also show that by controlling the amount of the macrocycle in the reaction vessel, materials with varying compositions can be prepared (Table 2). However, for the macrocycles used in this research, the interlayer spacing was found to be constant irrespective of the composition of the intercalated phase. This observation suggests that we might be forming micro- or mesoporous materials and we are currently performing BET surface area measurements to measure the surface area as well as the pore size distribution; this will be the subject of a future publication.
| Intercalate | Thermal stability/°C | |
|---|---|---|
| Air | N2 | |
| (L1)0.12MoS2 | 210 | 200 |
| (L2)0.14MoS2 | 400 | 200 |
| (L3)0.12MoS2 | 320 | 240 |
| (L4)0.14MoS2 | 200 | 200 |
| (L4)0.09MoS2 | 200 | 200 |
| (L4)0.08MoS2 | 200 | 200 |
| (L5)0.10MoS2 | 275 | 210 |
| (L5)0.02MoS2 | 275 | 210 |
| (L6)0.11MoS2 | 308 | 268 |
| (L7)0.13MoS2 | 200 | 200 |
| (L8)0.07MoS2 | 200 | 200 |
The room temperature electrical conductivities of the intercalated phases were determined by using the conventional four-probe technique. The values obtained were in the range 0.3–0.8 S cm−1 (Table 3). These values are approximate since the measurements were made on pressed pellets and account must be taken of the grain boundaries in the sample. Therefore, we would expect the actual conductivity of the samples to be much higher. True conductivities could be measured using sintered pellets.46 This is not possible, however, since sintering would cause a change in the structure of MoS2, resulting in loss of conductivity (vide infra). At first sight, it may be surprising to see that the nanocomposite materials are highly conductive, since conductivity measurements at room temperature on a pressed pellet of molybdenum disulfide shows that it has a low electrical conductivity value of 5 × 10−3 S cm−1. In addition, the macrocycles in isolation are discrete molecular species and are therefore non-conductors. The enhancement in electrical conductivity by a factor of 60–160 can only be explained by a structural transformation which takes place in the MoS2 during the intercalation process. In pristine MoS2, the molybdenum atoms are bonded to the sulfurs in a trigonal prismatic arrangement. Band structure calculations have shown that the material is a semiconductor,47 and it has been determined to have a band gap of ∼1.5 eV via photocurrent measurements in an electrochemical cell.48 In this form, MoS2 is referred to as 2H-MoS2, or D3h-MoS2 from point group considerations (Fig. 5). Upon treatment with n-BuLi, reduction of the layers takes place, along with a structural transformation of the MoS2 framework. The molybdenum atom is now bonded to the six sulfurs in an octahedral geometry. MoS2 in this form is referred to as 1T-MoS2 or Oh-MoS2. This structural modification confers a metallic character on the disulfide, as seen in its band diagram.49 The Oh-MoS2 form is actually metastable and has been shown to gradually lose its conductivity upon ageing. This loss in conductivity is due to the slow conversion of the Oh form to the thermodynamically more stable D3h form. The conversion is kinetically more rapid with increasing temperature. The conversion of Oh-MoS2 to D3h-MoS2 can also be probed by differential scanning calorimetry. For instance, DSC of (L5)0.02MoS2 reveals a broad exothermic peak with a peak maximum at ∼200 °C (Fig. 6). This exothermic peak corresponds to the conversion of metastable Oh-MoS2 to the thermodynamically more stable D3h form. The transition was found to be irreversible and occurs with constant mass. Restacked MoS2 has been shown to produce an exothermic peak at ∼100 °C.34 The 100 °C shift to higher temperature in (L5)0.02MoS2 is due to the presence of the intercalated macrocycle. In other words, the macrocycle stabilizes the Oh-MoS2 phase. Increasing the loading to 0.10 had no effect on the conversion temperature, keeping in mind that the interlayer spacings of both (L5)0.02MoS2 and (L5)0.10MoS2 are the same. Therefore, the maximum in the conversion temperature seems to be dependent on the interlayer spacing of the material, regardless of the loading of the guest species.
 | ||
| Fig. 5 Structures of (a) D3h-MoS2 and (b) Oh-MoS2. | ||
 | ||
| Fig. 6 DSC trace for (L5)0.02MoS2. | ||
| Intercalate | Conductivity/S cm−1 |
|---|---|
| (L1)0.12MoS2 | 0.3 |
| (L3)0.12MoS2 | 0.6 |
| (L4)0.14MoS2 | 0.8 |
| (L4)0.09MoS2 | 0.6 |
| (L4)0.08MoS2 | 0.4 |
| (L5)0.02MoS2 | 0.7 |
Conclusions
The exfoliation and restacking properties of LiMoS2 have proven to be very useful for producing intercalation compounds based on macrocycles. The guests are sandwiched between the host layers in a co-planar fashion, the interlayer expansions being due solely to the steric bulk of the guests. The compounds exhibit enhanced electronic conductivity, due to the alteration of the host’s band structure.We are currently extending this work to examine intercalation compounds formed between MoS2 and transition metal macrocycle complexes that have both square-planar and octahedral geometries in order to explore the steric effects on intercalation further. We are also studying the effect of metal type and guest charge on the intercalation process, with particular emphasis on cobalt systems, given the importance of this metal in the HDS process.
Acknowledgements
Financial support from the Natural Sciences and Engineering Research Council (NSERC) and the University of Prince Edward Island Senate Committee on Research are gratefully acknowledged.References
- ACS Symp. Ser., 1996, 622, and references therein Search PubMed.
- (a) T. Bein and P. Enzel, Synth. Met., 1989, 29, E163 CrossRef CAS; (b) P. Enzel and T. Bein, J. Phys. Chem., 1989, 93, 6270 CrossRef CAS.
- C.-G. Wu, H. O. Marcy, D. C. DeGroot, J. L. Schindler, C. R. Kannewurf and M. G. Kanatzidis, Synth. Met., 1991, 41(43), 693 CrossRef CAS.
- K. E. Strawhecker and E. Manias, Chem. Mater., 2000, 12, 2943 CrossRef CAS.
- T. Zheng and J. R. Dahn, Synth. Met., 1995, 73, 1 CrossRef CAS , and references therein.
- (a) Y. Matsuo, K. Tahara and Y. Sugie, Carbon, 1997, 35, 113 CrossRef CAS; (b) Y. Matsuo, K. Hatase and Y. Sugie, Chem. Mater., 1998, 10, 2266 CrossRef CAS; (c) T. Kyotani, H. Moriyama and A. Tomita, Carbon, 1997, 35, 1185 CrossRef CAS; (d) P. Liu, K. Gong, P. Xiao and M. Xiao, J. Mater. Chem., 2000, 10, 933 RSC.
- (a) K. Chatakondu, M. L. H. Green, J. Qin, M. E. Thompson and P. J. Wiseman, J. Chem. Soc., Chem. Commun., 1988, 223 RSC; (b) F. Leroux and L. F. Nazar, Solid State Ionics, 2000, 133, 37 Search PubMed.
- I. Kargina, B. Patel and D. Richeson, J. Chem. Res., 1996 Search PubMed , (S)72.
- L. Bernard, M. McKelvy and W. Glaunsinger, Solid State Ionics, 1985, 15, 301 Search PubMed.
- (a) J. K. Vassiliou, R. P. Ziebarth and F. J. DiSalvo, Chem. Mater., 1990, 2, 738 CrossRef; (b) F. J. DiSalvo, Science, 1990, 247, 649 CAS.
- (a) K. Holczer, O. Klein, G. Gruner, J. D. Thompson, F. Diederich and R. L. Whetten, Phys. Rev. Lett., 1991, 67, 271 CrossRef CAS; (b) K. Holczer, O. Klein, S-M. Huang, R. B. Kaner, K-J. Fu, R. L. Whetten and F. Diederich, Science, 1991, 252, 1154 CAS.
- M. S. Whittingham and A. J. Jacobson, Intercalation Chemistry, Materials Science Series, Academic Press, New York, 1982, and references therein Search PubMed.
- R. Bissessur, J. L. Schindler, C. R. Kannewurf and M. Kanatzidis, J. Chem. Soc., Chem. Commun., 1993, 1582 RSC.
- P. Aranda, B. Casal, J. J. Fripat and E. Ruiz-Hitzky, Langmuir, 1994, 10, 1207 CrossRef CAS.
- E. Ruiz-Hitzky and B. Casal, Nature, 1978, 7, 596.
- A. Okada, M. Kawasumi, A. Usuki, Y. Kojima, T. Kuraughi and O. Kamigaito, Mater. Res. Soc. Symp. Proc., 1990, 171, 45 Search PubMed.
- R. Bissessur, D. C. Degroot, J. L. Schindler, C. R. Kannewurf and M. G. Kanatzidis, J. Chem. Soc., Chem. Commun., 1993, 687 RSC.
- J. C. Hutchison, R. Bissessur and D. F. Shriver, Chem. Mater., 1996, 8, 1597 CrossRef.
- J. Xu, Y. Hu, L. Song, Q. Wang, W. Fan, G. Liao and Z. Chen, Polym. Degrad. Stab., 2001, 73, 29 CrossRef CAS.
- E. Benavente, M. Santa Ana, F. Mendizabal and G. Gonzalez, Coord. Chem. Rev., 2002, 224, 87 CrossRef CAS.
- N. N. Greenwood andA. Earnshaw, Chemistry of the Elements, Pergamon Press, New York, 1984, p.1168 Search PubMed.
- O. Weisser and S. Landa, Sulfided Catalysts: Their Properties and Applications, Pergamon Press, New York, 1973 Search PubMed.
- P. D. Fleischauer, Thin Solid Films, 1987, 154, 309 CrossRef CAS.
- T. Wieting and J. Werble, J. Phys. Rev. B, 1971, 3, 4286 Search PubMed.
- (a) C. Julien, S. I. Saikh and G. A. Nazri, Mater. Sci. Eng., B, 1992, 15, 73 Search PubMed; (b) H. Tributsch, Faraday Discuss. Chem. Soc., 1980, 70, 190 Search PubMed.
- (a) R. Schollhorn and A. Weiss, J. Common Met., 1974, 36, 229 Search PubMed; (b) R. B. Somoano, V. Hadek and A. Rembaum, J. Chem. Phys., 1973, 58, 697 CrossRef CAS; (c) R. B. Somoano, V. Hadek, A. Rembaum, S. Samson and J. A. Woollam, J. Chem. Phys., 1975, 62, 1068 CrossRef CAS; (d) R. B. Somoano and A. Rembaum, Phys. Rev. Lett., 1971, 27, 402 CrossRef CAS.
- M. S. Whittingham and F. R. Gamble, Jr., Mater. Res. Bull., 1975, 10, 363 CrossRef CAS.
- R. H. Friend and A. D. Yoffe, Adv. Phys., 1987, 36, 1 CAS , and references therein.
- (a) M. A. Gee, R. F. Frindt, P. Joensen and S. R. Morrison, Mater. Res. Bull., 1986, 21, 543 CrossRef CAS; (b) W. M. R. Divigalpitiya, S. Morrison and R. F. Frindt, Thin Solid Films, 1990, 186, 177 CrossRef CAS.
- (a) W. M. R. Divigalpitiya, R. F. Frindt and S. R. Morrison, Science, 1989, 246, 369 CAS; (b) L. Kosiodowski and A. V. Powell, Chem. Commun., 1998, 2201 RSC.
- (a) R. Bissessur, J. Heising, W. Hirpo and M. Kanatzidis, Chem. Mater., 1996, 8, 318 CrossRef CAS; (b) J. Brenner, C. L. Marshall, L. Ellis, N. Tomczyk, J. Heising and M. Kanatzidis, Chem. Mater., 1998, 10, 1244 CrossRef CAS.
- M. Danot, J. L. Mansot, A. S. Golub, G. A. Protzenko, P. B. Fabritchnyi, Y. N. Novikov and J. Rouxel, Mater. Res. Bull., 1994, 29, 833 CrossRef CAS.
- A. S. Golub, I. B. Shumilova, Y. V. Zubavichus, M. Jahncke, G. Süss-Fink, M. Danot and Y. N. Novikov, J. Mater. Chem., 1997, 7, 163 RSC.
- M. G. Kanatzidis, R. Bissessur, D. C. DeGroot, J. L Schindler and C. R. Kannewurf, Chem. Mater., 1993, 5, 595 CrossRef CAS.
- R. Bissessur, R. I. Haines, D. R. Hutching and R. Brüning, Chem. Commun., 2001, 1598 RSC.
- (a) J.-P. Collin and J.-P. Sauvage, J. Chem. Soc., Chem. Commun., 1987, 1075 RSC; (b) E. Kimura, T. Koike and M. Takahashi, J. Chem. Soc., Chem. Commun., 1985, 385 RSC.
- J. P. L. Cox, K. J. Jankowski, R. Kataky, D. Parker, N. R. A. Beeley, B.A. Boyce, M. A. W. Eaton, K. Miller, A. T. Millian, A. Harrison and C. Walker, J. Chem. Soc., Chem. Commun., 1989, 797 RSC.
- B. W. Clauberg and G. Sandstede, J. Electroanal. Chem., 1976, 74, 393 CrossRef.
- (a) J. P. Collman, M. Marrocco, P. Deisevich, C. Kooval and F. C. Anson, J. Electroanal. Chem., 1979, 101, 117 CrossRef CAS; (b) M. M. Burley, M. R. Rhodes and T. Meyer, Inorg. Chem., 1987, 26, 1746 CrossRef.
- J. Burgess, J. Fawcett, R. I. Haines, K. Singh and D. R. Russell, Transition Met. Chem., 1999, 24, 355 Search PubMed.
- B. E. Douglas, Inorg. Synth., 1978, 18, 10.
- J.-D. Xu and S.-S. Ni, Inorg. Chim. Acta, 1986, 111, 61 CrossRef.
- F. Wypych and R. Schollhorn, J. Chem. Soc., Chem. Commun., 1992, 1386 RSC.
- P. Scherrer, Nachr. Ges. Wiss. Gottingen, Math.-Phys., 1918, Kl.2, 96 Search PubMed.
- R. Bissessur, J. L. Schindler, C. Kannewurf and M. Kanatzidis, Mol. Cryst. Liq. Cryst., 1994, 245, 249–254 Search PubMed.
- R. I. Haines and D. G. Owen, J. Phys. Chem. Solids, 1986, 47, 647 CrossRef CAS.
- M. Kertesz and R. Hoffman, J. Am. Chem. Soc., 1984, 106, 3453 CrossRef CAS.
- K. K. Kam and B. A. Parkinson, J. Phys. Chem., 1982, 86, 463 CrossRef CAS.
- (a) L. F. Matthesis, Phys. Rev., 1973, 8, 3179 Search PubMed; (b) M. A. Py and R. R. Haering, Can. J. Phys., 1983, 61, 76 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: analytical data for L4–L8. See http://www.rsc.org/suppdata/jm/b2/b208237n/ |
| This journal is © The Royal Society of Chemistry 2003 |
