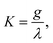Explorations of conical intersections and their ramifications for chemistry through the Jahn–Teller effect
Brian E.
Applegate
a,
Timothy A.
Barckholtz
b and
Terry A.
Miller
c
aDepartment of Chemistry, The University of North Carolina, Chapel Hill, NC 27599, USA. E-mail: beapple@unc.edu
bExxonMobil Research and Engineering, Annandale, NJ 08801, USA. E-mail: tim.barckholtz@exxonmobil.com
cLaser Spectroscopy Facility, Department of Chemistry, The Ohio State University, Columbus, OH 43210. E-mail: tamiller+@osu.edu
First published on 15th November 2002
Abstract
Much recent progress has been made theoretically and computationally towards understanding the importance of conical intersections for chemical reactions. Nonetheless, experimental characterization of conical intersections has proven extremely difficult with one striking exception: the Jahn–Teller conical intersection. This article overviews the fundamental similarity of a variety of conical intersections and demonstrates how the spectroscopy of Jahn–Teller active molecules can be used to characterize them. Specific results are reviewed for four representative Jahn–Teller active molecules, C5H5, C6H6+, Ag3 and CH3O.
 Brian E. Applegate Brian E. Applegate | Brian E. Applegate was born in Dayton, Ohio, USA, in 1970. He graduated from Wright State University in 1994 with a B.S. in chemistry. He attended graduate school at The Ohio State University earning a M.S. in 1998 and a Ph.D. in 2000 under the direction of Terry A. Miller. Currently he is a postdoctoral researcher at the University of North Carolina at Chapel Hill with Roger E. Miller. The main focus of his postdoctoral research is the study of cluster formation in superfluid liquid helium nanodroplets. |
 Timothy A. Barckholtz Timothy A. Barckholtz | Timothy A. Barckholtz was born in San Antonio, Texas, USA in 1970, and spent his childhood in Houston. He graduated from Trinity University, San Antonio, in 1992 with a degree in chemistry and mathematics. From there, he attended graduate school in chemistry at The Ohio State University as a National Science Foundation Pre-doctoral Fellow, studying quantum chemistry and laser spectroscopy with Bruce E. Bursten and Terry Miller. Following a post-doctoral fellowship at the University of Colorado, Boulder, he joined the staff of Corporate Strategic Research, ExxonMobil Research and Engineering Co., located in Clinton, New Jersey. His current research is centered around chemical kinetics modeling of internal combustion engines. |
 Terry A. Miller Terry A. Miller | Terry A. Miller received his undergraduate degree from the University of Kansas, and, with a Marshall Fellowship, attended Cambridge University where he obtained his Ph.D. degree. Thereafter he began a research program at AT&T Bell Laboratories. During that period he held visiting faculty positions at Princeton University, Stanford University, and the Institute for Molecular Science in Okazaki, Japan. In 1984, he became the Ohio Eminent Scholar Professor of Chemistry at The Ohio State University. He is a fellow of both the American Physical Society and the Optical Society of America and has been a councilor of the American Chemical Society. His research has been recognized by the William F. Meggars Award of the Optical Society of America in 1993, the Bomem–Michelson Award of the Coblentz Society in 1995, the Bourke Medal of the Royal Society of Chemistry in 1998, and the Broida Prize of the American Physical Society in 1999. His work centers on the spectroscopy and dynamics of reactive chemical intermediates, i.e., free radicals, molecular ions, etc. |
1 Introduction
The well-known ‘non-crossing rule’ guarantees for diatomic molecules that electronic states of the same symmetry cannot cross but must avoid one another.1 This rule fails for polyatomic molecules, for which electronic states of the same symmetry are allowed to cross,2 because of the additional degrees of freedom. When states do cross, they can form a conical intersection (CI), which strictly speaking is a (3N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)-dimensional seam (or hyperline) of the electronic energy for an N-atom molecule. One of the unique and special properties of a CI is that, at or near the geometry of the CI, the molecule can transfer with great facility from one electronic surface to the other. Due primarily to advances in ab initio calculations, CIs have recently been recognized to play important roles in organic photochemistry by providing a channel for the rapid radiationless decay of photoexcited states to a lower electronic state, typically the ground state, on which further chemistry occurs. A recent review detailing how reactions proceed through CIs, and the computational tools available to characterize this process, has been published in this journal.3 Reaction mechanisms involving CIs have been implicated in a number of well-known photochemical reactions including those involving the S1 and S2 states of benzene, carbene formation from diazerine and diazomethane, rearrangement of acylcyclopropenes to furans, and many others.
2)-dimensional seam (or hyperline) of the electronic energy for an N-atom molecule. One of the unique and special properties of a CI is that, at or near the geometry of the CI, the molecule can transfer with great facility from one electronic surface to the other. Due primarily to advances in ab initio calculations, CIs have recently been recognized to play important roles in organic photochemistry by providing a channel for the rapid radiationless decay of photoexcited states to a lower electronic state, typically the ground state, on which further chemistry occurs. A recent review detailing how reactions proceed through CIs, and the computational tools available to characterize this process, has been published in this journal.3 Reaction mechanisms involving CIs have been implicated in a number of well-known photochemical reactions including those involving the S1 and S2 states of benzene, carbene formation from diazerine and diazomethane, rearrangement of acylcyclopropenes to furans, and many others.
CIs even may have played a central role in the origin of life. The three most widely accepted explanations for the origin of life on earth are (i) creation by an omnipotent God, such as the account in the Book of Genesis; (ii) the panspermia theory, that life arrived on earth having been created in outer space; and (iii) the biopoiesis theory of abiogenic synthesis of living organisms on the early earth from prebiotic compounds. So pervasive are CIs in chemistry that they play critical roles in the latter two explanations.
A key argument for the panspermia theory is the discovery by radioastronomy of complex organic molecules, perhaps the precursors of life, in interstellar molecular clouds. Herschbach4 has pointed out that the existence of such molecules depends critically on the crossing or avoided crossing of certain potential curves. Because of the sparseness of the medium, interstellar chemistry requires exothermic reactions without activation barriers. This reaction class is dominated by ionic reactions, although in special cases neutral–neutral reactions involving atoms or radicals may play a role. Of the ions, only He+ is produced in great enough abundance by cosmic ray ionization to initiate the interstellar chemistry. He+ would be expected to pass its charge to the most abundant neutral molecule, H2, which in terms of producing complex organic molecules is an evolutionary dead end. Indeed, the curve (He![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2)+ coming asymptotically from He+
H2)+ coming asymptotically from He+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H
H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H appears at first glance to cross one leading asymptotically to H+
H appears at first glance to cross one leading asymptotically to H+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H
H![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) He, which should greatly facilitate the charge transfer. However, more detailed calculations indicate that the curves avoid crossing. Experiments confirm that this charge transfer reaction is at least four orders of magnitude slower than typical ion–molecule reactions. Thus, He+ is left to transfer its charge to the next most abundant interstellar molecule, CO, in which the electronic curves of the tri-atom system do cross. This reaction produces C+, which in turn drives the chemistry that produces the complex organic molecules observed in interstellar clouds.
He, which should greatly facilitate the charge transfer. However, more detailed calculations indicate that the curves avoid crossing. Experiments confirm that this charge transfer reaction is at least four orders of magnitude slower than typical ion–molecule reactions. Thus, He+ is left to transfer its charge to the next most abundant interstellar molecule, CO, in which the electronic curves of the tri-atom system do cross. This reaction produces C+, which in turn drives the chemistry that produces the complex organic molecules observed in interstellar clouds.
Curve crossings and CIs are also important to the detailed mechanism of biopoiesis. In their classic experiments, Miller and Urey5 demonstrated as early as the 1950s that electrical discharges in gases thought to resemble the Earth′s atmosphere of about a billion years ago, produce complex biological molecules, such as amino acids and nucleobases. However, until very recently it has been unclear how these prebiotic molecules could develop further, given the intense ultraviolet radiation to which the earth was subjected, because the protective O3 layer had not yet developed. However, recent experiments by Kohler and co-workers have shown6 that molecules such as the DNA base adenosine convert electronic excitation from UV radiation into heat in substantially less than 1 picosecond. They have further suggested, and recent calculations appear to confirm,7 that this ultra-fast conversion is made possible by a CI between the excited S1 state and the ground S0 state. Such a rapid conversion gives these molecules a high photostability, and may be nature′s original sunscreen to prevent biological damage from exposure to too much sun.
Recently there has been much effort3,8 to calculate by ab initio methods potential energy surfaces (PES) that contain conical intersections, such as the surfaces shown in Fig. 1. Such efforts, especially when combined with chemical dynamics calculations, show great promise for improving our understanding of the ramifications of CIs for chemistry. It would be desirable to assay the accuracy of such calculations by the experimental characterization of the region of the PES near the CI. However, such experiments are exceedingly difficult to perform, due in large part to the general lack of bound states in the region of the PES where chemical bonds form or break.
 | ||
| Fig. 1 Examples of conical intersections. (a) A cut through a molecule’s PES illustrating a conical intersection of two electronic surfaces, such as that found along the reaction path in many organic photochemical reactions. (b) An expanded view in three dimensions of the CI illustrated in (a). (c) A cut through a PES with a Jahn–Teller CI. (d) The three-dimensional form of the PES for a Jahn–Teller CI. | ||
However, for a CI such as that found in the PES of Fig. 1(c) and (d), experimental characterization may be possible because the region of the PES surrounding the CI does contain bound quantum states that can be probed in detail by spectroscopic methods. The PES of Fig. 1(c) and (d) is, of course, that of a molecule suffering the classic Jahn–Teller effect. Jahn and Teller9 first showed in 1937 that any non-linear polyatomic molecule in a degenerate electronic state would suffer a geometric distortion with a concomitant stabilization of the energy, ε, leading to a PES exhibiting a CI of precisely the sort depicted in Fig. 1(c) and (d).
While the CI of the Jahn–Teller PES is potentially amenable to spectroscopic characterization, it is still not an easy task to do so. Most isolated molecules that satisfy the requirements of the Jahn–Teller theorem are highly reactive, open-shell neutral or charged free radicals. However, in recent years considerable experimental progress in studying such molecules has been made using supersonic free jet expansions that cool the radicals to nearly 0 K, followed by interrogation via laser spectroscopy, e.g., laser induced fluorescence (LIF), resonantly enhanced multiphoton ionization (REMPI) and zero kinetic energy (ZEKE) photoelectron spectroscopy. Progress using the complementary experimental techniques in the time domain, i.e., ultrafast spectroscopy, has also been reported.
Even with observed spectra in hand, the connection to the PES, and hence comparison to ab initio calculations thereof, is far from trivial. The experiments typically measure the energies of the vibrational or vibronic (and in some cases the rotational) quantum states and their properties. These energies and properties can in principle be calculated via solving the appropriate Schrödinger equation for the nuclear motion on the (3N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6)-dimensional PES. However, this dynamical problem is generally still too difficult for numerical solution with values of N appropriate for most polyatomic molecules. Rather, over the years there has been much work done to formulate particular variations of the Jahn–Teller PES in terms of simple analytical models, thereby expressing the corresponding vibronic eigenenergies and eigenfunctions in terms of the molecular parameters characterizing these models. This work is much too detailed to be described here, but a number of excellent reviews10–13 summarize the work that has been done in this area.
6)-dimensional PES. However, this dynamical problem is generally still too difficult for numerical solution with values of N appropriate for most polyatomic molecules. Rather, over the years there has been much work done to formulate particular variations of the Jahn–Teller PES in terms of simple analytical models, thereby expressing the corresponding vibronic eigenenergies and eigenfunctions in terms of the molecular parameters characterizing these models. This work is much too detailed to be described here, but a number of excellent reviews10–13 summarize the work that has been done in this area.
In this article, we describe the results of some of this work with an emphasis on the qualitative understanding of these surfaces as examples of ones containing CIs, as well as emphasizing the consequences of these unusual PESs for spectroscopy and chemistry. In the following section, we briefly summarize some of the quantum mechanical results that are necessary for understanding recent experimental and theoretical progress. Thereafter, we describe the results for several key, even famous, Jahn–Teller active molecules: specifically, the cyclopentadienyl radical, C5H5; the benzene cation, C6H6+; the silver trimer, Ag3; and the methoxy radical, CH3O. Finally we summarize the present state of progress and prognosticate about possible future developments.
To give some perspective on the history and breadth of these phenomena, we note that our recent search of the scientific literature found over 8600 publications reporting Jahn–Teller effects in over 6000 substances. The four molecules that we use as examples have a long and active history, as indicated by the year (noted in parenthesis) in which Jahn–Teller effects were first reported experimentally: C5H5 (1956); C6H6+ (1964); Ag3 (1988) and CH3O (1977). For each of these four species, literally dozens of papers have been published, and the activity continues today with at least one paper describing Jahn–Teller effects having been published since the beginning of 2000 for each of these molecules. Nonetheless, progress in understanding has been slow. For instance, the calculated values of the Jahn–Teller stabilization energy, ε, that have been reported for C5H5 vary from <500 to >5000 cm−1, with experimental values being available for comparison only recently.
Several general conclusions emerge. One, the Jahn–Teller effect is among the oldest and most extensively studied problems in physical chemistry. Two, over the years there has been significant disagreement regarding the structure and energetics of Jahn–Teller active molecules. Three, there continues to be active research on Jahn–Teller molecules, and such research represents perhaps the most accessible experimental path to direct knowledge of CIs. Four, while the theoretical understanding of molecules with CIs has progressed tremendously in the last few years, it would be naive of us to conclude that there is now complete understanding; indeed we expect that the interest in, and activity studying, Jahn–Teller active molecules will continue for many years to come.
2 Potential energy surfaces (PES) with CIs
In this section we present a few mathematical results that allow us to describe CIs generally, and in more detail, the special case of the Jahn–Teller PES. These details are necessary for a quantitative understanding of these effects and we encourage the reader to work through this section. However the materials in Section 2.4 and beyond can be qualitatively understood without such mathematical detail, and some readers may find it desirable to skip directly to that material.2.1 A mathematical overview of CIs
It is instructive to build upon some concepts developed by Yarkony,8 Ruedenberg,14 and others to describe PESs near CIs. Let us consider a pair of electronic states (we could have more than two states, but the principles are illustrated well by a pair of states without complicating the details too much). The dependence of the electronic state energies upon the 3N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 ≡
M vibrational coordinates, Q = (q1, q2, ..., qM), can be represented by a 2
6 ≡
M vibrational coordinates, Q = (q1, q2, ..., qM), can be represented by a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 matrix representing the electronic Hamiltonian,
2 matrix representing the electronic Hamiltonian, ![[script letter H]](https://www.rsc.org/images/entities/i_char_e142.gif) (Q), where
(Q), where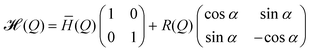 | (1) |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) , R (ΔH and H12), and α are functions of Q and defined as
, R (ΔH and H12), and α are functions of Q and defined as![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) (Q) = ½(H11 (Q) = ½(H11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H22); ΔH(Q) = ½(H11 H22); ΔH(Q) = ½(H11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H22) H22) | (2) |
R(Q) = (ΔH2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H212 )1/2 H212 )1/2 | (3) |
| α(Q) = cos−1(ΔH/R) = sin−1(H12/R) | (4) |
The general eigenvalues, E± and eigenfunctions, ψ±, of ![[script letter H]](https://www.rsc.org/images/entities/i_char_e142.gif) (Q), eqn. (1), are
(Q), eqn. (1), are
E±(Q) = ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R R | (5) |
ψ+ = cos(α/2)ϕ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(α/2)ϕ2 sin(α/2)ϕ2 | (6) |
ψ− = −sin(α/2)ϕ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(α/2)ϕ2, cos(α/2)ϕ2, | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2π then the electronic eigenfunctions,ψ±, change sign. This is a manifestation of the so-called ‘geometric’ or Berry′s phase.15 Since the overall eigenfunction cannot change upon rotation by 2π, there must be a compensatory change in the wavefunction describing the nuclei. Nonetheless the existence in the electronic wavefunction of the geometric phase for closed loops around a (single) CI has proved a powerful means of locating them along reaction paths.
2π then the electronic eigenfunctions,ψ±, change sign. This is a manifestation of the so-called ‘geometric’ or Berry′s phase.15 Since the overall eigenfunction cannot change upon rotation by 2π, there must be a compensatory change in the wavefunction describing the nuclei. Nonetheless the existence in the electronic wavefunction of the geometric phase for closed loops around a (single) CI has proved a powerful means of locating them along reaction paths.
Diabatic states of a molecule will cross when the energies of the two states become degenerate, i.e., for those geometries that satisfy E+(Q) = E−(Q), which requires
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = R = ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R. R. | (8) |
| ΔH(Q0) = 0 | (9) |
| H12(Q0) = 0 | (10) |
![[script letter H]](https://www.rsc.org/images/entities/i_char_e142.gif) (Q), eqn. (1), simplify to
(Q), eqn. (1), simplify toE+ = ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔH = E1; ψ+ = ϕ1 ΔH = E1; ψ+ = ϕ1 | (11) |
E− = ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔH = E2; ψ− = ϕ2 ΔH = E2; ψ− = ϕ2 | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 will occur. These conditions may be satisfied because of symmetry or because of accident or happenstance.8 (By happenstance we mean that Q0 exists for which eqns. (9) and (10) are satisfied, but no symmetry condition determines those values.) Conical intersections found along reaction paths most often correspond to happenstance occurences. Eqns. (9) and (10) are each satisfied on a surface of dimension M
2 will occur. These conditions may be satisfied because of symmetry or because of accident or happenstance.8 (By happenstance we mean that Q0 exists for which eqns. (9) and (10) are satisfied, but no symmetry condition determines those values.) Conical intersections found along reaction paths most often correspond to happenstance occurences. Eqns. (9) and (10) are each satisfied on a surface of dimension M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The happenstance intersection of those two surfaces creates a CI of dimension M
1. The happenstance intersection of those two surfaces creates a CI of dimension M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The shape and other details of the CI can be quite varied (see ref. 14 for an extensive discussion of the types of CIs). It is also possible that a CI is formed of dimension less than M
2. The shape and other details of the CI can be quite varied (see ref. 14 for an extensive discussion of the types of CIs). It is also possible that a CI is formed of dimension less than M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, a ‘doubly diabolical’ intersection, discussed at length in ref. 8.
2, a ‘doubly diabolical’ intersection, discussed at length in ref. 8.
Because eqns. (9) and (10) are independent, one could be satisfied by happenstance and the other by symmetry. For instance, the two lowest excited states, 1 1A″ and 2 1A″, of H2S have a CI where eqn. (10) is satisfied because of C2v geometry. However, the CI is restricted to that subset of C2v geometries where eqn. (9) is also satisfied.
2.2 Analytical descriptions of the PES
Further insight into the PES for a generic CI can be gained by developing approximate analytical descriptions, valid over limited regions of space. The simplest and most often used of these descriptions are power series expansions of the PES.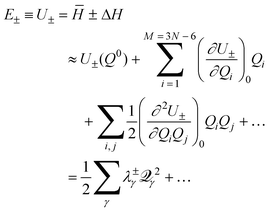 | (13) |
![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) and (iv) denoting (∂2U±/∂
and (iv) denoting (∂2U±/∂![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) 2γ) as λ±γ, which is the force constant for the normal mode in the electronic state with energy E±.
2γ) as λ±γ, which is the force constant for the normal mode in the electronic state with energy E±.
E±
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) U±
U±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R R | (14) |
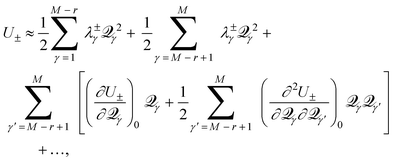 | (15) |
![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) M
M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r
r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, …,
1, …, ![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) M, but for the other M
M, but for the other M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r degrees of freedom, the first derivatives remain zero, and are thus omitted from eqn. (15). Inclusion of the last term in eqn. (15) involving the mixed partial derivatives is required because of the two-fold degeneracy of the vibrations. Distortion of the molecule away from Q0 along the M
r degrees of freedom, the first derivatives remain zero, and are thus omitted from eqn. (15). Inclusion of the last term in eqn. (15) involving the mixed partial derivatives is required because of the two-fold degeneracy of the vibrations. Distortion of the molecule away from Q0 along the M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r coordinates maintains the degeneracy of the intersection; only distortion along the remaining r coordinates will break the electronic degeneracy.
r coordinates maintains the degeneracy of the intersection; only distortion along the remaining r coordinates will break the electronic degeneracy.
The non-zero first derivatives of eqn. (15) have physical significance for the behavior of the molecule near the CI. In the case of CIs partially or wholly dependent on happenstance, not symmetry, such as are critical in reaction mechanisms, most of the important behavior is captured by this pair of first derivatives. As described by Yarkony,8 Bearpark, et al.,16 and others, a pair of linear combinations of coordinates, ![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) M
M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r
r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1,...,
1,..., ![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) M will describe the conical intersection exactly. Of particular significance is the linear combination (τ1, τ2) such that these two coordinates are the normals to the functions ΔH and H12 at Q0. When defined as such, the normal to H12 is called the derivative coupling vector, which allows molecules to ‘hop’ between surfaces, and the normal to ΔH is the gradient difference vector, which determines how fast a molecule moves through a CI.
M will describe the conical intersection exactly. Of particular significance is the linear combination (τ1, τ2) such that these two coordinates are the normals to the functions ΔH and H12 at Q0. When defined as such, the normal to H12 is called the derivative coupling vector, which allows molecules to ‘hop’ between surfaces, and the normal to ΔH is the gradient difference vector, which determines how fast a molecule moves through a CI.
2.3 The Jahn–Teller PES
For the Jahn–Teller CI, symmetry requires H11 and H22 of![[script letter H]](https://www.rsc.org/images/entities/i_char_e142.gif) (Q), eqn. (1), to be equal resulting in
(Q), eqn. (1), to be equal resulting in ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = H11 = H22 and R = H12. Using eqn. (15), we can write
= H11 = H22 and R = H12. Using eqn. (15), we can write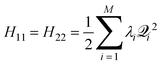 | (16) |
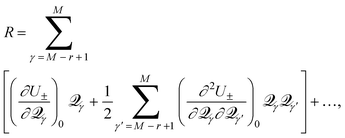 | (17) |
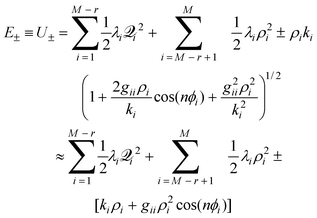 | (18) |
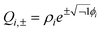 ,
, 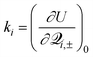 , and
, and 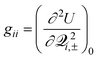 and reference the zero of energy to the conical intersection at E(Q0). Note that n is determined by the point group symmetry of the molecule, and, as has been typical, terms with γ
and reference the zero of energy to the conical intersection at E(Q0). Note that n is determined by the point group symmetry of the molecule, and, as has been typical, terms with γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ′
≠
γ in the last sum have been dropped.
′
≠
γ in the last sum have been dropped.
The parameters, ki and gii, may be, but are not required to be, non-zero as detailed in ref. 11. It is important to reiterate that, as for the generalized CI potential expansion, these derivatives are not defined at a minimum of the surface, but instead are defined at Q0, the CI.
As mentioned earlier, it may appear that there is a discrepancy between the use of r = 2p coordinates to describe the Jahn–Teller PES and the use of only two coordinates to describe its conical intersection. Resolution of this discrepancy lies in the recognition that the two coordinates (τ1, τ2) described earlier are a linear combination of the 2p coordinates of eqn. (17). The Jahn–Teller problem could be analyzed in terms of (τ1, τ2), but that would eliminate the use of the normal coordinates that describe the vibrations of the undistorted molecule. For a small to moderate Jahn–Teller effect, it is these coordinates that allow one to directly describe the resulting changes in the vibrational (vibronic) structures that are spectroscopically observed. In practice it has generally proven possible to deduce estimates for the values of the parameters of eqn. (18) by matching calculated quantized vibronic energy levels of the molecule as a function of these parameters, to spectroscopically observed structure. Elsewhere17,18 we have discussed the procedures for calculating the eigenvalues of the complete Hamiltonian obtained by adding the nuclear vibrational kinetic energy to the PES described by eqn. (18), as well as the relationship among these coordinates, in greater detail.
The first sum in eqn. (17) is worth considering in additional detail. As mentioned above it runs over all of the r components of the p normal modes (defined for the unperturbed symmetrical molecule) that transform as the appropriate irreducible representation of the group. Sometimes only a single normal mode will satisfy this criterion, and much of the early discussion19 of Jahn–Teller effects in molecules made this simplifying assumption. However, most molecules have several modes of the appropriate symmetry and all terms in the sum of eqn. (17) must be considered simultaneously in order to correctly calculate the vibronic eigenvalues.20 This is often referred to as the multi-mode effect.
2.4 Characteristics of the Jahn–Teller PES
In general, eqn. (18) represents a relatively simple analytical function which fairly accurately describes the PES surface in the vicinity of a typical Jahn–Teller CI. The full PES is M-dimensional, and difficult to envision. However the simple form of eqn. (18) allows us to easily visualize cuts through this surface along any of the 2p Jahn–Teller active normal coordinates. We can use these cuts, examples of which being depicted in Fig. 2, to illustrate some of the PES characteristics that play key roles in determining the experimentally observable vibronic energy level pattern. Alternatively, we can view the experimental results as determining the parameters, e.g., ki, gii, λi, that in turn characterize the PES, as described below.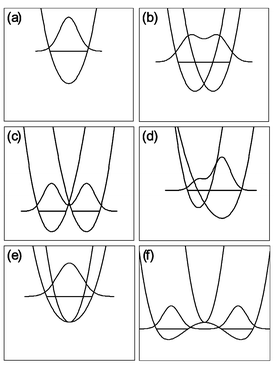 | ||
| Fig. 2 Example of cuts through representative Jahn–Teller PES; each is a slice through ϕ = 0 and the zero-point energy level is shown along with its wavefunction. (a) Harmonic oscillator, no Jahn–Teller coupling. (b) Linear Jahn–Teller coupling. (c) Linear Jahn–Teller coupling that is sufficiently large that the zero-point energy level lies below the CI. (d) Linear and quadratic Jahn–Teller coupling. (e) Small quadratic-only Jahn–Teller coupling. (f) Larger quadratic-only coupling. | ||
Let us consider a given Jahn–Teller active mode i and suppress the subscript. In the absence of quadratic Jahn–Teller coupling (i.e., g = 0, Fig. 2(b) and (c)), the minimum in the surface is located at
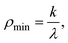 | (19) |
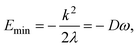 | (20) |
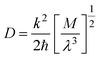 , where M is the reduced mass of the normal mode, and
, where M is the reduced mass of the normal mode, and 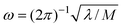 , is the vibrational frequency.
, is the vibrational frequency.
In the additional presence of non-zero quadratic coupling (g ≠ 0, Fig. 2(d)), eqn. (18) has a ϕ-dependence to the potential, creating n minima and maxima around the moat. The locations of the minima and maxima on the PES are now given by
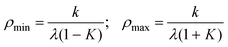 | (21) |
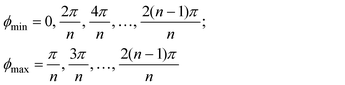 | (22) |
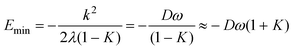 | (23) |
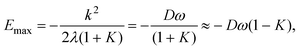 | (24) |
and assumed it is positive.
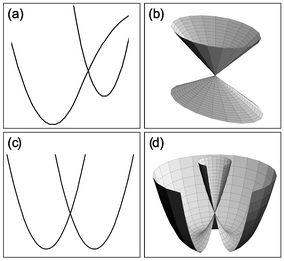
For a particular Jahn–Teller active mode i the Jahn–Teller stabilization energy,εi, is given by
εi = Diωi(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ki), Ki), | (25) |
| ε(2)i = 2DiωiKi. | (26) |
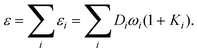 | (27) |
In the absence of linear coupling (D = 0), the Jahn–Teller portion of the potential, eqn. (18), simplifies to
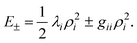 | (28) |
In the above description of the PESs, we have neglected one additional, complicating factor. Because Jahn–Teller activity requires an open-shell electronic configuration the majority of such molecules thus far examined also have a non-zero spin, most often S = ½. They thus possess spin and electronic orbital angular momentum and are subject to possibly significant first-order spin–orbit coupling, parameterized by the coupling constant aζe. Briefly, the effect of spin–orbit coupling is to diminish the effects of Jahn–Teller coupling on the molecule, and vice versa. The presence of spin–orbit coupling introduces several additional subtleties to the Jahn–Teller problem, which we have discussed in depth elsewhere,11 and which we will illustrate later in this article.
2.5 Qualitative implications of Jahn–Teller PESs
The preceding section describes PESs involving CIs in some degree of mathematical detail. Such a description is necessary for a quantitative understanding of these surfaces and their ramifications for spectroscopy and chemistry. However, much can still be understood qualitatively without invoking so much mathematics. Indeed the only results from Sections 2.1–2.4 that are critical to note is that ωe,i is the harmonic frequency of the ith Jahn–Teller active normal mode of the undistorted molecule and the linear and quadratic Jahn–Teller coupling terms for the ith mode are proportional to Di and Ki, respectively.The physical basis for these Jahn–Teller coupling terms can be easily illustrated for a specific example, e.g., the C5H5 radical. Fig. 3 shows the molecular distortion in terms of the dominant π electron configuration. As the figure shows the radical has three electrons to be distributed between a pair of degenerate e″1 orbitals. However the diagram also shows that if the molecule is distorted to the allylic or dienic C2v geometry, the degeneracy of the two e″1 orbitals will be removed which requires a non-zero value for k (or D) in the analytical potential, eqn. (18). Assuming the two molecular orbitals are repelled and stabilized by similar amounts, the net energy will be lowered by putting a pair of electrons in the depressed orbital. Cuts through the resulting PES, along with its lowest vibrational (vibronic) eigenvalue and a schematic representation of its wavefunction, are illustrated in Fig. 2(b) or (c).
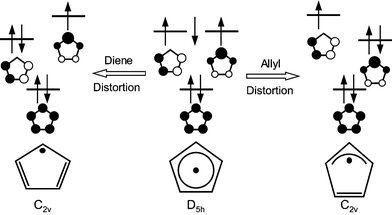 | ||
| Fig. 3 The five π molecular orbitals of the 2E″1 state of the C5H5 radical and their relative energies as a function of nuclear geometry. | ||
As Fig. 2(a) shows, the lowest energy wavefunction of a non-Jahn–Teller molecule has its maximum geometric probability at the symmetric geometry, Q0. In the absence of Jahn–Teller coupling the wavefunction for this level is a Gaussian function, appropriate for a harmonic oscillator potential, and is centered at the symmetrical geometry with no angular dependence, as shown in Fig. 2(a).
As the linear Jahn–Teller coupling (D ≠ 0) of C5H5 is introduced to the harmonic oscillator potential (Fig. 2(b)), the surface develops a minimum away from the D5h geometry. Consequently, the wavefunction spreads outward from the symmetrical point of the PES (Fig. 2(b)), such that the maximum in the probability distribution is over the center of the moat at the minimum of the PES. There is still no angular dependence of the energy, because the linear term in the potential (eqn. (18), with g = 0) has no angular dependence. Furthermore, the wavefunction still has a significantly non-zero value at the symmetrical geometry of the CI.
If the energy difference in the distorted geometry between the e″1 molecular orbitals increase, larger values of D result, and the stabilization becomes sufficiently large that the zero-point energy level lies below the CI (Fig. 2(c)). The wavefunction is still centered over the minimum moat, and does not have any angular dependence. The symmetric point now actually lies outside of the classical turning point on the PES for the zero-point level. Thus, only through tunneling does the wavefunction have a non-zero value at the symmetric geometry.
A more complete view of the C5H5 PES with the ‘position of the odd electron’ (as determined by the dominant electron configuration) and the corresponding, distorted nuclear geometry is shown in Fig. 4. The correlation between the electronic configuration and the Jahn–Teller PES allows us to understand several unique, and often confusing, features of the PESs and the vibrational (vibronic) eigenfunctions that result.
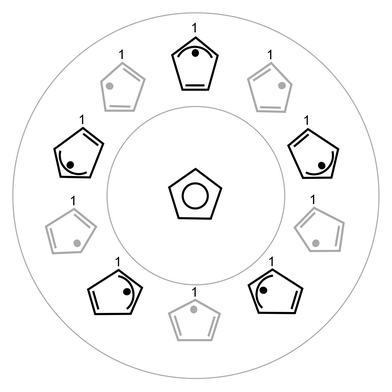 | ||
| Fig. 4 Schematic representation of the CI structure of C5H5 (center) and the five allylic and five dienic structures at the bottom of the moat encircling the CI. For C5H5, the allylic and dienic distorted structures are essentially isoenergetic. | ||
It is often stated that Jahn–Teller molecules ‘pseudo-rotate’ around the moat of the PES. This description is correct in that the molecules are constantly changing shape. However, all molecules are constantly changing shape due to their zero point motion. While the zero-point motion of the Jahn–Teller active molecule does have an angular portion to it, so does the zero-point motion of a two-dimensional harmonic oscillator of a non-Jahn–Teller molecule. The term ‘pseudo-rotation’ is misleading if it is taken to convey the notion that the nuclei in Jahn–Teller active molecules are moving significant distances, as occurs in rigid body rotation, while in fact they are not.
To clarify this point, Fig. 4 labels the top carbon atom to show that it is not the nuclei that rotate around the moat, but, in this drawing’s simplistic one-electron approximation to the wavefunction, it is the location of the odd electron that rotates, along with the resulting double and single C–C bond character. The C nuclei only move to the extent of the difference in bond lengths between a C–C single bond and a C–C double bond. In addition to this internal motion of the nuclei there is, of course, the external rotation of the molecule as a whole; these two motions of the nuclei can be coupled together, and at the finest level of detail this coupling can be experimentally resolved.
Fig. 2(b) and 2(c) describe another, often confusing, aspect of Jahn–Teller active molecules. It has been stated often that a ‘dynamic’ Jahn–Teller effect exists for D < 1, while the case of D > 1 results in a ‘static’ Jahn–Teller effect. However, in all cases where there is no quadratic Jahn–Teller coupling, the wavefunction of the molecule has no angular dependence. Because of the cylindrical symmetry of the PES in Fig. 2(b) or (c), a molecular property averaged around the moat will correspond to that of an undistorted molecule. Only a measurement made on a time scale short compared to the period of the zero-point motion will reveal any molecular distortion. Such ultra-fast time-resolved experiments have recently been reported by Zewail and co-workers for C5H5.21 They qualitatively detect the distortion which was previously quantitatively measured by high resolution spectroscopy22 (see Section 3.1 for details).
Although absent by symmetry in C5H5 (but present in the corresponding 5π electron system, C6H6+) the existence of unequal splitting for the degenerate orbitals between the diene and allyl conformation would result in a quadratic Jahn–Teller interaction and give rise to the PES of Fig. 2(d), which now clearly has an angular dependence and therefore requires gii ≠ 0 in eqn. (18). In this case, localization of the wave-functions around the moat can occur, because now the moat has distinct minima and maxima. If the barrier around the moat is high enough, the zero-point energy level can fall completely within one of the wells. In that case, only via tunneling, or via thermal or optical excitation to a vibronic level above the barrier, can the molecule transfer between wells. Measurements, even on long time scales comparable to vibronic motion, will reveal a ‘static’ molecular distortion for a PES of this nature. (Indeed the generalization of this statement appears to be that a ‘static’ distortion requires ‘high’ barriers along each of the dimensions involved in the CI.)
The potentials that we have discussed thus far are appropriate for isolated Jahn–Teller molecules, i.e., ones in the gas phase. In solution, in a matrix, or in the solid state, external perturbations can have a significant influence on the PES, especially in the case of quadratic Jahn–Teller coupling. For linear coupling, the molecule is always distorted, but also always changing the nature of that distortion. Thus, the molecule always has an instantaneous dipole moment, but the orientation of this dipole moment is constantly shifting. However, a molecule with linear and quadratic coupling has a partially localized distorted geometry with a permanent dipole moment. This permanent dipole moment causes a much more significant interaction with the surrounding molecules, which serves to deepen the quadratic Jahn–Teller well and give rise to a ‘static’ geometric distortion of the molecule in the condensed phase. This effect is much of the reason for the frequent discrepancies between condensed phase and gas phase spectra of the same Jahn–Teller active molecule. The condensed phase spectra can often be ascribed to a molecule suffering a ‘static’ Jahn–Teller distortion (enhanced by the environment), while the gas-phase results fit well with a ‘dynamic’ model.
3 The spectroscopy of the Jahn–Teller CI
Of course, a PES is not an observable in and of itself; experimentally only the quantum states of the molecule and their properties are observable, and we must model these observations to obtain the parameters that describe a PES. Herein, we illustrate how some of the various properties of the spectra of Jahn–Teller molecules, with the aid of modern quantum calculations, can be correlated with characteristics of the PES, and thus provide benchmarks for any computations of CI-containing PESs. We herein only discuss vibronic (and spin–orbit) energy levels that are most directly affected by Jahn–Teller interaction; (Jahn–Teller coupling can also indirectly affect the rotational energy levels, as is fully described in ref. 23).In the absence of Jahn–Teller coupling, the vibrational energy levels are evenly spaced by the vibrational frequency of the mode. The distortions of the PES illustrated in Fig. 2 dramatically alter this picture. Qualitatively, the energy levels are split as shown in Fig. 5. (For quantitative figures and more discussion, see the many figures and examples in ref. 11.) Linear Jahn–Teller coupling splits each vibrational level into v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 different levels (column (b) of Fig. 5). The magnitude of the splitting is dominated by the size of the coupling parameter D. Upon the introduction of a small to moderate quadratic coupling (column (c) of Fig. 5), most of the energy levels are only slightly perturbed in energy, but the degeneracy of some is raised. The splitting of these levels is determined largely by the value of K. Even a relatively small value of K can give rise to a large splitting, as illustrated later for the methoxy radical and benzene cation. The final example of Fig. 5, column (d), shows the inclusion of spin–orbit coupling to the problem. All energy levels are split, except for Kramer’s degeneracy or those already rendered non-degenerate by quadratic coupling, and the extent of the spin–orbit splitting (which varies by level) is determined by aζe.
1 different levels (column (b) of Fig. 5). The magnitude of the splitting is dominated by the size of the coupling parameter D. Upon the introduction of a small to moderate quadratic coupling (column (c) of Fig. 5), most of the energy levels are only slightly perturbed in energy, but the degeneracy of some is raised. The splitting of these levels is determined largely by the value of K. Even a relatively small value of K can give rise to a large splitting, as illustrated later for the methoxy radical and benzene cation. The final example of Fig. 5, column (d), shows the inclusion of spin–orbit coupling to the problem. All energy levels are split, except for Kramer’s degeneracy or those already rendered non-degenerate by quadratic coupling, and the extent of the spin–orbit splitting (which varies by level) is determined by aζe.
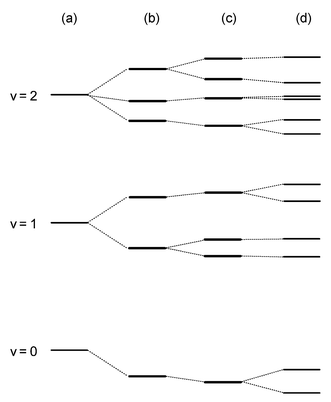 | ||
Fig. 5 Qualitative schematic diagram for the lowest few vibrational levels of a single mode of a Jahn–Teller active molecule. (a) Harmonic oscillator. (b) Harmonic oscillator![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) linear Jahn–Teller coupling. (c) Same as (b), plus quadratic coupling. (d) Same as (c), plus spin–orbit coupling. linear Jahn–Teller coupling. (c) Same as (b), plus quadratic coupling. (d) Same as (c), plus spin–orbit coupling. | ||
The four example molecules used to illustrate the connection between spectra, calculations, and PESs, are C5H5, C6H6+, Ag3 and CH3O. Respectively they illustrate a multi-mode linear Jahn–Teller effect without quadratic interactions or spin–orbit coupling, the same except with quadratic coupling, a linearly and quadratically active single-mode system with spin–orbit coupling, and finally a linearly and quadratically active multi-mode system with spin–orbit coupling.
3.1 Linear Jahn–Teller interactions: the cyclopentadienyl radical
The cyclopentadienyl radical (C5H5) is a planar five membered ring with the ground state electronic configuration| …(a″2 )2(e″1 )3(e″2 )0, | (29) |
The Jahn–Teller effect on the other hand turns out to be quite important for understanding the vibrational and rotational spectra. As noted above, our focus is on its effects for the vibrational energy levels because their analysis reveals far more about the PES, than does the rotational structure.
The cyclopentadienyl radical corresponds to the D5h point group which has four degenerate irreducible representations, e′1, e″1, e′2 and e″2. Of these four, only vibrational modes with e′2 symmetry may have a non-vanishing D. Likewise, only modes with e′1 and e″1 symmetry may have non-vanishing K. Cuts of the PES along the e′2 normal coordinates will therefore resemble Fig. 2(b); those along the e′1 and e″1 normal coordinates will resemble Fig. 2(e) or (f); and slices along the e″2 and the non-degenerate normal coordinates will resemble Fig. 2(a). Because there is no experimental evidence in C5H5 for quadratic Jahn–Teller activity in the e′1 and e″1 normal modes we will postpone discussion of such effects until the section on C6H6+, where there is significant experimental evidence for quadratic activity in comparable modes.
The best experimental evidence for the linear Jahn–Teller distortion in the e′2 modes of C5H5 arises from the LIF dispersed emission spectra18 taken using the electronic transition Ã2A″2
→ ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2E″1. The key to understanding the spectra is a good estimate of the D’s and ω’s obtained using high level ab initio calculations.18 Indeed, prior to these calculations the parameter space had proven far too great for a successful analysis of the spectra.
2E″1. The key to understanding the spectra is a good estimate of the D’s and ω’s obtained using high level ab initio calculations.18 Indeed, prior to these calculations the parameter space had proven far too great for a successful analysis of the spectra.
While spectra were obtained by dispersing each of the observed vibrational bands in the excited state (each of the spectra look different due to different selection rules and Frank–Condon factors), we illustrate the experimental results with the emission spectrum taken while pumping the e′2 symmetry ν11 vibrational mode (Fig. 6(a)). It features more than twenty bands in the first 2500 cm−1, whereas Fig. 6(c) shows that in the absence of Jahn–Teller interactions we would expect only transitions to three fundamental vibrational modes and one overtone. Indeed this dramatic increase in complexity is the spectral signature of the multimode Jahn–Teller effect.
 | ||
| Fig. 6 (a) Experimental dispersed emission spectrum of C5H5 from one quantum of ν11 excited in the à state. (b) Simulation of the Jahn–Teller active structure using the parameters given in the text. Some anomalies in the calculated intensities are due to the assumption of diagonal Frank–Condon factors. (c) Complete spectrum of C5H5 expected in the absence of Jahn–Teller activity. Summing scan B and C nicely reproduces the experimental spectrum A. | ||
Starting from the ab initio values of Di and ωi for each vibrational mode, it was possible to fit the ν11 spectrum using the Hamiltonian with a potential of the form of eqn. (18). The predicted spectrum of the Jahn–Teller active vibrations is depicted in Fig. 6(c). The experimental spectrum is well approximated as the sum of Fig. 6(b) and (c).
Two things are immediately apparent from Fig. 6. The density of states increases sharply with increasing energy, and there is a significant variation in the intensity of the Jahn–Teller levels. The first observation is a consequence of ‘lighting up’ all combinations and overtones of the Jahn–Teller active modes and the fact that each of these modes is split by the Jahn–Teller effect. The second observation is a product of the degree of mixing present in each level. Since ν11 is being pumped in the excited state, those Jahn–Teller levels with the most ground state ν11 mixed into them will have the strongest intensity. Of course since this is electronic spectroscopy the Frank–Condon factors also contribute to the variation in intensity.
From the analysis of spectra like Fig. 6, the constants Di and ωi, for each vibrational mode were determined, thereby characterizing the PES of the Jahn–Teller distortion. From this data we conclude that for C5H5, the cut of the PES along the Jahn–Teller distortion coordinates (τ1, τ2 or in polar coordinates ρT, ϕT) is much like Fig. 2(b) with an experimental moat depth of ε = 1237![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 cm−1. This stabilization energy is distributed among the 4 e′2 normal modes (9–12) approximately as follows: mode 12 (C–C–C bend), 166 cm−1; mode 11 (C–C–H bend), 594 cm−1; mode 10 (asymmetric C–C stretch), 477 cm−1 and mode 9 (asymmetric C–H stretch), ≈0 cm−1, where the approximate description of the normal coordinates in terms of symmetry coordinates is given in parenthesis. The barrier to pseudorotation around the moat is zero. The distance from the CI to the global minimum (moat bottom) on the PES is ρT = 0.265 amu1/2
Å, in mass weighted coordinates. Also, while the actual numbers quoted are from the experimental analysis, ab initio calculations give very consistent results for both the stabilization energy and geometric distortion. This distorted geometry is much more easily visualized in terms of internal coordinates as shown in Fig. 7. As the figure shows, the distortion is primarily in the C–C bond length, but with contributions from the C–C–C and C–C–H (not shown) angles. The geometric distortion is relatively small, of order 1° for the C–C–C angles and 0.1 Å for the C–C bond lengths. Despite its small size, the distortion clearly causes a great deal of havoc in the vibrational structure, as Fig. 6 shows.
50 cm−1. This stabilization energy is distributed among the 4 e′2 normal modes (9–12) approximately as follows: mode 12 (C–C–C bend), 166 cm−1; mode 11 (C–C–H bend), 594 cm−1; mode 10 (asymmetric C–C stretch), 477 cm−1 and mode 9 (asymmetric C–H stretch), ≈0 cm−1, where the approximate description of the normal coordinates in terms of symmetry coordinates is given in parenthesis. The barrier to pseudorotation around the moat is zero. The distance from the CI to the global minimum (moat bottom) on the PES is ρT = 0.265 amu1/2
Å, in mass weighted coordinates. Also, while the actual numbers quoted are from the experimental analysis, ab initio calculations give very consistent results for both the stabilization energy and geometric distortion. This distorted geometry is much more easily visualized in terms of internal coordinates as shown in Fig. 7. As the figure shows, the distortion is primarily in the C–C bond length, but with contributions from the C–C–C and C–C–H (not shown) angles. The geometric distortion is relatively small, of order 1° for the C–C–C angles and 0.1 Å for the C–C bond lengths. Despite its small size, the distortion clearly causes a great deal of havoc in the vibrational structure, as Fig. 6 shows.
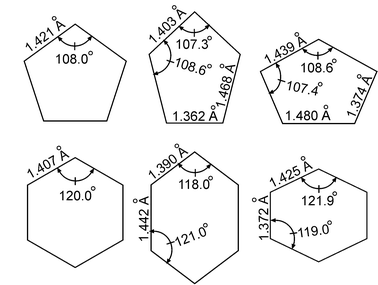 | ||
| Fig. 7 Experimentally determined geometries (left to right) of the CI, minima and maxima around the moat for (top) C5H5 and (bottom) C6H6+. The schematic distortions have been exaggerated to emphasize the differences. The distortions shown involve the ring skeleton (C–C stretches and C–C–C bends); the bending and stretching distortion of the hydrogens is not shown. The energy difference of the CI to the moat is ε = 1237 cm−1 for C5H5 and ε = 707 cm−1 for C6H6+. For C5H5 the energy difference between the minima and maxima in the moat is theoretically vanishing to high order; for C6H6+ it is smaller than the precision of the experiments. | ||
3.2 Linear plus quadratic Jahn–Teller interactions: the benzene cation
The benzene cation is perhaps the most famous molecule subject to the Jahn–Teller effect. It stands in stark contrast to its neutral relative, benzene, whose structure has been known for a century to be a planar regular hexagon with D6h symmetry. However, for the cation with a ground 2E1g electronic state, the minimum on the PES is not at the D6h geometry. Like C5H5, the benzene cation will suffer a distortion along a subset of its doubly degenerate normal modes. From group theory, only the e2g modes will have non-vanishing Di. Unlike C5H5, these linearly active Jahn–Teller modes in benzene cation are also quadratically Jahn–Teller active, i.e. they have both non-vanishing Diand Ki. Therefore a 2-D slice through the PES along any of the e2g normal coordinates resembles Fig. 2(d). Since the energy is now dependent upon ϕi the 3-D PES features three minima and three maxima around the moat. Note that the angular dependence of the e2g cut of the PES is due to the simultaneous presence of both a linear Jahn–Teller effect and a quadratic Jahn–Teller effect, because neither one taken independently produces any angular dependence.The remaining degenerate normal coordinates, of symmetry e1g, e1u and e2u, all have non-vanishing Ki, but vanishing Di. Hence, 2-D slices along any of these normal coordinates must resemble Fig. 2(e) or (f). For a small quadratic-only effect, the minimum remains at the D6h point on the PES. For any size quadratic-only effect, there is no angular dependence to the PES, and the 3-D PES is simply the 2-D PES rotated about the symmetry axis.
The first experiments to observe directly the Jahn–Teller effect in the benzene cation ground state were the photoeletron spectra of Williams and co-workers,25 though their low resolution hindered the analysis. More recent high resolution ZEKE26,27 spectra have done much to aid in the analysis; however, the spectrum is very complicated with over 40 spectral features observed within 1500 cm−1 of the origin. In fact, the original Jahn–Teller analysis included only the lowest frequency e2g mode, fitting only three of the observed lines, even though it is clear from symmetry arguments that all four e2g modes may have activity. Furthermore, at least three of the e2g modes were shown28 to be important for the closely related C6F6+.
As in C5H5, the use of high level ab initio calculations to obtain estimates of the Jahn–Teller constants have made a more complete assignment of this very dense spectrum possible. A recent analysis29 of the existing ZEKE spectra as well as IR spectra30 of C6H6+·Ne and C6H6+·Ar in light of these ab initio calculations has shown three of the four e2g modes to be important for describing the Jahn–Teller distortion in benzene cation. This analysis reiterates the need to simultaneously consider all of the active modes of a molecule. The active modes in C6H6+ are nominally the C–C stretch, the C–C–C bend, and the C–C–H bend (the C–H stretch while symmetry allowed shows little activity). Using the values of ωi, Di, and Ki from the fit, the Jahn–Teller geometric distortion is illustrated in Fig. 7. This distortion corresponds to a net energy stabilization of ε ≈ 707 cm−1 for C6H6+. With a very small barrier, (≲10 cm−1, on the order of the error in the fit) around the moat, the structure of benzene cation, while instantaneously D2h, will dynamically be D6h.
As mentioned earlier, the benzene cation has a number of vibrational modes that are subject to only quadratic Jahn–Teller interactions. One such mode is the lowest energy out-of-plane bending mode ν20. Several authors have fit experimental spectra to determine ω20 and K20 to be 307 cm−1 and 0.064, respectively. The energy difference between the two normally degenerate PES′s is 11 cm−1 at ρ = 0.25 amu1/2 Å. This fairly small splitting of the PES′s produced a splitting in the spectrum of the fundamental into three bands separated by approximately 17 cm−1. Again, this result illustrates how a small ripple in the PES can manifest itself as a relatively large splitting in experimental spectra.
3.3 Large single mode linear and quadratic Jahn–Teller interactions: the silver trimer
The alkali metals (Li, Na, K) and the coinage metals (Cu, Ag, Au) are known to form trimers, with nominally an equilateral triangular geometry (D3h). Simple molecular orbital arguments lead one to expect the ground state to be 2E′ with an allowed electronic transition to an excited 2E″ state. Both states would be expected to show Jahn–Teller activity with distortion of the equilateral triangular geometry.These metal trimers have been particularly attractive targets for both computational and experimental studies. From a theoretical point of view, their most distinctive feature is that the distortion path is entirely characterized by symmetry, as there is only one vibrational mode that transforms as the required irreducible representation (e′). At first it might appear that these would be ideal systems with which to compare theory and experiment. However, the reality is less than the ideal. With respect to all of the metal trimers, experimental data on the ground state is extremely sparse, as the spectroscopy of the 2E″–2E′ transition has produced mostly information on the excited 2E″ state and, even for the 2E″ state, there has been much debate over the interpretation of the data and even the nature of the state (for details see the discussion in ref. 10). What is likely the definitive interpretation of the alkali trimer data relies on a method unique to these molecules, i.e., direct integration of the Schrödinger equation in hyperspherical coordinates for the nuclei on an ab initio PES of sufficiently high quality to directly replicate experimental data. Because the Jahn–Teller distortion of the alkali trimers is large, the perturbative approach we have described is slow to converge and less applicable to these systems than almost any other isolated molecular system yet studied in detail. The direct integration is also presently only practical for a single mode system and rarely are ab initio PESs of this high quality available, so this treatment while being extremely elegant, is neither of great generality, nor of particular tutorial value since it focuses on large scale computations.
Nonetheless, the trimers display many interesting characteristics that can be generally informative. Therefore, we illustrate their behavior with the excited ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2E″ state of Ag3 which has been rather well characterized by both LIF31 and REMPI experiments.32,33 Like the alkali trimers, Ag3 has a sizable Jahn–Teller effect, but it has been treated by the approaches described in this review.
2E″ state of Ag3 which has been rather well characterized by both LIF31 and REMPI experiments.32,33 Like the alkali trimers, Ag3 has a sizable Jahn–Teller effect, but it has been treated by the approaches described in this review.
Even though the experimental results are relatively extensive, as shown by the Ag3 LIF spectrum31 in Fig. 8, the analysis is much less so. Indeed there are three distinct analyses in the literature which appear to ‘fit’ this spectrum comparably well. Respectively they ‘determine’ (i) the linear (D) and quadratic (K) Jahn–Teller coupling constants;32 (ii) D and the spin–orbit coupling constant (aζe);32 (iii) all three constants.33 Disconcertingly, the reported values of the parameters in the various fits are quite different. Qualitatively, fits (i) and (ii) yield small Jahn–Teller distortions, e.g., D < 0.05, while fit (iii) yields a large distortion D > 5.
For the purposes of this review, we shall discuss only fit (iii), as it is the most complete and most recent work and the large Jahn–Teller distortion it favors is consistent with a similar large distortion of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state predicted by ab initio calculations.34 Even if this fit ultimately is not the correct analysis for
state predicted by ab initio calculations.34 Even if this fit ultimately is not the correct analysis for ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2E″ Ag3, it is a plausible model that, for pedagogical purposes, illustrates a number of properties of Jahn–Teller systems not covered by the other examples in this review.
2E″ Ag3, it is a plausible model that, for pedagogical purposes, illustrates a number of properties of Jahn–Teller systems not covered by the other examples in this review.
Without going into detail, the first 250 cm−1 of the spectrum in Fig. 8 exhibits the simple vibrational structure expected of a molecule with two, approximately harmonic, vibrational modes (one a′1 and one e′ symmetry). However, above 27200 cm−1 the structure rapidly becomes very dense. Fit (iii)33 for the Jahn–Teller active structure yielded values for the e′ mode of ωe = 139.1 cm−1, D = 5.03, K = 0.354 and aζe = 1500 cm−1. These values correspond to a linear Jahn–Teller stabilization energy of ε ≈ 700 cm−1 (in the absence of spin–orbit coupling) and a barrier for motion around the moat of ≈560 cm−1. The barrier height is about four times the value of the vibrational frequency, indicating that approximately the first four vibrational levels will lie below the barrier. Thus, the simple low-frequency structure in Fig. 8 can be viewed in terms of the localized vibration of a ‘statically’ distorted molecule, as illustrated in Fig. 5(c). Because of tunneling between the barriers, each of these levels is in principle split into multiple components, but the splitting cannot be resolved with the experimental resolution. As the vibrational energy levels approach the barrier height, the splitting becomes larger and the delocalized motion gives rise to the extremely complex structure seen in the higher frequency regions of Fig. 8.
Interestingly, a large value of the spin–orbit coupling constant aζe ≈ 1500 cm−1 is suggested32 even though there is no sign of a spin–orbit splitting in the origin band or other low lying lines in Fig. 8. This can be rationalized in terms of the molecule being localized in a distorted geometry where the electronic angular momentum is quenched. Such a compression of the spin splitting by a Jahn–Teller distortion has long been known and often referred to as the Ham effect.10,11 As the vibrational energy increases and the vibrations delocalize, one expects this quenching to decrease, and indeed the analysis33 ascribes some of the complex high-lying structure in Fig. 8 to spin–orbit–split lines, but even here the purported splitting remains much smaller than 1500 cm−1, due to residual angular momentum quenching.
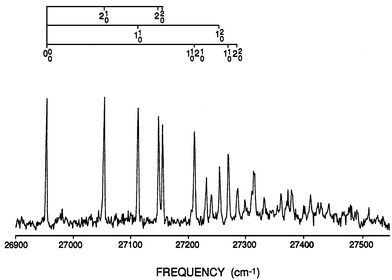 | ||
| Fig. 8 LIF excitation of the Ag3 trimer. Note the regular appearance of the vibrational structure below ≈27200 cm−1, compared to the irregular complex structure at higher frequencies. | ||
The analysis (iii) of Ag3 provides a convenient example illustrating a single mode system with a large Jahn–Teller effect, such that it nearly completely quenches the spin–orbit coupling. However, even in this simple trimer this analysis is not yet definitive. Moreover, the Jahn–Teller distortion in the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) state lacks almost any experimental characterization. A complete analysis of even the
state lacks almost any experimental characterization. A complete analysis of even the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2E″ state from the
2E″ state from the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) spectrum will require a much greater understanding of both the
spectrum will require a much greater understanding of both the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) states. This situation for even this simple trimer illustrates the abundant challenges that still exist in the area of Jahn–Teller spectroscopy.
states. This situation for even this simple trimer illustrates the abundant challenges that still exist in the area of Jahn–Teller spectroscopy.
3.4 The additional complication of spin–orbit coupling: the methoxy radical
The history of the spectroscopy and theoretical understanding of the methoxy radical, CH3O, is extremely rich, with greater than one hundred papers having been published on this topic. This radical has only two heavy atoms, making it a recurring target of the ever-evolving ab initio methods. Experimentally, it has one of the strongest and most easily observable LIF spectra, making it a favorite choice of spectroscopists. Furthermore, the methoxy radical is a key intermediate in combustion and atmospheric chemistry, which creates a broad interest in all of its properties. Despite these facts, a detailed understanding of the Jahn–Teller coupling in CH3O has only recently been revealed.There were two key experimental observations that were made in the 1990s that converged to elucidate this radical’s vibronic structure. The first was a relatively simple adjustment to the generation of the radical in a free jet expansion, such that the vibrational cooling of the radical was greatly enhanced.35 This additional cooling allowed the LIF spectroscopy of the electronically excited à state of the radical to be completely and definitively analyzed. Once the spectroscopy of the à state was finally on a firm foundation, the analysis of the ground state could be built thereupon.
The second key development in solving this radical’s Jahn–Teller structure was the high resolution, stimulated-emission-pumping experiments by Temps and coworkers.36 The superlative resolution of these experiments, which required a tremendous amount of tenacity and experimental finesse, resulted in the definitive assignment of the energies and spectral properties of an abundance of energy levels in the ground state of CH3O. Both of these experiments were also performed on the perdeuterated radical, which nearly doubled the available information.
Despite the increased wealth of data these experiments produced, these spectra were exceedingly difficult to analyze, for several reasons. In hindsight, many published ‘analyses’ of this radical’s spectra contained erroneous assignments, which heavily clouded the key issues. Many of these analyses used only a single active mode, rather than all three Jahn–Teller active e modes of CH3O. This simplification turned out to be a disastrously bad assumption. Additionally, the radical has a fairly large quadratic Jahn–Teller coupling in its lowest frequency vibrational mode. This coupling constant is so large that it splits an otherwise single level into two levels spaced ≈275 cm−1 apart. This large separation does not appear to be a simple splitting (which is normally expected to be small), but instead gives the illusion of being two completely separate energy levels. Finally, the spin–orbit coupling constant in CH3O is large enough (≈160 cm−1) to be of similar energy as the vibrational energy spacings, which caused several additional complications.
Upon the inclusion of a non-negligible spin–orbit coupling, many of the energy levels that were split by Jahn–Teller coupling are further split into doublets. (For vibrational modes with quadratic activity, some of the energy levels are not split but instead are mixed with each other, with only slight perturbations of the energy levels.) While the presence of these doublets can instantly be ascribed to the presence of spin–orbit coupling, the greater density of states adds significantly to the difficulty in assigning the spectral lines to the correct quantum states.
As with C5H5 and C6H6+, relatively large splittings in the vibrational energy levels of CH3O are derived from a relatively small geometric distortion. For methoxy, most of the distortion occurs in the O–C–H angles, which are about 110° at the C3v point. At the PES minima, of Cs symmetry, one of the O–C–H angles has decreased to about 105.5°, while the other two have increased to about 111°. At the maxima within the moat, these distortions are approximately reversed. The C–O and C–H bond lengths remain very close to their values at the C3v point, about 1.37 and 1.10 Å, respectively. The geometric distortion leads to a net linear energy stabilization of ε ≈ 400 cm−1.
Three other radicals similar to CH3O were also fully analyzed for their Jahn–Teller and spin–orbit coupling: CH3S, CF3O, and CF3S.11 As expected, the sulfur-centered radicals CH3S and CF3S have spin–orbit coupling constants that are approximately 2.5 times that of CH3O and CF3O. As mentioned earlier, the effect of a large spin–orbit coupling is to quench the Jahn–Teller coupling, and indeed this is the case. For example, while CF3S has non-negligible Jahn–Teller activity in its lowest frequency e vibrational mode, this activity does not lead to a stabilized PES such as Fig. 2(b). Instead, the spin–orbit coupling completely absorbs the stabilization, and the PES is actually a pair of surfaces similar to Fig. 2(a), but separated by about 360 cm−1.
4 Summary and outlook for future research directions
As briefly indicated in this review, the past few years have seen rapid progress in unifying experimental and computational approaches to elucidate one of the oldest and most actively pursued problems in chemical physics, the Jahn–Teller effect. For really the first time, experimental results have been sufficiently detailed and extensive enough to deduce PESs that could be compared to those from quantum chemistry calculations, which similarly moved forward at a rapid pace in this period. This work has now reached a point where detailed, nearly quantitative comparisons are possible with a corresponding enrichment of our understanding of the phenomena. Such comparisons are particularly useful since similar calculations of CIs to explain reaction mechanisms are increasingly prevalent, but scarcely amenable to experimental characterization.While recent progress has indeed been rather spectacular, there are still a number of remaining issues to be clarified with respect to the interpretation of spectral data for Jahn–Teller active molecules and its ramifications for CIs in general. Some of the remaining issues include the adequacy of the severely truncated power series representation of the PES, so often used to analyze spectra. Another area of future interest is in the interpretation of condensed phase spectra and examination of the interaction between the environment and the Jahn–Teller coupling. An area only briefly touched upon in this review are molecules subject to the pseudo-Jahn–Teller effect. Particularly interesting cases of the pseudo-Jahn–Teller effect that merit further investigation, occur when the degeneracy lifting of the CI is caused by an isotopic, or a minor chemical, substitution, e.g., ethyl for methyl, relatively remotely from the location of the ‘open-shell electron(s)’. Finally there is the intriguing possibility of Jahn–Teller molecules being isolated sufficiently long in distorted geometries to exhibit strongly different chemical reactivity. These issues as well as the fundamental problem of describing CI-containing PESs and their ramifications are likely to keep chemists occupied with the Jahn–Teller effect for many years to come.
5 Acknowledgements
T. A. M. is pleased to acknowledge the support of National Science Foundation via grants CHE-9974404 and CHE-0211281.References
- J. V. Neumann and E. P. Wigner, Phys. Z., 1929, 30, 467 Search PubMed.
- E. Teller, J. Phys. Chem., 1937, 41, 109 CrossRef CAS.
- F. Bernardi, M. Olivucci and M. A. Robb, Chem. Soc. Rev., 1996, 25, 321–328 RSC.
- D. Herschbach, Rev. Mod. Phys., 1999, 71, s411 CrossRef CAS.
- S. L. Miller and H. C. Urey, Science, 1959, 130, 245 CAS.
- J. Pecourt, J. Peon and B. Kohler, J. Am. Chem. Soc., 2000, 122, 9348 CrossRef CAS.
- N. Ismail, L. Blancafort, M. Olivucci, B. Kohler and M. A. Robb, J. Am. Chem. Soc., 2002, 124, 6818 CrossRef CAS.
- D. R. Yarkony, Acc. Chem. Res., 1998, 31, 511 CrossRef CAS.
- H. A. Jahn and E. Teller, Proc. R. Soc. London A, 1937, 161, 220 Search PubMed.
- I. Bersuker, Chem. Rev., 2001, 101, 1067 CrossRef CAS.
- T. Barckholtz and T. A. Miller, Int. Rev. Phys. Chem., 1998, 17, 435 CrossRef CAS.
- H. Köppel and W. Domcke, in Encyclopedia in Computational Chemistry, Wiley, New York, 1998 Search PubMed.
- H. Koppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59 Search PubMed.
- G. J. Atchity, S. S. Xantheas and K. Ruedenberg, J. Chem. Phys., 1991, 95, 1862 CrossRef.
- C. A. Mead, Rev. Mod. Phys., 1992, 64, 51 CrossRef CAS.
- M. J. Bearpark, M. A. Robb and H. B. Schlegel, Chem. Phys. Lett., 1994, 223, 269 CrossRef CAS.
- T. A. Barckholtz and T. A. Miller, J. Phys. Chem., 1999, 103, 2321 CrossRef CAS.
- B. E. Applegate, T. A. Miller and T. A. Barckholtz, J. Chem. Phys., 2001, 114, 4855 CrossRef CAS.
- H. C. Longuet-Higgins, Adv. Spectrosc., 1961, II, 429 Search PubMed.
- C. S. Sloane and R. Silbey, J. Chem. Phys., 1972, 56, 6031 CrossRef CAS.
- H. Ihee, J. S. Feenstra, J. Cao and A. H. Zewail, Chem. Phys. Lett., 2002, 353, 325 CrossRef CAS.
- B. E. Applegate, A. J. Bezant and T. A. Miller, J. Chem. Phys., 2001, 114, 4869 CrossRef CAS.
- X. Liu, C. P. Damo, T.-Y. Lin, S. C. Foster, P. Misra, L. Yu and T. A. Miller, J. Phys. Chem., 1989, 93, 2266 CrossRef CAS.
- L. Yu, D. W. Cullin, J. M. Williamson and T. A. Miller, J. Chem. Phys., 1993, 98, 2682 CrossRef CAS.
- A. W. Potts, W. C. Price, D. G. Streets and T. A. Williams, Discuss. Faraday. Soc., 1972, 54, 168 RSC.
- R. Linder, K. Muller-Dethlefs, E. Wedum, K. Haber and E. R. Grant, Science, 1996, 271, 1698.
- A. Held and E. Schlag, Acc. Chem. Res., 1998, 31, 467 CrossRef CAS.
- T. A. Miller and V. E. Bondybey, in Molecular Ions: Spectroscopy, Structure and Chemistry, North-Holland, Amsterdam, 1983 Search PubMed.
- B. E. Applegate and T. A. Miller, J. Chem. Phys., 2002, 117, XXXX CrossRef CAS , to be published December 2002.
- J. M. Bakker, R. G. Saterik, G. V. Helden and G. Meijer, Phys. Chem. Chem. Phys., 2002, 4, 24 RSC.
- A. M. Ellis, E. S. J. Robles and T. A. Miller, Chem. Phys. Lett., 1993, 201, 132 CrossRef CAS.
- E. E. Wedum, E. R. Grant, P. Y. Cheng, K. F. Willey and M. A. Duncan, J. Chem. Phys., 1994, 100, 6312 CrossRef CAS.
- F. Wallimann, H.-M. Frey, S. Leutwyler and M. Riley, Z. Phys. D, 1997, 1.
- K. Balasubramanian and M. Z.. Liao, Chem. Phys., 1988, 127, 313 CrossRef CAS.
- D. E. Powers, M. Pushkarsky and T. A. Miller, J. Chem. Phys., 1997, 106, 6863 CrossRef CAS.
- A. Geers, J. Kappert, F. Temps and J. Wiebrecht, J. Chem. Phys., 1994, 101, 3618 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2003 |