Dissipative wave packet dynamics of the intramolecular hydrogen bond in o-phthalic acid monomethylester
O.
Kühn
* and
H.
Naundorf
Institut für Chemie, Physikalische und Theoretische Chemie, Freie Universität Berlin, Takustrasse 3, D-14195, Berlin, Germany
First published on 18th November 2002
Abstract
We investigate the infrared laser-driven ultrafast dynamics of the carboxy-deuterated title compound in the condensed phase using a system–bath approach. The three-dimensional relevant system comprises the OD stretching and bending motion as well as a low-frequency out-of-plane twisting vibration modulating the hydrogen-bond strength. The dominant relaxation and dephasing channels are identified giving rise to three terms which contribute to the system–bath interaction: (i) A linear system-solvent coupling leading to the relaxation of the low-frequency mode. Here, a classical molecular dynamics simulation is performed to obtain the spectral density and thus the relevant relaxation time scale for this mode. (ii) A coupling which is quadratic in the system coordinates and responsible for pure dephasing. (iii) A fourth-order coupling which involves the release of vibrational energy into the environment by means of the simultaneous excitation of two intramolecular bath vibrations and a solvent mode. Using a quantum master equation approach it is demonstrated that this model is in accord with the results of recent infrared pump-probe and four-wave mixing experiments. The dynamics is discussed in terms of a diabatic representation defined with respect to the high-frequency stretching and bending modes. The behaviour of the low-frequency mode can be characterized as a dissipative wave packet motion in the diabatic ground state which contains contributions from bath-induced coherence transfer out of the initially excited diabatic state.
1 Introduction
Recent advances in ultrafast infrared (IR) spectroscopy paved the road to a better understanding of vibrational molecular dynamics in the condensed phase. Special attention has been focussed on H-bonded systems with liquid water being the most prominent example.1–8 The well-defined intramolecular H-bonds of the type A–H⋯B, on the other hand, are conceptually much simpler than the H-bonded network which characterizes liquid water. Nevertheless the interpretation of IR line shapes is notoriously difficult due to, for instance, the anharmonic coupling between the fast A–H vibration and the slow A⋯B motion which modulates the strength of the H-bond.9,10 In addition the coupling between A–H stretching and bending vibrations can give rise to typical Fermi-resonance features such as the so-called Evans window, see refs. 11–13. The richness of intramolecular H-bond dynamics which in principle can be burried underneath a broad IR absorption band was demonstrated by the Elsaesser group14–18 using the femtosecond IR spectroscopy. For carboxy-deuterated o-phthalic acid monomethylester (PMME-D, see Fig. 1)14,15 which exhibits an intramolecular H-bond of medium strength, the decay of the excited state absorption of the OD stretching vibration in C2Cl4 could be characterized by a time scale of 400 fs. A second slower component of 20 ps was attributed to vibrational cooling of the anharmonically coupled modes in the OD vibrational ground state. As a clear indication of the effect of anharmonic coupling between the fast OD stretching and a low-frequency mode modulating the H-bond geometry, an oscillatory component was observed in the signal. It was attributed to damped wave packet motion with respect to the low-frequency mode with the related dephasing time being about 600 fs. For the fundamental OH stretching transition in PMME-H, on the other hand, photon echo studies showed an extremely short dephasing time of about 40 fs.17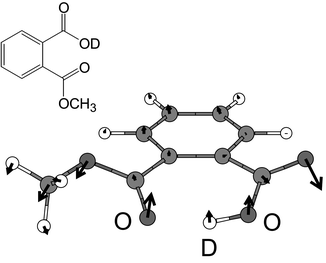 | ||
| Fig. 1 Most stable structure of PMME-D as obtained from a DFT/B3LYP (6-31+G(d,p)) geometry optimization. The arrows indicate the displacement vector for the low-frequency mode νlow which corresponds to an out-of-plane torsional motion. The O–O distance of 2.56 Å and the single minimum anharmonic shape of the potential surface indicate a H-bond of moderate strength. | ||
The theoretical investigation of intramolecular IR laser field induced H-bond dynamics requires a multidimensional treatment. For a molecule as large as PMME-D it is not clear a priori what is the relative importance of intramolecular and intermolecular processes for the observed relaxation and dephasing phenomena. Concerning the intramolecular dynamics we have shown that in principle a full-dimensional but approximate quantum simulation is possible if one uses the ab initio reaction surface Hamiltonian approach.19,20 The Schrödinger equation for this Hamiltonian can then be solved using the time-dependent Hartree method either in the mean-field21 or the numerically exact multiconfiguration22,23 limit. The latter of course requires to select a subset of important modes. For PMME-D this parameter-free approach was capable of predicting the character of the modes which are anharmonically coupled to the OD stretching vibration. Specifically, the mode responsible for the periodic low-frequency modulation of the H-bond dynamics, seen in the experiment, could be identified. However, the estimated decay time of the OD stretching excitation due to intramolecular vibrational energy randomization was about 20 ps, i.e. much longer than the experimental time of 400 fs. (The coincidence with the time scale of vibrational cooling is somewhat accidental as we will see below.) In other words, the interaction with the solvent must play an important role for the relaxation dynamics. In ref. 24 we have developed a system–bath model of PMME-D in the condensed phase. This approach combines an accurate description of the most relevant degrees of freedom, i.e. the OD stretch and bending modes as well as a low-frequency out-of-plane twisting mode, with a perturbational treatment of their interaction with the remaining intramolecular modes and the solvent. The key feature of the model was a fourth-order system–bath coupling which, by virtue of the interplay between two specific intramolecular and a solvent mode, could account for the ultrafast relaxation of the OD stretching vibration. This model has to be distinguished from previous considerations which were aimed mostly at the description of the dephasing of the A–H fundamental transition. Here two models have been discussed which differ in the way the solvent couples to the stretching mode. In the direct coupling case the related dipole moment interacts with the fluctuating field of the polar surroundings.25 Alternatively, an indirect coupling may occur via the damping of the low-frequency mode which has been described either quantum mechanically26,27 or stochastically.28 On the other hand, Rey and Hynes have considered a linear system–bath coupling model for vibrational relaxation of HOD in D2O leading, however, to a step-wise mechanism involving the HOD bending fundamental and first overtone transitions.29,30 Recently, this mechanism was shown to be dominant even if higher-order coupling terms are present.31 In the case of PMME-D the fourth-order order coupling opens a direct relaxation channel for the OD stretching vibration. Although of higher order it is a resonant process which can be rate-determining provided that lower order processes are not effective. This has been shown, although in a different context, in refs. 32–34.
Besides the fourth-order coupling our system–bath model includes a linear and a quadratic (in the system coordinate) interaction. From the latter we have taken only the contribution it gives to pure dephasing. While the dynamics of the OD stretching mode and the dephasing of the low-frequency mode could be fitted to the experimental results, the vibrational relaxation of the low-frequency mode could not be modelled without ambiguity. In ref. 24 we have tacitly assumed that the relaxation time for the low-frequency mode will be on the order of the vibrational cooling time of about 20 ps. However, our high-dimensional simulations of the intramolecular dynamics22 suggest that the latter may take place on a similar time scale. In other words, to assume that the 20 ps vibrational cooling time involves the release of energy from the low-frequency mode into the solvent only, is not straightforward. Clearly, to complete the model there is a need for an independent determination of the population relaxation time for the low-frequency mode.
Classical molecular dynamics simulations have been shown to provide an effective way for obtaining relaxation rates for complex solute-solvent situations. The conceptual framework goes back to early work of Landau and Teller and has been reviewed, e.g., in refs. 35 and 36 (see also ref. 37). The link between solute and solvent dynamics is established via time correlation functions of the force which is exerted on the relevant system coordinate by the solvent interactions. In a number of publications such correlation functions have been used to determine population relaxation rates as such29,30,38,39,40,41 or for use within density matrix theory.42,43 The validity of this approach was scrutinized, for instance, in refs. 44–47. In particular, for a bilinear coupling between an otherwise harmonic system and bath, Bader and Berne44 showed that classical and quantum relaxation rates coincide while a mixed quantum-classical treatment fails for high-frequency solutes. The conditions for the validity of the linear response theory assumed in this context where investigated by Makri on the basis of an influence functional approach.47 These considerations lead to the notion of an effective harmonic bath whose interaction with the relevant system, as manifested in the spectral density function, resembles the real anharmonic solvent environment.
In the present contribution we will extend our previous studies24 and combine the density matrix formulation of the dissipative H-bond dynamics in PMME-D with a molecular dynamics simulation of the solvent spectral density for the low-frequency system mode. This way we will be able to fix the time scale for the relaxation of the latter which will turn out to be much faster than the 20 ps required for the overall vibrational cooling. We start with reviewing our model as well as the link to the classical molecular dynamics simulation of spectral densities in Section 2. The determination of the system–bath interaction parameters is outlined in Section 3.1. In Section 3.2–3.3 the laser-driven dynamics is discussed in terms of a diabatic state representation with respect to the stretching and bending modes. The paper is summarized in Section 4.
2 Theory
2.1 System–bath Hamiltonian
In the following we briefly review the model for the dissipative nuclear dynamics in the adiabatic electronic ground state of PMME-D as put forward in ref. 24. All calculations have been performed using the DFT/B3LYP level of theory with a Gaussian 6-31+G(d,p) basis set.48 The most stable geometry is shown in Fig. 1. The potential energy surface for the O–D–O intramolecular H-bond is rather anharmonic, but has a single minimum only, i.e. the H-bond is of moderate strength. Previous investigations on the basis of a high-dimensional reaction surface Hamiltonian have led to the conclusion that the laser-driven dynamics takes place in the vicinity of the most stable configuration.21–23 This suggests to describe the nuclear motions in terms of normal mode coordinates. Specifically we will include three normal mode vibrational coordinates, {Qi}![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) {Qs,Qb,Qlow}, into the relevant system, i.e. those of the OD stretching (νs) and bending (νb) modes and a low-frequency mode (νlow) which modulates the strength of the H-bond as shown in Fig. 1. The choice of Qb and Qlow has been motivated by calculations of the forces acting on the normal modes given an elongated Qs mode.24 Additional support for the model comes from the double peak structure of the IR absorption spectrum in the OD stretch region (cf.Fig. 3 below) as well as from the experimental observation of low-frequency wave packet motion in ref. 15.
{Qs,Qb,Qlow}, into the relevant system, i.e. those of the OD stretching (νs) and bending (νb) modes and a low-frequency mode (νlow) which modulates the strength of the H-bond as shown in Fig. 1. The choice of Qb and Qlow has been motivated by calculations of the forces acting on the normal modes given an elongated Qs mode.24 Additional support for the model comes from the double peak structure of the IR absorption spectrum in the OD stretch region (cf.Fig. 3 below) as well as from the experimental observation of low-frequency wave packet motion in ref. 15.
The potential energy surface for the relevant system is obtained by performing additional single point calculations according to
V(Qs, Qb, Qlow)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≡ ≡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vsys({Qi}) Vsys({Qi})![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vs(Qs) Vs(Qs)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vsb(Qs,Qb) Vsb(Qs,Qb)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vsl(Qs,Qlow) Vsl(Qs,Qlow) | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V(Qs, Qb
V(Qs, Qb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, Qlow
0, Qlow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0). Notice that eqn. (1) is an approximation because instead of a full 3D grid only two 2D grids are spanned. (We used 18 points along Qs and 7 to 11 points along Qb and Qlow, depending on the shape of the potential. Subsequently the potential surface was fitted to a high-order polynomial.) We have checked that the direct coupling between modes νb and νlow is negligible for moderate elongations along Qs.
0). Notice that eqn. (1) is an approximation because instead of a full 3D grid only two 2D grids are spanned. (We used 18 points along Qs and 7 to 11 points along Qb and Qlow, depending on the shape of the potential. Subsequently the potential surface was fitted to a high-order polynomial.) We have checked that the direct coupling between modes νb and νlow is negligible for moderate elongations along Qs.
The interaction of the relevant 3D system with the external electric field E(t) has been included within the dipole approximation via the Hamiltonian
Hf(t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −E(t)d(Qs) −E(t)d(Qs) | (2) |
The 3D system Hamiltonian Hsys![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tsys
Tsys![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vsys has been diagonalized using an expansion of the total state vector in terms of zero-order states, |φ(k)i〉, i.e.
Vsys has been diagonalized using an expansion of the total state vector in terms of zero-order states, |φ(k)i〉, i.e.
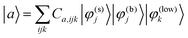 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, Qb), and Vsl(Qs
0, Qb), and Vsl(Qs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, Qlow) using the Fourier grid Hamiltonian method.49 To obtain convergence for the lower part of the spectrum up to energies corresponding to the νs overtone transition at about 4400 cm−1 it was sufficient to use 5, 8, and 25 basis states for the expansion in the Qs, Qb, and Qlow direction, respectively.
0, Qlow) using the Fourier grid Hamiltonian method.49 To obtain convergence for the lower part of the spectrum up to energies corresponding to the νs overtone transition at about 4400 cm−1 it was sufficient to use 5, 8, and 25 basis states for the expansion in the Qs, Qb, and Qlow direction, respectively.
The influence of the remaining intramolecular, {qm}, and solvent, {Zξ}, modes on the dynamics of the relevant system is taken into account using the formalism of dissipative quantum dynamics.50 Here, the system–bath interaction Hamiltonian is written as
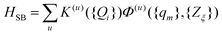 | (4) |
A related question concerns the choice of terms to be kept from the Taylor expansion. In ref. 24 we have shown that the experimental observations can be modelled by retaining three terms, i.e.HSB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H(I)SB
H(I)SB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H(II)SB
H(II)SB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H(III)SB, which open rather distinct phase and energy relaxation channels.
H(III)SB, which open rather distinct phase and energy relaxation channels.
The bilinear system–solvent coupling
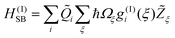 | (5) |
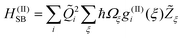 | (6) |
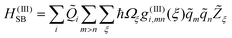 | (7) |
In eqns. (5)–(7) we introduced the dimensionless coupling strengths g(…)i,…(ξ) as well as the frequency of the ξth solvent bath mode Ωξ. Further, we use dimensionless coordinates according to ![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif) i
i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qi/λi. Below we will take λi
Qi/λi. Below we will take λi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (ħ/2ωi)1/2 with ωi being the fundamental transition frequency of the uncoupled mode νi. An analogous factor is introduced for the harmonic bath modes.
(ħ/2ωi)1/2 with ωi being the fundamental transition frequency of the uncoupled mode νi. An analogous factor is introduced for the harmonic bath modes.
As pointed out in ref. 24 this form of HSB represents a minimum model for the envisaged relaxation dynamics. The actual choice has been guided by the “rule” that only lowest-order terms for a particular mechanism should be taken into account (see also refs. 32 and 33).
2.2 Equations of motion
In the following we will focus on the time evolution of the reduced statistical operator ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) trBρtot. Assuming a weak system–bath interaction and the validity of the Markov approximation for the system–bath dynamics the equation of motion for ρ reads50
trBρtot. Assuming a weak system–bath interaction and the validity of the Markov approximation for the system–bath dynamics the equation of motion for ρ reads50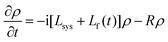 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Hsys,•]/ħ and Lf(t)•
[Hsys,•]/ħ and Lf(t)•![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Hf(t),•]ħ. The relaxation and dephasing due to the system–bath interaction is contained in the (Redfield) superoperator R. It can be expressed in the energy representation given by {|a〉} as50
[Hf(t),•]ħ. The relaxation and dephasing due to the system–bath interaction is contained in the (Redfield) superoperator R. It can be expressed in the energy representation given by {|a〉} as50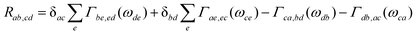 | (9) |
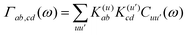 | (10) |
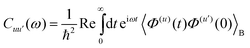 | (11) |
Neglecting the mixing between the three different contribution to HSB, eqns. (5)–(7) the damping matrix can be split into three terms which have been derived in ref. 24. For later reference we give the contribution of the bilinear coupling which reads:
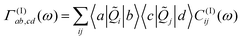 | (12) |
C(I)ij(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) πω2(1 πω2(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n(ω))[J(I)ij(ω) n(ω))[J(I)ij(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J(I)ij(−ω)] J(I)ij(−ω)] | (13) |
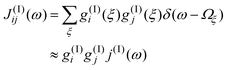 | (14) |
The quadratic coupling is treated in a similar fashion. However, we will only consider its contribution to pure dephasing, i.e. to those elements of the Redfield tensor which arise from Γ(II)ab,cd(ω) with the frequency argument being equal to zero. From the ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 limit of the correlation function one arrives at the following parameterization:52,53C(II)ij(ω
0 limit of the correlation function one arrives at the following parameterization:52,53C(II)ij(ω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0)
0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(II)ig(II)jγpd, i.e. the magnitude of the pure dephasing term is scaled by the parameter γpd which has the dimension of an inverse time.
g(II)ig(II)jγpd, i.e. the magnitude of the pure dephasing term is scaled by the parameter γpd which has the dimension of an inverse time.
The correlation function for the fourth-order relaxation contains again a spectral density which is approximated as J(III)ij(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(III)ig(III)jj(III)(ω). This implies that g(III)i,mn(ξ)
g(III)ig(III)jj(III)(ω). This implies that g(III)i,mn(ξ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(III)i(ξ), i.e. there is no difference in the coupling of the intramolecular modes. Following ref. 24 we will incorporate two intramolecular modes into eqn. (7) which are selected according to their coupling strength to the OD stretching vibration and the simultaneous requirement that, in combination with a low-frequency bath mode, they should provide a resonant transition for both the νs fundamental and the νb overtone excitation. The appropriate modes have frequencies of 620 cm−1 and 1329 cm−1.
g(III)i(ξ), i.e. there is no difference in the coupling of the intramolecular modes. Following ref. 24 we will incorporate two intramolecular modes into eqn. (7) which are selected according to their coupling strength to the OD stretching vibration and the simultaneous requirement that, in combination with a low-frequency bath mode, they should provide a resonant transition for both the νs fundamental and the νb overtone excitation. The appropriate modes have frequencies of 620 cm−1 and 1329 cm−1.
2.3 Spectral densities
The effect of the solvent on the system dynamics can be entirely characterized by the spectral densities introduced in Section 2.2. This quantity is defined by the density of states of the solvent weighted by the respective coupling strength for the considered mode. Eqn. (14) assumes the validity of a harmonic description of the solvent. Although real solvents are harmonic only under some limiting conditions, e.g., on a short time scale,51 the actual influence of the solvent can often be mapped onto that of an effective harmonic bath. This can be shown, for instance, by considering a second-order cumulant expansion of the influence functional within the path integral formalism.47 This so-called linear response treatment is possible for an arbitrary nonlinear solvent provided that quantum effects can be neglected and that the system–bath coupling is not solvent mode specific, i.e. there is a uniform distribution of coupling strengths over a large number of solvent modes. In the present context these conditions are most likely fulfilled for the low-frequency mode νlow. The respective correlation function for the low-frequency mode in eqn. (13) then reads47C(I)low(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) π(1 π(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n(ω))[J(eff)low(ω) n(ω))[J(eff)low(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J(eff)low(−ω)] J(eff)low(−ω)] | (15) |
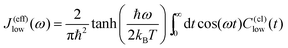 | (16) |
On the other hand, it is common practice to assume the validity of an effective harmonic bath description and to use a model spectral density within a fully quantum mechanical formulation. For the case of a rather unspecific low-frequency solvent environment the Ohmic spectral density with a cut-off frequency ω(…)c is widely used,50,54i.e.
ω2j(…)(ω)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ(ω)ωexp(−ω/ω(…)c) Θ(ω)ωexp(−ω/ω(…)c) | (17) |
3 Numerical results
3.1 System–bath interaction
Our relaxation model is characterized by twelve parameters, i.e. the nine coupling strengths g(…)i, the scaling factor for pure dephasing γpd, and the two cut-off frequencies ω(I)c and ω(III)c. From the experiment15,17 it is known that (i) the OD stretching vibration relaxes within 400 fs, (ii) the dephasing time for the OH vibration in the normal species PMME-H is about 40 fs (iii) the observed low-frequency wave packet dynamics is subject to a dephasing on a timescale of 600 fs, and (iv) the overall vibrational cooling takes place in about 20 ps. In addition one has the linear IR absorption spectrum which shows two distinct peaks in the OD stretching region.In ref. 24 it has been demonstrated that these experimental observations can be reasonably reproduced by the present model. Particularly it should be emphasized that the available parameter space is considerably reduced by the fact that each term in HSB has a distinct influence on the relaxation and dephasing rates for a given system mode. According to our model the IR spectrum in the OD stretch region is influenced by a Fermi resonance between the νs fundamental and the νb overtone transition (see Fig. 3 below). Its line width is mostly determined by the pure dephasing and the dephasing coming from the fourth-order coupling acting on the νs and νb modes. The relative importance of these dephasing channels can be scrutinized by the requirement for a 400 fs population relaxation time for the νs excitation. This in turn gives a dephasing time of about 100 fs for the νs 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 coherence.
1 coherence.
The situation is a little more complicated for the dynamics of the low-frequency mode. In ref. 24 we have assumed that the equilibration of νlow proceeds on a time scale longer than 10 ps, i.e. it is related to the vibrational cooling time of 20 ps observed in the experiment. The 600 fs dephasing time for this mode therefore is coming from the pure dephasing term only. However, in the light of our previous investigations22 one might argue that on a picosecond time scale intramolecular vibrational energy redistribution processes take place which are not captured by the present model for the system–bath interaction. In order to obtain a time scale for the population relaxation of the low-frequency mode due to the interaction with the solvent we have performed a classical molecular dynamics calculation of PMME-D in CCl4 solution at room temperature.†
A single PMME-D molecule frozen at its equilibrium geometry was put into a periodically continued simulation box containing 724 CCl4 molecules such that the solvent density at room temperature (1.5833 g ml−1) is reproduced. All calculations have been performed using GROMACS 2.0.55,56 The GROMACS force field is taken for the solute–solvent interactions and the intramolecular solvent dynamics. Electrostatic interactions are not considered. Also the relaxation due to Coriolis and centrifugal coupling is neglected. They have been shown to give a small contribution for HOD in D2O,29i.e. their effect should be negligible for the much heavier PMME-D. After a 6 ps equilibration of the solvent, a 1 ns production run was performed from which the components of the forces on the solute atoms, Fn(t), are obtained. Given the normal mode transformation matrix U the force on the ith mode can be obtained from 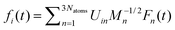 where the Mn are the respective masses (see also ref. 29).
where the Mn are the respective masses (see also ref. 29).
From these data the spectral density of the effective harmonic bath can be determined according to eqn. (16). The result is shown in Fig. 2 for the low-frequency region. Here J(eff)low(ω) is compared with an Ohmic spectral density (eqn. (17)) having a cut-off frequency of ωc/2πc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 cm−1. The spectral densities are rather similar, with the notable exception that J(eff)low has a small shoulder around 200 cm−1 which is due to an intramolecular CCl4 vibration.‡ As indicated by the arrow in Fig. 2 the relaxation of the νlow mode does not involve a direct excitation of this solvent mode. Having J(eff)low one can calculate state-to-state relaxation rates from kab
50 cm−1. The spectral densities are rather similar, with the notable exception that J(eff)low has a small shoulder around 200 cm−1 which is due to an intramolecular CCl4 vibration.‡ As indicated by the arrow in Fig. 2 the relaxation of the νlow mode does not involve a direct excitation of this solvent mode. Having J(eff)low one can calculate state-to-state relaxation rates from kab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2Γab,ba(ωab). For the transition between the two lowest states, |a
2Γab,ba(ωab). For the transition between the two lowest states, |a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2〉
2〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |b
|b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1〉, which are almost pure zero-order states of νlow one obtains 1/k21
1〉, which are almost pure zero-order states of νlow one obtains 1/k21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.67 ps, a value which is substantially shorter than the observed vibrational cooling time.
1.67 ps, a value which is substantially shorter than the observed vibrational cooling time.
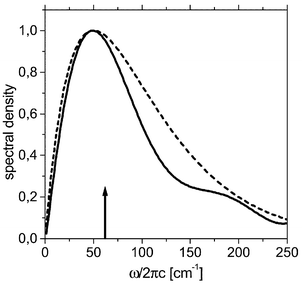 | ||
Fig. 2 Normalized spectral density for the interaction between the solvent and the low-frequency system mode νlow; solid-molecular dynamics result (eqn. (16), smoothed for visual clarity), dashed-Ohmic form with ω(I)c/2πc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 cm−1
(eqn. (17)). The arrow indicates the value of the transition frequency where the spectral density is “probed”. 50 cm−1
(eqn. (17)). The arrow indicates the value of the transition frequency where the spectral density is “probed”. | ||
It has already been emphasized that J(eff)low is close to the Ohmic spectral density in the range around 65 cm−1 which is relevant for the νlow relaxation. Therefore we will stay with the Ohmic form, eqn. (17) for all relaxation processes as in ref. 24. However, the parameters given in ref. 24 will be slightly modified to be conform with the present findings. Specifically, we chose ω(I)c/2πc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 cm−1 and g(I)i
50 cm−1 and g(I)i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.042 which reproduces the |2〉
0.042 which reproduces the |2〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |1〉 relaxation rate of the molecular dynamics simulation. In addition, the scaling parameter for the pure dephasing γpd is chosen as 0.5 s−1 instead of 0.6 s−124 in order to have a 500–600 fs dephasing time for the excited low-frequency oscillations. These parameter changes have only a small influence on the relaxation of the Qs and Qb modes, which is dominated by the (unchanged) fourth-order coupling.
|1〉 relaxation rate of the molecular dynamics simulation. In addition, the scaling parameter for the pure dephasing γpd is chosen as 0.5 s−1 instead of 0.6 s−124 in order to have a 500–600 fs dephasing time for the excited low-frequency oscillations. These parameter changes have only a small influence on the relaxation of the Qs and Qb modes, which is dominated by the (unchanged) fourth-order coupling.
3.2 Diabatic state dynamics
The time evolution of the relevant system is conveniently followed employing a diabatic state representation of the Hamiltonian Hsys which disentangles the information contained in the eigenstates. A suitable diabatic basis includes the two high-frequency vibrations νs and νb, i.e.[Ts![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Tb Tb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V(Qs,Qb,Qlow V(Qs,Qb,Qlow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0)]|ϕm〉 0)]|ϕm〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Em|ϕm〉 Em|ϕm〉 | (18) |
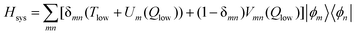 | (19) |
Um(Qlow)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Em Em![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈ϕm|Vsys({Qi}) 〈ϕm|Vsys({Qi})![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V(Qs,Qb,Qlow V(Qs,Qb,Qlow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0)|ϕm〉 0)|ϕm〉 | (20) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈ϕm|Vsys({Qi})
〈ϕm|Vsys({Qi})![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V(Qs,Qb,Qlow
V(Qs,Qb,Qlow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0)|ϕn〉. This figure also nicely illustrates the analogy to the treatment of electron-vibrational problems in optical spectroscopy. Stressing this point, the diabatic state populations and the vibrational dynamics along Qlow should be reflected in the IR pump–probe measurements (see, also ref. 15).
0)|ϕn〉. This figure also nicely illustrates the analogy to the treatment of electron-vibrational problems in optical spectroscopy. Stressing this point, the diabatic state populations and the vibrational dynamics along Qlow should be reflected in the IR pump–probe measurements (see, also ref. 15).
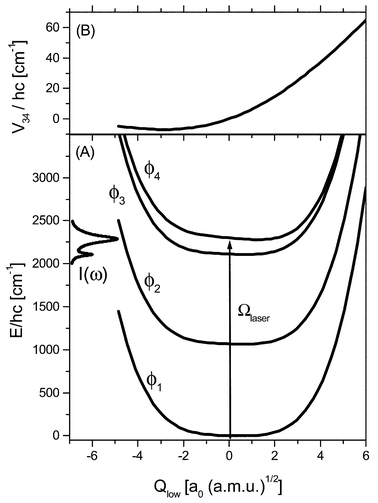 | ||
Fig. 3 Diabatic potential curves (A) and diabatic state coupling (B) along the low-frequency system coordinate Qlow. In the left part of panel (A) the IR absorption spectrum, I(ω), in the OD stretch region is shown (for a detailed discussion see ref. 24). The parameters of the relaxation model are: g(I)i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.042, g(II)s 0.042, g(II)s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005, g(II)b,low 0.005, g(II)b,low![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0001, γpd 0.0001, γpd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5 s−1, g(III)i 0.5 s−1, g(III)i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.02, ω(I)c/2πc 0.02, ω(I)c/2πc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 cm−1, and ω(III)c/2πc 50 cm−1, and ω(III)c/2πc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1. 250 cm−1. | ||
In ref. 24 it has been shown that the linear IR absorption spectrum in the OD-stretching region is dominated by a Fermi-resonance with the bending overtone transition. In terms of the present diabatic basis this is reflected in the fact that upon expansion in zero-order states as
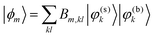 | (21) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∝
∝![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.32|φ(s)1〉|φ(b)0〉
−0.32|φ(s)1〉|φ(b)0〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.94|φ(s)0〉|ε(b)2〉 and |ϕ4〉
0.94|φ(s)0〉|ε(b)2〉 and |ϕ4〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∝
∝![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.94|φ(s)1〉|φ(b)0〉
0.94|φ(s)1〉|φ(b)0〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.32|φ(s)0〉|φ(b)2〉. In addition the diabatic states |ϕ3〉 and |ϕ4〉 are coupled with a strength depending on the value of the low-frequency coordinate, see Fig. 3B. In the energy representation of Hsys
(cf. Table 2 of ref. 24) this coupling is manifested in the various combination transitions contributing to the IR line shape of Fig. 3A.
0.32|φ(s)0〉|φ(b)2〉. In addition the diabatic states |ϕ3〉 and |ϕ4〉 are coupled with a strength depending on the value of the low-frequency coordinate, see Fig. 3B. In the energy representation of Hsys
(cf. Table 2 of ref. 24) this coupling is manifested in the various combination transitions contributing to the IR line shape of Fig. 3A.
The vibrational states of the low-frequency mode pertaining to a particular diabatic state |ϕm〉, i.e. the set {|χMm〉} can be obtained from diagonalization of the Hamiltonian Tlow![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Um(Qlow) which is conveniently done by expansion in the zero-order basis {|φ(low)k〉}, i.e.
Um(Qlow) which is conveniently done by expansion in the zero-order basis {|φ(low)k〉}, i.e.
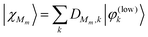 | (22) |
The propagation of the reduced density matrix is performed in the energy representation of the total system Hamiltonian, {|a〉}. For an analysis in terms of the more intuitive diabatic states one needs the diabatic representation of ρ, i.e.ρmMm,nNn, which is readily obtained from ρab using the transformation
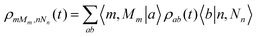 | (23) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |ϕm〉|χMm〉 and for the transformation matrix one has
|ϕm〉|χMm〉 and for the transformation matrix one has 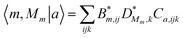 | (24) |
The equations of motion for the reduced density matrix have been solved using the Runge–Kutta–Verner fifth and sixth-order method with adaptive step size control. Following ref. 24 we invoked the Bloch approximation, where the dynamics of populations and coherences is decoupled;50 see Section 3.3. All 57 eigenstates up to a transition frequency of 3000 cm−1 have been included in the propagation. In Fig. 4 we have shown the diabatic state populations, Pm(t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∑MmρmMm,mMm(t) after resonant excitation of the νs dominated absorption peak at 2288 cm−1 with a laser field having a Gaussian envelope of width 130 fs and being centered at t
∑MmρmMm,mMm(t) after resonant excitation of the νs dominated absorption peak at 2288 cm−1 with a laser field having a Gaussian envelope of width 130 fs and being centered at t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 fs (see Fig. 3A). For this excitation condition the bending type diabatic state |ϕ3〉 is only marginally excited via those νlow states which overlap with the potential curve U4(Qlow). In the dissipation-free case, Fig. 4(A), there is a coherent flow of population between the stretching fundamental and the bending overtone states |ϕ4〉 and |ϕ3〉, respectively. The relatively long time required for maximum population transfer reflects the average state coupling as well as the excitation conditions. There is no noticeable population of the state |ϕ2〉
(bending fundamental). Switching on the system–bath interaction changes the situation dramatically, see Fig. 4(B). The fourth-order coupling causes a rapid relaxation of the |ϕ4〉 population back to |ϕ1〉. Note that the time scale for the relaxation of the diabatic state population P4(t) is about 340 fs, i.e. a little shorter than the overall relaxation time of the excited stretching and bending type eigenstates which is 400 fs.24 In the diabatic picture the linear system–bath coupling leads to a population transfer between |ϕ4〉 and the bending overtone state |ϕ3〉 as seen in Fig. 4(B). The relaxation of the latter back to the ground state is slower by a factor of about two. It should be noticed that also the bending fundamental state |ϕ2〉 is somewhat populated due to relaxation. It has, however, a small population already in the initial equilibrium state due to a mixing with the overall eigenstates.
0 fs (see Fig. 3A). For this excitation condition the bending type diabatic state |ϕ3〉 is only marginally excited via those νlow states which overlap with the potential curve U4(Qlow). In the dissipation-free case, Fig. 4(A), there is a coherent flow of population between the stretching fundamental and the bending overtone states |ϕ4〉 and |ϕ3〉, respectively. The relatively long time required for maximum population transfer reflects the average state coupling as well as the excitation conditions. There is no noticeable population of the state |ϕ2〉
(bending fundamental). Switching on the system–bath interaction changes the situation dramatically, see Fig. 4(B). The fourth-order coupling causes a rapid relaxation of the |ϕ4〉 population back to |ϕ1〉. Note that the time scale for the relaxation of the diabatic state population P4(t) is about 340 fs, i.e. a little shorter than the overall relaxation time of the excited stretching and bending type eigenstates which is 400 fs.24 In the diabatic picture the linear system–bath coupling leads to a population transfer between |ϕ4〉 and the bending overtone state |ϕ3〉 as seen in Fig. 4(B). The relaxation of the latter back to the ground state is slower by a factor of about two. It should be noticed that also the bending fundamental state |ϕ2〉 is somewhat populated due to relaxation. It has, however, a small population already in the initial equilibrium state due to a mixing with the overall eigenstates.
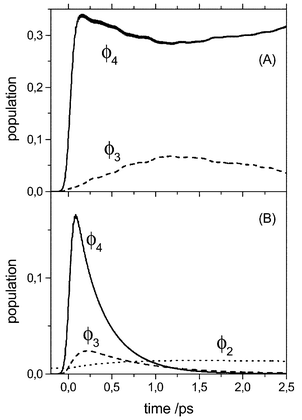 | ||
Fig. 4 Diabatic state populations after excitation with a laser field having a Gaussian envelope of width 130 fs and being centered at t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 fs. The excitation is resonant with the main νs dominated absorption peak at 2288 cm−1 and the field strength is taken as 0.001 Eh/(ea0√amu). Panel (A) and (B) correspond to the coherent and dissipative evolution, respectively, using the parameters given in Fig. 3. 0 fs. The excitation is resonant with the main νs dominated absorption peak at 2288 cm−1 and the field strength is taken as 0.001 Eh/(ea0√amu). Panel (A) and (B) correspond to the coherent and dissipative evolution, respectively, using the parameters given in Fig. 3. | ||
A more detailed look at the dynamics in the diabatic potentials can be obtained from the wave packets with respect to the low-frequency mode. They are obtained from
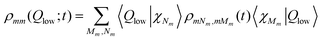 | (25) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4〉 and |3,M3
4〉 and |3,M3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5〉. In the dissipative case (Fig. 5D) essentially only these two states are substantially populated. However, this population starts to emerge already during the action of the laser pulse, i.e. in the diabatic state picture it is mostly due to interstate relaxation. Subsequently, the |ϕ3〉 wave packet is depleted due to the fourth-order relaxation back to the ground state |ϕ1〉.
5〉. In the dissipative case (Fig. 5D) essentially only these two states are substantially populated. However, this population starts to emerge already during the action of the laser pulse, i.e. in the diabatic state picture it is mostly due to interstate relaxation. Subsequently, the |ϕ3〉 wave packet is depleted due to the fourth-order relaxation back to the ground state |ϕ1〉.
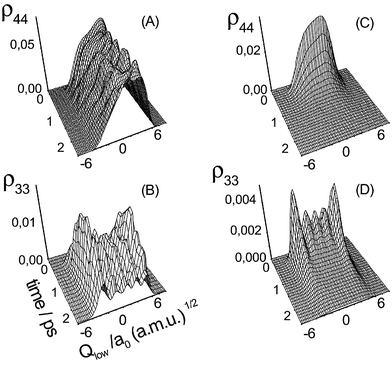 | ||
| Fig. 5 Diabatic state wave packet dynamics along the low-frequency mode according to eqn. (25) ((A) and (B) coherent limit, (C) and (D) dissipative limit). (Note that the grid along the time axis is wider in panel (C) for visual clarity.) | ||
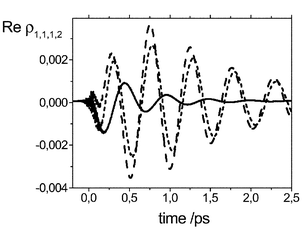 | ||
| Fig. 6 Time evolution of the coherence density matrix element ρ1,1,1,2 obtained using the Bloch (solid), secular (long dashed), and full (short dashed) Redfield theory. | ||
3.3 Beyond the Bloch limit
The Redfield equations of motion are commonly used in three limits: full Redfield tensor, secular and Bloch approximation. The Bloch limit discussed so far provides a convenient way for simulating the laser-driven dissipative dynamics of PMME-D. As already indicated the Bloch approximation implies a decoupling between coherence and population dynamics, i.e. ∑cdRab,cdρcd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1
(1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δab)Rab,abρab
δab)Rab,abρab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δab∑cRaa,ccρcc. It follows as an additional simplification of the Redfield equations in secular approximation.50 In the latter it is assumed that the actual relaxation dynamics of the relevant system is much slower than the time scale given by |ωab
δab∑cRaa,ccρcc. It follows as an additional simplification of the Redfield equations in secular approximation.50 In the latter it is assumed that the actual relaxation dynamics of the relevant system is much slower than the time scale given by |ωab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωcd|−1. In secular approximation the elements of Rab,cd of those pairs of transitions for which ωab
ωcd|−1. In secular approximation the elements of Rab,cd of those pairs of transitions for which ωab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωcd
ωcd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≠
≠![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 holds are neglected. Apparently, this condition is fulfilled for the Bloch limit. However, it can also hold, e.g., for systems having almost harmonic potentials. In such a case bath-induced coherence transfer, ρab
0 holds are neglected. Apparently, this condition is fulfilled for the Bloch limit. However, it can also hold, e.g., for systems having almost harmonic potentials. In such a case bath-induced coherence transfer, ρab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρcd, becomes possible (see, e.g., refs. 57 and 58. Beyond the secular approximation the conversion of populations into coherences, ρaa
ρcd, becomes possible (see, e.g., refs. 57 and 58. Beyond the secular approximation the conversion of populations into coherences, ρaa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρcd, and vice versa becomes possible as well (see, e.g., ref. 59). In passing we note that an intuitive phase-space picture of the effect of the secular approximation has been given by Tannor and co-workers in ref. 60.
ρcd, and vice versa becomes possible as well (see, e.g., ref. 59). In passing we note that an intuitive phase-space picture of the effect of the secular approximation has been given by Tannor and co-workers in ref. 60.
In order to study the dynamics beyond the Bloch approximation in the present case we have solved the full as well as the secular Redfield equations using the same parameters as before. Because the present system is sufficiently anharmonic such that there is no exact degeneracy between pairs of transitions we have used the criteria that |ωab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωcd|/2πc
ωcd|/2πc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 cm−1 for the secular limit. We find that the overall relaxation dynamics of P4(t) is somewhat accelerated as compared to the Bloch case. There is no noticeable difference between the secular and the full Redfield dynamics for this quantity. A more drastic influence, however, is observed for the dynamics of the coherences and here in particular for the diabatic ground state |ϕ1〉. This is conveniently illustrated by the matrix elements ρ1M1,1N1(t) which are responsible for nuclear wave packet motion along Qlow in state |ϕ1〉. In Fig. 6 we compare ρ1,1,1,2(t) for the full and approximate Redfield dynamics. Overall the magnitude of the coherence is much larger and the dephasing time is much longer when going beyond the Bloch limit. Apparently, this is due to the bath-induced coherence transfer, e.g., from the pair of diabatic states |4,2〉–|4,1〉 to |1,2〉–|1,1〉. Switching to the eigenstate picture the states having the largest overlap with these diabatic states obey |ωab
10 cm−1 for the secular limit. We find that the overall relaxation dynamics of P4(t) is somewhat accelerated as compared to the Bloch case. There is no noticeable difference between the secular and the full Redfield dynamics for this quantity. A more drastic influence, however, is observed for the dynamics of the coherences and here in particular for the diabatic ground state |ϕ1〉. This is conveniently illustrated by the matrix elements ρ1M1,1N1(t) which are responsible for nuclear wave packet motion along Qlow in state |ϕ1〉. In Fig. 6 we compare ρ1,1,1,2(t) for the full and approximate Redfield dynamics. Overall the magnitude of the coherence is much larger and the dephasing time is much longer when going beyond the Bloch limit. Apparently, this is due to the bath-induced coherence transfer, e.g., from the pair of diabatic states |4,2〉–|4,1〉 to |1,2〉–|1,1〉. Switching to the eigenstate picture the states having the largest overlap with these diabatic states obey |ωab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωcd|/2πc
ωcd|/2πc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 cm−1, which corresponds to a time scale much longer than the relaxation time of |ϕ4〉. In addition the respective matrix element of the Redfield tensor yields a time constant of 375 fs for the coherence transfer. In other words, this type of coherence transfer is likely to play a role in the present model of PMME-D. Comparing the secular approximation with the full Redfield result we notice that nonsecular contributions have an influence on the coherence dynamics as well. Here the ∼400 fs |ϕ4〉
2 cm−1, which corresponds to a time scale much longer than the relaxation time of |ϕ4〉. In addition the respective matrix element of the Redfield tensor yields a time constant of 375 fs for the coherence transfer. In other words, this type of coherence transfer is likely to play a role in the present model of PMME-D. Comparing the secular approximation with the full Redfield result we notice that nonsecular contributions have an influence on the coherence dynamics as well. Here the ∼400 fs |ϕ4〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |ϕ1〉 relaxation time competes with the time scale of ∼500 fs set by the difference |ωab
|ϕ1〉 relaxation time competes with the time scale of ∼500 fs set by the difference |ωab![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωcd|/2πc
ωcd|/2πc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 cm−1 for transitions, e.g., between the diabatic state pairs |4,1〉–|4,1〉 and |1,2〉–|1,1〉. However, the time scale for this conversion from a population to a coherence in terms of the respective Redfield tensor element is with about 1.4 ps much longer.
65 cm−1 for transitions, e.g., between the diabatic state pairs |4,1〉–|4,1〉 and |1,2〉–|1,1〉. However, the time scale for this conversion from a population to a coherence in terms of the respective Redfield tensor element is with about 1.4 ps much longer.
Finally, it should be emphasized that the experimental dephasing time for the low-frequency wave packet motion is about 600 fs. The results from this section demonstrate that bath-induced coherence transfer is an important part of the overall dynamics. Of course, in order to establish the relation between the full Redfield dynamics and the experiment would require to modify the parameter set entering our model. Because the population dynamics of the excited diabatic states is only slightly affected by non-Bloch terms, it is primarily the pure dephasing contribution for the low-frequency mode which would become more important in a revised parameter set.
4 Conclusions
The theoretical simulation of condensed phase intramolecular ultrafast H-bond dynamics demands for the combination of methods from quantum chemistry, molecular dynamics, and nonequilibrium statistical mechanics. This high level of description appears to be adequate to match the insight provided by current infrared nonlinear spectroscopies. For the specific example of carboxy-deuterated o-phthalic acid monomethylester we have shown that experimentally observed time scales and phenomena can not only be reproduced, but also related to microscopic processes involving nuclear wave packet motion accompanied by energy and phase relaxation. In the present contribution we have extended our previous model24 to account more accurately for the spectral density describing the interaction between the low-frequency mode modulating the strength of the H-bond and the solvent environment. As a result of a classical molecular dynamics simulation the relaxation time for this mode was determined to be about 1.7 ps. Therefore, it can be concluded that the vibrational cooling which is observed on a 20 ps time scale most likely involves many intramolecular degrees of freedom, in accord with our previous gas phase simulations.22 Thus, the applicability of the present model is limited to ultrafast processes as they occur immediately after laser excitation, i.e. approximately during the first 2 ps.The dynamics triggered by the laser field is conveniently analyzed in terms of a diabatic representation with respect to the fast stretching and bending modes. This picture facilitates an intuitive illustration of nuclear wave packet motion of the low-frequency coordinate. In the dissipation-free limit, the diabatic state coupling leads to a coherent flow of population between the stretching fundamental and bending overtone state on a time scale of 1–2 ps. Thus, the wave packet motion takes place on both potentials. Switching on the interaction with the bath leads to a rapid (∼400 fs) decay of the excited diabatic state populations and the wave packet motion occurs in the diabatic ground state. Here it dephases with a time constant of 500–600 fs. In this respect we have shown that, in principle, in the course of the excited state relaxation bath-induced coherence transfer and a conversion of populations into coherences can contribute to the ground state wave packet dynamics.
The present choice of expressing the relevant system potential in terms of normal mode coordinates relies on the fact that the H-bond in PMME-D is of moderate strength, i.e. there is no possibility for proton transfer. The theoretical description of proton transfer reactions, of course, requires the use of large amplitude coordinates at least for the moving proton. This can be achieved, for instance, by using a reaction surface description. Recently we have shown that an all-Cartesian formulation provides a convenient way for establishing a system–bath Hamiltonian and for identifying the contribution of specific intramolecular degrees of freedom to dephasing and relaxation rates.61 Combined with a linear response treatment of the interaction with the solvent this approach should allow for a realistic simulation of the IR spectroscopy of proton transfer systems.
Acknowledgements
This work has been supported by the Deutsche Forschungsgemeinschaft through the Sfb450 and by the Fonds der Chemischen Industrie (O.K.). The authors gratefully acknowledge stimulating discussions with J. Dreyer, T. Elsaesser, and E. Nibbering from the Max Born Institute Berlin.References
- H. Graener, G. Seifert and A. Laubereau, Phys. Rev. Lett., 1991, 66, 2092 CrossRef CAS.
- S. Woutersen, U. Emmerichs and H. J. Bakker, Nature, 1997, 278, 658 CrossRef CAS.
- S. Bratos and A. Laubereau, in Theoretical Treatments of Hydrogen Bonding, ed. D. Hadži, John Wiley, Chichester, 1997, p. 187 Search PubMed.
- G. M. Gale, G. Gallot, F. Hache, N. Lascoux, S. Bratos and J.-C. Leicknam, Phys. Rev. Lett., 1999, 82, 1068 CrossRef CAS.
- J. C. Deak, S. T. Rhea, L. K. Iwaki and D. D. Dlott, J. Phys. Chem. A, 2000, 104, 4866 CrossRef CAS.
- J. Stenger, D. Madsen, P. Hamm, E. T. J. Nibbering and T. Elsaesser, Phys. Rev. Lett., 2001, 87, 2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7401 CrossRef CAS.
7401 CrossRef CAS. - J. Stenger, D. Madsen, P. Hamm, E. T. J. Nibbering and T. Elsaesser, J. Phys. Chem. A, 2002, 106, 2341 CrossRef CAS.
- H. J. Bakker and H. K. Nienhuys, Science, 2002, 297, 587 CrossRef CAS.
- Y. Marechal and A. Witkowski, J. Chem. Phys., 1968, 48, 3697 CrossRef CAS.
- O. Henri-Rousseau and P. Blaise, Adv. Chem. Phys., 1998, 103, 1 Search PubMed.
- A. Witkowski and M. Wójcik, Chem. Phys., 1973, 1, 9 CrossRef CAS.
- S. Bratos, J. Chem. Phys., 1975, 63, 3499 CrossRef CAS.
- O. Henri-Rousseau, P. Blaise and D. Chamma, Adv. Chem. Phys., 2002, 121, 241 Search PubMed.
- J. Stenger, D. Madsen, J. Dreyer, E. T. J. Nibbering, P. Hamm and T. Elsaesser, in Ultrafast Phenomena XII, Springer Series in Chemical Physics, ed. T. Elsaesser, S. Mukamel, M. Murnane and N. Scherer, Springer, New York, 2000, p. 542 Search PubMed.
- J. Stenger, D. Madsen, J. Dreyer, E. T. J. Nibbering, P. Hamm and T. Elsaesser, J. Phys. Chem. A, 2001, 105, 2929 CrossRef CAS.
- D. Madsen, J. Stenger, J. Dreyer, E. T. J. Nibbering, P. Hamm and T. Elsaesser, Chem. Phys. Lett., 2001, 341, 56 CrossRef CAS.
- J. Stenger, D. Madsen, J. Dreyer, P. Hamm, E. T. J. Nibbering and T. Elsaesser, Chem. Phys. Lett., 2002, 354, 256 CrossRef CAS.
- D. Madsen, J. Stenger, J. Dreyer, P. Hamm, E. T. J. Nibbering and T. Elsaesser, Bull. Chem. Soc. Jpn., 2002, 75, 909 CrossRef CAS.
- B. A. Ruf and W. H. Miller, J. Chem. Soc., Faraday Trans. 2, 1988, 84, 1523 RSC.
- H. Naundorf, J. A. Organero, A. Douhal and O. Kühn, J. Chem. Phys., 1999, 110, 11
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 286 CrossRef CAS.
286 CrossRef CAS. - G. K. Paramonov, H. Naundorf and O. Kühn, Eur. J. Phys. D, 2001, 14, 205 Search PubMed.
- H. Naundorf, G. A. Worth, H.-D. Meyer and O. Kühn, J. Phys. Chem. A, 2002, 106, 719 CrossRef CAS.
- H. Naundorf and O. Kühn, in Femtochemistry and Femtobiology, eds. A. Douhal and J. Santamaria, World Scientific, Singapore, 2002, p. 438 Search PubMed.
- O. Kühn, J. Phys. Chem. A, 2002, 106, 7671 CrossRef.
- N. Rösch and M. A. Ratner, J. Chem. Phys., 1974, 61, 3344 CrossRef.
- B. Boulil, O. Henri-Rousseau and P. Blaise, Chem. Phys., 1988, 126, 263 CrossRef CAS.
- B. Boulil, J.-L. Dejardin, N. E. Ghandour and O. Henri-Rousseau, J. Mol. Struct. (THEOCHEM), 1994, 314, 83 CrossRef.
- G. N. Robertson and J. Yarwood, Chem. Phys., 1978, 32, 267 CrossRef CAS.
- R. Rey and J. T. Hynes, J. Chem. Phys., 1996, 104, 2356 CrossRef CAS.
- J. T. Hynes and R. Rey, in Ultrafast Infrared and Raman Spectroscopy, ed. M. D. Fayer, Marcel Dekker, New York, 2001, p. 593 Search PubMed.
- C. P. Lawrence and J. L. Skinner, J. Chem. Phys., 2002, 117, 5827 CrossRef CAS.
- V. M. Kenkre, A. Tokmakoff and M. D. Fayer, J. Chem. Phys., 1994, 101, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 618 CrossRef CAS.
618 CrossRef CAS. - A. Tokmakoff, B. Sauter and M. D. Fayer, J. Chem. Phys., 1994, 100, 9035 CrossRef CAS.
- S. A. Egorov and J. L. Skinner, J. Chem. Phys., 2000, 112, 275 CrossRef CAS.
- D. W. Oxtoby, Adv. Chem. Phys., 1981, 47, 487 Search PubMed.
- J. C. Owrutsky, D. Raftery and R. M. Hochstrasser, Annu. Rev. Phys. Chem., 1994, 45, 519 CrossRef CAS.
- R. Zwanzig, J. Chem. Phys., 1961, 34, 1931 CrossRef CAS.
- R. M. Withnell, K. R. Wilson and J. T. Hynes, J. Phys. Chem., 1990, 94, 8625 CrossRef CAS.
- M. Bruehl and J. T. Hynes, Chem. Phys., 1993, 175, 205 CrossRef CAS.
- S. Gnanakaran and R. M. Hochstrasser, J. Chem. Phys., 1996, 105, 3486 CrossRef CAS.
- S. A. Egorov and J. L. Skinner, J. Chem. Phys., 1996, 105, 7047 CrossRef CAS.
- F. E. Figueirido and R. M. Levy, J. Chem. Phys., 1992, 97, 703 CrossRef CAS.
- H. Gai and G. A. Voth, J. Chem. Phys., 1993, 99, 740 CrossRef CAS.
- J. S. Bader and B. J. Berne, J. Chem. Phys., 1994, 100, 8359 CrossRef CAS.
- S. A. Egorov and B. J. Berne, J. Chem. Phys., 1997, 107, 6050 CrossRef CAS.
- S. A. Egorov, K. F. Everitt and J. L. Skinner, J. Phys. Chem. A, 1999, 103, 9494 CrossRef CAS.
- N. Makri, J. Phys. Chem. B, 1999, 103, 2823 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. C. V. G. Zakrzewski, J. A. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 98 (Revision A.7), Gaussian Inc., Pittsburgh, PA, 1998 Search PubMed.
- C. C. Marston and G. G. Balint-Kurti, J. Chem. Phys., 1989, 91, 3571 CrossRef CAS.
- V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH, Berlin, 2000 Search PubMed.
- G. Goodyear and R. M. Stratt, J. Chem. Phys., 1996, 105, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 CrossRef CAS.
050 CrossRef CAS. - D. Reichman, R. J. Silbey and A. Suarez, J. Chem. Phys., 1996, 105, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 CrossRef CAS.
500 CrossRef CAS. - Y. Yan, F. Shuang, R. Xu, J. Cheng, X.-Q. Li, C. Yang and H. Zhang, J. Chem. Phys., 2000, 113, 2068 CrossRef CAS.
- A. J. Leggett, S. Chakravarty, A. T. Dorsey, M. P. A. Fisher, A. Garg and M. Zwerger, Rev. Mod. Phys., 1987, 59, 1 CrossRef CAS.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43 CrossRef CAS.
- D. van der Spoel, A. R. van Buuren, E. Apol, P. J. Meulenhoff, D. P. Tieleman, A. L. T. M. Sijbers, B. Hess, K. A. Feenstra, E. Lindahl, R. van Drunen and H. J. C. Berendsen, Gromacs User Manual version 2.0, Nijenborgh 4, 9747 AG Groningen, The Netherlands, http://md.chem.rug.nl./∼gmx/, 1999 Search PubMed.
- J. M. Jean and G. R. Fleming, J. Chem. Phys., 1995, 103, 2092 CrossRef CAS.
- D. Egorova, A. Kuhl and W. Domcke, Chem. Phys., 2001, 268, 105 CrossRef CAS.
- O. Kühn, V. Sundström and T. Pullerits, Chem. Phys., 2002, 275, 15 CrossRef CAS.
- D. Kohen, C. C. Marston and D. J. Tannor, J. Chem. Phys., 1997, 107, 5236 CrossRef CAS.
- R. Xu, Y.-J. Yan and O. Kühn, Eur. J. Phys. D, 2002, 19, 293 Search PubMed.
Footnotes |
| † Note that the experiment reported in ref. 15 has been performed in C2Cl4 solution. Concerning the main results, however, there is no substantial difference compared to CCl4 (E. T. J. Nibbering, personal communication). |
| ‡ For the isolated CCl4 one obtains this mode at 225 cm−1 (MP2/6-31+G(d,p)). |
| This journal is © the Owner Societies 2003 |
