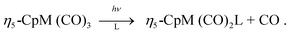Ultrafast non-adiabatic laser-induced photodissociation dynamics of CpMn(CO)3. An ab initio quantum chemical and dynamical study
Jürgen
Full
a,
Chantal
Daniel
*b and
Leticia
González
*a
aInstitut für Chemie-Physikalische und Theoretische Chemie, Freie Universität Berlin, Takustrasse 3, D-14195, Berlin, Germany
bLaboratoire de Chimie Quantique UMR 7551 CNRS/Université Louis Pasteur, Institut Le Bel, 4 Rue Blaise Pascal, 67 000, Strasbourg, France
First published on 20th November 2002
Abstract
The ultrafast laser driven dynamics of CpMn(CO)3, so-called cymantrene, have been investigated by wavepacket propagations on adiabatic coupled CASSCF/MR-CCI potential energy curves calculated for the electronic ground and low-lying metal-centered (MC) excited 1A′ and 1A″ states as a function of one Mn–CO bond elongation. The main features of the absorption spectrum as well as the electronic states populations are investigated by the time-dependent approach including numerical non-adiabatic couplings. The photo-induced simulations use selected laser pulse parameters close to the experimental ones (Daniel et al., Chem. Phys., 2001, 267, 247), where the frequencies correspond to the four main resonant Franck-Condon transitions which can prepare either the parent neutral molecule [CpMn(CO)3]* or the first photofragment [CpMn(CO)2]*.
1. Introduction
The photochemical reactivity of η5-CpM(CO)3 (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn, Re; Cp
Mn, Re; Cp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η5-C5H5) has been widely used in substitution reactions of CO by different nucleophilic ligands L′:
η5-C5H5) has been widely used in substitution reactions of CO by different nucleophilic ligands L′: These organometallics are good precursors of the Si–H bond activation for which a comparative mechanism has been proposed on the basis of femtosecond to nanosecond pump-probe TRIR (time resolved infra-red) experiments completed by ab initio calculations.1 It was found that photolysis of the manganese complex results in dicarbonyl fragments in both the singlet and triplet electronic states, whereas photolysis of the rhenium complex leads only to the singlet dicarbonyl. According to recent time-resolved experiments, the importance of dynamical effects (including solvation) at the early stage of the photolysis of these complexes1 and more generally of transition metal carbonyls2–6 cannot be neglected for the understanding of the primary relaxation and fragmentation processes. These experiments, based on femtosecond pump-probe spectroscopy combined with multi-photon ionization of the electronically excited states, constitute an excellent tool for investigating the fragmentation pattern of the molecule. The detection of unstable, unsaturated species of very short life-time (a few tens to a few hundreds of femtoseconds) used in subsequent catalytic processes, chemical substitutions or polymerisations is one of the many challenging tasks in this field of research. The ultimate goal of these experiments is the femtosecond quantum control of photoprocesses via chemically selective molecular excitation.7 The interplay between theory and experiments in this domain is based on the accurate knowledge of the potential energy surfaces associated with the various electronic excited states populated directly or indirectly during the course of the experiment. The propagation of selected wavepackets on these potentials allows one to determine several important quantities, some of them being directly comparable with the experimental data; including the time scale of the primary reactions occurring after irradiation, the main features of the absorption spectra, the branching ratio between concurrent reactions and the time-scale of intersystem crossing processes.8–10 From a joint theoretical/experimental study11 of the ultra-fast dynamics of electronically excited cymantrene, CpMn(CO)3, we extracted the lifetimes of the parent molecule on several electronic states to produce the fragment CpMn(CO)2. Pump-probe experiments together with preliminary theoretical simulations showed that the loss of this first CO ligand occurs on a time scale of less than 70 fs. Furthermore, the occurrence of a sequential mechanism leading to ion signals CpMn(CO)n+ (n
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3–0) has been demonstrated.
3–0) has been demonstrated.
The findings obtained from this exploratory work and the detailed knowledge of the electronic structure of ground and excited states in cymantrene12 have encouraged us to perform simulations using laser pulses with different frequencies and intensities in a systematic investigation of the behaviour of the molecular system after excitation with the pump pulse. The purpose of this work is to obtain more detailed information about electronically excited unstable intermediate species and to propose new experiments. Furthermore, the different ratios of primary products as a function of the initial electronic excitations and the nature of the observed species detected by the probe pulse will be predicted.
The first aim of the present work is the accurate calculation of the adiabatic potential energy curves associated with the low-lying singlet excited states of CpMn(CO)3 as a function of the “axial” Mn–CO bond elongation using the complete-active space/multireference contracted configuration interaction (CASSCF/MR-CCI) method. Triplet excited states are neglected since the time scale of the intersystem crossing cannot compete with the time scale of dissociation in this particular case. Within this limited one-dimensional model several aspects of the early dynamics (≈100 fs) will be investigated in detail in order to establish a connection between experiments and simulations. One aspect of the study is the determination of the main features of the absorption spectrum. In a second step, laser-induced quantum simulations are performed by propagating selected molecular wavepackets, which are prepared in a domain of energy accessible to the experimental pulses operating at a wavelength of 400 nm. Specifically, we use four different frequencies resonant to the relevant vertical transitions that were determined in our preliminary study devoted to the electronic spectroscopy of cymantrene.12
2. Methodology
Quantum chemistry
The quantum chemical calculations have been performed starting from the Cs staggered conformation of CpMn(CO)3 depicted in Fig. 1 and discussed in ref. 12.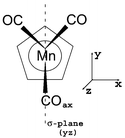 | ||
| Fig. 1 Molecular configuration of CpMn(CO)3 (see ref. 11). | ||
According to recent geometry optimizations performed at the DFT13 level without any symmetry constraints, the CpMn(CO)2 fragment has a geometry very close to Cs;14 it was therefore assumed that the Cs symmetry is retained along the reaction pathway, with the axial CO in the yz plane. The fragment CpMn(CO)2 has been kept frozen in the Franck-Condon geometry. This assumption is justified by the time-scale of the primary photoprocess investigated in the present study, namely the CO loss which occurs within a few tens of femtoseconds.11 Moreover, according to our recent gradient-CASSCF geometry optimizations of the low-lying excited states of CpMn(CO)3,12 the structures of the excited states do not differ significantly from that of the ground state. The elongation of the Mn–CO bond of the in-plane carbonyl is the main deformation accompanied by the opening of the bond angle between the two equatorial out-of-plane CO ligands in c1A′. In the other states, the elongation of the Mn–CO bond does not exceed 10% and the Mn–Cp bond distance is not affected when going from the electronic ground state to the excited states. In this preliminary study, the Mn–CO in-plane bond elongation will be the only degree of freedom taken into consideration. The one-dimensional CASSCF/MR-CCI15,16 potential energy curves V(qa)
(with qa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Mn–COax]) are calculated under the Cs symmetry constraint (Scheme 1).
[Mn–COax]) are calculated under the Cs symmetry constraint (Scheme 1).
 | ||
| Scheme 1 | ||
Because our interest focusses mostly on the metal-centered states of CpMn(CO)3, ten electrons are correlated in fourteen active orbitals including the highest πCp occupied orbitals, the 3dMn occupied orbitals and vacant orbitals, the 3d of correlation and the low-lying π*CO orbitals. Using this active space we have calculated the a1A′ electronic ground state potential associated with the (1πCp)2(3dz2)2(3dx2−y2)2(3dxy)2(2πCp)2(3dxz)0(3dyz)0 electronic configuration plus the b1A′, c1A′, d1A′, e1A′ and a1A″, b1A″, c1A″ and d1A″ potentials which correspond mainly to metal-centered excited states described at the Franck-Condon geometry by single excitations from the 3dMn to the 3dxz and 3dyz orbitals of symmetry a″ and a′, respectively. State-average CASSCF calculations (with equal weights) over 5 roots for 1A′ and 4 roots for 1A″ states were performed to obtain electronic wavefunctions used as references in the subsequent MR-CCI calculations. Single and double excitations to the whole virtual space were included in a multireference scheme keeping as references the configurations with CI coefficients larger than 0.08 in all roots along the complete reaction path.17 The vertical MR-CCI transition energies will be compared to the values reported in our previous work, calculated using multi-state second order perturbation CASPT2 treatment (MS-CASPT2)18 and time-dependent DFT (TD-DFT).19 The electronic transition dipole moments (TDM) were calculated either at the MR–CCI level for the A′ states or at the CASSCF level for the A″ states. MR–CCI and CASSCF results are in reasonable agreement for the A′ states.
The following basis sets were used in the relativistic effective core potential approximation ECP (small core): a (8s,7p,6d,1f) set contracted to [6s,5p,3d,1f]
(effective atomic number Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15.0) for the Mn atom,20 for the oxygen atoms a (4s,5p) set contracted to [2s,3p]
(Z
15.0) for the Mn atom,20 for the oxygen atoms a (4s,5p) set contracted to [2s,3p]
(Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.0)21 and for the carbon atoms a (4s,4p) set contracted to [2s,2p]
(Z
6.0)21 and for the carbon atoms a (4s,4p) set contracted to [2s,2p]
(Z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.0).21 The ANO basis set (7s,3p) contracted to [3s,1p] was used for the H atoms.22 According to a recent study of the electronic spectroscopy of a series of M(R)(CO)3(α-di-imine) complexes (R
4.0).21 The ANO basis set (7s,3p) contracted to [3s,1p] was used for the H atoms.22 According to a recent study of the electronic spectroscopy of a series of M(R)(CO)3(α-di-imine) complexes (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H, ethyl) the effect on the transition energies of d functions on the second row atoms is insignificant.23
H, ethyl) the effect on the transition energies of d functions on the second row atoms is insignificant.23
All the calculations were performed with the Molcas 4.1 quantum chemistry software.24
Quantum dynamics
The simulation of the photodissociation dynamics is based on laser driven molecular wavepackets propagated on the adiabatic ab initio potential energy curves in the non-adiabatic coupling scheme. Specifically, we solve the time dependent Schrödinger equation | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0,...,8) labelled a1A′, b1A′,..., e1A′, a1A″, b1A″, ... .d1A″, respectively.
0,...,8) labelled a1A′, b1A′,..., e1A′, a1A″, b1A″, ... .d1A″, respectively.
The laser coupling is treated in the semi-classical dipole approximation, so that the Hamiltonian Hij is written as:
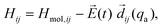 | (2) |
 is the laser field, and
is the laser field, and  are the electronic TDM if i
are the electronic TDM if i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≠
≠![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j, or the dipole moments of the molecule in each electronic potential if i
j, or the dipole moments of the molecule in each electronic potential if i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j. The diagonal Hamiltonian matrix elements of Hmol contain two terms,
j. The diagonal Hamiltonian matrix elements of Hmol contain two terms, Hmol,ii![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Vi(qa). Vi(qa). | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (−ħ2/2μa)(∂2/∂q2a) represents the kinetic energy and Vi(qa) is the adiabatic ab initio potential energy surfaces of each state i. The off-diagonal terms of the molecular Hamiltonian, Hmol,ij, contain the kinetic couplings T(1) and T(2), which govern the non-adiabatic dynamics,
(−ħ2/2μa)(∂2/∂q2a) represents the kinetic energy and Vi(qa) is the adiabatic ab initio potential energy surfaces of each state i. The off-diagonal terms of the molecular Hamiltonian, Hmol,ij, contain the kinetic couplings T(1) and T(2), which govern the non-adiabatic dynamics,  | (4) |
For simplicity, we consider our molecule modelled as a pseudodiatomic with one dissociative bond qa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [Mn–COax]
(cf.Scheme 1) and the remaining degrees of freedom frozen. Therefore, μa, the reduced mass corresponding to the bond qa, is expressed as follows:
[Mn–COax]
(cf.Scheme 1) and the remaining degrees of freedom frozen. Therefore, μa, the reduced mass corresponding to the bond qa, is expressed as follows:
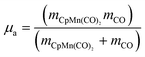 | (5) |
All other “spectator” modes are considered decoupled from qa. This decoupling should be reasonable for ultrafast dissociation time scales (less than 100 fs) as the energy remains in the dissociative bond and intramolecular vibrational redistribution (IVR) can be neglected.
For the initial state (t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0), we assume
0), we assume
|Ψ0(qa,0)〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |Φ0,0(qa)〉, Ψi(qa,0) |Φ0,0(qa)〉, Ψi(qa,0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 i 0 i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≠ ≠![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) in the electronic ground state a1A′
(i
0) in the electronic ground state a1A′
(i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0). The ground state vibrational eigenfunctions Φ0,v of Ψ0(qa) are evaluated using the Fourier grid Hamiltonian method,26 with a spatial discretization of 1024 grid points.
0). The ground state vibrational eigenfunctions Φ0,v of Ψ0(qa) are evaluated using the Fourier grid Hamiltonian method,26 with a spatial discretization of 1024 grid points.
The TDM corresponding to the A′ states contain two components, dy or dz
(dx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 for symmetry reasons). As a consequence, the initial wavepacket will be photoexcited using y- or z-linearly polarized laser pulses. In contrast, the A″ states will be photoexcited using x-polarized laser pulses. The general form of the pulses is given by
0 for symmetry reasons). As a consequence, the initial wavepacket will be photoexcited using y- or z-linearly polarized laser pulses. In contrast, the A″ states will be photoexcited using x-polarized laser pulses. The general form of the pulses is given by
 | (7) |
 , carrier frequency ω and analytical shape function
, carrier frequency ω and analytical shape function  | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) the initial wavefunction Ψi(qa,0) will be proportional to Φ0,0 and to the corresponding component of the transition dipole moment, di0,x, di0,y or di0,z, respectively. In any case, the resulting wavepacket is not a stationary state and will evolve as Ψi(qa,t) according to eqn. (1). The solution of eqn. (1) in the adiabatic representation is obtained using either the split-operator scheme27 with a time discretization of Δt
0) the initial wavefunction Ψi(qa,0) will be proportional to Φ0,0 and to the corresponding component of the transition dipole moment, di0,x, di0,y or di0,z, respectively. In any case, the resulting wavepacket is not a stationary state and will evolve as Ψi(qa,t) according to eqn. (1). The solution of eqn. (1) in the adiabatic representation is obtained using either the split-operator scheme27 with a time discretization of Δt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.02 fs when kinetic couplings are neglected (as a first approximation) or the second-order-differential (SOD) propagation scheme28 with a time step Δt
0.02 fs when kinetic couplings are neglected (as a first approximation) or the second-order-differential (SOD) propagation scheme28 with a time step Δt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.008 fs when non-adiabatic couplings are taken into account. In both cases, the fast Fourier transform (FFT) procedure29 has been employed.
0.008 fs when non-adiabatic couplings are taken into account. In both cases, the fast Fourier transform (FFT) procedure29 has been employed.
The corresponding laser driven population of the vibronic states Φi,v(qa) and the electronic states i are given by
Pi,v(t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |〈Φi,v(qa)|Ψi(qa,t)〉|2, |〈Φi,v(qa)|Ψi(qa,t)〉|2, | (9) |
 | (10) |
The total absorption spectrum, which measures the capability of the molecule to absorb radiation with a frequency ϖ, is obtained from the Fourier transformation of the total autocorrelation function Stot(t) summed over the individual autocorrelation functions corresponding to each of the excited states i, with E0,0 being the energy of the initial vibrational and electronic ground state.30
 | (11) |
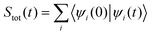 | (12) |
The absorption spectrum σtot(ϖ) is calculated imposing the initial condition at t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 for the excited states i
0 for the excited states i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≠
≠![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0
|Ψi(qa,t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0)〉 0)〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d′i0|Ψ0(qa,0)〉 d′i0|Ψ0(qa,0)〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d′i0|Ψ0,0(qa)〉, d′i0|Ψ0,0(qa)〉, | (13) |
 | (14) |
3. Results and discussion
Theoretical absorption spectrum
According to our recent MS-CASPT2 and TD-DFT calculations, the six low-lying metal-centered states of CpMn(CO)3 range between 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and 30
000 cm−1 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1
(3.13–3.80 eV), of which some are nearly degenerate around the Franck-Condon geometry.12 These states have been assigned to the first absorption band observed in the experimental spectrum between 410 nm and 290 nm (3.02–4.28 eV). The MR-CCI transition energies obtained in this work are reported in Table 1 together with the MS-CASPT2 and TD-DFT values calculated in our previous study. For instance, the b1A′ and c1A′ have been calculated at 25
000 cm−1
(3.13–3.80 eV), of which some are nearly degenerate around the Franck-Condon geometry.12 These states have been assigned to the first absorption band observed in the experimental spectrum between 410 nm and 290 nm (3.02–4.28 eV). The MR-CCI transition energies obtained in this work are reported in Table 1 together with the MS-CASPT2 and TD-DFT values calculated in our previous study. For instance, the b1A′ and c1A′ have been calculated at 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 cm−1 and 26
730 cm−1 and 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 cm−1, respectively at the MS-CASPT2 level (26
470 cm−1, respectively at the MS-CASPT2 level (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 cm−1 and 27
720 cm−1 and 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 cm−1 at the TD-DFT level and 25
240 cm−1 at the TD-DFT level and 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 cm−1 and 28
840 cm−1 and 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 at the MR-CCI level). The overall agreement between the different levels of calculation is satisfactory. The largest deviations between the MR-CCI and MS-CASPT2 values occur for the higher states, c1A″ and d1A′, which are overestimated by the MR-CCI method by ca. 3000 cm−1, in contrast with the MS-CASPT2 and TD-DFT values. In general, the transition energies obtained through the MR-CCI approach are overestimated with respect to the MS-CASPT2 transitions energies. These trends have been observed and discussed for other transition metal complexes.31 It is generally difficult to draw conclusions regarding the relative quality of the two approaches since this depends strongly on the zero-order wavefunction given by the CASSCF calculation. Indeed the reference wavefunction must not fulfil exactly the same criteria for assuring a balanced description of the different excited states depending on whether the remaining electronic correlation is added perturbationally (CASPT2) or variationally (MR-CCI). However, the overall agreement between the different methods validates the use of the MR-CCI method for the computation of the potential energy curves associated with the low-lying singlet excited states which are the only states playing a key role in the ultrafast dynamics.
400 cm−1 at the MR-CCI level). The overall agreement between the different levels of calculation is satisfactory. The largest deviations between the MR-CCI and MS-CASPT2 values occur for the higher states, c1A″ and d1A′, which are overestimated by the MR-CCI method by ca. 3000 cm−1, in contrast with the MS-CASPT2 and TD-DFT values. In general, the transition energies obtained through the MR-CCI approach are overestimated with respect to the MS-CASPT2 transitions energies. These trends have been observed and discussed for other transition metal complexes.31 It is generally difficult to draw conclusions regarding the relative quality of the two approaches since this depends strongly on the zero-order wavefunction given by the CASSCF calculation. Indeed the reference wavefunction must not fulfil exactly the same criteria for assuring a balanced description of the different excited states depending on whether the remaining electronic correlation is added perturbationally (CASPT2) or variationally (MR-CCI). However, the overall agreement between the different methods validates the use of the MR-CCI method for the computation of the potential energy curves associated with the low-lying singlet excited states which are the only states playing a key role in the ultrafast dynamics.
| Transition | MR-CCI | MS-CASPT2 | TD-DFT(B3LYP) |
|---|---|---|---|
a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a1A″ a1A″ |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 (3.13) 040 (3.13) |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970 (3.10) 970 (3.10) |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 (3.15) 200 (3.15) |
a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b1A′ b1A′ |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 (3.23) 840 (3.23) |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 (3.22) 730 (3.22) |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 (3.34) 720 (3.34) |
a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b1A″ b1A″ |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 (3.40) 200 (3.40) |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 020 (3.25) 020 (3.25) |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 (3.38) 040 (3.38) |
a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c1A′ c1A′ |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 (3.55) 400 (3.55) |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 (3.31) 470 (3.31) |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 (3.41) 240 (3.41) |
a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c1A″ c1A″ |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 (4.20) 600 (4.20) |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 (3.71) 950 (3.71) |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 (3.84) 720 (3.84) |
a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d1A′ d1A′ |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 (4.20) 600 (4.20) |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 (3.80) 370 (3.80) |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 960 (3.87) 960 (3.87) |
a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d1A″ d1A″ |
35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 (4.45) 600 (4.45) |
— | — |
According to the accessible domain of the experimental pulses (400 nm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.10 eV) we will concentrate on the lowest part of the spectrum corresponding to the four low-lying electronic states: a1A″, b1A′, b1A″ and c1A′. The kinetic couplings between these states are shown in Fig. 2. As seen, the coupling between the b1A′/c1A′ states is very small in the Franck-Condon (FC) region, qa(FC)
3.10 eV) we will concentrate on the lowest part of the spectrum corresponding to the four low-lying electronic states: a1A″, b1A′, b1A″ and c1A′. The kinetic couplings between these states are shown in Fig. 2. As seen, the coupling between the b1A′/c1A′ states is very small in the Franck-Condon (FC) region, qa(FC)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.85 Å, in comparison with the coupling between the states of A″ symmetry, a1A″/b1A″. Hence, the only dynamics affected by non-adiabatic coupling, as shown in the next section, will be those occurring in the A″ potentials.
1.85 Å, in comparison with the coupling between the states of A″ symmetry, a1A″/b1A″. Hence, the only dynamics affected by non-adiabatic coupling, as shown in the next section, will be those occurring in the A″ potentials.
 | ||
| Fig. 2 T ij (1) and Tij(2) numerical kinetic couplings between the states b1A′/c1A′ in panel (a) and (b), respectively, and between a1A″/b1A″ in panel (c) and (d). | ||
The theoretical absorption spectrum has been calculated using only the four lowest low-lying electronic excited states above mentioned which contribute to the first band of the experimental spectrum32 and for which the MR-CCI method closely resembles the MS-CASPT2 energetics. The resulting simulated spectra with and without (for the sake of comparison) kinetic couplings are shown in Fig. 3 together with the experimental one over the same range of energy (in dashed lines).32 The theoretical spectrum has been obtained by propagation of the initial one-dimensional wavepacket Ψi(qa,t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) prepared on each of the electronically excited potentials as stated in eqn. (13). Application of eqn. (14) for CpMn(CO)3 results in the following initial conditions:
0) prepared on each of the electronically excited potentials as stated in eqn. (13). Application of eqn. (14) for CpMn(CO)3 results in the following initial conditions:
 | (15) |
 | ||
| Fig. 3 Theoretical electronic absorption spectrum for CpMn(CO)3 normalized to 1 (solid line). Dashed line indicates the experimental absorption in solution. Panel (a) excludes kinetic couplings, (b) includes kinetic couplings. | ||
The experimental absorption spectrum exhibits two bands, the first with a maximum around 3.6 eV, the second starting at 4.5 eV. Our theoretical simulation concentrates on the first band (dashed lines) which extends from 3.00 eV to 3.80 eV and shows an intense peak at 3.4 eV, in rather good agreement with the experimental spectrum (by ca. 0.2 eV) according to the level of the calculations (MR-CCI with a limited number of correlated electrons and medium size basis sets). This peak corresponds to the absorption in the b1A″ state which, as shown in the next section, is a bound state. It is interesting to see the strong effects of the non-adiabatic couplings which transfer population from the b1A″![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a1A″ state via internal conversion, broadening and reducing this peak. Thus, since the spectrum is always normalized to one, the following peaks are much more pronounced in the coupled case (cf.Fig. 3b), in better agreement with the experimental spectrum. The upper band, not included in the present simulation, should consist not only of metal-centered excited states corresponding to dMn
a1A″ state via internal conversion, broadening and reducing this peak. Thus, since the spectrum is always normalized to one, the following peaks are much more pronounced in the coupled case (cf.Fig. 3b), in better agreement with the experimental spectrum. The upper band, not included in the present simulation, should consist not only of metal-centered excited states corresponding to dMn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dMn excitations which certainly contribute to the experimental absorption occurring beyond 280 nm (4.5 eV) but also to high-lying metal-to-ligand-charge-transfer excited states calculated between 4.51 eV and 5.58 eV (at the MS-CASPT2 level) and 4.15 eV and 4.98 eV at the TD-DFT level12 and not included in the present MR-CCI computations. In conclusion, the main features of the lowest part of the absorption spectrum of CpMn(CO)3, corresponding to the domain of energy accessible by the experimental pulses (between 3.2 eV and 3.6 eV), have been reproduced in the limit of this one-dimensional approach. The relative error of 0.2 eV is reasonable within the considered methodology and it can be taken as an indication of the quality of the ab initio potentials and the subsequent dynamics presented in the following sections.
dMn excitations which certainly contribute to the experimental absorption occurring beyond 280 nm (4.5 eV) but also to high-lying metal-to-ligand-charge-transfer excited states calculated between 4.51 eV and 5.58 eV (at the MS-CASPT2 level) and 4.15 eV and 4.98 eV at the TD-DFT level12 and not included in the present MR-CCI computations. In conclusion, the main features of the lowest part of the absorption spectrum of CpMn(CO)3, corresponding to the domain of energy accessible by the experimental pulses (between 3.2 eV and 3.6 eV), have been reproduced in the limit of this one-dimensional approach. The relative error of 0.2 eV is reasonable within the considered methodology and it can be taken as an indication of the quality of the ab initio potentials and the subsequent dynamics presented in the following sections.
Potential energy curves
The potential energy curves describing the CO loss in CpMn(CO)3 calculated under the Cs symmetry constraint for the a1A′ electronic ground state and the eight low-lying singlet excited states corresponding mainly to 3dMn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3dMn excitations are represented in Fig. 4. The reaction is calculated to be endothermic by 126.2 kJ mol−1
(1.34 eV). This value is in the range of the calculated values and experimental data available for the metal–carbonyl bond dissociation energy in first-row transition metal carbonyls.33
3dMn excitations are represented in Fig. 4. The reaction is calculated to be endothermic by 126.2 kJ mol−1
(1.34 eV). This value is in the range of the calculated values and experimental data available for the metal–carbonyl bond dissociation energy in first-row transition metal carbonyls.33
 | ||
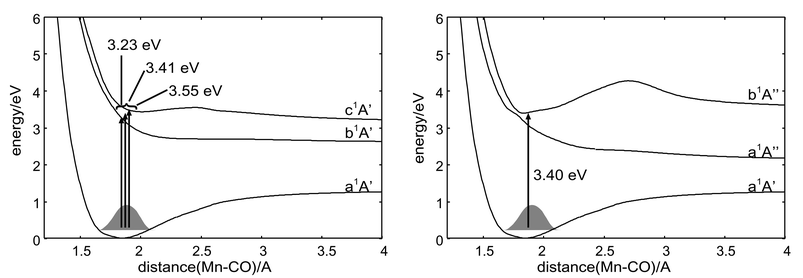
| Fig. 4 CASSCF/MR-CCI adiabatic non-relaxed potential energy curves as a function of the Mn–COax elongation in CpMn(CO)3, computed under Cs symmetry constraint. | ||
The set of potential energy curves depicted in Fig. 4 is characterized by several avoided crossings, two of them around the Franck-Condon geometry between the b1A′ and c1A′ states at ca. 1.70Å and between the a1A″ and b1A″ states at ca. 1.78 Å
(see the maximum of the corresponding kinetic couplings in Fig. 2). Whereas the b1A′ potential appears to be dissociative leading directly to the primary products CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MnCp(CO)2
[b1A′], the c1A′ state presents a small energy barrier around 2.5 Å, due to an avoided crossing with the d1A′ state, which prevents fast and total dissociation. The a1A″ and b1A″ states, which are nearly degenerate around the equilibrium geometry, avoid each other at this point; this leads to one dissociative potential towards the primary products CO
MnCp(CO)2
[b1A′], the c1A′ state presents a small energy barrier around 2.5 Å, due to an avoided crossing with the d1A′ state, which prevents fast and total dissociation. The a1A″ and b1A″ states, which are nearly degenerate around the equilibrium geometry, avoid each other at this point; this leads to one dissociative potential towards the primary products CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MnCp(CO)2
[a1A″] and to a quasi-bound potential which will trap the molecular system. The upper states d1A′, e1A′, c1A″ and d1A″ have been calculated in order to reproduce the main features of the absorption spectrum in the UV energy domain and they are included in the following laser driven wavepackets propagations, with the exception of the state e′A′. The calculated TDM values di0 as a function of the Mn–COax bond elongation are presented in Fig. 5 for the x, y and z components.
MnCp(CO)2
[a1A″] and to a quasi-bound potential which will trap the molecular system. The upper states d1A′, e1A′, c1A″ and d1A″ have been calculated in order to reproduce the main features of the absorption spectrum in the UV energy domain and they are included in the following laser driven wavepackets propagations, with the exception of the state e′A′. The calculated TDM values di0 as a function of the Mn–COax bond elongation are presented in Fig. 5 for the x, y and z components.
 | ||
| Fig. 5 X, Y and Z-components of the CASSCF/MR-CCI adiabatic electronic transition dipole moments in CpMn(CO)3. | ||
Laser-induced wavepacket simulations on adiabatic potentials
First exploratory multiphoton ionization pump and probe experiments on cymantrene were performed using a laser wavelength centered around 400 nm (3.1 eV) for the pump pulse and at 800 nm (1.55 eV) for the probe pulse.11 The goal of the present work is to systematically explore the behaviour of the system after photoexcitation with the first pump pulse. For this purpose we choose the following laser parameters: E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.5 GV m−1 equivalent to I
5.5 GV m−1 equivalent to I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 TW cm−2 for the A′ states and E0
4 TW cm−2 for the A′ states and E0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 GV m−1 and 1.0 GV m−1
(I
2.5 GV m−1 and 1.0 GV m−1
(I![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8 TW cm−2, and 0.1 TW cm−2, respectively) for the A″ states; tp
0.8 TW cm−2, and 0.1 TW cm−2, respectively) for the A″ states; tp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 fs equivalent to ca. 37 fs for full width at half maximum (FWHM) in I; and three different frequencies ħω
100 fs equivalent to ca. 37 fs for full width at half maximum (FWHM) in I; and three different frequencies ħω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.23 eV, 3.55 eV and 3.41 eV, for the simulations on the A′ potentials, and a single frequency, ħω
3.23 eV, 3.55 eV and 3.41 eV, for the simulations on the A′ potentials, and a single frequency, ħω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.40 eV, in the case of simulations on A″ curves. These frequencies correspond to the resonant FC a1A′
3.40 eV, in the case of simulations on A″ curves. These frequencies correspond to the resonant FC a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b1A′, a1A′
b1A′, a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c1A′ transitions, to some intermediate value bringing the molecular system between the b1A′ and c1A′ states, and to the resonant FC a1A′
c1A′ transitions, to some intermediate value bringing the molecular system between the b1A′ and c1A′ states, and to the resonant FC a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b1A″ transition, respectively, all of which are illustrated in Scheme 2. This region should be accessible within an experimental pulse centered around 400 nm. All the simulations have been done including the kinetic couplings, unless otherwise stated.
b1A″ transition, respectively, all of which are illustrated in Scheme 2. This region should be accessible within an experimental pulse centered around 400 nm. All the simulations have been done including the kinetic couplings, unless otherwise stated.
 | ||
| Scheme 2 | ||
The molecule is assumed to be non-rotating and can be photoexcited either with y- or with z-linearly polarized light when excited to the A′ states and with linearly polarized light in the x direction if excited to states of A″ symmetry. Due to the very different behaviour of the TDM around the FC window with dominant components on one or the other axis of polarization, the amount of population that will be transferred from the electronic ground state to some of the electronically excited states will depend strongly on the TDM component used. In this specific situation the non-rotating and free-rotating molecules descriptions should be nearly equivalent. Coincidentally, either the y or the z component of the TDM to the electronic excited states is always found to be close to zero (cf.Fig. 5). Within the states in which we are interested, b1A′ and c1A′, the marginal TDM are dz(a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b1A′)
b1A′)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dy(a1A′
dy(a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c1A′)
c1A′)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. Therefore, it is easy to predict that when the resonant frequency for the a1A′
0. Therefore, it is easy to predict that when the resonant frequency for the a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b1A′ or a1A′
b1A′ or a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c1A′ transitions is used, only y- or z-linearly polarized pulses, respectively, will transfer a significant amount of population using reasonable laser intensity. Indeed, for the aforementioned transitions the complementary z- and y-pulses, respectively, induce less than 10% population inversion with the present intensity.
c1A′ transitions is used, only y- or z-linearly polarized pulses, respectively, will transfer a significant amount of population using reasonable laser intensity. Indeed, for the aforementioned transitions the complementary z- and y-pulses, respectively, induce less than 10% population inversion with the present intensity.
The resulting population dynamics and wavepacket evolution on the three relevant states a1A′, b1A′ and c1A′ for ħω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.23 eV and 3.55 eV are shown in Figs. 6 and 7, respectively.
3.23 eV and 3.55 eV are shown in Figs. 6 and 7, respectively.
 | ||
Fig. 6 Laser driven simulations of the adiabatic time evolution of CpMn(CO)3 under y-linearly polarized light of ħϖ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.23 eV (frequency resonant with the b1A′ state). Panel (a) shows the population dynamics, as defined in eqn. (8). Panels (b), (c) and (d) show the time evolution of the wavepacket on the c1A′, b1A′ and a1A′ states, respectively. 3.23 eV (frequency resonant with the b1A′ state). Panel (a) shows the population dynamics, as defined in eqn. (8). Panels (b), (c) and (d) show the time evolution of the wavepacket on the c1A′, b1A′ and a1A′ states, respectively. | ||
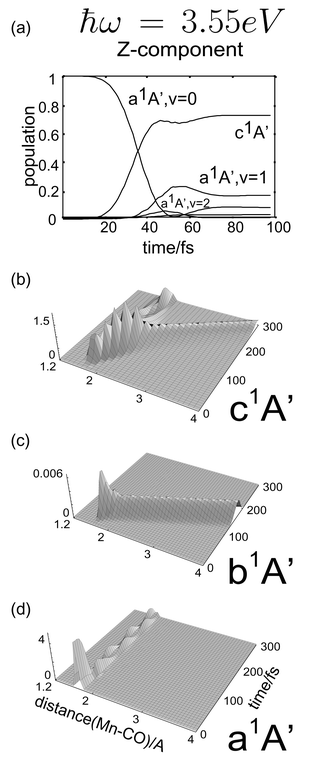 | ||
Fig. 7 Laser driven simulations of the adiabatic time evolution of CpMn(CO)3 under z-linearly polarized light of ħϖ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.55 eV (frequency resonant with the c1A′ state). Panel (a) shows the population dynamics. Panels (b), (c) and (d) show the time evolution of the wavepacket on the c1A′, b1A′ and a1A′ states, respectively. 3.55 eV (frequency resonant with the c1A′ state). Panel (a) shows the population dynamics. Panels (b), (c) and (d) show the time evolution of the wavepacket on the c1A′, b1A′ and a1A′ states, respectively. | ||
As shown in Fig. 6(a) the use of Ey together with the y component of the TDM and a laser energy of 3.23 eV results in ca. 70% population inversion from the electronic and vibrational ground state to b1A′. The laser is intense enough to return population to the ground state by stimulated emission, in a so-called intra-pulse-pump-dump process, as indicated by the residual population in |Φ0,1〉. Fig. 6(c) demonstrates direct dissociation as expected from a repulsive state. In contrast, using a z-linearly polarized laser pulse of energy of 3.55 eV the c1A′ state is populated by approximately the same amount. Likewise, small populations in |Φ0,1〉 and |Φ0,2〉 indicate stimulated emission (see Fig. 7(a)). The wavepacket simulations depicted in Fig. 7(b) and 7(c) indicate that the marginal population of the b1A′ state runs away as fast as when using 3.23 eV, cf.Fig. 6(c). On the contrary, the wavepacket on the c1A′ potential splits into two partial waves due to the small energy barrier at 2.5 Å. The main part remains trapped and oscillates in the potential well, whereas a smaller fraction overcomes the small barrier (0.2 eV) and dissociates, although slower than in the b1A′ state. These results are in agreement with the earlier simulations performed using a δ-pulse described in ref. 11.
When an intermediate frequency ħω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.41 eV is used, about half of the population is transferred to either the b1A′ or to the c1A′ states, depending on whether y- or z-polarized pulses are employed, respectively. The results are shown in Fig. 8 for y- and z-pulses. The y-polarized pulse transfers preferentially population from a1A′ to b1A′, and as in the case shown in Fig. 6(c), it dissociates rapidly on the repulsive state, see Fig. 8(a) and (c).
3.41 eV is used, about half of the population is transferred to either the b1A′ or to the c1A′ states, depending on whether y- or z-polarized pulses are employed, respectively. The results are shown in Fig. 8 for y- and z-pulses. The y-polarized pulse transfers preferentially population from a1A′ to b1A′, and as in the case shown in Fig. 6(c), it dissociates rapidly on the repulsive state, see Fig. 8(a) and (c).
 | ||
Fig. 8 Laser driven simulations of the adiabatic time evolution of CpMn(CO)3 under y- and z-linearly polarized light of ħϖ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.41 eV (averaged frequency between the b1A′ and c1A′ state). Panel (a) shows the population dynamics. Panels (b), (c) and (d) show the time evolution of the wavepacket on the c1A′, b1A′ and a1A′ states, respectively. 3.41 eV (averaged frequency between the b1A′ and c1A′ state). Panel (a) shows the population dynamics. Panels (b), (c) and (d) show the time evolution of the wavepacket on the c1A′, b1A′ and a1A′ states, respectively. | ||
The residual population which reaches the c1A′ state is trapped in the local well (Fig. 8(b)). The same effects can be observed if a z-polarized laser pulse is used. Half of the population is inverted from the a1A′ to the c1A′ state and it remains completely trapped in the local well and oscillates with a full period of ca. 170 fs, as depicted in Fig. 8(b). Also apparent is that the wavepacket located in the a1A′ potential exchanges amplitude during the laser pulse as demonstrated in the population dynamics of Fig. 8(a). The population of the c1A′ state clearly reveals a loss of amplitude when the pulse reaches its maximum of intensity, which is transferred to |Φ0,1〉, indicating an intra-pulse-pump-dump process.
In all the previous three scenarios, the Born–Oppenheimer (BO) dynamics coincides with the non-adiabatic one. The inclusion of the kinetic couplings in the simulations has negligible effects: no transfer from the c1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b1A′ state is observed.
b1A′ state is observed.
Next, let us consider the selective preparation of cymantrene in the excited A″ states. For this purpose the x-component of the TDM is used. As seen in Fig. 5, the value for the a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a1A″ in the Franck-Condon region is close to zero, and transitions to this state would require thus a very intense laser pulse, in comparison to the intensity needed to reach other accessible states, as i.e. b1A″. Note that the oscillator strength of this state reported in ref. 12 at CASSCF level was predicted to be of the same order of magnitude as for the a1A′
a1A″ in the Franck-Condon region is close to zero, and transitions to this state would require thus a very intense laser pulse, in comparison to the intensity needed to reach other accessible states, as i.e. b1A″. Note that the oscillator strength of this state reported in ref. 12 at CASSCF level was predicted to be of the same order of magnitude as for the a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b1A′ transition, and zero at TD-DFT level. The discrepancy between the previous CASSCF results and the present ones comes from the slight shift of the a1A′ potential minimum on going from CASSCF to MR-CCI level (from 1.81 Å to 1.85 Å at MR-CCI level). Thus, only simulations with a frequency resonant with the b1A″
(Fig. 9) state will be performed. For the sake of comparison, the BO dynamics is also presented.
b1A′ transition, and zero at TD-DFT level. The discrepancy between the previous CASSCF results and the present ones comes from the slight shift of the a1A′ potential minimum on going from CASSCF to MR-CCI level (from 1.81 Å to 1.85 Å at MR-CCI level). Thus, only simulations with a frequency resonant with the b1A″
(Fig. 9) state will be performed. For the sake of comparison, the BO dynamics is also presented.
 | ||
Fig. 9 Laser driven simulations of the adiabatic time evolution of CpMn(CO)3 under x-linearly polarized light of ħϖ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.40 eV (frequency resonant with the b1A″ state). In the left hand side, kinetic couplings have been excluded for comparison, while the right-hand side pictures include them. Panels (a) and (a′) show the population dynamics. Panels (b), (c) and (d) and counterparts (b′), (c′) and (d′), show the time evolution of the wavepacket on the b1A″, a1A″ and a1A′ states, respectively. 3.40 eV (frequency resonant with the b1A″ state). In the left hand side, kinetic couplings have been excluded for comparison, while the right-hand side pictures include them. Panels (a) and (a′) show the population dynamics. Panels (b), (c) and (d) and counterparts (b′), (c′) and (d′), show the time evolution of the wavepacket on the b1A″, a1A″ and a1A′ states, respectively. | ||
Since the value of the TDM for the a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b1A″ transition does not decay outside the Franck-Condon window as quickly as in the case of A′ transitions, an electric field of 2.5 GV m−1 is enough to invert ca. 100% of the population from the electronic and vibrational ground state a1A′ to the b1A″ state, as shown in Fig. 9(a). Most of the population is trapped in the b1A″ state due to its bound character in the absence of kinetic coupling, whereas the negligible population reaching the state a1A″ dissociates directly, cf.Fig. 9(b) and (c), respectively. Note that population trapped in the b1A″ state at the vibrational level v
b1A″ transition does not decay outside the Franck-Condon window as quickly as in the case of A′ transitions, an electric field of 2.5 GV m−1 is enough to invert ca. 100% of the population from the electronic and vibrational ground state a1A′ to the b1A″ state, as shown in Fig. 9(a). Most of the population is trapped in the b1A″ state due to its bound character in the absence of kinetic coupling, whereas the negligible population reaching the state a1A″ dissociates directly, cf.Fig. 9(b) and (c), respectively. Note that population trapped in the b1A″ state at the vibrational level v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 does not noticeably oscillate since the minimum position matches very much the one of the electronic ground state, a1A′. When the kinetic coupling is switched on, (electric field 1 GV m−1), there is a high yield of non-adiabatic population transfer from b1A″
0 does not noticeably oscillate since the minimum position matches very much the one of the electronic ground state, a1A′. When the kinetic coupling is switched on, (electric field 1 GV m−1), there is a high yield of non-adiabatic population transfer from b1A″![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a1A″, which steadily dissociates, as seen in the right panels of Fig. 9.
a1A″, which steadily dissociates, as seen in the right panels of Fig. 9.
In summary, these simulations illustrate that different products could be observed in the probe state depending on where the wavepacket is prepared. If the initial pump pulse prepares a state completely localized in the weakly bounded c1A′ state, no dissociation should occur and only a signal for the parent ion CpMn(CO)3+ should be observed after the probe pulse. The signal detection of the parent ion depends of course on the shape of its potential as a function of the Mn–CO bond elongation. In contrast, if the pump frequency is such that the wavepacket has enough kinetic energy to overcome the barrier, or if it selects the repulsive b1A′ and a1A″ states, or is transferred non-adiabatically from the b1A″![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a1A″ state, then it will undergo fast dissociation and the probe pulse would detect the fragment CpMn(CO)2+. These statements assume non-rotating molecules and specific polarizations. Obviously, in the case of free rotating molecules all components of the laser pulse would interact at the same time. However, in the present case the TDM which govern the electronic populations are characterized by a single dominant non zero component and consequently the computer simulations are still valid.
a1A″ state, then it will undergo fast dissociation and the probe pulse would detect the fragment CpMn(CO)2+. These statements assume non-rotating molecules and specific polarizations. Obviously, in the case of free rotating molecules all components of the laser pulse would interact at the same time. However, in the present case the TDM which govern the electronic populations are characterized by a single dominant non zero component and consequently the computer simulations are still valid.
Conclusion
The CASSCF/MR-CCI adiabatic potential energy curves associated with the low-lying singlet metal-centered (dMn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dMn) excited states of CpMn(CO)3 have been calculated as a function of the Mn–COax bond elongation under the Cs symmetry constraint. The main features of the absorption spectrum have been reproduced in the limit of this one-dimensional approach by means of wavepacket propagations on this set of coupled potentials. Wavepackets propagations induced by laser fields have been performed in the energy domain corresponding to the first absorption band (between 3.2 eV and 3.6 eV) assigned to MC states without any ambiguity. Four simulations have been proposed for future pump/probe experiments corresponding to different initial conditions governed by the laser parameters of the pump pulse with specific polarizations in the non-rotating molecule approximation. As far as the b1A′ and c1A′ states are concerned, three different frequencies have been used—ħω
dMn) excited states of CpMn(CO)3 have been calculated as a function of the Mn–COax bond elongation under the Cs symmetry constraint. The main features of the absorption spectrum have been reproduced in the limit of this one-dimensional approach by means of wavepacket propagations on this set of coupled potentials. Wavepackets propagations induced by laser fields have been performed in the energy domain corresponding to the first absorption band (between 3.2 eV and 3.6 eV) assigned to MC states without any ambiguity. Four simulations have been proposed for future pump/probe experiments corresponding to different initial conditions governed by the laser parameters of the pump pulse with specific polarizations in the non-rotating molecule approximation. As far as the b1A′ and c1A′ states are concerned, three different frequencies have been used—ħω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.23 eV, 3.55 eV and 3.41 eV—while only one simulation is reported for the 1A″ states using one frequency of 3.40 eV. When the pump pulse prepares the molecular system in the weakly bound c1A′ state characterized by a small energy barrier (using ħω
3.23 eV, 3.55 eV and 3.41 eV—while only one simulation is reported for the 1A″ states using one frequency of 3.40 eV. When the pump pulse prepares the molecular system in the weakly bound c1A′ state characterized by a small energy barrier (using ħω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.55 eV z-polarized), the only signal which will be observed using a second laser pulse should be [CpMn(CO)3]+, as long as fragmentation of the parent ion does not occur. In contrast, a laser frequency of ħω
3.55 eV z-polarized), the only signal which will be observed using a second laser pulse should be [CpMn(CO)3]+, as long as fragmentation of the parent ion does not occur. In contrast, a laser frequency of ħω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.23 eV (y-polarized) will prepare the system on the repulsive b1A′ potential leading to an ultra-fast dissociation of CpMn(CO)3 and to the detection of the [CpMn(CO)2]+ fragment after the probe experiment. An intermediate frequency ħω
3.23 eV (y-polarized) will prepare the system on the repulsive b1A′ potential leading to an ultra-fast dissociation of CpMn(CO)3 and to the detection of the [CpMn(CO)2]+ fragment after the probe experiment. An intermediate frequency ħω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.40 eV or 3.41 eV will populate both b1A′ and c1A′ states depending on the light polarization (y or z), as well as the b1A″ state (x polarization). The y polarized pulse will induce preferably the a1A′
3.40 eV or 3.41 eV will populate both b1A′ and c1A′ states depending on the light polarization (y or z), as well as the b1A″ state (x polarization). The y polarized pulse will induce preferably the a1A′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b1A′ transition leading to ultra-fast dissociation and formation of the [MnCp(CO)2]+ fragments whereas the z-polarized pulse will trap the system in the potential well of the c1A′ state. The x-polarized laser component will contribute to form [MnCp(CO)2]+ fragments by non-adiabatic transfer from b1A″
b1A′ transition leading to ultra-fast dissociation and formation of the [MnCp(CO)2]+ fragments whereas the z-polarized pulse will trap the system in the potential well of the c1A′ state. The x-polarized laser component will contribute to form [MnCp(CO)2]+ fragments by non-adiabatic transfer from b1A″![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a1A″. As a consequence, the ionized daughter molecule will be observed in the latter case.
a1A″. As a consequence, the ionized daughter molecule will be observed in the latter case.
The present paper is an important step towards the ultimate goal of designing laser pulses that maximize either the yield of the parent ion [CpMn(CO)3]+ or that of the fragments [CpMn(CO)2]+, [CpMn(CO)]+, etc., observed experimentally. In summary, the detailed investigation of electronic excited states dynamics of cymantrene has enabled us to obtain important information regarding the dissociative mechanism towards the formation of the first observed fragment as well as on non-dissociative channels. Obviously, a further step of the study should be devoted to the influence on the reactive pathways of other degrees of freedom (in particular the bond angle between the out-of-plane carbonyls). The branching ratio between CpMn(CO)3/CpMn(CO)2 has been predicted to be very sensitive to the initial pump frequency. Of course, the final nature of the ions detected by the probe experiment will depend on the topology and energetics of the ionic parent molecule CpMn(CO)3+. Indeed, it is difficult to discriminate experimentally between dissociation of the neutral excited species and fragmentation of the parent cation. As a further step, preliminary laser probe simulations have been performed on the basis of potential energy curves calculated for the lowest ionic states of [CpMn(CO)3]+. The interplay between quantum theory and new experiments that determine the origin of the observed fragments (pump or probe) would certainly be enlightening.
Acknowledgements
The authors kindly thank Prof. J. Manz and Prof. L. Wöste for fruitful discussions on the theoretical and experimental aspects of this work. The Deutsche Forschungsgemeinschaft SFB 450 “Analysis and Control of ultrafast photoinduced reactions” is gratefully acknowledged. All the calculations have been performed on HP workstations of the Theoretische Chemie group at FU-Berlin.References
- H. Yang, K. T. Kotz, M. C. Asplund and C. B. Harris, J. Am. Chem. Soc., 1997, 119, 9564 CrossRef CAS; H. Yang, M. C. Asplund, K. T. Kotz, M. J. Wilkers, H. Frei and C. B. Harris, J. Am. Chem. Soc., 1998, 120, 1015.
- S. K. Kim, S. Pedersen and A. H. Zewail, Chem. Phys. Lett., 1995, 233, 500 CrossRef CAS.
- S. A. Trushin, W. Fuss, W. E. Schmid and K. L. Kompa, J. Phys. Chem., 1998, 102, 4129 CrossRef CAS.
- S. A. Trushin, W. Fuss, K. L. Kompa and W. E. Schmid, J. Phys. Chem. A, 2000, 104, 1997 CrossRef CAS.
- L. Bañares, T. Baumert, M. Bergt, B. Kiefer and G. Gerber, J. Chem. Phys., 1997, 108, 5799 CrossRef CAS.
- M. Gutmann, J. M. Janello, M. S. Dickebohm, M. Grossekathöfer and J. Lindener-Roenneke, J. Phys. Chem., 1998, 102, 4138 CrossRef CAS.
- A. Assion, T. Baumert, M. Bergt, T. Brixner, B. Kiefer, V. Seyfried, M. Strehle and G. Gerber, Science, 1998, 282, 919 CrossRef CAS.
- M. C. Heitz, C. Ribbing and C. Daniel, J. Chem. Phys., 1997, 106, 1421 CrossRef CAS.
- M. C. Heitz and C. Daniel, J. Am. Chem. Soc., 1997, 119, 1269 CrossRef CAS.
- D. Guillaumont and C. Daniel, J. Am. Chem. Soc., 1999, 121, 11
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 733 CrossRef CAS.
733 CrossRef CAS. - C. Daniel, J. Full, L. González, C. Kaposta, M. Krenz, C. Lupulescu, J. Manz, S. Minemoto, M. Oppel, P. Rosendo-Francisco, Š. Vajda and L. Wöste, Chem. Phys., 2001, 267, 247 CrossRef CAS.
- J. Full, L. González and C. Daniel, J. Phys. Chem, 2001, 105, 184 CrossRef CAS.
- W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, Weinheim, 2000 Search PubMed.
- L. Miguet, C. Daniel and A. Dedieu, private communication.
- B. O. Roos, Adv. Chem. Phys, 1987, 69, 399 Search PubMed.
- P. E. M. Siegbahn, Int. J. Quantum Chem., 1983, 23, 1869 CrossRef CAS.
- Only the e1A′ state around the Franck-Condon region corresponds to a much higher energy state than those included in the CASSCF reference space and it is not converged in the present MR-CCI calculations.
- J. Finley, P.-A. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299 CrossRef CAS.
- M. E. Casida, Time-dependent Density Functional Response Theory for Molecules in Recent Advances in Density Functional Methods, Part I, ed. D. P. Chong, World Scientific, Singapore, 1995 Search PubMed.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys, 1987, 86, 866 CrossRef CAS.
- A. Bergner, M. Dolg, W. Kuechle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431 CAS.
- K. Pierloot, B. Dumez, P. O. Widmark and B. O. Roos, Theor. Chim. Acta, 1995, 90, 87 CrossRef CAS.
- I. Bruand-Cote, PhD Thesis, Université L. Pasteur, Strasbourg, 2002.
- K. Andersson et al., Molcas 4.1., University of Lund, Sweden, 1998.
- G. Hirsch, P. J. Bruna, R. J. Buenker and S. D. Peyerimhoff, Chem. Phys., 1980, 45, 335 CrossRef CAS.
- C. Marston and G. G. Balint-Kurti, J. Chem. Phys, 1989, 91, 3571 CrossRef CAS.
- M. D. Feit and G. A. Fleck, J. Comp. Chem., 1982, 47, 412 Search PubMed; M. D. Feit and G. A. Fleck, J. Chem. Phys., 1982, 78, 301 CrossRef CAS.
- A. Askar and A. S. Cakmak, J. Chem. Phys., 1978, 68, 2794 CrossRef CAS.
- D. Kosloff and R. Kosloff, J. Comput. Chem., 1982, 52, 35.
- R. Schinke, Photodissociation dynamics, Cambrigde University Press, Cambridge, 1993 Search PubMed.
- M. C. Heitz and C. Daniel, Chem. Phys. Letters, 1995, 246, 488 Search PubMed; M. R. J. Hachey and C. Daniel, Inorg. Chem., 1998, 37, 1387 CrossRef CAS.
- P. J. Giordano and M. S. Wrighton, Inorg. Chem., 1977, 16, 160 CrossRef CAS.
- W. A. Ehlers and G. Frenking, Organometallics, 1995, 14, 423 CrossRef CAS.
| This journal is © the Owner Societies 2003 |