View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/B209457F (Paper) Phys. Chem. Chem. Phys., 2003, 5, 12-17

Molecular parity violation in electronically excited states

Robert Berger
Chemistry Department, Technical University Berlin, Strasse des 17. Juni 135, D-10623 Berlin, Germany. E-mail: Robert.Berger@www.chem.tu-berlin.de

Received 30th September 2002 , Accepted 5th November 2002

First published on 25th November 2002

Abstract

One of the greatest challenges in the field of molecular physics is the still outstanding measurement of the parity violating energy difference (ΔEpv) which electroweak theory predicts to exist between the enantiomers of chiral molecules. Apparently, previous attempts to detect signals of parity violation in molecules almost exclusively focused on electronic ground state systems. But as this study reveals, there are good reasons to believe that compounds which are chiral in an electronically excited state are particularly suited for a possible proof of molecular parity violation. Here, first calculations of the parity violating energy difference in electronically excited states are presented and routes to its measurement are discussed.

1. Introduction

One of the most striking consequences of the electroweak theory1–3 is that a tiny energy difference ΔEpv between the left- and right-handed enantiomers of a chiral compound arises from the parity violating property of the electroweak force (see refs. 4 and 5 and literature cited therein). However, while several predictions of this theory have been successfully verified in the realms of nuclear and atomic physics, the proof of molecular parity violation in general and of this energy difference in particular still remains a challenging task for experimentalists.

In the past, several experimental approaches have been proposed and various, but in the outcome unsuccessful or at least doubtful, attempts have been made to measure parity violating effects in chiral molecules. These approaches can generally be classified as to detect certain frequency shifts for example in the nuclear magnetic resonance, in the microwave, infrared or even Mössbauer-spectra of the enantiomers6–14 or to measure the parity violating coupling in a special class of molecules with intermediate tunneling15 (see also ref. 16) or directly the spectroscopic energy difference between the left- and the right-handed compound17 (see also ref. 5). While compared to a direct measurement of the energy difference between enantiomers the detection of line splittings appears to be in principle less difficult, the interpretation of those splittings in terms of ΔEpv is complicated.

The intensified efforts over the past few years to detect parity violating effects in molecules have largely been motivated by the fact that opposed to early computations (see for instance refs. 18–21) more recent calculations4,22–27 predict the absolute value of the parity violating energy difference often to be larger by an order of magnitude, which has profound consequences for possible experiments.

Surprisingly, it seems that all experimental schemes proposed so far aim at a detection of molecular parity violation in the electronic ground state and that parity violating potentials have only been calculated for this state, with the following two exceptions: In a figure caption of ref. 28 it has been noted that the role of the ground and excited state could be reversed in the experiment proposed in ref. 17 (see below) and Ivanov and Letokhov29 performed explicit calculations of molecular parity violating effects in electronically excited states, namely on splittings of electronically excited states in optically inactive molecules.

As will be detailed later in this article, a different class of systems, that is molecules which are optically active in electronically excited states, is particularly attractive for a measurement of ΔEpv for the following reasons: Firstly, parity violating potentials in electronically excited states might be larger in magnitude than those in the electronic ground state. Secondly, direct measurements of parity violating energy differences in these states can in principle be performed with a simplified scheme (see also caption to Fig. 1 in ref. 28). Thirdly, a large pool of molecular systems becomes accessible for a possible measurement of ΔEpv.


One-dimensional cut through a multi-dimensional Born-Oppenheimer potential energy surface V(q⃑) (solid line) along the stereomutation coordinate q of a chiral compound. qL corresponds to the equilibrium geometry of the left-handed, qR of the right-handed enantiomer. In the left figure the wavefunctions Ψ(q) of the chiral states |L〉 and |R〉 (dotted and dashed line respectively) are indicated, which have in the absence of parity violation the same energy expectation value E (horizontal dotted and dashed lines), while in the right figure the wavefunctions of the parity eigenstates |+〉 and |−〉 (dashed and dotted lines respectively) are shown together with their corresponding energy levels E (respective horizontal lines).
Fig. 1 One-dimensional cut through a multi-dimensional Born-Oppenheimer potential energy surface V([q with combining right harpoon above (vector)]) (solid line) along the stereomutation coordinate q of a chiral compound. qL corresponds to the equilibrium geometry of the left-handed, qR of the right-handed enantiomer. In the left figure the wavefunctions Ψ(q) of the chiral states |L〉 and |R〉 (dotted and dashed line respectively) are indicated, which have in the absence of parity violation the same energy expectation value E (horizontal dotted and dashed lines), while in the right figure the wavefunctions of the parity eigenstates |+〉 and |−〉 (dashed and dotted lines respectively) are shown together with their corresponding energy levels E (respective horizontal lines).

Thus, first calculations of parity violating energy differences in electronically excited states are presented in this paper and an experimental approach to measure them is discussed.

2. Parity violating potentials in electronically excited states of prototype systems

Parity violating potentials in electronically excited states can be calculated within the multi-configuration linear response approach to electroweak theory presented in refs. 25 and 4. For details I refer to the original publication4 where the first realization within the DALTON program30 is described.

In the non-relativistic approximation the main contribution to the parity violating potential is expected to be due to the following one-electron operator (in atomic units)

 
ugraphic, filename = b209457f-t1.gif(1)
with GF[thin space (1/6-em)]=[thin space (1/6-em)]2.22254[thin space (1/6-em)]×[thin space (1/6-em)]10−14 au: Fermi coupling constant, α: fine structure constant, Qw(A)[thin space (1/6-em)]=[thin space (1/6-em)]ZA(1[thin space (1/6-em)]−[thin space (1/6-em)]4sin2θw)[thin space (1/6-em)]−[thin space (1/6-em)]NA, ZA: number of protons in nucleus A, NA: number of neutrons, sin2θw[thin space (1/6-em)]=[thin space (1/6-em)]0.2319: Weinberg parameter, 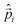ugraphic, filename = b209457f-t6.gif: linear momentum operator of electron i, ugraphic, filename = b209457f-t7.gif: spin operator, δ3([x with combining right harpoon above (vector)]): Dirac delta distribution, [r with combining right harpoon above (vector)]ν: position vector of particle ν, {·,·}+: anticommutator.

In order to obtain non-vanishing parity violating potentials, coupling between spin and coordinate space is essential. The most pronounced coupling effect is expected to be due to spin–orbit coupling, for which the corresponding operator reads in the Breit–Pauli form (in atomic units)

 
ugraphic, filename = b209457f-t2.gif(2)
where ugraphic, filename = b209457f-t10.gif refers to the orbital angular momentum operator of electron i with respect to the position of particle μ.

Within the multi-configuration linear response (MCLR) approach, the parity violating potential Vpv is then given by:

 
Vpv[thin space (1/6-em)]=[thin space (1/6-em)]〈〈Ĥso;Ĥpv〉〉ω1[thin space (1/6-em)]=[thin space (1/6-em)]0[thin space (1/6-em)]=[thin space (1/6-em)]〈〈Ĥpv;Ĥso〉〉ω1[thin space (1/6-em)]=[thin space (1/6-em)]0(3)
where 〈〈Â;[B with combining circumflex]ω1〉〉ω1 is the linear response function for operators  and [B with combining circumflex] at frequency ω1. In case of a coordinate independent Vpv for each enantiomer and an infinitely high barrier for interconversion of the two, the parity violating potential is related to the parity violating energy difference according to |ΔEpv|[thin space (1/6-em)]≈[thin space (1/6-em)]2|Vpv|.

In traditional second order perturbation theory, the parity violating potential reads as

 
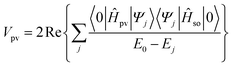ugraphic, filename = b209457f-t3.gif(4)
where |0〉 denotes the reference state of interest (not necessarily the ground state), E0 the corresponding energy and |Ψj〉 the jth (excited) state with energy Ej. For a singlet reference state non-vanishing contributions only arise from triplet states. By virtue of this sum-over-states expression, one could generally expect an increased parity violating potential in electronically excited states. While for closed-shell chiral molecules in their equilibrium structure the electronic ground state is usually energetically well removed from the manifold of triplet states, an electronically excited state typically resides in the close neighborhood of other electronic states, which results in a smaller denominator in the sum-over-states expression. It should be noted, however, that this does not necessarily lead to larger values for Vpv, since the various numerators may have alternating signs and vary in magnitude. Furthermore, the non-degenerate second order perturbation theory approach breaks down, if the matrix elements of the spin-orbit coupling operator are no longer small compared to the (de)excitation energies. Molecules composed of chemical elements from the first and second row of the periodic table typically show singlet–triplet spin–orbit coupling (SOC) values on the order of a few to a few hundred reciprocal centimeters with corresponding consequences on the validity of the second order perturbation theory approach for small energy gaps between the reference state and the perturbing states.

Molecules of interest for a calculation of parity violating potentials in electronically excited states and for the type of experiment to be outlined below are for instance those carbonyl compounds XYCO which are planar in the electronic ground state and pyramidal in the lowest excited singlet state. For several of these compounds the n[thin space (1/6-em)]→[thin space (1/6-em)]π* state is non-planar and, depending on the substituents, the barrier for stereomutation can be large. This in turn leads to a small tunneling splitting ΔE±, which is of advantage for an experimental detection of molecular parity violation (see below). Other suitable molecular systems are for instance formaldimine derivatives or 1,2-disubstituted ethylene with chiral equilibrium geometries in an electronically excited state.

In early spectroscopic studies of formyl fluoride,31–33 one of the simplest compounds of the type XYCO, it has been concluded that the first electronically excited singlet states of this molecule has a (chiral) pyramidal equilibrium structure as opposed to a planar nuclear arrangement in the electronic ground state. The corresponding double minimum potential in the first electronically excited singlet state was investigated in more detail in later studies34,35 and tunneling splittings in various vibronic states were reported. Stanton and Gauss36 in a computational study used the equation-of-motion coupled-cluster singles and doubles (EOM-CCSD) method to calculate the equilibrium structure of HFCO in the S1 state.

In the present study the complete active space-self consistent field (CASSCF) approach has been employed with all 18 valence electrons distributed in a set of 13 molecular orbitals described with the (atomic) augmented correlation consistent polarized valence triple-ζ basis set (usually referred to as aug-cc-pVTZ). Equilibrium structures and harmonic vibration wavenumbers obtained for the ground and the first electronically excited singlet state are shown in Table 1. Within the multi-configuration linear response approach to electroweak quantum chemistry the parity violating potential at the chiral equilibrium geometry of the lowest excited singlet state of formyl fluoride is computed to be −139[thin space (1/6-em)]×[thin space (1/6-em)]10−20Eh for the R-enantiomer. The parity violating potential in the electronic ground state at the same geometry is +37[thin space (1/6-em)]×[thin space (1/6-em)]10−20Eh and thus significantly smaller in magnitude. These findings are in accordance with what might be expected from sum-over-states arguments. SOC values between the first excited singlet state and the lowest two triplet states are on the order of 2 cm−1 and 46 cm−1, while the reference state is energetically sufficiently well-removed from the triplet states (corresponding (de)excitation wavenumbers[thin space (1/6-em)]>[thin space (1/6-em)]2600 cm−1). Results for ethylene and 1,2-difluoroethylene, which will be presented in a forthcoming publication, indicate the same trend of an increase of the parity violating potential in electronic singlet states with close lying triplet states. Here, however, the effect for the first electronically excited state is less pronounced since 90°-twisted ethylene is a perfect biradical with a large energy gap between the S1 and the S0 state whereas the splitting between the S0 and the lowest triplet state is very small.

Table 1 Structures, harmonic vibration wavenumbers and parity violating potentials of the ground (S0) and first electronically excited singlet state (S1) of formyl fluoride as obtained on the CASSCF level of theory with 18 electrons distributed in 13 orbitals and with the aug-cc-pVTZ basis set. Bond lengths (r) are reported in picometers, angles (∠,τ) in degrees, harmonic wavenumbers (ω) in reciprocal centimeters and parity violating potentials (Vpv) in 10−20Eh. τ corresponds to the angle between the CO bond and its projection on the CHF plane. Parity violating potentials in the ground and first electronically excited singlet state have been calculated for the R-enantiomer at the equilibrium geometry of the S1-state. These values have been obtained with a modified4 version of the DALTON program.30
Parameter S0 S1
CASSCF CCSDa CASSCF EOM-CCSDa
aug-cc-pVTZ cc-pVDZ aug-cc-pVTZ cc-pVDZ
a Ref. 36.
r(CO) 118.75 118.74 135.51 134.62
r(CF) 133.75 134.03 134.47 134.58
r(CH) 108.44 109.97 107.88 109.77
∠OCF 122.27 123.13 109.18 109.82
∠OCH 127.64 127.35 114.70 116.10
τ 0.0 0.0 46.51 46.3
ω 1 3206.85 3173.51 3254.24 3147.33
ω 2 1860.77 1923.85 1226.95 1217.57
ω 3 1457.77 1418.33 1421.64 1384.70
ω 4 1114.77 1126.65 1162.66 1149.10
ω 5 682.87 678.41 509.44 462.35
ω 6 1080.84 1046.72 1107.84 996.45
V pv(S0) 0   37  
V pv(S1) 0   −139  

In the following section the principle idea of a direct measurement of ΔEpv is outlined and a scheme for an observation of ΔEpv in molecules that are chiral in electronically excited states is discussed.

3. Outline of an experimental scheme for the measurement of ΔEpv in electronically excited states

Chiral compounds are of particular importance for the measurement of parity violating effects in molecular systems, since here the situation arises that a parity even state (denoted as |+〉) and a parity odd state (|−〉) become sufficiently close in energy. This is sketched in Fig. 1 (right hand side) where a one-dimensional cut through a multi-dimensional Born–Oppenheimer potential energy surface V([q with combining right harpoon above (vector)]) along the stereomutation coordinate q is shown. This coordinate connects the minima corresponding to the left-handed and right-handed enantiomer which are separated by a barrier with a maximum at an achiral geometry q[thin space (1/6-em)]=[thin space (1/6-em)]0.

In the absence of parity violation, the molecular Hamiltonian is parity conserving and thus commutes with the parity operator [P with combining circumflex] ([Ĥpc,[P with combining circumflex]][thin space (1/6-em)]=[thin space (1/6-em)]0). States |L〉 and |R〉 localized on the left- or the right-hand side respectively (henceforth referred to as chiral or handed states) and which are related by the parity operation (|L〉[thin space (1/6-em)]=[thin space (1/6-em)][P with combining circumflex]|R〉) then have identical energy expectation values (Fig. 1, left hand side). However, they are not eigenstates of the parity-conserving Hamiltonian Ĥpc since those must as well be eigenstates of the parity operator and thus be either symmetric or antisymmetric with respect to inversion at the origin. The parity eigenstates |+〉 and |−〉, which are proportional to the plus- and the minus-combination of the chiral states, will in contrast to the handed states differ in energy as a result of the chiral state's tunneling through the barrier. In the high barrier limit, however, this energy difference is negligibly small.

Due to parity violation, the states of well-defined parity will be perturbed by the parity violating part Ĥpv of the total electroweak Hamiltonian Ĥ[thin space (1/6-em)]=[thin space (1/6-em)]Ĥpc[thin space (1/6-em)]+[thin space (1/6-em)]Ĥpv. If we restrict ourselves to a two level system only and work in the basis of the parity eigenstates, the strength of the mixing depends on the tunneling splitting E± and on the parity violating coupling element Vpv[thin space (1/6-em)]=[thin space (1/6-em)]〈+|Ĥpv|−〉. Assuming real states for simplicity, we arrive at the following eigenvalue problem (see also refs. 15,17,5):

 
ugraphic, filename = b209457f-t4.gif(5)
where we have used E+, E− for the eigenvalues of the parity conserving Hamiltonian Ĥpc. This gives the eigenvalues Ei and eigenvectors |i〉
 
ugraphic, filename = b209457f-t5.gif(6)
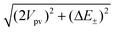where we have introduced D as a shorthand notation for ugraphic, filename = b209457f-t12.gif and sgn[x][thin space (1/6-em)]=[thin space (1/6-em)]x/|x|.

If the absolute value of the tunneling splitting ΔE±[thin space (1/6-em)]=[thin space (1/6-em)]E+[thin space (1/6-em)]−[thin space (1/6-em)]E− is much smaller than the absolute value of the parity violating matrix element Vpv, we obtain (assuming Vpv[thin space (1/6-em)]<[thin space (1/6-em)]0) D[thin space (1/6-em)]≈[thin space (1/6-em)]|2Vpv| as well as 1[thin space (1/6-em)]±[thin space (1/6-em)]ΔE±/D[thin space (1/6-em)]≈[thin space (1/6-em)]1. Consequently, the true eigenstates are the handed states (|1〉[thin space (1/6-em)]≈[thin space (1/6-em)]{|+〉[thin space (1/6-em)]+[thin space (1/6-em)]|−〉}/√2, |2〉[thin space (1/6-em)]≈[thin space (1/6-em)]{|+〉[thin space (1/6-em)]−[thin space (1/6-em)]|−〉}/√2) with E1[thin space (1/6-em)]−[thin space (1/6-em)]E2[thin space (1/6-em)]≈[thin space (1/6-em)]2Vpv. In the limit of an infinitely high barrier, E1[thin space (1/6-em)]−[thin space (1/6-em)]E2 corresponds to the parity violating energy difference ΔEpv. In the opposite case (assuming ΔE±, Vpv[thin space (1/6-em)]<[thin space (1/6-em)]0) we obtain D[thin space (1/6-em)]≈[thin space (1/6-em)]|ΔE±| and 1[thin space (1/6-em)]−[thin space (1/6-em)]ΔE±/D[thin space (1/6-em)]≈[thin space (1/6-em)]2, 1[thin space (1/6-em)]+[thin space (1/6-em)]ΔE±/D[thin space (1/6-em)]≈[thin space (1/6-em)]0. The true eigenstates are then the states of well-defined parity (|1〉[thin space (1/6-em)]≈[thin space (1/6-em)]|+〉, |2〉[thin space (1/6-em)]≈[thin space (1/6-em)]−|−〉) with E1[thin space (1/6-em)]−[thin space (1/6-em)]E2[thin space (1/6-em)]≈[thin space (1/6-em)]ΔE±.

Harris and Stodolski15 noted that when |2Vpv|[thin space (1/6-em)]≪[thin space (1/6-em)]|ΔE±|, a system initially prepared in a chiral state |L〉 or |R〉 would show time-dependent oscillations of the optical activity θ with a period τ of h/ΔE±. The time-averaged optical rotation 〈θ〉t however would vanish. When |Vpv| is no longer negligibly small compared to |ΔE±|, the optical activity would oscillate with a reduced time period around a non-vanishing average value. The time-dependence of the quantum beats gives experimental information about the parity violating coupling and thus indirectly also on ΔEpv by reference to the tunneling splitting according to 〈θ〉t/θmax[thin space (1/6-em)]=[thin space (1/6-em)]V2pv/[V2pv[thin space (1/6-em)]+[thin space (1/6-em)](ΔE±/2)2].

Quack17 suggested considering the reverse situation: When |ΔE±|[thin space (1/6-em)]≪[thin space (1/6-em)]|2Vpv|, which should be the case for typical chiral molecules, ΔEpv becomes a directly measurable quantity. A system initially prepared in a state of well-defined parity would show oscillations between the parity eigenstates. The time-period τ for these oscillations is then determined by the parity violating energy difference, according to τ[thin space (1/6-em)]=[thin space (1/6-em)]h/ΔEpv. It has been proposed to create this state of well-defined parity in the electronic ground state of a typical chiral molecule with a large barrier for stereomutation via optical excitation to and deexcitation from an electronically excited state with an achiral equilibrium geometry where the parity of the rovibrational eigenstates is well-defined, since |ΔE±|[thin space (1/6-em)]≫[thin space (1/6-em)]|2Vpv|. Due to the strong parity selection rules in optical dipole transitions, this excitation–deexcitation scheme can be used to create a state of well-defined parity in an initially unpopulated rovibrational level of the electronic ground state of the chiral molecule. Influenced by the parity violating energy difference in this rovibrational state, a transformation to the state of opposing parity will take place which can be probed with a third transition to a state of well-defined parity in the electronically excited state of the molecule.

There are several difficulties connected with this approach (see below and ref. 17) which one, however, could overcome under favorable conditions. Nevertheless, although this proposal is 15 years old and although various aspects of this approach can now be considered to be under control, the preparation step still seems to be a problematic aspect, to a lesser extent in view of technical difficulties, but rather because promising molecular candidates that are ideally suited for this scheme are apparently still to be discovered. For several chiral molecules the parity violating energy difference has been calculated (see for instance refs. 19,20,23,37–47) and for S2Cl247 it has been explicitly shown that the parity violating energy difference exceeds the tunneling splitting in the lowest vibrational levels of the electronic ground state by orders of magnitude, but for most of those molecules we do not expect that electronically excited states with an achiral equilibrium geometry exist for which a rotationally resolvable and analysable spectrum may be obtained, a necessary prerequisite to the experiment.

Therefore, I propose to search for molecular parity violation in electronically excited states. Since on the one hand we significantly enlarge our pool of systems applicable in our quest for molecular parity violation and on the other hand might even profit from a gain in order of magnitude for the quantity we are aiming at, electronically excited states appear to be promising for a successful measurement of |ΔEpv|: As illustrated in Fig. 2, for a molecule with an achiral equilibrium geometry in the electronic ground state (more precisely: for which |ΔE±|[thin space (1/6-em)]≫[thin space (1/6-em)]|2Vpv| holds in certain rovibrational levels of the electronic ground state) and with a chiral equilibrium geometry in an electronically excited state we can due to the strong parity selection rules directly prepare a state of well-defined parity in the electronically excited state via an optical dipole transition from the initial vibronic ground state. If |ΔE±| in this excited vibronic state is much smaller than |Vpv|, the time for parity change is almost exclusively determined by the parity violating energy difference. The time-dependent increase of the population p of the initially forbidden parity state, which is in the absence of decay processes given by p[thin space (1/6-em)]=[thin space (1/6-em)]sin2[ΔEpvt/(2ħ)], can then selectively be probed by a second transition to a level of well-defined parity, which may for instance be a rovibrational level of an achiral electronic state (not necessarily the electronic ground state) or a level of the electronically excited state in an energy region, where the tunneling splitting is large compared to |ΔEpv|. This scheme is in principle also applicable to states with different spin symmetry. Then, however, other selection rules apply. Note, that in this type of experiment it is not necessary to resolve the parity violating splitting since the strong parity selection rules for electric dipole transitions allow for a selective preparation and detection of one of the two parity eigenstates.


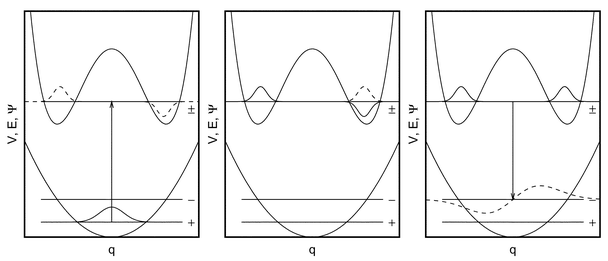Schematic representation of a measurement of the parity violating energy difference for systems which are chiral in an electronically excited state (|ΔE±| ≪ |2Vpv|) but achiral in the electronic ground state (|ΔE±| ≫ |2Vpv|). Starting from a state with well-defined parity in the electronic ground state, we create with the first electronic transition a rovibronic state of well-defined parity in the electronically excited state (left part of the figure; dashed curves are used for emerging, solid curves for already present states). Under the influence of the parity violating potential in this rovibronic state, a transformation to the state of opposing parity will take place (middle part) which can selectively be probed with a second transition to a state of well-defined parity, for instance in the electronic ground state of the molecule (right part of the figure).
Fig. 2 Schematic representation of a measurement of the parity violating energy difference for systems which are chiral in an electronically excited state (|ΔE±|[thin space (1/6-em)]≪[thin space (1/6-em)]|2Vpv|) but achiral in the electronic ground state (|ΔE±|[thin space (1/6-em)]≫[thin space (1/6-em)]|2Vpv|). Starting from a state with well-defined parity in the electronic ground state, we create with the first electronic transition a rovibronic state of well-defined parity in the electronically excited state (left part of the figure; dashed curves are used for emerging, solid curves for already present states). Under the influence of the parity violating potential in this rovibronic state, a transformation to the state of opposing parity will take place (middle part) which can selectively be probed with a second transition to a state of well-defined parity, for instance in the electronic ground state of the molecule (right part of the figure).

Compared to the experiment proposed in ref. 17 the preparation of a state of well-defined parity is greatly simplified, which is of particular importance, since up to now no definite molecular example has been presented that is according to explicit calculations of the tunneling splitting, the parity violating potential and either computations or experimental knowledge of the parity conserving potential of the intermediate electronic state qualified for the measurement suggested in ref. 17. While already in this reference it has been suggested, among other possibilities, to use allenes with achiral excited states for a spectroscopic experiment with this scheme, only very recently it has been calculated quantitatively in a different context that 1,3-dimethylallene has an achiral electronically excited state.48 With the approach outlined in the present paper (see also caption to Fig. 1 in ref. 28) we significantly increase the number of classes of molecular systems suitable for a parity violation experiment and can benefit from the presumably larger parity violating energy differences in electronically excited states.

These merits, however, come at the expense of further disadvantages specific for an experiment performed in electronically excited states, while other difficulties associated with the experiment outlined in ref. 17 (collisions; magnetic dipole, electric quadrupole transitions; electric fields etc.) which have already been examined more closely within that letter, continue to exist for the approach discussed here. The main complicating factors will be addressed briefly in the following:

(i) For an experiment conducted in the electronically excited state the most critical step will be the evolution phase. As has been discussed before, in the absence of decay processes the signal for parity change will evolve as p[thin space (1/6-em)]=[thin space (1/6-em)]sin2[ΔEpvt/(2ħ)]. Given that the value of Vpv computed for formyl fluoride in its first electronically excited singlet state translates to a time for parity change of about 30 s, it appears to be extremely difficult to record an entire period of the parity oscillation. However, this is not necessary. Since sin2(x) behaves approximately as x2 for small x, it has been noted for the electronic ground state17 that a measurement of the quadratically increasing signal in the initial time evolution (typically in the milli- or microsecond regime46) would be sufficient to determine ΔEpv. This also holds for electronically excited states although here additional complicating factors arise. For an isolated molecule, the prepared metastable state will decay due to internal conversion, intersystem crossing, predissociation as well as fluorescence and these processes will compete with the dynamics of parity change induced by Vpv. In order to ensure a significant population of the electronically excited state over this time span (milli- to microseconds) and thus a reasonably intense signal, the radiative lifetime should be at least of the same order of magnitude. Accordingly, the natural fluorescence (or phosphorescence) lifetime has to be long enough which requires a sufficiently small oscillator strength for a radiative transition between the electronically excited state and the ground state (see, however, below). The criterion for long radiative lifetimes (larger than microseconds) may for instance be met by various systems in their lowest electronically excited state with the same spin symmetry as the electronic ground state, by chiral high Rydberg states and in particular by electronically excited states with different spin symmetry showing phosphorescence lifetimes typically in the range of milliseconds to hundreds of seconds.

Interactions between the chiral molecular system and its environment especially due to collisions, however, will modify the dynamics of parity change considerably. An abundant literature on this particular point exists (see for instance refs. 5,15,49–52), since the hypothesis has been raised that environmental influences stabilize handed states of ordinary chiral molecules with respect to their states of well-defined parity. This necessitates working under single molecule conditions in the experiment outlined above, which can to a large extent be realized within a molecular beam or possibly within specially designed molecular traps. Severe consequences on the dynamics are due to parity changing collisions that result in a loss of phase coherence (so-called pure dephasing). Following the estimate in ref. 17 we would obtain after 1 ms time of flight in the molecular beam a relative signal of about 3[thin space (1/6-em)]×[thin space (1/6-em)]10−9 (here ΔEpv[thin space (1/6-em)]=[thin space (1/6-em)]2Vpv and Vpv[thin space (1/6-em)]=[thin space (1/6-em)]−139[thin space (1/6-em)]×[thin space (1/6-em)]10−20Eh as calculated for HFCO in its first electronically excited singlet state have been used), while for the traveling time of 100 ms used in ref. 17 the relative signal increases to 3[thin space (1/6-em)]×[thin space (1/6-em)]10−5. The probability for a collision within the 100 ms time of flight has been estimated as 2.5[thin space (1/6-em)]×[thin space (1/6-em)]10−7, which translates to 2.5[thin space (1/6-em)]×[thin space (1/6-em)]10−9 during the 1 ms flight. Even if these collisions have a high probability for parity change, which would lead to a significant background signal in the experiment, the signal caused by the incoherent collision events increases only linearly with time while the signal for coherent parity change displays quadratic dependence, so that the different contributions can be identified with additional measurements downstream the beam.17

Further dynamical information on the various decay channels including collisional deactivation of the electronically excited states can be obtained from control experiments which record the time evolution of the two states of well-defined parity after their direct preparation.

As has been noted in ref. 17, if a superselection rule exists for the handed states of chiral molecules (see ref. 53), this type of experiment can provide a sensitive check of this hypothesis.

(ii) The preparation phase has been significantly simplified compared to the experiment in ref. 17, since the state of well-defined parity is now prepared with a single electric dipole transition. However, excitations with other parity selection rules may occur due to accompanying magnetic dipole and electric quadrupole transitions. While these transitions are typically five or eight orders of magnitude weaker than electric dipole transitions, they nonetheless impose lower limits on the strength of the electric dipole transitions. A smaller electric dipole transition moment is on the one hand favorable as it provides long radiative lifetimes but on the other hand a larger oscillator strength is required to reduce the background as a result of transitions with other parity selection rules. A compromise between these two requirements appears to be well possible, since the population of the state of unwanted parity caused by accompanying transitions can be removed by “cleaning” the prepared state. This can be performed for instance via probing the initially forbidden component with a strongly allowed electric dipole transition immediately after the preparation step which may remove the states with contributions of the unwanted parity. This procedure may also be applied to avoid complications due to rovibronic coupling in these states with relatively high energy.

(iii) Calculations of parity violating potentials of chiral molecules in electronically excited states are in principle more difficult than for electronic ground state systems and this will also affect the interpretation of future experiments. The approach used here for the calculation of ΔEpv in electronically excited states marks the first step in the direction of reliable theoretical estimates.

As is evident from the discussion above, formyl fluoride itself is not well suited for this type of experiment since the tunneling splitting in the lowest vibrational level of the first electronically excited state is, at approximately 0.2 cm−1 (ref. 35), much larger than ΔEpv. Moreover the fluorescence lifetime ranges from 130 ns to <10 ns (ref. 35) and is therefore too small for this type of experiment. For the deuterated compound DFCO the fluorescence lifetime falls in the range of 400 ns to 800 ns (ref. 35) and we may expect a further increase for TFCO so that the microsecond regime might finally be reached. Nonetheless, according to preliminary calculations, the tunneling splitting in DFCO and TFCO are on the order of 10−2 cm−1 and consequently still orders of magnitude larger than the parity violating energy difference. A more favorable situation may however be realized in other compounds of the general type XYCO.

4. Conclusion and outlook

In this paper first calculations of parity violating potentials have been presented for molecules that are chiral in electronically excited states. A route to the observation of ΔEpv in those states has been discussed, which follows the spirit of the approach proposed in ref. 17, where ΔEpv is obtained directly via a measurement in the time domain. Compared to the experiment of ref. 17, the preparation of a state of well-defined parity, which is crucial for the experiment, is in the present approach (see also caption to Fig. 1 in ref. 28) significantly simplified. As might be expected from sum-over-states arguments and as is indicated by the calculations of parity violating potentials in electronically excited states with chiral equilibrium structures presented here, we may also benefit from a larger value of |ΔEpv| in excited states. These two aspects render this experiment particularly appealing for the first successful measurement of ΔEpv.

I shall note here that electronically excited molecular states are also of interest for other approaches to detect molecular parity violation, for instance in a measurement of the dispersion of optical rotation or of the electronic circular dichroism. One might also consider to search for parity violating signals in electronic transitions, where for both the initial and the final rovibronic state the parity violating potential prevails against the tunneling splitting. However, one would have to beat the natural linewidth in order to resolve possible linesplittings in electronic transitions of the enantiomers and even if one succeeds, frequency shifts due to molecular parity violation have to be distinguished from splittings of various other sources, a difficult task even in the infrared region as recent experiments indicate.54

Acknowledgements

I thank Jürgen Stohner for his comments on the manuscript and for fruitful discussions on various aspects of molecular parity violation. I am grateful to Martin Quack, who had previously informally suggested also to consider his scheme for the detection of parity violation in the reverse form with chiral excited states, for initial stimulus to the parity violation project and for sharing ideas and insight. Financial support by the Fonds der Chemischen Industrie and grant of computer time by the Konrad-Zuse-Zentrum Berlin are gratefully acknowledged.

References

  1. S. Glashow, Nucl. Phys., 1961, 22, 579–588 Search PubMed.
  2. S. Weinberg, Phys. Rev. Lett., 1967, 19, 1264–1266 CrossRef.
  3. A. Salam, in Proceedings of the Eighth Nobel Symposium, ed. N. Svartholm, Amkvist and Wiksell, Stockholm, 1968, pp. 367–377 Search PubMed.
  4. R. Berger and M. Quack, J. Chem. Phys., 2000, 112, 3148–3158 CrossRef CAS.
  5. M. Quack, Angew. Chem., Int. Ed. Engl., 1989, 28, 571–586 CrossRef; M. Quack, Angew. Chem., Int. Ed., 2002, 41, 5001–5012, recently published work CrossRef CAS.
  6. A. Barra, J. Robert and L. Wiesenfeld, Phys. Lett. A, 1986, 115, 443–447 CrossRef CAS.
  7. A. Barra, J. Robert and L. Wiesenfeld, Europhys. Lett., 1988, 5, 217–222 Search PubMed.
  8. A. Barra and J. Robert, Mol. Phys., 1996, 88, 875–886 CrossRef CAS.
  9. A. Bauder, A. Beil, D. Luckhaus, F. Müller and M. Quack, J. Chem. Phys., 1997, 106, 7558–7570 CrossRef CAS.
  10. V. Letokhov, Phys. Lett. A, 1975, 53, 275–276 CrossRef.
  11. O. Kompanets, A. Kukudzhanov, V. Letokhov and L. Gervits, Opt. Commun., 1976, 19, 414–416 CrossRef CAS.
  12. E. Arimondo, P. Glorieux and T. Oka, Opt. Commun., 1977, 23, 369–372 CrossRef CAS.
  13. C. Daussy, T. Marrel, A. Amy-Klein, C. Nguyen, C. Bordé and C. Chardonnet, Phys. Rev. Lett., 1999, 83, 1554–1557 CrossRef CAS.
  14. A. Lahamer, S. Mahurin, R. Compton, D. House, J. Laerdahl, M. Lein and P. Schwerdtfeger, Phys. Rev. Lett., 2000, 85, 4470–4473 CrossRef CAS.
  15. R. Harris and L. Stodolski, Phys. Lett. B, 1978, 78, 313–317 CrossRef.
  16. I. Khriplovich, Parity Nonconservation in Atomic Phenomena, Gordon and Breach Science, Philadelphia, 1991 Search PubMed.
  17. M. Quack, Chem. Phys. Lett., 1986, 132, 147–153 CrossRef CAS.
  18. D. Rein, R. Hegstrom and P. Sandars, Phys. Lett. A, 1979, 71, 499–502 CrossRef.
  19. R. Hegstrom, D. Rein and P. Sandars, J. Chem. Phys., 1980, 73, 2329–2341 CrossRef CAS.
  20. S. Mason and G. Tranter, Mol. Phys., 1984, 53, 1091–1111 CAS.
  21. G. Tranter, J. Chem. Soc. Chem. Commun., 1986, 60–61 RSC.
  22. A. Bakasov, T.-K. Ha, and M. Quack, in Chemical Evolution: Physics of the Origin and Evolution of Life, ed. J. Chela-Flores and F. Raulin,, Kluwer Academic Publisher, Netherlands, 1996, pp. 287–296 Search PubMed.
  23. A. Bakasov, T.-K. Ha and M. Quack, J. Chem. Phys., 1998, 109, 7263–7285 CrossRef CAS.
  24. A. Bakasov, T.-K. Ha and M. Quack, J. Chem. Phys., 1999, 110, 6081 CrossRef CAS.
  25. R. Berger and M. Quack, in Proc. 37th IUPAC Congress, GDCh, Berlin, 1999, vol. 2, p. 518 Search PubMed.
  26. P. Lazzeretti and R. Zanasi, Chem. Phys. Lett., 1997, 279, 349–354 CrossRef CAS.
  27. J. Laerdahl and P. Schwerdtfeger, Phys. Rev. A, 1999, 60, 4439–4453 CrossRef CAS.
  28. M. Quack, Faraday Discuss., 1994, 99, 389–394 Search PubMed.
  29. L. Ivanov and V. Letokhov, J. Chem. Phys., 1997, 106, 6045–6050 CrossRef CAS.
  30. T. Helgaker, H. J. Jensen, P. Jørgensen, J. Olsen, K. Ruud, H. Ågren, T. Andersen, K. L. Bak, V. Bakken, O. Christiansen, P. Dahle, E. K. Dalskov, T. Enevoldsen, B. Fernandez, H. Heiberg, H. Hettema, D. Jonsson, S. Kirpekar, R. Kobayashi, H. Koch, K. V. Mikkelsen, P. Norman, M. J. Packer, T. Saue, P. R. Taylor and O. Vahtras, Dalton release 1.0, an electronic structure program, University of Oslo, Norway, 1997 Search PubMed.
  31. L. Giddings and K. Innes, J. Mol. Spectrosc., 1961, 6, 528–549 CrossRef CAS.
  32. L. Giddings and K. Innes, J. Mol. Spectrosc., 1962, 8, 328–337 CrossRef CAS.
  33. G. Fischer, J. Mol. Spectrosc., 1969, 29, 37–53 CrossRef CAS.
  34. G. Fischer and Y. Sorek, J. Mol. Spectrosc., 1979, 74, 136–145 CrossRef CAS.
  35. J. Crane, H. Nam, H. Beal, H. Clauberg, Y. Choi, C. Moore and J. Stanton, J. Mol. Spectrosc., 1997, 181, 56–66 CrossRef CAS.
  36. J. Stanton and J. Gauss, Theor. Chim. Acta, 1995, 91, 267–289 CrossRef CAS.
  37. L. Wiesenfeld, Mol. Phys., 1988, 64, 739–745 CAS.
  38. O. Kiyonaga, K. Morihashi and O. Kikuchi, J. Chem. Phys., 1998, 108, 2041–2043 CrossRef.
  39. P. Lazzeretti, R. Zanasi and F. Faglioni, Phys. Rev. E, 1999, 60, 871–874 CrossRef CAS.
  40. R. Berger and M. Quack, Chem. Phys. Chem, 2000, 1, 57–60 CrossRef CAS.
  41. R. Berger, M. Quack and G. Tschumper, Helv. Chim. Acta, 2000, 83, 1919–1950 CrossRef CAS.
  42. M. Quack and J. Stohner, Phys. Rev. Lett., 2000, 84, 3807–3810 CrossRef CAS.
  43. M. Quack and J. Stohner, Z. Phys. Chem., 2000, 214, 675–703 Search PubMed.
  44. J. Laerdahl, R. Wesendrup and P. Schwerdtfeger, Chem. Phys. Chem, 2000, 1, 60–62 CrossRef CAS.
  45. M. Gottselig, D. Luckhaus, M. Quack, J. Stohner and M. Willeke, Helv. Chim. Acta, 2001, 84, 1846–1861 CrossRef CAS.
  46. R. Berger, M. Quack and J. Stohner, Angew. Chem., Int. Ed. Engl., 2001, 40, 1667–1670 CrossRef CAS.
  47. R. Berger, M. Gottselig, M. Quack and M. Willeke, Angew. Chem., Int. Ed. Engl., 2001, 40, 4195–4198 CrossRef CAS.
  48. E. Deretey, M. Shapiro and P. Brumer, J. Chem. Phys., 2001, 105, 9509–9517 CrossRef CAS.
  49. M. Simonius, Phys. Rev. Lett., 1978, 40, 980–983 CrossRef CAS.
  50. R. Harris and L. Stodolski, J. Chem. Phys., 1981, 74, 2145–2155 CrossRef.
  51. M. Cattani and J. Bassalo, Chirality, 1998, 10, 519–521 CrossRef CAS.
  52. A. Vardi, J. Chem. Phys., 2000, 112, 8743–8746 CrossRef CAS.
  53. P. Pfeifer, in Energy Storage and Redistribution in Molecules, ed. J. Hinze, Plenum, New York, 1983, pp. 315–326 Search PubMed.
  54. M. Ziskind, C. Daussy, T. Marrel and C. Chardonnet, Eur. Phys. J. D, 2002, 20, 219–225 Search PubMed.
This journal is © the Owner Societies 2003
Click here to see how this site uses Cookies. View our privacy policy here.