Ab initio calculations of vibrational spectra of 2-methoxy ethanol in the C–H stretching range

Abstract

Focussing on the range of the C–H stretching vibrations, spectra of 2-methoxy ethanol (HO–CH₂–CH₂–O–CH₃) were calculated at the MP2 level using the 6-31+G(d) basis set. The spectra exhibit a striking dependence on the molecular conformation which can cause shifts of mode frequencies by up to 80 cm⁻¹. Whereas vibrations above 2955 cm⁻¹ are very characteristic for OH in a gauche conformation, the spectral range between 2850–2900 cm⁻¹ is congested by numerous bands and, therefore, seems poorly suited for analytical purposes. In this range, even the unambiguous assignment of modes becomes impossible due to the overlap of symmetric and antisymmetric modes. The range between 2900 and 2955 cm⁻¹ is characterized by a grouping of the bands. The interaction of methoxy ethanol with water lifts this grouping and yields a more uniform distribution. The results are compared to a recent spectroscopic study of oligo(ethylene glycol) films (Dreesen et al., Chem Phys Lett., 2001, 333, 327). For the films in contact with air the characteristic spectral features are well reproduced and changes induced by water are also reflected in the calculations.

---

Introduction

Substances bearing ethylene glycol (EG) units are widely used as detergents, emulsifiers, or dispersants¹ and are intensively investigated due to their ability to render surfaces resistant to protein adsorption and cell adhesion.^2–9 In experimental studies which aim for an understanding of the interfacial properties of EG-based layers, vibrational spectroscopies play an important role, and IR spectroscopy and IR-vis sum frequency generation (SFG) have been applied to investigate alkyl poly(ethylene glycol) ethers,¹⁰ polyethylene glycol (PEG) films,^11,12 or self-assembled monolayers (SAM) where in the latter case an oligo (ethylene glycol) moiety (OEG) is linked to the surface via an alkyl thiolate.^6,8,13 These studies revealed a strong dependence of the spectra on the details of the experiments such as the number of ethylene moieties,⁸ the environment,¹³ or the substrate⁶ which can be understood by realizing that EG strands can adopt a variety of conformationally different structures whose ratios are determined by the energetics of the system. Ab initio studies of simple EG units such as 2-methoxy ethanol (1-hydroxy 2-methoxy ethane, HME)^14–24 and dimethoxyethane (DME)^23,25–27 already demonstrate that several conformations not too different in energy exist and that hydrogen bonding plays a significant role. The situation becomes even more complicated for larger systems such as OEG strands which have been studied by ab initio methods^28,29 or SAMs of OEG thiols modelled by Monte Carlo calculations^30–33 where the number of possible conformations further increases.

The ab initio studies presented here and in a forthcoming publication³⁴ were in particular triggered by SFG studies of films of PEG^11,12 and SAMs of OEG thiols.¹³ Vibrational spectra which were recorded in the range of the C–H stretching vibrations exhibit characteristic features for films under ambient atmosphere but change drastically if the PEG/OEG layers are exposed to water.^13,12 From an analytical point of view it is, therefore, of interest to correlate the spectral features with the conformations and to elucidate spectral alterations caused by interactions of EG with water.

The present study deals with the spectra of HME which is representative of the chain terminating unit of OH terminated PEG films¹² whereas a forthcoming paper³⁴ deals with DME as a representative unit of either a methoxy terminated strand¹³ or a “bulk” EG unit.

Due to the intrinsically high interface sensitivity of SFG, the terminating EG moiety is likely to dominate the signal^11,12 and, therefore, it can be expected that HME reflects to a significant extent the vibrational fingerprint of a PEG layer with OH terminated strands. To study the effect of water, the most simple case of a single water molecule interacting with an HME unit is considered. Even though the vibrational spectra of ethylene glycol fragments, i.e. DME and HME, have been studied theoretically to some extent^16–24,27 the C–H stretching region has barely been addressed and not been compared in detail with experimental data.

Methods

Selection of fragments, method, and basis set. The ab initio calculations were performed on an IBM RS6000 and a 400 MHz Pentium using the G98/G98W suite of programs.³⁵ To minimize the calculation effort, i.e. to determine the most appropriate basis set, method, and smallest molecular fragment which is representative of the EG terminus unit, a number of tests were performed prior to the conformational studies. Calculations using HO–(CH₂)₂–O–R with R = H, CH₃, CH₂CH₃ yield CH₃ as the best choice of the smallest terminating fragment. R = H yields significant frequency shifts whereas an ethylene unit does not significantly influence the vibrational spectra compared to a CH₃ unit. Therefore, the calculations were performed with 2-methoxy ethanol. As described in detail elsewhere³⁴ the selection of the calculation method is based on the comparison of the calculated spectra of DME with IR and SFG spectra of self-assembled monolayers of partially deuterated OEG thiols. RHF calculations being completely unsuitable, calculations at the MP2 level turned out to be superior to DFT calculations. Therefore, all calculations were performed at the MP2 level.

Exploring different basis sets for the frequency calculations, 6-31+G(d) was the best choice among the ones tested. Basis sets up to 6-311++G(d,p) were investigated but did not yield results which were significantly different, i.e., the band shifts were two to three wave numbers at maximum compared to 6-31+G(d).

All calculations were performed with very tight convergence criteria since the standard criteria gave, partially, significantly different, misleading energies. Convergence problems encountered with the very tight option were resolved by using the modified GDIIS algorithm.^35,36

The scaling factor was set to 0.927 and is based on the comparison of the SFG experiments of different partially deuterated OEG SAMs with the calculated spectra of DME.³⁴

As has been outlined by others^19,20,29 hydrogen bonding, both intra and intermolecular, can play an important role in EG moieties. In PEG films different types of hydrogen bonding are of interest: the intermolecular interaction between two terminating OH groups, the interaction of an OH with an inner EG oxygen, and in the case of contact with water the interaction of water with the OH and the EG oxygen of the same molecule. Hydrogen bonding between two PEG molecules was mimicked by calculating the interaction of CH₃OH with HME. For the calculation of selected conformations of the EG it turned out that the spectra of CH₃OH were within 2–3 cm⁻¹ compared to the spectra of water. Therefore, only water was further considered in the systematic study of the vibrational spectra.

Nomenclature. The labelling of the different conformations investigated is defined by Fig. 1 which shows the HME molecule in an all-trans conformation. Starting at the terminating methyl group the C and O atoms are labelled 1–5. Bonds are rotated as indicated, + and − denoting clockwise and counter-clockwise rotations. Deviations from the trans (t) conformations are indicated by ±g (gauche). The molecular conformation is defined by a three letter sequence, e.g. +g−gt, which denotes the conformation at bonds (O2–C3), (C3–C4), and (C4–O5). Signs are omitted if a structure does not depend on the direction of a bond rotation.

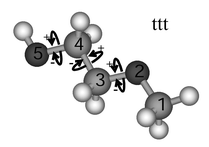Fig. 1 Nomenclature for 1-hydroxy-2-methoxy ethane (see text).

Results and discussion

Conformational energies. For HME without water all 14 possible combinations of gauche and trans conformations were calculated and the respective energies are compiled in Table 1 and graphically displayed in Fig. 3. Except for the conformers +g+g+g and +g−g+g which did not yield a minimum but transformed into +g+g−g and t−g+g, respectively, all 12 remaining structures gave stable local minima. With respect to the energies it is noted that, where a comparison with the literature is possible (ttt, ttg, t−g+g, +g+g−g), the relative energies of the conformers agree to within 2 kJ mol⁻¹ with published values which were calculated using MP2/6-31G(d).¹⁸ Additional energy calculations using significantly larger basis sets, up to aug-cc-pVTZ, resulted in variations of the relative energies by less than 20%. This deviation from the values provided in Table 1 might serve as indicator to what extent two conformers can be considered different in energy. In order to allow for a comparison of all conformers, all energies are given relative to the energy of the ttt-conformer (−268,72 hartrees) plus the energy of a water molecule (−76.21 hartrees). One should, however, keep in mind that such a comparison of the isolated HME with water complexated HME ignores basis set superposition effects (BSSE) and, thus, has its limitations. It should, therefore, be understood to infer trends rather than as a precise account of energy values.³⁷ Looking first at the isolated HME molecule, the introduction of a gauche conformation at the C4–O5 bond (ttg, Fig. 2a) does not appreciably change the energy compared to ttt. Rotating the C–C bond (tgt, Fig. 2b) causes only a small increase in energy whereas a more significant increase results if the O2–C3 bond is rotated (gtt, not shown). The energy decreases significantly if both the C4–O5 and the C3–C4 bonds are rotated (t+g−g, Fig. 2c) since the H is now oriented towards the O2-atom forming an intramolecular hydrogen bond. A very similar situation is met for the +g+g−g conformation (Fig. 2d). Note that the energy difference between t+g−g and +g+g−g is close to the difference of ttt and gtt, that is, the rotation of the methyl group is energy costly but for t+g−g is overcompensated by the intramolecular interaction of the hydroxyl H with the O2-atom. For a more detailed discussion of the H-bonding in HME it is referred to the literature.^17,18

Fig. 2 Different conformations of HME without (a,b) and with (c,d) intramolecular hydrogen bonding.

Fig. 3 Relative energies of the conformations of HME. Solid circles and diamonds denote values for the isolated HME molecule and its interaction with water, respectively. For assignment of the numbers see Table 1.

Table 1 Energies, relative occupation numbers, CH₂ mode frequencies, and IR intensities of different conformations of 2-methoxy ethanol (HME). #1–12 are values for the isolated molecule, #13–20 denote HME interacting with water. Frequencies are calculated with a CD₃ group. For changes of methylene mode frequencies due to coupling to the methyl modes see Table 2

	#	ΔE^a kJ mol^−1	N rel ^b	sym C3^c		asym C3^c		sym C4^c		asym C4^c
				cm^−1	I/km mole^−1	cm^−1	I/km mole^−1	cm^−1	I/km mole^−1	cm^−1	I/km mole^−1
a Values are referenced to the sum of an isolated ttt conformer plus a water molecule. b Separate relative values for HME with and without water; numbers are relative to the ttt conformer (#14 for water). Values calculated for T = 293 K. c Modes are coupled to varying extent. Assignment is to the dominating mode. For details see text.
ttt	1	0	1.00	2835	34.9	2881	19.2	2864	48.7	2920	55.7
ttg	2	0.9	0.68	2810	56.3	2867	22.8	2882	54.4	2970	21.5
tgt	3	2.6	0.35	2814	36.6	2868	45.6	2845	54.8	2905	38.2
gtt	4	6.6	0.07	2856	3.4	2951	32.7	2860	76.0	2907	27.3
−gt−g	5	8.2	0.03	2821	55.4	2943	14.2	2871	38.6	2967	26.3
−gt+g	6	6.5	0.07	2848	31.4	2919	20.6	2874	48.5	2964	30.8
+g+gt	7	9.5	0.02	2812	41.3	2948	23.9	2840	70.1	2886	36.3
+g−g−g	8	4.5	0.16	2807	55.2	2915	31.9	2845	53.5	2954	16.8
+g+g−g	9	−6.2	13	2842	37.5	2947	31.1	2856	52.8	2934	17.2
t+g−g	10	−13.6	268	2825	44.2	2880	70.9	2860	15.9	2946	25.1
+g−gt	11	1.5	0.55	2837	40.6	2921	30.7	2844	45.2	2899	39.9
t+g+g	12	5.1	0.12	2792	47.7	2833	38.4	2844	84.9	2959	16.2
ttt, H2O at O2	13	−32.6	1.56	2850	26.4	2901	15.3	2867	44.8	2932	33.6
ttt, H2O at O5	14	−31.5	1.00	2837	32.4	2893	12.4	2880	38.3	2940	34.5
ttg, H2O at O2	15	−33.2	1.94	2836	34.7	2897	35.6	2892	18.0	2968	21.1
ttg, H2O at O5	16	−32.5	1.51	2810	55.3	2888	8.7	2898	37.6	2977	16.3
gtt, H2O at O5	17	−28.2	0.25	2872	44.0	2960	25.0	2864	26.8	2926	8.5
tgt, ⋯H–O–H⋯	18	−39.9	31	2828	30.0	2880	38.6	2854	43.2	2912	31.2
+g+g−g, O⋯H2O⋯HO	19	−48.8	1175	2855	51.5	2947	19.8	2848	25.2	2920	34.6
t+g−g, O⋯H2O⋯HO	20	−57.1	35 178	2827	45.2	2889	45.8	2858	26.9	2927	33.8

---

In the calculation of the interaction of HME with water a selection of conformers was chosen to infer trends. This includes the attachment of water to either O2 or O4 of the all trans conformation to see the H-bonding induced differences between the two sites. Furthermore, the effect of water bonding on the two energetically lowest conformations was calculated. As a third type, a conformation was chosen where the water can bind via its two hydrogens (tgt). As seen from the comparison of the isolated conformers (#1–12) with the corresponding ones interacting with water (#13–20) the interaction is energetically favourable for all conformers (Table 1 and Fig. 3). Apart from this general preference of hydrogen bonding the energy sequence is not affected. Like for the isolated molecule (#9) the +g+g−g (#19) and the t+g−g (#10/#20) conformers are lowest in energy. The higher energy conformation gtt (#4/#17) remains higher relative to ttt. The only exception is tgt (#3/#18) which is slightly higher in energy than ttt (#1) in the isolated state but is lower than the all trans conformer by about 7.3 kJ mol⁻¹ when interacting with water. The reason is that, in contrast to the ttt or ttg (Fig. 4a) conformation where HME forms only one hydrogen bond with water, two hydrogen bonds are formed (Fig. 4b). This increased interaction of H₂O with the HME molecule is similar to the interaction of an oligoethylene glycol strand with water. In this case a significant difference was found between a planar and a helical structure due to the ability of the helical structure to interact with water via two oxygens.²⁸ For the +g+g−g (Fig. 4c) and t+g−g (Fig. 4d) conformers also two hydrogen bonds are formed and, consequently, the energy difference between isolated and H-bonded is essentially the same for all three conformers. However, the tgt conformer is different from the other two geometries since the water points with both hydrogens towards the HME, in contrast to the other two conformers where the OH group of the HME points with its hydrogen towards the water molecule. Thus, tgt-type intermolecular interaction cannot occur in two HME molecules interacting with each other. Concluding the presentation of the conformational energies it is noted that the conformers highest in energy are different for each series, +g+gt for the isolated and gtt for the water bonded HME.

Fig. 4 Relative energies of the conformations of HME. Solid circles and diamonds denote values for the isolated HME molecule and its interaction with water, respectively. For assignment of the numbers see Table 1.

Vibrational spectra.
Isolated molecule. Tables 1 and 2 compile the C–H stretching modes of all 12 conformers. It is stressed that the labelling of the modes as symmetric and antisymmetric does not reflect truly the situation. The symmetry of the modes significantly depends on the conformation, i.e. the local symmetry, and the amplitudes of the two H's of a methylene moiety vibrating against the C can become rather different.³⁸ Taking the asym C4 methylene mode as an example, the ratios of the two amplitudes vary between 1 and 3. It would, therefore, be more appropriate to refer to the vibrations as in phase and out of phase C–H modes, rather than symmetric and antisymmetric. The origin of this asymmetry comes from the lone pair effect of the oxygen³⁹ and also from the influence of the adjacent CH₂. Comparison of the asym C4 mode for the ttt (#1), ttg (#2), and tgt (#3) conformations with amplitude ratios of 1, 2.65, and 1.8 demonstrate this. Analogously, this also holds for the methyl modes. Another crucial point is concerned with coupling of vibrations. As is well known from polymethylene chains⁴⁰ the methylene modes are coupled, thus giving rise to bands with the same modes of the two CH₂ moieties being either in phase or out of phase. The vibrations of the ttt conformer (#1), where the 2881 cm⁻¹ and 2920 cm⁻¹ bands represent the asym CH₂ modes at C3 and C4 moving in phase and out of phase, respectively, illustrate this. However, due to the lower symmetry of the molecule compared to alkane chains the amplitudes are rather different. In the case of the ttt conformer, the amplitude ratios are about 7 ∶ 2 with the larger amplitude on the C4 (C3) for the 2920 cm⁻¹ (2881 cm⁻¹) band. Devations from the trans conformation give rise to further modifications of the coupling and to even larger amplitude ratios. Furthermore, also coupling between asym and sym modes can occur as the ttg (#2) conformer demonstrates. Even though the band at 2882 cm⁻¹ is predominantly a sym CH₂ vibration at C4 the asym CH₂ at C3 also contributes. However, there is always a dominance of a particular mode of one CH₂ group and it is this mode to which a frequency listed in Table 1 is assigned. Analogous to the methylene modes, also some of the conformations of the symmetric methylene vibrations at C3 and/or C4 and the symmetric methyl mode exhibit a significant coupling. The in phase and out of phase combinations are provided in Table 2 whereas the corresponding values for the isolated methylene vibrations, i.e. for HME with a CD₃ moiety are the ones listed in Table 1. With the comparison with ethylene glycol layers in mind, the discussion will focus on the methylene modes, all of which are presented graphically in Fig. 5a to give an impression of their spectral distribution. It is obvious that the vibrational frequencies of the methylene groups very much depend on the conformation. The range below 2890 cm⁻¹ is particularly congested and makes this range rather useless for analytical purposes. Above 2890 cm⁻¹ the band group to some extent with a block between 2900–2920 cm⁻¹ and above 2940 cm⁻¹. Beyond the rather high density of bands which makes a straightforward interpretation of experimental spectra already a demanding task, the assignment of a particular frequency range to a mode of a particular symmetry or to a vibration at a particular C atom is restricted, as Fig. 6a illustrates. Even for the C3 symmetric methyl mode which, for a particular conformation has always the lowest frequency, there is a substantial variation from 2807 cm⁻¹ to 2854 cm⁻¹ and there is overlap between this mode and the C4 sym CH₂ mode. Similarly, in the range between 2850 cm⁻¹ and 2890 cm⁻¹ which is the range where the C4 sym CH₂ mode is located, bands from the C3 asym CH₂ are found. However, only conformers with the methoxy group in trans conformation (#1–3, and 10) give rise to C3 asym CH₂ vibrations at frequencies overlapping with the C4 sym CH₂. Interestingly, even an inversion in the sequence can occur as is the case for the ttg conformation (#2) where the C3 asym CH₂ is lower than the C4 sym CH₂. The problem to assign bands to a particular methylene group becomes worse for the antisymmetric modes since the modes from both methylene groups exhibit a conformation dependent variation of up to 80 cm⁻¹. Such big shifts are clearly associated with gauche conformations of either the methoxy or the OH groups which cause a strong blue shift of the antisymmetric modes. For example, the change from t+g−g (#10) to +g+g−g (#9) shifts the C3 asym CH₂ mode by about 33 cm⁻¹. Another example which illustrates the problem of assignment is depicted in Fig. 7 which compares ttg (#2) with +g−gt (#11), two conformers which are essentially equal in energy (see Fig. 3). The sequence of the antisymmetric modes is inverted and the symmetric ones get very close to each other. Fig. 7 also highlights the fact that asym methylene modes can appear at frequencies unusually high compared to the normal position of methylene modes which range between 2900 and 2955 cm⁻¹.³⁹

Fig. 5 Compilation of all calculated mode frequencies for the isolated HME molecule (a) and HME interacting with water (b). Same column patterns of colours represent same conformer.

Fig. 6 The frequencies of the methylene modes as a function of the conformations. For assignment of the numbers see Table 1. ▼ sym C3, ▲ sym C4, ■ asym C3, ● asym C4.

Fig. 7 Comparison of the +g−gt (#11, hatched columns) and ttg (#2, solid columns) conformers of HME. The positions of the symmetric (s) and antisymmetric (as) modes of both the methylene adjacent to the OH and the methoxy moiety, respectively, vary strongly and illustrate the overlapping spectral region of modes which make an assignment of a spectral range to a particular mode questionable.

Table 2 Methyl modes of 2-methoxy ethanol (HME). Vibrational frequencies and IR intensities of different conformations. #1–12 are values for the isolated molecule, #13–20 denote HME interacting with water

Conformation	#	asym CH3, ip^a		asym CH3, op		sym CH3,
		cm^−1	I/km mole^−1	cm^−1	I/km mole^−1	cm^−1	I/km mole^−1
a ip = in C1–O2–C3 plane, op = out of C1–O2–C3 plane. b Where two values are given there is significant coupling of the sym CH3 with sym CH2 modes. 0° and 180° label in phase and out of phase coupling. Cn labels the CH2 mode of the respective C atom. Corresponding values in Table 1 for the CH2 vibration refer to HME with a deuterated CH3 group.
ttt	1	2982	22.3	2901	45.9	2838	66.6
						2833	27.6
ttg	2	2983	21.4	2902	42.3	2836	62.6
tgt	3	2981	22.1	2895	44.2	2831	70.0
gtt	4	2981	21.6	2911	36.9	2842	41.5
−gt−g	5	2982	20.5	2910	52.9	2841	49.7
−gt+g	6	2982	20.4	2913	44.1	2848 (0° C3)^b	35.2
						2843 (180°)	47.8
+g+gt	7	2978	21.9	2907	49.4	2831	37.8
+g−g−g	8	2984	19.6	2938	14.0	2843	70.9
+g+g−g	9	2984	17.4	2915	40.3	2857 (0° C3, 0° C4)	81.7
						2845 (0° C3, 180° C4)	16.7
						2842 (180° C3, 0° C4)	40.4
t+g−g	10	2984	19.5	2907	35.8	2840	62.9
+g−gt	11	2984	18.5	2941	31.4	2849	54.6
t+g+g	12	2983	20.2	2893	48.5	2831	66.2
ttt, H2O at O2	13	2987	18.0	2923	38.0	2852 (0° C3)	56.2
						2848 (180°)	22.1
ttt, H2O at O5	14	2983	21.9	2906	36.0	2840 (0° C3)	62.5
						2836 (180°)	30.0
ttg, H2O at O2	15	2987	18.1	2923	31.0	2850	52.9
ttg, H2O at O5	16	2984	21.7	2907	33.6	2839	58.4
gtt, H2O at O5	17	2987	16.5	2932	304	2855	27.6
tgt, ⋯H–O–H⋯	18	2991	13.6	2920	30.4	2847	54.3
+g+g−g, O⋯H2O⋯HO	19	2982	16.7	2930	35.3	2857 (0° C3,C4)	79.3
						2851 (180° C3, C4)	19.9
t+g−g, O⋯H2O⋯HO	20	2979	19.4	2918	30.0	2847	61.5

---

Despite the complex behavior of the C–H stretching modes some features can be identified which are useful in the interpretation of experimental spectra. Frequencies above 2930 cm⁻¹ are characteristic of an end group gauche conformation. Even more specific are bands which appear above 2955 cm⁻¹ since they indicate the presence of a gauche conformation of the OH. However, this does not mean that a conformer containing one necessarily appears above 2955 cm⁻¹. Bands appearing between 2930 cm⁻¹ and 2955 cm⁻¹ have either one or both ends in a gauche geometry as the examples of the two, energetically most favorable conformations (+g+g−g/#9, t+g−g/#10) show which have their highest frequency vibration around 2947 cm⁻¹. Note that all of the vibrations above 2955 cm⁻¹ belong to conformations (#2,5,6,12) which are higher in energy than ttt with however no correlation between the energy and the blue shift, as #2 shows which is energetically very close to ttt but has the highest frequency of all conformers.

From the data presented so far it is clear that the region below 2900 cm⁻¹ only gives little information. The most characteristic feature is the blue shift of the asym CH₂ upon a trans to gauche transition of one of the end groups.

Interaction with water. In analogy to the isolated molecule Fig. 5b shows all calculated conformers (see Table 1) of HME interacting with a water molecule and, not surprising, the different conformers cover the whole spectral range. Comparing Fig. 5b with Fig. 5a one notices that the interaction of HME with the H₂O molecule results in a more even distribution of the modes across the spectral range. In particular, the range between 2920 cm⁻¹ and 2940 cm⁻¹ is more regularly filled with bands compared to the isolated molecule. Another point is that the mode intensities vary less compared to HME alone where the vibrations below 2890 cm⁻¹ are overall more intense than those above. The high frequency region extends even further with the ttg conformer having the highest frequency at 2977 cm⁻¹ as for HME without H₂O.

As seen from Tables 1 and 2 and Fig. 6, water blue shifts most bands by up to 20 cm⁻¹. However, this is not necessarily true for all modes, as a comparison of the isolated with the water interacting molecule of the +g+g−g (#9/#19) and t+g−g (#10/20#) conformations reveals. In both cases two hydrogen bonds are formed, one via the OH of HME and one by the water (Fig. 4c and d). This is explained by a less strained geometry compared to the intermolecular hydrogen bonding without water (Fig. 2c and d).

Comparison with SFG spectra. Whereas the vibrational bands of Raman or IR spectra of poly(ethylene glycol) are dominated by the ethylene glycol units of the chain (–CH₂–CH₂–) rather than by the terminating moieties of which HME is representative in the case of OH terminated strands, studies of spectra of PEG films with SFG, which were recently reported,^11,12 suggest that the signal is dominated by the film surface, that is, one can expect that the dominating contribution comes from the chain terminating moieties. For the PEG/air interface the SFG spectrum of PEG400 (H–(O–CH₂–CH₂)₈–OH)¹² reproduced in Fig. 8c is characterized by five features located at 2970, 2930, 2913, 2872, and 2862 cm⁻¹. Comparing the experimental spectrum with the calculations, the band at 2970 cm⁻¹ clearly is an asym CH₂ vibration of the methylene group adjacent to the OH. As outlined above, such an unusually high frequency is characteristic of a conformation containing gauche OH⁴¹ and, thus, limits the number of conformations to contribute. At this point it is appropriate to discuss more generally which conformations are likely to contribute. One has to keep in mind that not only the spectra of the isolated HME fragment are relevant but also those where hydrogen bonding is involved. As mentioned above, the water molecule also mimics, to some extent, interactions between PEG molecules. Except for the tgt conformation where water points with its two hydrogens towards the oxygens of the HME (Fig. 4b) the other types of hydrogen bonding can also be realized by involving an OH group from a neighbouring PEG strand. Given that hydrogen bonding is energetically strongly favoured (Fig. 3) one would expect that the spectrum represents configurations involving hydrogen bonding. The other point is that the conformations are energetically different and, therefore, should exhibit different occupation numbers. A Boltzmann distribution (N_rel in Table 1) essentially yields conformers #19 and #20 which is not confirmed by the experiment since none of these conformations have vibrations above 2950 cm⁻¹, as demonstrated in Fig. 8. Additional factors seem to play a role which lead to significant contributions from energetically less favourable conformations. Not too surprising, the energy of the isolated HME fragment is inappropriate to infer the contribution of a particular conformation of the terminating moiety in a PEG strand. First of all, the conformational energy of the terminating moiety can be affected by the fragments attached. For example, the most stable conformation of DME changed from ttt to tgt upon substitution of one methyl group by additional EG units.^29,30 Other, probably even more important factors, are steric requirements and additional contributions to the total free energy of the systems such as the bonding of an EG strand to the substrate which might induce a transition from the lowest energy conformation of the isolated molecule to an energetically less favourable but sterically less demanding conformation.³⁰

Fig. 8 Comparison of calculated HME spectra with an experimental SFG spectrum of a PEG400 film in contact with air. (a) Energetically lowest conformations of isolated HME (#9/10), (b) HME/water (#18/19/20), (c) SFG spectrum.¹²

In the present case, the conformers which can contribute to the high frequency feature are ttg, gtg, −gt+g, t+g+g both with and without water all having significantly higher energies than t+g−g and +g+g−g. There is another point worth noting. The shape of the band is rather asymmetric implying that more than one conformer is involved and indeed both in the isolated (−gt+g #6, −gt−g #5, ttg #2) and water binding HME (gtt #17, ttg #16, ttg #15) there is a series of three bands. The intensities seem to follow the experimentally observed shape but this has to be taken as a fortuitous coincidence considering that the calculations represent the IR intensities whereas the intensities of experimental spectra contain both IR and Raman cross sections and, furthermore are dependent on experimental parameters and the orientation of the polymer chains.

The interpretation of the other vibrational features is less straightforward since, as inferred from Fig. 6, below 2955 cm⁻¹ different bands from both different modes and different methylene moieties can overlap. In particular, any detailed assignment of vibrational features below 2890 cm⁻¹ is a hopeless task due to the density of bands, keeping also in mind that the precision of the calculated band positions introduces additional uncertainties. The only rather safe statement is that the bands below 2830 cm⁻¹ arise from the C3 sym methylene modes. More details can only be inferred by comparison with partially deuterated substances. It is worth noting that in this range both experimental SFG^11,12 spectra of OH terminated PEG in contact with air report peaks around 2860–2865 cm⁻¹. However, the shape of the peaks indicate that more than one species contribute and looking at Fig. 6 and Fig. 8a and b a clear assignment of the peak to a particular mode (sym, asym) or CH₂ group seems questionable since in this range the conformers ttt, ttg, and tgt (#1–3), which are essentially equal in energy, have bands.

The third region between 2890 cm⁻¹ and 2955 cm⁻¹ even though it has a pronounced double peak structure also seems rather difficult to interpret at first glance since, again, different conformations are involved as seen from Fig. 5. In addition to bands of the isolated fragment, the ones originating from intermolecular H-bonded species should also be considered since from an energetic point of view they should be preferred. Focussing on the role of intermolecular hydrogen bonded conformers, the energetically most favourable conformers can hardly account for the structure as is obvious from the comparison of their band positions with the experimental spectrum (Fig. 8b and c). Taking the other conformers into account which are essentially equal in energy (#13–17, see Fig. 3) one would expect a rather structureless shape of the spectrum due to the rather uniform spread over the spectral range (see Fig. 5b). Interestingly, this is exactly what is observed when the PEG film as shown in Fig. 8c comes in contact with water.¹² The double peak structure (peaks at 2912 cm⁻¹ and 2930 cm⁻¹) and the minimum around 2955 cm⁻¹ vanish and the resulting spectrum exhibits two very broad maxima peaking at ∼2910 cm⁻¹ and ∼2850 cm⁻¹ the latter being the lower one. In contrast to the rather uniform distribution of bands for intermolecular hydrogen bonded HME, the bands of the isolated HME exhibits a significant grouping above 2890 cm⁻¹.

Comparing the experimental spectrum with the calculation of the isolated HME one, firstly, notices that the minimum in the experimental spectrum (Fig. 8c) is at the same position as a gap in the calculated spectra centered at ∼2895 cm⁻¹ (Fig. 5a). Secondly, there is another gap centered at ∼2927 cm⁻¹ which again agrees well with the minimum in the SFG spectrum of PEG400/air at ∼2923 cm⁻¹. Thirdly, there is a low density of bands between 2955 and 2960 cm⁻¹ which agrees with the minimum seen in the experiment at 2957 cm⁻¹. However, this cannot be taken as an argument for the isolated HME since the situation for the intermolecular H-bonded HME (Fig. 5b) is similar. It is the first two points which strongly suggest that the non-hydrogen bondend conformers are responsible for the characteristic shape of the PEG spectrum above 2900 cm⁻¹. This does not mean however, that H-bonded conformers are not present but they seem to play a minor role. To get an idea how well the calculated frequencies of the isolated HME can describe the PEG/air spectrum, a spectrum was calculated using a Gaussian line shape with a uniform half width of 12 cm⁻¹. Starting with the lowest energy conformation (#10) other conformers with increasing energy were added (#1–3,8,9,11) until the spectrum shown in Fig. 9a was obtained. It is stressed that this is not an attempt to interpret the spectrum quantitatively but to evaluate the agreement between experiment and calculations with respect to the band positions, i.e. the general shape of the experimental spectrum. A quantitative agreement cannot be expected since the ab initio data are IR data whereas the SFG spectrum involves both Raman and IR transitions. Furthermore, the SFG band intensities also depend on the molecular orientation and the SFG spectrum is a coherent superposition of bands whereas in the present case the bands are added incoherently like in a normal IR spectrum. The band intensities were simply adjusted to match the data. The degree of adjustment of the intensities can be inferred from the comparison between the used values (Fig. 9a) and the one resulting from the calculations (Fig. 9b). What is nicely described by the ab initio data is the high frequency band at 2970 cm⁻¹ and the double peak structure. Also the dip around 2895 cm⁻¹ is seen even though it is too deep. This mismatch in depth can have several reasons which are not clear at present. One is that the complete neglection of intermolecular H-bonded conformers which exhibit a rather high density of bands in this region oversimplifies the situation. Another reason could be that, besides the terminating unit modelled by the HME, the EG units as the main constituent of PEG make a contribution. Calculations of dimethoxy ethane (DME) as a representative fragment of the EG unit in PEG shows a band in exactly this range and it depends on the details of the film structure, that is the symmetry of the PEG strand how much this signal from the EG units contibute to the SFG signal.³⁴ There is another discrepancy at 2874 cm⁻¹ between the simulated and experimental spectra showing a dip instead of a peak. Obviously a significant band is missing. However, no attempt to improve this was undertaken for the following reason. As outlined above and seen from Fig. 5 there are many bands in this region and adding more conformers would remove the dip. However, nothing would be gained since, again, the chain EG units also have bands in this range.³⁴ This point merely underlines the statement made above that the region between 2890–2850 cm⁻¹ is useless for analytical purposes unless one knows a priori that the number of conformers is rather limited.

Fig. 9 Comparison of experimental SFG data of PEG400¹² with ab initio data for the isolated HME. (a) SFG data (□) and calculation (solid line) using adjusted intensities as reflected by the bars. (b) For comparison, intensities as obtained from the ab initio calculations.

Conclusions

The above calculations of 2-methoxy ethylene glycol show a pronounced dependence of the vibrational C–H stretching frequencies on the molecular conformation. Whereas the gauche conformations of the terminating OH group produces a clear signature, the identification of other conformations is more difficult since the bands partially overlap. This holds in particular for the region between 2850–2900 cm⁻¹ where an assignment of a band not only to a particular mode but also to a particular methylene group is hampered by the strong frequency variations as a function of the conformation. However, the calculations can help on a qualitative basis to identify characteristic vibrational features and to understand their changes such as the effect of water on the SFG spectrum of PEG, but any attempt for a more quantitative interpretation based on an equilibrium distribution of conformers of the model molecule is inappropriate as shown by the fact that energetically unfavourable conformers have to be taken into account to explain the experimentally observed spectrum. A more quantitative treatment requires to include additional contributions to the total energy such as packing effects and intermolecular interactions and, therefore, requires the comprehensive treatment at different levels including ab initio calculations of fragments or single strands and Monte Carlo simulations of the whole system.

Acknowledgements

The author is indebted to H. J. Kreuzer and R. Wang for helpful discussions and to L. Dreesen for making the SFG spectra available. Financial support from German Science Foundation, Fonds der Chemischen Industrie, and EPSRC is gratefully acknowledged.

References

1. M. R. Porter, Handbook of surfactants, 2nd edn., Blackie, London, 1994, ch. 7.
2. N. P. Desai and J. A. Hubbell, Biomaterials, 1991, 12, 144.
3. Poly(ethyleneglycol) Chemistry: Biotechnical and Biomedical Applications, ed. J. M. Harris, Plenum Press, New York, 1992.
4. K. L. Prime and G. M. Whitesides, Science, 1991, 252, 1164.
5. G. B. Sigal, M. Mrksich and G. M. Whitesides, J. Am. Chem. Soc., 1998, 120, 3464.
6. P. Harder, M. Grunze, R. Dahint, G. M. Whitesides and P. E. Laibinis, J. Phys. Chem. B, 1998, 102, 426.
7. K. Feldman, G. Hähner, N. D. Spencer, P. Harder and M. Grunze, J. Am. Chem. Soc., 1999, 121, 10 134.
8. R. Valiokas, S. Svedhem, S. C. T. Svensson and B. Liedberg, Langmuir, 1999, 15, 3390.
9. R. Valiokas, M. Ostblom, S. Svedhem, S. C. T. Svensson and B. Liedberg, J. Phys. Chem. B, 2000, 104, 7565.
10. S. R. Goates, D. A. Schofield and C. D. Bain, Langmuir, 1999, 15, 1400.
11. Z. Chen, R. Ward, Y. Tian, S. Baldelli, A. Opdahl, Y. R. Shen and G. A. Somorjai, J. Am. Chem. Soc., 2000, 122, 10 615.
12. L. Dreesen, C. Humbert, P. Hollander, A. A. Mani, K. Ataka, P. A. Thiry and A. Peremans, Chem. Phys. Lett., 2001, 333, 327.
13. M. Zolk, F. Eisert, J. Pipper, S. Herrwerth, W. Eck, M. Buck and M. Grunze, Langmuir, 2000, 16, 5849.
14. S. A. Vazquez, M. A. Rios and L. Carballeira, J. Comput. Chem., 1992, 13, 851.
15. S. Vazquez, R. A. Mosquera, M. A. Rios and C. Van Alsenoy, J. Mol. Struct. (THEOCHEM), 1989, 57, 95.
16. M. H. Langoor, L. M. J. Kroon-Batenburg and J. H. Van der Maas, J. Chem. Soc., Faraday Trans., 1997, 93, 4107.
17. F. P. S. C. Gil, R. Fausto, A. A. M. da Costa and J. J. Teixeira-Dias, J. Chem. Soc., Faraday Trans., 1994, 90, 689.
18. F. P. S. C. Gil and J. J. C. Teixeira-Dias, J. Mol. Struct. (THEOCHEM), 1995, 332, 269.
19. F. P. S. C. Gil, A. M. A. Da Costa and J. J. C. Teixeira-Dias, J. Phys. Chem., 1995, 99, 8066.
20. F. P. S. C. Gil, A. M. A. da Costa, R. E. Bruns and J. J. C. Teixeira-Dias, J. Phys. Chem., 1995, 99, 634.
21. F. P. S. C. Gil and J. J. C. Teixeira-Dias, J. Mol. Struct., 1999, 482/483, 621.
22. H. Yoshida, K. Takikawa, K. Ohno and H. Matsuura, J. Mol. Struct., 1993, 299, 141.
23. H. Yoshida, K. Takikawa, I. Kaneko and H. Matsuura, J. Mol. Struct. (THEOCHEM), 1994, 117, 205.
24. H. Yoshida, T. Harada and H. Matsuura, J. Mol. Struct., 1997, 413, 217.
25. M. A. Murcko and R. A. DiPaola, J. Am. Chem. Soc., 1992, 114, 10 010.
26. R. L. Jaffe, G. D. Smith and D. Y. Yoon, J. Phys. Chem., 1993, 97, 12 745.
27. H. Yoshida and H. Matsuura, J. Phys. Chem., 1998, 102, 2691.
28. R. L. C. Wang, H. J. Kreuzer and M. Grunze, J. Phys. Chem. B, 1997, 101, 9767.
29. R. L. C. Wang, H. J. Kreuzer and M. Grunze, Phys. Chem. Chem. Phys., 2000, 2, 3613.
30. A. J. Pertsin, M. Grunze and I. A. Garbuzova, J. Phys. Chem. B, 1998, 102, 4918.
31. A. Pertsin and M. Grunze, Langmuir, 2000, 16, 8829.
32. A. J. Pertsin, M. Grunze, H. J. Kreuzer and R. Wang, Phys. Chem. Chem. Phys., 2000, 2, 1729.
33. A. J. Pertsin, T. Hayashi and M. Grunze, Phys. Chem. Chem. Phys., 2001, 3, 1598.
34. M. Zolk, S. Herrwerth, W. Eck, M. Buck and M. Grunze, in preparation.
35. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 98 (Rev. A.7), Gaussian, Inc., Pittsburgh, PA, 1998.
36. O. Farkas and H. B. Schlegel, Phys. Chem. Chem. Phys., 2002, 4, 11.
37. The influence of basis set superposition effects (BSSE) on the relative energies of HME and water complexated HME was tested with counterpoise calculations using 6-31+G(d) and larger basis sets up to aug-cc-pVTZ. Whereas the counterpoise method did not yield any significant differences in energy compared to the simple scheme applied in Table 1, the aug-cc-pVTZ basis set produced deviations of up to 25%. For this reason two separate sets of N_rel, i.e. for HME and water complexated HME, are provided in Table 1.
38. Y. Dimitrova and D. Steele, Spectrochim. Acta, 1991, 47A, 75.
39. D. Lin-Vien, H. B. Colthup, W. G. Fateley and J. G. Grasselli, The Handbook of Infrared and Raman Characteristic Frequencies of Organic Molecules, Academic Press, San Diego, CA, 1991.
40. R. G. Snyder and J. R. Scherer, J. Chem. Phys., 1979, 71, 3221.
41. The contribution from the chain EG can be neglected since they do not have bands in this range as detailed in ref. 34.

---