Correlation between film properties and the purity of surfactants
Judith
Schlarmann
,
Cosima
Stubenrauch
* and
Reinhard
Strey
Institut für Physikalische Chemie, Universität zu Köln, Luxemburger Str. 116, D-50939 Köln, Germany
First published on 27th November 2002
Abstract
The disjoining pressure Π as a function of the film thickness h of aqueous tetraethyleneglycol-monodecylether (C10E4)-solutions was measured by means of a thin film pressure balance (TFPB). The Π(h)-curves were obtained for three surfactant concentrations for each of three samples, which differed in purity. Apart from a pure and an aged sample of C10E4, we investigated C10E4 solutions, which had been contaminated with decanol. In addition, the surface tension and the miscibility gap of the binary system water–C10E4 were measured. The aim of these investigations was to obtain a correlation between the above-mentioned properties, especially the disjoining pressure, of a non-ionic surfactant and its purity. We found that the impurities of the investigated sample strongly influence the position of the miscibility gap, whereas the effect on the surface tensions was unexpectedly low. With respect to the properties of thin films the impurities were found to decrease the electrostatic repulsion between the two monolayers of the film. As a consequence, common black films (CBF) are destabilized, whereas at concentrations around the c.m.c. an increasing stability of Newton black films (NBF) is observed. At first sight, these observations are in contrast to the results found by other groups, according to which the CBF is usually stabilized by the presence of impurities or the addition of alcohol. An explanation of this discrepancy is given.
1. Introduction
Foams are made of air bubbles dispersed in an aqueous solution, which forms the continuous phase. In a well-drained foam the single air bubbles are separated by thin films of the liquid containing a surface-active component, e.g. a surfactant. To understand the processes occurring in macroscopic foams the properties of these thin liquid films are of outstanding importance because factors playing a role in the microscopic system are believed to be relevant for foam stability.1–3 Thin liquid films can be studied by measuring the disjoining pressure Π, which acts in the liquid core of the film. The disjoining pressure is an excess force per unit area acting normal to the interface, thus preventing further film drainage. It mainly consists of three different interaction forces, namely van der Waals, electrostatic, and steric interactions.Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΠvdW ΠvdW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Πelec Πelec![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Πsteric Πsteric | (1) |
 | (2) |
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 Pa). An excellent overview is given in ref. 1.
40 Pa). An excellent overview is given in ref. 1.
Whereas reliable data for the influence of the surfactant concentration, the electrolyte concentration and the pH on the Π(h)-curves of non-ionic surfactants can be found in the quoted references, it is only in four studies that the effect of additives and/or impurities is considered.9,16–18 To our knowledge, the first study on the influence of impurities was done by Bergeron et al.16 who investigated aqueous solutions of the anionic surfactant sodium dodecylsulfate (SDS). A pronounced difference between the Π(h)-curve of a fresh and an aged solution was observed and interpreted as a consequence of the presence of dodecanol from SDS hydrolysis. At concentrations above the c.m.c. the films of the dodecanol contaminated sample are thinner than those of the fresh sample. An influence on the film stability and the step sizes of the thinning transitions is not reported. In contrast to these results, the presence of dodecanol in aqueous solutions of the cationic surfactant dodecyl trimethylammoniumbromide (C12TAB) does not alter the Π(h)-curve but strongly influences the film stability.17 These observations are consistent with those made by Monin et al.18 who found that adding octanol to sodium 1-octanesulfonate (C8SO3Na) solutions increases the stability of the corresponding thin liquid films. To complete the “confusion”, impurities in aqueous solutions of the sugar surfactant n-decyl-β-D-maltoside (β-C10G2) lead to both a change in the Π(h)-curve and an increase of the film stability.9 Surprisingly, a systematic study is completely missing although these investigations are expected to be of great relevance because technical products are usually based on mixtures. It is the interplay of the different components that determines the properties of the system; therefore studies of mixtures are indispensable to a deeper understanding of phenomena related to the stability of thin liquid films. In contrast to the small number of studies dealing with the influence of impurities on the Π(h)-curves, the influence of impurities on the surface tension9,19–22 and the miscibility gap of aqueous surfactant solutions22–24 has been investigated lextensively. At concentrations below the c.m.c., the surface tension of impure surfactants decreases as a function of time, whereas around the c.m.c. a minimum or a slow decay but no sharp bend is observed. In addition, for systems with a miscibility gap, the lower critical temperature Tc is very sensitive to traces of impurities and usually shifts to lower temperatures if the sample is contaminated. In a recent publication, both properties were investigated and compared systematically for the non-ionic surfactant tetraethyleneglycol–monooctylether (C8E4).22 It is shown that contaminants can have different influences on the miscibility gap and the surface tension isotherm, respectively. Thus it is only the combination of both measurements which can be taken as a reliable purity check.
The present paper is a study about the influence of impurities and additives on characteristic properties of the non-ionic surfactant tetraethyleneglycol-monodecylether (C10E4). The focus is on the miscibility gaps, the surface tension isotherms and Π(h)-curves of three different samples. Apart from a pure and an aged sample of C10E4, C10E4 solutions have been investigated, which had been contaminated with decanol to simulate the impurities of the aged sample. Whereas the miscibility gaps and the surface tension isotherms were measured to characterize the samples, the influence of impurities on properties of thin liquid films was intended to be studied with the Π(h)-curves. For that purpose, three different concentrations were chosen for which films of the pure, the impure and the contaminated sample were investigated. The study reveals the strong effect of impurities and additives and thus the necessity of detailed, systematic studies which are still missing. The results will be compared with literature data and related to the ongoing discussion about the stability of thin liquid soap films.
2. Experimental section
2.1 Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C by the DuNoüy ring method using a Krüss K10ST tensiometer. For the determination of the miscibility gap, water and surfactant were weighted in a glass tube, which was closed with a stopper. The samples were placed in a transparent water bath and the temperature was varied. After a period of constant stirring at a fixed temperature, the system was allowed to equilibrate and the number of phases were visually determined by inspection in scattered and transmitted light.
°C by the DuNoüy ring method using a Krüss K10ST tensiometer. For the determination of the miscibility gap, water and surfactant were weighted in a glass tube, which was closed with a stopper. The samples were placed in a transparent water bath and the temperature was varied. After a period of constant stirring at a fixed temperature, the system was allowed to equilibrate and the number of phases were visually determined by inspection in scattered and transmitted light.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3 (due to the dissolution of CO2 in the air). The error bars given for the Π(h)-curves are ±30 Pa for the pressure which results from the uncertainty in the hydrostatic pressure in the glass tube of the film holder and ±5% for the film thickness. The latter results from the uncertainty in the determination of the equilibrium intensity from which the film thickness is calculated.10
0.3 (due to the dissolution of CO2 in the air). The error bars given for the Π(h)-curves are ±30 Pa for the pressure which results from the uncertainty in the hydrostatic pressure in the glass tube of the film holder and ±5% for the film thickness. The latter results from the uncertainty in the determination of the equilibrium intensity from which the film thickness is calculated.10
2.2 Materials and cleaning procedure
The non-ionic surfactant tetraethyleneglycol-monodecylether (C10E4) was purchased from Bachem (Heidelberg, Germany). Two samples of different age were used. Decanol as well as sodium chloride were obtained from Merck (Germany) and the latter was roasted at 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C before use to remove impurities. All solutions were prepared with Milli-Q® water. All glassware (except the film holders) was cleaned with deconex® from Borer Chemie (as a replacement for chromic sulfuric acid) and rinsed thoroughly with water before use. The film holders were boiled two times in acetone, six times in water and eventually at least 0.5 l hot water were sucked through each disc.
°C before use to remove impurities. All solutions were prepared with Milli-Q® water. All glassware (except the film holders) was cleaned with deconex® from Borer Chemie (as a replacement for chromic sulfuric acid) and rinsed thoroughly with water before use. The film holders were boiled two times in acetone, six times in water and eventually at least 0.5 l hot water were sucked through each disc.
3. Results and discussion
Three different samples of the non-ionic surfactant tetraethyleneglycol–monodecylether (C10E4) were investigated, namely a fresh one, an aged one and a fresh sample to which decanol was added in the ratio nC10E4 : ndecanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 : 1 to simulate impurities that may emerge in this surfactant owing to degradation.23,25 In this way the influence of impurities and additives on the surface tension, the lower critical temperature Tc and the disjoining pressure Π of the water–C10E4 system could be studied. The results are shown and discussed in the following.
50 : 1 to simulate impurities that may emerge in this surfactant owing to degradation.23,25 In this way the influence of impurities and additives on the surface tension, the lower critical temperature Tc and the disjoining pressure Π of the water–C10E4 system could be studied. The results are shown and discussed in the following.
3.1 Miscibility gap and surface tension
As has been described in the introduction, the purity of non-ionic surfactants can be checked by measuring the surface tension and the lower critical temperature Tc of the miscibility gap of the binary water–surfactant system.22–24 The miscibility gaps for the binary water–C10E4 systems are shown in Fig. 1. The lower critical temperature of the fresh sample is Tc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20.1
20.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C at a critical composition of c
°C at a critical composition of c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.8 × 10−2 M. The critical temperature documented in literature is found to be Tc
7.8 × 10−2 M. The critical temperature documented in literature is found to be Tc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20.5
20.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C23 and Tc
°C23 and Tc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20.56
20.56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C,26 respectively. Although the Tc found in the present work is slightly shifted towards lower temperatures, the corresponding sample is named “pure”, which is justified by the measured surface tension isotherm (see below). For the aged sample Tc
°C,26 respectively. Although the Tc found in the present work is slightly shifted towards lower temperatures, the corresponding sample is named “pure”, which is justified by the measured surface tension isotherm (see below). For the aged sample Tc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18.8
18.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C was obtained, and a significant shift of the miscibility gap towards lower temperatures was observed. This shift is a clear indication of impurities in the sample, which will therefore be named “impure”. For the contaminated fresh sample an even lower Tc of 17.8
°C was obtained, and a significant shift of the miscibility gap towards lower temperatures was observed. This shift is a clear indication of impurities in the sample, which will therefore be named “impure”. For the contaminated fresh sample an even lower Tc of 17.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C and the corresponding shift of the miscibility gap were measured. This sample will be termed “pure
°C and the corresponding shift of the miscibility gap were measured. This sample will be termed “pure![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) decanol” or contaminated sample. Obviously, the contamination of the pure sample with decanol leads to properties comparable with the impure sample, at least with respect to the miscibility gap. In view of the fact that ionic surface-active impurities usually increase Tc,22 these results indicate that the impurities are of non-ionic nature. The surface activity of these impurities can be shown by measuring the corresponding surface tension isotherms.
decanol” or contaminated sample. Obviously, the contamination of the pure sample with decanol leads to properties comparable with the impure sample, at least with respect to the miscibility gap. In view of the fact that ionic surface-active impurities usually increase Tc,22 these results indicate that the impurities are of non-ionic nature. The surface activity of these impurities can be shown by measuring the corresponding surface tension isotherms.
 | ||
Fig. 1 Miscibility gaps of the binary water–C10E4 system for three different samples (○ pure sample, □ impure sample, ◇ pure sample![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) decanol). The lower critical points of the three miscibility gaps are marked with a filled symbol. decanol). The lower critical points of the three miscibility gaps are marked with a filled symbol. | ||
In Fig. 2 the surface tensions σ are presented as a function of the concentration c at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. As is expected for a pure sample, the surface tension decreases with increasing surfactant concentration down to the c.m.c., which is indicated by a sharp bend at 8.6 × 10−4 M. The isotherms for the two other samples are shifted so that the surface tension for a given concentration is lower than for the fresh sample. It is notable that it was not possible to measure the surface tension for the impure and the contaminated sample at 22
°C. As is expected for a pure sample, the surface tension decreases with increasing surfactant concentration down to the c.m.c., which is indicated by a sharp bend at 8.6 × 10−4 M. The isotherms for the two other samples are shifted so that the surface tension for a given concentration is lower than for the fresh sample. It is notable that it was not possible to measure the surface tension for the impure and the contaminated sample at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C for concentrations above 10−3 M, for the aqueous solution demixes. This is consistent with the shifted miscibility gaps (see Fig. 1). At concentrations above 10−3 M, a two-phase region is observed at 22
°C for concentrations above 10−3 M, for the aqueous solution demixes. This is consistent with the shifted miscibility gaps (see Fig. 1). At concentrations above 10−3 M, a two-phase region is observed at 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. In conclusion, one can say that the impurities are non-ionic surface active components, which can be simulated by decanol. These observations are in accordance with the postulated degradation from C10E4 to surfactants with shorter head groups, including C10E3, C10E2, C10E1, and the corresponding alcohol, namely decanol. In this context it has to be mentioned that Lang and Morgan investigated the influence of traces of C10E3 on the position of three-phase lines of the water–C10E4 system. A three-phase line occurs where three distinct phases simultaneously coexist. In a two-component system at constant pressure such a line is simply an isotherm at which a two-phase region is divided into two two-phase regions by a new third phase. Lang and Morgan found that a sample intentionally contaminated with 1% C10E3 had the three-phase lines translated by more than 1 K,26 in accordance with the shift of the miscibility gap in the presence of the non-ionic impurities mentioned above.
°C. In conclusion, one can say that the impurities are non-ionic surface active components, which can be simulated by decanol. These observations are in accordance with the postulated degradation from C10E4 to surfactants with shorter head groups, including C10E3, C10E2, C10E1, and the corresponding alcohol, namely decanol. In this context it has to be mentioned that Lang and Morgan investigated the influence of traces of C10E3 on the position of three-phase lines of the water–C10E4 system. A three-phase line occurs where three distinct phases simultaneously coexist. In a two-component system at constant pressure such a line is simply an isotherm at which a two-phase region is divided into two two-phase regions by a new third phase. Lang and Morgan found that a sample intentionally contaminated with 1% C10E3 had the three-phase lines translated by more than 1 K,26 in accordance with the shift of the miscibility gap in the presence of the non-ionic impurities mentioned above.
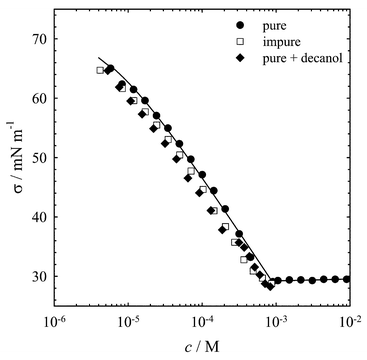 | ||
Fig. 2 Surface tension σ as a function of the C10E4 concentration c for three different samples (● pure sample, □ impure sample, ◆ pure sample![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) decanol) at T decanol) at T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. The error is about the size of the symbols. The line represents the best Langmuir–Szyskowski fit for the pure surfactant, leading to a c.m.c. of 8.6 °C. The error is about the size of the symbols. The line represents the best Langmuir–Szyskowski fit for the pure surfactant, leading to a c.m.c. of 8.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M. Note that for the impure samples surface tension measurements for c 10−4 M. Note that for the impure samples surface tension measurements for c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[greater than or equal, slant]](https://www.rsc.org/images/entities/char_2a7e.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 M were not possible at the chosen temperature. According to the lower miscibility gaps shown in Fig. 1 the solutions demix. 10−3 M were not possible at the chosen temperature. According to the lower miscibility gaps shown in Fig. 1 the solutions demix. | ||
A quantitative analysis of the surface tension isotherm is only reasonable for the pure surfactant. The corresponding data points were fitted with the Langmuir–Szyszkowski equation27,28
 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72.2 mN m−1 is the surface tension of the solvent, Γ∞ is the maximum surface concentration of surfactant and a represents the concentration at which 50% of Γ∞ has been reached. The best fitting parameters are Γ∞
72.2 mN m−1 is the surface tension of the solvent, Γ∞ is the maximum surface concentration of surfactant and a represents the concentration at which 50% of Γ∞ has been reached. The best fitting parameters are Γ∞![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.32 × 10−6 mol m−2 and a
3.32 × 10−6 mol m−2 and a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.48 × 10−6 M. With the results of this fit the surface excess Γ was calculated using the Gibbs equation:
4.48 × 10−6 M. With the results of this fit the surface excess Γ was calculated using the Gibbs equation: 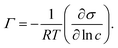 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.29 In the present case concentrations can be used because the c.m.c. of C10E4 is low enough to expect γs to be constant (but not to be 1!29,30) for c
0.29 In the present case concentrations can be used because the c.m.c. of C10E4 is low enough to expect γs to be constant (but not to be 1!29,30) for c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c.m.c. The results are shown in Fig. 3. The surface excess increases with increasing bulk concentration and reaches a plateau for concentrations around the c.m.c. Knowing Γ∞ and a the Gibbs' elasticities ε
c.m.c. The results are shown in Fig. 3. The surface excess increases with increasing bulk concentration and reaches a plateau for concentrations around the c.m.c. Knowing Γ∞ and a the Gibbs' elasticities ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −Γ(dσ/dΓ) can be calculated according to
−Γ(dσ/dΓ) can be calculated according to  | (6) |
 | ||
| Fig. 3 Surface excess Γ as a function of the bulk concentration c for aqueous solutions of the pure C10E4-sample calculated according to the Gibbs' adsorption equation. Inset: Calculated Gibbs' elasticities ε as a function of the surfactant concentration c derived from the fitted surface tension isotherm. | ||
3.2 Disjoining pressure
The disjoining pressure in films stabilized by C10E4 was examined for the effect of surfactant concentration, impurities, and additives. Film thicknesses were found to range from ca. 80 nm to less than 5 nm depending on the composition of the sample and the applied pressure, which ranges from 200 to 9000 Pa. The measured Π(h)-curves were compared with interaction curves calculated with the DLVO theory. To obtain the electrostatic component of the disjoining pressure the nonlinear Poisson–Boltzmann equation was solved. The calculations were done with the algorithm of Chan et al.,31 using constant charge boundary conditions and the theoretical Debye length κ−1.4 All surfactant solutions contained 10−4 M NaCl to have a fixed electrolyte concentration and thus a constant Debye length of κ−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30.4 nm. The van der Waals component of the disjoining pressure was calculated according to eqn. 2 with the Hamaker constant A
30.4 nm. The van der Waals component of the disjoining pressure was calculated according to eqn. 2 with the Hamaker constant A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.7 × 10−20 J for the air-water-air system.4 The parameter extracted from these calculations is the apparent surface potential ψ0, with which the corresponding surface charge density q0 can be calculated using the Grahame equation.4
3.7 × 10−20 J for the air-water-air system.4 The parameter extracted from these calculations is the apparent surface potential ψ0, with which the corresponding surface charge density q0 can be calculated using the Grahame equation.4
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.6 × 10−4 M), whereas the highest is around the c.m.c. Two different kinds of films were observed: thick common black films (CBF), stabilized by electrostatic repulsion and thin Newton black films (NBF), stabilized by steric repulsion. The thickness of the two CBFs decreases steadily as the capillary pressure increases, and the corresponding Π(h)-curves are nearly indistinguishable up to a pressure of around 2500 Pa. At higher pressures, however, the CBFs stabilized by the 2.5 × 10−4 M solution rupture around 4000 Pa, whereas those stabilized by the 5.0 × 10−4 M solution undergo a CBF–NBF transition at 2500 Pa. The increasing tendency to form NBFs with increasing surfactant concentration is well demonstrated in Fig. 4. For the highest surfactant concentration investigated, namely 7.5 × 10−4 M, the transition pressure is so low that under the experimental conditions only a NBF was seen. Note that the thickness of the NBF slightly decreases with increasing pressure, which indicates large flexible headgroups that can change their conformation and/or packing in the NBF.
8.6 × 10−4 M), whereas the highest is around the c.m.c. Two different kinds of films were observed: thick common black films (CBF), stabilized by electrostatic repulsion and thin Newton black films (NBF), stabilized by steric repulsion. The thickness of the two CBFs decreases steadily as the capillary pressure increases, and the corresponding Π(h)-curves are nearly indistinguishable up to a pressure of around 2500 Pa. At higher pressures, however, the CBFs stabilized by the 2.5 × 10−4 M solution rupture around 4000 Pa, whereas those stabilized by the 5.0 × 10−4 M solution undergo a CBF–NBF transition at 2500 Pa. The increasing tendency to form NBFs with increasing surfactant concentration is well demonstrated in Fig. 4. For the highest surfactant concentration investigated, namely 7.5 × 10−4 M, the transition pressure is so low that under the experimental conditions only a NBF was seen. Note that the thickness of the NBF slightly decreases with increasing pressure, which indicates large flexible headgroups that can change their conformation and/or packing in the NBF.
 | ||
Fig. 4 Disjoining pressure Π as a function of the film thickness h for three concentrations of the pure C10E4-sample in 10−4 M NaCl-solution. c1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M (○), c2 10−4 M (○), c2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M (□) and c3 10−4 M (□) and c3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.5 7.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M (◇). The two lower concentrations are below, the highest is around the c.m.c. (=8.6 10−4 M (◇). The two lower concentrations are below, the highest is around the c.m.c. (=8.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M). The solid lines are calculated according to the DLVO theory. The upper one corresponds to a surface potential of ψ0 10−4 M). The solid lines are calculated according to the DLVO theory. The upper one corresponds to a surface potential of ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 mV, the lower one to ψ0 40 mV, the lower one to ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 mV. 38 mV. | ||
First, we would like to discuss in detail the CBF properties. The present study provides further evidence for the general phenomenon that surfaces of foam films stabilized by non-ionic surfactants are charged.1,6,8–10,12,13,15,32,33 In the present work, the surface potentials are found to be ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and 38 mV for c
40 and 38 mV for c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 × 10−4 and 5.0 × 10−4 M, respectively, which correspond to surface charge densities of q0
2.5 × 10−4 and 5.0 × 10−4 M, respectively, which correspond to surface charge densities of q0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.01 and 0.95 mC m−2. The DLVO calculations are presented as solid lines in Fig. 4. At present, the specific adsorption of OH− ions at the water/air interface is the most convincing explanation of the origin of the charge although the mechanism is not known in detail and discrepancies are observed between the experimental and the theoretical data (for details see refs. 10,15,34,35). The observation that the Π(h)-curves of the two CBFs shown in Fig. 4 do not differ significantly means that a competitive adsorption between surfactant and the “surface ions”, which are responsible for the charge, does not take place. In other words, there is enough space at the surface for both components, which results in nearly the same surface charge densities for the films stabilized by a concentration of 2.5 × 10−4 and 5.0 × 10−4 M, respectively. To be more precise, the charge is usually found to be constant at low surfactant concentrations and decreases only significantly at concentrations around the c.m.c.6,10,15,32 Looking at Fig. 4, one expects a steep decrease of the surface charge for 5.0 × 10−4 M
1.01 and 0.95 mC m−2. The DLVO calculations are presented as solid lines in Fig. 4. At present, the specific adsorption of OH− ions at the water/air interface is the most convincing explanation of the origin of the charge although the mechanism is not known in detail and discrepancies are observed between the experimental and the theoretical data (for details see refs. 10,15,34,35). The observation that the Π(h)-curves of the two CBFs shown in Fig. 4 do not differ significantly means that a competitive adsorption between surfactant and the “surface ions”, which are responsible for the charge, does not take place. In other words, there is enough space at the surface for both components, which results in nearly the same surface charge densities for the films stabilized by a concentration of 2.5 × 10−4 and 5.0 × 10−4 M, respectively. To be more precise, the charge is usually found to be constant at low surfactant concentrations and decreases only significantly at concentrations around the c.m.c.6,10,15,32 Looking at Fig. 4, one expects a steep decrease of the surface charge for 5.0 × 10−4 M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c
c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.5 × 10−4 M as the surface charge of a NBF is negligible, which results in sterically stabilized films. However, it is not only a low charge, which is required for the NBF formation but also high elastic surfaces, i.e. high surface coverages. The transition from an electrostatically stabilized CBF to a sterically stabilized NBF is clearly seen for c
7.5 × 10−4 M as the surface charge of a NBF is negligible, which results in sterically stabilized films. However, it is not only a low charge, which is required for the NBF formation but also high elastic surfaces, i.e. high surface coverages. The transition from an electrostatically stabilized CBF to a sterically stabilized NBF is clearly seen for c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.0 × 10−4 M at pressures around 2500 Pa. For the lower concentration of 2.5 × 10−4 M the surface coverage and thus the surface elasticity is too low to stabilize a NBF so that the film ruptures around 4000 Pa instead of undergoing a CBF–NBF transition. The contrary is observed for the higher concentration of 7.5 × 10−4 M. In this case, the surface charge is too low to stabilize a CBF, whereas the surface coverage is high enough to stabilize a NBF, which is indeed formed immediately.
5.0 × 10−4 M at pressures around 2500 Pa. For the lower concentration of 2.5 × 10−4 M the surface coverage and thus the surface elasticity is too low to stabilize a NBF so that the film ruptures around 4000 Pa instead of undergoing a CBF–NBF transition. The contrary is observed for the higher concentration of 7.5 × 10−4 M. In this case, the surface charge is too low to stabilize a CBF, whereas the surface coverage is high enough to stabilize a NBF, which is indeed formed immediately.
An unexpected result is the strong up-turn of the Π(h)-curve at short separations, which was seen for the lowest concentration and reproduced three times. In contrast to these results, the Π(h)-curves of the intermediate concentration could be described satisfactorily with the classical DLVO theory. Although the reason for the up-turn is not known, the experimental observations are in perfect agreement with previous results obtained for β-C12G2.10 For this particular surfactant, six different concentrations were studied and an up-turn at concentrations below the c.m.c. was observed, which was most pronounced at c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ¼ c.m.c. and was not visible at concentrations around the c.m.c. Speculative as it may still be, a correlation between these results and those obtained for C10E4 seems to be likely. Work investigating this possible correlation is under way.
¼ c.m.c. and was not visible at concentrations around the c.m.c. Speculative as it may still be, a correlation between these results and those obtained for C10E4 seems to be likely. Work investigating this possible correlation is under way.
With the measured Π(h)-curves the different mechanisms stabilizing thin liquid films are not only well illustrated but clearly separated. The results for the two lower concentrations are a further example of the observation that similar surface forces do not automatically result in similar film stabilities. On the contrary, it was found that the stability increases steadily with increasing surfactant concentration, even in concentration ranges where no change of the surface forces is observed.6,10 In this case, the stability differences cannot be expressed in terms of electrostatic repulsive forces but depend on the elasticity of the films' surfaces.6,17 For the system at hand, it is shown in Fig. 3 that the Gibbs elasticity increases steeply from 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M to 5.0
10−4 M to 5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M, indicating a steep increase in the surface coverage and thus in the stability of the film.36 Whereas the CBF at c
10−4 M, indicating a steep increase in the surface coverage and thus in the stability of the film.36 Whereas the CBF at c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5
2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M ruptures around 4000 Pa, the corresponding NBF at c
10−4 M ruptures around 4000 Pa, the corresponding NBF at c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.0
5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M is stable over the whole pressure range studied. The comparison of these results with those obtained for β-C8G16 and β-C12G210 illustrates in a convincing way that the Gibbs elasticities explain the stability of thin liquid films only qualitatively but not quantitatively, as has been discussed by different scientists.6,10,17,37–40 Although the Gibbs elasticity of the 2.5
10−4 M is stable over the whole pressure range studied. The comparison of these results with those obtained for β-C8G16 and β-C12G210 illustrates in a convincing way that the Gibbs elasticities explain the stability of thin liquid films only qualitatively but not quantitatively, as has been discussed by different scientists.6,10,17,37–40 Although the Gibbs elasticity of the 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M solution is ten times higher than those reported for β-C8G1 and β-C12G2 in the studies mentioned above, the stabilities of the corresponding C10E4 films are similar to those of the β-C8G1 films and even lower than those of the β-C12G2 films, which have the lowest elasticities but the highest stabilities of the three surfactants compared above.
10−4 M solution is ten times higher than those reported for β-C8G1 and β-C12G2 in the studies mentioned above, the stabilities of the corresponding C10E4 films are similar to those of the β-C8G1 films and even lower than those of the β-C12G2 films, which have the lowest elasticities but the highest stabilities of the three surfactants compared above.
In literature some investigations on equilibrium foam films but only one complete Π(h)-curve of C10E4 can be found. Kolarov et al.12 studied the change in equilibrium film thickness heq of a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M C10E4 solution as a function of the electrolyte concentration cEl. They found that heq decreases with increasing cEl until a NBF is formed at cEl
10−4 M C10E4 solution as a function of the electrolyte concentration cEl. They found that heq decreases with increasing cEl until a NBF is formed at cEl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M. In a concentration range from 5
10−4 M. In a concentration range from 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 to 3
10−4 to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 M the formation of either a CBF or a NBF is observed until at cEl
10−3 M the formation of either a CBF or a NBF is observed until at cEl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 M a NBF is directly formed. Khristov et al.13 also investigated the equilibrium film thickness of C10E4 solutions. In this study, a concentration of 8
10−3 M a NBF is directly formed. Khristov et al.13 also investigated the equilibrium film thickness of C10E4 solutions. In this study, a concentration of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 M was chosen and heq was monitored as a function of pH. Starting from pH
10−5 M was chosen and heq was monitored as a function of pH. Starting from pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 they found that heq decreases with decreasing pH. In a pH-range from 3.6 to 4.7 they observed not only equilibrium but also rupturing films and named this region “zone of metastable films”. Below a pH of 3.6 no stable films were observed. As the instability is correlated with a steep decrease of the potential the points at which only rupturing films are observed have been named isoelectric points pH*.41 Furthermore, Khristov et al. investigated the foam lifetime as a function of the C10E4 concentration with a technique allowing to create a constant pressure in a macroscopic foam (foam pressure drop technique). However, nearly nothing is known about complete Π(h)-curves of C10E4 solutions. To our knowledge, only one Π(h)-curve has been measured, namely of a 5
6 they found that heq decreases with decreasing pH. In a pH-range from 3.6 to 4.7 they observed not only equilibrium but also rupturing films and named this region “zone of metastable films”. Below a pH of 3.6 no stable films were observed. As the instability is correlated with a steep decrease of the potential the points at which only rupturing films are observed have been named isoelectric points pH*.41 Furthermore, Khristov et al. investigated the foam lifetime as a function of the C10E4 concentration with a technique allowing to create a constant pressure in a macroscopic foam (foam pressure drop technique). However, nearly nothing is known about complete Π(h)-curves of C10E4 solutions. To our knowledge, only one Π(h)-curve has been measured, namely of a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M C10E4 solution at an electrolyte concentration of 3
10−4 M C10E4 solution at an electrolyte concentration of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M KCl. This particular composition was investigated independently by Kolarov et al.12 and Karraker and Radke.15 Whereas in the former work a transition from a CBF to a NBF was found at a film thickness of 11 nm and a pressure of around 5000 Pa, in the latter no transition was found. However, this inconsistency can simply be explained by the fact that Karraker and Radke investigated only pressures up to 5000 Pa. A NBF transition at higher pressures is likely. These results are in good agreement with the observations made in the present study. We found a CBF–NBF transition for a 5
10−4 M KCl. This particular composition was investigated independently by Kolarov et al.12 and Karraker and Radke.15 Whereas in the former work a transition from a CBF to a NBF was found at a film thickness of 11 nm and a pressure of around 5000 Pa, in the latter no transition was found. However, this inconsistency can simply be explained by the fact that Karraker and Radke investigated only pressures up to 5000 Pa. A NBF transition at higher pressures is likely. These results are in good agreement with the observations made in the present study. We found a CBF–NBF transition for a 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M C10E4 solution at a salt concentration of 10−4 M and a pressure of 2500 Pa. Compared to the compositions used in12,15 our electrolyte concentration was slightly lower. As the CBF–NBF transition is favoured at higher salt concentrations it is at first sight contradictory that we observed the CBF–NBF transition at lower pressures than reported by Kolarov et al. However, the film rupturing is a statistical process and it cannot be excluded that films made out of 10−4 M salt solutions are stable at pressures above 5000 Pa. Last but not least, Khristov et al. report the unsuccessful attempt to measure Π(h)-curves of C10E4 solutions at a concentration of 8
10−4 M C10E4 solution at a salt concentration of 10−4 M and a pressure of 2500 Pa. Compared to the compositions used in12,15 our electrolyte concentration was slightly lower. As the CBF–NBF transition is favoured at higher salt concentrations it is at first sight contradictory that we observed the CBF–NBF transition at lower pressures than reported by Kolarov et al. However, the film rupturing is a statistical process and it cannot be excluded that films made out of 10−4 M salt solutions are stable at pressures above 5000 Pa. Last but not least, Khristov et al. report the unsuccessful attempt to measure Π(h)-curves of C10E4 solutions at a concentration of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 M. In contrast to the investigations of the equilibrium films by means of the Sheludko cell it was impossible with the porous plate technique to obtain films since they ruptured at their formation. Obviously the films are not stable enough to resist the higher capillary pressure of film formation in the porous plate measuring cell. This observation is in accordance with our observation that the film stability decreases with decreasing C10E4 concentration. At 8
10−5 M. In contrast to the investigations of the equilibrium films by means of the Sheludko cell it was impossible with the porous plate technique to obtain films since they ruptured at their formation. Obviously the films are not stable enough to resist the higher capillary pressure of film formation in the porous plate measuring cell. This observation is in accordance with our observation that the film stability decreases with decreasing C10E4 concentration. At 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 M the Gibbs elasticity is a third of the value calculated for 2.5
10−5 M the Gibbs elasticity is a third of the value calculated for 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M (see Fig. 3) so that a very unstable film is expected.
10−4 M (see Fig. 3) so that a very unstable film is expected.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 : 1) and the impure sample were performed and compared with the results obtained for the pure sample. The corresponding Π(h)-curves for c
50 : 1) and the impure sample were performed and compared with the results obtained for the pure sample. The corresponding Π(h)-curves for c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5
2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M, 5.0
10−4 M, 5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M, and 7.5
10−4 M, and 7.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M are shown in Fig. 5(a), (b), and (c), respectively. The presence of decanol leads to a moderate decrease of the stability of the CBF and a small shift towards lower thicknesses is seen (Fig. 5(a), (b)). In contrast, the impurities significantly decrease both the stability and the thickness of the CBF. Therefore, for c
10−4 M are shown in Fig. 5(a), (b), and (c), respectively. The presence of decanol leads to a moderate decrease of the stability of the CBF and a small shift towards lower thicknesses is seen (Fig. 5(a), (b)). In contrast, the impurities significantly decrease both the stability and the thickness of the CBF. Therefore, for c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5
2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M a film rupture and for c
10−4 M a film rupture and for c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.0
5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M a CBF–NBF transition is observed at pressures which are much lower than those for the contaminated sample. The Π(h)-curve of the 7.5
10−4 M a CBF–NBF transition is observed at pressures which are much lower than those for the contaminated sample. The Π(h)-curve of the 7.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M solution is obviously not influenced by both the impurities and decanol.
10−4 M solution is obviously not influenced by both the impurities and decanol.
 | ||
Fig. 5 a: Disjoining pressure Π as a function of the film thickness h for the three investigated C10E4-samples (○ pure sample, ● impure sample, ⊙ pure sample![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) decanol) at a concentration of c decanol) at a concentration of c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M in 10−4 M NaCl-solution. The solid lines are calculated according to the DLVO theory. The upper one corresponds to a surface potential of ψ0 10−4 M in 10−4 M NaCl-solution. The solid lines are calculated according to the DLVO theory. The upper one corresponds to a surface potential of ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 mV, the intermediate one to ψ0 40 mV, the intermediate one to ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36 mV, and the lower one to ψ0 36 mV, and the lower one to ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 mV. b: Disjoining pressure Π as a function of the film thickness h for the three investigated C10E4-samples (□ pure sample, ■ impure sample, ⊡ pure sample 24 mV. b: Disjoining pressure Π as a function of the film thickness h for the three investigated C10E4-samples (□ pure sample, ■ impure sample, ⊡ pure sample![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) decanol) at a concentration of c decanol) at a concentration of c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M in 10−4 M NaCl-solution. The solid lines are calculated according to the DLVO theory. The upper one corresponds to a surface potential of ψ0 10−4 M in 10−4 M NaCl-solution. The solid lines are calculated according to the DLVO theory. The upper one corresponds to a surface potential of ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 mV, the lower one to ψ0 38 mV, the lower one to ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 mV. c: Disjoining pressure Π as a function of the film thickness h for the three investigated C10E4-samples (◇ pure sample, ◆ impure sample, 34 mV. c: Disjoining pressure Π as a function of the film thickness h for the three investigated C10E4-samples (◇ pure sample, ◆ impure sample, ![[diamond dotted]](https://www.rsc.org/images/entities/char_e084.gif) pure sample pure sample![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) decanol) at a concentration of c decanol) at a concentration of c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.5 7.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M in 10−4 M NaCl-solution. 10−4 M in 10−4 M NaCl-solution. | ||
First we would like to discuss the influence of decanol on the Π(h)-curves. The observations made can be interpreted in the following way: the adsorption of decanol at the surfaces of the film reduces both the surface charge and the surface elasticity. Note that under the chosen conditions of nC10E4 : ndecanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 : 1 only a slight decrease of the surface charge is observed, namely from q0
50 : 1 only a slight decrease of the surface charge is observed, namely from q0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.01 to 0.89 mC m−2 for c
1.01 to 0.89 mC m−2 for c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5
2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M and from q0
10−4 M and from q0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.95 to 0.84 mC m−2 for c
0.95 to 0.84 mC m−2 for c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.0
5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M. Apart from the film thickness it is also the CBF–NBF transition that is altered by lowering the surface charge (see Fig. 5(b)). As the electrostatic repulsion is decreased, the transition takes place at lower pressures compared to the pure system. However, the absence of the “up-turn”, which was observed for the pure sample at c
10−4 M. Apart from the film thickness it is also the CBF–NBF transition that is altered by lowering the surface charge (see Fig. 5(b)). As the electrostatic repulsion is decreased, the transition takes place at lower pressures compared to the pure system. However, the absence of the “up-turn”, which was observed for the pure sample at c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5
2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M, indicates that the lower stability of the CBF is probably not only due to a decrease of the surface charge but also to a decrease of the surface elasticity. Qualitatively this observation can easily be explained. In contrast to C10E4, decanol is not able to stabilize thin liquid films. In more general terms, the smaller the hydrophilic and hydrophobic part of the surfactant, the lower its ability to stabilize thin liquid films. Note that a reduction of the hydrophobic part from C10E4 to C8E4 also results in unstable films.14 Thus, an increase of the amount of decanol (or C8E4) in a C10E4/decanol- (or C10E4/C8E4-) mixture leads to a decreasing stability of the film, until it is no longer stable. However, we are not yet able to quantify the elasticity. In the discussion above it became clear that the Gibbs elasticity is not the appropriate value. Therefore we have to use the film stability as a measure for the surface elasticity. The more stable the film, the more elastic its surfaces. Knowing that the elasticity increases with the surfactant concentration, we can conclude from our results that films made of C10E4 solutions with c
10−4 M, indicates that the lower stability of the CBF is probably not only due to a decrease of the surface charge but also to a decrease of the surface elasticity. Qualitatively this observation can easily be explained. In contrast to C10E4, decanol is not able to stabilize thin liquid films. In more general terms, the smaller the hydrophilic and hydrophobic part of the surfactant, the lower its ability to stabilize thin liquid films. Note that a reduction of the hydrophobic part from C10E4 to C8E4 also results in unstable films.14 Thus, an increase of the amount of decanol (or C8E4) in a C10E4/decanol- (or C10E4/C8E4-) mixture leads to a decreasing stability of the film, until it is no longer stable. However, we are not yet able to quantify the elasticity. In the discussion above it became clear that the Gibbs elasticity is not the appropriate value. Therefore we have to use the film stability as a measure for the surface elasticity. The more stable the film, the more elastic its surfaces. Knowing that the elasticity increases with the surfactant concentration, we can conclude from our results that films made of C10E4 solutions with c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[greater than or equal, slant]](https://www.rsc.org/images/entities/char_2a7e.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.0
5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M are “elastic” enough to compensate for the slight elasticity decrease induced by the addition of decanol. With these results in mind, the data presented in Fig. 5(c) are not surprising. Small amounts of decanol have no influence on “non-charged” highly stable NBF.
10−4 M are “elastic” enough to compensate for the slight elasticity decrease induced by the addition of decanol. With these results in mind, the data presented in Fig. 5(c) are not surprising. Small amounts of decanol have no influence on “non-charged” highly stable NBF.
The effect of the impurities on the film properties is qualitatively the same as the effect of decanol. It is, however, much more pronounced. According to the DLVO calculations (see solid lines in Fig. 5) the CBFs become thinner and less stable because the surface charge is significantly reduced. In the case of c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5
2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M a reduction from q0
10−4 M a reduction from q0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.01 mC m−2 to q0
1.01 mC m−2 to q0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.57 mC m−2 is observed, whereas for c
0.57 mC m−2 is observed, whereas for c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.0
5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M the electrostatic interactions are so low that the stabilization of a CBF is not possible over a relevant pressure range. One difficulty in discussing these results derives from the ignorance of the kind and the amount of the impurities. We concluded from the miscibility gaps and the surface tension isotherms that decanol simulates the impurities very well. However, the shift of the miscibility gap of the impure sample can be interpreted in two different ways. Supposing that the impurities are only decanol (which is unlikely), the results shown in Fig. 1 indicate that the amount of impurities is less than nC10E4 : ndecanol
10−4 M the electrostatic interactions are so low that the stabilization of a CBF is not possible over a relevant pressure range. One difficulty in discussing these results derives from the ignorance of the kind and the amount of the impurities. We concluded from the miscibility gaps and the surface tension isotherms that decanol simulates the impurities very well. However, the shift of the miscibility gap of the impure sample can be interpreted in two different ways. Supposing that the impurities are only decanol (which is unlikely), the results shown in Fig. 1 indicate that the amount of impurities is less than nC10E4 : ndecanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 : 1 as the miscibility gap of the impure sample lies between the pure and the contaminated sample. However, this explanation is inconsistent with the measured Π(h)-curves. As the impurities have a much more pronounced effect than the contamination with decanol their amount has to be higher than nC10E4 : ndecanol
50 : 1 as the miscibility gap of the impure sample lies between the pure and the contaminated sample. However, this explanation is inconsistent with the measured Π(h)-curves. As the impurities have a much more pronounced effect than the contamination with decanol their amount has to be higher than nC10E4 : ndecanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 : 1. Another explanation of the intermediate position of the miscibility gap is that the impurities include all types of degradation products, namely C10E3, C10E2, C10E1, and decanol. In this case the shift of the miscibility gap is less pronounced even in the presence of significant amounts of impurities as far as the mixture is more hydrophilic than the C10E4/decanol-mixture. In view of the Π(h)-curves the second explanation is much more reasonable as a large amount of impurities is needed to explain the enormous decrease of the surface charge. Note that for the pure sample with c
50 : 1. Another explanation of the intermediate position of the miscibility gap is that the impurities include all types of degradation products, namely C10E3, C10E2, C10E1, and decanol. In this case the shift of the miscibility gap is less pronounced even in the presence of significant amounts of impurities as far as the mixture is more hydrophilic than the C10E4/decanol-mixture. In view of the Π(h)-curves the second explanation is much more reasonable as a large amount of impurities is needed to explain the enormous decrease of the surface charge. Note that for the pure sample with c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5
2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M neither an increase of the surfactant concentration to 5.0
10−4 M neither an increase of the surfactant concentration to 5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M nor the addition of highly surface-active decanol significantly changed the surface charge. The fact that the surface coverage of a “C10En<4” solution (to calculate an average headgroup length the total amounts of the single components are required) is higher than that of a C10E4 solution if equal bulk concentrations are considered explains the low surface charge density of the impure sample.
10−4 M nor the addition of highly surface-active decanol significantly changed the surface charge. The fact that the surface coverage of a “C10En<4” solution (to calculate an average headgroup length the total amounts of the single components are required) is higher than that of a C10E4 solution if equal bulk concentrations are considered explains the low surface charge density of the impure sample.
A direct comparison of our results with observations made by other groups is very difficult as different situations are considered. We found three papers in which the influence of non-ionic surface-active additives or impurities on the properties of films stabilized by ionic surfactants are investigated.16–18 In addition, one group reports the influence of ionic surface-active impurities on films stabilized by a non-ionic surfactant.9 However, examples similar to the situation investigated in the paper at hand, namely the influence of non-ionic additives and impurities on non-ionic foam films, were not found.
Let us first consider the influence of long chain alcohols on ionic foam films as studied in refs. 16–18. It was shown that highly purified dodecyl-trimethylammonium bromide (C12TAB) does not stabilize thin liquid foam films, whereas with the unpurified surfactant as well as with small amounts of added dodecanol stable C12TAB films were obtained.17 What is of crucial importance is that small amounts of impurities do not affect the surface forces but only the stability. A similar observation was made for the surfactant sodium 1-octanesulfonate (C8SO3Na). Whereas the pure C8SO3Na produces very unstable foams, the addition of small amounts of octanol stabilizes the foam.18 These results are attributed to an increasing elasticity of the surfaces.17 Although the monolayers are highly charged, which in turn generates relatively high activation barriers to rupture, the surface layers are not elastic enough to protect the film from fluctuations, which destabilize the film. It is shown that dense hydrocarbon layers are required to obtain stable films, which can be achieved by increasing the chain length of the surfactant (note that films stabilized by C14TAB are very stable) or by adding long-chain alcohols such as dodecanol.17 In both cases it is the cohesion (i.e. elasticity) within the monolayer that is increased, which enables the film to resist fluctuations. However, these results cannot be transferred to the system at hand, C10E4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) decanol. Instead of an increasing elasticity we observed the opposite when adding decanol. This can be explained by taking the structures of the surfactant and the alcohol into consideration. In the case of C12TAB and dodecanol the length of the hydrophilic and the hydrophobic part are comparable, whereas the hydrophilic E4-group of C10E4 is much more bulky than the OH-group of the alcohol. Thus the adsorption of decanol is expected to decrease the cohesion (i.e. the elasticity) within the hydrophilic part of the C10E4 monolayer as a dense packing at the surface is no longer possible. In contrast to the results obtained for C12TAB, the presence of dodecanol in solutions of sodium dodecylsulfate (SDS) has an influence on the thickness and thus on the forces of the SDS films.16 In this particular case, the amount of alcohol is so high that a remarkable displacement of surfactant at the interface takes place, which leads to less charged surfaces. Note that in the case of non-ionic foam films a simple displacement of surfactant by alcohol does not change the charge: it is only an increase in the total surface coverage that changes the charge if the charge giving surface ions are replaced.
decanol. Instead of an increasing elasticity we observed the opposite when adding decanol. This can be explained by taking the structures of the surfactant and the alcohol into consideration. In the case of C12TAB and dodecanol the length of the hydrophilic and the hydrophobic part are comparable, whereas the hydrophilic E4-group of C10E4 is much more bulky than the OH-group of the alcohol. Thus the adsorption of decanol is expected to decrease the cohesion (i.e. the elasticity) within the hydrophilic part of the C10E4 monolayer as a dense packing at the surface is no longer possible. In contrast to the results obtained for C12TAB, the presence of dodecanol in solutions of sodium dodecylsulfate (SDS) has an influence on the thickness and thus on the forces of the SDS films.16 In this particular case, the amount of alcohol is so high that a remarkable displacement of surfactant at the interface takes place, which leads to less charged surfaces. Note that in the case of non-ionic foam films a simple displacement of surfactant by alcohol does not change the charge: it is only an increase in the total surface coverage that changes the charge if the charge giving surface ions are replaced.
A different situation is considered by Persson et al.9 They investigated the influence of surface-active impurities on the surface properties of n-decyl-β-D-maltoside (β-C10G2)9 without knowing anything about the type of impurity in advance. As the presence of the impurities results in higher surface charges compared to the pure system, the authors conclude that the impurities are ionic surface-active components. A detailed analysis was not performed. The findings described so far allow us to speculate about the influence of impurities and/or additives. Additives that increase the surface elasticity stabilize the film. Whether a CBF or a NBF is stabilized depends on the charge of the additive. For example, in films stabilized by nonionic surfactants the addition of ionic surface-active components leads to higher surface charges and thus to more stable CBFs, whereas in the case of ionic foam films charges can be compensated by additives of opposite charge which destabilize the CBF but may favour a NBF formation. The effect non-ionic surface-active components have depends on their ability to increase the cohesion within in the monolayers, which in turn depends on the structure of the surfactant comprising the monolayer. It is obvious that each additive has to be considered separately with regard to both its influence on the surface charge and the surface elasticity. In order to understand the influence of additives, studies under defined conditions are needed, which means that both the kind and the amount of additive must be known.
4. Conclusions
The present work is the first systematic investigation into the influence additives and impurities have on the film properties of a non-ionic surfactant. We measured Π(h)-curves of thin liquid films stabilized by pure tetraethyleneglycol-monodecylether (C10E4) and compared the results with those obtained for an aged sample and for a sample, which was contaminated with decanol. In addition, we investigated the miscibility gaps and the surface tension isotherms of the respective solutions to obtain a more complete picture of the role the impurities play. With respect to the miscibility gaps we found a significant effect of the added decanol and the impurities, whereas the effect on the surface tension isotherms was unexpectedly low. Confining oneself to evaluating these results, one can argue that decanol simulates the impurities very well. However, the conclusion that the impurities are simply decanol is inconsistent with the Π(h)-curves. We found that adding decanol to pure C10E4 solutions has only a minor effect on the common black films (CBF) and no effect on the Newton black films (NBF). For the CBFs a small decrease of the surface charge and thus a slight decrease of the film stability were observed. The corresponding Π(h)-curves of the impure sample had a completely different appearance. An extremely low surface charge was found, even at the lowest concentration investigated, indicating a high surface coverage of non-ionic components, which at first sight seemed to conflict with the moderate decrease of the miscibility gap. However, this discrepancy can be easily explained if the impurities are not assumed to be simply decanol but a mixture of different degradation products including C10E3, C10E2, C10E1, and decanol.To conclude, one can say that the knowledge of the miscibility gaps and the surface tension isotherms is very important to interpret the influence of impurities on film properties. However, these results, especially the position of the miscibility gap, can also be misleading so that a prediction of the corresponding Π(h)-curves is not possible if the impurities are unknown. We believe that systematic studies combining bulk and surface properties as in the study at hand will allow us to identify, maybe even to quantify, impurities, which is important for a deeper understanding of the influence added surface-active components have. With regard to film properties the challenge is to control the surface charge and the film stability independently by tuning the appropriate parameters. Keeping in mind that the properties of thin liquid films are thought to be correlated to the properties of macroscopic foams, one realizes the great technical relevance investigations of film properties may have. In this respect, our next step will be to investigate the influence of additives and impurities on the properties of macroscopic foams with the foam pressure drop technique,3 which is expected to play an increasingly important role in thin film and foam studies.
Acknowledgements
We would like to thank Prof. P. Claesson for placing the program for the calculations of the DLVO interaction forces at our disposal. Lively and fruitful discussions with Dr T. Sottmann, Dr V. Bergeron and Prof. P. Claesson are gratefully acknowledged. C. Stubenrauch is indebted to the Fond der Chemischen Industrie and the Ministerium für Wissenschaft und Forschung des Landes NRW for financial support.References
- D. Exerowa and P. M. Kruglyakov, in Foam and Foam Films–Theory, Experiment, Application, ed. D. Möbius and R. Miller, Elsevier, Amsterdam, 1998 Search PubMed.
- R. J. Pugh, Adv. Colloid Interface Sci., 1996, 64, 67 CrossRef CAS.
- K. Khristov, D. Exerowa and K. Malysa, in Foams, Emulsions and their Application, ed. P. Zitha, J. Banhart and G. Verbist, Verlag MIT Publishing, Bremen, 2000 Search PubMed.
- J. Israelachvili, Intermolecular and Surface Forces, Academic Press, San Diego, 2nd edn., 1991 Search PubMed.
- V. Bergeron, J. Phys.: Condens. Matter, 1999, 11, R215 Search PubMed.
- V. Bergeron, A. Waltermo and P. M. Claesson, Langmuir, 1996, 12, 1336 CrossRef CAS.
- A. Waltermo, P. M. Claesson, S. Simonsson, E. Manev, I. Johansson and V. Bergeron, Langmuir, 1996, 12, 5271 CrossRef CAS.
- C. M. Persson, P. M. Claesson and I. Johansson, Langmuir, 2000, 16, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 227 CAS.
227 CAS. - C. M. Persson, P. M. Claesson and K. Lunkenheimer, J. Colloid Interface Sci., 2002, 251, 182 CrossRef CAS.
- C. Stubenrauch, J. Schlarmann and R. Strey, Phys. Chem. Chem. Phys., 2002, 4, 4504 RSC.
- D. Exerowa, M. Zacharieva, R. Cohen and D. Platikanov, Colloid Polym. Sci., 1979, 257, 1089.
- T. Kolarov, R. Cohen and D. Exerowa, Colloids Surf., 1989, 42, 49 CrossRef CAS.
- K. Khristov, D. Exerowa and R. Yankov, Colloids Surf. A, 1997, 129–130, 257 CrossRef.
- K. A. Karraker, PhD Thesis, University of California at Berkeley, 1999.
- K. A. Karraker and C. J. Radke, Adv. Colloid Interface Sci., 2002, 96, 231 CrossRef CAS.
- V. Bergeron and C. J. Radke, Langmuir, 1992, 8, 3020 CrossRef CAS.
- V. Bergeron, Langmuir, 1997, 13, 3474 CrossRef CAS.
- D. Monin, A. Espert and A. Colin, Langmuir, 2000, 16, 3873 CrossRef CAS.
- K. Lunkenheimer, H.-J. Pergande and H. Krüger, Rev. Sci. Instrum., 1987, 58, 2313 CrossRef CAS.
- K. Lunkenheimer and R. Miller, J. Colloid Interface Sci., 1987, 120, 176 CrossRef CAS.
- K. Lunkenheimer, K. Haage and R. Hirte, Langmuir, 1999, 15, 1052 CrossRef CAS.
- C. Stubenrauch, J. Schlarmann, T. Sottmann and R. Strey, J. Colloid Interface Sci., 2001, 244, 447 CrossRef CAS.
- K.-V. Schubert, R. Strey and M. Kahlweit, J. Colloid Interface Sci., 1991, 141, 21 CrossRef CAS.
- K.-V. Schubert, R. Strey and M. Kahlweit, Prog. Colloid Polym. Sci., 1991, 84, 103 Search PubMed.
- R. G. Laughlin, personal communication.
- J. C. Lang and R. D. Morgan, J. Chem. Phys., 1980, 73, 5849 CrossRef CAS.
- K. Lunkenheimer, G. Czichocki, R. Hirte and W. Barzyk, Colloid Surf. A, 1995, 101, 187 CrossRef CAS.
- R. Ribera and M. M. Velázquez, Langmuir, 1999, 15, 6686 CrossRef CAS.
- R. Strey, Y. Viisanen, M. Aratono, J. P. Kratohvil, Q. Yin and S. E. Friberg, J. Phys. Chem. B, 1999, 103, 9112 CrossRef CAS.
- J. Gracia-Fadrique, P. Brocos, A. Pineiro and A. Amigo, Langmuir, 2002, 18, 3604 CrossRef CAS.
- D. Y. Chan, R. M. Pashley and L. R. White, J. Colloid Interface Sci., 1980, 77, 283 CrossRef CAS.
- E. D. Manev and R. J. Pugh, Langmuir, 1991, 7, 2253 CrossRef CAS.
- R. Cohen and D. Exerowa, Colloids Surf. A, 1994, 85, 271 CrossRef CAS.
- K. G. Marinova, R. G. Alargova, N. D. Denkov, O. D. Velev, D. N. Petsev, I. B. Ivanov and R. P. Borwankar, Langmuir, 1996, 12, 2045 CrossRef CAS.
- C. Stubenrauch and R. V. Klitzing, J. Phys.: Condens. Matter, submitted Search PubMed.
- Note that the surface coverage can increase while the surface excess Γ remains constant. Whereas the latter is the interfacial excess of molecules related to the bulk concentration, the former is the total number of molecules at the interface. The change of total surface coverage at constant Γ is reflected in the steep decrease of the surface tension at concentrations around the c.m.c. from which the elasticities are calculated.
- D. Langevin, Adv. Colloid Interface Sci., 1998, 88, 29.
- D. Langevin, Curr. Opin. Colloid Interface Sci., 2000, 3, 600 Search PubMed.
- K.-D. Wantke, H. Fruhner, J. Fang and K. Lunkenheimer, Colloid Interface Sci., 1998, 208, 34 Search PubMed.
- H. Fruhner, K.-D. Wantke and K. Lunkenheimer, Colloids Surf. A, 1999, 162, 193 CrossRef CAS.
- D. Exerowa, Kolloid–Z. Z. Polym., 1969, 232, 703 Search PubMed.
| This journal is © the Owner Societies 2003 |
