Dependence of the mobility of tracer ions in aqueous perchlorate solutions on the hydrogen ion concentration
Received
22nd August 2002
, Accepted 25th October 2002
First published on 14th November 2002
Abstract
The dependence of the absolute individual ion mobility (AIIM) of the carrier-free radioactive ions [137Cs]Cs+, [201Tl]Tl+ and [57Co]Co2+ on the hydrogen ion concentration in aqueous perchlorate electrolyte mixtures was studied by means of the electromigration technique. The AIIM of the radioactive ions was found to decrease as the hydrogen ion concentration of the electrolyte mixture increases. Above pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 there is a fairly good agreement between experimental and calculated values. Below pH 4 the experimentally observed decrease of the AIIM is not explained by the extended Debye–Hückel–Onsager limiting law. The effect can possibly be explained by a change of the dynamical properties of electrolyte bulk water due to the increasing presence of an excess of hydrated protons in the bulk solution. From the variation of the rotational reorientation time of bulk water molecules in HClO4 electrolytes with the proton concentration, a value of 0.69 ps−1 is derived for the rate constant for proton transfer between the hydronium ions and the acceptor water molecules. For the proton hopping length a value of 2.46 Å was found. These two values are in good agreement with the literature values. Finally, we propose a relation for mobility of tracer ions in HClO4 electrolytes involving the proton hopping time and length.
4 there is a fairly good agreement between experimental and calculated values. Below pH 4 the experimentally observed decrease of the AIIM is not explained by the extended Debye–Hückel–Onsager limiting law. The effect can possibly be explained by a change of the dynamical properties of electrolyte bulk water due to the increasing presence of an excess of hydrated protons in the bulk solution. From the variation of the rotational reorientation time of bulk water molecules in HClO4 electrolytes with the proton concentration, a value of 0.69 ps−1 is derived for the rate constant for proton transfer between the hydronium ions and the acceptor water molecules. For the proton hopping length a value of 2.46 Å was found. These two values are in good agreement with the literature values. Finally, we propose a relation for mobility of tracer ions in HClO4 electrolytes involving the proton hopping time and length.
I Introduction
All ions are hydrated in aqueous solutions and the extent of hydration together with the ionic charge play an important role in many chemical reactions. Thus the investigation of the structural and dynamical properties of hydrated ions in aqueous solutions is of fundamental importance in physical chemistry.
The static properties of hydration, i.e. the hydration numbers and distances between the ions and oxygen atoms of hydrated water molecules, as well as the dynamical properties, i.e. the residence time and rotational behavior of water molecules in the first hydration shell, have been extensively investigated using X-ray and neutron diffraction, X-ray extended absorption fine structure, nuclear magnetic resonance, quasi-elastic neutron scattering and molecular dynamic simulation. A recent compilation of the results gained by the techniques mentioned above may be found elsewhere.1
Information on the dynamical properties of water molecules in the hydration shells of ions may also be deduced from the measurements of the transport properties of ions in solutions. The behavior of the limiting ionic mobility, u°, at zero concentration of added electrolyte reflects the complex relation existing between the water structure around the ion and the dynamics of ion-hydration. For a long time u° has been used as a probe to get insight into the dynamical aspects of ion–water interactions. Various theoretical models, from the initial solventberg model to molecular approach, have been employed to try to describe the dynamics of ions in solutions.2,3 More recently a self-consistent microscopic theory based on the microscopic version of the dielectric friction including rotational and translational friction of the solvent has been successfully employed to calculate the mobility of univalent ions in various polar solvents.4,5
At non-zero electrolyte concentrations, the ion atmosphere relaxation and electrophoretic effects contribute to a decrease of the ion mobility. In the range of very low electrolyte concentrations, the ion mobility is described without ambiguity by the well known Debye–Hückel–Onsager (DHO) limiting law.6,7 At higher electrolyte concentrations (c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ⩽
⩽![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 mol dm−3), an extension of the DHO limiting law based on the introduction of ion atmosphere parameters [see eqn. (11) in Section II B] leads to reasonable values for the ion mobility and diffusion coefficient for uni- and divalent ions in various neutral (pH
0.2 mol dm−3), an extension of the DHO limiting law based on the introduction of ion atmosphere parameters [see eqn. (11) in Section II B] leads to reasonable values for the ion mobility and diffusion coefficient for uni- and divalent ions in various neutral (pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∼
∼![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7) aqueous electrolytes.8,9 Recent molecular dynamics simulations of NaCl and KCl solutions show that the decrease of the ionic diffusion coefficient at increasing concentrations is correlated with the increase of the residence time τr of water molecules in the hydration shell of the ions as well as with the decrease of the bulk water diffusion coefficient, DH2O.10 At low electrolyte concentrations the product τrDH2O is constant and the hydration number remains unchanged.
7) aqueous electrolytes.8,9 Recent molecular dynamics simulations of NaCl and KCl solutions show that the decrease of the ionic diffusion coefficient at increasing concentrations is correlated with the increase of the residence time τr of water molecules in the hydration shell of the ions as well as with the decrease of the bulk water diffusion coefficient, DH2O.10 At low electrolyte concentrations the product τrDH2O is constant and the hydration number remains unchanged.
Most of the experimental and theoretical studies deal with the determination of the transport properties of ions in neutral aqueous electrolytes. Studies of the dynamical properties of ions in acidic aqueous electrolytes are scarce. In previous work,11 the absolute individual ion mobilities (AIIM) of carrier-free trivalent lanthanide ions, determined by means of the electromigration method, were found to be influenced by the hydrogen ion concentration in aqueous HClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaClO4 solutions at constant overall ionic strength, μ
NaClO4 solutions at constant overall ionic strength, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol dm−3 and T
0.1 mol dm−3 and T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1 K. Although the macroscopic properties of the two electrolytes, such as viscosity and density, are very close, the values of the AIIM of the lanthanide ions in 0.1 mol dm−3 HClO4 were about 15% lower than those in 0.1 mol dm−3 NaClO4. Thus transport of metal cations is affected by an excess of protons in the solution. The structure of acidic electrolytes is largely different from that of neutral electrolytes because the individual proton of the acid is directly transferred to a water molecule of the bulk and never returns as the nearest neighbour of its counter-ion.12 The interaction of protons with water molecules leads to the formation of complexes of the type H5O2+ or H9O4+.13,14 It is also well established that the migration of the excess proton in water occurs via a process of structural diffusion (Grötthus mechanism) in which charge transfer takes place through an interchange of covalent and hydrogen bonds.15 This mechanism is responsible for the proton's well known abnormally high mobility (up
298.1 K. Although the macroscopic properties of the two electrolytes, such as viscosity and density, are very close, the values of the AIIM of the lanthanide ions in 0.1 mol dm−3 HClO4 were about 15% lower than those in 0.1 mol dm−3 NaClO4. Thus transport of metal cations is affected by an excess of protons in the solution. The structure of acidic electrolytes is largely different from that of neutral electrolytes because the individual proton of the acid is directly transferred to a water molecule of the bulk and never returns as the nearest neighbour of its counter-ion.12 The interaction of protons with water molecules leads to the formation of complexes of the type H5O2+ or H9O4+.13,14 It is also well established that the migration of the excess proton in water occurs via a process of structural diffusion (Grötthus mechanism) in which charge transfer takes place through an interchange of covalent and hydrogen bonds.15 This mechanism is responsible for the proton's well known abnormally high mobility (up![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36.24
36.24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 m2 V−1 s−1 at T
10−8 m2 V−1 s−1 at T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1 K) . Fundamental results on the dynamics of the proton transfer in water may be found elsewhere.16–24 Since protons migrate very rapidly, they continuously interact with a great number of water molecules, in turn affecting the dynamics of bulk water. As the dynamical properties of the bulk water are coupled with those of the water molecules in the hydration shell of the ions, a difference in the transport properties of the ions in neutral and acidic media may be expected.
298.1 K) . Fundamental results on the dynamics of the proton transfer in water may be found elsewhere.16–24 Since protons migrate very rapidly, they continuously interact with a great number of water molecules, in turn affecting the dynamics of bulk water. As the dynamical properties of the bulk water are coupled with those of the water molecules in the hydration shell of the ions, a difference in the transport properties of the ions in neutral and acidic media may be expected.
In this paper, we investigate by means of the electromigration method the influence of the hydrogen ion concentration of chemically inert aqueous perchlorate electrolyte solutions on the absolute individual ion mobilities of the carrier-free radioactive ions [137Cs]Cs+, [201Tl]Tl+ and [57Co]Co2+ at tracer scale concentrations (≈10−11 mol). One major advantage of the radio-tracer technique is that the overall composition of the supporting electrolyte is not affected by the minute presence of the radioactive tracer ions. A change of the structural and dynamical properties of the supporting electrolyte on the other hand is then reflected by a modification of the mobility of the migrating radioactive ions.
The experimental values of the AIIM for the radioactive tracer ions investigated here are compared with the values predicted by the extended DHO limiting law. Using the migration data obtained in this work and those obtained for other radioactive ions in previous work,11,25 a systematic analysis of the variation of the AIIM with the hydrogen ion concentration of perchlorate electrolyte mixtures is performed assuming an equilibrium between two alternative dynamical states of the hydrated radioactive ion. This results in a semi-empirical relation for the dependence of the AIIM of the migrating ions on the overall electrolyte ionic strength and the hydrogen ion concentration.
The variation of the AIIM of the metal cations with increasing hydrogen ion concentration is also discussed in terms of a change of the dynamical properties of the electrolyte bulk water. The rate constant for proton transfer between the hydronium ions and water molecules is deduced from the hydrogen ion concentration dependence of the rotational reorientation time of bulk water molecules in HClO4 electrolytes. The proton hopping length is calculated from the proton mobility using the Einstein relation.
II Theory
A Ion mobility, ion micro-viscosity and rotational reorientation time of water molecules
The mobility of an ion can be related to the solution viscosity by the Stokes–Einstein equation for perfect sticking26,27| |  | (1) |
where e is the elementary charge (1.6022![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−19 C), zi the charge number of the ion, η the solution viscosity (kg m−1 s−1) and rS the Stokes radius (m). As the experimental results are generally difficult to interpret on the basis of the Stokes radius, Stokes’ law may be used in its microscopic form
10−19 C), zi the charge number of the ion, η the solution viscosity (kg m−1 s−1) and rS the Stokes radius (m). As the experimental results are generally difficult to interpret on the basis of the Stokes radius, Stokes’ law may be used in its microscopic form | |  | (2) |
which connects the ion mobility to the ion micro-viscosity, where ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i is the ion micro-viscosity (kg m−1 s−1), defined as the viscosity of the water molecules in the first hydration shell of the ion, and ri is the ionic radius (m).
i is the ion micro-viscosity (kg m−1 s−1), defined as the viscosity of the water molecules in the first hydration shell of the ion, and ri is the ionic radius (m).
The values of the ion micro-viscosity in pure water, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i° calculated from the ion mobility in pure water, ui° at 298.15 K28 for the ions investigated in this work are listed in Table 1. The ratio of
i° calculated from the ion mobility in pure water, ui° at 298.15 K28 for the ions investigated in this work are listed in Table 1. The ratio of ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i° against η°, the viscosity of water (η°
i° against η°, the viscosity of water (η°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.903
8.903![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 kg m−1 s−1 at 298.15 K29), reflects the effect of the ion on the structure of water. Here,
10−4 kg m−1 s−1 at 298.15 K29), reflects the effect of the ion on the structure of water. Here, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i°
i°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η° corresponds to the case of low charge density ions (Cs+, Tl+, etc.), referred to as structure-breakers, while
η° corresponds to the case of low charge density ions (Cs+, Tl+, etc.), referred to as structure-breakers, while ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i°
i°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η° corresponds to the case of high charge density ions (Sr2+, Co2+, La3+, etc.), classified as structure-makers. The ion micro-viscosity can be related to the vibrational frequency νi
(s−1) of the ion–water bond in the first hydration sphere as30
η° corresponds to the case of high charge density ions (Sr2+, Co2+, La3+, etc.), classified as structure-makers. The ion micro-viscosity can be related to the vibrational frequency νi
(s−1) of the ion–water bond in the first hydration sphere as30
| |  | (3) |
MH2O the molar mass of
H2O (kg mol
−1),
di the distance between the central ion and the oxygen atom of the hydrated water molecules (m), and
NA the Avogadro constant (6.022
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
23 mol
−1). The factor
χi takes into account the electrostriction,
i.e. the reduction of the effective radius of the water molecule caused by the electrostatic field of the ion. It can be calculated using Conway's equation:
31| |  | (4) |
where
ε0 is the permittivity of the vacuum (8.8541
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
−12 F m
−1), and
εr the dielectric constant of
water (78.36 at 298.15 K
28). Using the harmonic oscillator as a model for the ion-water system, the vibrational frequency of the ion–water bond may be connected to the hydration enthalpy Δ
Hhyd
(J mol
−1) as
30| | 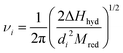 | (5) |
where
Mred is the reduced mass of the quasi-molecule ion–OH
2. For calculation of
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i
i° by means of
eqns. (3)–(5), the values of Δ
Hhyd obtained by means of the TATB extrathermodynamic assumption (Δ
Hhyd[C
6H
5)
4As
+]
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
ΔH
hyd[B(C
6H
5)
4−]) were employed.
32 The value of
di was set equal to
ri![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
+
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
(
δ/2), with
δ being the thickness of the hydration shell. For univalent, divalent and trivalent ions, the values of
δ were taken as 2.404, 2.334 and 2.276·10
−10 m, respectively.
33 As shown in
Table 1, the values of
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i
i° obtained by
eqn. (3) agree closely with those given by
eqn. (2), based on sticking conditions.
Table 1 Parameters of hydrated ions in pure water (T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.15 K). ui° is the absolute individual ion mobility at μ
298.15 K). ui° is the absolute individual ion mobility at μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 [refs. 28,49,50],
0 [refs. 28,49,50], ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i° the ion micro-viscosity, τi° the rotational reorientation time of water molecules in the first hydration shell of the ion, N the coordination number [ref. 1] and Δn the number of water molecules leaving the hydration shell during the exchange process with the bulk. ri is the ionic radius [refs. 51 and 52]. pK° is the first hydrolysis constant at 298.15 K for μ
i° the ion micro-viscosity, τi° the rotational reorientation time of water molecules in the first hydration shell of the ion, N the coordination number [ref. 1] and Δn the number of water molecules leaving the hydration shell during the exchange process with the bulk. ri is the ionic radius [refs. 51 and 52]. pK° is the first hydrolysis constant at 298.15 K for μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 [ref. 53]
0 [ref. 53]
| Ion |
r
i
/10−10 m |
u
i
°/10−8 m2 V−1 s−1 |
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i
°
[eqn. (2)]/10−4 kg−1 s−1
i
°
[eqn. (2)]/10−4 kg−1 s−1 |
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i
°
[eqn. (3)]/10−4 kg−1 s−1
i
°
[eqn. (3)]/10−4 kg−1 s−1 |
τ
i
°a/10−12 s |
N
|
Δn |
pK° |
|
Calculated from the data of column 4 with eqn. (6).
|
| Cs+ |
1.67 |
8.00 |
6.4 |
6.7 |
5.9 |
8 |
6.0 |
— |
| Tl+ |
1.50 |
7.74 |
7.3 |
8.0 |
6.8 |
6 |
4.2 |
13.2 |
| Na+ |
1.02 |
5.19 |
16.0 |
16.5 |
14.9 |
6 |
2.6 |
14.2 |
| Sr2+ |
1.26 |
6.16 |
21.9 |
20.5 |
20.4 |
8 |
2.7 |
13.3 |
| Co2+ |
0.65 |
5.70 |
45.9 |
42.2 |
42.8 |
6 |
1.0 |
9.7 |
| La3+ |
1.16 |
6.85 |
32.1 |
31.7 |
29.9 |
9 |
2.2 |
8.5 |
| Gd3+ |
1.05 |
6.62 |
36.7 |
35.6 |
34.2 |
8 |
1.7 |
8.0 |
| Tb3+ |
1.04 |
6.48 |
37.8 |
36.0 |
35.3 |
8 |
1.7 |
7.9 |
| Tm3+ |
0.99 |
6.48 |
39.8 |
38.0 |
37.0 |
8 |
1.6 |
7.7 |
| Yb3+ |
0.99 |
6.45 |
39.9 |
38.4 |
37.2 |
8 |
1.6 |
7.7 |
| Am3+ |
1.095 |
7.30 |
31.9 |
33.6 |
29.7 |
9 |
2.2 |
8.2 |
| ClO4− |
2.40 |
6.97 |
5.1 |
4.1 |
4.7 |
8 |
6.9 |
– |
It is also possible to determine the rotational reorientation time τi for water molecules in the hydration shell of the ion from the ion micro-viscosity using the Debye–Stokes–Einstein (DSE) relation:
| |  | (6) |
where
α is a numerical constant,
θ the effective radius of the
water molecule (1.38
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
−10 m),
k the Boltzmann constant (1.3807
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
−23 J K
−1) and
T the absolute temperature (K). Assuming that the DSE relation holds for pure
water and using a rotational reorientation time of
τH2O°
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
8.3 ps (the Debye relaxation time of
water at 298.15 K)
34,35 and a viscosity of 8.903
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
−4 kg m
−1 s
−1, we obtain
α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
4.65. The value of
α increases weakly as the temperature increases with a change of about 0.1% per degree in the range 273–328 K. The diffusion coefficient of pure
water calculated with the parameters above, (
DH2O°
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2
θ2/
τH2O°
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2.29
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
−9 m
2 s
−1) is in good agreement with the best known experimental value,
36 2.30
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
−9 m
2 s
−1. For the structure-breaker ions we find
τi°
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
<
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τH2O
τH2O° and for the structure-maker ions
τi°
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
>
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τH2O
τH2O°.
As the break-up of the first hydration shell is initiated principally by molecular reorientation, the number of water molecules leaving the hydration sphere over the period of time in which the outer bulk water shell is renewed, may be given by3
where
N is the number of
water molecules in the first hydration sphere at time zero,
i.e. the coordination number. The number of
water molecules remaining in the hydration shell during the exchange process is thus
N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
−
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
Δ
n. The values of
τi°
(in pure
water) as well as the values of
N and Δ
n for the ions investigated in this work are listed in
Table 1. The relative exchange rate of
water molecules between the hydration sphere and the bulk, Δ
n/
N, appears as an important quantity for the exchange process. As shown in
Fig. 1 for the
cations in pure
water, Δ
n/
N may be expressed as a complicated exponential function of the surface charge density of the ion,
σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
|
zi|
e/4π
r2i
(C m
−2):
| | 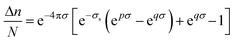 | (8) |
with
p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
11.65 (m
2 C
−1),
q![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
12.52 (m
2 C
−1) and
σs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
0.24 C m
−2. The surface charge density
σs corresponds to the maximum value of Δ
n/
N. Interestingly, the radii derived from
σs, which are 2.30, 3.26, and 4.00
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
−10 m for
zi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1, 2 and 3, respectively, are correlated through a proportionality factor of
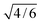
with the Hubbard–Onsager lengths,
RH–O, commonly used as
solvent parameters.
RH–O may be calculated using the following expression
37| |  | (9) |
with
ε∞ the high-frequency dielectric constant of
water (5.2 at 298.15 K).
28 From
eqns. (9) and (6), the surface charge density term
σs appears to be only dependent on the
solvent properties at a given temperature
| |  | (10) |
The value of
σs decreases weakly as the temperature increases with a change of about 0.1% per degree in the range 273–328 K. Finally, inserting the above expression
σs for in
eqn. (8) we obtain a general expression which describes well the transport properties of ions in pure
water as a function of the characteristics of the ions (ionic radius and charge) and of the
solvent properties. Furthermore, it is possible from
eqn. (8) to derive an analytical expression of the Stokes radius
rS using
eqn. (2).
![Relative exchange rate of water molecules between the first hydration sphere and the bulk, Δn/N, versus surface charge density σ of the ion in pure water at 298.15 K. The circles represent the univalent ions (Pe4N+, Bu4N+, Pr4N+, Et4N+, Me4N+, NH4+, Cs+, Rb+, K+, Tl+, Ag+, Na+, Li+); the squares the divalent ions (Ra2+, Ba2+, Pb2+, Sr2+, Hg2+, Ca2+, Cd2+, Mn2+, Zn2+, Cu2+, Mg2+, Ni2+, Co2+, Fe2+; Be2+) and the triangles the trivalent ions (La3+, Gd3+, Gd3+, Tb3+, Tm3+, Yb3+, Am3+, Sc3+, Fe3+, Al3+). The solid line is the fit of the data with eqn. (8). The ratio Δn/N was calculated by means of eqns. (7,6,2) using ionic radii from Shannon51 for monatomic ions and thermochemical radii from Jenkins and Thakur52 for polyatomic ions. The values of the ion mobility in pure water were taken from [ref. 28] except for lanthanide ions [ref. 49,50].](/image/article/2003/CP/b208227f/b208227f-f1.gif) |
| | Fig. 1 Relative exchange rate of water molecules between the first hydration sphere and the bulk, Δn/N, versus surface charge density σ of the ion in pure water at 298.15 K. The circles represent the univalent ions (Pe4N+, Bu4N+, Pr4N+, Et4N+, Me4N+, NH4+, Cs+, Rb+, K+, Tl+, Ag+, Na+, Li+); the squares the divalent ions (Ra2+, Ba2+, Pb2+, Sr2+, Hg2+, Ca2+, Cd2+, Mn2+, Zn2+, Cu2+, Mg2+, Ni2+, Co2+, Fe2+; Be2+) and the triangles the trivalent ions (La3+, Gd3+, Gd3+, Tb3+, Tm3+, Yb3+, Am3+, Sc3+, Fe3+, Al3+). The solid line is the fit of the data with eqn. (8). The ratio Δn/N was calculated by means of eqns. (7,6,2) using ionic radii from Shannon51 for monatomic ions and thermochemical radii from Jenkins and Thakur52 for polyatomic ions. The values of the ion mobility in pure water were taken from [ref. 28] except for lanthanide ions [ref. 49,50]. | |
B Ion mobility in electrolyte mixtures, ionic strength dependence
According to Onsager's theory based on the Debye–Hückel treatment of the ion atmosphere in dilute solutions38 and according to corrections proposed by Stokes et al. for finite ion-size effects39 in connection with dielectric saturation and local hydration of the ions,40 the ion mobility of an individual ion present at very low concentration (ci![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) in a chemically inert background electrolyte may be given by the following relation:
0) in a chemically inert background electrolyte may be given by the following relation: | |  | (11) |
where ui° is the limiting mobility of ion i
(m2 V−1 s−1), d(ωi) a mobility function, μ the overall ionic strength of the electrolyte (mol dm−3), κ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) √μ/3.041
√μ/3.041![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−10
(m−1) the reciprocal radius of the ion atmosphere,41 and a
(m) the distance of closest approach between oppositely charged ions of the background electrolyte.42 The mobility function may be expressed by:
10−10
(m−1) the reciprocal radius of the ion atmosphere,41 and a
(m) the distance of closest approach between oppositely charged ions of the background electrolyte.42 The mobility function may be expressed by: | |  | (12) |
where cj and zj are the concentration and the charge of the jth component of the background electrolyte. Eqn. (11), called the extended DHO limiting law, is valid only for electrolyte concentrations lower than about 0.2 mol dm−3. For higher electrolyte concentrations, the ion mobility (or the diffusion coefficient) increases and reaches a maximum value (generally higher than the limiting value in pure water) at about 1.2 mol dm−3 before it decreases again.9 Unfortunately, no pertinent law exists to describe the behavior of transport properties of an individual ion in electrolyte solutions of concentrations higher than 0.2 mol dm−3.
In the case of a mixed background electrolyte of type MX/HX composed of univalent ions (in our experiments NaClO4/HClO4), for which the overall ionic strength is kept constant, the change of the pH of the solution is obtained by replacing M+ ions by H+ ions (μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [M+]
[M+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [H+]
[H+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [X−]). The mobility function can then be expressed as a function of the hydrogen ion concentration [H+]
[X−]). The mobility function can then be expressed as a function of the hydrogen ion concentration [H+]
| |  | (13) |
where
d(
ωHXi) and
d(
ωMXi) are the mobility functions of the individual ions for the electrolytes HX and MX. The change in the parameter
a, the mean value of the distance between oppositely charged ions, with the pH of the electrolyte mixture may be expressed similarly by
| | 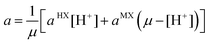 | (14) |
where
aHX and
aMX are the distances of closest approach for the ions of the electrolytes HX and MX.
For a mixed electrolyte of type NX2/MX/HX, composed of uni- and divalent ions (in our experiment Co(ClO4)2/NaClO4/HClO4), for which the overall ionic strength μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μNX2
μNX2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μMX is kept constant, and the change of the pH of the solution is achieved by replacing M+ ions by H+ ions, the mobility function is given as a function of the proton concentration [H+] by
μMX is kept constant, and the change of the pH of the solution is achieved by replacing M+ ions by H+ ions, the mobility function is given as a function of the proton concentration [H+] by
| |  | (15) |
where
 d
d(
ωHXi) and
d(
ωMXi) are the mobility functions of the individual ions for the electrolytes NX
2, HX and MX. The change of the parameter
a with the pH of the electrolyte mixture may be expressed by
| |  | (16) |
where
aNX2,
aHX and
aMX are the distances of closest approach for the individual electrolytes NX
2, HX and MX.
If the migrating tracer cations are not involved in hydrolysis equilibria (Mn+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mH2O
mH2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ⇔
⇔![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M(OH)m(n−m)+
M(OH)m(n−m)+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mH+), which is in fact the case for our experimental study (for the onset of the hydrolysis reactions see the pK°-values in Table 1), the AIIM of the cations can be calculated for various pH values of the mixed electrolyte (for overall ionic strength lower than 0.2 mol dm−3) using eqns. (11), (13) and (14) and (11), (15) and (16) respectively. The electrolyte parameters employed for the calculations are listed in Table 2. The pH-dependence of AIIM of Cs+, Tl+ and Co2+ ions is shown in Fig. 2.
mH+), which is in fact the case for our experimental study (for the onset of the hydrolysis reactions see the pK°-values in Table 1), the AIIM of the cations can be calculated for various pH values of the mixed electrolyte (for overall ionic strength lower than 0.2 mol dm−3) using eqns. (11), (13) and (14) and (11), (15) and (16) respectively. The electrolyte parameters employed for the calculations are listed in Table 2. The pH-dependence of AIIM of Cs+, Tl+ and Co2+ ions is shown in Fig. 2.
Table 2 Electrolyte parameters used to calculate the absolute individual ion mobilities by means of eqns. (9)–(14) at T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.15 K
298.15 K
|
u°/10−8 m2 V−1 s−1 |
a/10−10 m |
Ref. 28.
Ref. 42.
Interpolated from the relation a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75.56 (r+ 75.56 (r+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r−)−1
− 18.06 obtained for the perchlorate data: a(NaClO4) r−)−1
− 18.06 obtained for the perchlorate data: a(NaClO4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.04 Å, a(LiClO4) 4.04 Å, a(LiClO4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.63 Å, a(Zn(ClO4)2) 5.63 Å, a(Zn(ClO4)2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.18 Å
[ref. 41] with r+ the ionic radius of the cation and r− that of the anion/Å. 6.18 Å
[ref. 41] with r+ the ionic radius of the cation and r− that of the anion/Å.
|
| Na+ |
ClO4− |
Co2+ |
H+ |
NaClO4 |
HClO4 |
Co(ClO4)2 |
| 5.19a |
6.97a |
5.70a |
36.24a |
4.04b |
5.09b |
6.73c |
 |
| | Fig. 2 Variation of the ion mobility of Cs+, Tl+ and Co2+ ions according to the pH of inert electrolyte mixtures of overall ionic strength μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol dm−3
(solid line: Na(H)ClO4, dashed line: Co(ClO4)/Na(H)ClO4) calculated with the extended limiting law, eqn. (11). 0.1 mol dm−3
(solid line: Na(H)ClO4, dashed line: Co(ClO4)/Na(H)ClO4) calculated with the extended limiting law, eqn. (11). | |
III Experiment
A Sample preparation
The carrier-free radioisotopes 137Cs, 57Co, (CSI Diagnostik GmbH) and 201Tl (Mallinckrodt Medical BV) were used. Aliquots of solutions of 137Cs (400 MBq mL−1, 1 mol dm−3 HCl) and 57Co (80 MBq mL−1, 1 mol dm−3 HCl) were diluted with deionized water to obtain specific volume activities of about 40 MBq mL−1 for both cations. In the case of 201Tl, isotonic solutions of thallium chloride (37 MBq mL−1, 0.16 mol dm−3 NaCl) were used directly.
Background electrolyte mixtures of the type NaClO4/HClO4 and Co(ClO4)2/NaClO4/HClO4 were prepared from deionized water and analytical grade chemicals. The overall ionic strength was μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3 for all electrolytes. The concentration of Co(ClO4)2 was fixed to 0.023 mol dm−3.
0.10 mol dm−3 for all electrolytes. The concentration of Co(ClO4)2 was fixed to 0.023 mol dm−3.
The pH of the electrolytes was measured by means of pre-calibrated glass electrode using standard buffer solutions. The estimated uncertainty was ±0.02 in pH units.
B Measurement of the ion mobility
The measurement of the AIIM of the radioactive ions was performed by means of the free-electrolyte continuous electromigration technique. The apparatus used in this work as well as the analytical procedure for the on-line determination of the migration velocities of radioactive ions are described in detail elsewhere.8,43 In order to eliminate electroosmosis, the inner surface of the migration tube was coated with a monomolecular layer of non-cross-linked polyacrylamide according to the method proposed by Hjertén.44
The migration tube (id 3 mm, length 500 mm) was filled with the electrolyte mixture of a given composition. To exclude convection flows, the migration tube was connected to the electrode cells via hydrodynamic resistors (polycarbonate membranes). A bolus of 1–5 μL of the solution containing the radio-isotope (∼10−11 mol) under investigation was injected into the migration tube. An electric field intensity of 2.5 or 10 V cm−1 was applied over the migration zone by the use of platinum electrodes immersed in the electrode cells. To ensure a constancy of electrolyte composition and pH in the migration tube, the electrolyte solution in the electrode cells was continuously refreshed by means of a peristaltic pump. The electromigration experiments were carried out at a temperature of 298.1(5) K using an appropriate thermostatting system.
The migration of the radio-ions was studied over a period of 30 min by continuously scanning the migration tube with a well collimated bismuth germanate (BGO) scintillation detector. For each scan, the absolute position of the ions was determined by analysis of the recorded activity distribution with a Gaussian or Lorentzian, setting a preferential fit on the front of the migration. The migration velocity of the radioactive ions was calculated on-line from the slope of the linear relation obtained between the position of the radioactive ions and the time. The absolute individual ion mobility was determined by dividing the migration velocity by the intensity of the electric field.
Each value of the AIIM reported in this study is an average of two to four independent measurements with a precision ranging between 0.5 and 2%. The standard deviations on the average value of the AIIM range from 2 to 4%.
III Results
A pH dependence of the AIIM
The AIIM of the Cs+, Tl+ and Co2+ radioactive ions versus the pH of the inert electrolyte mixtures is plotted in Fig. 3. The AIIM increases as the pH is raised from pH 1 to pH 4. Up to pH 4 the AIIM is constant. The increase of the AIIM at decreasing hydrogen ion concentrations was not expected since changes of electrolyte parameters like density, viscosity, dielectric constant or others between pH 1 and 7 can be neglected. For example, the viscosity of 0.10 mol dm−3 NaClO4 is 9.001![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 kg−1 s−1 and that of 0.10 mol dm−3 HClO4 is 9.117
10−4 kg−1 s−1 and that of 0.10 mol dm−3 HClO4 is 9.117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 kg−1 s−1.45 The difference in the viscosity is only 1.3%, while the AIIM of the ions studied for the two electrolytes differ by 10 to 20%. Furthermore, no metal-ligand complexation equilibria, redox reactions or protonization equilibria may have an influence on the mobility of the investigated ions. The coating of the inner surface of the migration tube for suppression of the electroosmosis performed well since no change in the height and shape of the measured radioactive distributions was detected during the electromigration runs. No adsorption of the radioactive ions on the wall of the migration tube was observed. Similar dependences of the ion mobility on the pH of inert aqueous solutions have been found for the lanthanide ions in previous study (Fig. 4).11 The two levels of the migration data obtained for the neutral and acidic electrolytes are given in Table 3 and Table 4 respectively.
10−4 kg−1 s−1.45 The difference in the viscosity is only 1.3%, while the AIIM of the ions studied for the two electrolytes differ by 10 to 20%. Furthermore, no metal-ligand complexation equilibria, redox reactions or protonization equilibria may have an influence on the mobility of the investigated ions. The coating of the inner surface of the migration tube for suppression of the electroosmosis performed well since no change in the height and shape of the measured radioactive distributions was detected during the electromigration runs. No adsorption of the radioactive ions on the wall of the migration tube was observed. Similar dependences of the ion mobility on the pH of inert aqueous solutions have been found for the lanthanide ions in previous study (Fig. 4).11 The two levels of the migration data obtained for the neutral and acidic electrolytes are given in Table 3 and Table 4 respectively.
 |
| | Fig. 3 (a) Ion mobility of Cs+ in Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3). (b) Ion mobility of Tl+ in Na(H)ClO4
(μ 0.10 mol dm−3). (b) Ion mobility of Tl+ in Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3). (c) Ion mobility of Co2+ in Na(H)ClO4
(μ 0.10 mol dm−3). (c) Ion mobility of Co2+ in Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3), open symbols; ion mobility of Co2+ in Co(ClO4)2/Na(H)ClO4
(μ 0.10 mol dm−3), open symbols; ion mobility of Co2+ in Co(ClO4)2/Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3, μCo(ClO4)2 0.10 mol dm−3, μCo(ClO4)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.068 mol dm−3, μNa(H)ClO4 0.068 mol dm−3, μNa(H)ClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.032 mol dm−3), close symbols. The solid line is the fit of experimental data using eqn. (19), the dashed line is the ion mobility calculated using eqn. (11), the dotted line is the ion mobility calculated using eqn. (24). 0.032 mol dm−3), close symbols. The solid line is the fit of experimental data using eqn. (19), the dashed line is the ion mobility calculated using eqn. (11), the dotted line is the ion mobility calculated using eqn. (24). | |
 |
| | Fig. 4 (a) Ion mobility of La3+ in Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 mol dm−3). (b) Ion mobility of Gd3+ in Na(H)ClO4
(μ 0.01 mol dm−3). (b) Ion mobility of Gd3+ in Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3). (c) Ion mobility of Lu3+ in Na(H)ClO4
(μ 0.10 mol dm−3). (c) Ion mobility of Lu3+ in Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3). The solid line is the fit of experimental data using eqn. (21), the dotted line is the ion mobility calculated using eqn. (24). 0.10 mol dm−3). The solid line is the fit of experimental data using eqn. (21), the dotted line is the ion mobility calculated using eqn. (24). | |
Table 3 Parameters of hydrated ions in the neutral aqueous perchlorate electrolyte. ui is the experimental absolute individual ion mobility, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i the ion micro-viscosity, and τi the rotational reorientation time of water molecules in the first hydration shell. ri is the ionic radius. T
i the ion micro-viscosity, and τi the rotational reorientation time of water molecules in the first hydration shell. ri is the ionic radius. T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1(5) K
298.1(5) K
| Ion |
r
i
/10−10 m |
u
i/10−8 m2 V−1 s−1
|
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i
[eqn. (2)]/10−4 kg−1 s−1 i
[eqn. (2)]/10−4 kg−1 s−1 |
τ
i
[eqn. (6)]/10−12 s |
τ
i
[eqn. (26)]/10−12 s |
|
This work.
Ref. 25.
Ref. 11.
|
NaClO4, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 0.1 |
| Cs+ |
1.67 |
7.66(2)a |
6.6 |
6.2 |
6.1 |
| Tl+ |
1.50 |
7.51(4)a |
7.5 |
7.0 |
7.1 |
| Co2+ |
0.65 |
5.05(5)a |
51.8 |
48.3 |
44.6 |
| Sr2+ |
1.26 |
5.87(5)b |
23.0 |
21.4 |
21.3 |
| Gd3+ |
1.05 |
6.09(4)c |
39.9 |
37.2 |
35.6 |
| Tb3+ |
1.04 |
5.77(4)c |
42.5 |
39.6 |
36.8 |
| Tm3+ |
0.99 |
5.91(5)c |
43.6 |
40.6 |
38.6 |
| Yb3+ |
0.99 |
6.28(7)c |
41.0 |
38.2 |
38.8 |
| Lu3+ |
0.97 |
5.99(9)c |
43.9 |
40.9 |
— |
| Am3+ |
1.095 |
7.00(12)c |
32.0 |
29.8 |
31.0 |
NaClO4, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 0.01 |
| La3+ |
1.16 |
6.70(5)c |
32.8 |
30.6 |
30.5 |
Co(ClO4)/NaClO4, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 0.1 |
| Co2+ |
0.65 |
5.19(4)a |
50.4 |
46.9 |
45.9 |
Table 4 Parameter of hydrated ions in acidic aqueous pechlorate electrolytes. ui is the experimental absolute individual ion mobility, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i the ion micro-viscosity, and τi the rotational reorientation time of water molecules in the first hydration shell. ri is the ionic radius. T
i the ion micro-viscosity, and τi the rotational reorientation time of water molecules in the first hydration shell. ri is the ionic radius. T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1(5) K
298.1(5) K
| Ion |
r
i/10−10 m
|
u
i/10−8 m2 V−1 s−1
|
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i
[eqn. (2)]/10−4 kg−1 s−1
i
[eqn. (2)]/10−4 kg−1 s−1 |
τ
i
[eqn. (6)]/10−12 s |
τ
i
[eqn. (26)]/10−12 s |
|
this work
[Ref. 25]
[Ref. 11]
|
HClO4, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 0.1 |
| Cs+ |
1.67 |
6.78(16)a |
7.5 |
7.0 |
7.2 |
| Tl+ |
1.50 |
6.99(34)a |
8.1 |
7.6 |
8.3 |
| Co2+ |
0.65 |
4.14(8)a |
63.2 |
58.9 |
52.1 |
| Sr2+ |
1.26 |
5.38(3)b |
25.1 |
23.4 |
24.8 |
| Gd3+ |
1.05 |
5.24(10)c |
46.3 |
43.2 |
41.7 |
| Tb3+ |
1.04 |
5.12(10)c |
47.9 |
44.6 |
43.0 |
| Tm3+ |
0.99 |
5.16(10)c |
49.9 |
46.5 |
45.0 |
| Yb3+ |
0.99 |
5.08(10)c |
50.7 |
47.3 |
45.3 |
| Lu3+ |
0.97 |
5.10(10)c |
51.6 |
48.0 |
— |
| Am3+ |
1.095 |
5.63(8)c |
41.4 |
38.5 |
36.2 |
HClO4, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 0.01 |
| La3+ |
1.16 |
5.77(8)c |
38.1 |
35.5 |
32.6 |
Co(ClO4)2/HClO4, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 0.1 |
| Co2+ |
0.65 |
4.62(4)a |
56.6 |
52.7 |
51.3 |
Phenomenologically, the variation of the AIIM with the pH of the electrolyte mixtures may be divided into three zones whose characteristics depend significantly on the pH of the inert electrolyte mixture.
In the zone of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pH
pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to 5, the AIIM is constant. The value of the AIIM is in close agreement with the theoretical value given by the extended DHO limiting law for each of the Cs+, Tl+, and Co2+ ions. In the case of the trivalent lanthanide and actinide ions the experimentally determined AIIM11 are 10 to 20% higher than the value predicted by the extended limiting law.
3 to 5, the AIIM is constant. The value of the AIIM is in close agreement with the theoretical value given by the extended DHO limiting law for each of the Cs+, Tl+, and Co2+ ions. In the case of the trivalent lanthanide and actinide ions the experimentally determined AIIM11 are 10 to 20% higher than the value predicted by the extended limiting law.
In the intermediate zone of 3 to 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pH
pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the AIIM decreases at increasing hydrogen ion concentration and reaches a minimum at about pH 2.
2, the AIIM decreases at increasing hydrogen ion concentration and reaches a minimum at about pH 2.
In the acidic zone, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pH
pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, a small increase of the AIIM is observed, which is qualitatively in agreement with the prediction given by the extended limiting law.
1, a small increase of the AIIM is observed, which is qualitatively in agreement with the prediction given by the extended limiting law.
Furthermore, there is one important observation: As shown in Fig. 3(c), the variation of the AIIM of Co2+ ions with pH is less pronounced when the ions move in Co(ClO4)/Na(H)ClO4 electrolytes rather than in “Co-free” Na(H)ClO4 electrolytes. This indicates that the pH-mobility effect of the ions depends also on the structure affecting properties of the cation composing the electrolyte. As Na+ ions are replaced by hydrogen ions in the Co(ClO4)/Na(H)ClO4 electrolyte, not only the pH increases but also the “structureness” of the electrolyte bulk water increases, (i.e. the rotational freedom of the bulk water decreases, since Co2+ is a stronger structure-maker ion than Na+).
B Analysis of the migration data
For a first, qualitative interpretation of the change of the AIIM with the pH of the solution, two alternative dynamical states of the hydrated radioactive cation acting in equilibrium were assumed:11| |  | (17) |
Using the symbolic representations {M(H2O)Nn+} and {M(H2O)Nn+}{H+} we try to describe two different types of interaction of the migrating radioactive ion with the components of the chemically inert electrolyte, in particular the hydrogen ion concentration [H+]. We aim to reflect the change of the dynamical properties of the water molecules in the hydration shell of the ion. The phenomenological stoichiometric equilibrium constant of the system is represented by βψ
(dm3 mol−1).
For a quantitative discussion the overall ion mobility may be written as 45
| |  | (18) |
where
ui is the absolute individual ion mobility of the ionic species
i
(for
αi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1),
αi the partial mole fraction of the ionic species in the equilibrium and
φ a function taking into account the change of the activity coefficients
γ when switching from Na
+ to H
+ in the perchlorate solution of a constant overall ionic strength. Concerning the small increase of the AIIM of the radioactive
cations observed between pH 2 and pH 1, the function
φ can be expressed as
| |  | (19) |
The values of the activity coefficients
28 of the aqueous electrolyte of HClO
4 and NaClO
4 at 298.15 K are given in
Table 5. Since the activity coefficients are ionic strength dependent, the function
φ for a Na(H)ClO
4 electrolyte mixture can be expressed by
Using the equilibrium
expression (17) and
relation (18), the variation of the overall ion mobility of the radioactive
cation with the pH of the electrolyte may now be expressed by
| |  | (21) |
The ion mobility
u{M(H2O)Nn+}{H+} corresponds to the minimum value of the AIIM at about pH 2. The
experimental data were fitted with the equation above. The obtained results are included in
Table 5.
Table 5 Results of the fit of the experimental electromigration data according to eqn. (21). u{M(H2O)Nn+} is the ion mobility at the neutral level and u{M(H2O)Nn+}{H+} the ion mobility at the acidic level. βψ is the phenomenological stoichiometric equilibrium constant for eqn. (17). A is the ratio u{M(H2O)Nn+}/u{M(H2O)Nn+}{H+}. T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1(5) K
298.1(5) K
| Ion |
r
i
/10−10 m |
u
{M(H2O)Nn+}/10−8 m2 V−1 s−1 |
u
{M(H2O)Nn+}{H+}/10−8 m2 V−1 s−1 |
A
|
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ βψ |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ
[eqn. (23)] βψ
[eqn. (23)] |
NaClO4/HClO4, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1, γNaClO4 0.1, γNaClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.777, γHClO4 0.777, γHClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.803 0.803 |
| Cs+ |
1.67 |
7.66(3) |
6.44(6) |
0.84(1) |
2.43(23) |
2.54 |
| Tl+ |
1.50 |
7.52(6) |
6.48(8) |
0.86(1) |
3.42(46) |
2.71 |
| Co2+ |
0.65 |
5.05(5) |
3.98(5) |
0.79(1) |
4.00(26) |
3.69 |
| Sr2+ |
1.26 |
5.88(6) |
5.10(5) |
0.87(1) |
3.30(58) |
3.48 |
| Gd3+ |
1.05 |
6.09(4) |
5.10(3) |
0.84(1) |
3.79(23) |
3.64 |
| Tb3+ |
1.04 |
5.77(4) |
4.92(5) |
0.85(1) |
3.39(26) |
3.65 |
| Tm3+ |
0.99 |
5.92(5) |
4.94(4) |
0.83(1) |
3.56(27) |
3.66 |
| Yb3+ |
0.99 |
6.27(7) |
5.06(7) |
0.81(2) |
3.47(30) |
3.66 |
| Lu3+ |
0.97 |
5.99(8) |
4.98(5) |
0.83(2) |
3.76(36) |
— |
| Am3+ |
1.095 |
6.99(11) |
5.57(9) |
0.80(2) |
4.07(37) |
3.60 |
NaClO4/HClO4, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01, γNaClO4 0.01, γNaClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.903, γHClO4 0.903, γHClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.906 0.906 |
| La3+ |
1.16 |
6.70(5) |
5.77(8) |
0.86(1) |
3.18(41) |
3.61 |
Co(ClO4)2/NaClO4/HClO4, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1, γNaClO4 0.1, γNaClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.856, γHClO4 0.856, γHClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.860 0.860 |
| Co2+ |
0.65 |
5.19(4) |
4.62(4) |
0.89(1) |
3.67(41) |
3.69 |
While the experimentally determined AIIM are different for all the cations investigated, the ratio between u{M(H2O)Nn+}{H+} and u{M(H2O)Nn+} is constant for a given aqueous electrolyte and a given overall ionic strength. For the electrolyte mixture Na(H)ClO4, the mean value of this ratio is 0.83(3) at μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol dm−3 and 0.86(1) at μ
0.1 mol dm−3 and 0.86(1) at μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 mol dm−3
(the ratio is quoted by A in Table 5). As the ionic strength of the electrolyte mixture approaches zero (infinite dilution of the electrolyte) and thus the pH to 7, the value of A is expected to approach unity.
0.01 mol dm−3
(the ratio is quoted by A in Table 5). As the ionic strength of the electrolyte mixture approaches zero (infinite dilution of the electrolyte) and thus the pH to 7, the value of A is expected to approach unity.
Using the migration data obtained in this work and from the experimental AIIM of Am3+ in neutral (NaClO4) and acidic (HClO4) aqueous perchlorate electrolytes of various ionic strength,25 the variation of A with the overall ionic strength of the Na(H)ClO4 electrolyte mixture (μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 mol dm−3) may be given by:
0.2 mol dm−3) may be given by:
| |  | (22) |
To complete the analysis of the migration data we should find an analytical expression for the stoichiometric equilibrium constant βψ. The value of βψ
(Table 5) increases with increasing structure-making properties of the ion. This may reflect the interaction of the ion with the electrolyte bulk water. Thus an analytical expression for βψ was obtained by plotting the product log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ·(τi°/τH2O°)
versus
(τi°/τH2O°)
(Fig. 5). In fact log
βψ·(τi°/τH2O°)
versus
(τi°/τH2O°)
(Fig. 5). In fact log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ corresponds to the pH-value for which we have: [{M(H2O)Nn+}]
βψ corresponds to the pH-value for which we have: [{M(H2O)Nn+}]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [{M(H2O)Nn+}{H+}]. From the linear fit of the data plotted in Fig. 5 and using eqns. (6) and (2), the stoichiometric equilibrium constant may be expressed as a function of the diffusion coefficient of the ion in pure water, (Di°
[{M(H2O)Nn+}{H+}]. From the linear fit of the data plotted in Fig. 5 and using eqns. (6) and (2), the stoichiometric equilibrium constant may be expressed as a function of the diffusion coefficient of the ion in pure water, (Di°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kTui°/ez), and of the diffusion coefficient of water, DH2O°:
kTui°/ez), and of the diffusion coefficient of water, DH2O°:
| |  | (23) |
The log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ
βψ values calculated with the equation above are listed in
Table 5.
 |
| | Fig. 5 Plot log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ(τi°/τH2O°)
versusτi°/τH2O°) at T βψ(τi°/τH2O°)
versusτi°/τH2O°) at T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.15 K for the ions investigated. (Coefficient of correlation r 298.15 K for the ions investigated. (Coefficient of correlation r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.988). 0.988). | |
Finally, the variation of the ion mobility with the pH of the Na(H)ClO4 electrolyte mixture of a constant overall ionic strength μ can be expressed as follows
| |  | (24) |
where
f(
μ) corresponds to the second term on the right side of
relation (22). As
u{M(H2O)Nn+} for the uni- and divalent ions studied here may be calculated from
relation (9)
(or by a similar relation for the lanthanide and actinide ions), the
relation (24) reaches the general form:
u![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u
u°
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
−
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g
g(
μ,[H
+]). The variation of the AIIM with the pH of the inert electrolyte calculated by means of
eqn. (24) is represented by the dotted lines in
Fig. 4 and
Fig. 5.
IV Discussion
The extended DHO limiting law does not predict a change of the AIIM with the pH of the inert electrolyte mixture. However a systematic effect of the hydrogen ion concentration on the electrophoretic mobilities of radioactive cations on tracer scale (10−11 mol) has been observed by means of the electromigration technique. From the systematic analysis of the experimental migration data a semi-empirical relation (24) was deduced. It reproduces well the change of the AIIM with the hydrogen ion concentration. However the cause of this effect which in our mind has so far never been observed with other methods based on the measurement of the individual transport properties of ions, still remains unknown. A change of the dynamical properties of the electrolyte bulk water with regard to the hydrogen ion concentration could be a possible explanation for this effect.
In the zone of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pH
pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3–5, the hydrogen ion concentration appears to be too low to affect the dynamic properties of the bulk water. The values of the ion microviscosity
3–5, the hydrogen ion concentration appears to be too low to affect the dynamic properties of the bulk water. The values of the ion microviscosity ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i and of the reorientation time of water molecules in the hydration shell of the ion τi calculated from the experimental AIIM (Table 3) are somewhat higher than those obtained for pure water (Table 1). This is due mainly to the modification of the dynamical properties of bulk water induced by the hydrated ions of the electrolyte. We also observed that the pH value at which the decrease of the ion mobility begins appears to depend on the structure-affecting properties of the moving ion.
i and of the reorientation time of water molecules in the hydration shell of the ion τi calculated from the experimental AIIM (Table 3) are somewhat higher than those obtained for pure water (Table 1). This is due mainly to the modification of the dynamical properties of bulk water induced by the hydrated ions of the electrolyte. We also observed that the pH value at which the decrease of the ion mobility begins appears to depend on the structure-affecting properties of the moving ion.
According to the microscopic version of Stokes law, eqn. (2), the decrease of the AIIM could be explained by an increase of the frictional forces exerted on the migrating ion due to an excess of hydrated protons in the electrolyte bulk water. It is well established that the migration of an excess of protons in water does not occur through hydrodynamics Stokes diffusion but via a process of structural diffusion (Grötthus mechanism), in which charge transfer takes place through an interchange of covalent and hydrogen bonds.15 The mechanism of structural diffusion gives the proton a very high mobility, leading to the formation of hydrated protons, which are generally described with the limiting structures H5O2+
(Zundel cation13) or H9O4+
(Eigen cation14). Due to its high mobility, the proton can thus interact with a large number of water molecules. Hence, the non-negligible presence of hydrated protons could modify the dynamic (reorientation time) and structural properties (translational and orientational order) of the electrolyte bulk water. This results in an increase of the reorientation time of the water molecules in the hydration sphere of the ion and thus to a lowering of the ion mobility.
For the change of the rotational reorientation time of the electrolyte bulk water with the hydrogen ion concentration we propose the following relation
| |  | (25) |
where
cj is the concentration and
τj the rotational reorientation time of the
water molecule in the first hydration shell of the ion for the
jth ion composing the electrolyte, except for the
proton itself, (
j![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
≠
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
H
+). The variation of
τj with the hydrogen ion concentration at a given overall ionic strength of the electrolyte mixture is obtained using
relation (24). The values of the phenomenological stoichiometric equilibrium constants
βψ derived from
relation (22) are: 162(9), 2188(131), 4898(292) dm
3 mol
−1 for ClO
4−, Na
+ and Co
2+ respectively. The variation of the reorientation time of the bulk
water molecules
τH2O with the hydrogen ion concentration of the various electrolytes mixtures is shown in
Fig. 6. The values of
τH2O and of the corresponding diffusion coefficient of bulk
water DH2O for the neutral and acidic electrolyte solutions are listed in
Table 6. A consequence of
relation (25) is that the relative exchange rate of
water molecules between the first hydration sphere of the ion and the bulk, Δ
n/
N, remains constant for any electrolyte composition. We see no indication that more or less
water molecules leave the hydration shell of the ion as the hydrogen ion concentration of the electrolyte increases, only the dynamical properties are affected. Hence the rotational reorientation time of the
water molecules in the hydration shell of the migrating radioactive ion may be expressed as
| | τi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τi°(τH2O/τH2O°) τi°(τH2O/τH2O°) | (26) |
The values of
τi calculated by means of
eqn. (26) for the radioactive ions in neutral and acidic aqueous electrolytes are in fairly good agreement with the values derived from the experimental ion mobilities (
Tables 3 and 4).
 |
| | Fig. 6 Reorientation time of bulk water molecules of the electrolyte as function of the pH at 298.15 K. The solid line represents the electrolyte mixture Na(H)ClO4μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3; the dashed line the electrolyte mixture Na(H)ClO4μ 0.10 mol dm−3; the dashed line the electrolyte mixture Na(H)ClO4μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 mol dm−3 and the dotted line the electrolyte mixture Co(ClO4)2/Na(H)ClO4μ 0.01 mol dm−3 and the dotted line the electrolyte mixture Co(ClO4)2/Na(H)ClO4μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3. 0.10 mol dm−3. | |
Table 6 Rotational reorientation time τH2O and diffusion coefficients DH2O of bulk water molecules in neutral and acidic perchlorate electrolytes T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1(5) K
298.1(5) K
| Electrolyte |
μ/mol dm−3 |
τ
H2O
[eqn. (26)]/10−12 s |
D
H2O/10−9 cm2 s−1 |
| NaClO4 |
0.10 |
8.65(7) |
2.20(2) |
| NaClO4 |
0.01 |
8.47(7) |
2.25(2) |
| Co(ClO4)2/NaClO4 |
0.10 |
8.90(7) |
2.14(2) |
| HClO4 |
0.10 |
10.11(10) |
1.88(2) |
| HClO4 |
0.01 |
9.05(10) |
2.10(2) |
| Co(ClO4)2/HClO4 |
0.10 |
9.94(8) |
1.92(2) |
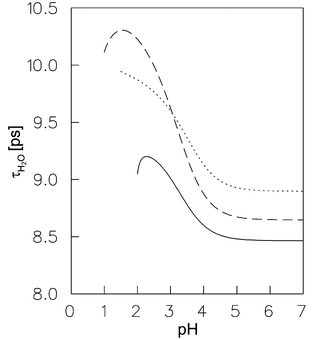
By means of eqn. (25), we can also calculate the value of the rotational reorientation time of bulk water, τH2O, in NaClO4 and HClO4 electrolytes of various ionic strength. The ionic strength dependence of τH2O for both electrolytes is displayed in Fig. 7. For the NaClO4 electrolyte the value of τH2O may be derived by a similar law as the extended DHO limiting law, since, as mentioned above, the hydrogen ion concentration is too low to affect the dynamical properties of the bulk water molecules. In the case of the HClO4-electrolyte, the value of τH2O increases significantly for increasing hydrogen ion concentrations and thus with the fraction of water molecules which exchange protons per unit time. The variation of the rotational reorientation time of bulk water with the proton concentration may be given by the following semi-empirical expression
| | 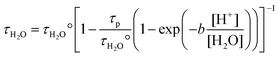 | (27) |
where
τp is the
proton hopping time, [
H2O]
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
55.5 mol dm
−3 and b a numerical constant. The fit of the
τH2O data for HClO
4 electrolytes according to the
relation (27)
(solid line in
Fig. 7) leads to a value for
τp of 1.44(18) ps at 298.1(5) K. The inverse of this number corresponds to the rate constant for
proton transfer between the hydronium ions and the acceptor water molecule. The value found here is 0.69(9) ps
−1 and compares well with the experimental value obtained from
NMR studies of
proton transfer in
water,
46 0.67 ps
−1 and with the values calculated by quantum molecular dynamic simulation
18 which are 0.69 ps
−1 for
proton transfer in the Eigen
cation and 0.60 ps
−1 for
proton transfer in the Zundel
cation. The ratio
b/[
H2O] in
expression (27) is 60.8(4) dm
3 mol
−1.
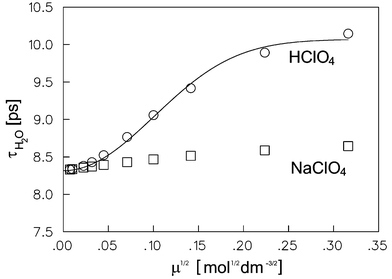 |
| | Fig. 7 Rotational reorientation time of bulk water versus ionic strength of the NaClO4 and HClO4 electrolytes. The solid line is eqn. (27). | |
From the value of τp it is also possible to determine the proton hopping length, rOO, defined as the oxygen–oxygen distance between the hydronium ion and the acceptor water molecule, by means of the Einstein relation:
| |  | (28) |
where
Dp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
7.01
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
−9 m
2 s
−1 is the abnormal
proton mobility, (difference between the
proton diffusion coefficient, 9.31
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
−9 m
2 s
−1, and water self-diffusion coefficient, 2.30
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
×
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
10
−9 m
2 s
−1).
15,28 With
τp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1.44(18) ps we find a value for the
proton hopping length of
rOO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2.46(15)
Å. This value agrees well with the experimental data obtained from thermal
neutron and X-ray scattering studies,
rOO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2.5 Å.
47 Molecular dynamic simulations lead to values of
rOO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2.40–2.49 Å for H
5O
2+ and r
OO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
2.50–2.60 Å for H
9O
4+.
16,17,20 For comparison it should be remembered that the oxygen–oxygen distance between two
water molecules in pure
water is larger, about 2.8 Å.
According to relations (26) and (27), the concentration dependence of the absolute individual ion mobility of an ion present at tracer scale in HClO4 may be written as:
| |  | (29) |
The experimental values of the AIIM of La
3+ ions in HClO
4,
48 the only migration data in acidic solutions found in the literature at the time of this work, are plotted as a function of the ionic strength of the electrolyte in
Fig. 8. The values of the AIIM given by
eqn. (29) using the parameters
τp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1.44 ps and
b/[
H2O]
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
60.8 dm
3 mol
−1 are represented by the solid line in
Fig. 8. The calculated values agree well with the experimental data. Thus, despite the great lack of absolute and accurate
tracer migration data in
perchloric acid for comparison, we can say that
eqn. (29) leads to a good estimation of the transport properties of ions on
tracer scale in HClO
4. For other acids such as HCl or
HNO3 for example,
eqn. (29) cannot be applied directly for all metal ions because of the formation of complex species of various charges which greatly influence the overall ion mobility.
IV Conclusion
In acidic inert aqueous electrolytes, metal cations, particularly at very low concentrations, migrate completely differently from predictions by standard theories. As this is not due to the intrinsic properties of the migrating ion themselves, the structure and dynamics of the aqueous electrolytes with an excess of protons must be responsible.
In this paper we have investigated the dependence of the absolute individual ion mobility (AIIM) of the radioactive ions [137Cs]Cs+, [201Tl]Tl+ and [57Co]Co2+ on the hydrogen ion concentration of inert aqueous perchlorate electrolyte mixtures by means of the electromigration technique. The AIIM of the radioactive ions is found to decrease as the hydrogen ion concentration of the electrolyte mixture increases. A similar behavior of the AIIM with regards to the hydrogen ion concentration of inert electrolytes was also observed in previous work for some di- and trivalent radioactive ions at tracer scale. The experimental values of the AIIM were compared to the theoretical values predicted by the extended DHO limiting law. For the neutral electrolyte mixtures of low hydrogen ion concentration (pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) there is a fairly good agreement between experimental and calculated values. The experimentally observed decrease of the AIIM of the radioactive ions for higher hydrogen ion concentrations (pH
4) there is a fairly good agreement between experimental and calculated values. The experimentally observed decrease of the AIIM of the radioactive ions for higher hydrogen ion concentrations (pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) is not explained by the extended DHO limiting law. A systematic analysis of the migration data was performed assuming a change of the dynamical properties of the water molecules in the hydration shell of the migrating radioactive ions. The resulting general relation for the variation of the AIIM with the hydrogen ion concentration as well as with the overall ionic strength μ of the electrolyte mixture is of the form: u
4) is not explained by the extended DHO limiting law. A systematic analysis of the migration data was performed assuming a change of the dynamical properties of the water molecules in the hydration shell of the migrating radioactive ions. The resulting general relation for the variation of the AIIM with the hydrogen ion concentration as well as with the overall ionic strength μ of the electrolyte mixture is of the form: u![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u°
u°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f(μ,[H+])
[see eqn. (24)].
f(μ,[H+])
[see eqn. (24)].
The effect of the hydrogen ion concentration on the AIIM can be explained by a possible change of the dynamical properties of electrolyte bulk water due to the increasing presence of an excess of hydrated protons in the bulk. From the variation of the rotational reorientation time of bulk water molecules in HClO4 electrolytes of various concentrations, a value of 0.69 ps−1 is derived for the rate constant of proton transfer between the hydronium ions and the acceptor water molecules. For the proton hopping length we find a value of 2.46 Å. These two values are in good agreement with the literature values. Finally we propose a relation for the ion mobility of radioactive ions at tracer scale in HClO4 electrolytes involving the values of the proton hopping time and length.
This study demonstrates the potential of the electromigration method to investigate the individual parameters of the migrating ion, but also to derive data on the dynamics of electrolyte systems. The approach might thus be applied to provide experimental data to check the validity of various theoretical models developed for understanding the dynamics of ions in solutions.
References
- H. Ohtaki, Monatsh. Chem., 2001, 132, 1237–1268 Search PubMed.
- P. G. Wolynes, Annu. Rev. Phys. Chem., 1980, 31, 345–376 CrossRef CAS.
- R. W. Impey, P. A. Madden and I. R. McDonald, J. Phys. Chem., 1983, 87, 5071–5083 CrossRef CAS.
- R. Biswas, S. Roy and B. Bagchi, Phys. Rev. Lett., 1995, 75, 1098–1101 CrossRef CAS.
- R. Biswas and B. Bagchi, J. Chem. Phys., 1997, 106, 5587–5598 CrossRef CAS.
- P. Debye and H. Hückel, Z. Phys., 1924, 25, 49 Search PubMed.
- L. Onsager, Z. Phys., 1924, 27, 388 Search PubMed; L. Onsager, Z. Phys., 1927, 28, 277 Search PubMed.
- E. Mauerhofer, O. Kling and F. Rösch, Radiochim. Acta, 2001, 89, 537–541 Search PubMed.
- S. F. Patil, A. V. Borhade and N. Munmun, Appl. Radiat. Isot., 1994, 45, 1–4 Search PubMed.
- S. Chowduhri and A. Chandra, J. Chem. Phys., 2001, 115, 3732–3741 CrossRef.
- F. Rösch and V. A. Khalkin, Radiochim. Acta, 1990, 51, 101–106 Search PubMed.
- C. Lee, C. Sosa, M. Planas and J. J. Novoa, J. Chem. Phys., 1996, 104, 7081–7085 CrossRef CAS.
- G. Zundel and H. Metzger, Z. Phys. Chem., 1968, 58, 225–245 Search PubMed.
- E. Wicke, M. Eigen and Th. Ackermann, Z. Phys. Chem., 1954, 1, 340–364 Search PubMed.
- N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462 CrossRef CAS.
- L. Ojamäe, I. Shavitt and S. J. Singer, J. Chem. Phys., 1998, 109, 5547–5564 CrossRef CAS.
- J. Lobaugh and G. A. Voth, J. Chem. Phys., 1996, 104, 2056–2069 CrossRef CAS.
- U. W. Schmitt and G. A. Voth, J. Chem. Phys., 1999, 111, 9361–9381 CrossRef CAS.
- R. R. Sadeghi and H. P. Cheng, J. Chem. Phys., 1999, 111, 2086–2094 CrossRef CAS.
- D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601–604 CrossRef CAS.
- S. Walbran and A. A. Kornyshev, J. Chem. Phys., 2001, 114, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 039–10
039–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048 CrossRef CAS.
048 CrossRef CAS.
- M. A. Lill and V. Helms, J. Chem. Phys., 2001, 115, 7993–8005 CrossRef CAS.
- H. P. Cheng and L. Krause, J. Chem. Phys., 1997, 107, 8461–8468 CrossRef CAS.
- B. Halle and G. Karlström, J. Chem. Soc., Faraday Trans. 2, 1983, 79, 1031–1046 RSC;
1983; 79, 1047–1076.
- F. Rösch, Zentralinst. Kernforsch. Rossendorf Dresden Ber., 1989, ZfK-664 Search PubMed.
- G. G. Stokes, Trans. Cambridge Philos. Soc., 1850, 9, 8 Search PubMed.
- A. Einstein, Ann. Phys., 1905, 17, 549 CAS.
-
Handbook of Chemistry and Physics, CRC Press, Boca Raton, FL, 78th edn., 1997–1998 Search PubMed.
-
R. H. Stokes and R. Mills, Viscosity of Electrolytes and Related Properties, Pergamon Press, Oxford, 1965 Search PubMed.
-
N. Gorskij, Bestimmung der physikalischen Eigenschaften der ersten Hydrathülle von Ionen in Lösung (German transl. C. Riedel), GSI, Darmstadt, 1989 Search PubMed.
-
B. E. Conway, Ionic Hydration in Chemistry and Biophysics, Elsevier, Amsterdam, 1981 Search PubMed.
- Y. Marcus, J. Chem. Soc., Faraday
Trans. 1, 1983, 83, 339–349 Search PubMed.
- R. L. Hahn, J. Phys. Chem., 1988, 92, 1668–1675 CrossRef CAS.
- U. Kaatze, Chem. Phys. Lett., 1993, 203, 1–4 CrossRef CAS.
- N. Nandi, S. Roy and N. Bagchi, J. Chem. Phys., 1995, 102, 1390–1397 CrossRef CAS.
- R. Mills, J. Phys. Chem., 1973, 77, 685–688 CrossRef CAS.
- M. Nakahara and K. Ibuki, J. Chem. Phys., 1986, 90, 3026–3030 CAS.
- L. Onsager, Ann. NY Acad. Sci., 1945, 46, 241 Search PubMed.
- R. H. Stokes, E. A. Woolf and R. Mills, J. Phys. Chem., 1957, 61, 1634–1636 CrossRef CAS.
- H. S. Franck, J. Am. Chem. Soc., 1958, 63, 1789.
-
H. S. Harned and B. Owen, The Physical Chemistry of Electrolytic Solutions, Rheinhold Publishing Co., New York and Chapman and Hall Ltd, London, 1958 Search PubMed.
- R. H. Stokes and R. A. Robinson, J. Am. Chem. Soc., 1948, 70, 1870–1878 CrossRef CAS.
- E. Mauerhofer, O. Kling, K. Hiller and F. Rösch, Radiochim. Acta, 2000, 88, 399–404 Search PubMed.
- S. Hjertén, J. Chromatogr., 1985, 347, 191–198 CrossRef.
- R. Lundqvist, Acta Chem. Scand. Ser. A, 1981, 35, 31–41 Search PubMed.
- Z. Luz and S. Meiboom, J. Am. Chem. Soc., 1964, 86, 4768–4769 CrossRef CAS.
- R. Triolo and A. H. Narten, J. Chem. Phys., 1975, 63, 3624–3631 CrossRef CAS.
- F. Rösch, V. A. Kalkin, M. Milanov and T. K. Hung, Z. Chem., 1987, 10, 358–366 Search PubMed.
- B. Fourest, J. Duplesis and F. David, Radiochim. Acta, 1984, 36, 191–195 Search PubMed.
- B. Fourest, J. Duplesis and F. David, Radiochim. Acta, 1989, 46, 131–135 Search PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, A32, 751–767 CAS.
- H. D. B. Jenkins and K. P. Thakur, J. Chem. Educ., 1979, 56, 576–577 Search PubMed.
-
C. F. Baes and R. E. Mesmer, The Hydrolysis of Cations, Robert E. Krieger Publishing Company, Malabar, FL, 1986 Search PubMed.
|
| This journal is © the Owner Societies 2003 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 there is a fairly good agreement between experimental and calculated values. Below pH 4 the experimentally observed decrease of the AIIM is not explained by the extended Debye–Hückel–Onsager limiting law. The effect can possibly be explained by a change of the dynamical properties of electrolyte bulk water due to the increasing presence of an excess of hydrated protons in the bulk solution. From the variation of the rotational reorientation time of bulk water molecules in HClO4 electrolytes with the proton concentration, a value of 0.69 ps−1 is derived for the rate constant for proton transfer between the hydronium ions and the acceptor water molecules. For the proton hopping length a value of 2.46 Å was found. These two values are in good agreement with the literature values. Finally, we propose a relation for mobility of tracer ions in HClO4 electrolytes involving the proton hopping time and length.
4 there is a fairly good agreement between experimental and calculated values. Below pH 4 the experimentally observed decrease of the AIIM is not explained by the extended Debye–Hückel–Onsager limiting law. The effect can possibly be explained by a change of the dynamical properties of electrolyte bulk water due to the increasing presence of an excess of hydrated protons in the bulk solution. From the variation of the rotational reorientation time of bulk water molecules in HClO4 electrolytes with the proton concentration, a value of 0.69 ps−1 is derived for the rate constant for proton transfer between the hydronium ions and the acceptor water molecules. For the proton hopping length a value of 2.46 Å was found. These two values are in good agreement with the literature values. Finally, we propose a relation for mobility of tracer ions in HClO4 electrolytes involving the proton hopping time and length.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ⩽
⩽![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 mol dm−3), an extension of the DHO limiting law based on the introduction of ion atmosphere parameters [see eqn. (11) in Section II B] leads to reasonable values for the ion mobility and diffusion coefficient for uni- and divalent ions in various neutral (pH
0.2 mol dm−3), an extension of the DHO limiting law based on the introduction of ion atmosphere parameters [see eqn. (11) in Section II B] leads to reasonable values for the ion mobility and diffusion coefficient for uni- and divalent ions in various neutral (pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∼
∼![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7) aqueous electrolytes.8,9 Recent molecular dynamics simulations of NaCl and KCl solutions show that the decrease of the ionic diffusion coefficient at increasing concentrations is correlated with the increase of the residence time τr of water molecules in the hydration shell of the ions as well as with the decrease of the bulk water diffusion coefficient, DH2O.10 At low electrolyte concentrations the product τrDH2O is constant and the hydration number remains unchanged.
7) aqueous electrolytes.8,9 Recent molecular dynamics simulations of NaCl and KCl solutions show that the decrease of the ionic diffusion coefficient at increasing concentrations is correlated with the increase of the residence time τr of water molecules in the hydration shell of the ions as well as with the decrease of the bulk water diffusion coefficient, DH2O.10 At low electrolyte concentrations the product τrDH2O is constant and the hydration number remains unchanged.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaClO4 solutions at constant overall ionic strength, μ
NaClO4 solutions at constant overall ionic strength, μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol dm−3 and T
0.1 mol dm−3 and T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1 K. Although the macroscopic properties of the two electrolytes, such as viscosity and density, are very close, the values of the AIIM of the lanthanide ions in 0.1 mol dm−3 HClO4 were about 15% lower than those in 0.1 mol dm−3 NaClO4. Thus transport of metal cations is affected by an excess of protons in the solution. The structure of acidic electrolytes is largely different from that of neutral electrolytes because the individual proton of the acid is directly transferred to a water molecule of the bulk and never returns as the nearest neighbour of its counter-ion.12 The interaction of protons with water molecules leads to the formation of complexes of the type H5O2+ or H9O4+.13,14 It is also well established that the migration of the excess proton in water occurs via a process of structural diffusion (Grötthus mechanism) in which charge transfer takes place through an interchange of covalent and hydrogen bonds.15 This mechanism is responsible for the proton's well known abnormally high mobility (up
298.1 K. Although the macroscopic properties of the two electrolytes, such as viscosity and density, are very close, the values of the AIIM of the lanthanide ions in 0.1 mol dm−3 HClO4 were about 15% lower than those in 0.1 mol dm−3 NaClO4. Thus transport of metal cations is affected by an excess of protons in the solution. The structure of acidic electrolytes is largely different from that of neutral electrolytes because the individual proton of the acid is directly transferred to a water molecule of the bulk and never returns as the nearest neighbour of its counter-ion.12 The interaction of protons with water molecules leads to the formation of complexes of the type H5O2+ or H9O4+.13,14 It is also well established that the migration of the excess proton in water occurs via a process of structural diffusion (Grötthus mechanism) in which charge transfer takes place through an interchange of covalent and hydrogen bonds.15 This mechanism is responsible for the proton's well known abnormally high mobility (up![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36.24
36.24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−8 m2 V−1 s−1 at T
10−8 m2 V−1 s−1 at T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1 K) . Fundamental results on the dynamics of the proton transfer in water may be found elsewhere.16–24 Since protons migrate very rapidly, they continuously interact with a great number of water molecules, in turn affecting the dynamics of bulk water. As the dynamical properties of the bulk water are coupled with those of the water molecules in the hydration shell of the ions, a difference in the transport properties of the ions in neutral and acidic media may be expected.
298.1 K) . Fundamental results on the dynamics of the proton transfer in water may be found elsewhere.16–24 Since protons migrate very rapidly, they continuously interact with a great number of water molecules, in turn affecting the dynamics of bulk water. As the dynamical properties of the bulk water are coupled with those of the water molecules in the hydration shell of the ions, a difference in the transport properties of the ions in neutral and acidic media may be expected.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−19 C), zi the charge number of the ion, η the solution viscosity (kg m−1 s−1) and rS the Stokes radius (m). As the experimental results are generally difficult to interpret on the basis of the Stokes radius, Stokes’ law may be used in its microscopic form
10−19 C), zi the charge number of the ion, η the solution viscosity (kg m−1 s−1) and rS the Stokes radius (m). As the experimental results are generally difficult to interpret on the basis of the Stokes radius, Stokes’ law may be used in its microscopic form 
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i is the ion micro-viscosity (kg m−1 s−1), defined as the viscosity of the water molecules in the first hydration shell of the ion, and ri is the ionic radius (m).
i is the ion micro-viscosity (kg m−1 s−1), defined as the viscosity of the water molecules in the first hydration shell of the ion, and ri is the ionic radius (m).
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i° calculated from the ion mobility in pure water, ui° at 298.15 K28 for the ions investigated in this work are listed in Table 1. The ratio of
i° calculated from the ion mobility in pure water, ui° at 298.15 K28 for the ions investigated in this work are listed in Table 1. The ratio of ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i° against η°, the viscosity of water (η°
i° against η°, the viscosity of water (η°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.903
8.903![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 kg m−1 s−1 at 298.15 K29), reflects the effect of the ion on the structure of water. Here,
10−4 kg m−1 s−1 at 298.15 K29), reflects the effect of the ion on the structure of water. Here, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i°
i°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η° corresponds to the case of low charge density ions (Cs+, Tl+, etc.), referred to as structure-breakers, while
η° corresponds to the case of low charge density ions (Cs+, Tl+, etc.), referred to as structure-breakers, while ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i°
i°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η° corresponds to the case of high charge density ions (Sr2+, Co2+, La3+, etc.), classified as structure-makers. The ion micro-viscosity can be related to the vibrational frequency νi
(s−1) of the ion–water bond in the first hydration sphere as30
η° corresponds to the case of high charge density ions (Sr2+, Co2+, La3+, etc.), classified as structure-makers. The ion micro-viscosity can be related to the vibrational frequency νi
(s−1) of the ion–water bond in the first hydration sphere as30
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1023 mol−1). The factor χi takes into account the electrostriction, i.e. the reduction of the effective radius of the water molecule caused by the electrostatic field of the ion. It can be calculated using Conway's equation:31
1023 mol−1). The factor χi takes into account the electrostriction, i.e. the reduction of the effective radius of the water molecule caused by the electrostatic field of the ion. It can be calculated using Conway's equation:31
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−12 F m−1), and εr the dielectric constant of water (78.36 at 298.15 K28). Using the harmonic oscillator as a model for the ion-water system, the vibrational frequency of the ion–water bond may be connected to the hydration enthalpy ΔHhyd
(J mol−1) as30
10−12 F m−1), and εr the dielectric constant of water (78.36 at 298.15 K28). Using the harmonic oscillator as a model for the ion-water system, the vibrational frequency of the ion–water bond may be connected to the hydration enthalpy ΔHhyd
(J mol−1) as30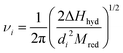
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i° by means of eqns. (3)–(5), the values of ΔHhyd obtained by means of the TATB extrathermodynamic assumption (ΔHhyd[C6H5)4As+]
i° by means of eqns. (3)–(5), the values of ΔHhyd obtained by means of the TATB extrathermodynamic assumption (ΔHhyd[C6H5)4As+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔHhyd[B(C6H5)4−]) were employed.32 The value of di was set equal to ri
ΔHhyd[B(C6H5)4−]) were employed.32 The value of di was set equal to ri![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (δ/2), with δ being the thickness of the hydration shell. For univalent, divalent and trivalent ions, the values of δ were taken as 2.404, 2.334 and 2.276·10−10 m, respectively.33 As shown in Table 1, the values of
(δ/2), with δ being the thickness of the hydration shell. For univalent, divalent and trivalent ions, the values of δ were taken as 2.404, 2.334 and 2.276·10−10 m, respectively.33 As shown in Table 1, the values of ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i° obtained by eqn. (3) agree closely with those given by eqn. (2), based on sticking conditions.
i° obtained by eqn. (3) agree closely with those given by eqn. (2), based on sticking conditions.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.15 K). ui° is the absolute individual ion mobility at μ
298.15 K). ui° is the absolute individual ion mobility at μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 [refs. 28,49,50],
0 [refs. 28,49,50], ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i° the ion micro-viscosity, τi° the rotational reorientation time of water molecules in the first hydration shell of the ion, N the coordination number [ref. 1] and Δn the number of water molecules leaving the hydration shell during the exchange process with the bulk. ri is the ionic radius [refs. 51 and 52]. pK° is the first hydrolysis constant at 298.15 K for μ
i° the ion micro-viscosity, τi° the rotational reorientation time of water molecules in the first hydration shell of the ion, N the coordination number [ref. 1] and Δn the number of water molecules leaving the hydration shell during the exchange process with the bulk. ri is the ionic radius [refs. 51 and 52]. pK° is the first hydrolysis constant at 298.15 K for μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 [ref. 53]
0 [ref. 53]
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i
°
[eqn. (2)]/10−4 kg−1 s−1
i
°
[eqn. (2)]/10−4 kg−1 s−1![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i
°
[eqn. (3)]/10−4 kg−1 s−1
i
°
[eqn. (3)]/10−4 kg−1 s−1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−10 m), k the Boltzmann constant (1.3807
10−10 m), k the Boltzmann constant (1.3807![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−23 J K−1) and T the absolute temperature (K). Assuming that the DSE relation holds for pure water and using a rotational reorientation time of τH2O°
10−23 J K−1) and T the absolute temperature (K). Assuming that the DSE relation holds for pure water and using a rotational reorientation time of τH2O°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.3 ps (the Debye relaxation time of water at 298.15 K)34,35 and a viscosity of 8.903
8.3 ps (the Debye relaxation time of water at 298.15 K)34,35 and a viscosity of 8.903![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 kg m−1 s−1, we obtain α
10−4 kg m−1 s−1, we obtain α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.65. The value of α increases weakly as the temperature increases with a change of about 0.1% per degree in the range 273–328 K. The diffusion coefficient of pure water calculated with the parameters above, (DH2O°
4.65. The value of α increases weakly as the temperature increases with a change of about 0.1% per degree in the range 273–328 K. The diffusion coefficient of pure water calculated with the parameters above, (DH2O°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2/τH2O°
θ2/τH2O°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.29
2.29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−9 m2 s−1) is in good agreement with the best known experimental value,36 2.30
10−9 m2 s−1) is in good agreement with the best known experimental value,36 2.30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−9 m2 s−1. For the structure-breaker ions we find τi°
10−9 m2 s−1. For the structure-breaker ions we find τi°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τH2O° and for the structure-maker ions τi°
τH2O° and for the structure-maker ions τi°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τH2O°.
τH2O°.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N[1
N[1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−τH2O/τi]
e−τH2O/τi]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δn. The values of τi°
(in pure water) as well as the values of N and Δn for the ions investigated in this work are listed in Table 1. The relative exchange rate of water molecules between the hydration sphere and the bulk, Δn/N, appears as an important quantity for the exchange process. As shown in Fig. 1 for the cations in pure water, Δn/N may be expressed as a complicated exponential function of the surface charge density of the ion, σ
Δn. The values of τi°
(in pure water) as well as the values of N and Δn for the ions investigated in this work are listed in Table 1. The relative exchange rate of water molecules between the hydration sphere and the bulk, Δn/N, appears as an important quantity for the exchange process. As shown in Fig. 1 for the cations in pure water, Δn/N may be expressed as a complicated exponential function of the surface charge density of the ion, σ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |zi|e/4πr2i
(C m−2):
|zi|e/4πr2i
(C m−2):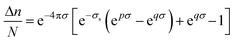
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11.65 (m2 C−1), q
11.65 (m2 C−1), q![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12.52 (m2 C−1) and σs
12.52 (m2 C−1) and σs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.24 C m−2. The surface charge density σs corresponds to the maximum value of Δn/N. Interestingly, the radii derived from σs, which are 2.30, 3.26, and 4.00
0.24 C m−2. The surface charge density σs corresponds to the maximum value of Δn/N. Interestingly, the radii derived from σs, which are 2.30, 3.26, and 4.00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−10 m for zi
10−10 m for zi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2 and 3, respectively, are correlated through a proportionality factor of
1, 2 and 3, respectively, are correlated through a proportionality factor of 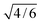 with the Hubbard–Onsager lengths, RH–O, commonly used as solvent parameters. RH–O may be calculated using the following expression37
with the Hubbard–Onsager lengths, RH–O, commonly used as solvent parameters. RH–O may be calculated using the following expression37

![Relative exchange rate of water molecules between the first hydration sphere and the bulk, Δn/N, versus surface charge density σ of the ion in pure water at 298.15 K. The circles represent the univalent ions (Pe4N+, Bu4N+, Pr4N+, Et4N+, Me4N+, NH4+, Cs+, Rb+, K+, Tl+, Ag+, Na+, Li+); the squares the divalent ions (Ra2+, Ba2+, Pb2+, Sr2+, Hg2+, Ca2+, Cd2+, Mn2+, Zn2+, Cu2+, Mg2+, Ni2+, Co2+, Fe2+; Be2+) and the triangles the trivalent ions (La3+, Gd3+, Gd3+, Tb3+, Tm3+, Yb3+, Am3+, Sc3+, Fe3+, Al3+). The solid line is the fit of the data with eqn. (8). The ratio Δn/N was calculated by means of eqns. (7,6,2) using ionic radii from Shannon51 for monatomic ions and thermochemical radii from Jenkins and Thakur52 for polyatomic ions. The values of the ion mobility in pure water were taken from [ref. 28] except for lanthanide ions [ref. 49,50].](/image/article/2003/CP/b208227f/b208227f-f1.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0) in a chemically inert background electrolyte may be given by the following relation:
0) in a chemically inert background electrolyte may be given by the following relation: 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) √μ/3.041
√μ/3.041![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−10
(m−1) the reciprocal radius of the ion atmosphere,41 and a
(m) the distance of closest approach between oppositely charged ions of the background electrolyte.42 The mobility function may be expressed by:
10−10
(m−1) the reciprocal radius of the ion atmosphere,41 and a
(m) the distance of closest approach between oppositely charged ions of the background electrolyte.42 The mobility function may be expressed by: 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [M+]
[M+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [H+]
[H+]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [X−]). The mobility function can then be expressed as a function of the hydrogen ion concentration [H+]
[X−]). The mobility function can then be expressed as a function of the hydrogen ion concentration [H+]

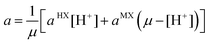
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μNX2
μNX2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μMX is kept constant, and the change of the pH of the solution is achieved by replacing M+ ions by H+ ions, the mobility function is given as a function of the proton concentration [H+] by
μMX is kept constant, and the change of the pH of the solution is achieved by replacing M+ ions by H+ ions, the mobility function is given as a function of the proton concentration [H+] by 
 d(ωHXi) and d(ωMXi) are the mobility functions of the individual ions for the electrolytes NX2, HX and MX. The change of the parameter a with the pH of the electrolyte mixture may be expressed by
d(ωHXi) and d(ωMXi) are the mobility functions of the individual ions for the electrolytes NX2, HX and MX. The change of the parameter a with the pH of the electrolyte mixture may be expressed by 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mH2O
mH2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ⇔
⇔![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M(OH)m(n−m)+
M(OH)m(n−m)+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mH+), which is in fact the case for our experimental study (for the onset of the hydrolysis reactions see the pK°-values in Table 1), the AIIM of the cations can be calculated for various pH values of the mixed electrolyte (for overall ionic strength lower than 0.2 mol dm−3) using eqns. (11), (13) and (14) and (11), (15) and (16) respectively. The electrolyte parameters employed for the calculations are listed in Table 2. The pH-dependence of AIIM of Cs+, Tl+ and Co2+ ions is shown in Fig. 2.
mH+), which is in fact the case for our experimental study (for the onset of the hydrolysis reactions see the pK°-values in Table 1), the AIIM of the cations can be calculated for various pH values of the mixed electrolyte (for overall ionic strength lower than 0.2 mol dm−3) using eqns. (11), (13) and (14) and (11), (15) and (16) respectively. The electrolyte parameters employed for the calculations are listed in Table 2. The pH-dependence of AIIM of Cs+, Tl+ and Co2+ ions is shown in Fig. 2.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.15 K
298.15 K
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75.56 (r+
75.56 (r+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r−)−1
− 18.06 obtained for the perchlorate data: a(NaClO4)
r−)−1
− 18.06 obtained for the perchlorate data: a(NaClO4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.04 Å, a(LiClO4)
4.04 Å, a(LiClO4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.63 Å, a(Zn(ClO4)2)
5.63 Å, a(Zn(ClO4)2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.18 Å
[ref. 41] with r+ the ionic radius of the cation and r− that of the anion/Å.
6.18 Å
[ref. 41] with r+ the ionic radius of the cation and r− that of the anion/Å.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol dm−3
(solid line: Na(H)ClO4, dashed line: Co(ClO4)/Na(H)ClO4) calculated with the extended limiting law, eqn. (11).
0.1 mol dm−3
(solid line: Na(H)ClO4, dashed line: Co(ClO4)/Na(H)ClO4) calculated with the extended limiting law, eqn. (11).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3 for all electrolytes. The concentration of Co(ClO4)2 was fixed to 0.023 mol dm−3.
0.10 mol dm−3 for all electrolytes. The concentration of Co(ClO4)2 was fixed to 0.023 mol dm−3.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 kg−1 s−1 and that of 0.10 mol dm−3 HClO4 is 9.117
10−4 kg−1 s−1 and that of 0.10 mol dm−3 HClO4 is 9.117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 kg−1 s−1.45 The difference in the viscosity is only 1.3%, while the AIIM of the ions studied for the two electrolytes differ by 10 to 20%. Furthermore, no metal-ligand complexation equilibria, redox reactions or protonization equilibria may have an influence on the mobility of the investigated ions. The coating of the inner surface of the migration tube for suppression of the electroosmosis performed well since no change in the height and shape of the measured radioactive distributions was detected during the electromigration runs. No adsorption of the radioactive ions on the wall of the migration tube was observed. Similar dependences of the ion mobility on the pH of inert aqueous solutions have been found for the lanthanide ions in previous study (Fig. 4).11 The two levels of the migration data obtained for the neutral and acidic electrolytes are given in Table 3 and Table 4 respectively.
10−4 kg−1 s−1.45 The difference in the viscosity is only 1.3%, while the AIIM of the ions studied for the two electrolytes differ by 10 to 20%. Furthermore, no metal-ligand complexation equilibria, redox reactions or protonization equilibria may have an influence on the mobility of the investigated ions. The coating of the inner surface of the migration tube for suppression of the electroosmosis performed well since no change in the height and shape of the measured radioactive distributions was detected during the electromigration runs. No adsorption of the radioactive ions on the wall of the migration tube was observed. Similar dependences of the ion mobility on the pH of inert aqueous solutions have been found for the lanthanide ions in previous study (Fig. 4).11 The two levels of the migration data obtained for the neutral and acidic electrolytes are given in Table 3 and Table 4 respectively.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3). (b) Ion mobility of Tl+ in Na(H)ClO4
(μ
0.10 mol dm−3). (b) Ion mobility of Tl+ in Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3). (c) Ion mobility of Co2+ in Na(H)ClO4
(μ
0.10 mol dm−3). (c) Ion mobility of Co2+ in Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3), open symbols; ion mobility of Co2+ in Co(ClO4)2/Na(H)ClO4
(μ
0.10 mol dm−3), open symbols; ion mobility of Co2+ in Co(ClO4)2/Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3, μCo(ClO4)2
0.10 mol dm−3, μCo(ClO4)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.068 mol dm−3, μNa(H)ClO4
0.068 mol dm−3, μNa(H)ClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.032 mol dm−3), close symbols. The solid line is the fit of experimental data using eqn. (19), the dashed line is the ion mobility calculated using eqn. (11), the dotted line is the ion mobility calculated using eqn. (24).
0.032 mol dm−3), close symbols. The solid line is the fit of experimental data using eqn. (19), the dashed line is the ion mobility calculated using eqn. (11), the dotted line is the ion mobility calculated using eqn. (24).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 mol dm−3). (b) Ion mobility of Gd3+ in Na(H)ClO4
(μ
0.01 mol dm−3). (b) Ion mobility of Gd3+ in Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3). (c) Ion mobility of Lu3+ in Na(H)ClO4
(μ
0.10 mol dm−3). (c) Ion mobility of Lu3+ in Na(H)ClO4
(μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3). The solid line is the fit of experimental data using eqn. (21), the dotted line is the ion mobility calculated using eqn. (24).
0.10 mol dm−3). The solid line is the fit of experimental data using eqn. (21), the dotted line is the ion mobility calculated using eqn. (24).![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i the ion micro-viscosity, and τi the rotational reorientation time of water molecules in the first hydration shell. ri is the ionic radius. T
i the ion micro-viscosity, and τi the rotational reorientation time of water molecules in the first hydration shell. ri is the ionic radius. T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1(5) K
298.1(5) K
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i
[eqn. (2)]/10−4 kg−1 s−1
i
[eqn. (2)]/10−4 kg−1 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01
0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i the ion micro-viscosity, and τi the rotational reorientation time of water molecules in the first hydration shell. ri is the ionic radius. T
i the ion micro-viscosity, and τi the rotational reorientation time of water molecules in the first hydration shell. ri is the ionic radius. T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1(5) K
298.1(5) K
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i
[eqn. (2)]/10−4 kg−1 s−1
i
[eqn. (2)]/10−4 kg−1 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01
0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pH
pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 to 5, the AIIM is constant. The value of the AIIM is in close agreement with the theoretical value given by the extended DHO limiting law for each of the Cs+, Tl+, and Co2+ ions. In the case of the trivalent lanthanide and actinide ions the experimentally determined AIIM11 are 10 to 20% higher than the value predicted by the extended limiting law.
3 to 5, the AIIM is constant. The value of the AIIM is in close agreement with the theoretical value given by the extended DHO limiting law for each of the Cs+, Tl+, and Co2+ ions. In the case of the trivalent lanthanide and actinide ions the experimentally determined AIIM11 are 10 to 20% higher than the value predicted by the extended limiting law.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pH
pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the AIIM decreases at increasing hydrogen ion concentration and reaches a minimum at about pH 2.
2, the AIIM decreases at increasing hydrogen ion concentration and reaches a minimum at about pH 2.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pH
pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, a small increase of the AIIM is observed, which is qualitatively in agreement with the prediction given by the extended limiting law.
1, a small increase of the AIIM is observed, which is qualitatively in agreement with the prediction given by the extended limiting law.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), αi the partial mole fraction of the ionic species in the equilibrium and φ a function taking into account the change of the activity coefficients γ when switching from Na+ to H+ in the perchlorate solution of a constant overall ionic strength. Concerning the small increase of the AIIM of the radioactive cations observed between pH 2 and pH 1, the function φ can be expressed as
1), αi the partial mole fraction of the ionic species in the equilibrium and φ a function taking into account the change of the activity coefficients γ when switching from Na+ to H+ in the perchlorate solution of a constant overall ionic strength. Concerning the small increase of the AIIM of the radioactive cations observed between pH 2 and pH 1, the function φ can be expressed as 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.321[H+]
0.321[H+]
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1(5) K
298.1(5) K
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ
βψ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ
[eqn. (23)]
βψ
[eqn. (23)]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1, γNaClO4
0.1, γNaClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.777, γHClO4
0.777, γHClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.803
0.803![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01, γNaClO4
0.01, γNaClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.903, γHClO4
0.903, γHClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.906
0.906![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1, γNaClO4
0.1, γNaClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.856, γHClO4
0.856, γHClO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.860
0.860![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol dm−3 and 0.86(1) at μ
0.1 mol dm−3 and 0.86(1) at μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 mol dm−3
(the ratio is quoted by A in Table 5). As the ionic strength of the electrolyte mixture approaches zero (infinite dilution of the electrolyte) and thus the pH to 7, the value of A is expected to approach unity.
0.01 mol dm−3
(the ratio is quoted by A in Table 5). As the ionic strength of the electrolyte mixture approaches zero (infinite dilution of the electrolyte) and thus the pH to 7, the value of A is expected to approach unity.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 mol dm−3) may be given by:
0.2 mol dm−3) may be given by: 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ·(τi°/τH2O°)
versus
(τi°/τH2O°)
(Fig. 5). In fact log
βψ·(τi°/τH2O°)
versus
(τi°/τH2O°)
(Fig. 5). In fact log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ corresponds to the pH-value for which we have: [{M(H2O)Nn+}]
βψ corresponds to the pH-value for which we have: [{M(H2O)Nn+}]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [{M(H2O)Nn+}{H+}]. From the linear fit of the data plotted in Fig. 5 and using eqns. (6) and (2), the stoichiometric equilibrium constant may be expressed as a function of the diffusion coefficient of the ion in pure water, (Di°
[{M(H2O)Nn+}{H+}]. From the linear fit of the data plotted in Fig. 5 and using eqns. (6) and (2), the stoichiometric equilibrium constant may be expressed as a function of the diffusion coefficient of the ion in pure water, (Di°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kTui°/ez), and of the diffusion coefficient of water, DH2O°:
kTui°/ez), and of the diffusion coefficient of water, DH2O°:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ values calculated with the equation above are listed in Table 5.
βψ values calculated with the equation above are listed in Table 5.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βψ(τi°/τH2O°)
versusτi°/τH2O°) at T
βψ(τi°/τH2O°)
versusτi°/τH2O°) at T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.15 K for the ions investigated. (Coefficient of correlation r
298.15 K for the ions investigated. (Coefficient of correlation r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.988).
0.988).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u°
u°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g(μ,[H+]). The variation of the AIIM with the pH of the inert electrolyte calculated by means of eqn. (24) is represented by the dotted lines in Fig. 4 and Fig. 5.
g(μ,[H+]). The variation of the AIIM with the pH of the inert electrolyte calculated by means of eqn. (24) is represented by the dotted lines in Fig. 4 and Fig. 5.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pH
pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3–5, the hydrogen ion concentration appears to be too low to affect the dynamic properties of the bulk water. The values of the ion microviscosity
3–5, the hydrogen ion concentration appears to be too low to affect the dynamic properties of the bulk water. The values of the ion microviscosity ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) i and of the reorientation time of water molecules in the hydration shell of the ion τi calculated from the experimental AIIM (Table 3) are somewhat higher than those obtained for pure water (Table 1). This is due mainly to the modification of the dynamical properties of bulk water induced by the hydrated ions of the electrolyte. We also observed that the pH value at which the decrease of the ion mobility begins appears to depend on the structure-affecting properties of the moving ion.
i and of the reorientation time of water molecules in the hydration shell of the ion τi calculated from the experimental AIIM (Table 3) are somewhat higher than those obtained for pure water (Table 1). This is due mainly to the modification of the dynamical properties of bulk water induced by the hydrated ions of the electrolyte. We also observed that the pH value at which the decrease of the ion mobility begins appears to depend on the structure-affecting properties of the moving ion.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≠
≠![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H+). The variation of τj with the hydrogen ion concentration at a given overall ionic strength of the electrolyte mixture is obtained using relation (24). The values of the phenomenological stoichiometric equilibrium constants βψ derived from relation (22) are: 162(9), 2188(131), 4898(292) dm3 mol−1 for ClO4−, Na+ and Co2+ respectively. The variation of the reorientation time of the bulk water molecules τH2O with the hydrogen ion concentration of the various electrolytes mixtures is shown in Fig. 6. The values of τH2O and of the corresponding diffusion coefficient of bulk water DH2O for the neutral and acidic electrolyte solutions are listed in Table 6. A consequence of relation (25) is that the relative exchange rate of water molecules between the first hydration sphere of the ion and the bulk, Δn/N, remains constant for any electrolyte composition. We see no indication that more or less water molecules leave the hydration shell of the ion as the hydrogen ion concentration of the electrolyte increases, only the dynamical properties are affected. Hence the rotational reorientation time of the water molecules in the hydration shell of the migrating radioactive ion may be expressed as
H+). The variation of τj with the hydrogen ion concentration at a given overall ionic strength of the electrolyte mixture is obtained using relation (24). The values of the phenomenological stoichiometric equilibrium constants βψ derived from relation (22) are: 162(9), 2188(131), 4898(292) dm3 mol−1 for ClO4−, Na+ and Co2+ respectively. The variation of the reorientation time of the bulk water molecules τH2O with the hydrogen ion concentration of the various electrolytes mixtures is shown in Fig. 6. The values of τH2O and of the corresponding diffusion coefficient of bulk water DH2O for the neutral and acidic electrolyte solutions are listed in Table 6. A consequence of relation (25) is that the relative exchange rate of water molecules between the first hydration sphere of the ion and the bulk, Δn/N, remains constant for any electrolyte composition. We see no indication that more or less water molecules leave the hydration shell of the ion as the hydrogen ion concentration of the electrolyte increases, only the dynamical properties are affected. Hence the rotational reorientation time of the water molecules in the hydration shell of the migrating radioactive ion may be expressed as ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τi°(τH2O/τH2O°)
τi°(τH2O/τH2O°)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3; the dashed line the electrolyte mixture Na(H)ClO4μ
0.10 mol dm−3; the dashed line the electrolyte mixture Na(H)ClO4μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 mol dm−3 and the dotted line the electrolyte mixture Co(ClO4)2/Na(H)ClO4μ
0.01 mol dm−3 and the dotted line the electrolyte mixture Co(ClO4)2/Na(H)ClO4μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.10 mol dm−3.
0.10 mol dm−3.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 298.1(5) K
298.1(5) K
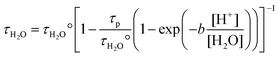
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55.5 mol dm−3 and b a numerical constant. The fit of the τH2O data for HClO4 electrolytes according to the relation (27)
(solid line in Fig. 7) leads to a value for τp of 1.44(18) ps at 298.1(5) K. The inverse of this number corresponds to the rate constant for proton transfer between the hydronium ions and the acceptor water molecule. The value found here is 0.69(9) ps−1 and compares well with the experimental value obtained from NMR studies of proton transfer in water,46 0.67 ps−1 and with the values calculated by quantum molecular dynamic simulation18 which are 0.69 ps−1 for proton transfer in the Eigen cation and 0.60 ps−1 for proton transfer in the Zundel cation. The ratio b/[H2O] in expression (27) is 60.8(4) dm3 mol−1.
55.5 mol dm−3 and b a numerical constant. The fit of the τH2O data for HClO4 electrolytes according to the relation (27)
(solid line in Fig. 7) leads to a value for τp of 1.44(18) ps at 298.1(5) K. The inverse of this number corresponds to the rate constant for proton transfer between the hydronium ions and the acceptor water molecule. The value found here is 0.69(9) ps−1 and compares well with the experimental value obtained from NMR studies of proton transfer in water,46 0.67 ps−1 and with the values calculated by quantum molecular dynamic simulation18 which are 0.69 ps−1 for proton transfer in the Eigen cation and 0.60 ps−1 for proton transfer in the Zundel cation. The ratio b/[H2O] in expression (27) is 60.8(4) dm3 mol−1.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.01
7.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−9 m2 s−1 is the abnormal proton mobility, (difference between the proton diffusion coefficient, 9.31
10−9 m2 s−1 is the abnormal proton mobility, (difference between the proton diffusion coefficient, 9.31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−9 m2 s−1, and water self-diffusion coefficient, 2.30
10−9 m2 s−1, and water self-diffusion coefficient, 2.30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−9 m2 s−1).15,28 With τp
10−9 m2 s−1).15,28 With τp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.44(18) ps we find a value for the proton hopping length of rOO
1.44(18) ps we find a value for the proton hopping length of rOO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.46(15)
Å. This value agrees well with the experimental data obtained from thermal neutron and X-ray scattering studies, rOO
2.46(15)
Å. This value agrees well with the experimental data obtained from thermal neutron and X-ray scattering studies, rOO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.5 Å.47 Molecular dynamic simulations lead to values of rOO
2.5 Å.47 Molecular dynamic simulations lead to values of rOO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.40–2.49 Å for H5O2+ and rOO
2.40–2.49 Å for H5O2+ and rOO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.50–2.60 Å for H9O4+.16,17,20 For comparison it should be remembered that the oxygen–oxygen distance between two water molecules in pure water is larger, about 2.8 Å.
2.50–2.60 Å for H9O4+.16,17,20 For comparison it should be remembered that the oxygen–oxygen distance between two water molecules in pure water is larger, about 2.8 Å.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.44 ps and b/[H2O]
1.44 ps and b/[H2O]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60.8 dm3 mol−1 are represented by the solid line in Fig. 8. The calculated values agree well with the experimental data. Thus, despite the great lack of absolute and accurate tracer migration data in perchloric acid for comparison, we can say that eqn. (29) leads to a good estimation of the transport properties of ions on tracer scale in HClO4. For other acids such as HCl or HNO3 for example, eqn. (29) cannot be applied directly for all metal ions because of the formation of complex species of various charges which greatly influence the overall ion mobility.
60.8 dm3 mol−1 are represented by the solid line in Fig. 8. The calculated values agree well with the experimental data. Thus, despite the great lack of absolute and accurate tracer migration data in perchloric acid for comparison, we can say that eqn. (29) leads to a good estimation of the transport properties of ions on tracer scale in HClO4. For other acids such as HCl or HNO3 for example, eqn. (29) cannot be applied directly for all metal ions because of the formation of complex species of various charges which greatly influence the overall ion mobility.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) there is a fairly good agreement between experimental and calculated values. The experimentally observed decrease of the AIIM of the radioactive ions for higher hydrogen ion concentrations (pH
4) there is a fairly good agreement between experimental and calculated values. The experimentally observed decrease of the AIIM of the radioactive ions for higher hydrogen ion concentrations (pH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4) is not explained by the extended DHO limiting law. A systematic analysis of the migration data was performed assuming a change of the dynamical properties of the water molecules in the hydration shell of the migrating radioactive ions. The resulting general relation for the variation of the AIIM with the hydrogen ion concentration as well as with the overall ionic strength μ of the electrolyte mixture is of the form: u
4) is not explained by the extended DHO limiting law. A systematic analysis of the migration data was performed assuming a change of the dynamical properties of the water molecules in the hydration shell of the migrating radioactive ions. The resulting general relation for the variation of the AIIM with the hydrogen ion concentration as well as with the overall ionic strength μ of the electrolyte mixture is of the form: u![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) u°
u°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f(μ,[H+])
[see eqn. (24)].
f(μ,[H+])
[see eqn. (24)].![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 039–10
039–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048 CrossRef CAS.
048 CrossRef CAS.