Gas-phase rate coefficients and activation energies for the reaction of NO3 radicals with selected branched aliphatic aldehydes
B.
Cabañas
*,
S.
Salgado
,
P.
Martín
,
M. T.
Baeza
,
J.
Albaladejo
and
E.
Martínez
Facultad de Químicas, Universidad de Castilla-La Mancha, Avda, Camilo José Cela 10, 13071, Ciudad-Real, Spain. E-mail: Beatriz.Cabanas@uclm.es
First published on 15th November 2002
Abstract
Using a fast-flow-discharge technique, absolute rate coefficients for the gas-phase reactions of the NO3 radical with a series of branched aldehydes (2-methylpropanal, 2,2-dimethylpropanal, 2-methylbutanal and 3-methylbutanal) have been determined. The experiments were carried out monitoring the NO3 radical by laser induced fluorescence (LIF). The temperature dependence of the reaction was studied in the range between 298 and 433 K. The proposed Arrhenius expressions, are respectively:
k
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.0
(1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5)
0.5)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−10exp[−(2598
10−10exp[−(2598![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384)/T]/cm3 molecule−1 s−1,
384)/T]/cm3 molecule−1 s−1,
k
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (2.7
(2.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2)
1.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11exp[−(2063
10−11exp[−(2063![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 356)/T]/cm3 molecule−1 s−1,
356)/T]/cm3 molecule−1 s−1,
k
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (5.5
(5.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.1)
3.1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11exp[−(2296
10−11exp[−(2296![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 555)/T]/cm3 molecule−1 s−1,
555)/T]/cm3 molecule−1 s−1,
k
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (3.7
(3.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4)
1.4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11exp[−(2184
10−11exp[−(2184![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230)/T]/cm3 molecule−1 s−1.
230)/T]/cm3 molecule−1 s−1.
Tropospheric lifetimes for these aldehydes have been calculated at night and during the daytime for typical NO3 and OH average concentrations.
Introduction
Aldehydes, as other carbonyl compounds are emitted into the atmosphere from anthropogenic and natural sources.1,2 They are emitted as primary pollutants from partial oxidation of hydrocarbon fuels and they are the first stable products (secondary pollutant) from the atmospheric oxidation of different anthropogenic and biogenic organic compounds.3–5 Also vegetation has been found to be a significant source of aldehydes, mainly high molecular weight aldehydes (> C5), emitted from a variety of arboreous plants, shrubs, herbaceous plants and mosses.6,7 Depending on the plant species, the emission rates can be comparable to those of monoterpenes.8,9 Finally an additional source of volatile aldehydes are forest fires and biomass burning.10Principal representatives of aldehydes in the atmosphere are the low molecular weight1,2,11–14 compounds such as formaldehyde,15–17 which has been the subject of numerous studies in view of its importance in the tropospheric oxidation of hydrocarbons and acetaldehyde,17–19 detected in urban and rural areas of particular interest as a precursor of peroxyacetylnitrate (PAN), a photooxidant, well known for its adverse effects on human health and plant growth.20,21
Aldehydes are removed from the troposphere by wet and dry deposition, photolytic processes yielding radicals as primary products or by chemical reactions with the OH radical during the day-time or by reaction with the NO3 radical during the night-time. The night-time reactions of NO3 radicals with aldehydes have been object of several kinetic studies,22–29 but, at the present time, kinetic data are still scarce especially for larger aldehydes (> C5).30–34 These reactions lead to the formation of hydroperoxy (HO2) and organic peroxy (RO2) radicals, and in the presence of NO to the formation of OH. The reaction of unsaturated aldehydes with NO3, can provide a mechanism for the transport of NO2 species between different parts of the atmosphere through the formed peroxyacyl nitrates and also these radicals participate in chemical cycles which produce OH radicals during the night.24
In this work, we have studied the NO3 reaction with some branched aldehydes (2-methylpropanal, 2,2-dimethylpropanal, 2-methylbutanal and 3-methylbutanal) continuing the systematic investigation of the NO3 reaction with aldehydes developed in our laboratory and completing the former studies on the reactivity of the NO3 radical with linear aliphatic aldehydes and unsaturated aldehydes.33,34 Kinetic data for the NO3 reaction with different series of aldehydes are needed to get a better understanding about the role of aldehydes in the atmospheric chemistry and to develop a reliable structure–reactivity relationship for these compounds.
The following reactions have been investigated:
2-methylpropanal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NO3 NO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Products Products | (1) |
2,2-dimethylpropanal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NO3 NO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Products Products | (2) |
2-methylbutanal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NO3 NO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Products Products | (3) |
3-methylbutanal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NO3 NO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Products Products | (4) |
The experiments have been performed in a fast flow system and using laser induced fluorescence (LIF) detection of the NO3 radical. The absolute rate coefficients at different temperatures have been measured and the Arrhenius parameters calculated for the four reactions studied, (1)–(4).
Experimental
The absolute rate coefficients were measured using a discharge-flow tube reactor with LIF detection for the nitrate radical. The experimental set up was described in detail in previous articles,35,36 therefore only the relevant details are given here.Nitrate radicals were generated in a side-arm tube by the reaction, F![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HNO3
HNO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NO3
NO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HF, and they were admitted at the upstream end of the flow tube through a fixed port. Fluorine atoms were obtained by passing F2–He mixtures through a microwave discharge. The dissociation of F2 into F atoms was close to 100% and a massive excess of HNO3
([HNO3]
HF, and they were admitted at the upstream end of the flow tube through a fixed port. Fluorine atoms were obtained by passing F2–He mixtures through a microwave discharge. The dissociation of F2 into F atoms was close to 100% and a massive excess of HNO3
([HNO3]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50[F]) was immediately added to remove all the atomic fluorine. The initial concentrations of NO3 were in the range of 5 to 13
50[F]) was immediately added to remove all the atomic fluorine. The initial concentrations of NO3 were in the range of 5 to 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1012 molecule cm−3. Quantitative detection of NO3 was carried out by monitoring the fluorescence emitted after exciting the (0–0) 2E′
1012 molecule cm−3. Quantitative detection of NO3 was carried out by monitoring the fluorescence emitted after exciting the (0–0) 2E′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ←
←![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2A′2 transition of NO3 pumping with λ
2A′2 transition of NO3 pumping with λ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 662.0 nm radiation from a dye laser (Quantel, TDL90). Under our experimental conditions, the reactor being coated with halocarbon wax, the wall loss of the nitrate radical was found to be negligible, with a kw
662.0 nm radiation from a dye laser (Quantel, TDL90). Under our experimental conditions, the reactor being coated with halocarbon wax, the wall loss of the nitrate radical was found to be negligible, with a kw![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 s−1.
0.1 s−1.
The aldehydes were introduced through a sliding injector, the position of which varied up to 70 cm from the center of the observation region. The concentrations of the studied aldehydes ranged from 0.5 to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1014 molecule cm−3 and were measured by the drop in pressure with respect to time on delivery from their calibrated volume storage bulbs.
1014 molecule cm−3 and were measured by the drop in pressure with respect to time on delivery from their calibrated volume storage bulbs.
Variation of the reaction time was provided by changing the distance between the injector and the detection cell. Contact times between NO3 and the reactant were in the range of 10 to 110 ms.
Helium was used as a carrier gas, and the experiments were carried out at a total pressure of 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 Torr. The flow tube was heated between room temperature (298 K) and 433 K by an electronically regulated heating tape. The temperature was measured with an accuracy of ±1 K. Direct measurements of the temperature inside the flow tube showed that it dropped rapidly at approximately 7 cm upstream from the detection cell. The temperature profiles as a function of distance from the cell were obtained in the same way as is reported by Canosa-Mas et al.37
0.2 Torr. The flow tube was heated between room temperature (298 K) and 433 K by an electronically regulated heating tape. The temperature was measured with an accuracy of ±1 K. Direct measurements of the temperature inside the flow tube showed that it dropped rapidly at approximately 7 cm upstream from the detection cell. The temperature profiles as a function of distance from the cell were obtained in the same way as is reported by Canosa-Mas et al.37
Helium (Carburos Metálicos C50) was passed through an oxygen-removing columm (Oxisorb, Messer Griesheim) trap and through a molecular-sieve trap at room temperature. Molecular fluorine (5% in He) was supplied by Praxair. Anhydrous gaseous HNO3 in a He carrier was prepared by bubbling He through a mixture of H2SO4–HNO3 (P.A. Panreac).
All the organic reactants, 2-methylpropanal (99.5%), 2,2-dimethylpropanal (97%), 2-methylbutanal (95%), and 3-methylbutanal (97%) were obtained from Sigma Aldrich Chemical Co.
Results
The desired bimolecular rate coefficient for the reactions between the branched aldehydes and the NO3 radical, k is defined by eqn. (I). | (I) |
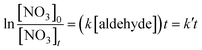 | (II) |
where k′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k
[reactant] k
[reactant] | (III) |
The temperature dependence of the reactions of 2-methylpropanal, 2,2-dimethyilpropanal, 2-methylbutanal and 3-methylbutanal with NO3 radical, reactions (1)–(4), were investigated over the range of temperature 298–433 K and due to the existence of a temperature profile in the flow-tube, the rate coefficients at elevated temperatures were calculated assuming that the entire flow tube was at the same high temperature and the cell was at room temperature. Thus the adequate standard kinetic equation is applied separately to both regions at the different temperatures. Airds et al.39 and Martinez et al.40 have shown that this method leads to good results in systems with a profile of temperature in the flow tube similar to our profile.
At each temperature graphs of ln([NO3]0/[NO3])tvs. time (first-order plot) were obtained. The slopes of these plots yield the corresponding pseudo-first order rate coefficients k′ in accordance with eqn. (II). Fig. 1 shows typical first-order plots for the reaction of NO3 with 2,2-dimethylpropanal at 345 K and different aldehyde concentrations. The first-order rate coefficients k′ for each compound at a given temperature were plotted against the reactant concentration, and the second-order rate coefficients were obtained as the slopes of least-squares fit of these data. Fig. 2 shows plots of the pseudo-first order rate coefficients, k′ vs. the reactant concentration for the reaction of NO3 with 2,2-dimethylpropanal at four different temperatures.
![Pseudo-first order plots for the reactions of NO3 with 2,2-dimethylpropanal at 433 K, and at different concentrations. [2,2DMP] = 2,2-dimethylpropanal concentration, in units of molecule cm−3.](/image/article/2003/CP/b205495g/b205495g-f1.gif) | ||
Fig. 1 Pseudo-first order plots for the reactions of NO3 with 2,2-dimethylpropanal at 433 K, and at different concentrations. [2,2DMP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,2-dimethylpropanal concentration, in units of molecule cm−3. 2,2-dimethylpropanal concentration, in units of molecule cm−3. | ||
 | ||
| Fig. 2 Second-order plots for the reaction of NO3 with 2,2-dimethylpropanal at different temperatures. | ||
A summary of the absolute second order rate coefficient obtained for reactions (1)–(4) presented in this work is given in Table 1.
| T/K | k/10−14 cm3 molecule−1 s−1 (this work) | k/10−14 cm3 molecule−1 s−1 (other work) | E a/kJ mol−1 | A/10−11 molecule−1 cm3 s−1 |
|---|---|---|---|---|
a [NO3]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (5–13) (5–13)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1012 molecule cm−3, PT 1012 molecule cm−3, PT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.1 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 Torr, t 0.2 Torr, t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10–110 ms, v 10–110 ms, v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4–7 m s−1. Indicated errors are two least-squares standard deviations (2σ).
b From ref. 30, relative rate coefficient (RR).
c From ref. 32, absolute rate coefficient (A).
d From ref. 31, relative rate coefficient (RR). 4–7 m s−1. Indicated errors are two least-squares standard deviations (2σ).
b From ref. 30, relative rate coefficient (RR).
c From ref. 32, absolute rate coefficient (A).
d From ref. 31, relative rate coefficient (RR).
|
||||
Reaction NO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-methylpropanal 2-methylpropanal |
||||
| 298 | 1.61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.13 0.13 |
1.21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.06b 0.06b |
||
3.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5c 0.5c |
||||
| 345 | 8.82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.20 1.20 |
21.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.2 3.2 |
10.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.0 5.0 |
|
| 389 | 14.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.12 2.12 |
|||
| 433 | 25.96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.15 1.15 |
|||
Reaction NO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,2-methylpropanal 2,2-methylpropanal |
||||
| 298 | 2.80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35 0.35 |
2.29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.09b 0.09b |
||
| 345 | 7.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.97 0.97 |
17.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6 1.6 |
2.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4 1.4 |
|
| 389 | 13.44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.14 0.14 |
|||
| 433 | 27.30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.76 2.76 |
|||
Reaction NO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2-methylbutanal 2-methylbutanal |
||||
| 298 | 2.56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.49 0.49 |
– | ||
| 345 | 5.92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.50 0.50 |
19.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.6 4.6 |
5.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.1 3.1 |
|
| 389 | 14.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.24 0.24 |
|||
| 433 | 22.42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.99 1.99 |
|||
Reaction NO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-methylbutanal 3-methylbutanal |
||||
| 298 | 2.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.20 0.20 |
1.20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3d 0.3d |
||
| 345 | 7.17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.38 0.38 |
18.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.9 1.9 |
3.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4 1.4 |
|
| 389 | 11.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.93 0.93 |
|||
| 433 | 25.74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.85 1.85 |
|||
As the rate coefficients of the reactions investigated are fairly small the possible influence of secondary chemistry on the absolute measurement for the calculated rate coefficients has been investigated. A set of simulation calculations for reactions (1)–(4) was made, using the FACSIMILE code.41 In the calculations, for each primary reaction (1)–(4) a consecutive pathway of reactions between the organic product radicals (RCO, RO and R) and the nitrate radical was considered, as well as the reaction of the nitrate radical with NO2. The best fits of the NO3 experimental data were obtained when the weight of the secondary chemistry was minimized, thus confirming a negligible effect of the secondary reactions under the experimental working conditions used in the present work.
The data for the reaction of the nitrate radical with 2,2-dimethylpropanal is shown in Fig. 3 in the form of an Arrhenius plot, where ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k has been plotted vs. 1/T. A linear least-square analysis of the data yields the activation energy and the pre-exponential factor. The rate coefficients at different temperatures for such reactions, with the corresponding activation energy and pre-exponential factor are also summarized in Table 1.
k has been plotted vs. 1/T. A linear least-square analysis of the data yields the activation energy and the pre-exponential factor. The rate coefficients at different temperatures for such reactions, with the corresponding activation energy and pre-exponential factor are also summarized in Table 1.
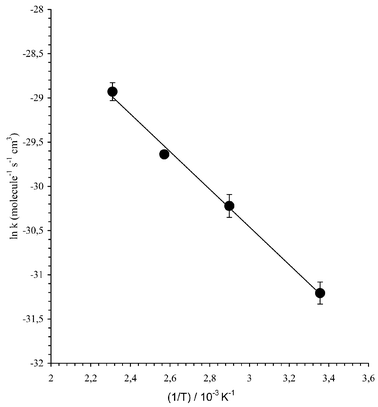 | ||
| Fig. 3 Example of Arrhenius plots for the reactions of NO3 with 2,2-dimethylpropanal. | ||
From the data obtained in these experiments, the following Arrhenius expressions were derived:,
k
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (1.0
(1.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5)
0.5)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−10exp[−(2598
10−10exp[−(2598![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384)/T]/cm3 molecule−1 s−1,
384)/T]/cm3 molecule−1 s−1,
k
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (2.7
(2.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2)
1.2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11exp[−(2063
10−11exp[−(2063![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 356)/T]/cm3 molecule−1 s−1,
356)/T]/cm3 molecule−1 s−1,
k
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (5.5
(5.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.1)
3.1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11exp[−(2296
10−11exp[−(2296![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 555)/T]/cm3 molecule−1 s−1,
555)/T]/cm3 molecule−1 s−1,
k
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (3.7
(3.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4)
1.4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11exp[−(2184
10−11exp[−(2184![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230)/T]/cm3 molecule−1 s−1.
230)/T]/cm3 molecule−1 s−1.
These expressions are able to predict the rate coefficients of the reactions of 2-methylpropanal, 2,2-dimethylpropanal 2-methylbutanal, and 3-methylbutanal with NO3, respectively, in the temperature range 298–433 K.
Discussion
The published rate coefficients for the reaction of NO3 with aldehydes, are around 10−15–10−13 cm3 molecule−1 s−1. In previous work on the NO3–aldehyde reactivity33,34 it has been pointed out that the obtained rate coefficients are also in the range of the rate constants for the reactions of NO3 with alkenes (between 10−16 and 10−11 cm3 molecule−1 s−1). The absolute rate constants at room temperature measured in this work for branched aldehydes, shown in Table 1, are in the range (1.6–2.8)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−14 cm3 molecule−1 s−1. These values are compared with the available literature data in Table 1. The reaction of the nitrate radical with 2-methylpropanal has been studied, with both, absolute and relative techniques. It can be seen that our absolute experimental value of the rate coefficient is higher than the relative values given by D'Anna et al.,30 and much lower than the absolute value obtained for Ullerstram et al.32 The absolute rate coefficient obtained in the present work for the reaction of nitrate radical with 2,2-dimethylpropanal is (within the experimental error) slightly higher than the one obtained by the relative technique by D'Anna et al.30 No data for the reaction of NO3 with 2-methylbutanal has been found and for the reaction of 3-methylbutanal the rate coefficients presented in this article is much higher than the relative value calculated by Glasius et al.31 The reason for these discrepances remain unclear.
10−14 cm3 molecule−1 s−1. These values are compared with the available literature data in Table 1. The reaction of the nitrate radical with 2-methylpropanal has been studied, with both, absolute and relative techniques. It can be seen that our absolute experimental value of the rate coefficient is higher than the relative values given by D'Anna et al.,30 and much lower than the absolute value obtained for Ullerstram et al.32 The absolute rate coefficient obtained in the present work for the reaction of nitrate radical with 2,2-dimethylpropanal is (within the experimental error) slightly higher than the one obtained by the relative technique by D'Anna et al.30 No data for the reaction of NO3 with 2-methylbutanal has been found and for the reaction of 3-methylbutanal the rate coefficients presented in this article is much higher than the relative value calculated by Glasius et al.31 The reason for these discrepances remain unclear.
Regarding the dependence of the rate coefficient on temperature for the reactions of NO3 with branched aldehydes, only the work of Ullerstram et al.32 for the reaction of NO3 wit 2-methylpropanal has been reported.
So, this is the first study on the temperature dependence for the reactions of NO3 with 2,2-dimethylpropanal, 2-methylbutanal and 3-methylbutanal. As can be expected for an abstraction process, a positive activation energy for all the reactions of NO3 with such compounds has been obtained: 2-methylpropanal, (21.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.2 kJ mol−1), 2,2-dimethylpropanal (17.2
3.2 kJ mol−1), 2,2-dimethylpropanal (17.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6 kJ mol−1), 2-methylbutanal, (19.1
1.6 kJ mol−1), 2-methylbutanal, (19.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.6 kJ mol−1) and 3-methylbutanal, (17.7
4.6 kJ mol−1) and 3-methylbutanal, (17.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4 kJ mol−1). These positive values of the activation energies are of the same order as the values obtained for the NO3 abstraction process with alkanes,24,33 and similar to those for the reactions of NO3 with aliphatic aldehydes.33,34 The value calculated by Ullerstam et al. for the reaction with 2-methylpropanal is lower (14
1.4 kJ mol−1). These positive values of the activation energies are of the same order as the values obtained for the NO3 abstraction process with alkanes,24,33 and similar to those for the reactions of NO3 with aliphatic aldehydes.33,34 The value calculated by Ullerstam et al. for the reaction with 2-methylpropanal is lower (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 kJ mol−1) than that obtained in this work for the reaction of this compound and lower than the activation energy for the other reactions of different saturated aldehydes reported in the literature.24–33,42
1 kJ mol−1) than that obtained in this work for the reaction of this compound and lower than the activation energy for the other reactions of different saturated aldehydes reported in the literature.24–33,42
For a better understanding of the reactivity of aldehydes with NO3 it is necessary to analyze the result obtained in this work together with those obtained for other series of aldehydes. Table 2 shows the room temperature rate coefficient and activation energy for different aldehydes, obtained in our laboratory.33 It can be observed that the rate constant increases with the length of the organic chain. Comparing the rate coefficients for the reactions of 2-methylpropanal and 2,2-dimethylpropanal with the corresponding value for propanal we also can observe an increase in the rate coefficient due to the presence and number of substituents in the organic chain. The same effect can be seen in the data of butanal, 2-methylbutanal and 3-methylbutanal. All the values of activation energy are of the same order (around 20 kJ mol−1). The values of rate coefficients and activation energies obtained in the present work appear entirely consistent with the available literature data for the reactions of the NO3 radical with other aliphatic aldehydes.24–33,42 All the data available for these reactions indicate that the reaction with aliphatic aldehydes is an overall abstraction process but not only a simple H-abstraction process. The reaction could proceed via the formation of an exothermic adduct before C–Hald bond cleavage and the subsequent elimination of nitric acid. Then the rate coefficient will depend upon the stability of the adduct that will also depend itself upon the electronic properties of the alkyl group and its ability to distribute the reaction energy and not just the C–Hald bond dissociation energy. This suggestion is in accordance with the positive temperature dependence (for the abstraction process of the aldehydic-H) observed for the reactions of the NO3 radical with aldehydes. At present all these ideas have to be considered with caution because of the lack of data about these reactions; therefore more kinetics data and in particular information about the products of the reactions of NO3 radicals with aldehydes should to be obtained to enable elucidation of the reaction mechanism.
| Compound | k 298/10−14 cm3 molecule−1 s−1 | E a/kJ mol−1 |
|---|---|---|
| a From ref. 33. b The rate constants are from this work. | ||
| Acetaldehydea | 0.32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.08 0.08 |
23.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.2 7.2 |
| Propanala | 0.60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.06 0.06 |
18.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6 1.6 |
| Butanala | 1.46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.16 0.16 |
20.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.2 4.2 |
| Pentanala | 1.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.06 0.06 |
18.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.3 1.3 |
| Hexanala | 1.83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.36 0.36 |
19.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.3 8.3 |
| Heptanala | 2.37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.42 0.42 |
20.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 0.4 |
| 2-Methylpropanalb | 1.61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.13 0.13 |
21.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.2 3.2 |
| 2-Methylbutanalb | 2.56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.46 0.46 |
19.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.6 4.6 |
| 3-Methylbutanalb | 2.45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.20 0.20 |
18.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.9 1.9 |
| 2,2-Dimethyl-propanalb | 2.80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.35 0.35 |
17.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6 1.6 |
The rate coefficients at room temperature for the gas-phase reactions of the aldehydes studied here with NO3, and the room temperature rate coefficients for the reactions of such compounds with OH obtained from literature references, given in Table 3, can be combined with estimated ambient tropospheric concentrations of NO3 and OH in order to derive estimated chemical lifetimes for these compounds. These lifetimes are also shown in Table 3. It can be clearly seen that the calculated tropospheric lifetimes of these aldehydes with respect to the OH-reaction are shorter than those of the NO3 but both are of the order of hours. Although the lifetimes of these aldehydes towards the reactions with NO3 at night are larger than the corresponding process for the OH radical, the night-time reactions with the NO3 radical have to be taken into account to understand the global processes in atmospheric chemistry.
| Compound | k NO3/10−14 cm3 molecule−1 s−1b | k OH/10−11 cm3 molecule−1 s−1c | τ OH/day-time hours | τ NO3/night-time hours |
|---|---|---|---|---|
a [NO3]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 108 molecule cm−3
(12 h average), from ref. 43, [OH] 108 molecule cm−3
(12 h average), from ref. 43, [OH]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6 1.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106 molecule cm−3
(12 h average) from ref. 44.
b Measured in this work.
c From ref. 45. 106 molecule cm−3
(12 h average) from ref. 44.
b Measured in this work.
c From ref. 45.
|
||||
| 2-Methylpropanal | 1.61 | 2.90 | 5.9 | 34 |
| 2,2-Dimethyl-propanal | 2.80 | 2.20 | 7.9 | 19.8 |
| 2-Methylbutanal | 2.56 | – | – | 21.7 |
| 3-Methylbutanal | 2.45 | 2.89 | 6.0 | 22.7 |
Acknowledgements
The authors wish to thank C.I.C.Y.T (Comision Interministerial de Ciencia y Tecnologia) for the financial support, under project PB97-0432.References
- D. Kotzias, C. Konidari and C. Spartá, Volatile carbonyl compounds of biogenic origin, ed. G. Helas, J. Slanina and R. Steinbrecher, SPB Academic Publishing, Amsterdam, The Netherlands, 1997 Search PubMed.
- A. Guenther, N. C. Hewitt, R. Fall, C. Geron, T. Graedel, P. Harley, L. Klinger, M. Lerdan, N. A. McKay, T. Pierce, B. Schoeles, R. Steinbrecher, R. Tallamraju, J. Taylor and P. Zimmerman, J. Geophys Res., 1995, 100, 8873–8875 CrossRef CAS.
- P. Carlier, H. Hannachi, A. Kartoudis, A. Martinet and G. Mouvier, Air Poll. Res. Rep., 1987, 9, 133–141 Search PubMed.
- J. Hahn, R. Steinbrech and J. Slemr, EUROTRAC, Annual Report, Part 4, ed. P. Borrell and P. M. Borrell, BIATEX, SPB, The Hague, 1991, 230–235.
- V. A. Isidorov, I. G. Zenkevich and B. V. Ioffe, Atmos. Environ., 1985, 19, 1–8 CrossRef CAS.
- J. Arey, A. M. Winer, R. Atkinson, S. M. Aschmann, W. D. Long and C. L. Morrison, Atmos. Environ., 1991, 25A, 1063–1065 CAS.
- R. R. Arnts, B. W. Gay and J. J. Bufalini, in Atmospheric Biogenic Hydrocarbons, ed. J. J. Bufalini and R. R. Arnts, Ann Arbor Science Publishers, Inc., Michigan, 1981, vol. 2, p. 117 Search PubMed.
- P. R. Zimmerman, R. B. Chatfield, J. Fishman, P. J. Crutzen and P. L. Hanst, Geophys. Res. Lett., 1978, 5, 676–680.
- K. Nagai, K. Naka, B. Matsuoayashi, M. Takatsuka and M. Murata, Odor Res., 1975, 4, 23–32 Search PubMed , APTIC NO. 74561.
- H. T. Prates, R. C. Leite, A. A. Craveiro and A. B. Oliveira, J. Braz. Chem. Soc., 1998, 9, 193–197 Search PubMed.
- P. Carlier, P. Fresnet, V. Lescoat, S. Pashalidis and G. Mouvier, Proceedings of the 5th European Symposium on “Physico-chemical behaviour of atmospheric pollutants”, ed. G. Restelli and G. Angeletti, Kluwer, Dordrecht, 1989, p. 582 Search PubMed.
- P. Ciccioli, A. Cecinato, B. Brancaleoni and M. Frattoni, Fresenius' Envir. Bull., 1992, 1, 73–75 Search PubMed.
- P. Ciccioli, E. Brancaleoni, M. Frattoni, A. Cecinato and A. Brachetti, Atmos. Environ., 1993, 27A, 1891–1894 CAS.
- J. S. Gaffney, G. E. Streit, W. D. Spall and J. H. Hall, Environ. Sci. Technol., 1987, 21, 519–529 CAS.
- G. Shuster, S. Wilson and G. Helas, Proceedings of the 5th European Symposium on “Physicochemical behaviour of atmospheric polutants”, ed. G. Restelli and G. Angeletti, Kluwer, Dordrecht, 1989, pp. 553–559 Search PubMed.
- D. Grosjean, Environ. Sci. Technol., 1991, 25, 710–715 CAS.
- S. Solberg, N. Schmidbauer, U. Pedersen and J. Schang, VOC measuraments, August 1992–June 1993, EMEP/CCC-Report 6/93, NILU, Lillestrom, 1993 Search PubMed.
- R. L. Tanner and B. Zylinska, Atmos. Environ., 1994, 28, 1113–1120 CrossRef CAS.
- G. Koening, M. Brunda, H. Puxbaum, C. N. Hewitt, S. C. Duckham and J. Rudolph, Atmos. Environ., 1995, 25A, 861–874 CrossRef.
- Committee on Medical and Biologic Effects of Environmental Pollutants. Vapor-phase Organic Pollutants, National Academy of Sciences, Washington, DC, 1976 Search PubMed.
- A. Roussel, Impact médical des pollutions d'origine automobile (Rapport) Revue pollution atmosphérique N° 99, ed. G. Restelli and G. Angeletti, Kluwer, Dordrecht, 1983 Search PubMed.
- W. Kristine, I. Galbally, Y. Ye and M. Hooper, J. Geophys. Res., 1998, 103, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605–10
605–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 619.
619. - M. M. O'Mara, J. Fire Flammability, 1974, 5, 34–37 Search PubMed.
- R. J. Atkinson, Phys. Chem. Ref. Data Monogr. 2, 1994 Search PubMed.
- R. Atkinson, D. L. Baulch, R. A. Cox, R. F. Hampson, J. A. Kerr, Jr., M. J. Rossi and J. Troe, J. Phys. Chem. Ref. Data, 1997, 26, 521 CAS.
- E. J. Duglockencky and C. J. Howard, J. Phys. Chem., 1989, 93, 1091–1096 CrossRef CAS.
- C. A. Cantrell, W. R. Stockwell, L. G. Anderson, K. L. Busanow, D. Perner, A. Schmeltekopf, J. G. Calvert and H. S. Johnston, J. Phys. Chem., 1985, 89, 139–146 CrossRef CAS.
- P. Carlier, H. Hannachi, A. Kartoudis, A. Martinet and G. Mouvier, Air Poll. Res. Rep. 9, 1987, 133–141 Search PubMed.
- J. Hjorth, G. Ottobrini and G. Restelli, J. Phys. Chem., 1988, 92, 2669–2672 CrossRef CAS.
- B. D'Anna and C. J. Nielsen, J. Chem. Soc., Faraday Trans., 1997, 93, 3479–3483 RSC.
- M. Glasius, A. Caligirou, N. R. Jensen, J. Hjorth and C. J. Nielsen, Int. J. Chem. Kinet., 1997, 29, 527–531 CrossRef CAS.
- M. Ullerstram, S. Langer and E. Ljungström, Int. J. Chem. Kinet., 2000, 32, 294–298 CrossRef CAS.
- B. Cabañas, S. Salgado, P. Martin, M. T. Baeza and E. Martinez, J. Phys. Chem. A, 2001, 18, 4440–4445 CrossRef.
- B. Cabañas, S. Salgado, P. Martin, B. Ballesteros and E. Martinez, J. Atmos. Chem. A, 2001, 40, 23–39 Search PubMed.
- E. Martinez, B. Cabañas, A. Aranda and R. P. Wayne, J. Chem. Soc., Faraday Trans., 1996, 92, 53–58 RSC.
- E. Martinez, E. Cabañas, A. Aranda, P. Martin and R. P. Wayne, Recent Res. Dev. Photochem. Photobiol., 1997, 1, 63–75 Search PubMed.
- C. E. Canosa-Mas, S. J. Smith, S. J. Waygood and R. P. Wayne, J. Chem. Soc., Faraday Trans. 2, 1991, 87, 3473–3478 Search PubMed.
- J. K. Laidler, Chemical Kinetics, Harper Collins Publisher, Inc., 3rd edn, 1987 Search PubMed.
- S. Airds, C. E. Canosa-Mas, D. J. Cook, G. Marston, P. S. Monk, R. P. Wayne and E. Ljungström, J. Chem. Soc., Faraday Trans., 1992, 88, 1093–1099 RSC.
- E. Martinez, B. Cabañas, A. Aranda and P. Martin, Environ. Sci. Technol., 1998, 32, 3730–3734 CrossRef CAS.
- E. M. Chance, A. R. Curtis, I. P. Jones and C. R. Kirdy, FACSIMILE, AUKAEA, Harwell Report, AERE-R8775.
- R. P. Wayne, I. Barnes, P. Biggs, J. P. Burrows, C. E. Canosa-Mas, J. Hjorth, G. LeBras, G. K. Moortgat, D. Perner, G. Poulet, G. Restelli and H. Sidebottom, Atmos. Environ., Part A, 1991, 25, 1.
- Y. Shu and R. Atkinson, J. Geophys. Res., 1995, 100, 7275–7281 CrossRef CAS.
- R. Prinn, R. F. Weiss, B. R. Miller, J. Huang, F. N. Alyea, D. M. Cunnold, P. J. Fraser, D. E. Hartley and P. G. Simmonds, Science, 1995, 269, 187–192 CAS.
- R. Atkinson, J. Phys. Chem. Ref. Data Monogr., 1989 Search PubMed.
| This journal is © the Owner Societies 2003 |
