Dynamics of electronic energy transfer from the S2 state of azulene to the S2 state of zinc porphyrin
Edwin K. L.
Yeow
and
Ronald P.
Steer
*
Department of Chemistry, University of Saskatchewan, Saskatoon, Saskatchewan, Canada S7N 5C9. E-mail: ron.steer@usask.ca; Fax: +1 306 966 4730
First published on 19th November 2002
Abstract
Electronic energy transfer between the S2 state of azulene as donor and the S2 state of zinc porphyrin as acceptor in dichloromethane and CTAB micelles has been investigated. In dichloromethane high S2–S2 energy transfer efficiency, which cannot be explained using the Förster theory, is observed. An inhomogeneous distribution of acceptors surrounding the donor, leading to short-range exchange interaction and higher multipole interaction is proposed. In CTAB micelles, Förster's mechanism is found to agree well with the observed energy transfer efficiency when a surface-uniform distance distribution between donor and acceptor is assumed. The implications of S2–S2 energy transfer in our system for designing efficient molecular devices is discussed.
Introduction
Azulene and porphyrin based systems have received much attention because of their unique photophysical properties. In contravention of Kasha's rule, azulene displays an intense fluorescence (S2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0) from a higher electronic state, while undergoing an ultrafast internal conversion from its S1 to its S0 states.1 A negligibly small quantum yield of S1
S0) from a higher electronic state, while undergoing an ultrafast internal conversion from its S1 to its S0 states.1 A negligibly small quantum yield of S1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 fluorescence is thus observed. This anomalous behaviour has led to several studies devoted to the spectroscopic characterisation of azulene.2,3 Recently, several azulenic derivatives were synthesised,4 and used to understand the colour properties of their bacteriorhodopsin analog.5 Porphyrin-based systems are commonly employed for gaining further insight into the efficient photon-harvesting and electron transfer dynamics of the photosynthetic apparatus.6–9 In many diamagnetic metalloporphyrins (e.g. zinc tetraphenylporphyrin), weak S2
S0 fluorescence is thus observed. This anomalous behaviour has led to several studies devoted to the spectroscopic characterisation of azulene.2,3 Recently, several azulenic derivatives were synthesised,4 and used to understand the colour properties of their bacteriorhodopsin analog.5 Porphyrin-based systems are commonly employed for gaining further insight into the efficient photon-harvesting and electron transfer dynamics of the photosynthetic apparatus.6–9 In many diamagnetic metalloporphyrins (e.g. zinc tetraphenylporphyrin), weak S2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S0 fluorescence is also known,10,11 and has been correlated with the modest (ca. 1 eV) energy gap between their S2 and S1 electronic states.12
S0 fluorescence is also known,10,11 and has been correlated with the modest (ca. 1 eV) energy gap between their S2 and S1 electronic states.12
The investigation of electronic energy transfer (EET) from upper excited states (Sn, n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is both important and challenging. In the light-harvesting complexes of photosynthetic systems, energy transfer from the initially excited S2 state of carotenoids to chlorophylls is found to be important.13 Furthermore, molecules that exhibit S2 fluorescence would be of particular significance in the design of molecular photonic switches and molecular logic gates.14,15 Levine and co-workers have described the concept of using EET from the S2 state of azulene to develop suitable logic gates and circuits.14 The full potential of such molecular devices is realised when the number of electronic states of the component molecule that can undergo photophysical reactions (e.g. energy transfer) is large. Therefore, EET involving both higher electronic states (e.g. S2–S2 EET) and S1 states of the energy donor and acceptor chromophores is advantageous in this respect.
1) is both important and challenging. In the light-harvesting complexes of photosynthetic systems, energy transfer from the initially excited S2 state of carotenoids to chlorophylls is found to be important.13 Furthermore, molecules that exhibit S2 fluorescence would be of particular significance in the design of molecular photonic switches and molecular logic gates.14,15 Levine and co-workers have described the concept of using EET from the S2 state of azulene to develop suitable logic gates and circuits.14 The full potential of such molecular devices is realised when the number of electronic states of the component molecule that can undergo photophysical reactions (e.g. energy transfer) is large. Therefore, EET involving both higher electronic states (e.g. S2–S2 EET) and S1 states of the energy donor and acceptor chromophores is advantageous in this respect.
Previous studies of energy transfer involving high excited states have been mainly centered around EET from the donor S2 state to the acceptor S1 state.16–23 There are only a few reports of S2–S2 energy transfer.24–26 For example, Oster and Kallmann used X-rays to excite the S2 state of benzene, and then examined the subsequent energy transfer to the S2 state of phenylbiphenylyl oxadiazole.24 Osuka et al. have synthesised a series of porphyrin dimers and trimers consisting of a zinc porphyrin donor and a zinc diphenylethynyl porphyrin acceptor.25,26 In their systems, S2–S2 EET from donor to acceptor followed by back EET from the S2 state of the acceptor to the S1 state of the donor was reported.
In this paper, we examine the energy transfer dynamics from the S2 state of azulene to the S2 state of zinc porphyrins in dichloromethane and in aqueous CTAB micelles. Due to its relatively large S2 fluorescence quantum yield and S2 emission lifetime, azulene can act as an excellent S2 energy donor. 1,3-difluoroazulene, with a significantly higher S2 fluorescence quantum yield,4 is also used here as an energy donor. The choice of zinc porphyrin as an energy acceptor is driven by the fact that after the initial S2–S2 EET, subsequent back S1–S1 energy transfer is probable which results in a bidirectional and cyclic energy transfer process. This inadvertently has important implications in the design of efficient molecular devices as discussed by Levine and co-workers.14 To understand the S2–S2 energy transfer process occuring in dichloromethane and CTAB micelles, the EET efficiency was determined from the fluorescence quenching of azulene in the presence of zinc porphyrin under steady-state conditions.
Experimental section
Azulene (Az, Aldrich), zinc tetraphenylporphyrin (ZnTPP, Alfa Aesar), zinc tetra(4-sulfonatophenyl) porphyrin (ZnTPPS, Frontier Scientific Porphyrin Products), cetyltrimethylammonium bromide surfactant (CTAB, Aldrich), dichloromethane (CH2Cl2, Aldrich, spectroscopy grade), and ethanol (EM Science, spectroscopy grade) were used as received. 1,3-difluoroazulene (DFAz) was kindly supplied by Dr Alfred Asato (University of Hawaii).Solutions of Az and DFAz with concentrations ca. 3.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 M were first prepared in CH2Cl2. Stock solutions of ZnTPP were then introduced into the Az/DFAz solutions using a microlitre syringe to achieve a quencher concentration between ca. 10−5 and 10−4 M. Dissolved air was removed by bubbling the samples with solvent-saturated Ar for 15 min before taking any measurements.
10−5 M were first prepared in CH2Cl2. Stock solutions of ZnTPP were then introduced into the Az/DFAz solutions using a microlitre syringe to achieve a quencher concentration between ca. 10−5 and 10−4 M. Dissolved air was removed by bubbling the samples with solvent-saturated Ar for 15 min before taking any measurements.
The micelle solutions were prepared by dissolving an appropriate amount of CTAB in Millipore-purified (Milli-Q) water such that the concentration of the surfactant was well above the critical micelle concentration (c.m.c.) of CTAB (c.m.c.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9.2
9.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 M).27 Az was dissolved in the CTAB micellar solution by stirring for about 24 h, and any undissolved Az was then removed by filtering the solution. The final concentration of solubilised Az was 2.8
10−4 M).27 Az was dissolved in the CTAB micellar solution by stirring for about 24 h, and any undissolved Az was then removed by filtering the solution. The final concentration of solubilised Az was 2.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 M. Stock solutions of ZnTPPS were added into the micellised Az solutions via a microlitre syringe. In this way, the concentration of ZnTPPS was in the range of ca. 10−5 and 10−4 M. Finally, the sample solutions were allowed to stand for about 12 h. Since the oxygen concentration within a micelle is low,27,28 effects of oxygen quenching on the relatively short-lived Az emission can be neglected. Fluorescence measurements were therefore performed in aerated micellar solutions. All samples, both in CH2Cl2 and CTAB solutions, were protected from room light at all times.
10−5 M. Stock solutions of ZnTPPS were added into the micellised Az solutions via a microlitre syringe. In this way, the concentration of ZnTPPS was in the range of ca. 10−5 and 10−4 M. Finally, the sample solutions were allowed to stand for about 12 h. Since the oxygen concentration within a micelle is low,27,28 effects of oxygen quenching on the relatively short-lived Az emission can be neglected. Fluorescence measurements were therefore performed in aerated micellar solutions. All samples, both in CH2Cl2 and CTAB solutions, were protected from room light at all times.
Absorption spectra were recorded with a Varian Cary 500 UV-Vis spectrometer, and corrected steady-state fluorescence measurements were recorded on a SPEX 212 spectrofluorometer. All measurements were conducted in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cm cuvettes at room temperature. The fluorescence of the donor molecule after excitation was observed at right angles to the incident light. At the donor excitation wavelength (λex
1 cm cuvettes at room temperature. The fluorescence of the donor molecule after excitation was observed at right angles to the incident light. At the donor excitation wavelength (λex![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 nm for Az and DFAz in CH2Cl2, and λex
327 nm for Az and DFAz in CH2Cl2, and λex![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 nm for Az in CTAB solution), some of the incident light is absorbed by the quencher chromophore (i.e. ZnTPP and ZnTPPS). This results in an attenuation of the excitation beam reaching the donor molecules (primary inner filter effect).29 Furthermore, ZnTPP and ZnTPPS can absorb a fraction of the emitted donor fluorescence at the observation wavelength (λem
325 nm for Az in CTAB solution), some of the incident light is absorbed by the quencher chromophore (i.e. ZnTPP and ZnTPPS). This results in an attenuation of the excitation beam reaching the donor molecules (primary inner filter effect).29 Furthermore, ZnTPP and ZnTPPS can absorb a fraction of the emitted donor fluorescence at the observation wavelength (λem![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 374 nm for Az and 380 nm for DFAz in CH2Cl2, and λem
374 nm for Az and 380 nm for DFAz in CH2Cl2, and λem![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 374 nm for Az in CTAB solution), causing a secondary inner filter effect.29
374 nm for Az in CTAB solution), causing a secondary inner filter effect.29
Inner filter effects were corrected for by using a correction factor.30–32
Fcorr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10(Aexlex+Aemlem) 10(Aexlex+Aemlem) | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.44 was determined for our experimental set-up. Taking lex
0.44 was determined for our experimental set-up. Taking lex![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lem, which is typical for most commercial spectrofluorometers, the fluorescence intensity corrected for inner filter effects is given by,
lem, which is typical for most commercial spectrofluorometers, the fluorescence intensity corrected for inner filter effects is given by, Icorr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Iexpt100.44(Aex+Aem) Iexpt100.44(Aex+Aem) | (2) |
The quantum yield of Az in CTAB micelle, ΦCTABAz, was determined using DFAz in degassed ethanol as a reference (Φref![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.197):4
0.197):4
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−Aex) is the factor used to correct for different absorbances at the excitation wavelength used (325 nm). The refractive index of the CTAB micelle was assumed to be the average value of ηCTAB determined using pyrene, anthracene, and perylene as probe molecules (i.e.ηCTAB
10−Aex) is the factor used to correct for different absorbances at the excitation wavelength used (325 nm). The refractive index of the CTAB micelle was assumed to be the average value of ηCTAB determined using pyrene, anthracene, and perylene as probe molecules (i.e.ηCTAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.52).34
1.52).34
Theory
Förster energy transfer
The most common mechanism of non-radiative singlet–singlet EET between two chromophores (D and A) is the Coulombic interaction described by Förster.35 The rate constant of EET (keet) between D and A separated by a distance R is,35,36 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6), and the corresponding R0 is defined by
6), and the corresponding R0 is defined by  | (5) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ) is the spectral overlap integral of the emission of D with the absorption of A.
) is the spectral overlap integral of the emission of D with the absorption of A.
The energy transfer efficiency, E, can be calculated from the emission intensity of D, in the absence (I0), and presence (IA) of A. Accounting for inner filter effects (eqn. (2)), such as radiative energy transfer, the experimental non-radiative EET efficiency is readily obtained from eqn. (6):32
 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IAFcorr.
IAFcorr.
The fluorescence decay of a donor surrounded by a homogeneous distribution of acceptor was also obtained by Förster:37
IA(s)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IA(0)exp(−s IA(0)exp(−s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2γs1/2) 2γs1/2) | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ/τD, and γ
τ/τD, and γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cA/c0. cA is the acceptor concentration and c0 is the critical concentration given by
cA/c0. cA is the acceptor concentration and c0 is the critical concentration given by  | (8) |
 | (9) |
Gösele and Sipp–Voltz models
In a fluid medium of low solvent viscosity, the effects of translational diffusion on the donor fluorescence quenching may be significant.38 Gösele et al.39–41 took into account translational diffusion, and obtained an expression for the donor fluorescence decay as shown in eqn. (10):IA(s)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IA(0) exp(−s IA(0) exp(−s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αs αs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2γs1/2) 2γs1/2) | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4π
4π![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) rFnAτD, rF
rFnAτD, rF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.676(R60/τD
0.676(R60/τD![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) )1/4 is an effective trapping radius, nA is the acceptor number density and
)1/4 is an effective trapping radius, nA is the acceptor number density and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) is the sum of the diffusion coefficients of D and A. By integrating eqn. (10) over time, the steady-state fluorescence intensity is given by IA/I0
is the sum of the diffusion coefficients of D and A. By integrating eqn. (10) over time, the steady-state fluorescence intensity is given by IA/I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∫∞0IA(s)ds, and an exact expression for the theoretical EET efficiency is obtained,
∫∞0IA(s)ds, and an exact expression for the theoretical EET efficiency is obtained,  | (11) |
Using the time-dependent Smoluchowski quenching rate constant, Sipp and Voltz42 derived a time-dependent donor fluorescence decay function given by eqn. (12):
IA(s)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IA(0)exp(−s IA(0)exp(−s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βs βs![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2δs1/2) 2δs1/2) | (12) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4πr
4πr![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) τDnA, δ
τDnA, δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4r2(π
4r2(π![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) )1/2τ1/2DnA and r, the reaction length, provides useful information about the bimolecular quenching dynamics. An expression for r consisting of factors arising from diffusion, short-range energy transfer, and long-range energy transfer reactions shows that the common but ill-defined encounter distance (i.e.r
)1/2τ1/2DnA and r, the reaction length, provides useful information about the bimolecular quenching dynamics. An expression for r consisting of factors arising from diffusion, short-range energy transfer, and long-range energy transfer reactions shows that the common but ill-defined encounter distance (i.e.r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rA
rA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rD, where rA(D) is the radius of A(D)) underestimates the true short-range reaction length, re. In general, the long-range dipole–dipole reaction length, rd, is given by42
rD, where rA(D) is the radius of A(D)) underestimates the true short-range reaction length, re. In general, the long-range dipole–dipole reaction length, rd, is given by42 | (13) |
EET models in micelles
When D and A are separated by a distance R, the probability of finding at time t an excitation remaining on D averaged over the distance distribution (ω(R)) is43,44 | (14) |
The distance distribution, ω(R), is defined as the probability of finding an acceptor at a distance between R and R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dR from the donor. For a spherical micelle with radius Rm, the most common distance distributions are:45,46 (1) surface–surface distribution (i.e. both D and A are randomly distributed on the surface of the micelle, ωss(R)
dR from the donor. For a spherical micelle with radius Rm, the most common distance distributions are:45,46 (1) surface–surface distribution (i.e. both D and A are randomly distributed on the surface of the micelle, ωss(R)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R/2R2m), (2) surface–uniform distribution (i.e. one of the chromophore is randomly distributed on the surface of the micelle, while the other is uniformly distributed within the micelle, ωsu(R)
R/2R2m), (2) surface–uniform distribution (i.e. one of the chromophore is randomly distributed on the surface of the micelle, while the other is uniformly distributed within the micelle, ωsu(R)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3R2(2Rm
3R2(2Rm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R)/4R4m), and (3) uniform–uniform distribution (i.e. both D and A are uniformly distributed within the micelle, ωuu(R)
R)/4R4m), and (3) uniform–uniform distribution (i.e. both D and A are uniformly distributed within the micelle, ωuu(R)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3R2(2Rm
3R2(2Rm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R)2(4Rm
R)2(4Rm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R)/16R6m). In all of the above cases, the limit of integration in eqn. (14) is from 0 to 2Rm.
R)/16R6m). In all of the above cases, the limit of integration in eqn. (14) is from 0 to 2Rm.
When the probability of finding ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) acceptors in a micelle follows a Poissonian distribution with mean occupation number μ, the average donor fluorescence decay is written as45,46
acceptors in a micelle follows a Poissonian distribution with mean occupation number μ, the average donor fluorescence decay is written as45,46
 | (15) |

Results and discussion
EET in dichloromethane
The steady-state absorption and emission spectra for Az, DFAz, and ZnTPP in CH2Cl2 are shown in Figs. 1 and 2. The absorption spectra for Az, and DFAz were not affected by the addition of the quencher ZnTPP, and new absorption or emission bands were not observed (figure not shown), strongly suggesting that no complexes between donor and acceptor were formed. Furthermore, no splitting or shifting of the absorption bands of ZnTPP were observed in CH2Cl2, in accordance with previous reports that self-aggregates of ZnTPP in non-aqueous solvents can be excluded at the concentrations used.47 Self-aggregation of Az at low concentration is also not known to occur.48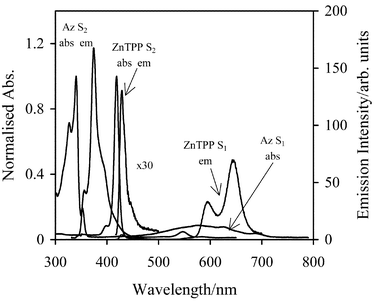 | ||
| Fig. 1 The absorption and emission spectra for Az and ZnTPP in CH2Cl2. The absorbances are normalised to the maximum optical density. ZnTPP S2 emission peak is amplified 30 times. abs is the absorption band, while em is the emission band. | ||
 | ||
| Fig. 2 The absorption and emission spectra for DFAz and ZnTPP in CH2Cl2. The absorbances are normalised to the maximum optical density. abs is the absorption band, while em is the emission band. | ||
Note, in Figs. 1 and 2, that there is a substantial amount of overlap between the S2 emission spectrum of the donor (i.e. Az or DFAz), and the S2 absorption spectrum of the acceptor ZnTPP. This indicates that efficient resonance energy transfer from the excited S2 state of Az/DFAz to the S2 state of ZnTPP is feasible. The spectral overlap integral values (J(![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) ), see eqn. (5)), calculated using the PhotochemCAD software,49 for Az-ZnTPP and DFAz-ZnTPP systems are 9.93
), see eqn. (5)), calculated using the PhotochemCAD software,49 for Az-ZnTPP and DFAz-ZnTPP systems are 9.93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−14 cm3 M−1 and 1.21
10−14 cm3 M−1 and 1.21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−13 cm3 M−1, respectively. The molar absorption coefficients of ZnTPP in CH2Cl2 were taken from ref. 6. Given further that the quantum yields of Az and DFAz in CH2Cl2 are 0.041 and 0.158,4 respectively, the Förster critical distance, R0, determined from eqn. (5) are 28.9 Å and 37.4 Å for Az-ZnTPP and DFAz-ZnTPP systems, respectively. The orientation factor, κ2, was assumed to be 2/3 for randomly oriented chromophores in a fluid medium.
10−13 cm3 M−1, respectively. The molar absorption coefficients of ZnTPP in CH2Cl2 were taken from ref. 6. Given further that the quantum yields of Az and DFAz in CH2Cl2 are 0.041 and 0.158,4 respectively, the Förster critical distance, R0, determined from eqn. (5) are 28.9 Å and 37.4 Å for Az-ZnTPP and DFAz-ZnTPP systems, respectively. The orientation factor, κ2, was assumed to be 2/3 for randomly oriented chromophores in a fluid medium.
In the presence of ZnTPP, the fluorescence intensities for both Az, and DFAz are reduced from I0 to IA,corr by energy transfer to ZnTPP. Using eqn. (6), and the maximum fluorescence intensities of Az (at 374 nm), and DFAz (at 380 nm), the EET efficiency, E, is obtained and presented in Fig. 3 for different concentrations of ZnTPP. We observe that E increases with [ZnTPP] for both donors, and that the excitation transfer is more efficient for the DFAz–ZnTPP system.
![The experimental S2–S2 energy transfer efficiency, E, for DFAz (■) and Az (●) at different concentrations of the quencher ([ZnTPP]) in CH2Cl2. Lines a, b and c are Gösele's theoretical energy transfer efficiency, EG, computed using the critical distances R0 = 92.2 Å
(for Az), 37.4 Å
(for DFAz), and 28.9 Å
(for Az), respectively.](/image/article/2003/CP/b208135k/b208135k-f3.gif) | ||
Fig. 3 The experimental S2–S2 energy transfer efficiency, E, for DFAz (■) and Az (●) at different concentrations of the quencher ([ZnTPP]) in CH2Cl2. Lines a, b and c are Gösele's theoretical energy transfer efficiency, EG, computed using the critical distances R0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 92.2 Å
(for Az), 37.4 Å
(for DFAz), and 28.9 Å
(for Az), respectively. 92.2 Å
(for Az), 37.4 Å
(for DFAz), and 28.9 Å
(for Az), respectively. | ||
We examine the mean diffusion length, (2![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) τD)1/2, by first defining the diffusion coefficients of D and A using the Stokes–Einstein equation,32 such that
τD)1/2, by first defining the diffusion coefficients of D and A using the Stokes–Einstein equation,32 such that
 | (16) |
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.449 cP is the viscosity of CH2Cl2.The molecular radii for the reactants are rAz
0.449 cP is the viscosity of CH2Cl2.The molecular radii for the reactants are rAz![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.3 Å, rDFAz
3.3 Å, rDFAz![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.52 Å, and rZnTPP
3.52 Å, and rZnTPP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.1 Å.9,48 The translational diffusion coefficients,
5.1 Å.9,48 The translational diffusion coefficients, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , calculated from eqn. (16) are 2.39
, calculated from eqn. (16) are 2.39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 cm2 s−1, and 2.30
10−5 cm2 s−1, and 2.30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 cm2 s−1 for Az-ZnTPP, and DFAz-ZnTPP, respectively. From the ratio z
(=(2
10−5 cm2 s−1 for Az-ZnTPP, and DFAz-ZnTPP, respectively. From the ratio z
(=(2![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) τD)1/2/R0) obtained for both Az-ZnTPP (z
τD)1/2/R0) obtained for both Az-ZnTPP (z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8), and DFAz-ZnTPP (z
0.8), and DFAz-ZnTPP (z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.7), which are close to 1, both translational diffusion and EET may play important roles in the quenching dynamics.39 The theoretically calculated values of the EET efficiency according to Gösele's model (eqn. (11)), EG, are given in Fig. 3. The fluorescence lifetimes (τD) in CH2Cl2, needed to compute α and rF, are 1.17 ns and 8.84 ns for Az (rF
1.7), which are close to 1, both translational diffusion and EET may play important roles in the quenching dynamics.39 The theoretically calculated values of the EET efficiency according to Gösele's model (eqn. (11)), EG, are given in Fig. 3. The fluorescence lifetimes (τD) in CH2Cl2, needed to compute α and rF, are 1.17 ns and 8.84 ns for Az (rF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25.7 Å) and DFAz (rF
25.7 Å) and DFAz (rF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23.0 Å),4 respectively. Clearly, from Fig. 3, Gösele's model based on the experimental Förster R0 values underestimates the observed energy transfer efficiencies in both systems. A good fit to the observed EET efficiency (E) is achieved when R0 is increased from 28.9 Å to 92.2 Å for Az-ZnTPP (see Fig. 3). Similarly, for DFAz-ZnTPP, Gösele's model (EG) agrees well with E when R0 lies between ca. 100 Å and 120 Å, depending on the concentration of ZnTPP (see Table 1). Large discrepancies between observed and Förster critical distances for other systems have been reported. Some examples are given below.
23.0 Å),4 respectively. Clearly, from Fig. 3, Gösele's model based on the experimental Förster R0 values underestimates the observed energy transfer efficiencies in both systems. A good fit to the observed EET efficiency (E) is achieved when R0 is increased from 28.9 Å to 92.2 Å for Az-ZnTPP (see Fig. 3). Similarly, for DFAz-ZnTPP, Gösele's model (EG) agrees well with E when R0 lies between ca. 100 Å and 120 Å, depending on the concentration of ZnTPP (see Table 1). Large discrepancies between observed and Förster critical distances for other systems have been reported. Some examples are given below.
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ) for DFAz at various ZnTPP concentrations in CH2Cl2
) for DFAz at various ZnTPP concentrations in CH2Cl2
| [ZnTPP]/10−5M | E a | R 0/Åb |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) /10−3 cm2 s−1c /10−3 cm2 s−1c |
|---|---|---|---|
a calculated from eqn. (6).
b obtained from Gösele model, eqn. (11), with ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.30 2.30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 cm2 s−1.
c obtained from Gösele model, eqn. (11), with R0 10−5 cm2 s−1.
c obtained from Gösele model, eqn. (11), with R0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37.4 Å. 37.4 Å.
|
|||
| 0.981 | 0.054 | 101.4 | 0.91 |
| 2.224 | 0.106 | 97.5 | 0.81 |
| 3.072 | 0.164 | 103.7 | 1.04 |
| 4.004 | 0.205 | 103.4 | 1.05 |
| 5.718 | 0.314 | 110.4 | 1.41 |
| 6.502 | 0.373 | 114.8 | 1.69 |
| 7.363 | 0.443 | 120.3 | 2.11 |
Pandey, Pant, and co-workers have previously studied energy transfer between different dye molecules (e.g., EET from trypaflavine to rhodamine 6G).50–52 They found that a reasonable fit to their donor fluorescence decay, using Gösele's model (eqn. (10)), is attained only when a larger than Förster critical distance (e.g., for the trypaflavine–rhodamine 6G system with Förster critical distance![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 Å, an observed critical distance as large as 158 Å was obtained), or a larger than donor-acceptor translational diffusion coefficient
54 Å, an observed critical distance as large as 158 Å was obtained), or a larger than donor-acceptor translational diffusion coefficient ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) in eqn. (10) is used. Pandey et al. argued that when the acceptor concentration is low enough, donor–donor energy migration can result in a faster quenching by the acceptors. In this case, the effective diffusion coefficient,
in eqn. (10) is used. Pandey et al. argued that when the acceptor concentration is low enough, donor–donor energy migration can result in a faster quenching by the acceptors. In this case, the effective diffusion coefficient, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , found in eqn. (10) and (11) is given by the sum of donor–acceptor translational diffusion coefficient (eqn. (16)), and donor–donor excitation migration diffusion coefficient (
, found in eqn. (10) and (11) is given by the sum of donor–acceptor translational diffusion coefficient (eqn. (16)), and donor–donor excitation migration diffusion coefficient (![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) E).53 Gochanour, Anderson, and Fayer (GAF) have found that at long times, the energy migration process becomes diffusive with a limiting diffusion coefficient given by54
E).53 Gochanour, Anderson, and Fayer (GAF) have found that at long times, the energy migration process becomes diffusive with a limiting diffusion coefficient given by54
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) E E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.428C4/30ER20Eτ−1D 0.428C4/30ER20Eτ−1D | (17) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4πnDR30E/3 is a reduced concentration, R0E is the donor–donor Förster critical distance, and nD is the number density of donors. From eqn. (17), we obtain a value of
4πnDR30E/3 is a reduced concentration, R0E is the donor–donor Förster critical distance, and nD is the number density of donors. From eqn. (17), we obtain a value of ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.9
1.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11 cm2 s−1 for Az (R0E
10−11 cm2 s−1 for Az (R0E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10.4 Å), and
10.4 Å), and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4
1.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11 cm2 s−1 for DFAz (R0E
10−11 cm2 s−1 for DFAz (R0E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13.8 Å).
13.8 Å).
When R0 is fixed to the Förster critical distance, Gösele's model returned a value of ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.2
6.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 cm2 s−1 in order to adequately explain the experimental E values observed for Az–ZnTPP. Likewise,
10−3 cm2 s−1 in order to adequately explain the experimental E values observed for Az–ZnTPP. Likewise, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ranged between 9.1
ranged between 9.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 cm2 s−1 and 2.1
10−4 cm2 s−1 and 2.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 cm2 s−1
(depending on [ZnTPP], see Table 1) for DFAz–ZnTPP. Clearly, the sum of the calculated donor-acceptor translational diffusion coefficient (eqn. (16)), and the GAF excitation migration diffusion coefficient (eqn. (17)) is insufficient to fully explain the apparent higher
10−3 cm2 s−1
(depending on [ZnTPP], see Table 1) for DFAz–ZnTPP. Clearly, the sum of the calculated donor-acceptor translational diffusion coefficient (eqn. (16)), and the GAF excitation migration diffusion coefficient (eqn. (17)) is insufficient to fully explain the apparent higher ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) values for our systems.
values for our systems.
The GAF model suffers from the assumption that donor molecules are immobile during energy migration. Jang et al.55 removed GAF's assumption, by formulating an expression for ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) E based on the combined effects of donor translational diffusion, and energy migration among donors. It was found that translational motion reduces the distance between donors, and hence increases the efficiency of energy migration and quenching. Jang's expression for
E based on the combined effects of donor translational diffusion, and energy migration among donors. It was found that translational motion reduces the distance between donors, and hence increases the efficiency of energy migration and quenching. Jang's expression for ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) E is
E is ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (2πτD−1R60EnD)/3rc, where rc is a cutoff distance for self-transfer. Here a value of rc
(2πτD−1R60EnD)/3rc, where rc is a cutoff distance for self-transfer. Here a value of rc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.81
1.81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−6 cm for Az, and a
10−6 cm for Az, and a ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) E value of 2.71
E value of 2.71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−11 cm2 s−1 have been calculated using Jang's model. Although Jang's energy migration diffusion coefficient is larger than GAF's, it is still insignificant compared to the donor–acceptor translational diffusion coefficient. This is easily rationalised from the fact that R0E for Az (i.e. 10.4 Å) is very much smaller than the Az-ZnTPP critical distance (R0
10−11 cm2 s−1 have been calculated using Jang's model. Although Jang's energy migration diffusion coefficient is larger than GAF's, it is still insignificant compared to the donor–acceptor translational diffusion coefficient. This is easily rationalised from the fact that R0E for Az (i.e. 10.4 Å) is very much smaller than the Az-ZnTPP critical distance (R0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28.9 Å). The very low R0E implies that energy migration among Az is highly inefficient. Similar behaviour is also observed for DFAz, which lead us to believe that the effects of donor energy migration on
28.9 Å). The very low R0E implies that energy migration among Az is highly inefficient. Similar behaviour is also observed for DFAz, which lead us to believe that the effects of donor energy migration on ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) , and hence E is negligible.
, and hence E is negligible.
As discussed by Sipp and Voltz,42 short-range exchange interaction, in addition to long-range Coulombic coupling, can contribute to the overall energy transfer quenching dynamics. The classical Dexter mechanism is often used to interpret the orbital-overlap dependent interaction.56 The importance of considering exchange interaction for a D–A pair with large Förster critical distance in a highly diffusive medium has been highlighted by Bandyopadhyay and Rao.57 Their study compliments those of Ali and co-workers.58,59 Birks and Leite60 found a larger than Förster's critical distance for EET between naphthalene and 9,10-diphenylanthracene in a series of solvents with varying viscosities. Adams et al.61 obtained large experimental R0
(e.g. 152 Å) values for EET from DODCI dye to malachite green in ethanol, which could not be explained using Förster's theory (Förster critical distance![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59 Å). Stevens and Dubois62 have also reported a two fold increase in the experimental critical distance (31 Å) compared to Förster's R0
(16 Å) for the quenching of the S2 state of Az by anthracene in ether solvent. In all of the above studies, the breakdown of considering solely Förster's theory was attributed to extra contributions arising from higher order Coulombic terms, and distributed transition-monopole theory.63–66 Both factors are known to become significant for large chromophores (e.g. porphyrin) when the D–A separation approaches the size of the molecules.
59 Å). Stevens and Dubois62 have also reported a two fold increase in the experimental critical distance (31 Å) compared to Förster's R0
(16 Å) for the quenching of the S2 state of Az by anthracene in ether solvent. In all of the above studies, the breakdown of considering solely Förster's theory was attributed to extra contributions arising from higher order Coulombic terms, and distributed transition-monopole theory.63–66 Both factors are known to become significant for large chromophores (e.g. porphyrin) when the D–A separation approaches the size of the molecules.
We examine the effects of short-range interaction for Az-ZnTPP using the Sipp–Voltz model, where the effective reaction length is defined by42
 | (18) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25.7 Å), Iy(x) is the modified Bessel function of the first kind, and χ is given by
25.7 Å), Iy(x) is the modified Bessel function of the first kind, and χ is given by  | (19) |
An effective reaction length of r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.56
1.56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−6 cm was determined from our experimental E values, and using eqns. (18) and (19), we obtain a short-range exchange interaction length of re
10−6 cm was determined from our experimental E values, and using eqns. (18) and (19), we obtain a short-range exchange interaction length of re![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 86.9 Å. We note that re is unreasonably large compared to rd, and we conclude that short-range interaction cannot be used to explain the efficient energy transfer observed, at least not when a homogeneous distribution of A around D is assumed.
86.9 Å. We note that re is unreasonably large compared to rd, and we conclude that short-range interaction cannot be used to explain the efficient energy transfer observed, at least not when a homogeneous distribution of A around D is assumed.
Kaschke and Vogler67,68
(KV) were the first to propose an inhomogeneous distribution of A around D. They developed a model whereby a raised acceptor concentration (n′A) is found around the donor (say between two spheres of radii R1 and R2, such that D is located in the centre of the spheres, and R1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R2
R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Förster R0) which exceeds the bulk acceptor concentration (nA) found outside this region. The raised acceptor concentration is due to mutual attraction between the molecules caused by weak van der Waals interactions. Kaschke and Vogler were able to explain the efficient EET observed between rhodamine 6G donor and several acceptors (DOTC, cresyl violet, oxazine) in ethanol using their model. For an example, in the case of rhodamine 6G-cresyl violet, an observed critical distance as large as 94 Å was reported compared to a Förster critical distance of 56 Å. Using an inhomogeneous acceptor distribution, whereby the raised acceptor concentration is 57 times higher than the bulk acceptor concentration, Kaschke and Vogler were able to rationalise the more efficient energy transfer observed.
Förster R0) which exceeds the bulk acceptor concentration (nA) found outside this region. The raised acceptor concentration is due to mutual attraction between the molecules caused by weak van der Waals interactions. Kaschke and Vogler were able to explain the efficient EET observed between rhodamine 6G donor and several acceptors (DOTC, cresyl violet, oxazine) in ethanol using their model. For an example, in the case of rhodamine 6G-cresyl violet, an observed critical distance as large as 94 Å was reported compared to a Förster critical distance of 56 Å. Using an inhomogeneous acceptor distribution, whereby the raised acceptor concentration is 57 times higher than the bulk acceptor concentration, Kaschke and Vogler were able to rationalise the more efficient energy transfer observed.
We adopt the KV approach to model our experimental results. Apart from van der Waals forces, weak π–π interactions can also induce ZnTPP to form a raised acceptor concentration around the donor (Az or DFAz).69 It must be stressed, as Kaschke and Vogler have,67,68 that this does not mean the formation of complexes or aggregates. However, in the region of raised acceptor concentration, the D and A are often close enough to effect short-range exchange interaction (e.g. Dexter mechanism), and higher multipole–higher multipole interactions. We therefore include two more terms in the KV model to account for the latter mechanisms. The time-dependent donor fluorescence decay, taking into consideration an inhomogeneous distribution of acceptors, and ignoring the effects of diffusion, is given by
 | (20) |
A(t) is the result of the modified Förster theory, and is given by67,68
 | (21) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n′A/nA, xi(t)
n′A/nA, xi(t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (R30/R3i)/(t/τD)1/2, and
(R30/R3i)/(t/τD)1/2, and  | (22) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, and n′A
0, and n′A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nA, A(t) coincides with Förster's 2γ expression (see eqn. (7)). B(t) is the contribution from Dexter's short-range exchange interaction given by70
nA, A(t) coincides with Förster's 2γ expression (see eqn. (7)). B(t) is the contribution from Dexter's short-range exchange interaction given by70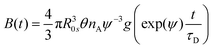 | (23) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2R0s/L with L being the so-called Bohr radius, and
2R0s/L with L being the so-called Bohr radius, and  | (24) |
 | (25) |
We illustrate the effects of an inhomogeneous distribution of ZnTPP around Az by considering only the self-decay, A(t), and B(t) terms in eqn. (20). Owing to the experimental difficulties in obtaining R1, R2, and R0s, our results will be semi-quantitative at best. Nonetheless, the implications of the results are generally true for all cases. A(t) has been shown to be insensitive to R1,67 and the latter is assigned a value of 10 Å. R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Förster's R0 was given a value of 20 Å. Dexter's mechanism is generally valid as long as the interchromophoric separation between D and A is smaller than ca. twice the encounter distance.71 Therefore, we chose R0s
Förster's R0 was given a value of 20 Å. Dexter's mechanism is generally valid as long as the interchromophoric separation between D and A is smaller than ca. twice the encounter distance.71 Therefore, we chose R0s![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 Å. Fig. 4 shows that when the ratio between raised acceptor concentration and bulk acceptor concentration, θ, equals 119, the theoretical EET efficiencies agree well with experimental E values. Even though the KV approach shows a vast improvement over Förster's model, both yield theoretical E values which are lower than the experimental ones (see Fig. 4). Clearly, the inclusion of Dexter's B(t) term in eqn. (20) cannot be ignored. The higher multipole interaction factor C will further reduce the value of θ. Two other short-range interaction mechanisms (i.e. the distributed transition-monopole and the through-configuration interactions) were left out in eqn. (20), which will further affect the value of θ. The through-configuration interaction term arising from interactions between ionic charge configurations and locally excited states have been previously shown to be just as important as Dexter's mechanism.72,73
16 Å. Fig. 4 shows that when the ratio between raised acceptor concentration and bulk acceptor concentration, θ, equals 119, the theoretical EET efficiencies agree well with experimental E values. Even though the KV approach shows a vast improvement over Förster's model, both yield theoretical E values which are lower than the experimental ones (see Fig. 4). Clearly, the inclusion of Dexter's B(t) term in eqn. (20) cannot be ignored. The higher multipole interaction factor C will further reduce the value of θ. Two other short-range interaction mechanisms (i.e. the distributed transition-monopole and the through-configuration interactions) were left out in eqn. (20), which will further affect the value of θ. The through-configuration interaction term arising from interactions between ionic charge configurations and locally excited states have been previously shown to be just as important as Dexter's mechanism.72,73
 | ||
Fig. 4 The experimental S2–S2 energy transfer efficiency, E, for Az (●) is compared with various theoretical models: a: Förster's model assuming a homogeneous acceptor distribution (EF, eqn. (9)), b: Kaschke and Vogler (KV) model assuming an inhomogeneous acceptor distribution (i.e., eqn. (20) with B(t) and C terms![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0), and c: modified KV model taking into account Dexter's mechanism (i.e., eqn. (20) with C 0), and c: modified KV model taking into account Dexter's mechanism (i.e., eqn. (20) with C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0). The value of θ is 119 for b and c. 0). The value of θ is 119 for b and c. | ||
The more efficient quenching observed for DFAz when compared to Az (Fig. 3) is now rationalised using the modified KV model. The DFAz emission spectrum is red-shifted with respect to Az, thus increasing the amount of overlap with ZnTPP absorption spectrum. Along with a higher fluorescence quantum yield, all the relevant resonance energy transfer critical distances (i.e., Förster, Dexter, higher-multipole interactions) for DFAz are larger than Az's. Furthermore, the π-donating effect of the two fluoro substituents to the azulenic aromatic system in DFAz will enhance the weak π-π interaction with ZnTPP. Therefore, a greater raised acceptor concentration around DFAz will amplify the quenching efficiency.
So far, we have reported energy transfer as the only quenching mechanism. The feasibility of electron transfer from Az to ZnTPP, especially in the region of raised acceptor concentration, is examined via the Gibbs free energy change (ΔG°) involved in the charge separation process,74
 | (26) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.88 V for Az,75 and Ered
0.88 V for Az,75 and Ered![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1.30 V for ZnTPP76 in acetonitrile. From eqn. (26), we get ΔG°
−1.30 V for ZnTPP76 in acetonitrile. From eqn. (26), we get ΔG°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −118.2 kJ mol−1, indicating an energetically favourable electron transfer process from D to A in CH2Cl2. Elucidation of the relative importance of energy and electron transfer reactions in our systems is currently being investigated using time-resolved emission, and flash photolysis experiments, and will be reported in a forthcoming paper.
−118.2 kJ mol−1, indicating an energetically favourable electron transfer process from D to A in CH2Cl2. Elucidation of the relative importance of energy and electron transfer reactions in our systems is currently being investigated using time-resolved emission, and flash photolysis experiments, and will be reported in a forthcoming paper.
EET in CTAB micelles
The steady-state absorption and emission spectra for Az and ZnTPPS in CTAB micelles are shown in Fig. 5. Monomeric ZnTPPS in CTAB shows characteristic absorbance maxima at 426 nm, 560 nm, and 599 nm, in accordance with literature values.77,78 No new absorption or emission bands were observed upon increasing the concentrations of ZnTPPS, strongly suggesting the absence of complex formation (figure not shown). Furthermore, premicellar aggregates between CTAB and ZnTPPS are excluded by working at surfactant concentration well above the c.m.c.79,80 | ||
| Fig. 5 The absorption and emission spectra for Az and ZnTPPS in CTAB micelles. The absorbances are normalised to the maximum optical density. The ZnTPPS S2 emission peak is amplified 20 times. abs is the absorption band, while em is the emission band. | ||
The spectral overlap integral between the emission spectrum of donor Az and the absorption spectrum of acceptor ZnTPPS is 6.40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−14 cm3 M−1. The molar absorption coefficients of solubilised ZnTPPS in CTAB were taken from ref. 77. Given further that the quantum yield of Az is determined to be 0.02 in CTAB micelles, the Förster critical distance calculated from eqn. (5) is 21.6 Å. Molecular motions are known to be greatly impeded upon encapsulation of the molecules in micelles.43,81 Hence, in the event of restricted rotation, a value of κ2
10−14 cm3 M−1. The molar absorption coefficients of solubilised ZnTPPS in CTAB were taken from ref. 77. Given further that the quantum yield of Az is determined to be 0.02 in CTAB micelles, the Förster critical distance calculated from eqn. (5) is 21.6 Å. Molecular motions are known to be greatly impeded upon encapsulation of the molecules in micelles.43,81 Hence, in the event of restricted rotation, a value of κ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.476 is assumed for randomly oriented chromophores.82
0.476 is assumed for randomly oriented chromophores.82
Using the maximum fluorescence intensity of Az at 374 nm, the experimental energy transfer efficiency, E, is calculated from eqn. (6), and the results are presented in Fig. 6 for different concentrations of ZnTPPS. To compare our experimental results with the model discussed in Section 2, the theoretical energy transfer efficiencies, ET, were obtained by integrating eqn. (15) over time. The numerical computation was performed using Maple 7 (Waterloo Maple Inc.) software. J(s) for the various distance distributions are given by:45,46
 | (27) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) s(R0/2Rm)6. The mean acceptor occupation number is defined to be μ
s(R0/2Rm)6. The mean acceptor occupation number is defined to be μ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ZnTPPS]/[CTAB]m, where [CTAB]m is the concentration of CTAB micelles. From the surfactant concentration ([CTAB]), c.m.c., and micellar aggregation number ρ
(=60 for CTAB),27
[CTAB]m
[ZnTPPS]/[CTAB]m, where [CTAB]m is the concentration of CTAB micelles. From the surfactant concentration ([CTAB]), c.m.c., and micellar aggregation number ρ
(=60 for CTAB),27
[CTAB]m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.2
2.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 M is easily obtained from the expression,83
10−5 M is easily obtained from the expression,83 | (28) |
![The experimental S2–S2 energy transfer efficiency, E, for Az (●) at different concentrations of the quencher ([ZnTPPS]) in CTAB micelles is compared with the theoretical model, ET, given by eqn. (15). A surface-uniform distance distribution (eqn. (27)) with micellar radius of 31.8 Å shows good agreement with E.](/image/article/2003/CP/b208135k/b208135k-f6.gif) | ||
| Fig. 6 The experimental S2–S2 energy transfer efficiency, E, for Az (●) at different concentrations of the quencher ([ZnTPPS]) in CTAB micelles is compared with the theoretical model, ET, given by eqn. (15). A surface-uniform distance distribution (eqn. (27)) with micellar radius of 31.8 Å shows good agreement with E. | ||
From Fig. 6, we see that when the radius of the micelle Rm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31.8 Å, for a surface–uniform (su) distance distribution, the theoretical ET values, based on Förster's theory, are in excellent agreement with the experimental ones. Similarly, good agreement between ET and E is obtained when Rm
31.8 Å, for a surface–uniform (su) distance distribution, the theoretical ET values, based on Förster's theory, are in excellent agreement with the experimental ones. Similarly, good agreement between ET and E is obtained when Rm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30.6 Å, and 38.8 Å for the surface–surface (ss), and uniform–uniform (uu) distance distributions, respectively. An interesting feature is the sensitivity of Rm to the distance distribution function. As discussed by Barzykin,45 the mean distance between D and A is largest for the s–s distribution, and smallest for the s–u distribution. Therefore, in order for eqn. (15) to appropriately describe E, a larger Rm is required for the s–u distribution. As discussed earlier, energy migration among Az chromophores is insignificant. An R0E value of 10.5 Å for Az–Az energy transfer implies a D–D Förster transfer rate of only 1.3% of that of the D–A one.
30.6 Å, and 38.8 Å for the surface–surface (ss), and uniform–uniform (uu) distance distributions, respectively. An interesting feature is the sensitivity of Rm to the distance distribution function. As discussed by Barzykin,45 the mean distance between D and A is largest for the s–s distribution, and smallest for the s–u distribution. Therefore, in order for eqn. (15) to appropriately describe E, a larger Rm is required for the s–u distribution. As discussed earlier, energy migration among Az chromophores is insignificant. An R0E value of 10.5 Å for Az–Az energy transfer implies a D–D Förster transfer rate of only 1.3% of that of the D–A one.
The sites of solubilisation of aromatic molecules, such as benzene and higher arenes, have been found to be located at the interface of ionic micelles near the polar head groups.84–86 Cardinal and Mukerjee85 have ascribed the micellar surface activity of aromatic molecules to the interaction beween water dipoles and π-electron system of the aromatic molecules. The Az chromophores are thus taken to be absorbed at the CTAB micellar surface. On the other hand, several studies have shown that porphyrin systems tend to be embedded in the hydrophobic core of micelles.77,78,81,87 In particular, Kadish et al.77 have reported that significant perturbation of the 1H NMR peaks of the CTAB's surfactant head group, terminal methyl group, and intermediate methylene groups are seen upon inclusion of free-base tetra-(4-sulfonatophenyl) porphyrins. This suggests that the ZnTPPS molecules interact throughout the surfactant chain, and are probably distributed uniformly within the micelle. Therefore, the surface–uniform distance distribution seems to be the most suitable description for our Az-ZnTPPS system.
The radius of CTAB micelle in the absence of solubilizate has been independently determined to be ca. 24 Å
(i.e. hydrophobic core radius![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) head group radius).88 The CTAB micelle radius obtained from this study, assuming a surface–uniform distance distribution, is 31.8 Å, which is not unreasonable. Two plausible explanations of the slightly larger observed Rm can be offered. Micellar structures are known to be modified by the addition of solubilizates.89,90 In our case, ZnTPPS which are solubilised within the CTAB micelles can produce a swelling of the latter,89 hence increasing the radii of micelles. Recently, Zhao et al.91 have studied the hydrocarbon chain packing behaviour of CTAB micelles using a 1H NMR relaxation technique. They found that intermediate methylene groups of CTAB have some probability of spending time at the micellar surface layer. This means that the interior of CTAB micelle is inhomogeneous, and a uniform distribution of ZnTPPS becomes a simplified picture of the true acceptor distribution.
head group radius).88 The CTAB micelle radius obtained from this study, assuming a surface–uniform distance distribution, is 31.8 Å, which is not unreasonable. Two plausible explanations of the slightly larger observed Rm can be offered. Micellar structures are known to be modified by the addition of solubilizates.89,90 In our case, ZnTPPS which are solubilised within the CTAB micelles can produce a swelling of the latter,89 hence increasing the radii of micelles. Recently, Zhao et al.91 have studied the hydrocarbon chain packing behaviour of CTAB micelles using a 1H NMR relaxation technique. They found that intermediate methylene groups of CTAB have some probability of spending time at the micellar surface layer. This means that the interior of CTAB micelle is inhomogeneous, and a uniform distribution of ZnTPPS becomes a simplified picture of the true acceptor distribution.
Conclusion and final comments
We have observed electronic energy transfer from the S2 state of a donor (azulene) to the S2 state of an acceptor (zinc porphyrin) in dichloromethane solvent and CTAB micelles. The high energy transfer efficiencies observed in dichloromethane are attributed to an inhomogeneous distribution of acceptors. On the other hand, Förster kinetics is followed when the chromophores are solubilised in CTAB micelles.The possible fate of the excitation energy after the initial S2–S2 transfer is worth mentioning here. The porphyrin in its S2 state will subsequently undergo rapid relaxation to its S1 state (see Fig. 7). The internal conversion rate from the S2 to the S1 states of the acceptor corresponds to its S2 fluorescence decay rate (i.e.τ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ca. 2 ps for ZnTPP,92 and ca. 1.3 ps for ZnTPPS93). Thereafter, the excited molecule can either emit radiatively as acceptor fluorescence (i.e.τ4
ca. 2 ps for ZnTPP,92 and ca. 1.3 ps for ZnTPPS93). Thereafter, the excited molecule can either emit radiatively as acceptor fluorescence (i.e.τ4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5–3 ns),6 or return to the donor via a radiationless back energy transfer from the S1 state of A to the S1 state of D (Fig. 7). From Figs. 1, 2, and 5, we find significant spectral overlap between the S1 emission spectrum of zinc porphyrin, and the S1 absorption spectrum of azulene, strongly suggesting probable resonance back-EET. Finally, the system returns quickly to the ground state by the S1–S0 conical intersection (i.e.τ3
1.5–3 ns),6 or return to the donor via a radiationless back energy transfer from the S1 state of A to the S1 state of D (Fig. 7). From Figs. 1, 2, and 5, we find significant spectral overlap between the S1 emission spectrum of zinc porphyrin, and the S1 absorption spectrum of azulene, strongly suggesting probable resonance back-EET. Finally, the system returns quickly to the ground state by the S1–S0 conical intersection (i.e.τ3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ps for Az).94 The cyclic energy transfer process, seen in Fig. 7, has very important implications in the design of molecular logic gates. Levine et al.14 have discussed how one can utilise bidirectional intermolecular EET to perform logical operations on different chromophores. We are presently investigating the cyclic EET dynamics for a series of linked (flexible and rigid) systems, consisting of azulene donor and zinc porphyrin acceptor chromophores, which will shed further insight into the functionality of such molecular logic gates.
2 ps for Az).94 The cyclic energy transfer process, seen in Fig. 7, has very important implications in the design of molecular logic gates. Levine et al.14 have discussed how one can utilise bidirectional intermolecular EET to perform logical operations on different chromophores. We are presently investigating the cyclic EET dynamics for a series of linked (flexible and rigid) systems, consisting of azulene donor and zinc porphyrin acceptor chromophores, which will shed further insight into the functionality of such molecular logic gates.
 | ||
| Fig. 7 Energy levels of donor (D) and acceptor (A) chromophores, and the various EET and energy relaxation pathways. Solid lines are radiative processes, while broken lines are non-radiative processes. τ1 is the fluorescence lifetime of the donor S2 state (e.g., 1.17 ns for Az, and 8.84 ns for DFAz in CH2Cl2).4 | ||
Another interesting issue concerns the choice of the orientation factor (κ2, eqn. (5)) for the back S1–S1 EET. In a random array of chromophores, κ2 is usually assigned a value of 2/3 in a fluid medium. However, because the porphyrin S2 state is very short-lived, there will be a photoselection of porphyrin S1 states after S2–S2 EET, invalidating the assumption of random S1 transition dipole moments. This problem will be tackled by us in a future publication.
Acknowledgements
We would like to thank Dr Alfred Asato for kindly supplying a sample of 1,3-difluoroazulene. We are also grateful to Professor R. E. Verrall for useful discussions regarding micelles.References
- N. J. Turro, V. Ramamurthy, W. Cherry and W. Farneth, Chem. Rev., 1978, 78, 125 CrossRef CAS.
- O. K. Abou-Zied, H. K. Sinha and R. P. Steer, J. Phys. Chem., 1996, 100, 4375 CrossRef CAS.
- O. K. Abou-Zied, H. K. Sinha and R. P. Steer, J. Mol. Spectrosc., 1997, 183, 42 CrossRef CAS.
- N. Tétreault, R. S. Muthyala, R. S. H. Liu and R. P. Steer, J. Phys. Chem. A, 1999, 103, 2524 CrossRef CAS.
- R. S. H. Liu, R. S. Muthyala, X. Wang, A. E. Asato, P. Wang and C. Ye, Org. Lett., 2000, 2, 269 CrossRef CAS.
- S. Takagi and H. Inoue, in Multimetallic and Macromolecular Inorganic Photochemistry, ed. V. Ramamurthy and K. S. Schanze, Marcel Dekker, New York, 1999, p. 215 Search PubMed.
- E. K. L. Yeow, K. P. Ghiggino, J. N. H. Reek, M. J. Crossley, A. W. Bosman, A. P. H. J. Schenning and E. W. Meijer, J. Phys. Chem. B, 2000, 104, 2596 CrossRef CAS.
- E. K. L. Yeow, P. J. Sintic, N. M. Cabral, J. N. H. Reek, M. J. Crossley and K. P. Ghiggino, Phys. Chem. Chem. Phys., 2000, 2, 4281 RSC.
- E. K. L. Yeow and S. E. Braslavsky, Phys. Chem. Chem. Phys., 2002, 4, 239 RSC.
- G. G. Gurzadyan, T.-H. Tran-Thi and T. Gustavsson, J. Chem. Phys., 1998, 108, 385 CrossRef CAS.
- N. Mataga, Y. Shibata, H. Chosrowjan, N. Yoshida and A. Osuka, J. Phys. Chem. B, 2000, 104, 4001 CrossRef CAS.
- H. Kobayashi and Y. Kaizu, in Porphyrins: Excited States and Dynamics, eds. M. Gouterman, P. M. Rentzepis and K. D. Straub, American Chemical Society, Washington DC, 1986, p. 105 Search PubMed.
- C. C. Gradinaru, I. H. M. van Stokkum, A. A. Pascal, R. van Grondelle and H. van Amerongen, J. Phys. Chem. B, 2000, 104, 9330 CrossRef CAS.
- F. Remacle, S. Speiser and R. D. Levine, J. Phys. Chem. B, 2001, 105, 5589 CrossRef CAS.
- F. Remacle and R. D. Levine, J. Chem. Phys., 2001, 114, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 239 CrossRef CAS.
239 CrossRef CAS. - I. Kaplan and J. Jortner, Chem. Phys., 1978, 32, 381 CrossRef CAS.
- D. W. Gordon and W. F. Coleman, J. Lumin., 1980, 22, 23 CrossRef CAS.
- V. A. Lyubimtsev, Opt. Spectrosc. (Transl. of Opt. Spektrosk.), 1983, 55, 624 Search PubMed.
- V. A. Lyubimtsev, Opt. Spectrosc. (Transl. of Opt. Spektrosk.), 1987, 62, 622 Search PubMed.
- E. N. Bodunov, M. N. Berberan-Santos and J. M. G. Martinho, Chem. Phys. Lett., 1997, 274, 171 CrossRef CAS.
- M. S. Gudipati and M. Kalb, J. Inf. Rec., 1998, 24, 445 Search PubMed.
- A. Harriman, M. Hissler, O. Trompette and R. Ziessel, J. Am. Chem. Soc., 1999, 121, 2516 CrossRef CAS.
- T. Theodossiou, E. Georgiou, V. Hovhannisyan, K. Politopoulos and D. Yova, J. Opt. A: Pure Appl. Opt., 2001, 3, L1 Search PubMed.
- G. K. Oster and H. Kallmann, J. Chim. Phys., 1967, 64, 28 Search PubMed.
- S. Akimoto, T. Yamazaki, I. Yamazaki, A. Nakano and A. Osuka, Pure Appl. Chem., 1999, 71, 2107 CAS.
- A. Nakano, Y. Yasuda, T. Yamazaki, S. Akimoto, I. Yamazaki, H. Miyasaka, A. Itaya, M. Murakami and A. Osuka, J. Phys. Chem. A, 2001, 105, 4822 CrossRef CAS.
- K. Kalyanasundaram, Photochemistry in Microheterogeneous Systems, Academic Press, Orlando, FL, 1987 Search PubMed.
- M. N. Berberan-Santos and M. J. E. Prieto, J. Chem. Soc., Faraday Trans. 2, 1987, 83, 1391 RSC.
- R. Frank and H. Rau, J. Photochem., 1982, 18, 281 Search PubMed.
- M. Kubista, R. Sjöback, S. Eriksson and B. Albinsson, Analyst, 1994, 119, 417 RSC.
- B. C. MacDonald, S. J. Lvin and H. Patterson, Anal. Chim. Acta, 1997, 338, 155 CrossRef CAS.
- J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Kluwer Academic, New York, 2nd edn., 1999 Search PubMed.
- J. F. Holland, R. E. Teets, P. M. Kelly and A. Timnick, Anal. Chem., 1977, 49, 706 CrossRef CAS.
- R. J. Kavanagh, K.-K. Iu and J. K. Thomas, Langmuir, 1992, 8, 3008 CrossRef CAS.
- Th. Förster, in Modern Quantum Chemistry, ed. O. Sinanoglu, Academic Press, New York, 1965, p. 93 Search PubMed.
- E. K. L. Yeow, D. J. Haines, K. P. Ghiggino and M. N. Paddon-Row, J. Phys. Chem. A, 1999, 103, 6517 CrossRef CAS.
- Th. Förster, Discuss. Faraday Soc., 1959, 27, 7 RSC.
- N. Tamai, T. Yamazaki and I. Yamazaki, Chem. Phys. Lett., 1985, 120, 24 CrossRef CAS.
- S. Speiser, Chem. Rev., 1996, 96, 1953 CrossRef CAS.
- U. Gösele, M. Hauser, U. K. A. Klein and R. Frey, Chem. Phys. Lett., 1975, 34, 519 CrossRef.
- U. K. A. Klein, R. Frey, M. Hauser and U. Gösele, Chem. Phys. Lett., 1976, 41, 139 CrossRef CAS.
- B. Sipp and R. Voltz, J. Chem. Phys., 1985, 83, 157 CrossRef CAS.
- K. Kasatani, M. Kawasaki, H. Sato and N. Nakashima, J. Phys. Chem., 1985, 89, 542 CrossRef CAS.
- M. H. Gehlen and F. C. De Schryver, Chem. Rev., 1993, 93, 199 CrossRef CAS.
- A. V. Barzykin, Chem. Phys., 1991, 155, 221 CrossRef CAS.
- A. V. Barzykin and M. Tachiya, Heterogen. Chem. Rev., 1996, 3, 105 CrossRef CAS.
- W. I. White, in The Porphyrins, ed. D. Dolphin, Academic Press, New York, 1978, vol. V, p. 303 Search PubMed.
- A. T. Reis e Sousa, J. M. G. Martinho, F. Baros and J. C. Andáe, J. Photochem. Photobiol. A: Chem., 1994, 83, 199 Search PubMed.
- H. Du, R.-C. A. Fuh, J. Li, L. A. Corkan and J. S. Lindsey, Photochem. Photobiol., 1998, 68, 141 Search PubMed.
- K. K. Pandey and T. C. Pant, Chem. Phys. Lett., 1990, 170, 244 CrossRef CAS.
- K. K. Pandey, Chem. Phys., 1992, 165, 123 CrossRef CAS.
- H. C. Joshi, H. Mishra, H. B. Tripathi and T. C. Pant, J. Lumin., 2000, 90, 17 CrossRef CAS.
- D. P. Millar, R. J. Robbins and A. H. Zewail, J. Chem. Phys., 1981, 75, 3649 CrossRef CAS.
- C. R. Gochanour, H. C. Andersen and M. D. Fayer, J. Chem. Phys., 1979, 70, 4254 CrossRef CAS.
- S. Jang, K. J. Shin and S. Lee, J. Chem. Phys., 1995, 102, 815 CrossRef CAS.
- D. L. Dexter, J. Chem. Phys., 1953, 21, 836 CrossRef CAS.
- T. Bandyopadhyay and K. V. S. Rama Rao, Chem. Phys., 1992, 167, 131 CrossRef CAS.
- M. A. Ali and S. A. Ahmed, J. Chem. Phys., 1989, 90, 1484 CrossRef CAS.
- M. A. Ali, S. A. Ahmed and A. S. Chokhavatia, J. Chem. Phys., 1989, 91, 2892 CrossRef CAS.
- J. B. Birks and M. S. S. C. P. Leite, J. Phys. B, 1970, 3, 513 Search PubMed.
- M. C. Adams, D. J. Bradley, W. Sibbett and J. R. Taylor, Chem. Phys. Lett., 1979, 66, 428 CrossRef CAS.
- B. Stevens and J. T. Dubois, Trans. Faraday Soc., 1966, 62, 1525 RSC.
- G. D. Scholes and K. P. Ghiggino, in Advances in Multiphoton Processes and Spectroscopy, ed. S. H. Lin, A. A. Villaeys and Y. Fujimura, World Scientific, Singapore, 1996, vol. 10, p. 95 Search PubMed.
- J. C. Chang, J. Chem. Phys., 1977, 67, 3901 CrossRef CAS.
- D. E. LaLonde, J. D. Petke and G. M. Maggiora, J. Phys. Chem., 1988, 92, 4746 CrossRef CAS.
- C. A. Hunter, J. K. M. Sanders and A. J. Stone, Chem. Phys., 1989, 133, 395 CrossRef CAS.
- M. Kaschke and K. Vogler, Chem. Phys., 1986, 102, 229 CrossRef CAS.
- M. Kaschke and K. Vogler, Laser Chem., 1988, 8, 19 Search PubMed.
- H. Scheer and J. J. Katz, in Porphyrins and Metalloporphyrins, ed. K. M. Smith, Elsevier Scientific, Amsterdam, 1975, p. 399 Search PubMed.
- M. Inokuti and F. Hirayama, J. Chem. Phys., 1965, 43, 1978 CrossRef CAS.
- N. J. Turro, Modern Molecular Photochemistry, Benjamin Cummings, Menlo Park, 1978 Search PubMed.
- R. D. Harcourt, G. D. Scholes and K. P. Ghiggino, J. Chem. Phys., 1994, 101, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521 CrossRef CAS.
521 CrossRef CAS. - E. K. L. Yeow and K. P. Ghiggino, J. Phys. Chem. A, 2000, 104, 5825 CrossRef CAS.
- G. J. Kavarnos, Fundamentals of Photoinduced Electron Transfer, VCH, New York, 1993 Search PubMed.
- T. Kurihara, T. Suzuki, H. Wakabayashi, S. Ishikawa, K. Shindo, Y. Shimada, H. Chiba, T. Miyashi, M. Yasunami and T. Nozoe, Bull. Chem. Soc. Jpn., 1996, 69, 2003 CAS.
- G. R. Seely, D. Gust, T. A. Moore and A. L. Moore, J. Phys. Chem., 1994, 98, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 659 CAS.
659 CAS. - K. M. Kadish, G. B. Maiya, C. Araullo and R. Guilard, Inorg. Chem., 1989, 28, 2725 CrossRef CAS.
- S. C. M. Gandini, V. E. Yushmanov and M. Tabak, J. Inorg. Biochem., 2001, 85, 263 CrossRef CAS.
- T. Hinoue, J. Kobayashi, T. Ozeki and H. Watarai, Chem. Lett., 1997, 8, 763 CrossRef.
- T. Tominaga, S. Endoh and H. Ishimaru, Bull. Chem. Soc. Jpn., 1991, 64, 942 CAS.
- N. C. Maiti, S. Mazumdar and N. Periasamy, J. Phys. Chem., 1995, 99, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 708 CAS.
708 CAS. - R. E. Dale and J. Eisinger, Proc. Natl. Acad. Sci. USA, 1976, 73, 271 CAS.
- S. J. Formosinho and M. M. Miguel, J. Chem. Soc., Faraday Trans. 1, 1985, 81, 1891 RSC.
- J. C. Eriksson, U. Henriksson, T. Klason and L. Ödberg, in Solution Behavior of Surfactants, ed. K. L. Mittal and E. J. Fendler, Plenum Press, New York, 1982, vol. 2, p. 907 Search PubMed.
- P. Mukerjee and J. R. Cardinal, J. Phys. Chem., 1978, 82, 1620 CrossRef.
- M. Gonzâlez, J. Vera, E. B. Abuin and E. A. Lissi, J. Colloid Interface Sci., 1984, 98, 152 CAS.
- M. Vermathen, E. A. Louie, A. B. Chodosh, S. Ried and U. Simonis, Langmuir, 2000, 16, 210 CrossRef CAS.
- M. Alauddin and R. E. Verrall, J. Phys. Chem., 1986, 90, 1647 CrossRef CAS.
- P. Mukerjee, in Solution Chemistry of Surfactants, ed. K. L. Mittal, Plenum Press, New York, 1979, vol. 1, p. 153 Search PubMed.
- M. Almgren and S. Swarup, J. Colloid Interface Sci., 1983, 91, 256 CrossRef CAS.
- S. Zhao, H.-Z. Yuan, J.-Y. Yu and Y.-R. Du, Colloid Polym. Sci., 1998, 276, 1125 CrossRef CAS.
- G. G. Gurzadyan, T.-H. Tran-Thi and T. Gustavsson, Proc. SPIE, 2000, 4060, 96 Search PubMed.
- M. Andersson, J. Davidsson, L. Hammarström, J. Korppi-Tommola and T. Peltola, J. Phys. Chem. B, 1999, 103, 3258 CrossRef CAS.
- B. D. Wagner, M. Szymanski and R. P. Steer, J. Chem. Phys., 1993, 98, 301 CrossRef CAS.
| This journal is © the Owner Societies 2003 |
