Electronic spectroscopy of the CaCCCH₃ and SrCCCH₃ free radicals

Abstract

The first spectroscopic observation of the free radicals CaCCCH₃ and SrCCCH₃ is reported. Vibrationally-resolved laser-induced fluorescence spectra, which were recorded under supersonic jet conditions, reveal two band systems for each molecule which have been assigned to the à ²E–X̃ ²A₁ and B̃ ²A₁–X̃ ²A₁ electronic transitions. The vibrational structure in each system is limited to a short progression in the metal–carbon stretching mode. The ÖX̃ origin is blue-shifted relative to the monoacetylides of Ca and Sr. Furthermore, in contrast to CaCCH and SrCCH, where predissociation seems to reduce the fluorescence quantum yield to near zero, the B̃ states of both CaCCCH₃ and SrCCCH₃ show strong fluorescence. Although relatively remote from the chromophore (the metal atom), the methyl group perturbs the electronic structure sufficiently to shift the low lying vibrational levels of the B̃ state out of the predissociative region.

---

Introduction

The monoacetylides of alkaline earth metals have recently attracted considerable interest. These free radicals were first observed by Bopegedera et al. in 1987 using laser-induced fluorescence (LIF) spectroscopy.¹ CaCCH and SrCCH were prepared by reaction of metal vapour with acetylene in a Broida oven. Relatively low resolution spectra were obtained showing spin–orbit splittings and some vibrational structure, from which it was deduced that CaCCH and SrCCH are linear in both their ground (X̃ ²Σ⁺) and first excited (à ²Π) electronic states. Subsequently, Bopegedera et al., followed by a number of other groups, reported rotationally-resolved LIF spectra of CaCCH.^2–6 In addition, Ziurys and co-workers have obtained pure rotational spectra of the X̃ ²Σ⁺ state of CaCCH and SrCCH using millimetre/submillimetre absorption spectroscopy.^7,8 A variety of properties, particularly for CaCCH, have now been firmly established including the structure, vibrational frequencies of several modes, spin–rotation and lambda-doubling parameters, and the electric dipole moments in the à ²Π_1/2 and X̃ ²Σ⁺ states.

MgCCH is another metal acetylide which has generated interest. Stimulated by the possibility of observing this molecule in interstellar space, the first spectroscopic data on MgCCH, obtained using millimetre absorption spectroscopy, was reported by Anderson and Ziurys.⁹ Shortly afterwards the first LIF spectra of MgCCH were recorded in our laboratory.^10,11 The study by Anderson and Ziurys showed that MgCCH is linear in its ground electronic state (²Σ⁺) while our LIF data showed that linearity is maintained in the first excited state (²Π). One of the interesting features of the alkaline earth monoacetylides is the scope they offer for characterising the Renner–Teller effect in tetra-atomic molecules. Indeed, several detailed studies of the Renner–Teller effect in CaCCH have recently appeared in the literature.^12–14 Other published work on MgCCH includes a matrix isolation IR study by Thompson and Andrews¹⁵ and high level ab initio calculations by Woon.^16,17

In this paper we present the first LIF spectra of the monomethylacetylides of calcium and strontium. In their initial work on the monoacetylides, Bopegedera and co-workers also attempted to obtain LIF spectra of the metal methylacetylide free radicals using methylacetylene instead of acetylene as the reagent.¹ They could find no evidence for formation of CaCCCH₃ but did observe spectral features which may have been due to SrCCCH₃, although these spectra were not published. The signal apparently due to SrCCCH₃ was weak and obscured by SrOH bands. We have been able to obtain rather strong vibrationally-resolved LIF spectra of both CaCCCH₃ and SrCCCH₃ using a laser ablation source combined with supersonic expansion. The cooling in the jet is particularly important as it allows vibronic bands of other species, particularly the metal hydroxides, to be distinguished from the methylacetylides. We have observed the à ²E–X̃ ²A₁ and B̃ ²A₁–X̃ ²A₁ transitions of CaCCCH₃ and SrCCCH₃ and report our findings here.

Experimental

The experimental apparatus and procedure have been described in detail elsewhere.¹¹ Briefly, the metal methylacetylides were produced in a pulsed supersonic expansion using excimer laser (193 nm) ablation of a calcium or strontium target in the presence of a suitable volatile organic precursor. Spectra were obtained by crossing the jet with the beam from a tunable pulsed dye laser (linewidth 0.2 cm⁻¹) approximately 4 cm downstream of the nozzle exit. Excitation spectra were recorded by detection of the unfiltered fluorescence gathered by a f/1.3 lens using a photomultiplier tube (PMT), while dispersed fluorescence spectra were obtained using a 0.27 m monochromator (Acton Research) also equipped with a PMT detector. For both excitation and dispersed fluorescence spectra, the PMT output was digitised and then transferred to a PC on a shot-to-shot basis for gated integration and averaging.

The precursor was seeded into helium carrier gas by flowing helium through a temperature-controlled sample bomb. A variety of organic precursors successfully yielded the desired species, including toluene, hexane and benzene. Methylacetylene was also employed in some experiments but no advantage accrued over the liquid precursors. Since the latter were easier to handle, most of the work was carried out with benzene (99.99% purity).

Computational details

To assist in the assignment of vibrational structure, calculations were carried out on several free radicals composed of a calcium atom and a hydrocarbon ligand. DFT calculations using the B3LYP functional were carried out using MOLPRO.^18,19 B3LYP was chosen because it has been widely characterised and is known to be superior to the Hartree–Fock method for the prediction of vibrational frequencies.^20,21

The triple zeta basis sets developed by Schäfer et al. were selected for these calculations.²² For calcium, the basis set chosen was that optimised for the ³P excited state of calcium rather than the ¹S ground state. This gives a better description of the valence p space, something which is known to be important for molecules containing an alkaline earth atom. Three d polarisation functions were added with exponents of 0.2, 0.15, and 0.05. For carbon the triple zeta basis set was supplemented with two diffuse p functions (exponents 0.035 and 0.012) to help describe the negatively charged C atom closest to the metal atom, and two d polarisation functions with exponents 0.4 and 1.6. For hydrogen, two p polarisation functions with exponents of 0.4 and 1.6 were added.

Results and discussion

A. Calcium

Laser ablation of metals in the presence of an organic precursor usually produces a variety of gas phase species. For example, during experiments using a calcium ablation target and benzene as the added precursor, we have observed LIF spectra of a number of well-known calcium-containing molecules. CaH, CaCH₃, CaCCH, and CaOH were all easily identified under these conditions. CaOH was always seen despite efforts to minimise water contamination in the carrier gas/precursor mixture and elsewhere in the vacuum system.

However during the same experiments, which were being carried out to optimise the nozzle conditions for radical production, the LIF spectrum of a previously unidentified species was also observed. Fig. 1 shows a laser excitation scan of the relevant spectral region. In addition to bands due to CaOH and CaCH₃, several new bands are present in this spectrum. Any variation of experimental conditions, including using the alternative organic precursors toluene or hexane, produced no change in the relative intensities of these new bands, thus showing that they arise from the same molecule. The spectral carrier is undoubtedly a calcium-containing free radical for a number of reasons including:

(i) The spectrum disappears when another metal is substituted for the calcium target.

(ii) The bands are very close to the ÖX̃ transitions of a wide variety of calcium-containing free radicals,²³ including CaCCH.^1,2

(iii) A spin–orbit doubling of ∼70 cm⁻¹ (see below) is seen in the first excited electronic state which is typical of that found for orbitally degenerate first excited states of calcium-containing free radicals.²³

Fig. 1 Excitation spectrum showing the ÖX̃ and B̃–X̃ regions of CaCCCH₃. Vibrational mode ν₅ is the Ca–C stretch. This spectrum was recorded with benzene as precursor seeded in helium at a total stagnation pressure of 10 bar. In addition to bands due to CaCCCH₃, contributions from CaOH (*) and CaCH₃ (+) can also be identified in the spectrum.

However, although the carrier is undoubtedly a free radical of type CaR, the identity of the substituent R is not immediately apparent. Rotational structure would be of considerable assistance but could not be resolved in these experiments. Isotope substitution is also potentially valuable, and some experiments were carried out with benzene-d₆ as precursor. However, these did not prove to be definitive. Despite using pure benzene-d₆, the extent of deuteration of the spectral carrier was small. Weak shoulders on the low frequency side of certain bands (the 5¹₀ bands; see later) in the excitation spectra were observed, indicating the presence of hydrogen and a small isotope shift. However, this does not allow a firm identification of the spectral carrier, since many conceivable Ca–R radicals would show the same behaviour. The reason for the ineffective deuteration is unknown, but it may be related to the abundant CaOH signal seen in these experiments (see below). In any event, the absence of firm evidence from rotational structure and isotope substitution experiments meant that alternative arguments had to be employed to identify the spectral carrier. Fortunately, as detailed below, there is other evidence that helps in the assignment of R.

The origin transition of the first electronic band system consists of a pair of intense bands at 16 103 and 16 172 cm⁻¹. From their separations and relative intensities, these resemble the spin–orbit doublets commonly found in ÖX̃ systems of calcium-containing free radicals. Confirmation is provided by a second, weaker, pair of bands at 16 471 and 16 542 cm⁻¹, which share the same spin–orbit splitting and are attributable to vibrational excitation in the à state (see later). The importance of the spin–orbit splitting is that it shows that the spectral carrier has an equilibrium geometry with a symmetry sufficiently high for electronic degeneracies to occur (or alternatively that the symmetry-lowering parts of the molecule are too distant from the orbital in which the unpaired electron resides to resolve the orbital degeneracy). This symmetry constraint severely restricts the number of possible spectral carriers.

Having eliminated closed-shell molecules, and recognising the need for a high local symmetry in the vicinity of the calcium atom, it is now possible to identify likely substituents. The observation of strong bands of CaCCH and CaCH₃ alongside the new CaR species is an important clue. The likelihood is that the substituent R is a hydrocarbon fragment, particularly given that benzene was used as the precursor for the spectrum in Fig. 1. Although CaOH contributes to the LIF spectrum, and therefore an alternative substituent containing one or more O atoms must also be considered, the evidence against this is strong. CaOH presumably forms either from direct laser ablation of Ca(OH)₂ from the surface of the ablation target, or by gas-phase reaction of Ca atoms with H₂O or OH (the latter will be formed in the laser ablation plasma). Water vapour leads to very efficient mopping up of calcium atoms. Even when small leaks were present in our gas delivery manifold the spectra were almost completely dominated by CaOH. Spectra such as that shown in Fig. 1 were difficult to obtain and required considerable effort to minimise air leaks and to remove adsorbed water from gas pipes. When such conditions were achieved, there would be little opportunity for other oxygen-containing ligands to form in the laser ablation plasma. This is borne out by the lack of observation of LIF signals of calcium alkoxy radicals,²⁴ including CaOCH₃, under our experimental conditions. The evidence is therefore overwhelmingly in favour of a hydrocarbon substituent R.

If CCH and CH₃ can be formed during the laser ablation process, then more complex ligands, such as CCCCH, CCCH₃, or C(CH₃)₃ could conceivably be present. The corresponding CaR radicals would all be expected to possess or exceed the minimum three-fold rotational symmetry required for doubly degenerate electronic states. The arguments made so far do not allow us to distinguish between these possibilities, but when the vibrational structure is investigated more closely, as is done in the next section, CaCCCH₃ becomes the only feasible carrier.

Vibrational structure in the ÖX̃ system. The prominent bands at 16 101 and 16 172 cm⁻¹ in Fig. 1 are the lowest wavenumber features observed for the new calcium-containing free radical. As mentioned earlier, these clearly constitute a spin–orbit doublet and, assuming the carrier is CaCCCH₃, can be assigned to the à ²E_1/2–X̃ ²A₁ and à ²E_3/2–X̃ ²A₁ 0⁰₀ transitions, respectively. The ÖX̃ transitions in CaR free radicals involve an electron of mainly non-bonding character moving between metal-localised orbitals.^23,25 As a result, extensive vibrational structure is not expected in the ÖX̃ system and the only mode likely to yield any substantial structure is the Ca–R stretch, since this is the mode which is most strongly perturbed by the electronic transition.

Consequently, the assignment of the doublet centred at 16 507 cm⁻¹ is to excitation of the Ca–R stretching vibration in the à state, which gives a frequency of ∼370 cm⁻¹ for this mode. To confirm that this doublet is due to excitation of ν_Ca–R in the à state, we have also recorded dispersed fluorescence spectra. The dispersed fluorescence spectrum is essentially the same, apart from a wavelength shift, if the laser is tuned to either the 16 471 or 16 542 cm⁻¹ transition, as would be expected if they constitute a spin–orbit doublet. The strongest feature is a band 364 cm⁻¹ to the red of the laser wavelength (see Fig. 2). The intensity of this band and its position clearly shows that it is due to single quantum excitation of the Ca–C stretch. We therefore determine ν_Ca–C to be 364 and 370 cm⁻¹ in the ground and first excited electronic states, respectively. The small change in vibrational frequencies between the à and X̃ states is consistent with the idea that a non-bonding electron is involved in the electronic transition.

Fig. 2 Dispersed fluorescence spectrum of CaCCCH₃ obtained by laser pumping the 16 537 cm⁻¹ transition (Ã ²E_3/2–X̃ ²A₁ 5¹₀ band). The strongest band corresponds to single quantum excitation of the Ca–C stretch (ν₅) in the ground electronic state.

Having measured the Ca–R stretching frequencies, this information can now be used to identify R. To put this on a firmer footing, density functional theory (DFT) calculations were carried out. Attention was restricted to the calcium acetylides CaCCH, CaCCCH₃, and CaCCCCH. The last two molecules were chosen because they were viewed as the most likely candidates for the spectral carrier. CaCCH was also included because the Ca–C stretching frequency in the ground electronic state of this molecule is known, and therefore serves as a useful reference point.

Given that the bonding in CaR radicals in their ground and low-lying excited electronic states is primarily ionic,^23,25 the identity of R is not expected to have a major effect on the strength of the Ca–R bond, especially when the ligands are from the same family (as the acetylides considered above are). In other words, the Ca–R bond force constant will show minor variations with ligand identity, but the Ca–R stretching frequency will be strongly dependent on the effective reduced mass. The similarity in binding is confirmed by the DFT calculations, which predict only small variations in Ca–C equilibrium bond lengths (see Table 1) and diagonal Ca–C stretching force constants (not shown). Consequently, ν(Ca–R) will be largely determined by the mass of substituent R.

Table 1 Geometrical parameters and Ca–C stretching vibrational frequencies for CaCCH, CaCCCH₃, and CaCCCCH, from DFT calculations^ab

	CaCCH	CaCCCH3^c	CaCCCCH
a The B3LYP functional was employed. See text for further details. b The DFT and experimental data refer to the ground electronic states of these molecules. The full set of vibrational frequencies for each molecule is available from the authors on request. c The calculated CCH bond angle was 111.56°.
r Ca–C/Å	2.419	2.408	2.426
r C1–C2/Å	1.220	1.223	1.229
r C2–C3/Å	—	1.461	1.365
r C3–C4/Å	—		1.208
r C–H/Å	1.064	1.092	1.065
ν(Ca–C)/cm^−1	375	325	298

---

Given the similarities of these molecules, the DFT calculations should systematically underestimate or overestimate the Ca–C stretching frequencies. We can therefore take the known Ca–C fundamental frequency of CaCCH and employ it as a scaling parameter for the DFT results to determine the frequency of the same mode in CaCCCCH and CaCCCH₃. In other words, we place no reliance on the absolute frequencies from the DFT calculations, but instead use them to deduce the differences in the Ca–R stretching frequencies from one acetylide to another.

Table 1 summarises the calculated vibrational frequencies. The DFT calculations underestimate the experimental (fundamental) Ca–C stretching frequency in CaCCH (399 cm⁻¹)¹ by approximately 6%. Scaling the frequencies of the other molecules by the same proportion gives predictions of ca. 346 and 317 cm⁻¹ for CaCCCH₃ and CaCCCCH, respectively. The latter value is far smaller than the observed ground state fundamental vibrational frequency in this work (364 cm⁻¹) and eliminates CaCCCCH as the spectral carrier. On the other hand, the discrepancy for CaCCCH₃ is only 18 cm⁻¹ and could easily be accounted for by limitations in the DFT calculations and the scaling procedure. It should also be borne in mind that the precision in measuring the vibrational frequency from the dispersed fluorescence spectrum is estimated as ±5 cm⁻¹. When all of these factors are taken into account, CaCCCH₃ is a plausible candidate for the spectral carrier.

Although other hydrocarbon substituents with similar masses are conceivable, none satisfy the additional requirement of high symmetry necessary to generate spin-orbit splitting. Consequently, the new electronic system is assigned to the à ²E–X̃ ²A₁ transition of CaCCCH₃.

B̃–X̃ system. The excitation spectrum of CaCCCH₃ shows another strong band at 16 861 cm⁻¹. Unlike the ÖX̃ system, there is no evidence of a spin-orbit partner and therefore, by analogy with other CaR radicals, the only reasonable assignment is to the B̃ ²A₁–X̃ ²A₁ 0⁰₀ transition. A weaker band is also observed at 17 223 cm⁻¹ which, like the origin, shows no spin-orbit doubling. This band is 360 cm⁻¹ from the origin, very similar to the Ca–C stretching frequency in the à ²E state. We therefore assign this 360 cm⁻¹ interval to excitation of the Ca–C stretch in the B̃ ²A₁ state.

Although the B̃–X̃ transitions of many calcium-containing free radicals have been reported, the B̃ ²Σ⁺–X̃ ²Σ⁺ system of CaCCH has not been observed by LIF spectroscopy. From their rotational analysis of the ÖX̃ system,² Bopegedera et al. argued that the absence of an observable B̃ ²Σ⁺ state is most likely due to predissociation, a conclusion drawn from the Λ-doubling parameters determined for the à ²Π state. More recent work by Li and Coxon has revealed errors in the analysis of Bopegedera et al.⁵ In particular, the p_ν Λ-doubling parameter was found to be positive, rather than negative as reported by Bopegedera et al. The new value for p_ν gave an estimated B̃ ²Σ⁺–à ²Π separation of 1080 cm⁻¹ in the pure precession limit. This value, which is reasonable when compared with other CaR molecules,²³ supports the proposition that predissociation is responsible for the non-observation of LIF spectra for the B̃ ²Σ⁺ state of CaCCH.

The B̃–Ã separation in CaCCCH₃ is found to be 758 cm⁻¹. The substitution of a methyl group in place of the hydrogen atom in CaCCH is unlikely to have a major impact on the calcium-localised orbitals. However, its effect clearly cannot be negligible since the B̃ state of CaCCCH₃ has a substantial fluorescence quantum yield, unlike that of CaCCH. The methyl group presumably decreases the predissociation rate by altering the relative energies of the B̃ state and the potentially predissociating state, pushing the latter above the former.

Table 2 summarises the positions and assignments of all CaCCCH₃ bands observed in this work.

Table 2 Band positions and assignments for CaCCCH₃

Band centre/cm^−1	Assignment
16 103	Ã ^2E1/2–X̃ ^2A1 0^00
16 172	Ã ^2E3/2–X̃ ^2A1 0^00
16 471	Ã ^2E1/2–X̃ ^2A1 5^10
16 542	Ã ^2E3/2–X̃ ^2A1 5^10
16 861	B̃ ^2A1–X̃ ^2A1 0^00
17 223	B̃ ^2A1–X̃ ^2A1 0^00

---

B. Strontium

The observations with strontium as ablation target are qualitatively similar to calcium. Fig. 3 shows an excitation spectrum obtained with benzene as the precursor. New bands attributable to SrCCCH₃ can be seen in addition to contributions from SrCCH and SrOH. The positions of the SrCCCH₃ bands are listed in Table 3. The à ²E state of SrCCCH₃ is expected to exhibit a larger spin–orbit splitting than that of CaCCCH₃ due to the presence of the heavier metal atom in the former molecule. The pair of strong bands at 14 831 and 15 128 cm⁻¹ are therefore assigned to the à ²E_1/2–X̃ ²A₁ and à ²E_3/2–X̃ ²A₁ 0⁰₀ transitions of SrCCCH₃, respectively. This gives a value of 297 cm⁻¹ for the spin–orbit coupling constant in the à ²E state of SrCCCH₃, which is clearly much larger than that observed for CaCCCH₃ but is quite similar to that reported for the corresponding state in SrCCH (275 cm⁻¹).¹

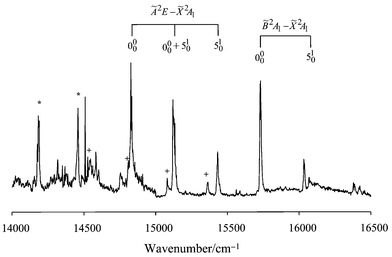Fig. 3 Laser excitation spectrum showing the ÖX̃ and B̃–X̃ systems of SrCCCH₃. Contributions from SrOH and SrCH₃ are marked * and + on the spectrum, respectively. Two laser dyes were used to scan the range shown, the changeover being evident from the discontinuity in the baseline at 15 000 cm⁻¹.

Table 3 Band positions and assignments for SrCCCH₃

Band centre/cm^−1	Assignment
a This is an estimated position due to overlap by the much stronger à ^2E3/2–X̃ ^2A1 0^00 band.
14 831	Ã ^2E1/2–X̃ ^2A1 0^00
15 128	Ã ^2E3/2–X̃ ^2A1 0^00
(15 128)^a	à ^2E1/2–X̃ ^2A1 5^10
15 435	Ã ^2E3/2–X̃ ^2A1 5^10
15 732	B̃ ^2A1–X̃ ^2A1 0^00
16 036	B̃ ^2A1–X̃ ^2A1 0^00

---

By analogy with CaCCCH₃, some activity in the Sr–C stretching mode is expected in the LIF spectrum of SrCCCH₃. The substitution of Sr for Ca will substantially lower the frequency of this vibration. A candidate is the band at 15 435 cm⁻¹, which is ∼307 cm⁻¹ from the à ²E_3/2–X̃ ²A₁ 0⁰₀ band. Notice that this value is similar to the spin–orbit splitting in the origin band. It is therefore likely that the band due to single quantum excitation of ν_Sr–C in the à ²E_1/2–X̃ ²A₁ system overlaps the à ²E_3/2–X̃ ²A₁ 0⁰₀ band, and this is consistent with the broadening of the band at 15 128 cm⁻¹.

A prominent B̃ ²A₁–X̃ ²A₁ system is also observed for SrCCCH₃. The strongest band at 15 732 cm⁻¹ is assigned to the 0⁰₀ transition while that at 16 036 cm⁻¹ is due to excitation of one quantum in the Sr–C stretch, giving a value of 304 cm⁻¹ for ν_Sr–C in the B̃ ²A₁ electronic state.

Mechanism for formation of MCCCH₃. Considerable chemistry is required to produce MCCCH₃, and indeed other species detected in these experiments such as MCH₃ and MCCH, from precursors such as benzene. The formation of these radicals must result from the reaction of metal atoms with decomposition products of the organic precursor. Broadly speaking, fragmentation of the precursor may occur in two ways, (i) direct excimer laser photolysis, or (ii) subsequent reactions in the plasma ejected from the surface of the ablation target. Although both are likely in our experiments, in attempting to propose a mechanism we will concentrate on those reactions induced by photolysis since the underlying chemistry is better understood. The focus will be on benzene, since it was the main precursor used in this work and its photodissociation mechanism has been extensively studied.

The most recent work on benzene photodissociation, carried out by Tsai and co-workers using ion imaging,²⁶ has established that there is only one single-photon decomposition process at 193 nm, viz.

C₆H₆ + hν → C₆H₆* → C₆H₅ + H (1)

The reaction proceeds through a ‘hot’ benzene intermediate (C₆H₆*) which has a relatively long lifetime (∼10 μs) under collision-free conditions.

Other fragments formed in the photolysis of benzene, which were previously thought to be the result of minor single-photon channels,²⁷ were found by Tsai et al. to be due to two-photon processes proceeding via the ‘hot’ benzene:

C₆H₆* + hν → C₆H₄ + H₂ (2)

C₆H₆* + hν → C₄H₃ + C₂H₃ (3)

C₆H₆* + hν → C₅H₃ + CH₃ (4)

These ring opening channels will probably be the dominant fragmentation processes under our conditions because of the relatively long lifetime of the ‘hot’ benzene coupled with the high intensity of the focussed excimer laser radiation.

Secondary photodissociation of the products of reactions (2)–(4) will yield other fragments. For example, loss of H from C₂H₃ will generate acetylene, and this is a well-known product from the photolysis of benzene.²⁸ Although this is a minor product under normal low light intensity conditions, under our conditions it is expected to be a major product. Acetylene itself will undergo photodissociation at 193 nm and the resulting reaction

C₂H₂ + hν → C₂H + H (5)

is known to occur with almost unit quantum yield.²⁹

Recombination of the products of reactions (4) and (5) will then lead to the formation of methylacetylene, viz.

C₂H + CH₃ + M → CH₃CCH (6)

All the ingredients are now in place for formation of MCH₃, MCCH, and MCCCH₃. These molecules could form by direct reaction between the metal atoms and the corresponding organic radical (e.g. CH₃ from reaction (4) yielding MCH₃). Alternatively, metal atoms in metastable excited electronic excited states can react directly with closed-shell organic molecules to displace a hydrogen atom, e.g.

M* + C₂H₂ → MCCH + H (7)

M* + CH₃CCH → MCCCH₃ + H (8)

The production of metastable electronic excited states of metal atoms via laser ablation is a well-known phenomenon.^30,31 Equally, reactions of the type (7) and (8) are well-known from the Broida oven experiments on M–R radicals by Bernath and co-workers. The latter group have used a tunable laser to excite alkaline earth atoms to a long-lived triplet excited state, which in turn drives the reaction between M and R–H.²³

Conclusions

The first laser-induced fluorescence spectra of the CaCCCH₃ and SrCCCH₃ free radicals have been reported. The à ²E–X̃ ²A₁ and B̃ ²A₁–X̃ ²A₁ systems have been observed for both molecules. The vibrational structure is sparse, with only short progressions being identified in the metal-carbon stretching mode. The observation of strong B̃–X̃ transitions contrasts sharply with CaCCH and SrCCH, where the analogous bands are not observable by LIF spectroscopy. Detailed rotationally-resolved studies would be valuable in shedding light on this apparent anomaly.

Acknowledgements

The authors acknowledge the support of this work by the UK Engineering and Physical Sciences Research Council.

References

1. A. M. R. P. Bopegedera, C. R. Brazier and P. F. Bernath, Chem. Phys. Lett., 1987, 136, 97.
2. A. M. R. P. Bopegedera, C. R. Brazier and P. F. Bernath, J. Mol. Spectrosc., 1988, 129, 268.
3. C. J. Whitham, B. Soep, J. P. Visticot and A. Keller, J. Chem. Phys., 1990, 93, 991.
4. A. J. Marr, J. Perry and T. C. Steimle, J. Chem. Phys., 1995, 103, 3861.
5. M. Li and J. A. Coxon, J. Mol. Spectrosc., 1996, 176, 206.
6. M. G. Li and J. A. Coxon, J. Mol. Spectrosc., 1997, 184, 395.
7. M. A. Anderson and L. M. Ziurys, Astrophys. J., 1995, 444, L57.
8. B. Nuccio, A. J. Apponi and L. M. Ziurys, Chem. Phys. Lett., 1995, 247, 283.
9. M. A. Anderson and L. M. Ziurys, Astrophys. J., 1995, 439, L25.
10. G. K. Corlett, A. M. Little and A. M. Ellis, Chem. Phys. Lett., 1996, 249, 53.
11. G. K. Corlett, M. S. Beardah and A. M. Ellis, J. Mol. Spectrosc., 1997, 185, 202.
12. M. G. Li and J. A. Coxon, J. Mol. Spectrosc., 1996, 180, 287.
13. M. G. Li and J. A. Coxon, J. Mol. Spectrosc., 1997, 183, 250.
14. M. G. Li and J. A. Coxon, J. Mol. Spectrosc., 1999, 196, 14.
15. C. A. Thompson and L. Andrews, J. Am. Chem. Soc., 1996, 118, 10242.
16. D. E. Woon, Astrophys. J., 1996, 456, 602.
17. D. E. Woon, Chem. Phys. Lett., 1997, 274, 299.
18. MOLPRO, a package of ab initio programs designed by H-J. Werner and P. J. Knowles, version 2002.1, R. D. Amos, A. Bernhardsson, A. Berning, P. Celani, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, P. J. Knowles, T. Korona, R. Lindh, A. W. Lloyd, S. J. McNicholas, F. R. Manby, W. Meyer, M. E. Mura, A. Nicklass, P. Palmieri, R. Pitzer, G. Rauhut, M. Schütz, U. Schumann, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and H-J. Werner.
19. G. Rauhut, A. El Azhary, F. Eckert, U. Schumann and H.-J. Werner, Spectrochim. Acta, 1999, 55, 651.
20. G. Rauhut and P. Pulay, J. Phys. Chem., 1995, 99, 3093.
21. A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502.
22. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
23. P. F. Bernath, in Advances in Photochemistry, ed. D. C. Neckers, D. H. Volman and G von Bünau, Wiley, 1997, vol. 23, pp. 1–62.
24. C. R. Brazier, L. C. Ellingboe, S. Kinsey-Nielson and P. F. Bernath, J. Am. Chem. Soc., 1986, 108, 2126.
25. A. M. Ellis, Int. Rev. Phys. Chem., 2001, 20, 551.
26. S.-T. Tsai, C.-L. Huang, Y. T. Lee and C.-K. Ni, J. Chem. Phys., 2001, 115, 2449.
27. A. Yokoyama, X. Zhao, E. J. Hintsa, R. E. Continetti and Y. T. Lee, J. Chem. Phys., 1990, 92, 4222.
28. J. K. Foote, M. H. Mallon and J. N. Pitts, J. Am. Chem. Soc., 1966, 88, 3698.
29. A. Läuter, K. S. Lee, K. H. Lung, R. K. Vatsa, J. P. Mittal and H.-R. Volpp, Chem. Phys. Lett., 2002, 358, 314.
30. V. S. Burakov, N. V. Tarasenko and N. A. Savastenko, Spectrochim. Acta, Part B, 2001, 56, 961.
31. T. J. Hughes and M. R. Levy, Phys. Chem. Chem. Phys., 2000, 2, 651.

---