Proton solvation and self-dissociation of 100% sulfuric acid: The quantum-chemical analysis
V.
Kazansky
and
V.
Solkan
Zelinsky Institute of Organic Chemistry, Russian Academy of Sciences, Leninsky prospect 47, Moscow, 119991, Russia. E-mail: vbk@ioc.ac.ru
First published on 14th November 2002
Abstract
Ab initio quantum-chemical calculations of solvation energies of H3SO4+ cation and HSO4− anion by one or two molecules of sulfuric acid in the gas phase have been performed at the Hartree–Fock (HF) level using the 6-31++G** basis set. Additional contributions to the solvation energy of the acid arising from electrostatic interactions with the surrounding molecules in the liquid were estimated in the framework of the polarizable continuum models (PCM or IPCM models). Together with the experimental values for the energies of protonation and deprotonation of sulfuric acid in the gas phase the calculated solvation energies were then used to estimate the heats of self-dissociation of the liquid sulfuric acid and of proton solvation by the anhydrous acid. An almost quantitative agreement of the calculated heat of self-dissociation with the experimental value of +15 kJ mol−1 indicates a rather high accuracy of the calculations. A remarkable feature of the anhydrous sulfuric acid is a low value of solvation energy of protons that is about 85 kJ mol−1 smaller than in the aqueous solution. This result explains why anhydrous sulfuric acid, despite the low value of dissociation constant, behaves as a superacid.
Introduction
It is well known that the energies of homolytic dissociation of various acids in the gas phase fall in the range of 300–600 kJ mol−1. For heterolytic dissociation, the corresponding values are twice or three times higher. In contrast, heterolytic dissociation of most of the acids in aqueous solution is thermoneutral or even weakly exothermic. The reason for such a difference is connected with solvation effects. Indeed, in aqueous solution the very high energy required for heterolytic dissociation in the gas phase is almost completely compensated by the sum of the heats of proton and anion hydration. The heat of proton hydration in this case is equal to 1090 kJ mol−1, whereas the heats of solvation of various anions are lower by 2.5–3.5 times.1,2Unlike in aqueous solutions, the energetics of heterolytic dissociation of acids in nonaqueous solutions have been much less investigated. In particular, this is true for such superacids as anhydrous sulfuric acid, liquefied hydrofluoric acid or sulfuric and hydrofluoric acids modified with such Lewis acid additives as SO3, BF3, or SbF5.
It is quite clear that the specific properties of superacids arise from the unusual properties of solvated protons instead of the high degrees of dissociation. For instance, the dissociation constant of anhydrous sulfuric acid is equal to only 10−4 whereas for liquid hydrofluoric acid it is as low as 10−10.2 Therefore, since both HF and H2SO4 behave as superacids only in anhydrous solution, extremely high chemical activity of protons is associated with the relatively weak solvation in comparison with solvation by the more basic water molecules.3,4
Bearing this in mind, the aim of the present work was to apply the ab initio quantum chemical calculations to estimate proton solvation energies in 100% sulfuric acid and to analyze the energetic of sulfuric acid self-dissociation with account of solvation effects. Anhydrous sulfuric acid was chosen for this study, because it is generally considered as a standard superacid, whereas the value of the H0 Hammett acidity function for anhydrous sulfuric acid is often used as a minimal value for superacids. In addition, starting from the 1940s, concentrated sulfuric acid has been used in chemical industry as a catalyst for isoparaffin–olefin alkylation. Therefore, the enthalpy of proton solvation by this acid is of interest for the better understanding of the mechanism of formation of alkylcarbenium ions, which are believed to play the role of active intermediates in sulfuric acid catalyzed transformations of hydrocarbons.
Method for quantum-chemical calculations
Quantum-chemical calculations of solvation energies of H3SO4+ cations and HSO4− anions by anhydrous sulfuric acid were carried out in two consecutive steps. First, we calculated the structure and the formation energies of the above-mentioned cations and anions interacting with one or two molecules of sulfuric acid in the gas phase in a cluster model approximation using the Hartree–Fock method with the 6-31++G** basis set and full optimization of geometry of solvated species. Zero-point vibrational energy (ZPE) corrections were introduced both for H3SO4+ and HSO4− ions solvated with one or two sulfuric acid molecules. These ab initio calculations were carried out using the GAMESS package.5 The optimized geometries of the neutral and charged complexes are presented in Figs. 1–4. The calculated total energies and the zero-point vibrational corrections for different neutral complexes are listed in Table 1. In a similar way, the calculated total energies, zero-point vibrational energies and solvation energies for the stable charged complexes and for cations and anions are collected in Table 2.| Molecule or complexes | Total RHF/631++G** energy/au | Zero-point energy in the gas phase/kJ mol−1 | Interaction energy in the gas phase/kJ mol−1 |
|---|---|---|---|
| H2SO4 | −698.05985093 | 110.2 | — |
| [H2SO4 H2SO4] | −1396.15073365 | 229.9 | 71.9 |
| [3H2SO4] | −2094.23923480 | 347.8 | 139.6 |
| Complexes or ions | Total RHF/6-31++Gb energy/au | Zero-point energy in the gas phase/kJ mol−1 | Interaction energy in the gas phase/kJ mol−1 | Electrostatic contribution in solvation energy/kJ mol−1 | Total solvation energy in liquid H2SO4/kJ mol−1 |
|---|---|---|---|---|---|
| a Calculated by means of PCM model. b Calculated by means of IPCM model. | |||||
| H3SO4+ | −698.3474724 | 141.2 | — | — | — |
| HSO4− | −697.5527652 | 77.7 | — | — | — |
| [H3SO4+ H2SO4] | −1396.4538124 | 237.8 | 115.4 | 268.7a | 334 |
| [HSO4− H2SO4] | −1395.6825880 | 199.1 | 172.2 | 212.3a | 334.5 |
| [H3SO4+ 2H2SO4] | −2094.5440256 | 370.6 | 192.7 | 224.9b | 317.3 |
| [HSO4− 2H2SO4] | −2093.7751496 | 314.3 | 253.3 | 168b | 321.3 |
Additional electrostatic contributions to solvation energies due to interaction of the charged clusters with surrounding molecules of liquid sulfuric acid were estimated in the framework of the continuum PCM6,7 or IPCM8 models. In both of them liquid sulfuric acid was considered as a homogeneous medium with a high dielectric constant equal to 110. PCM calculations for the dimeric [H3SO4 H2SO4]+ or [HSO4 H2SO4]− complexes were carried out using a standard GAMESS program. In this case the cavities occupied by the charged clusters in the liquid acid were built assuming van der Vaals diameters for the atoms in these ionic species.
This model obviously does not take into account the different dimensions of positively or negatively charged solvated ions. Therefore, for the bigger clusters with two solvating molecules of sulfuric acid, the electrostatic contribution into solvation energy was calculated by means of the modified IPCM model.8 In this case dimensions of cationic and anionic clusters were estimated more precisely with account of distribution in these species of electron density. These calculations were performed using the GAUSSIAN-98 program9 with the iso-density value equal to 0.0001 au. The MOLDEN program10 was used for molecular graphics visualization.
Results
(a) Association energies of neutral molecules in liquid sulfuric acid
It is well known that liquid sulfuric acid is strongly associated due to formation of intermolecular hydrogen bonds. In particular, this follows from the high dielectric constant of the acid which is equal to 110. Bearing this in mind, we performed ab initio quantum-chemical calculations of the structures and of the formation energies of dimeric and trimeric complexes in which sulfuric acid molecules are linked with each other by intermolecular hydrogen bonds.The calculated structures of the neutral double hydrogen bonded dimeric complexes are shown in Fig. 1, whereas formation energies of these complexes are given in Table 1. As follows from these data, the energy of two equivalent hydrogen bonds, accounting for the zero-point vibrational energy correction in the symmetric dimeric complex shown in Fig. 1(a), is equal to 71.9 kJ mol−1.
 | ||
Fig. 1 Structure of the most stable electroneutral dimers of sulfuric acid. (a)
ΔHform![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −71.9 kJ mol−1. (b)
ΔHform −71.9 kJ mol−1. (b)
ΔHform![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −41.4 kJ mol−1. −41.4 kJ mol−1. | ||
The complex shown in Fig. 1(b) is much less stable, whereas its formation energy is equal only to 41.4 kJ mol−1. In addition, the hydrogen bond is considerably longer than in complex 1(a). Our attempt to estimate formation energy of the dimeric complex with three hydrogen bonds between two H2SO4 molecules was unsuccessful: three hydrogen bonds, that were preassigned for the initial complex, transformed upon optimization of the complex geometry in two hydrogen bonds. Hence, among dimeric complexes, that one represented by the structure 1(a) with two equal hydrogen bonds between sulfuric acid molecules is most stable.
Addition of a third molecule of sulfuric acid to such dimeric complexes results in the formation of the symmetric trimeric complex shown in Fig. 2. The association energy with the third molecule of sulfuric acid calculated, taking into account zero point energy corrections, is equal to 67.7 kJ mol−1 resulting in a total solvation energy of 139.6 kJ mol−1. The calculated heat of evaporation of one molecule of sulfuric acid from the liquid acid due to decomposition of such complexes should amount to one third of this value i.e. 46.5 kJ mol−1. This is slightly lower than the experimental value of 50 kJ mol−1 reported in ref. 11. Therefore, one has to conclude that the hydrogen bonded associates in liquid sulfuric acid contain three and four hydrogen bonded molecules of the acid.
 | ||
Fig. 2 Structure of the most stable trimer of sulfuric acid. ΔHform![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −139.6 kJ mol−1. −139.6 kJ mol−1. | ||
(b) Solvation energy of H3SO4+ cations with liquid sulfuric acid
A quantum-chemical cluster calculation of the interaction energy of H3SO4+ cation with one molecule of sulfuric acid in the gas phase indicates that formation of the symmetric [HOSO3(HO)3SOH]+ positively charged dimer with three equivalent hydrogen bonds does not correspond to a local minimum of energy. The lack of the energy minimum is most likely connected with some steric hindrance. Instead, the most stable structure of the protonated sulfuric acid dimer corresponds to the asymmetric [H3SO4+ H2SO4] ion with two short equivalent hydrogen bonds between the sulfate groups with the almost equal lengths of 1.818 and 1.819 Å (Fig. 3(a)). | ||
Fig. 3 Structure of the most stable positively charged cationic dimer and trimer of sulfuric acid. (a)
ΔHform![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −115.4 kJ mol−1. (b)
ΔHform −115.4 kJ mol−1. (b)
ΔHform![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −192.7 kJ mol−1. −192.7 kJ mol−1. | ||
The calculated formation energy of this complex in the gas phase is equal to 115.4 kJ mol−1. This value is by about 35 kJ mol−1 higher than for the neutral asymmetric dimeric complex. However, the higher association energy does not result from the stronger hydrogen bonding, since the lengths of hydrogen bonds in the solvated cation and in the neutral dimer are nearly the same (compare Figs. 1(a) and 3(a)). Therefore, the higher solvation energy of the cation most likely originates from the additional ion–molecule interaction of the positively charged ion with a polarized neutral molecule of sulfuric acid.
The results of our calculations also revealed that addition of a third molecule of sulfuric acid to such dimeric complexes takes place from the side of the H3SO4+ cation giving rise to the linear [H2SO4 H3SO4 H2SO4]+ structure of Fig. 3(b). As one may expect, the second acid molecule is bonded to the H3SO4+ cation through a single hydrogen bond. This results in some increase of the length of the double hydrogen bond of H3SO4+ ion with the first solvating molecule of the acid.
Formation energy of this complex from the dimeric complex and the free sulfuric acid molecule in the gas phase is equal to 77.3 kJ mol−1. Thus, the total interaction energy of the H3SO4+ cation with two neutral molecules of sulfuric acid is equal to 192.7 kJ mol−1. This is higher by 53 kJ mol−1 than the association energy of three neutral molecules. Taking account of the additional solvation of the positively charged dimeric complexes with the surrounding molecules of liquid sulfuric acid results in an entire solvation energy of the dimeric complex of 268.8 kJ mol−1.
To estimate the full solvation energy of the dimeric H3SO4+ H2SO4 cation with liquid sulfuric acid, one needs to add to this value the above mentioned gas phase interaction energy of the H3SO4+ cation with the first molecule of sulfuric acid of 115.4 kJ mol−1 and subtract from this sum the energy of transfer of one molecule of sulfuric acid from the liquid acid into the gas phase, which is equal to 50 kJ mol−1:11
 | (1) |
 | (2) |
(c) Solvation of the HSO4− anion
The energy of HSO4− anion solvation by liquid sulfuric acid was calculated in a similar way, also in two consecutive steps. First, the structure and formation energies of HSO4− anion in the gas phase solvated by one or two molecules of sulfuric acid were calculated in a cluster approximation. Then similar to cations the electrostatic contribution to the total solvation energy due to interaction with the surrounding molecules of the liquid acid was estimated in the framework of the PCM or IPCM models.The structure of the most stable dimeric complex that is formed in the gas phase upon interaction of HSO4− anion with the first molecule of sulfuric acid is shown in Fig. 4(a). The binding between the anion and the second molecule of sulfuric acid results from the formation of three hydrogen bonds. The two equivalent bonds are shorter and have a length of 1.659 Å. The third hydrogen bond is longer, at 2.054 Å, and makes a smaller contribution to the energy of the intermolecular interaction.
 | ||
Fig. 4 Structure of the most stable negatively charged anionic dimer and trimer of sulfuric acid. (a)
ΔHform![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −172.2 kJ mol−1. (b)
ΔHform −172.2 kJ mol−1. (b)
ΔHform![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −253.3 kJ mol−1. −253.3 kJ mol−1. | ||
The two shorter hydrogen bonds and the formation of the third bond between the anion and a sulfuric acid molecule definitely indicate that the solvation energy of the anion is greater than that of the cation. This conclusion agrees with the calculated value of the solvation energy for the anion of 172.2 kJ mol−1 that is higher than that for the cation by 56.8 kJ mol−1.
The structure of the complex solvated with two sulfuric acid molecules is shown in Fig. 4(b). As one might expect, the third molecule of the acid is bonded to the negatively charged ion through a weaker single hydrogen bond. This result in the increase of the total solvation energy by 81.1 kJ mol−1. Simultaneously the triple hydrogen bond becomes somewhat longer.
For the dimeric [HSO4 H2SO4]− complexes, the PCM-calculated additional electrostatic contribution to the total solvation energy is equal to 212.3 kJ mol−1. The similar IPCM electrostatic contribution in the solvation energy of the trimeric complex is equal to 168 kJ mol−1. These and above calculated energies obtained for solvation of the HSO4− anion with one or two molecules of sulfuric acid resulted in the following total energies of solvation. For the clusters with one solvating sulfuric acid molecule:

| (3) |
For the clusters with two solvating sulfuric acid molecules:
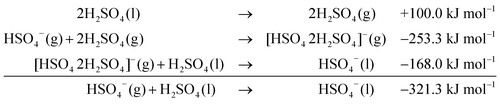 | (4) |
Discussion
The obtained results allowed the calculation of the self-dissociation energy of liquid sulfuric acid. For this purpose, in addition to the above calculated solvation energies of H3SO4+ and HSO4− ions we used the experimental value for self-dissociation of sulfuric acid in the gas phase of 589.4 kJ mol−1.13 Then for the dimeric solvated complexes, the energy balance of self-dissociation of anhydrous acid appears as follows: | (5) |
 | (6) |
Both calculated heats of self-dissociation are somewhat higher than the experimental value of +15 kJ mol−1.12 However, the heat of acid evaporation of 50 kJ mol−1 reported in ref. 11 is not very precise. On the other hand, lower evaporation energy decreases the heat of self-dissociation only by 5 kJ mol−1, for the dimeric complexes by 20 kJ mol−1, and for the trimeric complexes by 30 kJ mol−1. Then the resulting range of the calculated values of +0.9 kJ mol−1 for dimeric complexes and +20.8 kJ mol−1 for trimeric complexes almost quantitatively fits the experiment. However, even without such corrections, the agreement between calculated and experimental values of the self-dissociation energy is quite reasonable pointing to the rather high accuracy of our calculations.
Similar to solvation by liquid sulfuric acid of the H3SO4+ cation and HSO4− anion, the estimation of solvation energy of the proton by anhydrous sulfuric acid can be also made in two consecutive steps. First the proton is added to one molecule of sulfuric acid in the gas phase. This corresponds to the experimental value of the proton affinity of the free sulfuric acid molecule of 720.2 kJ mol−1.14 Then the resulting H3SO4+ cation is solvated by the liquid acid. Taking account of the transfer of one sulfuric acid molecule from the liquid acid to the gas phase results in the following energy balance:
 | (7) |
The average value of proton solvation by anhydrous acid of about −995 kJ mol−1 is approximately 95 kJ mol−1 lower than the proton affinity of liquid water (−1090 kJ mol−1). This evidently points to the specific properties of protons in anhydrous sulfuric acid.
Indeed, the enormously high chemical activity of protons in anhydrous or very concentrated sulfuric acid has been emphasized many times in the literature.15–17 The nonlinear growth of the Hammett acidity function for highly concentrated sulfuric acid also indicates the specificity of proton properties.18 The results of the present work concerning the much lower solvation energy of protons in anhydrous sulfuric acid than in aqueous solution provide a quantitative interpretation of these findings.
In this context it should be also underlined that although solvation is an absolutely necessary requirement for heterolytic dissociation of various acids, interaction with solvating molecules simultaneously lowers the chemical activity of the proton. Indeed, it is well known that the electron affinity of a free proton in the gas phase is equal to 13.6 eV. By contrast, in water solution it is only a few electronvolts. This difference originates from the much lower solvation energy by water of the hydrogen atom resulting after neutralization of the positive charge of proton by electron. It amounts to only few kJ mol−1 in comparison with the proton hydration energy of −1090 kJ mol−1. Therefore, the chemical properties of the free proton and hydrated proton are drastically different. In this connection, by about 90 kJ mol−1 lower solvation energy of proton in 100% sulfuric in comparison with aqueous solution is quite appreciable since a pKa of unity at room temperature corresponds to the energy difference of only about 6 kJ mol−1.
Thus, the results of the present work confirm our earlier conception according to which the specific properties of superacids are associated with the lower energies of proton solvation in comparison with solvation in aqueous solution.3,4 This conclusion appears to be very reasonable, because the solvation energy of protons by superacids is certainly lower than that by the more basic water. In contrast, solvation by superacids of the basic negatively charged anions is stronger than in water solution. Therefore, superacids represent a compromise between the lowest possible solvation of protons and the highest possible solvation of anions. The former requirement results in a high chemical activity of protons, whereas the latter provides a satisfactory energy balance of heterolytic dissociation of superacids.
Acknowledgements
This work was supported by grant from the RFBR (01-03-32555).References
- F. A. Cotton and G. Wilkinson, Advanced Inorganic Chemistry. A Comprehensive Text, John Wiley & Sons, New York, 1965, part 2 Search PubMed.
- R. P. Bell, The Proton in Chemistry, Chapman and Hall, London, 1973 Search PubMed.
- V. B. Kazansky and V. N. Solkan, Kinet. Catal. (Transl. Kinet. Katal.), 2000, 41, 38–43 Search PubMed.
- V. B. Kazansky, Top. Catal., 2000, 11/12, 55 Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117 CrossRef CAS.
- V. Barone, M. Cossi and J. Tomasi, J. Chem. Phys., 1997, 107, 3210–3221 CrossRef CAS.
- J. B. Foresman, T. A. Keith, K. B. Wiberg, J. Snoonian and M. J. Frisch, J. Phys. Chem., 1996, 100, 16
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098 CrossRef CAS.
098 CrossRef CAS. - M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Lui, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, Gaussian 98, Revision A 7, Gaussian, Inc., Pittsburgh PA, 1998 Search PubMed.
- G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Design, 2000, 14, 123–134 Search PubMed.
- K. M. Malin, N. L. Arkin, G. K. Boreskov and M. G. Slinko, Technology of Sulfuric Acid (in Russian), Goschimisdat, Moscow, 1950, p. 570 Search PubMed.
- R. J. Gillespie, E. A. Robinson and C. Solomons, J. Chem. Soc., 1960, 4320–4326 RSC.
- S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W. G. Mallard, J. Phys. Chem. Ref. Data, Suppl., 1988, 17, 1 Search PubMed.
- K. Do, T. P. Klein, C. A. Pommerening, S. M. Bachrach and L. S. Sunderlin, J. Am. Chem. Soc., 1998, 120, 6093–6096 CrossRef CAS.
- B. V. Nekrasov, Fundamentals of General Chemistry (in Russian), Chimia, Moscow, 1965, vol. 1, p. 334–336 Search PubMed.
- L. P. Hammett, Physical Organic Chemistry, McGraw Hill Co., New York, 1970 Search PubMed.
- M. I. Vinnik, Usp. Khim., 1966, 35, 1922–1952 Search PubMed.
- M. A. Paul and F. A. Long, Chem. Rev., 1957, 57, 1–45 CrossRef CAS.
| This journal is © the Owner Societies 2003 |
