Ferromagnetic bonding in high-spin alkali-metal clusters. How does sodium compare to lithium?

Abstract

High-spin sodium clusters (ⁿ⁺¹Na_n; n = 2–12) are studied using a combined density functional (B3P86/cc-pVDZ) and UCCSD(T)/cc-pVDZ approach. In agreement with previous findings for high-spin lithium clusters, here too the minimum energy clusters are compact species with a high coordination number for each atom in the cluster. Generally, though, high-spin bonding in sodium clusters is much weaker than in the corresponding high-spin lithium clusters. Furthermore, the electronic configuration and the ordering of the molecular orbitals of high-spin sodium clusters differ from those in the high-spin lithium clusters. The electronic states of high-spin sodium clusters have much less p-character than corresponding high-spin lithium clusters. Molecular orbital and valence bond considerations show that the reduced p-participation in bonding is the root cause of the weak ferromagnetic bonding in sodium vs. lithium clusters.

---

Introduction

Ferromagnetic (FM) bonding is a special type of bonding in which the molecules or clusters are devoid of electron pairs.^1–5 This peculiar bonding type, for instance, occurs in the triplet lithium dimer (³Li₂),^1–4 which in its lowest lying state has two singly occupied orbitals, namely the bonding and anti-bonding combination formed from the two atomic 2s orbitals on the two lithium centers. Although the covalent wave function which involves pure 2s orbital occupation produces a repulsive potential, the mixing in of covalent and ionic structures which involve 2p atomic orbital occupation into the 2s-only wave function provides the bonding interaction.^2,4 For a series of high-spin lithium clusters (ⁿ⁺¹Li_n; n = 2–12), we showed⁴ that the FM-bonding energy rises steeply and reaches a value of as much as 12 kcal mol⁻¹ per atom. Thus, FM-bonding can be very strong despite the absence of electron pairing. Furthermore, these ferromagnetic clusters were found to prefer highly symmetrical egg-shaped structures with high coordination numbers. Do other alkali atoms form ferromagnetically bound clusters? This question is the focus of the present study.

Despite the fact that alkali-metal clusters are widely studied, the amount of work done on the high-spin clusters is limited. Early theoretical work using the MCSCF technique was performed by Konowalow et al.^6,7 who studied a series of low lying electronic states of the sodium dimer. The bond dissociation energy of the lowest triplet energy state (x ³Σ⁺_u) was calculated to be 0.52 kcal mol⁻¹ at an interatomic distance of 5.206 Å. Using an experimental Rydberg–Klein–Rees potential Friedman-Hill and Field⁸ determined a dissociation energy of 0.50 kcal mol⁻¹ at an equilibrium bond length of 5.011 Å for the ³Σ⁺_u state. This bond dissociation energy was reproduced by Ho et al.⁹ using the Reproducing Kernel Hilbert Space (RKHS) method and by Gutowski¹⁰ at the CCSD(T) level of theory. The optimized equilibrium bond lengths using these methods were 5.089 Å and 5.192 Å, respectively.

Higgins and coworkers have performed laser induced emission spectroscopy experiments of sodium dimers¹¹ and trimers^12–15 in helium droplets. In the case of the trimer, the emission spectrum for the 2 ⁴E′ ← 1 ⁴A₂′ transition was studied. In addition, the vibrational spectra were calculated using the Reproducing Kernel Hilbert Space (RKHS) methodology and CCSD(T) calculations. The obtained spectra compared best with ⁴Na₃ in D_3h symmetry. The bond dissociation energy was found to be 2.43 kcal mol⁻¹ with a bond distance of 4.406 Å. Other experimentally studied high-spin ferromagnetic clusters are the ³Rb₂ and ³Cs₂ dimers, which were also found to be weakly bound.^16,17

Since our previous work on high-spin lithium clusters^2–4 showed that these type of clusters can be strongly bound, we decided to investigate high-spin sodium clusters (ⁿ⁺¹Na_n; n = 2–12) using a density functional theoretic (DFT) approach. The aim of the study is to delineate the differences and similarities between FM-bonds in lithium vs. sodium clusters.

Theoretical methods

All calculations presented here were performed with the Gaussian 98 program package.¹⁸ Following our experience with high-spin lithium clusters, the calculations were performed with B3P86 method using Becke's 3 parameter exchange functional¹⁹ in combination with the correlation functional due to Perdew (P86)²⁰ and a cc-pVDZ basis set.^21–23 In the case of the dimer, the correlation function of Perdew and Wang²⁴ was also tested but found less suitable, based on the experimental data and the benchmark values obtained by the UCCSD(T) method (see below). Full geometry optimization followed by a complete frequency analyses were performed in all cases. Many different geometrical configurations were tested with a variety of symmetry groups but only the local minima are discussed here. In all situations, it was checked that the doubly occupied orbitals correspond to the core 1s, 2s and 2p orbitals only. For the smaller clusters additional UCCSD(T)/cc-pVDZ optimizations were performed as a benchmark for the DFT calculations. We emphasize that our studies of the lithium clusters demonstrated that the high-spin species invariably prefer different geometries than the low-spin ground state species. For example, while ⁵Li₄ prefers a tetrahedral structure,^2–4 the low-spin state ¹Li₄ assumes a rhombic (D_2h) structure.^25,26 This trend was found, during the present study, also for sodium clusters in a few test cases, ^5,1Na₄ and ^12,2Na₁₁. A rationale for the different geometries was given in ref. 2.

Valence bond calculations of the covalent and ionic energy gaps (Fig. 4, see later) for square ⁵Li₄vs.⁵Na₄ were done with the Xiamen VB package.²⁷

Results

Many different high-spin sodium clusters, ⁿ⁺¹Na_n in the range between n = 2–12, were studied with a variety of techniques ranging from DFT (B3P86 and B3PW91) to UCCSD(T). In the following, BDE stands for bond dissociation energy of the cluster of size n into n individual atoms in their ground states.

The triplet sodium dimer is optimized using the B3P86 and B3PW91 hybrid density functional methods as well as with UHF, UMP2 and UCCSD(T) ab initio methods and the results are summarized in Table 1. Similarly to the triplet lithium dimer, here too in the sodium dimer the lowest triplet state converged to a ³Σ⁺_u state in all cases.

Table 1 Bond dissociation energies and bond distances of optimized ³Na₂ dimers using different methods and basis sets

Method	Basis set	BDE/kcal mol^−1	Bond distance/Å
a From Friedman-Hill and Field (ref. 8).
B3P86	cc-pVDZ	0.46	4.697
B3P86	cc-pVTZ	0.40	4.721
B3PW91	cc-pVDZ	0.21	4.804
UCCSD(T)	cc-pVDZ	0.45	5.187
UCCSD(T)	cc-pVTZ	0.55	5.161
UHF	6-311G(d)	0.01	8.001
UMP2	6-311G(d)	0.03	6.507
Experiment^a		0.50

---

BDEs calculated with the density functional method B3P86 seem to be in excellent agreement with UCCSD(T) calculations. Bond lengths, however, are considerably underestimated by up to 10%. Changing the basis set from cc-pVDZ to cc-pVTZ does not improve the quality of the bond length. Notwithstanding the large discrepancy in bond lengths, the bond dissociation energy and the vibrational frequency are similar to the UCCSD(T)/cc-pVDZ result. Other density functional methods like B3PW91 give a slightly better bond distance but underestimate the bond dissociation energy. Since, the calculated bond dissociation energy and the vibrational frequency are of good quality with B3P86/cc-pVDZ we decided to continue with this method alone.

As a comparison, calculations on ³Na₂ using UHF and UMP2 methods are added to Table 1. Bond lengths are even further off than the corresponding DFT obtained values. Furthermore, the energetics are extremely poor in comparison to the UCCSD(T) result. Therefore, the best cost-effective method for treating high-spin sodium clusters is the B3P86 density functional method in combination with a cc-pVDZ basis set.

Bond dissociation energies and geometric parameters of optimized ⁴Na₃ and ⁵Na₄ structures are written in Table 2. Geometry optimization of the minimum energy structures is repeated with the UCCSD(T)/cc-pVDZ method. Bond dissociation energies of 2.6 kcal mol⁻¹ for the cyclic ⁴Na₃ isomer and of 1.0 kcal mol⁻¹ for the linear isomer are obtained. The B3P86 values (2.4 and 1.0 kcal mol⁻¹) are in excellent agreement with the UCCSD(T) results. The bond distances, however, are underestimated with DFT, for the linear isomer, where we obtain r = 4.561 Å (B3P86), vs.r = 5.051 Å with UCCSD(T). In the case of the triangle a much better agreement between B3P86 and UCCSD(T) is observed, namely 4.222 Å vs. 4.351 Å, respectively. Our values compare very well with the calculated value of Higgins et al.¹⁴ who obtained a BDE = 2.4 kcal mol⁻¹ at an equilibrium distance of 4.406 Å for the D_3h symmetrical sodium trimer for the ⁴A₂′ state. Our calculations, however, gave a ⁴A₁′ ground state. All our attempts to locate the ⁴A₂′ state failed and resulted in ⁴A₁′.

Table 2 Geometries and BDEs of optimized ⁴Na₃ and ⁵Na₄ isomers

Isomer^a	B3P86/cc-pVDZ		UCCSD(T)/cc-pVDZ
	BDE/kcal mol^−1	Bond distance/Å	BDE/kcal mol^−1	Bond distance/Å
a After each isomer is written the electronic state and the symmetry point group. All isomers correspond to local minima and had real frequencies only.
^4Na3
Triangle ^4A1′; D3h	+2.4	4.222	+2.6	4.351
Linear ^4Σu; D∞h	+1.1	4.561	+1.0	5.051
^5Na4
Pyramid ^5A1; Td	+8.3	3.854	+10.2	3.947
Linear ^5Σg; D∞h	+1.9	r 12 = 4.508	+1.7	r 12 = 5.063
		r 23 = 4.410		r 23 = 4.767

---

Optimized ⁵Na₄ geometries and energies calculated with B3P86/cc-pVDZ compare favorably with UCCSD(T)/cc-pVDZ data, as found for the smaller clusters. The UCCSD(T) calculated total BDEs are reproduced within 2 kcal mol⁻¹ with the hybrid DFT method (B3P86). The bond length of the lowest lying quintet tetramer is reproduced reasonable well with B3P86, while the distances in the linear entity are underestimated by roughly 10%. In agreement with our previous results on the quintet lithium tetramer,^3,4 the pyramidal configuration in T_d symmetry is the lowest energy structure. The bond dissociation energy of the lithium tetramer, however, is substantially higher than the one obtained for the corresponding sodium cluster. At the UCCSD(T) level of theory BDEs of 29.6 kcal mol⁻¹ (⁵Li₄) and 10.2 kcal mol⁻¹ (⁵Na₄) were obtained.

The optimized high-spin sodium clusters in the range between the pentamer and the dodecamer are collected in Table 3. In agreement with our previous calculations on the sextet lithium pentamer,^3,4 the linear and cyclic configurations are local minima also for ⁶Na₅. The most stable ⁶Li₅ cluster, however, was the pyramidal structure with C_4v symmetry. In contrast, in the case of sodium the bipyramid in D_3h symmetry is the most stable structure and is 3.7 kcal mol⁻¹ lower in energy than the ⁶Na₅ pyramid in C_4v symmetry. The ⁶Na₅ pyramid has one imaginary frequency of 32 cm⁻¹ corresponding to a b₂ vibrational mode which distorts the system toward C_2v symmetry. A geometry optimization using the Cartesian coordinates of the vibrational mode added to the optimized pyramidal Cartesian led to a geometry identical in energy and geometrical parameters to the bipyramid. Consequently, the imaginary frequency of the pyramid leads to a distortion toward the bipyramid.

Table 3 Geometries and BDEs of optimized ⁿ⁺¹Na_n (n = 5–12) isomers calculated with the B3P86/cc-pVDZ method

Isomer^a	BDE/kcal mol^−1	Geometric parameters/Å
a After each isomer is written the electronic state and the symmetry point group. All isomers have real frequencies only.
^6Na5
Bipyramid ^6A2″; D3h	9.8	r 12 = 3.789; r15 = 4.227
Cyclo ^6A1′; D5h	5.2	r = 4.010
Linear ^6Σg; D∞h	2.7	r 12 = 4.481; r23 = 4.346; r34 = 4.268
^7Na6
Compact ^7A; C1	12.1	See Fig. 1.
Octahedral ^7A1g; Oh	7.1	r = 4.543
Linear ^7Σu; D∞h	3.6	r 12 = 4.462; r23 = 4.304; r34 = 4.268
Cyclo ^7B2u; D6h	2.8	r = 3.809
^9Na8
Compact ^9A; C2	20.1	See Fig. 1.
Linear ^9Σg; D∞h	5.5	r 12 = 4.429; r23 = 4.242; r34 = 4.167
		r 45 = 4.145
^10Na9
Compact ^10A2; C2v	29.6	See Fig. 1.
^11Na10
Compact ^11B2; D4d	35.0	See Fig. 1.
Linear ^11Σu; D∞h	7.7	r 12 = 4.382; r23 = 4.172; r34 = 4.082
		r 45 = 4.041; r56 = 4.029
^12Na11
Compact ^12A; C1	35.8	See Fig. 1.
^13Na12
Compact ^13A; C1	39.1	See Fig. 1.
Linear ^13Σg; D∞h	10.3	r 12 = 4.329; r23 = 4.105; r34 = 4.012
		r 45 = 3.967; r56 = 3.947; r67 = 3.940

---

The difference between the pyramidal ⁶Li₅ and ⁶Na₅ systems is the ordering of the electronic states. In the pyramidal ⁶Li₅ cluster⁴ the ground state is ⁶B₁, whereas in ⁶Na₅ this state is higher lying and the ⁶B₂ state is the ground state. The highest singly occupied orbital of the ⁶B₁ electronic state is a molecular orbital (with b₁ symmetry) made up of the bonding combination of 3p_x and 3p_y atomic orbitals on the bottom plane of the pyramid containing four sodium atoms, i.e. the 3pσ orbital. The ⁶B₂ electronic state, on the other hand, has singly occupied orbitals which involve only linear combination of the 3s atomic orbitals. In ⁶Na₅ clusters the 3pσ bonding molecular orbital is higher in energy than the 3sσ* antibonding orbital. In the corresponding lithium clusters, the 2pσ orbital is lower in energy than the 2sσ*.⁴ Therefore, the ⁶B₂ electronic state in sodium clusters is lower in energy than the ⁶B₁ electronic state.

The most stable high-spin clusters of the sodium hexamer, octamer, nonamer decamer, undecamer and dodecamer are depicted in Fig. 1, while Table 3 contains some additional structures. The septuplet sodium hexamer has local minima in C₁, O_h, D_∞h and D_6h point group symmetries. The ⁷Na₆ minimum is a bicapped tetrahedron and close to being C_2v symmetry, but all attempts to optimize this structure under the geometry constraint failed, leading to the C₁ structure depicted in Fig. 1. In contrast to the lithium hexamer for which BDE = 43.9 kcal mol⁻¹, the ⁷Na₆ octahedral system is a local minimum albeit with a considerably smaller BDE of 7.1 kcal mol⁻¹, at the B3P86/cc-pVDZ level of theory. For high-spin sodium clusters from size n = 8–12 we located two types of minima per cluster size, namely a linear structure and a structure with a maximum amount of intramolecular bonds, see Table 3.

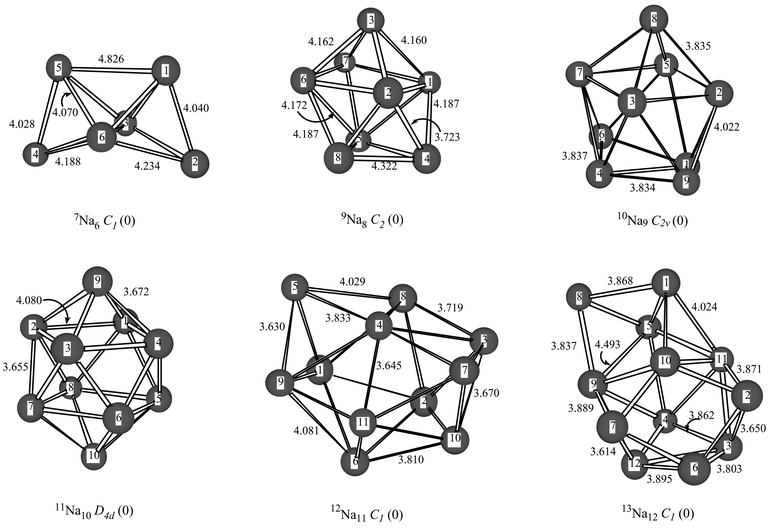Fig. 1 Optimized geometries of ⁷Na₆ (C₁ symmetry), ⁹Na₈ (C₂ symmetry), ¹⁰Na₉ (C_2v symmetry), ¹¹Na₁₀ (D_4d symmetry), ¹²Na₁₁ (C₁ symmetry) and ¹³Na₁₂ (C₁ symmetry) at the B3P86/cc-pVDZ level of theory. Bond lengths are in Å.

Discussion

In agreement with the high-spin lithium clusters the most stable high-spin sodium cluster is generally a compact system with a high and uniform coordination number. Fig. 2 shows the progression of the most stable clusters for the two atom systems. The similarities and differences are apparent. The most stable cluster gradually evolves to an egg-shaped structure with a high and uniform coordination number. However, the Li clusters are much more strongly bonded than their Na analogs.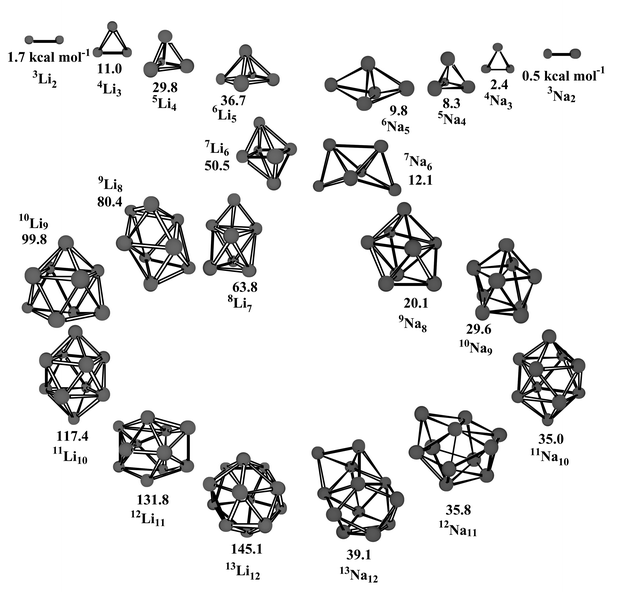

Fig. 2 Evolution of the most stable ⁿ⁺¹Li_nvs.ⁿ⁺¹Na_n clusters. BDEs (in kcal mol⁻¹) are shown under each structure.

In Fig. 3, the relative bond dissociation energy (BDE/n) is plotted as a function of cluster size for both the minimum energy sodium and lithium clusters. The relative bond dissociation energy is defined as the total bond dissociation energy divided by the number of atoms in the cluster. As can be seen from Fig. 3, the relative bond dissociation energies of the lithium and sodium clusters gradually increase and reach a flat region at around 10–12 atoms. In the case of sodium the maximum stabilization energy is around 3.3–3.5 kcal mol⁻¹, the values obtained for the dodecamer and decamer, while in the case of lithium the value is approximately 12.0–12.1 kcal mol⁻¹. In agreement with the high-spin lithium clusters, the relative bond dissociation energy for the tetrahedral sodium tetramer shows a small peak due to the relative short M–M distances and the high-symmetry.⁴

Fig. 3 Relative bond dissociation energies (BDE/n) of minimum energy sodium and lithium clusters (ⁿ⁺¹Li_n and ⁿ⁺¹Na_n; n = 2–12) as a function of cluster size. The BDE/n values are indicated for the flat regions of the two curves. Energies calculated with B3P86/cc-pVDZ.

In order to compare the differences in electronic properties of high-spin lithium and sodium clusters, we investigated several low lying states of the square ⁵Li₄ and ⁵Na₄ configurations. The square species have high symmetry (D_4h symmetry) and therefore, the orbital shapes are easier to interpret than in three-dimensional structures like the pyramidal configuration. In the case of the quintet cyclic tetramer, three low lying electronic states were investigated. The relative ordering of the lowest electronic states in cyclic lithium and sodium tetramers are depicted on the left-hand-side of Fig. 4. The right-hand-side of this figure shows the relevant orbitals for the lithium clusters. The 3sσ, 3pσ and 3pπ orbitals on sodium show much similarity to the corresponding lithium 2sσ, 2pσ and 2pπ orbitals, and are therefore not drawn. All investigated electronic states have singly occupied sσ(a_1g), e_u and e_u orbitals.

Fig. 4 Low-lying electronic states of ⁵Li₄ and ⁵Na₄ in D_4h symmetry calculated with the UCCSD(T) and B3P86 (in brackets) methods. The shape of the orbitals of the lithium clusters are plotted on the right-hand-side. The 2pσ(b_2g) and 2pσ(a_1g) orbitals show only interstitial lobes. Relative energies are in kcal mol⁻¹.

The lowest lying electronic state in the lithium square has a highest singly occupied orbital that possesses electron densities in between the atoms⁵ and is a 2pσ orbital generated from the bonding combination of 2p_x and 2p_y atomic orbitals with b_2g symmetry, 2pσ(b_2g). An excited state corresponding to a b_2g → a_2u transition is 3.1 kcal mol⁻¹ (UCCSD(T)) above the ground state and leads to filling of the 2pπ(a_2u) bonding orbital made from a linear combination of 2p_z atomic orbitals. Above this 2pπ(a_2u) molecular orbital is another bonding orbital which is the result of a linear combination of 2p_x and 2p_y atomic orbitals and has a_1g symmetry, 2pσ(a_1g). We were not able to locate the corresponding electronic state (⁵A_1g) with the UCCSD(T) method. However, using B3P86 this state was found to lie 9.5 kcal mol⁻¹ above the lowest square conformation. Finally, the b_1g molecular orbital is the result of the antibonding combination of 2s atomic orbitals and occupation of this particular orbital (2sσ*(b_1g)) leads to a highly excited state, 16.0 kcal mol⁻¹ (UCCSD(T)) above the ⁵B_2g electronic state, see Fig. 4.

In contrast to the lithium square, in the sodium square configuration the ⁵B_1g state is the lowest electronic state in Fig. 4. Replacing the 3sσ*(b_1g) orbital with either the 3pπ(a_2u) or the 3pσ(b_2g) orbitals gives excited states which are 3.7 and 4.7 kcal mol⁻¹ higher lying. The difference in ordering of the molecular orbitals is due to the difference in splitting of 2s/2p atomic orbitals and 3s/3p atomic orbitals. This in turn derives from the interatomic distances, which are short in ⁿ⁺¹Li_n and considerably longer in ⁿ⁺¹Na_n.

Fig. 5 illustrates the splitting of 2s and 2p atomic orbitals into molecular orbitals for lithium vs. the 3s and 3p atomic orbitals of sodium, into the corresponding molecular orbitals. In lithium clusters with the shorter distances the splitting is large and the 2pσ and 2pπ bonding type orbitals drop below the 2sσ* anti-bonding orbital. In sodium clusters where the distances are long this is not the case and the 3pσ orbital remains well above the 3sσ*. Consequently, in lithium clusters the highest filled orbital is the bonding 2pσ orbital, while in the sodium cluster the highest filled orbital is 3sσ*. With occupation in the bonding 2pσ orbital, the net ferromagnetic bonding energy in ⁵Li₄ is large, BDE = 19.8 kcal mol⁻¹. In contrast, with 3sσ* occupancy in ⁵Na₄ the ferromagnetic bonding diminishes to a mere 2.1 kcal mol⁻¹.

Fig. 5 Orbital splitting in lithium (left) and sodium (right) clusters.

The valence bond (VB) model in our previous papers^2,4 offers a complementary insight into the diminished ferromagnetic bonding in ⁿ⁺¹Na_nvs.ⁿ⁺¹Li_n. Fig. 6 shows the main VB structures which participate in the ferromagnetic (FM) bonding, for the example of the square ⁵M₄ (M = Li, Na) species. The lowest configuration (Φ_cov) is the covalent all-s wave function where all the electrons occupy the s(2s, 3s) orbitals of the atoms and have the same spin. This configuration is repulsive and at a finite distance lies above the separate atoms.^2,4 Above the covalent s-only there is a group of ionic configurations, Φ_ion. As we showed before,⁴ it is enough to consider the mono ionic configurations. Each such ionic structure involves an excited ³M⁻ atom with s¹p¹ occupancy. Still higher in energy are the excited covalent structures, Φ_cov* where adjacent pairs of atoms involve p¹p¹ occupancy due to excitations from s to p on these atoms. The FM-bonding arises due to mixing of the ionic and excited covalent configurations into the repulsive all-s structure. The ionic structures were shown to be crucial for attaining net bonding. The Φ_ion–Φ_cov mixing is inversely proportional to the energy gap, ΔE_cov–ion, between the corresponding configurations. The smaller the gap, the stronger the mixing and the more significant is the FM-bonding. An important factor that sets the gap, ΔE_cov–ion, is the electrostatic stabilization of the ionic structures. Since the ionic radii of sodium (Na⁺ and ³Na⁻) are significantly larger than those of lithium, ionic structures of the sodium cluster will undergo a much lesser electrostatic stabilization compared with the lithium case. Indeed, the computed energy gaps show a much smaller ΔE_cov–ion for the lithium tetramer. Consequently, the Φ_cov–Φ_ion mixing in sodium will be much smaller than in lithium. The resulting ferromagnetic bond energy, BDE(FM) will accordingly be much smaller for sodium. The weakening in Φ_cov–Φ_ion mixing for ⁵Na₄ will in turn correspond to a diminished p-contribution to FM-bonding in ⁵Na₄ and in general in high-spin sodium clusters, ⁿ⁺¹Na_n, compared with their lithium analogs, ⁿ⁺¹Li_n.

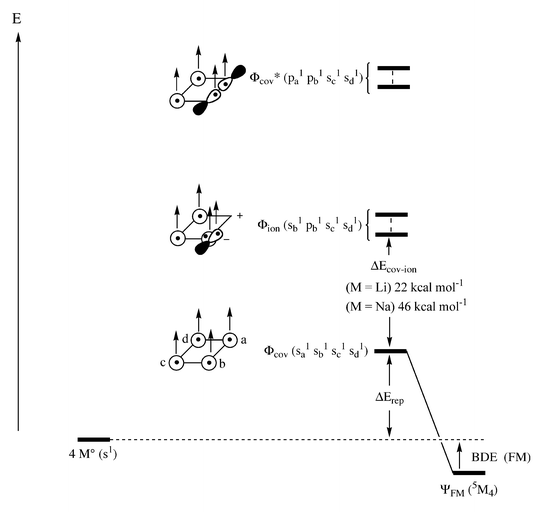Fig. 6 The mixing of covalent (Φ_cov) structure with higher lying ionic (Φ_ion) and excited covalent (Φ_cov*) structures to generate a bonding wave function (Ψ_FM) for ⁵M₄ (M = Li, Na). The occupancies of one Φ_ion and Φ_cov configurations are shown explicitly.

Conclusions

A DFT study of high-spin sodium clusters is performed for the first time, yielding an extended set of FM-bond energies and structures. In contrast to high-spin lithium clusters, the corresponding sodium clusters are weakly bound. The differences between high-spin lithium and sodium clusters are associated with the relative ordering of the molecular orbitals and derive from the longer Na–Na distances in comparison with Li–Li. Due to the shorter Li–Li distances the 2pσ orbitals cross below the 2sσ* type orbitals and become populated. This endows the high-spin lithium clusters with a significant FM-bonding energy. In high-spin sodium clusters, on the contrary, the distances are longer and the 3pσ orbitals remain higher than the 3sσ* orbitals. Therefore, the set of singly occupied orbitals in the high-spin clusters contain the same number of bonding as antibonding orbitals, hence causing the high-spin sodium clusters to be only marginally stable. Using a VB description^2,4 the diminished p-contribution to the FM-bonding is associated with a smaller-extent of mixing of the ionic structures into the all s-covalent structure (Fig. 6).

Except for the quantitative aspect, the high-spin sodium and lithium clusters exhibit the same general trends. In both cases, the FM-bond energy per atom increases with the cluster size and converges at clusters with 10–12 atoms. Furthermore, in both cases the clusters tend to maximize the coordination number of the constituent atoms in order to optimize FM-bonding. Although going from lithium to sodium caused weakening of ferromagnetic bonding, this may not necessarily be the case when going further down to potassium as nonregularities are often observed down a column in the periodic table.²⁸ Important new factors such as 3d and 4f contractions, as well as relativistic effects may disturb the regularity. Therefore, further mapping of the occurrence and strength of ferromagnetic bonding will have to follow in order to explore FM-bonding trends in the periodic table.

Acknowledgements

The authors wish to thank the Ministry of Sciences of the Niedersachsen States and the Robert Szold Fund for support.

References

1. M. N. Glukhovtsev and P. von Ragué Schleyer, Isr. J. Chem., 1993, 33, 455.
2. D. Danovich, W. Wu and S. Shaik, J. Am. Chem Soc., 1999, 121, 3165.
3. S. P. de Visser, Y. Alpert, D. Danovich and S. Shaik, J. Phys. Chem. A, 2000, 104, 11 223.
4. S. P. de Visser, D. Danovich, W. Wu and S. Shaik, J. Phys. Chem. A, 2002, 106, 4961.
5. M. H. McAdon and W. A. Goddard III, J. Phys. Chem., 1988, 92, 1352.
6. D. D. Konowalow, M. E. Rosenkrantz and M. L. Olson, J. Chem. Phys., 1980, 72, 2612.
7. D. D. Konowalow and M. E. Rosenkrantz, J. Phys. Chem., 1982, 86, 1099.
8. E. J. Friedman-Hill and R. W. Field, J. Chem. Phys., 1992, 96, 2444.
9. T.-S. Ho, H. Rabitz and G. Scoles, J. Chem. Phys., 2000, 112, 6218.
10. M. Gutowski, J. Chem. Phys., 1999, 110, 4695.
11. J. Higgins, C. Callegari, J. Reho, F. Stienkemeier, W. E. Ernst, M. Gutowski and G. Scoles, J. Phys. Chem. A, 1998, 102, 4952.
12. J. Higgins, C. Callegari, J. Reho, F. Stienkemeier, W. E. Ernst, K. K. Lehmann, M. Gutowski and G. Scoles, Science, 1996, 273, 629.
13. J. Higgins, W. E. Ernst, C. Callegari, J. Reho, K. K. Lehmann and G. Scoles, Phys. Rev. Lett., 1996, 77, 4532.
14. J. Higgins, T. Hollebeek, J. Reho, T.-S. Ho, K. K. Lehmann, H. Rabitz, G. Scoles and M. Gutowski, J. Chem. Phys., 2000, 112, 5751.
15. J. H. Reho, J. Higgins, M. Nooijen, K. K. Lehmann and G. Scoles, J. Chem. Phys., 2001, 115, 10 265.
16. F. R. Brühl, R. A. Miron and W. E. Ernst, J. Chem. Phys., 2001, 115, 10 275.
17. A. Fiortti, D. Comparati, A. Crubelier, O. Dulieu, F. Mansou-Seeuws and P. Pillet, Phys. Rev. Lett., 1998, 80, 4402.
18. Gaussian 98, Revision A.9, Gaussian Inc., Pittsburgh PA, 1998.
19. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
20. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822.
21. T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007.
22. D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 98, 1358.
23. D. E. Woon, private communication.
24. J. P. Perdew and Y. Wang, Phys. Rev. B, 1992, 45, 13 244.
25. F. Gardet, F. Rogemond and H. Chermette, J. Chem. Phys., 1996, 105, 9933.
26. V. Bonacic-Koutecky, P. Fantucci and J. Koutecky, Chem. Rev., 1991, 91, 1035.
27. W. Wu, L. Song, Y. Mo and Q. Zhang, XIAMEN—an ab initio spin-free valence bond program, Xiamen University, Xiamen, P. R. of China.
28. P. Pyykkö, Int. J. Quantum Chem., 2001, 85, 18.

---