A phase transition in H2O due to electrostriction pressure
Received
26th April 2002
, Accepted 29th October 2002
First published on 15th November 2002
Abstract
It is predicted that water at ambient conditions should undergo a phase transition to a dense phase of H2O at a transition value Πt of the local electrostriction pressure. The transition is accompanied by a latent heat as well as discontinuity in entropy and electric field. The values of the field in which recent X-ray scattering at a charged RuO2/water interface revealed phase transitions to very dense ordered H2O layers are met without adjustable parameters. The latent heat has been observed earlier at a Hg/aqueous electrolyte interface. An attempt at an explanation of the hydration of Sr2+ ions is undertaken.
1 Introduction
The phase behaviour of water in high electric field seems to be an important open question in physics. Recently, specular X-ray scattering investigation1,2 of water at a charged Ag electrode revealed water layers polarized and compressed to a density as high as twice the normal one. This observation has been explained qualitatively by the authors1,2 and later quantitatively by others3 as due to electrostriction. Some intuition concerning possibly different water phases in high electric fields at ambient conditions seems to have existed since more than a decade: a “solid water layer” at the highly polar TiO2 surface4 was first reported in 1989. Very recently, by the off-specular X-ray scattering technique, it was possible to reveal phase transitions in water layers compressed vertically to the surface of a RuO2 charged electrode.5 This observation gives an incentive for a theoretical approach to the problem of phase transitions in water under the influence of an electric field.
In a preliminary short account,6 we have presented a theoretical evidence for a phase transition of water in a high field at an electrode and discussed it in the context of the recent X-ray scattering experiments.5 In the current paper, additional theoretical evidence is presented, namely a latent heat and discontinuities of entropy and permittivity at the transition point. Also, the discussion is extended to the hydration shells of ions in solution. It is argued that the origin of the hitherto unexplained peculiar behaviour of the Sr2+ ion hydration shell found in a neutron scattering study7 is related to the vicinity of the phase transition predicted in the current work. The electrostriction pressure Πt at which the transition occurs is found and the permittivity ε and relative mass density d of H2O phases are given. In the discussion of the hydration of ions infinite dilution is assumed. Ambient conditions only are admitted.
2 Method
2.1 Equilibrium condition
Water placed in a local high electric field of strength E: water in hydration shells of ions and that in the double layers at electrodes, is considered (cf.refs. 3 and 8 and references therein). It forms a common system with the remaining water localized in a weak field or outside the field. The thermodynamic law describing the state of this system is the equilibrium condition with respect to the mass transport between the regions within and outside the field. It follows from the condition of equality of the chemical potentials ζ:| | ζi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζo. ζo. | (1) |
Henceforth, the superscripts i and o mark the quantities inside and outside the field, respectively. The chemical potential of a water molecule placed in a high electric field is reduced by ζW with respect to that of a molecule outside the field. To attain an equilibrium, the potential gradient thus created induces the pull of the dipoles into the field. We are interested in a new equilibrium state with water density increased in the high field (say, in the first hydration shell of the ion, or in a double layer) due to this process. The work L related to water compression in the field, the electrostriction work, enhances the chemical potential of water by ζL. After reaching the equilibrium, the latter compensates the negative increment ζW: | | −ζW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζL. ζL. | (2) |
With the electrostriction effect as a connection between the mechanical (mass density) and electric (electric field strength) quantities, and the experimental X-ray data of refs. 1 and 2 at hand, there arises a possibility to find the electric characteristics of the first layer of molecules (and possibly ions) at the electrode. This has been done in ref. 9 profiting from the fact that the mass density–charge density relationship was derived previously in ref. 3. Note that eqn. (19) below (obtained from a detailed form of eqn. (2)) allowing calculation of some parameters of the system from the values of other parameters represents an equation of state. In the current work it will be shown that the same equation that relates electric quantities with the mechanical ones implies the existence of a phase transition: normal water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) compressed H2O. Note that very recently new X-ray data on the RuO2/water interface were interpreted as evidence of phase transitions in water monolayers in a high electric field via changes in the chemical potential.5
compressed H2O. Note that very recently new X-ray data on the RuO2/water interface were interpreted as evidence of phase transitions in water monolayers in a high electric field via changes in the chemical potential.5
2.2 Equation of state of H2O expressed in the variables T, Π, E
The change in the chemical potential ζW is calculated in a way similar to that described earlier.3,8 The strength E of the field around the ions (Coulomb field) is | |  | (3) |
q is the elementary charge, ε is the permittivity, ε0 is the permittivity of vacuum, x is a reduced distance from the centre of the ion x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r|Z|−1/2, r is a distance from the centre of the ion and Z is the number of excess elementary charges of an ion (valence). In the immediate neighbourhood of the electrode (first layer of water molecules, the Helmholtz layer) the field strength E is
r|Z|−1/2, r is a distance from the centre of the ion and Z is the number of excess elementary charges of an ion (valence). In the immediate neighbourhood of the electrode (first layer of water molecules, the Helmholtz layer) the field strength E is | |  | (4) |
where σ0 is the surface charge density on the electrode.
The work W done by the electric field is:3,8
| |  | (5) |
V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
const. is the volume of the system,
V d
y is the increment of the polarization of the whole system. The increment of the grand free energy,
i.e., grand potential
Ω
(related to the canonical grand partition function,
cf.ref. 10a, §24) is:
where
N is the number of molecules in the volume
V.
Let us introduce the notation
| |  | (7) |
The work W performed leads to a change ΔΩ in the value of the grand potential Ω of water
| | 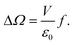 | (8) |
For ζW, the change in ζ as a result of the work W, one obtains
| |  | (9) |
The increment
| | 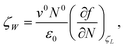 | (10) |
where
v0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V
V/
N0 and
N0 is the Avogadro number. The volume
V of the system is taken as equal to the molar volume of
water at ambient conditions. It follows from
eqn. (10) that
| | 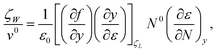 | (11) |
where
The derivatives (∂σ/∂ε) and (∂ε/∂N) have been calculated in a way similar to that given in ref. 3. They are obtained basing on our so called statistical model approach to the permittivity of hydrogen bonded liquids (including water) proposed earlier11,12 at relatively low temperatures (close to the melting temperature; this includes the ambient temperature). The mean cosine 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 of the angle θ between the direction of the external field E and the electric dipole moment μ of the water molecule has to be expressed by the hyperbolic tangent and not the Langevin function. In the hydration shells and double layers the strengths of the electric field are so high that the linear approximation to 〈cos
θ〉 of the angle θ between the direction of the external field E and the electric dipole moment μ of the water molecule has to be expressed by the hyperbolic tangent and not the Langevin function. In the hydration shells and double layers the strengths of the electric field are so high that the linear approximation to 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 is no longer sufficient, and the mean cosine has to be expressed by the full tanh function and not the first term in its expansion in a power series. The relation between the permittivity ε and the electric field strength E is, according to the Onsager field model (cf. Section 5 below for the question of the Onsager field in discrete systems), expressed as
θ〉 is no longer sufficient, and the mean cosine has to be expressed by the full tanh function and not the first term in its expansion in a power series. The relation between the permittivity ε and the electric field strength E is, according to the Onsager field model (cf. Section 5 below for the question of the Onsager field in discrete systems), expressed as
| |  | (12) |
where 〈cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ〉
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
=
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
tanh(
Ξ),
n is the refraction index and
where
k is the Boltzmann constant. From
eqn. (12) we obtain the derivatives occurring in
eqn. (11):
| |  | (13) |
and
| |  | (14) |
Let us now turn to the change in the chemical potential ζL due to the compression work L which, according to eqn. (2) shall compensate ζW. The compression work L is calculated, similarly as in refs. 3 and 8, by integrating the area under the isotherm V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V(P) with P pressure:
V(P) with P pressure:
| |  | (15) |
The change in the chemical potential ζL due to this work is
| |  | (16) |
One can re-write eqn. (2) in the form
| | 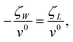 | (17) |
which, taking into account
eqns. (11) and (16), is the same as
| |  | (18) |
The integrals on the right hand sides of eqns. (16) and (18) have been found by substituting the room temperature isotherms13,14,15V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V(P) of water in the liquid, ice VI and ice VII phases under pressure P in the absence of field. Of course, the use of the data measured in the absence of the field introduces an approximation. Its validity can only be judged a posteriori, as has been done with a positive result in ref. 3. The upper integral limit (Pi, see eqn. (16)) was matched so as to fulfil eqn. (18). This is equivalent to putting the pressure value Pi in the field equal to the local electrostriction pressure value Π:
V(P) of water in the liquid, ice VI and ice VII phases under pressure P in the absence of field. Of course, the use of the data measured in the absence of the field introduces an approximation. Its validity can only be judged a posteriori, as has been done with a positive result in ref. 3. The upper integral limit (Pi, see eqn. (16)) was matched so as to fulfil eqn. (18). This is equivalent to putting the pressure value Pi in the field equal to the local electrostriction pressure value Π:
| |  | (19) |
In other words, we assume that the external pressure applied without an electric field would produce water compression comparable to that due to the local electrostriction pressure. Note that a similar approach has also been adopted by other authors, e.g., a neutron scattering experiment with isotopic substitution on a 10 M NaOH solution was said to “indicate that ions in aqueous solutions induce a change in water structure equivalent to the application of high pressure”.16
Eqn. (19) represents the equation of state of H2O in implicit variables T, Π, and E. Dependence on temperature is present through the relation ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε(T) as expressed in eqn. (12) and through introducing into eqn. (19) of the isotherm V
ε(T) as expressed in eqn. (12) and through introducing into eqn. (19) of the isotherm V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V(P) for the same temperature T, for which ε is calculated. The dependence on the value of the local electric field strength E is present through f and y
(cf.eqns. (4), (5) and (7)). The electrostriction pressure Π
V(P) for the same temperature T, for which ε is calculated. The dependence on the value of the local electric field strength E is present through f and y
(cf.eqns. (4), (5) and (7)). The electrostriction pressure Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pi is a local quantity, too.
Pi is a local quantity, too.
We have dropped the subscripts T and V in the eqns. (10), (11), (13), (14), (18) and (19), keeping in mind that isothermal and constant volume conditions are maintained throughout this study.
2.3 Change of entropy ΔS in the field E. Electrocaloric effect
In addition to electrostriction, the field E induces also a change ΔS in entropy of the system:17,18,10 The entropy change in the process of water adapting itself to the high field conditions is: | |  | (20) |
The quantity f
(see eqn. (7)) depends on temperature viaε(T). Eqn. (20) takes the form:
| |  | (21) |
From the latter equation it is possible to derive the expression ΔQ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TΔS for the heat absorbed by the dielectric substance during a change in the electric field (related to the appearance of an ion inside the water) at a constant temperature:
TΔS for the heat absorbed by the dielectric substance during a change in the electric field (related to the appearance of an ion inside the water) at a constant temperature:
| |  | (22) |
If (∂ε/∂T)y,ζL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, which is usually the case, we have ΔQ
0, which is usually the case, we have ΔQ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and ΔS
0 and ΔS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. Thus, heat is evolved by the dielectric and given off to the heat bath. At the same time the entropy decreases, that is the field orders the directions of the dipoles of the system. The release of heat by the dielectric as a consequence of a change in the applied field in isothermal conditions is called the isothermal electrocaloric effect. The heat due to this effect will be found from eqn. (22). The product of the derivatives:
0. Thus, heat is evolved by the dielectric and given off to the heat bath. At the same time the entropy decreases, that is the field orders the directions of the dipoles of the system. The release of heat by the dielectric as a consequence of a change in the applied field in isothermal conditions is called the isothermal electrocaloric effect. The heat due to this effect will be found from eqn. (22). The product of the derivatives:
is known from
eqns. (11) and (13). The derivative (∂
ε/∂
T)
y,ζL will be calculated from
eqn. (24) below.
As already shown (eqn. (21)), the expression for ΔS related to the electrocaloric effect contains the derivative ∂ε/∂T. Locally, neither this quantity nor ε itself are known from experiment. Hence, the necessity of a theoretical approach arises.
Taking into account that
we obtain from
eqn. (12) the following:
| |  | (23) |
From the latter implicit formula (eqn. (23)) of permittivity ε as a function of temperature T, the derivative ∂ε/∂T is found for various field strengths. After some algebra one arrives at the formula:
| |  | (24) |
where
σ is given by
eqns. (3) and (4) and
αp is the thermal expansion coefficient. The values of
αp were taken from
ref. 19; For local electrostriction pressures exceeding 10
8 Pa we applied the values of
αp extrapolated from the data of
ref. 19. The electrocaloric effect accompanying the changes in entropy of
water in the field of ions is the subject of
ref. 20, where consistency with the experimental results obtained by the electrospray method
21 as well as a density functional calculation
22 is discussed.
3 Phase transition in H2O induced by an electrostriction pressure Π
The left hand side of eqn. (19) is equal to −ζW/v0. The quantity −ζW/v0 is plotted in Fig. 1 as a function of x, which in turn is related to the field strength E
(cf.eqn. (3)). A kink is apparent in the plot of −ζW(x)/v0 in Fig. 1 at −ζW/v0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.17
0.17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 J m−3 about the value of the argument x
109 J m−3 about the value of the argument x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.2 Å. The 293 K isotherm v(P) in the integral on the right hand side of eqn. (19) concerns liquid water under pressures from atmospheric to about 1 GPa and is taken from ref. 15. The integral of v(P)dP is a continuous function. Hence, the electrostriction pressure Π
2.2 Å. The 293 K isotherm v(P) in the integral on the right hand side of eqn. (19) concerns liquid water under pressures from atmospheric to about 1 GPa and is taken from ref. 15. The integral of v(P)dP is a continuous function. Hence, the electrostriction pressure Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Π(x) as a function of x plotted in Fig. 2 reveals a plateau stemming from that kink viaeqn. (19). A simple interchange of coordinate axes from Π as a function of x
(or E) into x
(or E) as a function of Π shows that the plateau of Π(x) becomes a jump of x(Π)
(or E(Π)) at the transition value Πt of the electrostriction pressure. The result of the interchange of coordinates for the case of E is shown in Fig. 3.
Π(x) as a function of x plotted in Fig. 2 reveals a plateau stemming from that kink viaeqn. (19). A simple interchange of coordinate axes from Π as a function of x
(or E) into x
(or E) as a function of Π shows that the plateau of Π(x) becomes a jump of x(Π)
(or E(Π)) at the transition value Πt of the electrostriction pressure. The result of the interchange of coordinates for the case of E is shown in Fig. 3.
 |
| | Fig. 1 −ζW/vo as a function of the reduced distance x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r|Z|−1/2 from the centre of the ion (cf.eqn. (11)). r|Z|−1/2 from the centre of the ion (cf.eqn. (11)). | |
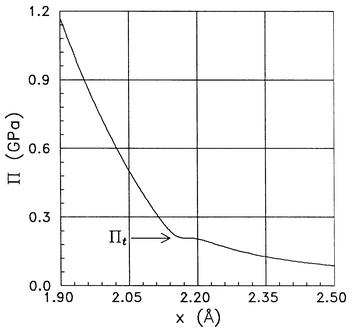 |
| | Fig. 2 Electrostriction pressure Π(x) as a function of the reduced distance x from the centre of the ion. The arrow marks the transition value Πt of the electrostriction pressure. | |
 |
| | Fig. 3 Electric field strength E(Π) as a function of the electrostriction pressure. The numbers in the brackets mark the coordinates (Π,E) of the lower and upper limits of the discontinuity at the transition value Πt of the electrostriction pressure. | |
By definition, a first-order phase transition is characterized by a finite discontinuity in a first derivative of the grand potential Ω
(cf.eqn. (6)). Hence, one can expect discontinuities in the electric field strength and entropy:
| |  | (25) |
The variable responsible for the transition is the electrostriction pressure Π, related to the remaining state variables by eqn. (19). From eqn. (19) the relation E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(Π) shown in Fig. 3 has been found. The plot shows that an electric field strength discontinuity occurs at Πt
E(Π) shown in Fig. 3 has been found. The plot shows that an electric field strength discontinuity occurs at Πt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.208 GPa (≈0.21 GPa), where the subscript t stands for transition. The range of the discontinuity (Fig. 3) is 0.77
0.208 GPa (≈0.21 GPa), where the subscript t stands for transition. The range of the discontinuity (Fig. 3) is 0.77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36 (109 V m−1). In other words, an increase in the electric field strength E from 0.77 to 1.36 (109 V m−1) does not change the value of the electrostriction pressure Π. At Πt and at a value of E comprised in this range two phases coexist.
1.36 (109 V m−1). In other words, an increase in the electric field strength E from 0.77 to 1.36 (109 V m−1) does not change the value of the electrostriction pressure Π. At Πt and at a value of E comprised in this range two phases coexist.
From eqns. (19) and (21) the dependence of entropy change −ΔS(Π) on Π in Fig. 4 has been obtained. A discontinuity in entropy at Πt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.21 GPa is seen. The range of this discontinuity is: 0.97
0.21 GPa is seen. The range of this discontinuity is: 0.97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |ΔS|
|ΔS|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.9 (J mol−1 K−1), and is accompanied by a latent heat of −277 J mol−1. On increasing Π from a value equal to atmospheric pressure up to 0.1 GPa (E
1.9 (J mol−1 K−1), and is accompanied by a latent heat of −277 J mol−1. On increasing Π from a value equal to atmospheric pressure up to 0.1 GPa (E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4
0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 V m−1), the entropy of the system of dipoles decreases (cf.Fig. 4) due to the process of orientational ordering of the dipoles. On the further increase of Π up to the value Πt
109 V m−1), the entropy of the system of dipoles decreases (cf.Fig. 4) due to the process of orientational ordering of the dipoles. On the further increase of Π up to the value Πt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.21 GPa entropy increases: the lowering of entropy due to the process of orientational ordering of the dipoles is overwhelmed by its increase. At Π
0.21 GPa entropy increases: the lowering of entropy due to the process of orientational ordering of the dipoles is overwhelmed by its increase. At Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Πt one can notice a discontinuous increase in entropy due to the coexistence of two phases. On further increasing Π
Πt one can notice a discontinuous increase in entropy due to the coexistence of two phases. On further increasing Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Πt the entropy of the newly created phase decreases.
Πt the entropy of the newly created phase decreases.
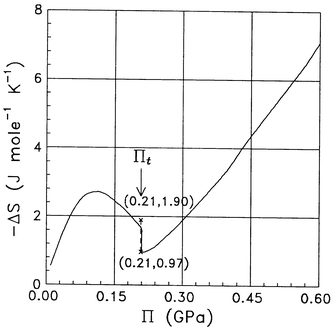 |
| | Fig. 4 Change in entropy −ΔS(Π) as a function of the electrostriction pressure. The numbers in the brackets mark the coordinates (Π,−ΔS) of the lower and upper limits of the discontinuity at the transition value Πt of the electrostriction pressure. | |
It is important to note that the value of Πt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.21 GPa corresponds neither to water
0.21 GPa corresponds neither to water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VI nor ice VI
ice VI nor ice VI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VII transitions under external pressure. In Fig. 5, along the line marked d, the d(P) data points are shown corresponding to the values of the pressure Π
ice VII transitions under external pressure. In Fig. 5, along the line marked d, the d(P) data points are shown corresponding to the values of the pressure Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pi found with the help of eqn. (19) from the experimental data of refs. 13–15. Between parts of the line with dense points two gaps are seen corresponding to water
Pi found with the help of eqn. (19) from the experimental data of refs. 13–15. Between parts of the line with dense points two gaps are seen corresponding to water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VI (marked by 1) and ice VI
ice VI (marked by 1) and ice VI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VII (marked by 2) transitions under pressure Pi applied in no field (E
ice VII (marked by 2) transitions under pressure Pi applied in no field (E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0). They are far apart the discontinuity in ε
0). They are far apart the discontinuity in ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε(Πt) characteristic of the phase transition found in this study. Hence, the discontinuous phase transition found above is not an artifact resulting from the use of the input data.
ε(Πt) characteristic of the phase transition found in this study. Hence, the discontinuous phase transition found above is not an artifact resulting from the use of the input data.
 |
| | Fig. 5 Relative mass density d(P) as a function of pressure and permittivity ε
(Π) as a function of electrostriction pressure. Discontinuity in permittivity ε is marked by an arrow, numbers 1 and 2 mark the water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VI and ice VI ice VI and ice VI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → →![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VII transitions, respectively. The points at the line marked d represent the input data based on the experiment13–15
(see text). ice VII transitions, respectively. The points at the line marked d represent the input data based on the experiment13–15
(see text). | |
Some limited similarity can be noted between the phase transition described here and the transition ice VII![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VIII for which no change in the molar volume was observed (ref. 19, Table 3.6 therein): Δv
ice VIII for which no change in the molar volume was observed (ref. 19, Table 3.6 therein): Δv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.000
0.000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0005 cm3 mol−1 and ΔQ
0.0005 cm3 mol−1 and ΔQ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 kJ mol−1. Ice VIII is an ordered form of ice VII.
1 kJ mol−1. Ice VIII is an ordered form of ice VII.
4 Comparison with experiment
To come close to a phase transition due to the electrostriction pressure Πt one should essentially vary electric field strength E in a continuous way. It is feasible in a limited range by a gradual charging of an electrode immersed in an electrolyte as done, e.g., in the X-ray scattering experiments.1,2,5 Although the earlier publications reporting experiments of this kind1,2 provided results for two discrete field values only, the very recent investigations are more detailed and indeed phase transitions were observed “under the extremely high interfacial electric field (∼109 V/m)”.5 It appears helpful for applying our considerations to neutron scattering studies of ions in D2O solution to apply the variable x as an abscissa when plotting the isotherm of Π. Fig. 2 presents the isotherm Π(x) at 293 K as a function of the reduced distance x from the centre of an ion, a quantity related to the field strength E
(cf.eq. (3) and Table 1). Note that with increasing x the field strength E decreases (eqn. (3)). In the plot of Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Π(x) in Fig. 2, the discontinuity in the electric field strength is extended over the range of x from 2.154 Å
Π(x) in Fig. 2, the discontinuity in the electric field strength is extended over the range of x from 2.154 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å. For x
2.217 Å. For x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.154 Å, water is in phase A with complete orientational order due to the field (cf.ref. 23, Table 1 therein). The plots of the relations Π
2.154 Å, water is in phase A with complete orientational order due to the field (cf.ref. 23, Table 1 therein). The plots of the relations Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Π(x) are steeper for x
Π(x) are steeper for x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.154 Å than for x
2.154 Å than for x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å. For x
2.217 Å. For x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å one finds phase B with incomplete orientational order (ref. 23, Table 1). In addition to the x discontinuity, the change in slope of the isotherm plotted in Fig. 2 can be interpreted as testifying to a phase transition: phase A
2.217 Å one finds phase B with incomplete orientational order (ref. 23, Table 1). In addition to the x discontinuity, the change in slope of the isotherm plotted in Fig. 2 can be interpreted as testifying to a phase transition: phase A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) phase B under the electrostriction pressure Πt
phase B under the electrostriction pressure Πt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.21 GPa. A rich series of experimental results can be found in literature on hydration shells of various ions. The fields acting on their hydration shells are E
0.21 GPa. A rich series of experimental results can be found in literature on hydration shells of various ions. The fields acting on their hydration shells are E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.77
0.77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 V m−1
(x
109 V m−1
(x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å) as well as E
2.217 Å) as well as E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36
1.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 V m−1
(x
109 V m−1
(x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.154 Å). Hence, we consider it sound to provide a discussion of literature neutron scattering experiments (Subsection 4.2) and relate them to the present results. We argue that the phase of H2O compressed in a high field can represent a layer (close to a monomolecular layer) at an electrode,5 or portions of a phase dispersed in space in the form of hydration shells of ions.
2.154 Å). Hence, we consider it sound to provide a discussion of literature neutron scattering experiments (Subsection 4.2) and relate them to the present results. We argue that the phase of H2O compressed in a high field can represent a layer (close to a monomolecular layer) at an electrode,5 or portions of a phase dispersed in space in the form of hydration shells of ions.
Table 1 Lower and upper values of the electric field strength E, change in entropy −ΔS, permittivity ε and reduced distance x at discontinuity
|
E
(109 V m−1) |
0.77 |
1.36 |
| −ΔS
(J mol−1 K−1) |
1.90 |
0.97 |
|
ε
|
38 |
22.8 |
|
x
(10−10 m) |
2.217 |
2.154 |
4.1 Comparison with X-ray surface scattering studies
As discussed in a preliminary short account,6 the results obtained on the basis of the thermodynamic and electrostatic approach applied in the current work may be related to very recently reported phase transitions at the RuO2/water interface.5 Here, we present additional theoretical evidence of a phase transition in H2O at the conditions encountered in the experiment.5 This new evidence is shown in Figs. 4, 5 and 2. As previously noted, the transition field strength range: 0.77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36 (109 V m−1) found in this study and seen in Fig. 3 at the transition value Πt of the electrostriction pressure falls well in the range where the phase transitions were observed by Chu et al..5 The discontinuous transition at the same Πt value is seen in entropy change (Fig. 4) and permittivity (Fig. 5) plots, too. Also, the calculated mass density of the compressed H2O phase can be shown by using methods developed earlier3 to attain the observed twice the ambient water density and more than that.1,5
1.36 (109 V m−1) found in this study and seen in Fig. 3 at the transition value Πt of the electrostriction pressure falls well in the range where the phase transitions were observed by Chu et al..5 The discontinuous transition at the same Πt value is seen in entropy change (Fig. 4) and permittivity (Fig. 5) plots, too. Also, the calculated mass density of the compressed H2O phase can be shown by using methods developed earlier3 to attain the observed twice the ambient water density and more than that.1,5
4.2 Comparison with the neutron scattering studies
To the electrostriction pressure Πt
(Fig. 2) there corresponds an electric field strength range 0.77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36 (109 V m−1)
(or a reduced radial distance range 2.154 Å
1.36 (109 V m−1)
(or a reduced radial distance range 2.154 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å). It will be argued that the discontinuity of the transition which allows for a whole range of x to correspond to the transition value Πt of the electrostriction pressure explains the destroyed hydration structure phenomenon of Sr2+ ion (ref. 24 and references cited therein). The calculated properties of the phases A and B are in our opinion also consistent with the known results of neutron scattering studies of other ions in D2O solution. These results for shells in phase A and B conform to an additivity rule. Marcus25 has indicated the following additivity relation between the distance ion-water (r1, equal to the radius of the first hydration shell) and the ionic radius Rion, as well as the radius of a water molecule (Rwater
2.217 Å). It will be argued that the discontinuity of the transition which allows for a whole range of x to correspond to the transition value Πt of the electrostriction pressure explains the destroyed hydration structure phenomenon of Sr2+ ion (ref. 24 and references cited therein). The calculated properties of the phases A and B are in our opinion also consistent with the known results of neutron scattering studies of other ions in D2O solution. These results for shells in phase A and B conform to an additivity rule. Marcus25 has indicated the following additivity relation between the distance ion-water (r1, equal to the radius of the first hydration shell) and the ionic radius Rion, as well as the radius of a water molecule (Rwater![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4 Å): Hence, the corresponding reduced distance
1.4 Å): Hence, the corresponding reduced distance| |  | (27) |
4.2.1 Transition behaviour of a hydration shell: destroyed hydration structure of the Sr2+ ion.
The lack of resolved two peak structure in the neutron scattering radial distribution function (RDF) of hydration shells of ions together with the accompanying lack of additivity of the ion and H2O radii (violation of eqn. (26)) has been found in the shell of Ni2+ ion at 573 K and called destroyed hydration structure.26,27 A RDF showing destroyed hydration structure characteristics had been found earlier in ref. 7 by the neutron scattering method for the Sr2+ ions at ambient conditions (see Fig. 6b), although at the time the term “destroyed hydration structure” was not coined yet. The radial distribution function GSr(x) about the Sr2+ ions is characterized by a single broad peak centered at x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.23 Å. This value does not fulfill eqn. (27), which indicates a lack of additivity of ionic and molecular radii. The discontinuity in x
(2.154 Å
2.23 Å. This value does not fulfill eqn. (27), which indicates a lack of additivity of ionic and molecular radii. The discontinuity in x
(2.154 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å) at Πt falls entirely within a broader range of x values under the single broad peak of the neutron scattering RDF GSr(x)
(Fig. 6b). Let us recall that in our description the state of H2O in the hydration shell is defined by the state variables T,Π,x . To each value of Π on the 293 K isotherm Π(x) in Fig. 2 there corresponds a given x value except for Πt, where x takes any value along the segment 2.154 Å
2.217 Å) at Πt falls entirely within a broader range of x values under the single broad peak of the neutron scattering RDF GSr(x)
(Fig. 6b). Let us recall that in our description the state of H2O in the hydration shell is defined by the state variables T,Π,x . To each value of Π on the 293 K isotherm Π(x) in Fig. 2 there corresponds a given x value except for Πt, where x takes any value along the segment 2.154 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å. We propose an interpretation of the apparently hitherto unexplained peculiar character of the neutron scattering RDF called the destroyed hydration structure: RDF smearing and lack of additivity of ionic and water radii. According to this interpretation, it can be a consequence of a discontinuity in x at the phase transition point. In such a case water in the neighbourhood of the ion is in the state determined by Πt and a water molecule can choose any possible value of the reduced radius x along the segment (Fig. 2) mentioned above. Hence, there is no specific unique value of xt corresponding to Πt, but any x value in the range of the segment is acceptable instead. As follows, H2O molecules in this state can statistically take positions in different distances from the ion. This statistical freedom of taking different distances results in the effect called destroyed hydration structure: the peaks in RDF attributed to oxygen and deuterium are smeared and shifted so as to give a common broad peak with a maximum not fulfilling the criterion given by eqn. (26). Now, as we have drawn a picture of hydration of Sr2+ ions in terms of a state at the transition between two H2O phases (A and B), what would be the meaning of these phases in the hydration problem of other ions? This will be the subject of the two next paragraphs.
2.217 Å. We propose an interpretation of the apparently hitherto unexplained peculiar character of the neutron scattering RDF called the destroyed hydration structure: RDF smearing and lack of additivity of ionic and water radii. According to this interpretation, it can be a consequence of a discontinuity in x at the phase transition point. In such a case water in the neighbourhood of the ion is in the state determined by Πt and a water molecule can choose any possible value of the reduced radius x along the segment (Fig. 2) mentioned above. Hence, there is no specific unique value of xt corresponding to Πt, but any x value in the range of the segment is acceptable instead. As follows, H2O molecules in this state can statistically take positions in different distances from the ion. This statistical freedom of taking different distances results in the effect called destroyed hydration structure: the peaks in RDF attributed to oxygen and deuterium are smeared and shifted so as to give a common broad peak with a maximum not fulfilling the criterion given by eqn. (26). Now, as we have drawn a picture of hydration of Sr2+ ions in terms of a state at the transition between two H2O phases (A and B), what would be the meaning of these phases in the hydration problem of other ions? This will be the subject of the two next paragraphs.
 |
| | Fig. 6 Total cation (Ni2+, Mg2+, Sr2+ and K+) distribution functions GNi(x) and GMg(x)
(Ni2+ is isomorphic with Mg2+ in D2O solution), GSr
(x) and GK
(x)
(in barn sr−1); after ref. 24. | |
4.2.2 Phase A with complete orientational order due to the field.
Fig. 6a shows the total RDF's GNi(x) and GMg(x)
(Ni2+ is isomorphic with Mg2+ in aqueous solution) typical of cations with the reduced radii x1 of the first hydration shells x1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.154 Å. The first of the two sharp peaks in the plot of GNi(x) is attributed to the distance Ni–O (cation–oxygen of heavy water molecule), the other one, to Ni–D. Such a shape of the function Gcation(x) follows the well-defined hydration structures in solution. The additivity relation (eqn. (27)) is well fulfilled by such ions. These are ions with double, triple (and larger) elementary charge with addition of Li+
(cf.ref. 25, table XIII therein). Ni2+ and Mg2+ form fairly well-defined long-lived24 hydration structure in solutions. These characteristics of the well-defined hydration structures24
(first hydration shell), learned from the RDF’s, is consistent with the characteristics of phase A following from our approach: its 〈cos
2.154 Å. The first of the two sharp peaks in the plot of GNi(x) is attributed to the distance Ni–O (cation–oxygen of heavy water molecule), the other one, to Ni–D. Such a shape of the function Gcation(x) follows the well-defined hydration structures in solution. The additivity relation (eqn. (27)) is well fulfilled by such ions. These are ions with double, triple (and larger) elementary charge with addition of Li+
(cf.ref. 25, table XIII therein). Ni2+ and Mg2+ form fairly well-defined long-lived24 hydration structure in solutions. These characteristics of the well-defined hydration structures24
(first hydration shell), learned from the RDF’s, is consistent with the characteristics of phase A following from our approach: its 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉
θ〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ε
1, ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23, and it is compressed: d
23, and it is compressed: d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The densities of the hydration shells calculated within the present approach can be expressed in terms of coordination numbers of specific ions and have been reported elsewhere.8 The values of coordination numbers calculated in ref. 8 compared well with literature data. Thus we conclude that although there are other ways of looking at the hydration of the above class of ions, the picture involving the concept of the phase (A) of water in a field does not conflict with the known data and can be treated at least as a complementary one.
1. The densities of the hydration shells calculated within the present approach can be expressed in terms of coordination numbers of specific ions and have been reported elsewhere.8 The values of coordination numbers calculated in ref. 8 compared well with literature data. Thus we conclude that although there are other ways of looking at the hydration of the above class of ions, the picture involving the concept of the phase (A) of water in a field does not conflict with the known data and can be treated at least as a complementary one.
4.2.3 Phase B with incomplete orientational order.
The comparable data for K+ are shown in Fig. 6c. The reduced radius of its first hydration shell is x1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å. The RDF GK(x) is characterized by a single maximum,24 whose position is close to the reduced distance x1
2.217 Å. The RDF GK(x) is characterized by a single maximum,24 whose position is close to the reduced distance x1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.8 Å, obtained from eqn. (27). From Table XIII in ref. 25, it follows that ions bearing single elementary charges (for which x1
2.8 Å, obtained from eqn. (27). From Table XIII in ref. 25, it follows that ions bearing single elementary charges (for which x1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å) fulfil eqn. (27), too. The absence of clearly resolved peaks in GK(x) is a clear evidence that K+ is weakly hydrated. This characteristics of weakly hydrated ions24 read from GK(x) is consistent with the characteristics of phase B following from our approach: 〈cos θ〉
2.217 Å) fulfil eqn. (27), too. The absence of clearly resolved peaks in GK(x) is a clear evidence that K+ is weakly hydrated. This characteristics of weakly hydrated ions24 read from GK(x) is consistent with the characteristics of phase B following from our approach: 〈cos θ〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ε
1, ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38, and there is no remarkable compression: d
38, and there is no remarkable compression: d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Again, the concept of phase B, a weakly ordered liquid water phase, does not conflict with the previous knowledge.
1. Again, the concept of phase B, a weakly ordered liquid water phase, does not conflict with the previous knowledge.
4.3 Thermal effect at the transition
Yet another study concerned the mercury/aqueous electrolyte interface. By laser temperature jump method at 293 K thermal phenomena have been observed28,29 which were interpreted by the Authors as accompanying a phase transition. In a field of strength 109 V m−1 changes in entropy S have been found of the same order of magnitude as that seen in our Fig. 4. In Fig. 4, a discontinuity in S is seen thanks to the fact that it shows −ΔS as a function of electrostriction pressure Π and not the charge surface density at the electrode, as in ref. 28. Hence, one encounters here a latent heat of a discontinuous transition. Note that if the entropy S were plotted as a function of E, its discontinuous character at the transition would not have been apparent (cf.Fig. 3 in ref. 6), since the field E itself (treated as a thermodynamic variable) also experiences a jump at the same point as S.
5 Remarks on the method
We shall discuss the statistical calculation of average quantities as applied to the case of hydrated ions. Strong electric fields generated by the charges of the ions decay rapidly with the radial distance into water according to the Coulomb law. As a consequence, the molecules within the first hydration shells are in the fields of a considerably higher strength than those outside them. In this way the first hydration shells about the ions are distinguished in respect to the field from the whole electrolyte. Taken together, the first shells form a subsystem of molecules in the same physical conditions, although they do not have a common macroscopic boundary. The chemical potentials of various parts of the system in equilibrium, including the set of the first hydration shells, the sets of the further more or less well defined shells, and the rest in zero field, are equal. The subsystem of all first shells of ions of one kind forms a macroscopically large ensemble of molecules in the same physical conditions and thus can be subjected to the procedure of statistical averaging leading to values of their thermodynamic parameters. Although dispersed in space, the set of the hydration shells can be treated in much the same way as a layer of molecular thickness in the theory of electrolytes at an electrode discussed in the current work and in refs. 3 and 30. Thus, one can derive thermodynamic quantities concerning the dispersed in space, but otherwise macroscopic, set of hydration shells by statistical methods, as done throughout this paper. Another point is the applicability of the Onsager field approximation, frequently conceived after popular textbooks as forming a part of the continuum theory,31 to discrete microscopic systems such as those considered here. Note in this context that this approximation in the statistical calculations appears in the literature of atomically discrete dielectric and magnetic systems, to mention only refs. 32–34. Let us still mention that the electric field strength E occurring in the current work represents a thermodynamic variable stemming from the statistical mechanics calculations based on our model’s assumptions in the Onsager approximation.
6 Conclusion
We have presented a theoretical evidence of a phase transition in H2O at ambient conditions in a local field of strength taking the values in the range 0.77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36 (109 V m−1). The experimental evidence of phase transitions in H2O in a high electric field has been provided by Chu et al..5 The latent heat accompanying the transition has also been observed at a Hg/aqueous electrolyte interface.28,29 The above E values fall well into the range where Chu et al.5 observed the transitions at the RuO2 electrode by synchrotron radiation X-ray scattering methods. Also, these values fall very close to the field acting on the water molecules lying at the maximum of RDF in the first hydration shell of the Sr2+ ion, which enabled us to provide a tentative explanation of its peculiar properties revealed by neutron scattering.7
1.36 (109 V m−1). The experimental evidence of phase transitions in H2O in a high electric field has been provided by Chu et al..5 The latent heat accompanying the transition has also been observed at a Hg/aqueous electrolyte interface.28,29 The above E values fall well into the range where Chu et al.5 observed the transitions at the RuO2 electrode by synchrotron radiation X-ray scattering methods. Also, these values fall very close to the field acting on the water molecules lying at the maximum of RDF in the first hydration shell of the Sr2+ ion, which enabled us to provide a tentative explanation of its peculiar properties revealed by neutron scattering.7
References
- M. F. Toney, J. N. Howard, J. Richer, G. L. Borges, J. G. Gordon, O. R. Melroy, D. G. Wiesler, D. Yee and L. B. Sorensen, Nature, 1994, 368, 444 CrossRef CAS.
- M. F. Toney, J. N. Howard, J. Richer, G. L. Borges, J. G. Gordon, O. R. Melroy, D. G. Wiesler, D. Yee and L. B. Sorensen, Surf. Sci., 1995, 335, 326 CrossRef CAS.
- I. Danielewicz-Ferchmin and A. R. Ferchmin, J. Phys. Chem., 1996, 100, 17
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 281 CrossRef CAS.
281 CrossRef CAS.
- J. J. Kasinski, L. A. Gomez-Jahn, K. J. Faran, S. M. Gracewski and R. J. Dwayne Miller, J. Chem. Phys., 1989, 90, 1253 CrossRef CAS.
- Y. S. Chu, T. E. Lister, W. G. Cullen, H. You and Z. Nagy, Phys. Rev. Lett., 2001, 86, 3364 CrossRef CAS.
- I. Danielewicz-Ferchmin and A. R. Ferchmin, Chem. Phys. Lett., 2002, 351, 397 CrossRef CAS; I. Danielewicz-Ferchmin and A. R. Ferchmin, Chem. Phys. Lett., 2002, 358, 357 CrossRef CAS , errata.
- G. W. Neilson and R. D. Broadbent, Chem. Phys. Lett., 1990, 167, 429 CrossRef CAS.
- I. Danielewicz-Ferchmin and A. R. Ferchmin, Physica B, 1998, 245, 34 CrossRef CAS.
- I. Danielewicz-Ferchmin, A. R. Ferchmin and A. Szlaferek, Chem. Phys. Lett., 1998, 288, 197 CrossRef CAS.
-
(a)
L. D. Landau and E. M. Lifshits, Statisticheskaya fizika, Izd. Tekh.-Teor. Lit., Moscow, 1951, section 25, in Russian Search PubMed;
(b)
L. D. Landau and E. M. Lifshits, Elektrodinamika sploshnych sred, Izd. Tekh.-Teor. Lit., Moscow, 1957, section 15, in Russian Search PubMed.
- I. Danielewicz-Ferchmin, J. Phys. Chem., 1990, 94, 4335 CrossRef CAS.
- I. Danielewicz-Ferchmin and A. R. Ferchmin, J. Chem. Phys., 1998, 109, 2394 CrossRef CAS.
- A. Polian and M. Grimsditch, Phys. Rev. B, 1983, 27, 6409 CrossRef CAS.
- R. J. Hemley, A. P. Jephcoat, H. K. Mao, C. S. Zha, L. W. Finger and D. E. Cox, Nature, 1987, 330, 737 CrossRef CAS.
-
Handbook of Physical Constants, ed. Sydney P. Clark, Jr., The Geological Society of America, New York, revised edn., 1966 Search PubMed.
- F. Bruni, M. A. Ricci and A. K. Soper, J. Chem. Phys., 2001, 114, 8056 CrossRef CAS.
- H. S. Frank, J. Chem. Phys., 1955, 23, 2023 CAS.
-
C. J. F. Böttcher, Theory of Electric Polarization, Elsevier, Amsterdam, 2nd edn., 1973, vol. 1 ch. 3 Search PubMed.
-
D. Eisenberg and W. Kauzmann, Structure and Properties of Water, Oxford University Press, London, 1969 Search PubMed.
- I. Danielewicz-Ferchmin and A. R. Ferchmin, J. Solution Chem., 2002, 31, 81 Search PubMed.
- M. Peschke, A. T. Blades and P. Kebarle, J. Phys. Chem. A, 1998, 102, 9978 CrossRef CAS.
- M. Pavlov, P. E. M. Siegbahn and M. Sandström, J. Phys. Chem. A, 1998, 102, 219 CrossRef CAS.
- I. Danielewicz-Ferchmin, J. Phys. Chem., 1995, 99, 5658 CrossRef CAS.
- I. Howell, G. W. Neilson and P. Chieux, J. Mol. Struct., 1991, 250, 281 CrossRef CAS.
- Y. Marcus, Chem. Rev., 1988, 88, 1475 CrossRef CAS.
- I. Howell and G. W. Neilson, J. Chem. Phys., 1996, 104, 2036 CrossRef CAS.
- P. H. K. de Jong, G. W. Neilson and M.-C. Bellisent-Funel, J. Chem. Phys., 1996, 105, 5155 CrossRef CAS.
- V. A. Benderskii, A. M. Brodsky, G. I. Velichko, L. I. Daikhin, N. S. Lidorenko and G. F. Muchnik, Dokl. Akad. Nauk SSSR, 1986, 286(3), 648 Search PubMed.
- A. M. Brodsky and L. I. Daikhin, Elektrokhimiya, 1989, 25(4), 435 Search PubMed.
- S. Romanowski, W. Stasiak and L. Wojtczak, Electrochim. Acta, 1982, 27, 511 CrossRef CAS.
- In-Chul Yeh and M. L. Berkowitz, J. Chem. Phys., 2000, 112, 10
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 491 CrossRef CAS.
491 CrossRef CAS.
- T. Kaneyoshi, Prog. Theor. Phys., 1969, 41, 577 Search PubMed.
- T. Kaneyoshi, Prog. Theor. Phys., 1971, 45, 1340 Search PubMed.
- D. E. Logan, Y. H. Szczech and M. A. Tusch, Europhys. Lett., 1995, 30, 307 Search PubMed.
|
| This journal is © the Owner Societies 2003 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζo.
ζo.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζL.
ζL.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) compressed H2O. Note that very recently new X-ray data on the RuO2/water interface were interpreted as evidence of phase transitions in water monolayers in a high electric field via changes in the chemical potential.5
compressed H2O. Note that very recently new X-ray data on the RuO2/water interface were interpreted as evidence of phase transitions in water monolayers in a high electric field via changes in the chemical potential.5

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r|Z|−1/2, r is a distance from the centre of the ion and Z is the number of excess elementary charges of an ion (valence). In the immediate neighbourhood of the electrode (first layer of water molecules, the Helmholtz layer) the field strength E is
r|Z|−1/2, r is a distance from the centre of the ion and Z is the number of excess elementary charges of an ion (valence). In the immediate neighbourhood of the electrode (first layer of water molecules, the Helmholtz layer) the field strength E is 

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) const. is the volume of the system, V dy is the increment of the polarization of the whole system. The increment of the grand free energy, i.e., grand potential Ω
(related to the canonical grand partition function, cf.ref. 10a, §24) is:
const. is the volume of the system, V dy is the increment of the polarization of the whole system. The increment of the grand free energy, i.e., grand potential Ω
(related to the canonical grand partition function, cf.ref. 10a, §24) is: ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −S
−S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dT
dT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EV
EV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dy
dy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N
N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dζL,
dζL,
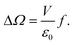

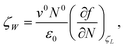
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V/N0 and N0 is the Avogadro number. The volume V of the system is taken as equal to the molar volume of water at ambient conditions. It follows from eqn. (10) that
V/N0 and N0 is the Avogadro number. The volume V of the system is taken as equal to the molar volume of water at ambient conditions. It follows from eqn. (10) that 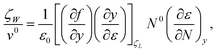
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 of the angle θ between the direction of the external field E and the electric dipole moment μ of the water molecule has to be expressed by the hyperbolic tangent and not the Langevin function. In the hydration shells and double layers the strengths of the electric field are so high that the linear approximation to 〈cos
θ〉 of the angle θ between the direction of the external field E and the electric dipole moment μ of the water molecule has to be expressed by the hyperbolic tangent and not the Langevin function. In the hydration shells and double layers the strengths of the electric field are so high that the linear approximation to 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 is no longer sufficient, and the mean cosine has to be expressed by the full tanh function and not the first term in its expansion in a power series. The relation between the permittivity ε and the electric field strength E is, according to the Onsager field model (cf. Section 5 below for the question of the Onsager field in discrete systems), expressed as
θ〉 is no longer sufficient, and the mean cosine has to be expressed by the full tanh function and not the first term in its expansion in a power series. The relation between the permittivity ε and the electric field strength E is, according to the Onsager field model (cf. Section 5 below for the question of the Onsager field in discrete systems), expressed as 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉
θ〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tanh(Ξ), n is the refraction index and
tanh(Ξ), n is the refraction index and

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V(P) with P pressure:
V(P) with P pressure:

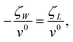

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V(P) of water in the liquid, ice VI and ice VII phases under pressure P in the absence of field. Of course, the use of the data measured in the absence of the field introduces an approximation. Its validity can only be judged a posteriori, as has been done with a positive result in ref. 3. The upper integral limit (Pi, see eqn. (16)) was matched so as to fulfil eqn. (18). This is equivalent to putting the pressure value Pi in the field equal to the local electrostriction pressure value Π:
V(P) of water in the liquid, ice VI and ice VII phases under pressure P in the absence of field. Of course, the use of the data measured in the absence of the field introduces an approximation. Its validity can only be judged a posteriori, as has been done with a positive result in ref. 3. The upper integral limit (Pi, see eqn. (16)) was matched so as to fulfil eqn. (18). This is equivalent to putting the pressure value Pi in the field equal to the local electrostriction pressure value Π:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε(T) as expressed in eqn. (12) and through introducing into eqn. (19) of the isotherm V
ε(T) as expressed in eqn. (12) and through introducing into eqn. (19) of the isotherm V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V(P) for the same temperature T, for which ε is calculated. The dependence on the value of the local electric field strength E is present through f and y
(cf.eqns. (4), (5) and (7)). The electrostriction pressure Π
V(P) for the same temperature T, for which ε is calculated. The dependence on the value of the local electric field strength E is present through f and y
(cf.eqns. (4), (5) and (7)). The electrostriction pressure Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pi is a local quantity, too.
Pi is a local quantity, too.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TΔS for the heat absorbed by the dielectric substance during a change in the electric field (related to the appearance of an ion inside the water) at a constant temperature:
TΔS for the heat absorbed by the dielectric substance during a change in the electric field (related to the appearance of an ion inside the water) at a constant temperature: 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, which is usually the case, we have ΔQ
0, which is usually the case, we have ΔQ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 and ΔS
0 and ΔS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0. Thus, heat is evolved by the dielectric and given off to the heat bath. At the same time the entropy decreases, that is the field orders the directions of the dipoles of the system. The release of heat by the dielectric as a consequence of a change in the applied field in isothermal conditions is called the isothermal electrocaloric effect. The heat due to this effect will be found from eqn. (22). The product of the derivatives:
0. Thus, heat is evolved by the dielectric and given off to the heat bath. At the same time the entropy decreases, that is the field orders the directions of the dipoles of the system. The release of heat by the dielectric as a consequence of a change in the applied field in isothermal conditions is called the isothermal electrocaloric effect. The heat due to this effect will be found from eqn. (22). The product of the derivatives: 

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.17
0.17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 J m−3 about the value of the argument x
109 J m−3 about the value of the argument x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.2 Å. The 293 K isotherm v(P) in the integral on the right hand side of eqn. (19) concerns liquid water under pressures from atmospheric to about 1 GPa and is taken from ref. 15. The integral of v(P)dP is a continuous function. Hence, the electrostriction pressure Π
2.2 Å. The 293 K isotherm v(P) in the integral on the right hand side of eqn. (19) concerns liquid water under pressures from atmospheric to about 1 GPa and is taken from ref. 15. The integral of v(P)dP is a continuous function. Hence, the electrostriction pressure Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Π(x) as a function of x plotted in Fig. 2 reveals a plateau stemming from that kink viaeqn. (19). A simple interchange of coordinate axes from Π as a function of x
(or E) into x
(or E) as a function of Π shows that the plateau of Π(x) becomes a jump of x(Π)
(or E(Π)) at the transition value Πt of the electrostriction pressure. The result of the interchange of coordinates for the case of E is shown in Fig. 3.
Π(x) as a function of x plotted in Fig. 2 reveals a plateau stemming from that kink viaeqn. (19). A simple interchange of coordinate axes from Π as a function of x
(or E) into x
(or E) as a function of Π shows that the plateau of Π(x) becomes a jump of x(Π)
(or E(Π)) at the transition value Πt of the electrostriction pressure. The result of the interchange of coordinates for the case of E is shown in Fig. 3.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) r|Z|−1/2 from the centre of the ion (cf.eqn. (11)).
r|Z|−1/2 from the centre of the ion (cf.eqn. (11)).


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E(Π) shown in Fig. 3 has been found. The plot shows that an electric field strength discontinuity occurs at Πt
E(Π) shown in Fig. 3 has been found. The plot shows that an electric field strength discontinuity occurs at Πt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.208 GPa (≈0.21 GPa), where the subscript t stands for transition. The range of the discontinuity (Fig. 3) is 0.77
0.208 GPa (≈0.21 GPa), where the subscript t stands for transition. The range of the discontinuity (Fig. 3) is 0.77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36 (109 V m−1). In other words, an increase in the electric field strength E from 0.77 to 1.36 (109 V m−1) does not change the value of the electrostriction pressure Π. At Πt and at a value of E comprised in this range two phases coexist.
1.36 (109 V m−1). In other words, an increase in the electric field strength E from 0.77 to 1.36 (109 V m−1) does not change the value of the electrostriction pressure Π. At Πt and at a value of E comprised in this range two phases coexist.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.21 GPa is seen. The range of this discontinuity is: 0.97
0.21 GPa is seen. The range of this discontinuity is: 0.97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |ΔS|
|ΔS|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.9 (J mol−1 K−1), and is accompanied by a latent heat of −277 J mol−1. On increasing Π from a value equal to atmospheric pressure up to 0.1 GPa (E
1.9 (J mol−1 K−1), and is accompanied by a latent heat of −277 J mol−1. On increasing Π from a value equal to atmospheric pressure up to 0.1 GPa (E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4
0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 V m−1), the entropy of the system of dipoles decreases (cf.Fig. 4) due to the process of orientational ordering of the dipoles. On the further increase of Π up to the value Πt
109 V m−1), the entropy of the system of dipoles decreases (cf.Fig. 4) due to the process of orientational ordering of the dipoles. On the further increase of Π up to the value Πt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.21 GPa entropy increases: the lowering of entropy due to the process of orientational ordering of the dipoles is overwhelmed by its increase. At Π
0.21 GPa entropy increases: the lowering of entropy due to the process of orientational ordering of the dipoles is overwhelmed by its increase. At Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Πt one can notice a discontinuous increase in entropy due to the coexistence of two phases. On further increasing Π
Πt one can notice a discontinuous increase in entropy due to the coexistence of two phases. On further increasing Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Πt the entropy of the newly created phase decreases.
Πt the entropy of the newly created phase decreases.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.21 GPa corresponds neither to water
0.21 GPa corresponds neither to water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VI nor ice VI
ice VI nor ice VI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VII transitions under external pressure. In Fig. 5, along the line marked d, the d(P) data points are shown corresponding to the values of the pressure Π
ice VII transitions under external pressure. In Fig. 5, along the line marked d, the d(P) data points are shown corresponding to the values of the pressure Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Pi found with the help of eqn. (19) from the experimental data of refs. 13–15. Between parts of the line with dense points two gaps are seen corresponding to water
Pi found with the help of eqn. (19) from the experimental data of refs. 13–15. Between parts of the line with dense points two gaps are seen corresponding to water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VI (marked by 1) and ice VI
ice VI (marked by 1) and ice VI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VII (marked by 2) transitions under pressure Pi applied in no field (E
ice VII (marked by 2) transitions under pressure Pi applied in no field (E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0). They are far apart the discontinuity in ε
0). They are far apart the discontinuity in ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε(Πt) characteristic of the phase transition found in this study. Hence, the discontinuous phase transition found above is not an artifact resulting from the use of the input data.
ε(Πt) characteristic of the phase transition found in this study. Hence, the discontinuous phase transition found above is not an artifact resulting from the use of the input data.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VI and ice VI
ice VI and ice VI![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VII transitions, respectively. The points at the line marked d represent the input data based on the experiment13–15
(see text).
ice VII transitions, respectively. The points at the line marked d represent the input data based on the experiment13–15
(see text).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ice VIII for which no change in the molar volume was observed (ref. 19, Table 3.6 therein): Δv
ice VIII for which no change in the molar volume was observed (ref. 19, Table 3.6 therein): Δv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.000
0.000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0005 cm3 mol−1 and ΔQ
0.0005 cm3 mol−1 and ΔQ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 kJ mol−1. Ice VIII is an ordered form of ice VII.
1 kJ mol−1. Ice VIII is an ordered form of ice VII.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Π(x) in Fig. 2, the discontinuity in the electric field strength is extended over the range of x from 2.154 Å
Π(x) in Fig. 2, the discontinuity in the electric field strength is extended over the range of x from 2.154 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å. For x
2.217 Å. For x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.154 Å, water is in phase A with complete orientational order due to the field (cf.ref. 23, Table 1 therein). The plots of the relations Π
2.154 Å, water is in phase A with complete orientational order due to the field (cf.ref. 23, Table 1 therein). The plots of the relations Π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Π(x) are steeper for x
Π(x) are steeper for x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.154 Å than for x
2.154 Å than for x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å. For x
2.217 Å. For x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å one finds phase B with incomplete orientational order (ref. 23, Table 1). In addition to the x discontinuity, the change in slope of the isotherm plotted in Fig. 2 can be interpreted as testifying to a phase transition: phase A
2.217 Å one finds phase B with incomplete orientational order (ref. 23, Table 1). In addition to the x discontinuity, the change in slope of the isotherm plotted in Fig. 2 can be interpreted as testifying to a phase transition: phase A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) phase B under the electrostriction pressure Πt
phase B under the electrostriction pressure Πt![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.21 GPa. A rich series of experimental results can be found in literature on hydration shells of various ions. The fields acting on their hydration shells are E
0.21 GPa. A rich series of experimental results can be found in literature on hydration shells of various ions. The fields acting on their hydration shells are E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.77
0.77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 V m−1
(x
109 V m−1
(x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å) as well as E
2.217 Å) as well as E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36
1.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 V m−1
(x
109 V m−1
(x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.154 Å). Hence, we consider it sound to provide a discussion of literature neutron scattering experiments (Subsection 4.2) and relate them to the present results. We argue that the phase of H2O compressed in a high field can represent a layer (close to a monomolecular layer) at an electrode,5 or portions of a phase dispersed in space in the form of hydration shells of ions.
2.154 Å). Hence, we consider it sound to provide a discussion of literature neutron scattering experiments (Subsection 4.2) and relate them to the present results. We argue that the phase of H2O compressed in a high field can represent a layer (close to a monomolecular layer) at an electrode,5 or portions of a phase dispersed in space in the form of hydration shells of ions.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36 (109 V m−1) found in this study and seen in Fig. 3 at the transition value Πt of the electrostriction pressure falls well in the range where the phase transitions were observed by Chu et al..5 The discontinuous transition at the same Πt value is seen in entropy change (Fig. 4) and permittivity (Fig. 5) plots, too. Also, the calculated mass density of the compressed H2O phase can be shown by using methods developed earlier3 to attain the observed twice the ambient water density and more than that.1,5
1.36 (109 V m−1) found in this study and seen in Fig. 3 at the transition value Πt of the electrostriction pressure falls well in the range where the phase transitions were observed by Chu et al..5 The discontinuous transition at the same Πt value is seen in entropy change (Fig. 4) and permittivity (Fig. 5) plots, too. Also, the calculated mass density of the compressed H2O phase can be shown by using methods developed earlier3 to attain the observed twice the ambient water density and more than that.1,5
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36 (109 V m−1)
(or a reduced radial distance range 2.154 Å
1.36 (109 V m−1)
(or a reduced radial distance range 2.154 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å). It will be argued that the discontinuity of the transition which allows for a whole range of x to correspond to the transition value Πt of the electrostriction pressure explains the destroyed hydration structure phenomenon of Sr2+ ion (ref. 24 and references cited therein). The calculated properties of the phases A and B are in our opinion also consistent with the known results of neutron scattering studies of other ions in D2O solution. These results for shells in phase A and B conform to an additivity rule. Marcus25 has indicated the following additivity relation between the distance ion-water (r1, equal to the radius of the first hydration shell) and the ionic radius Rion, as well as the radius of a water molecule (Rwater
2.217 Å). It will be argued that the discontinuity of the transition which allows for a whole range of x to correspond to the transition value Πt of the electrostriction pressure explains the destroyed hydration structure phenomenon of Sr2+ ion (ref. 24 and references cited therein). The calculated properties of the phases A and B are in our opinion also consistent with the known results of neutron scattering studies of other ions in D2O solution. These results for shells in phase A and B conform to an additivity rule. Marcus25 has indicated the following additivity relation between the distance ion-water (r1, equal to the radius of the first hydration shell) and the ionic radius Rion, as well as the radius of a water molecule (Rwater![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≈
≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4 Å):
1.4 Å): ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rion
Rion![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rwater .
Rwater .
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.23 Å. This value does not fulfill eqn. (27), which indicates a lack of additivity of ionic and molecular radii. The discontinuity in x
(2.154 Å
2.23 Å. This value does not fulfill eqn. (27), which indicates a lack of additivity of ionic and molecular radii. The discontinuity in x
(2.154 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å) at Πt falls entirely within a broader range of x values under the single broad peak of the neutron scattering RDF GSr(x)
(Fig. 6b). Let us recall that in our description the state of H2O in the hydration shell is defined by the state variables T,Π,x . To each value of Π on the 293 K isotherm Π(x) in Fig. 2 there corresponds a given x value except for Πt, where x takes any value along the segment 2.154 Å
2.217 Å) at Πt falls entirely within a broader range of x values under the single broad peak of the neutron scattering RDF GSr(x)
(Fig. 6b). Let us recall that in our description the state of H2O in the hydration shell is defined by the state variables T,Π,x . To each value of Π on the 293 K isotherm Π(x) in Fig. 2 there corresponds a given x value except for Πt, where x takes any value along the segment 2.154 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å. We propose an interpretation of the apparently hitherto unexplained peculiar character of the neutron scattering RDF called the destroyed hydration structure: RDF smearing and lack of additivity of ionic and water radii. According to this interpretation, it can be a consequence of a discontinuity in x at the phase transition point. In such a case water in the neighbourhood of the ion is in the state determined by Πt and a water molecule can choose any possible value of the reduced radius x along the segment (Fig. 2) mentioned above. Hence, there is no specific unique value of xt corresponding to Πt, but any x value in the range of the segment is acceptable instead. As follows, H2O molecules in this state can statistically take positions in different distances from the ion. This statistical freedom of taking different distances results in the effect called destroyed hydration structure: the peaks in RDF attributed to oxygen and deuterium are smeared and shifted so as to give a common broad peak with a maximum not fulfilling the criterion given by eqn. (26). Now, as we have drawn a picture of hydration of Sr2+ ions in terms of a state at the transition between two H2O phases (A and B), what would be the meaning of these phases in the hydration problem of other ions? This will be the subject of the two next paragraphs.
2.217 Å. We propose an interpretation of the apparently hitherto unexplained peculiar character of the neutron scattering RDF called the destroyed hydration structure: RDF smearing and lack of additivity of ionic and water radii. According to this interpretation, it can be a consequence of a discontinuity in x at the phase transition point. In such a case water in the neighbourhood of the ion is in the state determined by Πt and a water molecule can choose any possible value of the reduced radius x along the segment (Fig. 2) mentioned above. Hence, there is no specific unique value of xt corresponding to Πt, but any x value in the range of the segment is acceptable instead. As follows, H2O molecules in this state can statistically take positions in different distances from the ion. This statistical freedom of taking different distances results in the effect called destroyed hydration structure: the peaks in RDF attributed to oxygen and deuterium are smeared and shifted so as to give a common broad peak with a maximum not fulfilling the criterion given by eqn. (26). Now, as we have drawn a picture of hydration of Sr2+ ions in terms of a state at the transition between two H2O phases (A and B), what would be the meaning of these phases in the hydration problem of other ions? This will be the subject of the two next paragraphs.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.154 Å. The first of the two sharp peaks in the plot of GNi(x) is attributed to the distance Ni–O (cation–oxygen of heavy water molecule), the other one, to Ni–D. Such a shape of the function Gcation(x) follows the well-defined hydration structures in solution. The additivity relation (eqn. (27)) is well fulfilled by such ions. These are ions with double, triple (and larger) elementary charge with addition of Li+
(cf.ref. 25, table XIII therein). Ni2+ and Mg2+ form fairly well-defined long-lived24 hydration structure in solutions. These characteristics of the well-defined hydration structures24
(first hydration shell), learned from the RDF’s, is consistent with the characteristics of phase A following from our approach: its 〈cos
2.154 Å. The first of the two sharp peaks in the plot of GNi(x) is attributed to the distance Ni–O (cation–oxygen of heavy water molecule), the other one, to Ni–D. Such a shape of the function Gcation(x) follows the well-defined hydration structures in solution. The additivity relation (eqn. (27)) is well fulfilled by such ions. These are ions with double, triple (and larger) elementary charge with addition of Li+
(cf.ref. 25, table XIII therein). Ni2+ and Mg2+ form fairly well-defined long-lived24 hydration structure in solutions. These characteristics of the well-defined hydration structures24
(first hydration shell), learned from the RDF’s, is consistent with the characteristics of phase A following from our approach: its 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉
θ〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ε
1, ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23, and it is compressed: d
23, and it is compressed: d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The densities of the hydration shells calculated within the present approach can be expressed in terms of coordination numbers of specific ions and have been reported elsewhere.8 The values of coordination numbers calculated in ref. 8 compared well with literature data. Thus we conclude that although there are other ways of looking at the hydration of the above class of ions, the picture involving the concept of the phase (A) of water in a field does not conflict with the known data and can be treated at least as a complementary one.
1. The densities of the hydration shells calculated within the present approach can be expressed in terms of coordination numbers of specific ions and have been reported elsewhere.8 The values of coordination numbers calculated in ref. 8 compared well with literature data. Thus we conclude that although there are other ways of looking at the hydration of the above class of ions, the picture involving the concept of the phase (A) of water in a field does not conflict with the known data and can be treated at least as a complementary one.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å. The RDF GK(x) is characterized by a single maximum,24 whose position is close to the reduced distance x1
2.217 Å. The RDF GK(x) is characterized by a single maximum,24 whose position is close to the reduced distance x1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.8 Å, obtained from eqn. (27). From Table XIII in ref. 25, it follows that ions bearing single elementary charges (for which x1
2.8 Å, obtained from eqn. (27). From Table XIII in ref. 25, it follows that ions bearing single elementary charges (for which x1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.217 Å) fulfil eqn. (27), too. The absence of clearly resolved peaks in GK(x) is a clear evidence that K+ is weakly hydrated. This characteristics of weakly hydrated ions24 read from GK(x) is consistent with the characteristics of phase B following from our approach: 〈cos θ〉
2.217 Å) fulfil eqn. (27), too. The absence of clearly resolved peaks in GK(x) is a clear evidence that K+ is weakly hydrated. This characteristics of weakly hydrated ions24 read from GK(x) is consistent with the characteristics of phase B following from our approach: 〈cos θ〉![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ε
1, ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38, and there is no remarkable compression: d
38, and there is no remarkable compression: d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) →
→![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Again, the concept of phase B, a weakly ordered liquid water phase, does not conflict with the previous knowledge.
1. Again, the concept of phase B, a weakly ordered liquid water phase, does not conflict with the previous knowledge.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.36 (109 V m−1). The experimental evidence of phase transitions in H2O in a high electric field has been provided by Chu et al..5 The latent heat accompanying the transition has also been observed at a Hg/aqueous electrolyte interface.28,29 The above E values fall well into the range where Chu et al.5 observed the transitions at the RuO2 electrode by synchrotron radiation X-ray scattering methods. Also, these values fall very close to the field acting on the water molecules lying at the maximum of RDF in the first hydration shell of the Sr2+ ion, which enabled us to provide a tentative explanation of its peculiar properties revealed by neutron scattering.7
1.36 (109 V m−1). The experimental evidence of phase transitions in H2O in a high electric field has been provided by Chu et al..5 The latent heat accompanying the transition has also been observed at a Hg/aqueous electrolyte interface.28,29 The above E values fall well into the range where Chu et al.5 observed the transitions at the RuO2 electrode by synchrotron radiation X-ray scattering methods. Also, these values fall very close to the field acting on the water molecules lying at the maximum of RDF in the first hydration shell of the Sr2+ ion, which enabled us to provide a tentative explanation of its peculiar properties revealed by neutron scattering.7
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 281 CrossRef CAS.
281 CrossRef CAS.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 491 CrossRef CAS.
491 CrossRef CAS.





