Batch process monitoring using on-line MIR spectroscopy
Eric N. M.
van Sprang
a,
Henk-Jan
Ramaker
a,
Hans F. M.
Boelens
a,
Johan A.
Westerhuis
*a,
David
Whiteman
b,
David
Baines
b and
Ian
Weaver
b
aProcess Analysis and Chemometrics, Department of Chemical Engineering, University of Amsterdam, Nieuwe Achtergracht 166, 1018 WV Amsterdam, The Netherlands. E-mail: westerhuis@science.uva.nl
bSpectraprobe Ltd, Dawley Road, Middlesex, UK UB2 1HH
First published on 3rd December 2002
Abstract
Many high quality products are produced in a batch wise manner. One of the characteristics of a batch process is the recipe driven nature. By repeating the recipe in an identical manner a desired end-product is obtained. However, in spite of repeating the recipe in an identical manner, process differences occur. These differences can be caused by a change of feed stock supplier or impurities in the process. Because of this, differences might occur in the end-product quality or unsafe process situations arise. Therefore, the need to monitor an industrial batch process exists. An industrial process is usually monitored by process measurements such as pressures and temperatures. Nowadays, due to technical developments, spectroscopy is more and more used for process monitoring. Spectroscopic measurements have the advantage of giving a direct chemical insight in the process. Multivariate statistical process control (MSPC) is a statistical way of monitoring the behaviour of a process. Combining spectroscopic measurements with MSPC will notice process perturbations or process deviations from normal operating conditions in a very simple manner. In the following an application is given of batch process monitoring. It is shown how a calibration model is developed and used with the principles of MSPC. Statistical control charts are developed and used to detect batches with a process upset.
Introduction
The batch wise production of high quality products such as pharmaceuticals, polymers or bio-chemicals plays an important role in process industry. A batch process is a recipe driven approach, that is, if a new process is operated in a similar manner as the previous one, according to the recipe, it is expected that a similar end-product will be obtained. Since batch processes are often highly complex, it is not straightforward to maintain identical operating conditions and (undesired) variations between the batches may occur. There are many sources in a process that can cause these variations. As an example, a different initial feedstock or a change in heat exchange due to impurities. This uncontrolled variation may lead to poor quality end-products or unsafe process situations. It is therefore desirable to keep the batch to batch variation in control.The batch to batch variation can be monitored using multivariate statistical batch process control (MSPC). MSPC for batch processes or batch process monitoring was initially developed by Nomikos and MacGregor,1–3 and, since then many extensions and applications have been presented in the literature.4–7
A very convenient tool is the use of on-line spectroscopic measurements for batch process monitoring. It is a fast and non-destructive measurement giving direct chemical insight of the spectroscopic active compounds present in the system. This is in contrast to engineering variables such as temperatures and pressures which are indirectly related to the chemistry in the process. A list of examples of on-line spectroscopic measurements can be found in the review of Workman et al.8
In the present study, batch process monitoring is performed. A batch polymerisation process of poly(methylmethacrylate) (PMMA) has been monitored using mid infrared (MIR) spectroscopy and a calibration model, combined with the principles of batch MSPC. The calibration model and the statistical theory are explained in the following section before considering the experimental set-up and instrumentation used.
Theory
Notation
Matrices are denoted as boldface uppercase characters, vectors by boldface lowercase characters and italic characters denote scalars.Calibration
Projection to latent structures (or partial least squares, PLS) is a commonly used technique in spectroscopy to model a block of predictors X (spectra) and a response variable y (concentration).9,10 PLS is a decomposition which maximises the covariance between the X (I × J) and y (I × 1) block. The matrices X and y are decomposed into a number of R score vectors T (I × R), loading vectors P (J × R) and q (R × 1), and residual matrices E (I × J) and f (I × 1).The PLS decomposition is given in matrix notation in eqn. (1) to (3)| X = TP′ + E | (1) |
| y = Tq + f | (2) |
| T = XW(P′W)−1 | (3) |
Using the model parameters W, P and q, the concentration y is predicted on-line each time a new observation xnew (J × 1) is measured according to eqn (4) and (5).
| t′new = x′newW(P′W)−1 | (4) |
ŷ = ![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) ′newq ′newq | (5) |
On-line monitoring
The principle of multivariate statistical batch process monitoring (BPM) is used to monitor the batch polymerisation reaction. Statistical batch process monitoring is divided in three phases; the initial phase, the training phase and the application phase.11,12The first phase is the initial phase. This phase consists of measuring and collecting historical process data from previous batch runs. In this study, the process measurements are MIR spectra. An example of the measured process spectra is given in Fig. 1.
 | ||
| Fig. 1 Measured process spectra. | ||
The second phase is the training phase. In this phase it is determined which of the historical batch runs are assigned as batches that were operated under normal conditions (NOC). After the selection, a process model based on a calibration set is developed to predict the concentration during the evolution of the process. Since the model is based on a calibration set which is representative for the batch process under NOC, it can also be used for statistical batch process monitoring.
The third phase, is monitoring a new batch using the control charts developed in phase two.
The model combined with a historical data set is used to determine the statistical control limits. The data set consists of batches that are operated under normal operating conditions. A new batch is monitored by using eqn. (4). With every new observation x′new a new score vector ![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) new (R
× 1) is computed according to eqn. (4). The model parameter P is used to compute model residuals enew (J
× 1) for each observation.
new (R
× 1) is computed according to eqn. (4). The model parameter P is used to compute model residuals enew (J
× 1) for each observation.
e′new = x′new
−
![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) ′newP′ ′newP′ | (6) |
![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) new and the residuals enew are used to compute the monitoring statistics.
new and the residuals enew are used to compute the monitoring statistics.
In order to develop control charts with proper control limits, the historical NOC batches must follow the same procedure as a new batch would do. This results in the vector yi (N
× 1), consisting of the predicted concentrations at each interval i. The matrices ![[T with combining circumflex]](https://www.rsc.org/images/entities/b_char_0054_0302.gif) i (N
×
R), consisting of the score vectors from the N batch runs at interval i and the residual matrix Ei (N
×
J), which consists of the model residuals computed corresponding to interval i. The NOC matrices are used to develop three types of control charts; the concentration chart, the D chart and the SPE chart.
i (N
×
R), consisting of the score vectors from the N batch runs at interval i and the residual matrix Ei (N
×
J), which consists of the model residuals computed corresponding to interval i. The NOC matrices are used to develop three types of control charts; the concentration chart, the D chart and the SPE chart.
Concentration chart
The control limits of the concentration chart are determined using the vector yi. The mean (ȳi) and standard deviation (si) are computed from yi. The upper and lower control limits for each time interval i are given by| UCLi = ȳi + t(N−1,α/2)si | (7) |
| LCLi = ȳi − t(N−1,α/2)si | (8) |
The concentration chart monitors deviations in the predicted concentration compared to the average monomer decrease.
D chart
The D-statistic is the Hotelling statistic T2 in a reduced space R. This statistic is a Mahalanobis distance between the center of that space and the new obtained scores![[t with combining circumflex]](https://www.rsc.org/images/entities/b_char_0074_0302.gif) new. The Di statistic for each interval i is computed by
new. The Di statistic for each interval i is computed by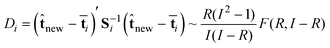 | (9) |
![[t with combining macron]](https://www.rsc.org/images/entities/b_char_0074_0304.gif) i are the mean scores obtained from the historical score matrix
i are the mean scores obtained from the historical score matrix ![[T with combining circumflex]](https://www.rsc.org/images/entities/b_char_0054_0302.gif) i. The matrix Si (R
×
R) is the variance–covariance matrix computed with the historical score matrix
i. The matrix Si (R
×
R) is the variance–covariance matrix computed with the historical score matrix ![[T with combining circumflex]](https://www.rsc.org/images/entities/b_char_0054_0302.gif) i and F(R,I
−
R) represents the F distribution with R and I
−
R degrees of freedom. The control limits are obtained from the F distribution with 99% significance level.
i and F(R,I
−
R) represents the F distribution with R and I
−
R degrees of freedom. The control limits are obtained from the F distribution with 99% significance level.
The concentration chart and the D chart are directly correlated. That is, the D chart defines a statistic based on the score vector and monitors the batch process in the reduced space. Whereas the concentration chart monitors the concentration which is predicted using the score vector. Therefore, the concentration chart and D chart will give more or less similar results.
The SPE chart
The SPEi statistic is a residual statistic and equals the sum of squared residuals summed over all wavelengths J at interval i.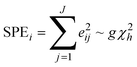 | (10) |
Experimental
The reaction of interest is a batch polymerisation of methylmethacrylate (MMA) to polymethylmethacrylate (PMMA) via a free radical polymerisation process. Azobisisobutyronitrile (AIBN) has been used as the free radical initiator. The reaction scheme is shown in Fig. 2.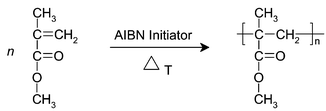 | ||
| Fig. 2 AIBN initiated polymerisation of methylmethacrylate. | ||
The polymerisation was performed in a 500 ml reactor with heating/cooling jacket under a nitrogen atmosphere to prevent termination or inhibition by impurities. The reaction was constantly stirred using a magnetic stirrer and kept at a temperature of 80 °C using a temperature controlled water bath (Thermo NESLAB). An initial solution of 0.36 mole methylmethacrylate in 0.89 mole toluene was heated at 80 °C prior to the start of the reaction. The reaction was initiated using a solution of 0.9 mmole azobisisobutyronitrile in 0.04 mole toluene.
The reaction was monitored by collecting MIR spectra using the SpectraProbe Linx MID spectrometer from SpectraProbe Ltd. (UK).The instrument utilised a two bounce silicon attenuated total reflection (ATR) crystal yielding spectra in the range 1020 cm−1 to 1936 cm−1. The detector is a patented mid IR detector which operates at room temperature and requires no cooling elements. The detector is a fixed 128 pixel pyroelectric array which SpectraProbe has developed for use in the mid IR range and could collect radiation from 2.5 to 10 microns. Although the detector is currently fixed to see the 5 to 10 micron range. The detector uses a grating rather than an FTIR system to address the detector array. The spectral resolution of the detector is in the range of 4 cm−1 @ 1020 cm−1 and 16 cm−1 @ 1923 cm−1.
Spectra were collected over a 4 min period and compared against a 10 min background spectra previously acquired in toluene as an auto-zero of the instrument.
Results and discussion
An example of the measured process spectra are given in Fig. 3. The spectra are taken from a single batch run prior to injecting the initiator and the bands of the spectroscopic active compounds have been assigned according to Olinga et al.13A PLS calibration model has been constructed to predict the monomer concentration during the polymerisation.The calibration model was based on 12 standard solutions with known concentrations of methylmethacrylate (MMA)/polymethylmethacrylate (PMMA). Each calibration sample was measured five times at 80 °C.
Prior to modelling, wavenumber selection and data pre-processing were performed, resulting in the use of the wavenumber range of 1450 cm−1–1140 cm−1. This range was chosen to follow the decrease of MMA. Data preprocessing was applied by taking the first derivative spectra using a Savitsky-Golay filter (window size 3) and the number of PLS components was determined by cross validation. Three components were used in the PLS model and the concentration was predicted with a 5% precision. The calibration concentrations versus the estimated concentrations are given in Fig. 4.
 | ||
| Fig. 4 Standard concentrations versus the concentrations estimated by the model. | ||
The results of monitoring the monomer concentration of batch 1 are given in Fig. 5 where the decrease of the monomer during the process is shown. After the initial five measurements, the initiator was added to the system and the reaction started. This is reflected by the decrease of the monomer concentration in time from this point.
 | ||
| Fig. 5 The methylmethacrylate (MMA) concentration during a reaction. | ||
A total of 18 batch runs obtained under normal operating conditions (NOC) were available for developing statistical control charts. One batch is used to validate the model and 2 batch runs with known process perturbations were available for testing the control charts. A description of the faulty batches is given in Table 1.
| Batch no. | Process upsets |
|---|---|
| 1 | Normal batch, no upsets |
| 2 | Different operating temperature |
| 3 | Small addition of styrene in the system |
The behaviour of the batch was analysed and checked under normal operating conditions and the developed control charts used to study the behaviour. The batch 1 measurements, given in Fig. 5 were monitored and are presented in Fig. 6A, B and C. In Fig. 6A, the concentration chart is given with 99% control limits. The first measurement prior to injecting the initiator is set as time t = 1. It can be seen that the batch behaves within the specified limits and therefore is statistically in control. The D chart in Fig. 6B, which is correlated with the concentration chart, gives a similar picture. Fig. 6C shows the normalised SPE chart with 99% control limits. From this figure it can be seen that the process has no unknown phenomena or unmodelled variation. The batch behaves under normal conditions.
 | ||
| Fig. 6 Monitoring batch 1 using statistical control charts. | ||
The control charts have been used to monitor the perturbed batches given in Table 1. Batch 2 has been run at a lower temperature (70 °C). The three control charts are given in Fig. 7A, B and C. The concentration chart and D chart indicate that the first measurement is on the border of acceptable variation, the second measurement is clearly out of control. The concentration chart shows that the monomer is decreasing very slowly indicating that there is a slow conversion. The D chart supports the concentration chart and shows that the process is deviating from normal conditions as time evolves. The SPE chart shows that no unmodelled or non-linear variation is detected. This is expected since the absorbing compounds do not change and therefore the spectra fit the model.
 | ||
| Fig. 7 Monitoring batch 2 using statistical control charts. | ||
Batch 3 had a small fraction polystyrene added to the system. The results are given in Fig. 8A, B and C. The fraction polystyrene is added after 10 min. It seems that the addition of polystyrene is affecting the process kinetics. This is shown in the concentration chart and the D chart. The conversion of MMA is slowing down due to the polystyrene addition. Polystyrene is a new compound in the system. A new or unknown compound should be observed in the SPE chart. However, in this specific situation, this is not the case. The SPE chart gives no out of control signal since polystyrene absorbs around 699 cm−1. This wavenumber is not used in the current calibration model and is therefore not detected in the SPE chart.
 | ||
| Fig. 8 Monitoring batch 3 using statistical control charts. | ||
Conclusion
A batch polymerisation process was monitored on-line using mid infrared spectroscopy with a Spectraprobe Linx spectrometer. The instrument is compact and easy to hand over to an industrial process. A calibration model has been constructed and used to monitor the decrease of the monomer concentration. The concentration is predicted with a 5% precision. Furthermore, the calibration model is used together with the principles of statistical batch process monitoring and different batches are monitored using control charts. It has been shown that unusual behaviour is easily detected by the control charts and that statistical process control is therefore a useful method for monitoring batch to batch variation.References
- P. Nomikos and J. F. MacGregor, AIChE J., 1994, 40, 1361 Search PubMed.
- P. Nomikos and J. F. MacGregor, Technometrics, 1995, 37, 41.
- P. Nomikos and J. F. MacGregor, Chemom. Intell. Lab. Syst., 1995, 30, 97 CrossRef CAS.
- S. Ränner, J. F. MacGregor and S. Wold, Chemom. Intell. Lab. Syst., 1998, 41, 73 CrossRef.
- S. Wold, N. Kettaneh, H. Friden and A. Holmberg, Chemom. Intell. Lab. Syst., 1998, 44, 331 CrossRef CAS.
- D. Neogi and C. E. Schlags, Ind. Eng. Chem. Res., 1998, 37, 3971 CrossRef CAS.
- A. A. Tates, D. J. Louwerse and A. K. Smilde, Ind. Eng. Chem. Res., 1999, 38, 4769 CrossRef CAS.
- J. Workman, Jr, D. F. Veltkamp, S. Doherty, B. B. Anderson, K. E. Creasy, M. Koch, J. F. Tatera, A. L. Robinson, L. Bond, L. W. Burgess, G. N. Bokerman, A. H. Ullman, G. P. Darsey, F. Mozayeni, J. A. Bamberger and M. Stautberg Greenwood, Anal. Chem., 1999, 71, 121R–180R CrossRef.
- S. Wold, M. Sjostrom and L. Eriksson, Chemom. Intell. Lab. Syst., 2001, 58, 109 CrossRef CAS.
- P. Geladi and B. R. Kowalski, Anal. Chem., 1986, 185, 1 CrossRef CAS.
- H. J. Ramaker, E. N. M. van Sprang, S. P. Gurden, J. A. Westerhuis and A. K. Smilde, J. Process Control, 2002, 12, 569 CrossRef CAS.
- J. A. Westerhuis, S. P. Gurden and A. K. Smilde, Anal. Chem., 2000, 72, 5322 CrossRef CAS.
- A. Olinga, R. Winzen, H. Rehage and H. W. Siesler, J. Near Infrared Spectrosc., 2001, 9, 19 Search PubMed.
| This journal is © The Royal Society of Chemistry 2003 |

