Solvation and nucleophilic reactivity of 2-nitrobenzoate and of 2,6-dichlorobenzoate ions in acetonitrile–methanol mixtures

Abstract

Rate constants and activation parameters for the reactions of the 2-nitrobenzoate and 2,6-dichlorobenzoate ions with ethyl iodide have been determined in acetonitrile–methanol mixtures. The activation parameters for the two reactions indicated different responses to solvent compositions. Single-ion enthalpies of transfer for the two anions have also been determined in the same solvent mixtures and on the basis of the results single-ion enthalpies of transfer for the transition-state anion for the two reactions have also been calculated and separated into their components. By empirical analysis of the transfer enthalpies due to the “more physical” interaction for the transition-state anion, Δ_tH_PHYS^AN→MeOH (TS⁻), the approach of solvent molecules to the α-carbon atom and the central carbon atom in carboxylate group in the carboxylate ion, together with the number of partial dipoles in the anion, have been suggested to account for the various transfer enthalpies.

---

Nucleophilic substitution reactions are among the most studied reactions in organic chemistry and through these studies such fundamental concepts as steric effects, polar effects, nucleophilicity, solvent effects and structure–reactivity correlations have been developed.^1–6 Recent progress in gas phase ion chemistry has helped to develop more advanced ideas such as intrinsic nucleophilicity, double-well potential, non-statistical and non-RRKM (Rice–Ramsperger–Kassel–Marcus) effects in S_N2 reactions.^7–10 Dipolar aprotic vs. protic solvent effects on reaction rates,¹¹ which have been quantified through the solvent activity coefficient term, log⁰γ^S, have been put on a more molecular mechanistic basis through the quantitative separation of observed solute–solvent interactions into components, i.e., “more physical” and specific interactions between a solute and solvents.^12,13 This separation made it possible to empirically classify anions on the basis of solvation patterns¹⁴ and to give a molecular thermodynamic understanding of the entropy of dissociation for weak acids in the aqueous phase.¹⁵

With respect to the specific interaction, through the introduction of the concept of “effective atomic charge on oxygen” a molecular mechanistic understanding of the origin of the interaction has been formulated on a quantitative basis encompassing anionic nucleophiles and transition-state anions.^16,17 However, partly because of the involvement of various molecular mechanistic factors contributing to “more physical” interactions, even qualitative understanding of “more physical” interactions has proved to be difficult.

Introduction of a bulky substituent near to a reaction center in a nucleophile is supposed to produce perturbations not only in reaction behavior but also in solvation patterns¹⁸ and an analysis of these effects will help to understand solute–solvent interactions and reaction behavior in solution. In this work, rate behavior and solute–solvent interactions will be determined for the reaction of 2-nitrobenzoate ion and of 2,6-dichlorobenzoate ion with ethyl iodide in acetonitrile–methanol mixtures and the solvation patterns will be discussed for transition-state anions of reaction (1).

Nu⁻ + Et–I → Nu–Et + I⁻ (1)

Results

Rate constants and activation parameters for the reaction of the 2-nitrobenzoate and 2,6-dichlorobenzoate ions with ethyl iodide in acetonitrile are compared with those for 4-nitrobenzoate and 3,4-dichlorobenzoate ion reactions in Table 1. The rate retarding effects of the 2-nitro and 2,6-dichloro substituents are comparable, i.e., (6.08/10.7) for the former and (6.35/12.0) for the latter. However, analysis of the activation parameters indicates that for the former reaction the effect is governed by the increase in the activation enthalpy on going from the 4-nitrobenzoate to the 2-nitrobenzoate ion reaction, while for the latter reaction the effect is governed by the decrease in the activation entropy on going from 3,4-dichlorobenzoate to 2,6-dichlorobenzoate, in other words, the ortho-effects have a different molecular mechanistic origin.

Table 1 Effects of ortho-substituents on rate constants and on activation parameters in acetonitrile (30 °C)

Reaction	k/10^−3 dm^3 mol^−1 s^−1	ΔH^≠/kJ mol^−1	ΔS^≠/J K^−1 mol^−1
a Ref. 19.
4-Nitrobenzoate^− + EtI^a	10.7	68.0	−58.3
2-Nitrobenzoate^− + EtI	6.08	73.2	−46.0
3,4-Dichlorobenzoate^− + EtI	12.0	69.9	−51.2
2,6-Dichlorobenzoate^− + EtI	6.35	69.9	−56.5

---

Rate constants and activation parameters for the reactions of 2-nitrobenzoate and of 2,6-dichlorobenzoate with ethyl iodide in acetonitrile–methanol mixtures are summarized in Table 2. Both reactions show a very sharp decrease in rate constant and a very sharp increase in activation enthalpy on going from acetonitrile to acetonitrile–methanol mixtures with a small mole fraction of methanol. This is a very characteristic feature of reactions whose rates are significantly governed by the hydrogen-bonding of the nucleophile with methanol.^12,13,16,17 However, the contrasting behavior of the two reactions is reflected in the variation of activation entropy, that is, for the 2-nitrobenzoate ion reaction the activation entropy decreases on going from acetonitrile to methanol, while for the 2,6-dichlorobenzoate ion reaction, the entropy significantly increases.

Table 2 Rate constants and activation parameters in acetonitrile–methanol mixtures (30 °C)

x MeOH ^a	2-Nitrobenzoate^− + EtI			2,6-Dichlorobenzoate^− + EtI
	k/10^−6 dm^3 mol^−1 s^−1	ΔH^≠/kJ mol^−1	ΔS^≠/J K^−1 mol^−1	Δk/10^−6 dm^3 mol^−1 s^−1	ΔH^≠/kJ mol^−1	ΔS^≠/J K^−1 mol^−1
a x MeOH is the mole fraction of methanol in the solvent mixtures.
0.0	6.08 × 10^3	73.2	−46.0	6.35 × 10^3	69.9	−56.5
0.10	1.39 × 10^2	89.9	−22.3	1.35 × 10^2	89.5	−23.9
0.25	28.1	93.3	−24.4	25.3	94.4	−21.7
0.50	7.81	91.9	−39.6	7.57	88.1	−52.5
0.75	3.43	90.5	−51.0	3.00	101.4	−16.3
1.0	1.67	89.2	−61.4	1.03	101.6	−24.5

---

Enthalpies of solution for three tetramethylammonium salts, Δ_sH, in acetonitrile–methanol mixtures are summarized in Table 3. Single ion enthalpies of transfer from acetonitrile to solvent mixtures, Δ_tH^AN→mix were calculated on the basis of the TBA/TBB (tetrabutylammonium/tetrabutyl borate) assumption^12,13 and are summarized in Table 4. These values are characterized by a sharp decrease for small mole fractions of methanol followed by a steady increase for larger mole fractions of methanol and suggest that these are a composite of two types of interactions. The results were analyzed using eqns. (2) and (3), ^13–16

Δ_tH^AN→mix = Δ_tH_PHYS^AN→MeOH × x_MeOH × [1 − 1.23 × x_MeOH × (1 − x_MeOH)] + Δ_tH_SI^AN→MeOH × K_se × x_MeOH/(x_AN + K_se × x_MeOH) (2)

Δ_tH^AN→MeOH = Δ_tH_PHYS^AN→MeOH + Δ_tH_SI^AN→MeOH (3)

where Δ_tH_PHYS^AN→MeOH, Δ_tH_SI^AN→MeOH, K_se, x_AN and x_MeOH stand for enthalpy of transfer from acetonitrile to mechanol due to “more physical” interaction, enthalpy of transfer from acetonitrile to mechanol due to specific interaction, equilibrium constant for the solvent exchange process on the solvation site around the anion, the mole fraction of acetonitrile and of methanol.^13–16 The first term on the right hand side of eqn. (2) expresses the enthalpy of transfer from acetonitrile to mixed solvents due to the “more physical interaction” such as electrostatic and hydrophobic interactions of the anion with solvents and the monotonic variation of the enthalpy according to the composition of the solvent mixtures.^12,13 The second term on the right hand side of eqn. (2) expresses the enthalpy of transfer from acetonitrile to mixed solvents due to a more specific or chemical interaction such as hydrogen-bonding and charge-transfer, which are effective only for a specific pair of anion and solvent, and simulates the sharp change of enthalpy for a low methanol content.^12,13 Plausible sets of parameters were determined through the following procedure: (1) for an assumed set of parameters, i.e., K_se and Δ_tH_SI^AN→MeOH, enthalpies of transfer were calculated on the basis of eqns. (2) and (3); (2) these were compared with observed quantities; (3) procedures (1) and (2) were repeated until optimum fits were attained. The most plausible set of parameters is given in Table 4 (results for the 4-nitrobenzoate ion are also given for comparison¹⁴). The experimental values could be reproduced by the calculated values with a maximum deviation of ca. ± 0.5 kJ mol⁻¹. It is noteworthy that the introduction of a substituent into the position ortho to a carboxylate group leads to a significant decrease of Δ_tH_SI^AN→MeOH for the nitro group, but to a small decrease for the 2,6-dichloro group, i.e., −31.0 for 2-nitrobenzoate vs. −28.0 for 4-nitrobenzoate and −31.5 for 2,6-dichlorobenzoate vs. −31.0 for 3,4-dichlorobenzoate (in kJ mol⁻¹), in other words, an increase in hydrogen-bonding with methanol by the ortho-substituent. Thus, the larger hydrogen-bond accepting basicity for ortho-substituted anions by comparison to para-substituted anions, as observed above, can lead to a better understanding of ortho-effects on benzoic acid dissociation in the aqueous phase.

Table 3 Enthalpies of solution, Δ_sH in acetonitrile–methanol mixtures at 25 °C (in kJ mol⁻¹)

x MeOH	TMA^a 2-nitrobenzoate	TMA 3,4-dichlorobenzoate	TMA 2,6-dichlorobenzoate
a TMA = tetramethylammonium.
0.0	25.0	21.9	18.3
0.10	0.025	−5.70	−7.60
0.25	−3.21	−8.33	−10.9
0.50	−0.992	−6.00	−8.86
0.75	2.78	−3.07	−6.28
1.0	9.82	0.64	0.080

---

Table 4 Single ion enthalpies of transfer from acetonitrile to solvent mixtures, Δ_tH^AN→mix (in kJ mol⁻¹) and interaction parameters

x MeOH	4-Nitrobenzoate^−^a	2-Nitrobenzoate^−	3,4-Dichlorobenzoate^−	2,6-Dichlorobenzoate^−	TS anion (4-nitrobenzoate^− + EtI)^b	TS anion (2-nitrobenzoate^− + EtI)	TS anion (2,6-dichlorobenzoate^− + EtI)
a Ref. 14. b Ref. 19.
0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
0.10	−23.8	−24.1	−26.7	−25.0	−4.0	−7.4	−5.4
0.25	−25.9	−26.9	−28.9	−27.9	−2.0	−6.9	−3.5
0.50	−23.5	−25.65	−27.55	−26.85	2.9	−7.35	−9.05
0.75	−19.95	−22.5	−25.3	−24.9	10.25	−6.1	5.7
1.0	−16.7	−17.9	−24.0	−20.9	25.0	−3.5	9.2
ΔtHPHYS^AN→MeOH	11.3	13.1	7.0	10.6	35.0	6.5	24.2
ΔtHSI^AN→MeOH	−28.0	−31.0	−31.0	−31.5	−10.0	−10.0	−15.0
K se	58.0	42.0	65.0	45.0	18.0	22.0	7.0
Z	2.7	2.8	—	2.9	1.0	0.8	1.2

---

On the basis of a thermodynamic cycle, enthalpies of transfer for the transition state anion from acetonitrile to mixed solvents, Δ_tH^AN→mix (TS⁻) have been calculated using eqn. (4),^12,13 and are summarized in Table 4.

ΔH^≠_mix − ΔH^≠_AN = Δ_tH^AN→mix (TS⁻) − Δ_tH^AN→mix (Nu⁻) − Δ_tH^AN→mix (EtI) (4)

These values were also analyzed by eqns. (2) and (3) and the most plausible sets of parameters are also summarized in Table 4 (results of the 4-nitrobenzoate ion reaction are given for comparison). For the 4- and 2-nitrobenzoate ion reactions, experimental values could be reproduced using these parameters with a maximum deviation of ±0.8 kJ mol⁻¹, while for the 2,6-dichlorobenzoate ion reaction, calculated values indicated a deviation of ca. 5 kJ mol⁻¹ at x_MeOH = 0.5 and 0.75. Although at the transition-state, hydrogen-bonding interactions with methanol are still significant, that is, the specific interaction enthalpy amounts to −10 to −15 kJ mol⁻¹, the physical interaction enthalpy, Δ_tH_PHYS^AN→MeOH, is the major term, and covers a wider range, 6.5–35.0 kJ mol⁻¹ (see Table 4).

Discussion

The decrease in reactivity, k, along the sequence, i.e., 4.78 × 10⁻² for the benzoate ion reaction,¹⁹ 1.20 × 10⁻² for the 3,4-dichlorobenzoate ion and 1.07 × 10⁻² dm³ mol⁻¹ s⁻¹ for the 4-nitrobenzoate ion¹⁹ and the decrease in the hydrogen-bond accepting basicity, Δ_tH_SI^AN→MeOH, i.e., −36.0 for the benzoate ion,¹⁴ −31.0 for the 3,4-dichlorobenzoate ion and −28.0 kJ mol⁻¹ for the 4-nitrobenzoate ion¹⁴ can be understood on the basis of the Hammett σ values i.e., σ_H = 0, σ_m-Cl + σ_p-Cl = 0.59 and σ_p-NO2 = 0.78.²⁰ The significant ortho-effects on the nitrobenzoate ion, in comparison to the small effects on the dichlorobenzoate ion, on hydrogen-bond accepting basicity Δ_tH_SI^AN→MeOH (i.e., −31.0 for 2-nitrobenzoate vs. −28.0 for 4-nitrobenzoate and −31.5 for 2,6-dichlorobenzoate vs. −31.0 kJ mol⁻¹ for 3,4-dichlorobenzoate) have their counterpart in the effects on the activation parameters of their reaction in acetonitrile, i.e., a stronger influence on the activation enthalpy for the former, and a stronger effect on the activation entropy for the latter (see Table 1).

For the methyl group, the substituent effects on benzoic acid dissociation change the direction from decreasing acidity to increasing acidity on shifting from the para- to the ortho-position both in the gas phase and in the aqueous phase.^21,22 In contrast, for the nitro group and for the chlorine atom the effect is increasing acidity, irrespective of the position of the substituent, with the effect being more prominent at the ortho-position.²³ In addition, increasing acidity for ortho-substituted acids in comparison to para-substituted acids is brought about through a decreasing enthalpy of dissociation, partly being compensated by decreasing entropy: ΔH° values for para- and ortho-substituted acids are 1.25 and −5.86 for the methyl group, 0.29 and −14.0 for the nitro group, and 0.96 and −10.3 kJ mol⁻¹ for the chlorine atom.²³ The larger hydrogen-bond accepting basicity for ortho-substituted anions as judged from the specific interaction enthalpy (i.e., −28.0 for 4-nitrobenzoate vs. −31.0 for 2-nitrobenzoate, −34.0 for 4-chlorobenzoate vs. −35.5 for 2-chlorobenzoate,²⁴ −31.0 for 3,4-dichlorobenzoate vs. −31.5 kJ mol⁻¹ for 2,6-dichlorobenzoate) is analogous to the trend observed for the enthalpy change, ΔH°, in the aqueous phase. Kulhanek and Exner ascribed the larger acidity for ortho-substituted benzoic acids in comparison to the relevant para-substituted acids to the intramolecular stabilization of the conjugate-base anions by electrostatic interaction in the anions.²²

Determination of the number of methanol molecules participating in hydrogen-bonding interactions with the nucleophilic and transition-state anion, Z(Nu⁻) and Z(TS⁻) is the next step to be carried out in our quantitative analysis of the reaction behavior.^19,25 Solvent effects on the activation parameter, δΔY^≠ ≡ ΔY^≠_mix − ΔY^≠_AN, can be separated into its constituents, that is, the activation parameters due to physical interaction and those due to specific interaction, δΔY^≠_PHYS and δΔY^≠_SI, using eqn. (5), where Y stands for entropy or enthalpy.^19,25

δΔY^≠ ≡ δΔY^≠_PHYS + δΔY^≠_SI (5)

The enthalpy of transfer from acetonitrile to mixed solvent due to specific interaction is given by eqn. (6) and the entropy of transfer due to specific interaction is given by eqns. (7) and (8), where ΔH_se stands for the enthalpy change for the solvent exchange process at a solvation site around an anion.^19,24

Δ_tH_SI^AN→mix = Δ_tH_SI^AN→MeOH × K_se × x_MeOH/(x_AN + K_se × x_MeOH) (6)

Δ_tS_SI^AN→mix = (ZΔH_se/T)(K_sex_MeOH)/(x_AN + K_sex_MeOH) + ZRln (x_AN + K_sex_MeOH) (7)

Δ_tH_SI^AN→MeOH = ZΔH_se (8)

When the number of methanol molecules participating in hydrogen-bonding interactions with the nucleophilic anion and transition-state anion, Z(Nu⁻) and Z(TS⁻), has been determined, the transfer entropy due to specific interaction can be calculated by substituting the value into eqn. (7) for the nucleophilic anion and for the transition-state anion. The following iterative procedures start by assuming the solvation numbers, Z(Nu⁻) and Z(TS⁻).

The activation parameter due to specific interaction is a composite of transfer quantities for the nucleophilic anion and for the transition-state anion [eqn. (9)] and then the expression for the activation parameter due to the “more physical” interaction, δΔY^≠_PHYS [eqn. (10)] can be obtained by substituting eqn. (9) into eqn. (5).

δΔY^≠_SI = Δ_tY_SI^AN→mix (TS⁻) − Δ_tY_SI^AN→mix (Nu⁻) (9)

δΔY^≠_PHYS = δΔY^≠ − Δ_tY_SI^AN→mix (TS⁻) + Δ_tY_SI^AN→mix (Nu⁻) (10)

The term δΔY^≠_PHYS is calculated by substituting into eqn. (10) the observed transfer activation parameter, δΔY^≠, and the relevant single ion quantities, which have been calculated using eqns. (6) and (7).

When a linear relationship holds between the activation enthalpy and the activation entropy due to the “ more physical” interaction, then the isokinetic temperature due to the “more physical” interaction, β_PHYS is given by eqn. (11).^19,25

δΔH^≠_PHYS = β_PHYS × δΔS^≠_PHYS (11)

Whether the empirical correlation [eqn. (11)] holds or not can be tested by systematically varying the two solvation numbers, Z(Nu⁻) and Z(TS⁻). The solvation numbers which satisfy eqn. (11) are given in Table 4, and the isokinetic temperatures due to the “more physical” interaction, β_PHYS, are summarized in Table 5. The empirical correlations [eqn. (11)] are shown in Figs. 1, 2 and 3.

Table 5 Physical interaction enthalpies for the nucleophile and transition-state anion, Δ_tH_PHYS^AN→MeOH (Nu⁻) and Δ_tH_PHYS^AN→MeOH (TS⁻), and β_PHYS

Nucleophile	ΔtHPHYS^AN→MeOH (Nu^−)/kJ mol^−1	ΔtHPHYS^AN→MeOH (TS^−)/kJ mol^−1	β PHYS/K
a Ref. 19. b Ref. 17.
Adamantanecarboxylate^−^a	6.9	3.7	(360)
Pivalate^−^a	9.5	5.5	360
2-Nitrobenzoate^−	13.1	6.5	260
Diethylacetate^−^b	8.7	15.6	340
Diphenylacetate^−^b	11.1	13.4	290
4-Methoxybenzoate^−^b	12.0	19.0	330
Benzoate^−^a	10.1	24.1	340
2,6-Dichlorobenzoate^−	10.6	24.2	300
4-Nitrobenzoate^−^a	11.3	35.0	358

---

Fig. 1 Activation enthalpy vs. activation entropy correlations for the reaction of the 4-nitrobenzoate ion with ethyl iodide in acetonitrile–methanol mixtures. ○, overall quantity; ●, “more physical” interaction quantity; curve, calculated values following procedures (1)–(4) using the parameters given in Tables 4 and 5 (see text). 1, Acetonitrile; 2, methanol. Experimental data were taken from ref. 19.

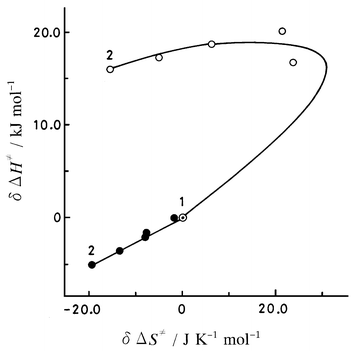Fig. 2 Activation enthalpy vs. activation entropy correlations for the reaction of the 2-nitrobenzoate ion with ethyl iodide in acetonitrile–methanol mixtures. ○, overall quantity; ●, “more physical” interaction quantity; curve, calculated values following procedures (1)–(4) using the parameters given in Tables 4 and 5 (see text). 1, Acetonitrile; 2, methanol.

Fig. 3 Activation enthalpy vs. activation entropy correlations for the reaction of the 2,6-dichlorobenzoate ion with ethyl iodide in acetonitrile–methanol mixtures. ○, overall quantity; ●, “more physical” interaction quantity; curve, calculated values following procedures (1)–(4) using the parameters given in Tables 4 and 5 (see text). 1, Acetonitrile; 2, methanol. The arrows indicate the shift of the point which would have been induced when the experimental error increased the activation enthalpy by 3.0 kJ mol⁻¹ at x_MeOH = 0.50 and decreased by 3.0 kJ mol⁻¹ at x_MeOH = 0.75.

In order to test the internal consistency of the treatment, the theoretical values of the solvent effects on the activation parameter, δΔY^≠ have been back-calculated using the following procedures.^16,25

(1) The activation enthalpy due to the “more physical” interaction can be calculated through substitution into eqn. (12) of the relevant parameters in Table 4 and the enthalpy of transfer for ethyl iodide given elsewhere.¹³

δΔH^≠_PHYS = [Δ_tH_PHYS^AN→MeOH (TS⁻) − Δ_tH_PHYS^AN→MeOH (Nu⁻)] × x_MeOH × [1 − 1.23 × x_MeOH × (1 − x_MeOH)] − Δ_tH^AN→mix (EtI) (12)

(2) The activation entropy due to the “more physical” interaction, δΔS^≠_PHYS can be calculated by substituting δΔH^≠_PHYS calculated above and β_PHYS summarized in Table 5 into eqn. (11).

(3) The activation parameters due to the more specific interaction, δΔY^≠_SI can be calculated by substituting relevant quantities calculated by eqns. (6) or (7) into eqn. (9).

(4) Finally, the overall quantities, δΔY^≠ can be obtained by substitution of the component quantities calculated above, ΔY^≠_PHYS and δΔY^≠_SI, into eqn. (5).

Comparisons of the calculated quantities with the observed ones are shown in the form of correlations between the activation enthalpy, δΔH^≠ and activation entropy, δΔS^≠ in Figs. 1, 2, and 3. The pattern of δΔH^≠vs. δΔS^≠ correlation for the 4-nitrobenzoate ion reaction (Fig. 1) is rather similar to that for the 2,6-dichlorobenzoate ion reaction (Fig. 3), but is quite different from that for the 2-nitrobenzoate ion reaction (Fig. 2). For the first two reactions the physical interaction enthalpy, Δ_tH_PHYS^AN→MeOH, increases on being transformed from a nucleophilic anion to a transition-state anion, while for the last reaction the enthalpy decreases. This is very characteristic of the 2-nitrobenzoate ion reaction. For the 4-nitrobenzoate ion reaction and for the 2-nitrobenzoate ion reaction, the observed trends are successfully simulated by the calculated quantities (Figs. 1 and 2), while for the 2,6-dichlorobenzoate ion reaction (Fig. 3) rather larger deviations are observed at x_MeOH = 0.5 and 0.75. Even though the patterns of the correlations between the overall quantities are different for the three reactions, the linear correlations hold between the “more physical” interaction quantities. This suggests that the separation of the overall quantities into their components is crucial for a molecular mechanistic understanding of the reaction behavior, and that the characteristics of the reaction system are incorporated into the parameters derived through the present analysis.

The enthalpy change accompanying the solvent exchange at a solvation site around the anion, ΔH_se (= Δ_tH_SI^AN→MeOH/Z), is very similar for both the nucleophilic anions and transition-state anions, as observed elsewhere,¹⁵i.e., with respect to the reactions discussed in this work, the average value is −10.8 for the former and −11.7 kJ mol⁻¹ for the latter. This suggests that the characteristics of the hydrogen-bonding interaction do not change much on going from the reactant to the transition-state. The physical interaction enthalpies, Δ_tH_PHYS^AN→MeOH, for nucleophilic anions in which the anionic charge is distributed over a smaller number of atoms are quite comparable, while for transition-state anions in which the charge is dispersed over a larger number of atoms characteristic molecular properties are reflected in the enthalpy (Table 5) Except for the ortho-substituted transition-state anions, the enthalpy increases according to the character of α-carbon along the sequence: tertiary, 3.7–5.5 < secondary, 13.4–15.6 < aromatic with an electron-donating substituent at the para-position, 19.0 < unsubstituted aromatic, 24.1 < aromatic with an electron-withdrawing substituent at the para-position, 35.0. This observation suggests that for transition-state anions that have an aliphatic carbon moiety, the approach of the solvent molecules to the α-carbon and to the central carbon atom in the carboxylate group is crucial for determining the physical interaction enthalpy, Δ_tH_PHYS^AN→MeOH. Although an aromatic carbon moiety provides the chance of a larger number of solvent molecules to sense the presence of the partial dipole in a solute, the increased distribution of negative charge along the longitudinal direction induced by an electron-withdrawing substituent at the para-position seems to be vital. When a nitro group is introduced into the position ortho to the carboxylate group, the carboxylate group is twisted out of the molecular plane, which thus reduces the resonance interaction between the phenyl ring and the carboxylate group. As a result, the electron-withdrawing effect of the nitro group is reduced, resulting in an increased hydrogen-bond accepting basicity in comparison with the 4-nitrobenzoate ion (Table 4). In addition, especially at the transition state, the approach of solvent molecules to the carboxylate carbon and to one of the oxygen atoms in the carboxylate group is sterically hindered. This leads to a reduced physical interaction enthalpy. In the 2,6-dichlorobenzoate ion, the carboxylate group is twisted out of the plane of the phenyl ring by the two chlorine atoms substituted at the ortho-positions. This results in an increased hydrogen-bond accepting basicity, although it is less significant in comparison to that of the 2-nitrobenzoate ion (Table 4). These chlorine atoms play a dual role: firstly to sterically hinder the approach of solvent molecules to the α-carbon atom and to the central carbon atom in the carboxylate group, and secondly to enable a larger number of solvent molecules surrounding the chlorine atoms to sense the charge of the carboxylate group through their polarization over wider areas, especially at the transition state. The second factor seems to be important in an increased physical interaction for the transition-state anion of the 2,6-dichlorobenzoate ion reaction in comparison to that of the 2-nitrobenzoate ion reaction.

Concluding remarks

The separation of the solute–solvent interaction into, at least, two components, i.e., a “more physical” interaction and a specific interaction, is indispensable for the quantitative molecular mechanistic understanding of the reaction behavior in mixed solvents. In nucleophiles where the negative charge is more concentrated on two oxygen atoms, a specific interaction, in which a restricted number of solvent molecules around the oxygen atoms can participate, plays the major role. In transition-state anions where the negative charge is distributed over a larger number of atoms (although specific interaction is still significant), the more characteristic solute–solvent interaction is that of a “more physical” interaction in which an unrestricted number of solvent molecules surrounding the partial dipoles in a solute can participate. Comparable isokinetic temperatures due to the “more physical” interaction indicate that the enthalpy vs. entropy compensation law holds for weak interactions, which are really the basis of “more physical” interactions. The results provide practical cases for the view that the enthalpy–entropy compensation is a consequence of weak interactions where the binding enthalpy is much lower than the typical covalent bond strength.^26,27

Experimental

Materials

Tetramethylammonium salts containing the conjugate-base anions of substituted benzoic acid were prepared from tetramethylammonium hydroxide and the relevant acid in methanol as described elsewhere²⁸ and recrystallized three times from acetonitrile; the results of elemental analysis are shown in Table 6. Other materials were treated as described elsewhere.^12,13,16,17

Table 6 Solvents for recrystallization and results of elemental analysis

	Solvents	Obs. (%)			Formula	Calc. (%)
		C	H	N		C	H	N
Tetramethylammonium 2-nitrobenzoate	Acetonitrile	54.9	6.72	11.70	C11H16N2O4	55.0	6.71	11.66
Tetramethylammonium 3,4-dichlorobenzoate	Acetonitrile	49.9	5.48	5.31	C11H15NO2Cl2	50.02	5.72	5.30
Tetramethylammonium 2,6-dichlorobenzoate	Acetonitrile	49.9	5.60	5.46	C11H15NO2Cl2	50.02	5.72	5.30

---

Enthalpy of solution measurements

Enthalpies of solution, Δ_sH, for tetramethylammonium salts were measured at 25.0 ± 0.1 °C with a Tokyo Riko twin isoperibol calorimeter.^12–15 Final concentration ranges of the salts were (0.4–1.5) × 10⁻² mol dm⁻³ and the experimental errors were estimated to be ca. 0.7 kJ mol⁻¹.

Product analysis and kinetic procedures

Stock solutions of ethyl iodide and of the relevant tetraalkylammonium salts were mixed in a round-bottomed flask and kept overnight. After near completion of the reaction, the reaction mixture was carefully evaporated to dryness and the solid precipitate was washed several times with several portions of ether. The solvent ether was evaporated to near dryness and the uncharged reaction product was dissolved in chloroform. The ¹H NMR spectra of the uncharged reaction product agreed with those of the relevant ethyl benzoate.

Reaction rates were calculated by the determination of amount of iodide ion formed from the reaction by means of potentiometric titration using silver nitrate solution and rates were measured at four of the following temperatures, 20.0, 30.0, 40.0, 50.0 and 60.0 °C. Experimental errors were estimated to be ca. 1.4%, 0.5 kJ mol⁻¹ and 1.6 J K⁻¹ mol⁻¹ respectively for rate constants, activation enthalpies and activation entropies in acetonitrile and a little larger in mixed solvents: 3%, 1.7 kJ mol⁻¹ and 5.2 J K⁻¹ mol⁻¹.

Acknowledgements

Y. K. thanks Dr M. H. Abraham, University College, London for helpful discussions and for his critical reading of the original version of this manuscript.

References

1. E. L. Eliel, in Steric Effects in Organic Chemistry, ed. M. S. Newman, John Wiley & Sons, Inc., NY, 1956, ch. 2, p. 62.
2. C. K. Ingold, Structure and Mechanism in Organic Chemistry, 2nd edn., Cornell University Press, Ithaca and London, 1969.
3. L. P. Hammett, Physical Organic Chemistry, 2nd edn., McGraw-Hill, NY, 1970.
4. R. W. Taft, Jr., in Steric Effects in Organic Chemistry, ed. M. S. Newman, John Wiley & Sons, Inc., N.Y., 1956, ch. 13, p. 556.
5. J. M. Harris and S. P. McManus, in Nucleophilicity, eds. J. M. Harris and S. P. McManus, Advances in Chemistry Series, No. 215, American Chemical Society, Washington DC, 1987, ch. 1.
6. F. G. Bordwell, J. A. Cripe and D. L. Hughes, in Nucleophilicity, eds. J. M. Harris and S. P. McManus, Advances in Chemistry Series, No. 215, American Chemical Society, Washington DC, 1987, ch. 9.
7. W. N. Olmsted and J. I. Brauman, J. Am. Chem. Soc., 1977, 99, 4219.
8. J. I. Brauman, J. A. Dodd and C.-C. Han, in Nucleophilicity, eds. J. M. Harris and S. P. McManus, Advances in Chemistry Series, No. 215, American Chemical Society, Washington DC, 1987, ch. 2, p. 23.
9. W. L. Hase, H. Wang and G. L. Peslherbe, in Advances in Gas-Phase Ion Chemistry, eds. N. G. Adams and L. M. Babcock, JAI Press, London, 1998, ch. 3, p. 125.
10. V. F. DeTuri, P. A. Hintz and K. M. Ervin, J. Phys. Chem., 1997, 101, 5969.
11. A. J. Parker, Chem. Rev., 1969, 69, 1.
12. Y. Kondo, K. Yuki, T. Yoshida and N. Tokura, J. Chem. Soc., Faraday Trans. 1, 1980, 76, 812.
13. Y. Kondo, M. Ittoh and S. Kusabayashi, J. Chem. Soc., Faraday Trans. 1, 1982, 78, 2793.
14. Y. Kondo, T. Fujiwara, A. Hayashi and S. Kusabayashi, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 2931.
15. Y. Kondo, W. Sugitani and M. Tokui, J. Chem. Soc., Faraday Trans., 1992, 88, 3019.
16. Y. Kondo, O. Nonaka, K. Iwasaki, K. Kuwamoto and T. Takagi, J. Chem. Soc., Perkin Trans. 2, 1994, 437.
17. Y. Kondo, W. Sugitani, M. Tokui and T. Takagi, J. Chem. Soc., Perkin Trans. 2, 1995, 1049.
18. J. Shorter, Correlation Analysis of Organic Reactivity. With particular reference to multiple regression, Research Studies Press, Chichester, 1982.
19. Y. Kondo, T. Fujiwara, A. Hayashi, S. Kusabayashi and T. Takagi, J. Chem. Soc., Perkin Trans. 2, 1990, 741.
20. H. Maskill, The physical basis of organic chemistry, Oxford University Press, Oxford, 1985, ch. 5, p. 156.
21. M. Decouzon, P. Ertl, O. Exner, J.-F. Gal and P.-C. Maria, J. Am. Chem. Soc., 1993, 115, 12071.
22. J. Kulhanek and O. Exner, J. Chem. Soc., Perkin Trans. 2, 1998, 1397.
23. J. W. Larson and L. G. Hepler, in Solute–Solvent Interactions, eds. J. F. Coetzee and C. D. Ritchie, Marcel Dekker, New York and London, 1969, vol. 1, ch. 1, p. 1.
24. Y. Kondo, N. Imazaike and R. Ichino, unpublished results.
25. Y. Kondo, K. Kondo and S. Kusabayashi, J. Chem. Soc., Perkin Trans. 2, 1993, 1141.
26. M. S. Searle, M. S. Westwell and D. H. Williams, J. Chem. Soc., Perkin Trans. 2, 1995, 141.
27. C. T. Calderone and D. H. Williams, J. Am. Chem. Soc., 2001, 123, 6262.
28. Y. Kondo, S. Kusabayashi and T. Mitsuhashi, J. Chem. Soc., Perkin Trans. 2, 1988, 1799.

---