EPR and computational studies of the formation and β-scission of cyclic and acyclic dialkoxyalkyl radicals
Received
(in Cambridge, UK)
11th July 2001
, Accepted 6th November 2001
First published on 3rd December 2001
Abstract
EPR spectroscopy and density functional theory have been applied to study the formation and subsequent β-scission of a series of dialkoxyalkyl radicals. Abstraction of hydrogen by photochemically-generated tert-butoxyl radicals from acyclic acetals R1O(R2O)CHR3, and from cyclic analogues derived from diols, takes place mainly from the acetal carbon atom to give radicals of the type R1O(R2O)ĊR3 and relative rates of abstraction have been determined in competition experiments. When R3
= phenyl or vinyl, the activating influence of these substituents on hydrogen-atom abstraction is smaller than might be expected, probably because delocalisation of the unpaired electron on to the unsaturated group comes at the expense of planarisation at Cα, in opposition to the natural pyramidalising tendency of the two α-alkoxy groups. Absolute rate constants and Arrhenius
activation parameters for β-scission of R1O(R2O)ĊR3 have been determined by a steady-state EPR method and the results can be understood in terms of angle-strain and stereoelectronic effects. β-Scission of selected cyclic dialkoxyalkyl radicals that carry a phenyl or vinyl substituent at the radical centre has been investigated using density functional theory at the UB3LYP/6-31G(d,p) level. Computed activation parameters are in good agreement with the experimental results, where comparison is possible. Both experiment and theory indicate that benzylic 2-phenyl-1,3-dioxan-2-yl radicals undergo β-scission more readily than the corresponding allylic 2-vinyl-1,3-dioxan-2-yl radicals.
Ongoing research in our laboratory is concerned with the application of polarity-reversal catalysis1 (PRC) by thiols to mediate the radical-chain deoxygenation of alcohols, diols and related compounds.2–4 For example, in the presence of an initiator and a thiol catalyst, an acetal 1 formally derived from two alcohols R1OH and R2OH (or from the diol HOR1R2OH) can undergo a radical-chain redox reaction that affords a reduced product R1H and an ester of R2OH, as shown in eqn. (1). In the case of a cyclic acetal derived from a diol, the two product functional groups are joined, such that the overall reaction represents a redox rearrangement process.
| |

| (1) |
The propagation stage of the chain mechanism is shown in Scheme 1 and abstraction of hydrogen from the acetal by the thiyl radical (step a) and β-scission of dialkoxyalkyl radical 2 (step b) are key elementary processes that must both be rapid if the overall reaction is to be effective; step c is uniformly fast for abstraction of hydrogen from thiols by simple alkyl radicals. In general, in order to plan successful radical-chain reactions it is necessary to understand the factors that are important in determining the rates of the elementary steps involved. In the present paper we report an EPR spectroscopic study of hydrogen-atom abstraction by tert-butoxyl radicals from acyclic and cyclic acetals to form the corresponding dialkoxyalkyl radicals. Although tert-butoxyl radicals abstract hydrogen much more rapidly from CH groups than do thiyl radicals, both species are electrophilic and their
reactivity patterns should be qualitatively similar. We have also used EPR spectroscopy to determine the absolute rates of β-scission for selected dialkoxyalkyl radicals (Scheme 1, step b) and have carried out density functional calculations to compute the activation barriers for selected examples of these cleavage processes.
 |
| | Scheme 1 | |
Results and discussion
Reaction kinetics
Relative rate constants were determined using well-established kinetic EPR methods,5–7 in which transient radical intermediates are generated continuously and their steady-state concentrations are monitored directly. Di-tert-butyl peroxide (DTBP) was subjected to photolysis with high-intensity UV light in the presence of an acetal hydrogen-atom donor RH and, if appropriate, a reference hydrogen donor SH to permit the determination of the relative reactivity of RH. The relevant reactions are generalised in Scheme 2, where hydrogen abstraction from RH is shown as taking place at two sites to give radicals A˙ and B˙, respectively, and the radical B˙ is transformed (by β-scission) into the radical C˙. It is assumed that all the radicals present in detectable concentrations are removed at the diffusion-controlled rate by self- and cross-reactions with other such radicals
with rate constants 2kt and kx, respectively, which are independent of the nature of the radicals involved; it is further assumed that 2kt
=
kx.5–7 Under these conditions, eqns. (2) and (3) apply to the steady-state radical concentrations determined by EPR spectroscopy.
| | |
(k1/k2) = [A˙]/([B˙] + [C˙])
| (2) |
| | |
(k1/kS) = ([A˙]/[S˙]) × ([SH]/[RH])
| (3) |
| | |
(kβ/2kt) = ([C˙]/[B˙]) × ([A˙] + [B˙] + [C˙])
| (4) |
| | |
2kt(But˙)solvent
= 2kt(But˙)heptane
× (ηheptane/ηsolvent)
| (5) |
 |
| | Scheme 2 | |
In the absence of SH, the rate constant for β-scission of B˙ can be determined relative to 2kt using eqn. (4).8,9 The value of 2kt for all the transient radicals is taken as equal to the corresponding value for the tert-butyl radical in the same solvent at the same temperature, obtained from the reliable measurements reported by Schuh and Fischer.10 For tert-butylbenzene and fluorobenzene solvents, experimental values of 2kt(But˙) are not available and the published data for heptane solvent were scaled using solvent viscosities11 according to eqn. (5).10 The Arrhenius relationship for 2kt obtained in this way by Walton12 for tert-butylbenzene
solvent is given in eqn. (6), where θ
= 2.303RT kJ mol−1. The corresponding relationship for fluorobenzene, obtained by us in the same manner, is given in eqn. (7). Schuh and Fischer10 have reported experimental values for 2kt(But˙) in 3-methylpentan-3-ol (3MP) and their results in the temperature range 330–370 K, appropriate for this work, conform to the Arrhenius relationship shown in eqn. (8).
| | |
log10 [2kt(PhBut)/M−1 s−1] = 12.17 − 14.64/θ
| (6) |
| | |
log10 [2kt(PhF)/M−1 s−1] = 11.59 − 10.17/θ
| (7) |
| | |
log10 [2kt(3MP)/M−1 s−1] = 12.81 − 18.41/θ
| (8) |
Hydrogen-atom abstraction from acetals
Relative molar rate constants for abstraction of hydrogen from cyclic and acyclic acetals by tert-butoxyl radicals were determined by competition experiments at 229 K in fluorobenzene solvent. One of the two competing acetals was always either 1,3-dioxolane or 2-methyl-1,3-dioxolane, chosen to avoid line overlap with the radical(s) derived from the second acetal. Stock mixtures of the two compounds were made up by weight and aliquots were mixed with DTBP (15–20% v/v) and diluted with fluorobenzene; the total acetal concentration was ca. 1.5 M. The sample was cooled in an ice bath, to avoid evaporative loss, in a standard Suprasil quartz EPR tube and de-oxygenated by bubbling a fine stream of argon through the liquid. EPR spectra were monitored during continuous UV irradiation of samples positioned in the variable-temperature insert of the spectrometer; relative radical concentrations were determined by double integration of appropriate lines and confirmed
by computer simulation of the spectra. Relative rates of hydrogen-atom abstraction from the acetals 3–12 to give the radicals 13–25 were investigated and the results are summarised in Table 1. The radicals 26–36 were also generated in this work, either by hydrogen abstraction from the parent acetals or by β-scission of the dialkoxyalkyl radicals derived from them; the EPR parameters of all radicals are collected in Table 2.
Table 1 Relative and absolute rate constants for hydrogen abstraction from acetals by tert-butoxyl radicals in fluorobenzene at 229 Ka
| Entry |
Acetal |
Site of reaction |
k(relative) |
k(absolute)b/M−1 s−1 |
|
Rate constants are not statistically corrected on the basis of the number of equivalent abstractable hydrogen atoms.
Obtained by taking the rate constant for abstraction from 2-methyl-1,3-dioxolane to be 4.34 × 106 M−1 s−1 at 229 K.
|
| 1 |
(MeO)2CH23 |
CH2 |
(1) |
5.2 × 104 |
| |
|
CH3O |
1.0 |
5.2 × 104 |
| 2 |
ButO(MeO)CH24 |
CH2 |
1.5 |
7.8 × 104 |
| |
|
CH3O |
0.6 |
3.1 × 104 |
| 3 |
(MeO)2CHMe 5 |
CHMe |
3.4 |
1.8 × 105 |
| |
|
CH3O |
1.6 |
8.4 × 104 |
| 4 |
(MeO)2CHPh 6 |
CHPh |
6.5 |
3.4 × 105 |
| 5 |
1,3-Dioxolane 7 |
C(2)H2 |
37 |
1.9 × 106 |
| 6 |
2-Methyl-1,3-dioxolane 8 |
C(2)HMe |
83 |
(4.3 × 106) |
| 7 |
2-Phenyl-1,3-dioxolane 9 |
C(2)HPh |
40 |
2.1 × 106 |
| 8 |
2-Phenyl-1,3-dioxane 10 |
C(2)HPh |
48 |
2.5 × 106 |
| 9 |
2-Vinyl-1,3-dioxolane 11 |
C(2)HVin |
69 |
3.6 × 106 |
| 10 |
2-Vinyl-1,3-dioxane 12 |
C(2)HVin |
92 |
4.8 × 106 |
Table 2 EPR parameters for dialkoxyalkyl radicals and for the radicals produced by their β-scission
| Radicala |
Solvent |
T/K |
Hyperfine splittings/Gb |
|
The g-values of all dialkoxyalkyl radicals are 2.0031 ± 0.0002; those of the alkyl radicals formed by β-scission are all 2.0028 ± 0.0001.
Generally ±0.05 G, except where the lines were relatively broad. However, simulations of the spectra of allylic and benzylic radicals were often very sensitive to the exact relationships between the coupling constants.
Ref. 20.
Relatively broad lines.
syn- and anti-Isomers were detectable; the coupling constants for the major (65%) isomer are given. The minor isomer (35%) showed 14.99 (1 H), 14.01 (1 H), 2.28 (1 H) and 0.91 (2 H).
The EPR spectra of the syn- and anti-isomers,
assuming that both are present, could not be resolved within the line-width.
|
|
13
|
PhF |
223 |
12.9 (1 Hα), 0.81 (6 Hγ) |
|
14
|
PhF |
223 |
18.3 (2 Hα), 0.78 (2 Hγ) |
|
15
|
PhF |
213 |
11.3 (1 Hα), 0.91 (3 Hγ) |
|
16
|
PhF |
213 |
18.0 (2 Hα), 0.87 (2 Hγ) |
|
17
|
PhF |
223 |
14.1 (3 Hβ), 0.68 (6 Hγ) |
|
18
|
PhF |
223 |
17.8 (2 Hα), 0.30 (1 Hγ) |
|
19
|
PhF |
223 |
6.15 (1 Hp), 5.04 (2 Ho), 1.60 (2 Hm), 0.23 (6 Hγ) |
|
20
|
PhF |
223 |
22.1 (1 Hα), 1.46 (4 Hγ) |
|
21
|
PhF |
223 |
13.2 (3 Hβ), 1.19 (4 Hγ) |
|
22
|
PhF |
223 |
6.88 (1 Hp), 5.25 (2 Ho), 1.64 (2 Hm), 0.96 (4 Hγ) |
|
23
|
PhF |
260 |
6.40 (1 Hp), 4.90 (2 Ho), 1.52 (2 Hm), 0.76 (4 Hγ) |
|
24
|
PhF |
200 |
15.06 (1 H), 14.32 (1 H), 2.26 (1 H), 1.20 (2 H), 0.84 (2 H) |
|
25
|
PhF |
229 |
13.97 (1 H), 13.36 (1 H), 2.70 (1 H), 0.68 (2 H), 0.56 (2 H) |
|
26
c
|
c-C3H6 |
233 |
21.3 (1 Hα) |
|
27
b
|
PhH |
353 |
21.8 (6 Hβ), 0.7 (6 Hγ), 2.2 (CHO) |
|
28
|
PhBut |
203 |
6.93 (1 Hp), 5.32 (2 Ho), 1.68 (2 Hm), 1.16 (2 Hγ) |
|
29
|
PhBut |
388 |
23.3 (6 Hβ), 15.9 (2 Hβ) |
|
30
|
PhBut |
229 |
6.14 (1 Hp), 4.96 (2 Ho), 1.55 (2 Hm), 1.15 (2 Hγ) |
|
31
|
PhBut |
340 |
23.3 (6 Hβ), 17.3 (2 Hβ) |
|
32
d
|
PhBut |
230 |
5.99 (1 Hp), 5.15 (2 Ho), 1.61 (2 Hm), 1.04 (2 Hγ) |
|
33
|
PhBut |
320 |
33.0 (4 Hβ), 19.1 (2 Hβ) |
|
34
e
|
PhBut |
229 |
14.94 (1 H), 14.15 (1 H), 2.27 (1 H), 1.26 (2 H) |
|
35
f
|
PhBut |
229 |
14.14 (1 H), 13.50 (1 H), 2.64 (1 H), 1.03 (2 H) |
|
36
|
PhBut |
229 |
6.47 (1 Hp), 5.25 (2 Ho), 1.70 (2 Hm) |
The temperature-dependence of the rate constant k3 for hydrogen-atom abstraction from 2-methyl-1,3-dioxolane 8 by tert-butoxyl radicals has been measured by Malatesta and Scaiano13 using the laser-flash photolysis method and the Arrhenius relationship obtained is given in eqn. (9). Our EPR results show that abstraction of hydrogen from 8 takes place effectively exclusively from C(2) and so the value of k3 at 229 K (4.34 × 106 M−1 s−1) obtained from eqn. (9) can be used to put our relative rate data on to an absolute basis; these results are included in Table 1.
| | |
log10 (k3/M−1 s−1) = (8.63 ± 0.26) − (8.74 ± 1.34)/θ
| (9) |
Abstraction of hydrogen from 3–5 takes place competitively from the acetal CH and O-methyl groups and the relative reactivities of 3 and 4 are essentially as expected on statistical grounds (entries 1 and 2). The methyl group attached to the acetal carbon atom in 5 (entry 3) exerts a significant activating effect on abstraction of the remaining tertiary hydrogen atom. The effect of the phenyl group at the acetal carbon atom in 6 (entry 4) is even more activating towards abstraction of the tertiary hydrogen and it was not possible to measure the much lower reactivity of the O-methyl groups. Cyclic and acyclic dialkoxyalkyl radicals, in which hydrogen or an alkyl group is attached to the trivalent carbon atom, are strongly pyramidal at this centre.14,15 However, if an α-phenyl group is present then the radical centre is believed to be effectively planar.16 Such planarity allows full benzylic delocalisation of the unpaired electron on to the phenyl group (as indicated by the ring-proton hyperfine splittings), but this comes at the expense of frustrating the inherent pyramidalising effect of the two α-oxygen substituents. Thus, the activating effect of the phenyl group in 6 is not as large as might be expected by comparison with molecules in which the product radical centre is naturally close to planar.
The high reactivity of the hydrogen atom attached to the acetal carbon C(2) in 1,3-dioxolane 7 (entry 5) is probably mainly a consequence of stereoelectronic effects.13 Thus, the C(2)–H bonds subtend a relatively small and fixed dihedral angle with the lone pairs on the adjacent oxygen atoms and the transition state is effectively stabilised by charge transfer (polar effects) of the type [RO− H˙
+CH(OR)2].13,17 The activating effect of the 2-methyl group in 8 (entry 6) is similar to that found for the acyclic analogue 5 in comparison with 3.
The relatively low reactivities of the C(2)–H groups in the benzylidene acetals 9 and 10 (entries 7 and 8), compared with that in 2-methyl-1,3-dioxolane 8, is surprising at first sight, in view of the fact that the phenyl group in 6 is more activating than the 2-methyl group in acetal 5. However, the radical centres in the cyclic benzylic radicals 22 and 23 are both planar16 (see Table 2 and the computational section), which introduces angle strain into the 5- and 6-membered rings when hydrogen is abstracted from C(2) in their protic parents 9 and 10.
In contrast, the OCO angle in the acyclic analogue 19 derived from 6 is free to open to ca. 120°.
2-Vinyl-1,3-dioxolane 11 (entry 9) is intermediate in reactivity between the 2-phenyl analogue 9 and the 2-methyl analogue 8. 2-Vinyl-1,3-dioxane 12 (entry 10) is similarly more reactive than 2-phenyl-1,3-dioxane 10 but, nevertheless, the 2-vinyl groups in 11 and 12 are still less activating than might be expected. The radical centres in the derived allylic radicals 24 and 25 must be near-planar (as judged from their EPR spectra) and presumably the reason for the relatively low reactivities of the allylic CH groups in 11 and 12
is analogous to that given for the low reactivity of the benzylic CH groups in the 2-phenyl derivatives. The low reactivities of 11 and 12 towards hydrogen-atom abstraction at C(2) are consonant with the relatively small amount of isomerisation of these acetals to the corresponding enol ethers observed under radical-chain conditions.18 Both results can be seen as a consequence of the strain developed in the rings when C(2) becomes a planar, sp2-hybridised centre.
β-Scission of dialkoxyalkyl radicals
The β-scission processes shown in eqns. (10)–(15) were considered. Samples usually consisted of the acetal (ca. 15% v/v) and DTBP (ca. 20% v/v) in fluorobenzene, tert-butylbenzene or 3-methylpentan-3-ol as solvent and absolute radical concentrations were determined by comparison with the signal obtained from a standard solution of 2,2,6,6-tetramethylpiperidine-N-oxyl (TEMPO) in fluorobenzene. Values of kβ over a range of temperatures, for which EPR spectra of both the parent radical and its β-scission product were detectable, were obtained using eqn. (4) in conjunction with the appropriate value of 2kt derived from eqns. (6)–(8). The Arrhenius plots are shown in Figs. 1–6
and the linear regression lines correspond to the activation parameters given in Table 3. For the dialkoxyalkyl radicals 15, 28, 30 and 32, in which the alkoxy substituents differ, only cleavage of the tertiary carbon–oxygen bond was observed. For the dioxolanyl and dioxanyl radicals 20–25 without substituents on the alkoxy carbon atoms, β-scission was not detectable by EPR spectroscopy below ca. 390 K.
| |

| (10) |
| |

| (11) |
| |

| (12) |
| |

| (13) |
| |

| (14) |
| |

| (15) |
Table 3 Arrhenius parameters for β-scission of dialkoxyalkyl radicals
| Entry |
Dialkoxyalkyl radical |
Product radical |
Solvent |
log10 (Aβ/s−1)a |
E
a
β/kJ mol−1b |
k
β(298 K)/s−1 |
|
Estimated error ±0.3.
Estimated error ±1.0 kJ mol−1.
Values of log10 (Aβ/2At) and (Eβ
−
Et) taken from ref. 20.
Taking log10 (2kt/M−1 s−1) = 11.19 − 4.19/θ in cyclopropane solvent, calculated from viscosity data as described in the text.
log10 (kβ/M−1 s−1) = 13.0 − 66.9/θ (kβ
= 19 M−1 s−1 at 298 K) is recommended in ref. 22a.
|
| 1 |
15
|
But˙ |
PhF |
12.0 |
33.8 |
1.2 × 106 |
| 2 |
37
c
|
But˙ |
c-C3H6 |
12.2c,d |
36.4c,d |
6.7 × 105 |
| 3 |
26
|
27
|
PhBut |
14.5 |
66.1 |
8.3 × 102 |
| 4 |
26
|
27
|
3MP |
14.3 |
63.4 |
1.6 × 103 |
| 5 |
28
|
29
|
PhBut |
13.1e |
62.0e |
1.7 × 102e |
| 6 |
28
|
29
|
3MP |
13.4 |
62.4 |
2.9 × 102 |
| 7 |
30
|
31
|
PhBut |
13.2 |
59.8 |
5.3 × 102 |
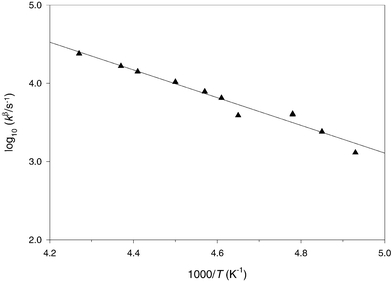 |
| | Fig. 1 Arrhenius plot for the β-scission of the tert-butoxy(methoxy)methyl radical 15 in fluorobenzene | |
 |
| | Fig. 2 Arrhenius plot for the β-scission of the 4,4,5,5-tetramethyl-1,3-dioxolan-2-yl radical 26 in tert-butylbenzene | |
 |
| | Fig. 3 Arrhenius plot for the β-scission of the 4,4,5,5-tetramethyl-1,3-dioxolan-2-yl radical 26 in 3-methylpentan-3-ol | |
 |
| | Fig. 4 Arrhenius plot for the β-scission of the 2-phenyl-4,4-dimethyl-1,3-dioxolan-2-yl radical 28 in tert-butylbenzene | |
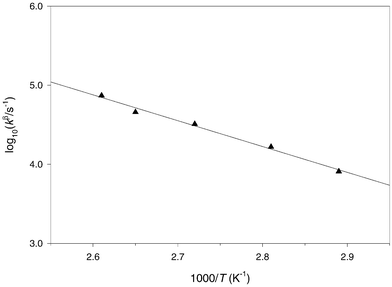 |
| | Fig. 5 Arrhenius plot for the β-scission of the 2-phenyl-4,4-dimethyl-1,3-dioxolan-2-yl radical 28 in 3-methylpentan-3-ol | |
 |
| | Fig. 6 Arrhenius plot for the β-scission of the 2-phenyl-4,4-dimethyl-1,3-dioxan-2-yl radical 30 in tert-butylbenzene | |
In this context, it is important not to focus solely on the nature of the radical centre in the product and caution must be exercised when qualitatively assessing the enthalpy changes associated with alternative modes of homolytic cleavage.3,4 For example, while 31 contains a stabilised tertiary alkyl radical centre, it is also a primary alkyl benzoate. The alternative mode of β-scission of 30 would give BzOCMe2CH2CH2˙ and, although this species contains a less stabilised primary radical centre, it is also a tertiary alkyl benzoate. Since, provided steric crowding is unimportant, branched molecules are generally more stable than their straight-chain isomers,11,19 the relative stabilities of the ester moieties will act to offset the relative stabilities of the alkyl radical moieties and
tend to make the enthalpies of reaction for the two modes of cleavage for 30 more similar than would be anticipated by consideration of the radical centres alone. At the UB3LYP/6-31G(d,p) level (see computational section), the enthalpy of formation of the tertiary alkyl radical 31 is calculated to be lower than that of the primary radical BzOCMe2CH2CH2˙, but by only 14.7 kJ mol−1, less than might be expected in view of the difference in enthalpies of formation11 of the tert-butyl and the n-butyl radicals (29.1 kJ mol−1). To illustrate the point further using experimental data,11 although the tert-butyl radical is more stable than the n-butyl radical by 29.1 kJ mol−1, the C–Cl bond dissociation enthalpies for
But–Cl and Bun–Cl are almost the same at 355 and 357 kJ mol−1, respectively, because tert-butyl chloride is more stable than n-butyl chloride by 27.8 kJ mol−1. The difference in stability of But–X and Bun–X decreases as X becomes less electronegative11,19c but, even with a methyl substituent attached to carbon, the But–Me and Bun–Me bond strengths (366 and 374 kJ mol−1, respectively) differ by only 8 kJ mol−1. Thus, the increased stability of the branched molecules compared to their straight-chain counterparts11,19 acts in opposition to the increased stability of the tert-butyl radical relative to the n-butyl radical to render the C–X bonds relatively similar in strength.
β-Scission of the tert-butoxy(methoxy)methyl radical 15 [eqn. (10)] to give the tert-butyl radical (entry 1) is very rapid above room temperature, in accord with our demonstration that tertiary alcohols can be successfully deoxygenated via thiol-catalysed radical-chain decomposition of their methoxymethyl ethers.2 The activation parameters for the β-scission of 15 are very similar to those obtained previously20 for the corresponding cleavage of the di-tert-butoxymethyl radical 37 [eqn. (11), entry 2], when the latter are recalculated using revised values for log10(2At) and Et applicable to cyclopropane as solvent (see Table
3) and consistent with the values used in the present work.
Our quantitative kinetic data for the ring opening of the dioxolanyl radical 26 [eqn. (12), entry 3] support the previous qualitative conclusion20 that this cyclic radical undergoes β-scission much less readily than analogous acyclic dialkoxyalkyl radicals such as 15 and 37. The transition states for this type of β-scission process appear to be product-like (see computational section) and the rate difference can be attributed in part to the angle strain that develops at C(2) in the transition structure for β-scission of the cyclic radical, as a result of planarisation at this centre. Stereoelectronic factors probably also play a part, because the need to achieve maximum overlap between the O–CMe2 bond undergoing cleavage and the orbital of the unpaired electron is
frustrated by the constraints imposed by the cyclic nature of the transition state.
β-Scission of alkoxyl radicals [eqn. (16)] is facilitated by polar solvents, particularly by hydrogen-bond donor solvents, that stabilise the transition state more than the ground state.21
β-Scission of an alkoxyalkyl radical [eqn. (17)] is a closely related process and so the ring opening of 26 to give the β-formyloxyalkyl radical 27 was also studied in 3-methylpentan-3-ol as solvent (entry 4). Although the rate of β-scission was greater in the alcohol solvent, the increase was relatively small.
| |

| (16) |
| |
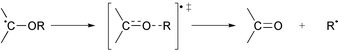
| (17) |
The β-scission of the 2-phenyl-1,3-dioxolanyl radical 28 in tert-butylbenzene solvent [eqn. (13), entry 5] has been studied previously by Ingold and co-workers.22 Our results indicate that ring opening of 28 to give the β-benzoyloxyalkyl radical 29 is rather more rapid than reported previously and the difference is attributable mainly to a lower activation energy determined in the present work. β-Scission of the benzylic radical 28 is only about 6 times slower at 298 K than opening of the unsubstituted analogue 26, which would be expected to cleave twice as fast as 28 simply on statistical grounds. The geometry at C(2) is planar in 28, as it is at this carbon atom in the product ester radical 29, while in 26 C(2) is strongly pyramidal and this centre has to become planar in the product formate. Thus, there is less structural reorganisation on going to the transition structure for cleavage of 28, compared with the situation for 26, and this will act to offset the loss of benzylic stabilisation that accompanies β-scission. The effect of the substituent at C(2) on the stability of the emerging C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in the transition state is probably also important in determining the activation energy for β-scission. As was found for β-scission of 26, there is only a modest increase in the rate of ring opening of 28 on moving from tert-butylbenzene
to 3-methylpentan-3-ol as solvent (entry 6).
O bond in the transition state is probably also important in determining the activation energy for β-scission. As was found for β-scission of 26, there is only a modest increase in the rate of ring opening of 28 on moving from tert-butylbenzene
to 3-methylpentan-3-ol as solvent (entry 6).
β-Scission of 30 [eqn. (14), entry 7], the six-membered-ring analogue of 28, takes place more readily than cleavage of the latter. The ring opening of 30 to give 31 is calculated to be more exothermic by 5 kJ mol−1 than corresponding β-scission of 28 (see computational section) and, since the transition states are product-like, this is probably the most important factor controlling the relative rates. The observed rate difference may also be partly stereoelectronic in origin, because the presence of the larger ring permits better overlap of the β-O–CMe2 bond with the orbital of the unpaired electron on moving to the transition state.
β-Scission of the spirocyclic radical 32 to give 33 [eqn. (15)] was included in this study because we have found evidence from end-product analysis that constraining the bond angles at the emerging radical centre can have a major effect on the rate of ring opening of bicyclic carbohydrate-derived 2-phenyl-1,3-dioxan-2-yl radicals.4 Unfortunately, because of the relatively broad (and therefore weak) EPR signal from the benzylic radical 32 it was not possible to obtain accurate kinetic data. However, the temperature at which the concentration of 32 is approximately equal to that of 33 is ca. 20 K lower than that (ca. 312 K) at which [30] = [31], implying that the spirocyclic 32 undergoes β-scission more rapidly than its 4,4-dimethyl analogue 30.†
No EPR spectroscopic evidence was found for β-scission of the benzylic radical 36 and its spectrum was still readily detectable at 400 K in tert-butylbenzene. Although other effects may also be operative, the slow β-scission of 36 seems likely to be mainly stereoelectronic in origin, in that the ring system will be quite rigidly planar thus preventing overlap of the β-O–CMe2 bond with the SOMO. Likewise, no EPR evidence was found for β-scission of the allylic radicals 2-vinyl-4,4-dimethyl-1,3-dioxolan-2-yl 34 or 2-vinyl-4,4-dimethyl-1,3-dioxan-2-yl 35 and their spectra were still readily observable at 400 K, some 50 K above the highest temperature at which 30, the 2-phenyl analogue of 35,
could be detected. This implies that 34 and 35 undergo β-scission more slowly than the 2-phenylated derivatives. However, we note that ring opening of 34 and 35 would yield radicals that contain acrylate ester functions and it would be difficult in any case to obtain quantitative kinetic data for cleavage of such allylic radicals, because of the ease of alkyl radical addition to acrylates.
Density functional calculations
To aid interpretation of the experimental results, a number of calculations were carried out at the UB3LYP/6-31G(d,p) level of density functional theory, using the GAUSSIAN 98 package of programs.23 Ground-state radicals and transition structures were fully optimised with respect to all geometrical variables with no symmetry constraints. The set of normal harmonic frequencies was computed for each structure, first in order to confirm it as a local minimum or a transition state and then to obtain the zero-point vibrational energy (ZPVE), third-law entropy and thermal contribution to the enthalpy at 298 K. In addition to selected examples of the β-scission processes studied experimentally, the prototypical reactions shown in eqns. (18) and (19) were examined computationally. The reactions investigated proceed via the transition structures 40–45
and the results are presented in Table 4. The ring-opening β-scission of the unsubstituted 1,3-dioxolan-2-yl radical 20, along with similar cleavage of its 2-methyl derivative 21 and of the 2-trifluoromethyl analogue, have been examined theoretically by Zipse24 as part of a study of the 1,2-acyloxy rearrangement that takes place for β-acyloxyalkyl radicals.| |  | (18) |
| |  | (19) |
Table 4 Results of density functional molecular orbital calculations at the UB3LYP/6-31G(d,p) levela
| Radical |
Electronic energy/hartree |
Number of imag. freqs. (cm−1) |
r(C–O)b/Å |
r(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)c/Å O)c/Å |
ZPVEd,e/kJ mol−1 |
H(298 K)e/hartree |
S(298 K)e/J mol−1 K−1 |
1 hartree = 2625.5 kJ mol−1.
Length of the C–O single bond that will undergo cleavage or is undergoing cleavage in the transition state.
Length of the C–O single bond that will become a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond in the product, or the length of the developing carbonyl C O double bond in the product, or the length of the developing carbonyl C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in the transition state or length of the C O bond in the transition state or length of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in the product radical.
Negative vibrational frequencies are ignored in the calculation of ZPVE.
Low frequency normal modes are treated as vibrations, rather than rotations. Any errors caused by this approximation are expected to be small.
See Fig. 7.
Effective Cs symmetry.
Both non-equivalent bonds are the same length.
Length of the cis-C–O bond is 1.364 Å, that of the trans-C–O bond is 1.366 Å. O bond in the product radical.
Negative vibrational frequencies are ignored in the calculation of ZPVE.
Low frequency normal modes are treated as vibrations, rather than rotations. Any errors caused by this approximation are expected to be small.
See Fig. 7.
Effective Cs symmetry.
Both non-equivalent bonds are the same length.
Length of the cis-C–O bond is 1.364 Å, that of the trans-C–O bond is 1.366 Å.
|
|
28
|
−577.425324 |
0 |
1.433 |
1.368 |
567.6 |
−577.196291 |
452.4 |
|
TS
40
|
−577.399773 |
1 (−729.5) |
1.894 |
1.276 |
560.2 |
−577.173400 |
457.4 |
|
29
|
−577.434344 |
0 |
|
1.218 |
562.0 |
−577.205958 |
507.0 |
|
30
|
−616.738966 |
0 |
1.462 |
1.362 |
644.2 |
−616.479889 |
467.9 |
|
TS
41
f
|
−616.714120 |
1 (−536.7) |
1.953 |
1.264 |
636.1 |
−616.457826 |
477.9 |
|
31
|
−616.749305 |
0 |
|
1.217 |
637.5 |
−616.491079 |
527.0 |
|
32
|
−694.156809 |
0 |
1.467 |
1.360 |
741.2 |
−693.859921 |
496.5 |
|
TS
42
|
−694.134808 |
1 (−549.5) |
1.940 |
1.267 |
734.1 |
−693.840648 |
494.5 |
|
23
g
|
−498.779591 |
0 |
1.437 |
1.365 |
422.1 |
−498.608834 |
416.0 |
|
TS
43
|
−498.750911 |
1 (−842.7) |
1.921 |
1.265 |
414.1 |
−498.583331 |
420.3 |
|
25
|
−384.439491 |
0 |
1.437h |
1.365i |
372.2 |
−384.289209 |
361.1 |
|
TS
44
|
−384.403444 |
1 (−658.8) |
1.955 |
1.262 |
362.5 |
−384.256671 |
366.8 |
|
TS
45
|
−384.402531 |
1 (−686.4) |
1.949 |
1.261 |
362.1 |
−384.255841 |
367.7 |
Calculated activation parameters and rate constants were obtained using eqns. (20) and (21),25 in which kB is Boltzmann's constant and e is the base of natural logarithms; the transmission constant in classical transition state theory is taken to be unity and the temperature is 298 K throughout. The computed activation parameters and rate constants are given in Table 5.
| | |
A
β
= (kBTe/h)exp(ΔS‡/R)
| (20) |
Table 5 Calculated activation parameters for β-scission of cyclic dialkoxyalkyl radicals in the gas phase at 298 K
| Reaction |
ΔH‡(298 K)/kJ mol−1 |
ΔS‡(298 K)/J mol−1 K−1 |
E
a
β
a/kJ mol−1 |
log10(Aβ/s−1)a |
k
β
calc./s−1 at 298 Ka |
|
Experimental values determined in tert-butylbenzene given in parentheses.
The statistical factor of 2, because there are two equivalent β-C–O bonds, has not been included.
Via transition state 44 to give the s-trans-acrylate ester.
|
|
28
→
29 |
60.1 |
+5.0 |
62.6 (62.0) |
13.5 (13.1) |
3.3 × 102 (1.7 × 102) |
|
30
→
31 |
57.9 |
+10.0 |
60.4 (59.8) |
13.8 (13.2) |
1.5 × 103 (5.3 × 102) |
|
32
→
33 |
50.6 |
−2.0 |
53.1 |
13.1 |
6.6 × 103 |
|
23
→
38 |
74.2 |
+4.3 |
76.7 |
13.5b |
1.0 |
|
25
→
39c |
85.4 |
+5.7 |
87.9 |
13.6 |
1.3 × 10−2 |
In agreement with the conclusions based on their EPR spectra, the parent benzylic or allylic 1,3-dioxolanyl and 1,3-dioxanyl radicals are all predicted to be effectively planar at C(2) (angle sums ≥ 358°): the configuration at C(2) in all the transition states 40–45 is also planar (angle sum > 359.5°). The configuration at the emerging alkyl radical centres in the transition structures are all strongly flattened (angle sums 352.6 ± 0.4°) in comparison with those centres in the starting radicals. The developing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is relatively short (1.263–1.276 Å) and the rupturing C–O bond is relatively long (1.894–1.953 Å), structural features which suggest that the transition states should be regarded as ‘product-like’. The computed lengths of the C
O bond is relatively short (1.263–1.276 Å) and the rupturing C–O bond is relatively long (1.894–1.953 Å), structural features which suggest that the transition states should be regarded as ‘product-like’. The computed lengths of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds in the product radicals 29 and 31 are 1.218 and 1.217 Å, respectively. The developing C
O bonds in the product radicals 29 and 31 are 1.218 and 1.217 Å, respectively. The developing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is shorter and the C–O bond undergoing cleavage is longer in the 6-membered transition structure 41, as compared with the 5-membered analogue 40. Within the series of 6-membered transition states, the developing C
O bond is shorter and the C–O bond undergoing cleavage is longer in the 6-membered transition structure 41, as compared with the 5-membered analogue 40. Within the series of 6-membered transition states, the developing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance varies very little, while the length of the rupturing C–O bond increases with increasing methylation of the new radical centre. The computed structure of 41 is shown in Fig. 7 and this typifies the stereochemical and geometrical features of all the transition states.
O bond distance varies very little, while the length of the rupturing C–O bond increases with increasing methylation of the new radical centre. The computed structure of 41 is shown in Fig. 7 and this typifies the stereochemical and geometrical features of all the transition states.
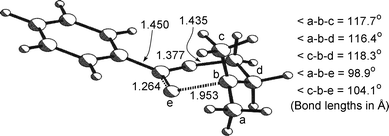 |
| | Fig. 7 UB3LYP/6-31G(d,p)-optimised structure of the transition state 41 | |
Ring-opening of 28 to give 29 is computed to be appreciably exothermic (ΔH
=
−25.4 kJ mol−1) and, as expected, the associated entropy change is large and positive (ΔS
=
+54.6 J mol−1 K−1). Ring opening of 30, the 6-membered-ring analogue of 28, to give 31 is more favourable (ΔH
=
−29.4 kJ mol−1, ΔS
=
+59.1 J mol−1 K−1). The reverse of these ring openings, namely 6-endo-cyclisation of the benzoyloxyalkyl radicals 29 and 31, is thus predicted to be relatively unfavourable (e.g.
ΔH‡
=
+87.3
kJ mol−1, ΔS‡
=
+69.1 J mol−1 K−1 for the cyclisation of 31 to give 30).
The computed activation entropies for ring opening are small, corresponding to Arrhenius pre-exponential factors in the region of 1013.4 s−1. For the two benzylic radicals for which experimental data are available, the agreement with the computed activation parameters is gratifying and gives credence to both sets of values.
The spirocyclic 1,3-dioxan-2-yl radical 32 is computed to undergo β-scission to give the tertiary radical 33 more rapidly than its non-spirocyclic analogue 30 cleaves to give 31, in accord with the experimental results. The allylic 1,3-dioxan-2-yl radical 25 is predicted to undergo β-scission significantly less readily than its benzylic analogue 23, consistent with the experimental observation that 4,4-dimethylated derivatives of these two prototypes (30 and 35, respectively) show the same trend. β-Scission of 25 is predicted to take place preferentially via the anti-transition
state 44 to give the trans-acrylate radical 39; the activation energy via the syn-transition state 45 is calculated to be greater by 2.2 kJ mol−1.
Conclusion
EPR spectroscopic studies, complemented by density functional calculations, can provide a basis for understanding the rates of the elementary reactions involved in the deoxygenation of alcohols and diols by way of their acyclic and cyclic acetal derivatives. For the β-scission processes studied by both experiment and theory, agreement between the two approaches is good. The results obtained from this work should facilitate development of a more complete understanding of the unexpected regioselectivity that has been observed for the β-scission of certain bicyclic 1,3-dioxan-2-yl radicals during the radical-chain redox ring opening of carbohydrate-derived benzylidene acetals.4
Experimental
EPR spectra were recorded during continuous UV irradiation of samples positioned in a standard variable temperature insert in the microwave cavity of a Varian E-109 or a Bruker ESP-300 spectrometer operating at 9.1–9.4 GHz.26 The light source was a 500 W mercury discharge lamp (Osram HBO 500 W/2) and the optical system has been described previously.26a The temperature of the sample during photolysis was determined, using the method described previously,26 by measurement of the value of a(Hβ) for the isobutyl radical. The heating effect at full light intensity was ca. 7 K.
Relative radical concentrations were determined by double integration of appropriate lines in each spectrum and confirmed by computer simulation of the composite spectrum; care was taken to avoid selective saturation of the spectra. Computer simulations were obtained using a modified version of ESRSPEC2,27 extended to handle composite spectra from up to four radicals with different centres, second-order shifts for coupling to single nuclei with I > ½, and lineshapes continuously variable between 100% Gaussian and 100% Lorentzian. The experimental methods for determination of relative rate constants using the steady-state EPR method have been described in detail previously.26,28 Absolute radical concentrations were determined by comparison with the EPR signal obtained from a standard solution of 2,2,4,4-tetramethylpiperidine-N-oxyl (TEMPO, Aldrich) in fluorobenzene, using the
signal from a piece of synthetic ruby fixed to the inside wall of the microwave cavity as a sensitivity reference.
NMR spectra were recorded for samples in CDCl3 using a Bruker ADVANCE 500 instrument (500 MHz for 1H, 125.7 MHz for 13C). Chemical shifts are reported relative to Me4Si, J values are quoted in Hz and the use of [multiplet] indicates an apparent multiplet associated with an averaged coupling constant.
Materials
Di-tert-butyl peroxide (98%, Aldrich) was washed repeatedly with 5% w/v aqueous sodium iodide containing 2% w/v sulfuric acid, until no more iodine was liberated. It was then washed successively with water, saturated aqueous sodium hydrogen carbonate, and saturated brine, before being dried (MgSO4), passed down a column of basic alumina (activity 1) and finally distilled (bp 46–47 °C/76 Torr); it was stored under argon at 4 °C. Fluorobenzene and tert-butylbenzene were distilled from calcium hydride and stored under argon; 3-methylpentan-3-ol was distilled from sodium and stored similarly.
The acetals 3, 5–9, and 11 were commercial products (Aldrich) and were used as received.
tert-Butyl methoxymethyl ether29 was prepared by the reaction of chloromethyl methyl ether with potassium tert-butoxide in dimethyl formamide at 0 °C; bp 100–101 °C at atmospheric pressure. 2-Phenyl-1,3-dioxane 10,30 2-phenyl-4,4-dimethyl-1,3-dioxolane31 and 2-phenyl-5,5-dimethyl-1,3-dioxolan-4-one32 were prepared from benzaldehyde and the corresponding diol or hydroxy acid in the presence of toluene-p-sulfonic acid catalyst and with azeotropic removal of water, as described in the literature. 2-Vinyl-1,3-dioxane33 and 2-vinyl-4,4-dimethyl-1,3-dioxolane34 were prepared in a similar fashion from acrolein and the appropriate diol, using pyridinium toluene-p-sulfonate as catalyst. 4,4,5,5-Tetramethyl-1,3-dioxolane35 was prepared from pinacol and paraformaldehyde using syrupy phosphoric acid as catalyst. The 1,3-dioxanes that have not been reported previously are described below; they were prepared from benzaldehyde or acrolein and the appropriate 1,3-diol in refluxing benzene, in the presence of pyridinium toluene-p-sulfonate as catalyst, by azeotropic removal of water using a Dean and Stark separator.30
2-Phenyl-4,4-dimethyl-1,3-dioxane.
Bp 75–78 °C/0.1 mmHg. δH 1.33 (3H, s, CH3), 1.40 (1H, d[t], J 13.4 and 2.0, Heq-5), 1.43 (3H, s, CH3), 2.01 (1H, ddd, J 13.4, 10.4 and 8.0, Hax-5), 4.07 (2H, m, H-6), 5.71 (1H, s, PhCH), 7.28–7.36 (3H, m, aromatic-H), 7.47–7.49 (2H, m, aromatic-H); δC 21.5, 31.7, 35.8, 63.5, 72.1, 95.2, 126.1, 128.1, 128.5, 139.2. (Found: C, 74.9; H, 8.7. C12H16O2 requires C, 75.0; H, 8.4%.)
2-Phenyl-4,4-spiropentyl-1,3-dioxane.
This was prepared from 1-(2-hydroxyethyl)cyclopentanol;36 bp 69–70 °C/0.4 mmHg. δH 1.42 (1H, d[t], J 13.3 and 1.9, Heq-5), 1.57–1.97 (7H, m, CH2), 2.19 (2H, m, CH2), 4.01 (1H, ddd, J 13.0, 11.5 and 2.4, Hax-6), 4.15 (1H, ddd, J 11.5, 5.3 and 1.5, Heq-6), 5.64 (1H, s, PhCH), 7.33 (3H, m, aromatic-H), 7.50 (2H, m, aromatic-H); δC 23.0, 24.4, 32.9, 34.9, 41.6, 64.9, 84.0, 96.3, 126.0, 128.1, 128.5, 139.3. (Found: C, 76.7; H, 8.3. C14H18O2 requires C, 77.0; H, 8.3%).
2-Vinyl-4,4-dimethyl-1,3-dioxane.
Bp 56 °C/12 mmHg. δH 1.25 (3H, s, CH3), 1.29 (1H, d[t], J 13.3 and 1.9, Heq-5), 1.31 (3H, s, CH3), 1.87 (1H, ddd, J 13.3, 12.8 and 5.8, Hax-5), 3.89 (1H, ddd, J 13.0, 11.7 and 2.4, Hax-6), 3.95 (1H, ddd, J 11.7, 5.8 and 1.4, Heq-6), 5.13 (1H, d, J 4.8, vinylCH), 5.22 (1H, dd, J 10.6 and 1.2, vinyl-H), 5.40 (1H, dd, J 17.4 and 1.2, vinyl-H), 5.79 (1H, ddd, J 17.4, 10.6 and 4.8, vinyl-H); δC 21.4, 31.6, 35.7, 62.9, 71.7, 94.4, 118.2, 135.5. (Found: C, 67.8; H, 9.9. C8H14O2 requires C, 67.6; H, 9.9%).
Acknowledgements
We acknowledge support from the EPSRC for this research and one of us (PF) thanks the University of Bologna for study leave during which this work was carried out. We are grateful to Ms Penny Bryant for carrying out some preliminary experiments.
References
- B. P. Roberts, Chem. Soc. Rev., 1999, 28, 25 RSC.
- H.-S. Dang, P. Franchi and B. P. Roberts, Chem. Commun., 2000, 499 RSC.
- B. P. Roberts and T. M. Smits, Tetrahedron Lett., 2001, 42, 137 CrossRef CAS.
- B. P. Roberts and T. M. Smits, Tetrahedron Lett., 2001, 42, 3663 CrossRef CAS.
- A. G. Davies, D. Griller and B. P. Roberts, J. Chem. Soc. B, 1971, 1823 RSC.
- D. Griller and K. U. Ingold, Acc. Chem. Res., 1980, 13, 193 CrossRef CAS.
- H. Fischer and H. Paul, Acc. Chem. Res., 1987, 20, 200 CrossRef CAS.
- D. Griller and B. P. Roberts, J. Chem. Soc., Perkin Trans. 2, 1972, 747 RSC.
- D. Griller and K. U. Ingold, Acc. Chem. Res., 1980, 13, 317 CrossRef CAS.
- H.-H. Schuh and H. Fischer, Helv. Chim. Acta, 1978, 61, 2130 CrossRef CAS.
-
CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC
Press, Boca Raton, 82nd edn., 2001 Search PubMed.
- J. C. Walton, J. Chem. Soc., Perkin Trans. 2, 1987, 231 RSC.
- V. Malatesta and J. C. Scaiano, J. Org. Chem., 1982, 47, 1455 CrossRef CAS.
- A. J. Dobbs, B. C. Gilbert and R. O. C. Norman, J. Chem. Soc. A, 1971, 124 RSC.
- G. Brunton, K. U. Ingold, B. P. Roberts, A. L. J. Beckwith and P. J. Krusic, J. Am. Chem. Soc., 1977, 99, 3177 CrossRef CAS.
- C. Gaze, B. C. Gilbert and M. C. R. Symons, J. Chem. Soc., Perkin Trans. 2, 1978, 235 RSC; C. Gaze and B. C. Gilbert, J. Chem. Soc., Perkin Trans. 2, 1979, 763 RSC.
- B. P. Roberts and A. J. Steel, J. Chem. Soc., Perkin Trans. 2, 1994, 2155 RSC; B. P. Roberts, J. Chem. Soc., Perkin Trans. 2, 1996, 2719 RSC.
- A. J. Fielding and B. P. Roberts, Tetrahedron Lett., 2001, 43, 4061 CrossRef CAS and unpublished work.
-
(a) S. W. Benson and M. Luria, J. Am. Chem. Soc., 1975, 97, 704 CrossRef CAS;
(b) N. Laurencelle and P. D. Pacey, J. Am. Chem. Soc., 1993, 115, 625 CrossRef CAS;
(c) Y. R. Luo and P. D. Pacey, Can. J. Chem., 1993, 71, 572 CAS;
(d) Y.-R. Luo and S. W. Benson, J. Phys. Chem. A, 1997, 101, 3042 CrossRef CAS.
- M.
J. Perkins and B. P. Roberts, J. Chem. Soc., Perkin Trans. 2, 1975, 77 RSC.
- D. V. Avila, C. E. Brown, K. U. Ingold and J. Lusztyk, J. Am. Chem. Soc., 1993, 115, 466 CrossRef CAS; D. V. Avila, K. U. Ingold, J. Lusztyk, W. H. Green and D. R. Procopio, J. Am. Chem. Soc., 1995, 117, 2929 CrossRef CAS; Y. P. Tsentalovich, L. V. Kulik, N. P. Gritsan and A. V. Yurkovskaya, J. Phys. Chem. A, 1998, 102, 7975 CrossRef CAS.
-
(a) L. R. C. Barclay, D. Griller and K. U. Ingold, J. Am. Chem. Soc., 1982, 104, 4399 CrossRef CAS;
(b) L. R. C. Barclay, J. Lusztyk and K. U. Ingold, J. Am. Chem. Soc., 1984, 106, 1793 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98, revision A.3, Gaussian, Inc., Pittsburgh PA, 1998 Search PubMed.
- H. Zipse, J. Am. Chem. Soc., 1997, 119, 1087 CrossRef CAS; H. Zipse and M. Bootz, J. Chem. Soc., Perkin Trans. 2, 2001, 1566 RSC.
-
H. Maskill, The Physical Basis of Organic Chemistry, Oxford University Press, Oxford, 1990 Search PubMed.
-
(a) J. A. Baban and B. P. Roberts, J. Chem. Soc., Perkin Trans. 2, 1981, 161 RSC;
(b) V. Diart and B. P. Roberts, J. Chem. Soc., Perkin Trans. 2, 1992, 1761 RSC;
(c) B. P. Roberts and A. J. Steel, J. Chem. Soc., Perkin Trans. 2, 1992, 2025 RSC (corrigendum, 1993, 1003).
-
P. J. Krusic, QCPE program no. 210, Chemistry Department, Indiana
University, USA Search PubMed.
- P. E. Elford and B. P. Roberts, J. Chem. Soc., Perkin Trans. 2, 1996, 2247 RSC.
- G. Parc, M. Davidson, M. Hellin and F. Coussemant, Bull. Soc. Chim. Fr., 1964, 1325 Search PubMed; D. A. Goff, R. N. Harris, J. C. Bottaro and C. D. Bedford, J. Org. Chem., 1986, 51, 4711 CrossRef CAS.
- E. S. Huyser and Z. Garcia, J. Org. Chem., 1962, 27, 2716 CAS.
- B. E. Leggetter and R. K. Brown, Can. J. Chem., 1964, 42, 990 CAS.
- M. Farines and J. Soulier, Bull. Soc. Chim. Fr., 1970, 332 Search PubMed.
- R. F. Fischer and C. W. Smith, J. Org. Chem., 1960, 25, 319 CrossRef CAS.
- C. K. Ikeda, R. A. Brown and B. E. Sorenson, J. Org. Chem., 1964, 29, 286 CAS.
- R. L. Leutner, Monatsh. Chem., 1935, 66, 222 CAS.
- G. Carr and D. Whittaker, J. Chem. Soc., Perkin Trans. 2, 1989, 359 RSC.
Footnote |
| † When B˙ and C˙ are the only radicals present in significant concentrations and [B˙] = [C˙], eqn. (4) reduces to (kβ/2kt) = 2[B˙]. Since radical concentrations will be approximately the same in the two experiments, it follows that the value of kβ for 30 at 312 K is approximately equal to the value of kβ for 32 at 292 K. |
|
| This journal is © The Royal Society of Chemistry 2002 |
Click here to see how this site uses Cookies. View our privacy policy here. 















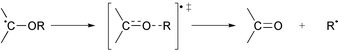
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in the transition state is probably also important in determining the activation energy for β-scission. As was found for β-scission of 26, there is only a modest increase in the rate of ring opening of 28 on moving from tert-butylbenzene
to 3-methylpentan-3-ol as solvent (entry 6).
O bond in the transition state is probably also important in determining the activation energy for β-scission. As was found for β-scission of 26, there is only a modest increase in the rate of ring opening of 28 on moving from tert-butylbenzene
to 3-methylpentan-3-ol as solvent (entry 6).

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)c/Å
O)c/Å![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond in the product, or the length of the developing carbonyl C
O double bond in the product, or the length of the developing carbonyl C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in the transition state or length of the C
O bond in the transition state or length of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in the product radical.
d
Negative vibrational frequencies are ignored in the calculation of ZPVE.
e
Low frequency normal modes are treated as vibrations, rather than rotations. Any errors caused by this approximation are expected to be small.
f
See Fig. 7.
g
Effective Cs symmetry.
h
Both non-equivalent bonds are the same length.
i
Length of the cis-C–O bond is 1.364 Å, that of the trans-C–O bond is 1.366 Å.
O bond in the product radical.
d
Negative vibrational frequencies are ignored in the calculation of ZPVE.
e
Low frequency normal modes are treated as vibrations, rather than rotations. Any errors caused by this approximation are expected to be small.
f
See Fig. 7.
g
Effective Cs symmetry.
h
Both non-equivalent bonds are the same length.
i
Length of the cis-C–O bond is 1.364 Å, that of the trans-C–O bond is 1.366 Å.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is relatively short (1.263–1.276 Å) and the rupturing C–O bond is relatively long (1.894–1.953 Å), structural features which suggest that the transition states should be regarded as ‘product-like’. The computed lengths of the C
O bond is relatively short (1.263–1.276 Å) and the rupturing C–O bond is relatively long (1.894–1.953 Å), structural features which suggest that the transition states should be regarded as ‘product-like’. The computed lengths of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds in the product radicals 29 and 31 are 1.218 and 1.217 Å, respectively. The developing C
O bonds in the product radicals 29 and 31 are 1.218 and 1.217 Å, respectively. The developing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is shorter and the C–O bond undergoing cleavage is longer in the 6-membered transition structure 41, as compared with the 5-membered analogue 40. Within the series of 6-membered transition states, the developing C
O bond is shorter and the C–O bond undergoing cleavage is longer in the 6-membered transition structure 41, as compared with the 5-membered analogue 40. Within the series of 6-membered transition states, the developing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance varies very little, while the length of the rupturing C–O bond increases with increasing methylation of the new radical centre. The computed structure of 41 is shown in Fig. 7 and this typifies the stereochemical and geometrical features of all the transition states.
O bond distance varies very little, while the length of the rupturing C–O bond increases with increasing methylation of the new radical centre. The computed structure of 41 is shown in Fig. 7 and this typifies the stereochemical and geometrical features of all the transition states.



