Application of Marcus cross-relation to mixed inorganic–organic redox couples. A stopped-flow study of the oxidation of N,N,N′,N′-tetramethyl-p-phenylenediamine with various oxidants†
Received
(in Cambridge, UK)
23rd May 2001
, Accepted 2nd November 2001
First published on 7th December 2001
Abstract
The rate constants of the oxidation of N,N,N′,N′-tetramethyl-p-phenylenediamine (TMPPD) are measured in water by means of stopped-flow techniques using different inorganic ions, like Fe(CN)63−, MnO4−, Co(NH3)63+, Ru(OH)3+6. The rates do not depend on the different oxidation potentials, but can be correlated well with calculated rate constants from the Marcus cross-relation.
The electron self-exchange rates of the inorganic oxidants range over nine orders of magnitude. Measurements were performed at T
= 293 K within a pH-range of 7–9.
Introduction
Great progress is achieved in understanding both the kinetics and thermodynamics of redox reactions [eqn. (1)] by applying the Marcus cross-relation.| |  | (1) |
For redox reactions, like eqn. (1), with the rate expression given in eqn. (2),
| | | k12
=
Z12 exp (−ΔG12*/RT) | (2) |
the cross-relation predicts the rate constant
k12 from the electron self-exchange rates of the electron exchange couples involved and the equilibrium constant
K12 of the reaction.
1
Rate constants of various inorganic redox reactions spanning twelve orders of magnitude have been reported and correlated with the predictions of the Marcus cross-relation1e,2 using pure inorganic redox couples. Papers on pure organic redox reactions are rare; additionally the electron self-exchange rates of organic redox couples cover only a relatively small range.3 Reports on mixed inorganic–organic redox reactions are also rare. In an extensive study, Nelsen et al.4 published the kinetics of the oxidation of various hydrazines by different oxidants and compared the results with the Marcus cross-relation.
Reactions like eqn. (1) can be described by Marcus' theory using the cross-relation in eqn. (3),
| | | kcalc12
= (k11k22K12f12)1/2W12 | (3) |
where
k11 and
k22 are the corresponding electron self-exchange rates of the reactants involved [
eqn. (4) and
(5)].
| |  | (4) |
| |  | (5) |
K
12 denotes the equilibrium constant, f12 is a constant normally close to unity and W12 reflects the coloumbic work terms involved in reactions (1), (4) and (5), if there are any [see eqn. (6)].
| | | W12
= exp [−(w12
+
w21
−
w11
−
w22)/2RT] | (6) |
w
12 is the work term for reaction (1), w21 that for the reverse reaction. w11 and w22 are that for reaction (4) and (5), respectively. The factor f12 is given by eqn. (7).
| |  | (7) |
With the pre-exponential factor Z12
=
d2NL (8kBT/μ)1/2, where d
=
rox
+
rred denotes the reaction distance and μ the reduced mass of the reactants, the equilibrium constant K12 can be calculated from eqn. (8).
| | | ln K12
= (Eox
−
Ered) zRT/F | (8) |
Eberson5 first pointed out that these relations can also be used to explain organic redox reactions and organic reaction mechanisms. This paper reports on the oxidations of N,N,N′,N′-tetramethyl-p-phenylenediamine (R) to the corresponding semiquinone radical cation (Wurster's Blue Cation, S˙+) and further from S˙+ to the quinone diimine T2+ by different inorganic oxidants with oxidation potentials, 0.06 ≤
Eox/V ≤ 0.56, and self-exchange rates between 1.2 × 103 M−1 s−1 (Fe(CN)63−/4−) and 8 × 10−6 M−1 s−1 (Co(NH3)62+/3+). The cross-relation is sometimes used in the literature, to determine unknown electron self-exchange
rate constants which are not easily measured. For inorganic redox couples radioactive tracer methods are used sometimes. For very few optically active transition metal complexes do polarisation measurements lead to electron self-exchange rates. NMR- or ESR-linebroadening effects are the tools for organic redox couples.6 This paper compares measured and calculated rate constants of mixed organic–inorganic redox couples, based only on separately measured electron self-exchange rate constants. The aim of this paper is to show that mixed inorganic–organic outer-sphere redox reactions can also be treated with Marcus' theory over a large range of rates since reports of that kind are rare.
Experimental
Measurements were made with a self-constructed stopped-flow machine consisting of six different syringes and various delay lines and pre-mixing chambers.7 Optical detection with optical fibre arrangements gave the absorption versus time profiles. Monochromatic light generated by a stabilized tungsten lamp (Osram 12 V, 100 W) in connection with a monochromator were used for optical detection. The signals from the photomultiplier (RCA, type 1P28) were stored in a Hameg digital oscilloscope, type HM 205-2, and transferred to a PC where data evaluation took place. N,N,N′,N′-Tetramethyl-p-phenylenediamine (TMPPD, Fluka 98%) was recrystallized from water under N2 atmosphere. K3Fe(CN)6 and KMnO4 were also from Fluka (p.a. grade), RuCl3 came from Aldrich and Co(NH3)5Cl3 was synthesised according to the literature
procedure.8 To avoid oxidation by oxygen, solutions must be prepared and handled under nitrogen atmosphere. Optical detection of the semiquinone radical S˙+ and the quinone diimine (T2+) was achieved at λ
= 610 nm with εS
= 1.3 × 104 M−1 cm−1 and λ
= 315 nm with εT
= 3.1 × 104 M−1 cm−1.9Fig. 1 shows the optical absorption spectra of R, S+ and T2+ from N,N,N′,N′-tetramethyl-p-phenylenediamine.
Phosphate buffer was used to establish a constant pH, controlled by a pH-meter (WTP, type pH 522). Buffer concentrations were always 1/15 M. The ionic strength was kept constant at I
= 0.2 M around pH = 8. Rate constants k12 were obtained using the method of initial rates at T
= 293K. The disproportionation reaction of the semiquinone radical cation (S˙+) according to eqn. (9) and Scheme 1 was taken into account for rate evaluation. The equilibrium constant K3 and the corresponding forward and backward rate constants, k3/k−3
=
K3, are described in the literature as K3
= 8.3 × 10−8 and k3
= 1.8 × 102 M−1 s−1.10,11
| |  | (9) |
Using the isolation method, it is shown that the reaction order is one for each reactant for the different redox reactions investigated [eqn. (10)].
| |  | (10) |
This is also valid for the formation of the quinone diimine (T2+), formed by the oxidation of the semiquinone radical cation (S˙+) with MnO4−.12
 |
| | Scheme 1 | |
Results and discussion
Observed rate constants kobs12 for reactions (11) and (12)| |  | (11) |
| |  | (12) |
are listed in Table 1 for the different redox couples together with Eox, the various electron self-exchange rates of the reactants k11 and k22. Note that the values of kobs12 do not depend on the oxidation potential and therefore not on the driving force ΔG°
=
−RT ln K12.
Table 1 Observed and calculated rate constants, kobs12 and kcalc12, in water at T
= 298 K, standard redox potentials E° and the equilibrium constants K12
| Redox reaction |
ox |
r/pm13,i |
k
22(ox)/M−1 s−1 |
E
oox/Vd |
K
12
|
pH |
k
obs12/M−1 s−1 |
k
calc12/M−1 s−1 |
|
E°(R/S˙+) = 0.265 V vs. NHE;14k11 (R/S˙+) = 8.9 × 108 M−1 s−1;15 red1
= R, ox1
= S˙+.
Interpolation of data reported for various ionic strengths.16
Ref. 13, 17;
Vs. NHE.
E°(S˙+/T2+) = 0.679 V vs. NHE).14k11 (S˙+/T2+) =
5.6 × 107 M−1 s−1;15 red1
= S+, ox1
= T2+.
Ref. 18.
Ref. 15b, 12
From ln K12
= (Eoox
−
Eored)nF/RT.
r (S˙+) =
r (T2+) = 406 pm.13
Oxidation of TMPPD with Ru (OH2)3+ contains at least two different
rates. kcalc12 is obtained by simulation of the first part (<100 ms) of the time dependent absorption signal.
|
| R + ox → S˙+
+ reda |
I) Fe(CN)63− |
465 |
1.2 × 103b |
0.38 |
90 ± 0.1 |
9 ± 0.1 |
1.6 × 107 |
4.5 × 107 |
| |
II) Ru(OH2)63+ |
325 |
2 × 101c |
0.23 |
0.26 ± 0.1 |
8 ± 0.1 |
≈105j |
8.1 × 105 |
| |
III) Co(NH3)63+ |
335 |
8 × 10−6c |
0.06 |
(3.3 ± 1.8) × 10−4 |
8 ± 0.1 |
0.11 |
4.5 |
| S˙+
+ ox → T2+
+ rede |
IV) MnO4− |
309 |
7.9 × 102f |
0.56 |
9.6 × 10−3 |
7 ± 0.1 |
1.6 × 105g |
1.5 × 105 |
To get kcalc12 from eqn. (3), the work term must be calculated according to eqn. (13).
| | 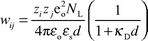 | (13) |
κ
D is the inverse Debye length and is given by κD
= (2NLeo2I/εoεskT)1/2, where I expresses the ionic strength of the solution. The theoretical calculated rate constants kcalc12 are listed in Table 1. The correlation with kcalc12 is quite good and ranges over seven orders of magnitude, indicating the validity of Marcus' theory. Fig. 2 gives a graphic plot of log kobs12versus log kcalc12 showing the applicability of Marcus' theory to mixed inorganic–organic redox reactions. Also different
oxidation states of the reactants are well described by the theory. The one-electron redox reactions (11) and (12) start from different oxidation states. Uncharged TMPPD (R) is oxidized by Fe(CN)63− (I), Rn(OH2)62− (II) and Co(NH3)63+ (III) to the semiquinone radical cation S˙+. For these reactions the work terms w11 and w12 are zero. The situation is different for reaction (12), where the semiquinone radical cation S˙+ is further oxidized to the quinone diimine (T2+) by MnO4− (IV). For this redox reaction all work terms are non-zero. For reaction (IV), a relatively large value of w21 appears because of the twofold charged quinone diimine (T2+)
is involved. The use of spherical radii (see Table 1) is quite acceptable for the inorganic oxidants, but this can not done for the aromatic, semiquinoid or quinoid systems R, S˙+ and T2+. An ellipsoidal model is used to calculate a mean radius from the semiaxes a, b and c. For details see ref. 15. The influence of these additional work terms and the approximation for the radii of organic molecules may be the reason of the small deviation of reaction (IV) in Fig. 2. Also the simple electrostatic treatment might not be adequate to describe reaction (IV) with all its charged reactants caused by specific solvation of the differently charged cations. But nevertheless the results obtained show that Marcus' theory describes the influence of the corresponding work terms quite well.
![Comparison of calculated kcalc12 [eqn. (3)] and experimental rate constants kcalc12. ko
= 1 M−1 s−1. The line corresponds to the theoretical prediction.](/image/article/2002/P2/b104564b/b104564b-f2.gif) |
| | Fig. 2 Comparison of calculated kcalc12 [eqn. (3)] and experimental rate constants kcalc12. ko
= 1 M−1 s−1. The line corresponds to the theoretical prediction. | |
Conclusions
The kinetic of the oxidation of N,N,N′,N′-tetramethyl-p-phenylenediamine with various inorganic oxidants showing a large range of electron-self exchange rates can be well described with the Marcus cross-relation. The cross-relation also describes well the behaviour of mixed organic–inorganic redox processes. All rates of the separate oxidation steps of this redox system including different charged species like the neutral p-phenylendiamine, the positively charged semiquinone radical and the doubly charged quinone diimine are well described by the theory. This is in agreement with a recently published paper, also using experimental self-exchange rates.4
Acknowledgements
G.G. and S.L. would like to thank the VW-Foundation, Germany, the Austrian Academic Exchange Service (ÖAD) and the Austrian Federal Ministry of Education, Science and Culture, Vienna, for financial supports. D.S. and D.D. thank the Austrian CEEPUS-exchange programme for scholarships.
References
-
(a) R. A. Marcus, Angew. Chem., Int. Ed. Engl., 1993, 32, 1111 CrossRef;
(b) R. A. Marcus, Disc. Faraday Soc., 1960, 29, 21 RSC;
(c) R. A. Marcus, J. Phys. Chem., 1986, 72, 891;
(d) R. A. Marcus and N. Sutin, Inorg. Chem., 1975, 14, 219 CrossRef;
(e) R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265 CAS.
-
(a) M. Chou, C. Creutz and N. Sutin, J. Am. Chem. Soc., 1977, 99, 5615 CrossRef CAS;
(b) M. J. Weaver and E. L. Yee, Inorg. Chem., 1980, 19, 1936 CrossRef CAS;
(c) R. D. Cannon, Inorg. React. Mech., 1981, 7, p. 3 Search PubMed;
(d) N. Sutin, Annu. Rev. Phys. Chem., 1966, 17, 119 CrossRef CAS;
(e) N. Sutin, Acc. Chem. Res., 1968, 1, 225 CrossRef CAS.
-
(a) J. R. Brandon and L. M. Dorfman, J. Chem. Phys., 1982, 53, 3849 CrossRef CAS;
(b) A. Yamagishi, Chem. Lett., 1975, 595 CAS;
(c) A. Yamagishi, Bull. Chem. Soc. Jpn., 1975, 48, 3475 CAS;
(d) A. Yamagishi, Bull. Chem. Soc. Jpn., 1980, 53, 1340 CAS.
- S. F. Nelsen, M. T. Ramm, R. F. Ismagilov, M. A. Nagy, D. A. Trieber, II, D. R. Powell, Xi Chen, J. J. Gengler, Q. Qu, J. L. Brandt and J. R. Pladziewicz, J. Am. Chem. Soc., 1997, 119, 5900 CrossRef CAS.
-
L. Eberson, Electron Transfer Reactions in Organic Chemistry, Springer, Berlin, 1987 Search PubMed.
-
(a) G. Grampp, Spectrochim. Acta, 1998, A54, 2349 Search PubMed;
(b) G. Grampp, Spec. Period. Rep. Electron Paramagn. Reson., 1998, 16, 234 Search PubMed.
- U. Nickel, K. Kemnitz and W. Jaenicke, J. Chem. Soc., Perkin Trans. 2, 1978, 1188 RSC.
-
E. Jander and Blasius, Lehrbuch der analytischen und präparativen anorganischen Chemie, 8th edn., S. Hirzel, Stuttgart, 1969, p. 411 Search PubMed.
- U. Nickel, E. Haase and W. Jaenicke, Ber. Bunsenges. Phys. Chem., 1977, 81, 849 Search PubMed.
- U. Nickel, M. Borchardt, M. R. Bapat and W. Jaenicke, Ber. Bunsenges. Phys. Chem., 1979, 83, 877 Search PubMed.
-
H. Gareis, PhD thesis, University of Erlangen, Germany 1986.
-
J. Porst, PhD thesis, University
of Erlangen, Germany, 1982.
- S. J. Formosinho, L. G. Arnant and R. Fausto, Prog. React. Kin., 1998, 23, 1 Search PubMed.
-
P. Pluschke, PhD thesis, University of Erlangen, Germany, 1981.
-
(a) G. Grampp and W. Jaenicke, Ber. Bunsenges. Phys. Chem., 1991, 95, 904 Search PubMed;
(b) G. Grampp and W. Jaenicke, Ber. Bunsenges. Phys. Chem., 1984, 88, 325, 335 Search PubMed;
(c)
kij-values in H2O extrapolated from homogeneous electron self-exchange measurements: ln kijvs.γ. γ
= 1/n2–1/εs.
-
(a) T. W. Swaddle and P. A. Treglon, Coord. Chem. Rev., 1999, 187, 255 CrossRef CAS;
(b) Y. Fu and T. W. Swaddle, J. Am. Chem. Soc., 1997, 119, 7177 CrossRef CAS;
(c) Y. Fu and T. W. Swaddle, Chem. Commun., 1996, 117 RSC;
(d) H. Takagi and T. W. Swaddle, Inorg. Chem., 1992, 31, 4669 CrossRef;
(e) R. J. Campion, C. F. Deck, P. King and A. Wahl, Inorg. Chem., 1967, 6, 672 CrossRef CAS.
- P. Bernhard, L. Helm, A. Ludi and A. E. Merbach, J. Am Chem. Soc., 1985, 107, 312 CrossRef CAS.
- J. C. Sheppard, J. Am. Chem. Soc., 1957, 79, 1020 CrossRef CAS.
Footnotes |
| † In memory of Lennart Eberson. |
| ‡ On leave from: Babes-Bolyai University Cluj-Napoca, Faculty of Chemistry, Dept. of Physical Chemistry, Cluj, Romania. |
| § On leave from: Slovak Technical University, Dept. of Physical Chemistry, Bratislava, Slovak Republic. |
|
| This journal is © The Royal Society of Chemistry 2002 |
Click here to see how this site uses Cookies. View our privacy policy here. 









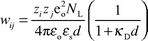
![Comparison of calculated kcalc12 [eqn. (3)] and experimental rate constants kcalc12. ko
= 1 M−1 s−1. The line corresponds to the theoretical prediction.](/image/article/2002/P2/b104564b/b104564b-f2.gif)
