EPR and UV/VIS spectroscopic investigations of VO²⁺ complexes and compounds formed in alkali pyrosulfates

Abstract

The catalytically important molten salt–gas system M₂S₂O₇–M₂SO₄–V₂O₅/SO₂(g) (M = Na, K, Rb, Cs) has been investigated by X- and Q-band EPR spectroscopy. In order to obtain information about the V(IV) complex formation in the melts, samples rather dilute in V₂O₅ were quenched from the molten state at 450–460 °C to 0 °C. EPR spectra of the quenched samples were recorded on samples with alkali to vanadium (M/V) ratios 40, 80 and 160. The spectra show that two V(IV) complexes dominate in the melt regardless of the type of alkali metal ion. In systems with low activity of sulfate a paramagnetic V(IV) complex with g_∥ = 1.915, g_⊥ = 1.978 and line widths 5–15 Gauss is observed. In systems saturated with M₂SO₄ the obtained EPR spectra show a paramagnetic complex with the g-tensors g_∥ = 1.930, g_⊥ = 1.980 and line widths 20–60 Gauss. These results fit very well with the assumption that the species VO(SO₄)₂²⁻ and SO₄²⁻ are in equilibrium with VO(SO₄)₃⁴⁻. It has also been shown for the system M₂S₂O₇–M₂SO₄(sat)–V₂O₅/SO₂(g) that the line widths in the system increase with higher cation radius, and depend linearly on the volume fraction of the sample occupied by the cation. This indicates that spin–spin relaxation effects are the major contribution to line broadening. Combining information from UV/VIS and EPR spectra shows that the VO²⁺ unit in the molten salt solvent exhibits electronic properties close to aqueous solutions of V(IV).

---

Introduction

The molten salt–gas system M₂S₂O₇/M₂SO₄/V₂O₅–SO₂/O₂/SO₃/N₂ (M = Na, K and/or Cs) is generally accepted as a realistic model system of the sulfuric acid catalyst.¹ Earlier work² has shown that during catalyst working conditions, an equilibrium between V(IV) and V(V) is found in the catalyst dependent on the SO₂/SO₃ partial pressure ratio. Not much is generally known about the structure of vanadium complexes in pyrosulfate melts. However, recent multi-nuclear NMR investigations^3,4 have shown that V(V) is present as slightly distorted octahedral complexes in the catalytically important concentration range (molar ratio M/V = 2–4). Particularly important has been the X-ray investigation⁵ of the compound Cs₄(VO)₂O(SO₄)₄ and the subsequent confirmation by NMR spectroscopy that the (VO)₂O(SO₄)₄⁴⁻ complex exists in the molten state as well as in the solid. A recent Raman spectroscopic investigation⁶ on these systems is in accordance with these results. The dimeric anion (VO)₂O(SO₄)₄⁴⁻ is believed to be the catalytically active component in the catalyst.⁷

The paramagnetic ([Ar]3d¹) vanadyl complex has been thoroughly investigated by EPR for years, however almost entirely in apolar organic solvents or water. The EPR spectra of most vanadyl complexes can be described by a spin Hamiltonian, H, including the electron-Zeeman interaction and the electron-vanadium nuclear hyperfine interaction (1):

H = βH(g_xxŜ_x + g_yyŜ_y + g_zzŜ_z) + hc(A_xxŜ_xÎ_x + A_yyŜ_yÎ_y + A_zzŜ_zÎ_z) (1)

where x, y and z is the axis system which diagonalizes both the g and nuclear hyperfine A tensors. A is here expressed in cm⁻¹. β, h, c and H are the Bohr magneton, Planck's constant, the speed of light and the applied magnetic field, respectively. Ŝ_i and Î_i (i = x, y, z) are the electron and nuclear spin operators. Often X-band spectra can be described by axially symmetric tensors, in which case g_∥ = g_zz, g_⊥ = g_xx = g_yy. For many complexes with symmetry lower than C_4v in-plane magnetic anisotropy becomes more evident for Q-band spectra. On the vanadyl cation in molten pyrosulfate, very little is known. Early in-situ EPR work⁸ indicated two types of V(IV) species present in the catalysts–monomeric and dimeric/polymeric VO²⁺ complexes. Later EPR work has confirmed^9,10 and extended² this by showing exclusively monomeric V(IV) complexes at vanadium concentrations far below the catalytically relevant concentration range. Spectroscopic and potentiometric investigations^2,11 have confirmed the existence of an equilibrium between dimeric V(V) and monomeric V(IV) at low vanadium concentrations.

This paper presents the results of an EPR investigation on V(IV) complexes in M₂S₂O₇–M₂SO₄–V₂O₅/SO₂(g) (M = Na, K, Rb or Cs) melts at low vanadium concentrations and on precipitating V(IV) compounds at higher concentrations. Melts with low vanadium concentrations allow recording of well resolved EPR spectra on both molten and quenched samples leading to more detailed information on the nature of the complexes, whereas melts with higher concentrations allow the formation of sufficient amounts of crystals to record their powder EPR spectra.

Experimental

Chemicals

Alkali pyrosulfate was made by thermal decomposition of the corresponding peroxodisulfate (analytical grade) as earlier described.¹² Cs₂S₂O₈ and Rb₂S₂O₈ are not commercially available and were synthesized as described for Cs₂S₂O₈.¹³ It proved necessary to recrystallize Na₂S₂O₈ before decomposition to obtain sufficient purity (>99.9%). V₂O₅ was from Cerac (Pure >99.9%) and used without any further treatment. SO₂ was from AGA (>99.9%). All handling of the chemicals was performed in a dry air glove box with a typical water content less than 10 ppm.

The M₂S₂O₇–M₂SO₄(sat)–V₂O₅/SO₂(g) system

Mixtures of M₂S₂O₇ and M₂SO₄ were prepared by melting and mixing the components in a sealed ampoule. The solubility of sulfates in pyrosulfates is rather low,^11,12e.g. the solubility of K₂SO₄ in K₂S₂O₇ is around 4 mole % at 450 °C. In order to ensure sulfate saturation even after a possible coordination of sulfate to V(IV), a mole fraction of sulfate, X(M₂SO₄) ⩾ 0.06 (of the binary system), was chosen, regardless of the alkali metal. Visual inspection of the molten samples confirmed excess sulfate as a white precipitate. V₂O₅ was added to this mixture at a M/V (M₂S₂O₇/V₂O₅) molar ratio of 40. The chemicals were filled into a quartz ampule (diameter = 12 mm, 300 mm length) in the glove box and sealed immediately under ca. 0.7 bar SO₂. The sealed ampules were transferred to a home made quartz tubular furnace wound with kanthal wire and were equilibrated for at least 100 h above the melting point of the mixture, i.e. 450–460 °C dependent on the type of alkali metal. From the furnace the ampules were dropped directly into icy water. Several attempts to quench into liquid nitrogen proved less successful, probably due to slow heat transfer through the N₂ gas film formed on the surface of the hot ampule. A too slow cooling of the samples resulted partly in formation of crystalline V(IV) compounds in the samples obscuring the EPR spectrum.

After quenching, the ampules were cut open in the glove box and some of the mixture ground and transferred to quartz capillary tubes (2.0 mm outer diameter, 0.5 mm wall thickness). The samples were sealed under vacuum. The capillary tubes were of unspecified quality, but tested negative for any EPR background signal (e.g. Fe(III)).

Samples with other M/V ratios were made by dilution of the M/V = 40 mixture with a premixed M₂S₂O₇–M₂SO₄ mixture.

The M₂S₂O₇–V₂O₅/SO₂(g) system

Samples without SO₄²⁻-saturation are sensitive to the decomposition of the solvent melt, i.e. [eqn. (2)]

S₂O₇²⁻ ⇄ SO₃ + SO₄²⁻ (2)

which causes SO₄²⁻ contamination of the M₂S₂O₇. Only carefully selected batches of pyrosulfate of high purity were used. The mixing procedure was the same as in the previous case, except that the samples were not remelted and requenched after being transferred to the capillaries as in the case of the M₂S₂O₇–M₂SO₄(sat)–V₂O₅/SO₂(g) system. This was avoided in order not to decompose the pyrosulfate further. For the same reason no spectra of molten samples have been recorded. It was not possible to record well resolved spectra with M/V ratios smaller than 160, the spectra smeared out due to increased spin–spin relaxation.

Compound formation and isolation

The V(IV) compounds were synthesised in M₂S₂O₇–V₂O₅ melts with the alkali–vanadium ratios M/V = 3–5 in a pyrex flow cell and washed out with water (except for the mixed valence V(IV)–V(V) salt K₆(VO)₄(SO₄)₈ which is rather water soluble and prepared otherwise¹⁴) as described in detail earlier. The gas composition used was 10% SO₂, 11% O₂ and 79% N₂, corresponding to the synthesis gas in a traditional sulfuric acid plant. In the case of preparation of K₆(VO)₄(SO₄)₈, this gas was converted more than 90%, i.e. containing more than 9% SO₃.

EPR spectroscopy

The EPR spectra were recorded on a Bruker EMX spectrometer with a 12 kW 10″ magnet. Room temperature X-band spectra were recorded with a Bruker ER4102ST cavity. High temperature X-band spectra were recorded with a Bruker ER4114HT cavity whereas the room temperature Q-band spectra were obtained with a Bruker ER5106Q cavity.

Selected EPR spectra were simulated using the Simpow¹⁵ computer program.

Spectrophotometric measurements

The optical spectrum was obtained using a Jasco 570 UV/VIS/NIR spectrophotometer. A sample of M₂S₂O₇–V₂O₅/SO₂(g) with M/V molar ratio of 40 was measured by placing the quartz capillary sample used for EPR measurements in the beam. Since a significant background signal was measured due to reflexions from the cylindrical quartz capillary tube the spectrum was fitted to a function with three gaussian terms and one constant (y₀) [eqn. (3)], where C_i, ν_i, σ_i are the pre-exponential constant, the wave number of the peak and the line width parameter respectively for each peak, i, in the spectrum.

The spectrum was recorded in the range ν = 25000 cm⁻¹ (400 nm) to 8000 cm⁻¹ (1250 nm).

Results and discussion

The composition and structure of the V(IV) complexes in pyrosulfate melts are as mentioned not as well known as the V(V) complexes. Based on the knowledge of the V(V) complexes and a very recent investigation on V(IV) in pyrosulfate, the following reactions (4) and (5) will be considered for the rest of the discussion:

Dissolution: V₂O₅ + 2S₂O₇²⁻ ⇄ (VO)₂O(SO₄)₄⁴⁻ (4)

Reduction: (VO)₂O(SO₄)₄⁴⁻ + SO₂ ⇄ 2VO(SO₄)₂²⁻ + SO₃ (5)

Furthermore, in presence of excess sulfate the V(IV) complex will coordinate one additional sulfate [eqn. (6)]:

Complex reaction: VO(SO₄)₂²⁻ + SO₄²⁻ ⇄ VO(SO₄)₃⁴⁻ (6)

At the applied SO₂ pressure the equilibrium, eqn. (5), is almost completely shifted to the right, i.e. towards V(IV). A short V=O bond and four equatorial oxygen ligands from two bidentate sulfate ions are expected for VO(SO₄)₂²⁻, since unidentate sulfate groups would lead to an unlikely coordination number of three instead of five where the trans position may coordinate additional sulfate (unidentately) to form the hexa-coordinated VO(SO₄)₃⁴⁻, which is coordinatively saturated. In VO(SO₄)₂²⁻ the trans position will be free or loosely coordinated to the solvent. This type of coordination is common for the vanadyl(IV) cation.

The M₂S₂O₇–M₂SO₄(sat)–V₂O₅/SO₂(g) system

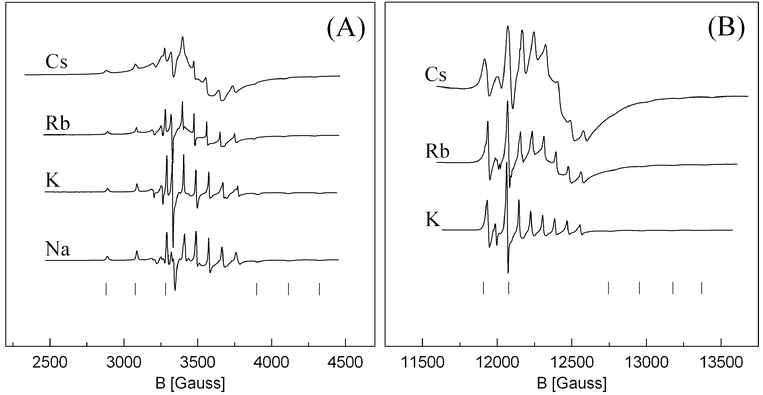
Fig. 1 shows the EPR spectra of samples with M/V = 40, 80 and 160 recorded in the X- and Q-band. All spectra are recorded at room temperature after quenching from 450–460 °C to 0 °C, except for the samples with M/V = 160 which in addition are recorded in the X-band in the molten state at 450–460 °C. The Q-band spectra of the samples with M/V = 160 have been simulated using the Simpow computer program.

Fig. 1 X-band (A) and Q-band (B) EPR spectra of VO(SO₄)₃⁴⁻ in the M₂S₂O₇–M₂SO₄(sat)–V₂O₅/SO₂(g) system with M/V = 40, 80 and 160 (M = Na, K, Rb and Cs). All spectra are recorded at room temperature after quenching from 450–460 °C except for the indicated M/V = 160 samples recorded at 450–460 °C in the X-band. Simulated spectra are shown stipulated.

The general EPR features of the quenched samples are quite similar with two general trends. The X- and Q-band spectra both show axial symmetry typical for octahedral VO²⁺ complexes with the hyperfine structure (due to coupling to the ⁵¹V nucleus, I = 7/2), best resolved in the Q-band spectra. The line width of the spectra increases with increasing vanadium concentration (lower M/V ratio) and with the molar weight of the alkali cation. The samples Rb/V = 40, Rb/V = 80, Cs/V = 40 and Cs/V = 80 could not be recorded with well resolved hyperfine structure in the X-band and are therefore not shown in Fig. 1.

The quenched spectra are typical immobilized axial symmetric spectra also known from, e.g., frozen vanadyl-containing Schiff bases.^16,17 Axial symmetric spectra can be well characterized by g-tensors and hyperfine coupling constants, i.e. the parameters g_⊥, g_∥, a_⊥, a_∥ and one line width. The Q-band spectra, stipulated in Fig. 1, are computer simulations using these five parameters and assuming Lorentzian line shapes. The initial parameter sets for the iterations were obtained by an algorithm¹⁶ using the well-resolved Q-band spectra. No differences were found in the parameters dependent on the vanadium concentration (within experimental error), hence the best resolved spectrum for each alkali metal was used for the accurate calculation of the EPR parameters, regardless of the concentration. The final parameters of the simulations are listed in Table 1. It can be seen that the parameters for the quenched samples are identical within the experimental error of ±0.005 and ±10 for g and a respectively, i.e.g_∥ = 1.930, g_⊥ = 1.980, a_∥ = 200 Gauss, a_⊥ = 70 Gauss. Only the parameters of the parallel feature for the Cs-based samples deviate slightly. It should be stressed that observable in-plane anisotropy rarely occurs in EPR spectra, even though some rhombicity is present.

Table 1 Spin Hamiltonian parameters, g and a (Gauss), of quenched and molten samples in the M₂S₂O₇–M₂SO₄(sat)–V₂O₅/SO₂ system

M	g ⊥	g ∥	Δg∥/Δg⊥^a	g 0 (450 °C)	g 0 (calc)^b	a ⊥	a ∥	a 0 (450 °C)	a 0 (calc)^c
a Δg∥/Δg⊥ = ge − g∥/ge − g⊥. b g 0(calc) = 1/3(2g⊥ + g∥). c a 0(calc) = 1/3(2a⊥ + a∥).
Na	1.982	1.930	3.36	1.970	1.966	71.7	200	110	115
K	1.980	1.930	3.29	1.970	1.963	70.7	202	108	114
Rb	1.980	1.930	3.24	1.967	1.963	67.1	194	108	109
Cs	1.981	1.940	3.16	1.968	1.966	65.3	187	108	106

---

However, the line width changes significantly by increasing size of the cation (Fig. 2). In order to discuss this, the line width for the M/V = 160 series has been plotted versus the void fraction (%), i.e. the volume fraction of the sample which is not occupied by the cation, 1 − (⁴ /₃N_A)V_m⁻¹r³π, r being the ionic radius of the cation, N_A Advogadro's number and V_m the molar volume of the sample. Since the samples are very dilute in vanadium, the molar volumes of the pure alkali pyrosulfates have been used.¹⁸ The molar volume of the solid has been extrapolated from the liquid state. Fig. 2 shows this dependency both in the solid state at room temperature using the well resolved perpendicular components and in the molten state at 450–460 °C using the isotropic line width. Table 1 summarizes the parameters. Both in the solid and the liquid state an excellent linear correlation (R² > 0.95) is found, indicating that the line broadening can be explained solely by a spin–spin relaxation effect.

Fig. 2 Line width dependence on void fraction (see text) of the alkali metal cations M = Na, K, Rb, Cs in the M₂S₂O₇–M₂SO₄(sat)–V₂O₅/SO₂(g) system for samples with molar ratios M/V = 160 in the liquid state at 450 °C (open circles) and in the solid state at room temperature (filled circles).

The high temperature X-band EPR spectra (Fig. 1A) of the molten samples with M/V = 160 exhibit eight isotropic lines of varying intensity as always found for monomeric vanadyl complexes in solution. The different alkali pyrosulfate solvents seem not to affect the first coordination sphere of the complex. Thus no variation in the isotropic g value or the isotropic hyperfine structure constant is observed as with respect to the type of the alkali cation. In some of the spectra, a skew baseline can be seen, probably due partly to formation of dimeric or polymeric V(IV) species where coupling along the chains may smear out the hyperfine structure. The measured isotropic parameters fit well with the calculated isotropic values from the quenched samples—considering the large temperature difference—as it can be seen in Table 1, indicating that we are dealing with the same complex in both phases.

The M₂S₂O₇–V₂O₅/SO₂ system

The X- and Q-band EPR spectra of the vanadyl complexes without sulfate saturation are shown in Fig. 3. The spectra represent axial symmetric complexes as in the sulfate saturated system, but the line width is much smaller, 5–15 G vs. 20–60 G for samples with sulfate saturation. This indicates that there is less distortion of the VO²⁺ unit for VO(SO₄)₂²⁻ compared to VO(SO₄)₃⁴⁻ complexes present in the sulfate saturated system. Furthermore, the EPR parameters of the parallel features are—not surprisingly—changed, as can be seen from Table 2. The value of g_∥ is typically about 0.015 smaller in the case of VO(SO₄)₂²⁻ compared to VO(SO₄)₃⁴⁻. The perpendicular components are less affected. This shows that the character of the V=O bond is important for the relaxation path of the unpaired electron.

Table 2 Spin Hamiltonian parameters, g and a (Gauss), of quenched samples in the M₂S₂O₇–V₂O₅/SO₂ system

M	g ⊥	g ∥	g 0 (calc)^a	Δg∥/Δg⊥	a ⊥	a ∥	a 0 (calc)^a
a See Table 1.
Na	1.978	1.912	1.956	3.714	81.6	210	124
K	1.977	1.912	1.955	3.567	81.7	211	125
Rb	1.976	1.917	1.956	3.242	79.9	206	122
Cs	1.978	1.918	1.958	3.467	78.4	204	120

---

Fig. 3 X-band (A) and Q-band (B) EPR spectra of VO(SO₄)₂²⁻ in the M₂S₂O₇–V₂O₅/SO₂(g) system with M/V = 160. All spectra are recorded at room temperature after quenching from 450–460 °C. Parallel features are indicated by “|” below the spectra.

This system seems to show the same trend on line width versus alkali metal as the sulfate saturated system, and even more pronounced. However it was not possible to record well resolved spectra of the Cs based system for proper determination of line widths, even at Cs/V = 160. An attempt to increase the Cs/V ratio further did not increase the resolution significantly, but decreased the S/N ratio unacceptably. The Rb based system suffered to some extent from the same problems. Furthermore it was impossible to expose the samples to high temperature without decomposition of the complex, and in the case of M = Na decomposition occurred already at room temperature which made it impossible to obtain pure spectra of Na/V = 160 in Q-band. Consequently, it was not possible to construct a line width vs. void fraction plot.

Properties of VO²⁺ compounds crystallized from pyrosulfate melts

The g-values for seven different compounds synthesized in our laboratories^19–21 have been determined by optimization using the Simpow program as shown in Table 3. The powder EPR spectra of several of the compounds have been given elsewhere. A varying degree of tetragonal distortion is found, judged from the g-anisotropy. These results show that EPR powder spectra of such compounds, which might appear isotropic from the immediate appearance of the spectra, actually exhibit anisotropy, which, however, becomes unresolved because of the relatively large line widths observed in these systems.

Table 3 EPR parameters for crystalline VO²⁺ compounds

Compound	g ⊥	g ∥	g iso ^a	Ref.
a Only where applicable. b Mixed valence V(IV)–V(V) compound. c Unpublished.
β-VOSO4	1.972	1.922		19
Na2VO(SO4)2	1.970	1.939		20
K4(VO)3(SO4)5	1.962	1.969	1.964	21
K6(VO)4(SO4)8^b	1.978	1.930	1.972	14
Rb2(VO)2(SO4)3	1.977	1.917		^c
Cs2(VO)2(SO4)3	1.977	1.913		^c
Na26(VO)5(SO4)18	1.980	1.925		^c

---

Electronic properties of VO²⁺ in pyrosulfate melts

According to the classic works^22,23 on the electronic assignment of VO²⁺ complexes, the 3d¹ electron occupies the d_xy orbital in the ground state. Having a compressed octahedral geometry, the following simplified relations (7) and (8) between the paramagnetic and electronic transitions apply,^17,24,25

Δg_∥ = g_∥ − g_e = −8λβ₁*²β₂*²/Δ (7)

Δg_⊥ = g_⊥ − g_e = −2λβ₂*²ε_π*²/δ (8)

λ being the spin–orbit coupling constant, where λ is estimated to be 170 cm⁻¹ for the free V⁴⁺ ion, β_i*² and ε_π*² the wavefunction coefficients, Δ = E_{x² − y²} − E_xy and δ = E_xz,yz − E_xy are the energies for the electronic transitions between the indicated orbitals. The ratio Δg_∥/Δg_⊥ is very sensitive to tetragonal distortion—e.g. the strength of the vanadyl bond—of the octahedrons²⁶ since it is directly related to the energy ratio Δ/δ. From the data in Tables 1 and 2 it seems that the sulfate saturated vanadyl complexes are less distorted (Δg_∥/Δg_⊥ = 3.2–3.5) than the sulfate free complexes (Δg_∥/Δg_⊥ = 3.5–3.7), which shows that the trans coordinated sulfate in the saturated samples weakens the VO²⁺ bond, as expected. These complexes, however, are more distorted than VO²⁺ on oxide surfaces (Δg_∥/Δg_⊥ = 1–3), but less distorted than VO²⁺ in silicate glasses (Δg_∥/Δg_⊥ = 3–4.4).²⁷

The value of β₂*² can be obtained by equation (9):

where P is proportional to the expectation value of r⁻³ in the 3d orbitals of a free V⁴⁺ ion. A value of 184.5 Gauss is used in these calculations, as used by Sharma and co-workers.²⁶

In Fig. 4, the optical spectrum of the complex present in the acidic quenched melt, VO(SO₄)₂²⁻, is shown. The spectrum has been resolved in three gaussian components as shown by resolved curves and a constant contribution for background correction. The summarized function (10) is

f(ν) = 1.56 + 0.89exp(−(ν − 11350)²/(2 × 1100²)) + 0.72exp(−(ν − 14050)²/(2 × 1930²)) + 18500exp(−(ν − 77000)²/(2 × 12780²)). (10)

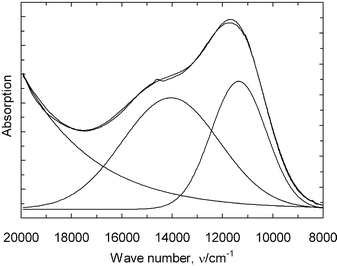Fig. 4 Absorption spectrum of the vanadyl complex VO(SO₄)₂²⁻ in the quenched M₂S₂O₇–V₂O₅/SO₂(g) system.

The last term has no physical/chemical meaning, but provides a mathematical fit of the absorption from the charge transfer and strong V(V) bands in the UV region.

The transition assigned as Δ in eqn. 7 corresponds to d_xy → d_{x² − y²} and appears at 14050 cm⁻¹ in VO(SO₄)₂²⁻, while the transition assigned δ in eqn. (8) corresponds to d_xy → d_xz,yz, for the complex and is found at 11350 cm⁻¹. In the region above 20000 cm⁻¹, charge transfer bands well described^17,22,28 for VO²⁺ are seen, but contributions from traces of V(V) complexes in this region cannot be ruled out, since V(V) is known to absorb strongly in this region. Using the estimated value for λ of 170 cm⁻¹ together with the observed energies for the d–d transition band from the optical spectra and the observed g- and A-values from the EPR measurements on the quenched melts, the wave function coefficients can be estimated for the complex VO(SO₄)₂²⁻ in the frozen solution using eqns. (7)–(9).

This leads to the wave functions parameters, β₁*² = 1.028, β₂*² = 0.907 and ε_π*² = 0.894. β₁*² characterize the in-plane σ-bonding of VO(SO₄)₂²⁻ and a value of one shows that there is no, or only very weak, covalent σ-bonding between the vanadium atom and the oxygen atoms in the equatorial ligand plane. The quantity 1 − β₂*² = 0.093 corresponds to the fraction of unpaired d electrons delocalised over ligand orbitals. This indicates a weaker V=O bond in this complex compared to VO(H₂O)₅²⁺ and VO(acac)₂ but a possible effect from packing of the vanadyl units in the Na₂S₂O₇ structrure during quenching of the samples can't be ruled out. The term (1 − ε_π*²) = 0.106 indicates some influence of π-bonding between vanadium and the vanadyl oxygen not unlike VO(acac)₂ which has chelating ligands such as VO(SO₄)₂²⁻ is likely to have.

All wave function parameters, however, are close to unity compared to for example VO²⁺ on oxide surfaces. This indicates that the electronic properties of the vanadyl unit is well preserved even in this molten salt with high ionic strength of the solvent compared to aqueous solutions. This also gains support from the very similar molar absorptivity found to be around 19.0 l mol⁻¹ cm⁻¹ for VO²⁺ formed in both aqueous and pyrosulfate solvents.^2,27

Conclusions

It has been shown that two VO²⁺ complexes exist in M₂S₂O₇–M₂SO₄–V₂O₅/SO₂(g) (M = Na, K, Rb or Cs) melts in the molar ratio range M/V = 40–160. The spin Hamiltonian parameters have been derived, and it has been shown that line broadening of the EPR spectra of these complexes due to spin–spin relaxation is evident. The electronic properties of VO²⁺ in pyrosulfate melts have been discussed by calculating wave function parameters, β₁*², β₂*² and ε_π*², using the obtained spin Hamiltonian parameters and energy levels obtained from an absorption spectrum of VO(SO₄)₂²⁻ in Na₂S₂O₇.

Acknowledgements

The authors wish to thank I. Laursen and K. Nielsen, Technical University of Denmark, for helpful discussions. NATO Science for Peace Programme (SfP 971984) has supported this investigation.

References

1. S. Boghosian, R. Fehrmann, N. J. Bjerrum and G. N. Papatheodorou, J. Catal., 1989, 119, 121.
2. D. A. Karydis, K. M. Eriksen, R. Fehrmann and S. Boghosian, J. Chem. Soc., Dalton Trans., 1994, 2151.
3. O. B. Lapina, V. M. Mastikhin, A. A. Shubin, K. M. Eriksen and R. Fehrmann, J. Mol. Catal., 1995, 99, 123.
4. O. B. Lapina, V. V. Terskikh, A. A. Shubin, V. M. Mastikhin, K. M. Eriksen and R. Fehrmann, J. Phys. Chem., 1997, 101, 9188.
5. K. Nielsen, R. Fehrmann and K. M. Eriksen, Inorg. Chem., 1993, 32, 4825.
6. S. Boghosian, F. Borup and A. Chrissanthopoulos, Catal. Lett., 1997, 48, 145.
7. O. B. Lapina, B. S. Bal'zhinimaev, S. Boghosian, K. M. Eriksen and R. Fehrmann, Catal. Today, 1999, 51, 469.
8. V. M. Mastikhin, G. M. Polyakova, Ya. Zyulkovskii and G. K. Boreskov, Kinet. Katal, 1970, 11, 1463, (Engl. Transl., 1971, 11, 1219).
9. K. M. Eriksen, D. A. Karydis, S. Boghosian and R. Fehrmann, J. Catal., 1995, 155, 32.
10. K. M. Eriksen, R. Fehrmann and N. J. Bjerrum, J. Catal, 1991, 132, 263.
11. S. B. Rasmussen, K. M. Eriksen and R. Fehrmann, J. Phys. Chem, 1999, 103, 11282.
12. N. H. Hansen, R. Fehrmann and N. J. Bjerrum, Inorg. Chem., 1982, 21, 744.
13. G. E. Folkmann, G. Hatem, R. Fehrmann, M. Gaune-Escard and N. J. Bjerrum, Inorg. Chem., 1991, 30, 4057.
14. K. M. Eriksen, K. Nielsen and R. Fehrmann, Inorg. Chem., 1996, 35, 480.
15. M. Nilges, Program SIMPOW, Illinois ESR Research Center NIH, Illinois, IL, Division of Research Resources Grant No. RR0181.
16. N. D. Chasteen, in Biological Magnetic Resonance, ed. L. J. Berliner and J. Reubens, Plenum Press, New York, 1981, pp. 53(please note misprints in formulas pp. 71–72).
17. D. Kivelson and S-K. Lee, J. Chem. Phys., 1964, 41, 1896.
18. G. Hatem, F. Abdoun, M. Gaune-Escard, K. M. Eriksen and R. Fehrmann, Thermochim. Acta., 1998, 319, 33.
19. S. Boghosian, K. M. Eriksen, R. Fehrmann and K. Nielsen, Acta Chem. Scand., 1995, 49, 703.
20. R. Fehrmann, S. Boghosian, G. N. Papatheodorou, K. Nielsen and R. W. Berg, Inorg. Chem., 1991, 29, 3294.
21. R. Fehrmann, S. Boghosian, G. N. Papathedorou, K. Nielsen and R. W. Berg, Inorg. Chem., 1989, 28, 1847.
22. C. J. Ballhausen and H. B. Gray, Inorg. Chem., 1962, 1, 111.
23. C. K. Jørgensen, Acta Chem. Scand., 1957, 11, 73.
24. N. M. Atherton, in Principles of Electron Magnetic Resonance, ed. T. J. Kemp, Ellis Horwood, Chichester, 1993.
25. K. Dyrek and M. Che, Chem. Rev., 1997, 97, 305.
26. V. K. Sharma, A. Wokaun and A. Baiker, J. Phys. Chem., 1986, 90, 2715.
27. H. Farah, M. P. Brungs, D. J. Miller and G. R. Belton, Phys. Chem. Glasses, 1998, 39, 318.
28. J. Selbin, Coord. Chem. Rev., 1966, 1, 293.

---