Infrared photodissociation spectroscopy of benzene–Ne,Ar complex cations

Abstract

The infrared (IR) absorption spectrum of the jet-cooled benzene cation complexed with Ne has been recorded throughout the 275–1600 cm⁻¹ and the 2800–3200 cm⁻¹ ranges via IR-laser induced vibrational dissociation spectroscopy. Measuring the spectrum of the complex ion rather than the spectrum of the bare benzene cation, leads to the appearance of weak Van der Waals sidebands. In addition, subtle effects of the symmetry lowering in the complex, giving rise to additional lines in the spectrum, have been observed for the benzene–Ar complex. To obtain a more detailed picture of the vibrational structure of the benzene cation in the region up to 1500 cm⁻¹, IR absorption spectra of benzene complex cations prepared in selected low-lying vibrationally excited levels have been recorded.

---

1 Introduction

A detailed understanding of the vibrational structure of the benzene cation is both interesting and relevant for a variety of reasons. The benzene cation, with its doubly degenerate electronic ground state, is of fundamental interest as it is the prototypical system for studies of the Jahn–Teller interaction.^1,2 In the vibrational spectrum the Jahn–Teller effect manifests itself as a splitting of certain vibrational modes. This splitting can be rather large, of the order of the vibrational energy, and it is often difficult to discern a clear vibrational energy level pattern, complicating assignment of vibrational modes. The benzene cation might also be of astrophysical interest. Recently, neutral benzene has been identified as an emitter of infrared (IR) radiation in a proto-planetary nebula.³ It is therefore not unlikely that the benzene cation can be identified in astrophysical objects via its IR emission spectrum as well. After all, the polycyclic aromatic hydrocarbons (PAHs), and specifically their cations, have been proposed as carriers of the unidentified infrared bands (UIBs), a series of distinct IR emission bands observed from the interstellar medium.^4,5

The use of direct IR absorption techniques to obtain information on the vibrational structure of the benzene cation, for instance on benzene cations deposited in rare gas matrices, has thus far not been successful. Another commonly used method to study vibrational structure, laser induced fluorescence (LIF) on ionic species either in the gas phase or in matrices, has not proven to be viable for the benzene cation either, due to an unfavorably low quantum yield for fluorescence.⁶ As a consequence, much of the early experimental work on benzenoid systems consisted of dispersed fluorescence studies of partly or completely halogenated benzene ions, for which the fluorescence quantum yield is close to one. For an overview, the reader is referred to the work by Miller and Bondybey.⁷

With the advent of the dye laser and with the development of supersonic molecular beam cooling techniques, other methods for studying benzene cations became available. By recording the gas phase one color (1+1) photoelectron spectrum, Long et al. identified several low-lying fundamental vibrational frequencies in the benzene cation.⁸ The spectral resolution in this original work was limited by the resolution of the electron energy analyzer to about 3 meV. In later studies, in which a second tunable dye laser photon was used to induce ionization, the resolution was largely improved, making a more detailed analysis possible. These studies include accurate determination of photoionization thresholds via resonance enhanced multi photon ionization (REMPI) spectroscopy,^9,10 zero electron kinetic energy (ZEKE) spectroscopy,¹¹ and mass analyzed threshold ionization (MATI) spectroscopy.^12,13 More recently, the measurement of rotationally resolved high-n Rydberg spectra of neutral benzene allowed for the extrapolation to the various ionization thresholds, leading to a very precise determination of some vibrational frequencies in the ion.¹⁴

Although the methods mentioned above yield accurate vibrational frequencies, definite assignment of the modes involved might nevertheless be complicated. This is because in the electronic transitions involved in the detection process, the relative line intensities are mainly governed by Franck–Condon overlap and there are no strict vibrational selection rules. Additional information can therefore be obtained when the true vibrational absorption spectrum of the cation is measured instead. For this, a sensitive IR absorption detection scheme is required, for instance a scheme based on the IR induced photodissociation of weakly bonded complexes of the benzene cations with rare gas atoms.¹⁵ Although the IR absorption spectrum of the complex ions, rather than of the bare ions, is measured in this case, it is expected that these spectra will closely resemble each other; this is substantiated by the good agreement between the observed MATI spectra for bare benzene and those of its argon complexes.¹⁶ To be able to efficiently induce photodissociation of these complexes, an intense (pulsed) IR source, tunable throughout the relevant portion of the spectrum, is required. Using a pulsed laser system tunable in the 3 µm region, Dopfer et al. measured the IR active C–H stretch mode via IR laser induced photodissociation of the benzene–Ar cation.¹⁷ In a complementary study, using a free electron laser (FEL) as a source of widely tunable IR radiation, we reported on the IR absorption spectrum of the same species in the 450–1500 cm⁻¹ range.¹⁸

In this work we present the results of a more elaborate study on the IR spectrum of the benzene cation complexed with either Ne or Ar. There are two main advantages of using Ne over Ar as a messenger atom. First, the binding energy of the benzene–Ne complex is significantly lower than that of benzene–Ar, enabling the detection of IR absorption lines at lower frequencies. Second, the lower polarizability of Ne is expected to yield a spectrum that is more closely resembling the spectrum of the bare benzene cation. In the spectra of the complex ions Van der Waals sidebands have been observed, yielding information on the intermolecular potential energy surface. Finally, IR absorption spectra of benzene–Ar cations prepared in selected low-lying vibrationally excited levels have been recorded to obtain a more detailed picture of the complex vibrational structure of the benzene cation in the region up to 1500 cm⁻¹.

2 Spectroscopic details

The neutral benzene molecule in its electronic ground state belongs to the D_6h molecular symmetry group. Its 30 vibrational modes are of the species Γ_ν = 2a_1g ⊕ 1a_2g ⊕ 2b_2g ⊕ 1e_1g ⊕ 4e_2g ⊕ 1a_2u ⊕ 2b_1u ⊕ 2b_2u ⊕ 3e_1u ⊕ 2e_2u. Throughout this paper the commonly used Wilson notation¹⁹ is adopted rather than Herzberg’s more systematic one.²⁰ In the neutral ground state there are four IR active modes, one of a_2u and three of e_1u symmetries. The fundamental frequencies of these modes are experimentally found at 671 cm⁻¹ for the a_2uν₁₁ mode [out-of-plane C–H bending], at 1037 cm⁻¹ for the e_1uν₁₈ mode [in-plane C–H bending], at 1485 cm⁻¹ for the e_1uν₁₉ mode [C–C stretching] and at 3099 cm⁻¹ for the e_1uν₂₀ mode [C–H stretching].²⁰ The electronic configuration of neutral benzene is (a_2u)² (e_2g)⁴(e_1g)⁴ and upon removal of one electron from one of the e_1g orbitals, the cation is left in a degenerate E_1g state. When the vibrational symmetry is combined with the E_1g electronic symmetry of the ground state of the cation, the number of vibrational states is greatly increased. In particular, six ungerade states of electronic-vibrational A symmetry and ten of E symmetry result; all are expected to lie in the spectral range covered in this study.

In a classic paper published in 1937, Jahn and Teller pointed out that for any nonlinear molecule with a threefold (or higher) rotational symmetry axis in an orbitally degenerate electronic state there will be at least one normal coordinate whose potential energy minimum does not coincide with the symmetrical position, thus effectively distorting the nuclear framework, lowering the symmetry and lifting the degeneracy.¹ The benzene cation in its electronic ground state is a prototypical system for this. For molecules of D_6h symmetry, vibrations of e_2g symmetry will cause a distortion that is linear in the corresponding normal coordinate whereas vibrations of e_1g, e_1u and e_2u symmetry will cause a quadratic distortion. In the benzene cation, there are four e_2g modes that are linearly Jahn–Teller active. Of course, none of these four modes can be directly observed in IR absorption spectroscopy of the bare cation. Using photoelectron spectroscopy and the more sophisticated ZEKE and MATI methods, only the frequency and Jahn–Teller activity of the lowest energy e_2g mode, the ν₆ in-plane ring-bending mode, have been identified thus far. The benzene molecule is distorted along this coordinate and two possible structures of D_2h symmetry result. No theoretical agreement has been reached so far as to which of the two structures has the lowest energy.^2,21 Experimentally, however, ZEKE spectroscopy studies revealed that the barriers between these structures are so low that ν₆ acts as a pseudorotational coordinate linking the two. The resulting system as a whole is then necessarily viewed as D_6h.¹¹ Of the quadratic Jahn–Teller active modes, only the lowest frequency e_2u mode, the ν₁₆ out-of-plane ring-bending mode around 300 cm⁻¹, has been identified. It is split up into two non-degenerate and one doubly degenerate mode, of which only the latter is IR active.¹¹

The low frequencies of the linear and quadratic Jahn–Teller active ν₆ and ν₁₆ modes give rise to a rich energy level structure in the ion, even when only overtones and combinations of these two modes are included. Due to the possibility of interaction of such combination modes with IR active fundamental modes via Fermi resonances, this might lead to unexpected features in the IR spectrum of the ion.¹⁸ In Fig. 1, a schematic representation of the energy level structure originating from the ν₆ and ν₁₆ modes of the benzene ion is given. The two-mode interaction model we have used to produce this figure is the same as used by Goode et al.¹³ For interpretation of their spectroscopic data on halogenated benzenoid systems, Miller and Bondybey developed a theoretical framework, based on a treatment by Longuet-Higgins,²² to explain the observed energy level structure.⁷ This work was used and refined for the benzene cation by various groups.^8,11,13 The method consists of diagonalization of a Hamiltonian matrix representing the two degenerate electronic states coupled through the Jahn–Teller active vibrational states. For a complete treatment the reader is referred to the original work.⁷ In Fig. 1, the linear and quadratic Jahn–Teller coupling parameters are simultaneously increased from left to right, going from the situation of no Jahn–Teller interaction (left axis) to the situation that is in best agreement with experimental observations (right axis).¹³ From this figure, level assignments can be deduced.

In addition to the various energy levels resulting from the ν₆ and ν₁₆ modes as shown in the figure, the ν₄, ν₁₁, ν₁ and ν₁₇ modes are also expected below 1000 cm⁻¹. For completeness, all presently known vibrational frequencies are listed in Table 1, both for C₆H₆⁺ and for C₆D₆⁺. The numbers in this table are taken from MATI studies by Krause et al.^12,23 and Goode et al.,¹³ ZEKE spectroscopy by Lindner et al.,^11,24 Rydberg spectroscopy by Siglow et al.¹² as well as from the present work. Though the photoelectron studies by Long et al.⁸ are among the landmark works on benzene, the values obtained from these low-resolution studies have not been included. Mode assignments are given in the table, either based on assignments previously made in the literature or based on the present work, as will be discussed below.

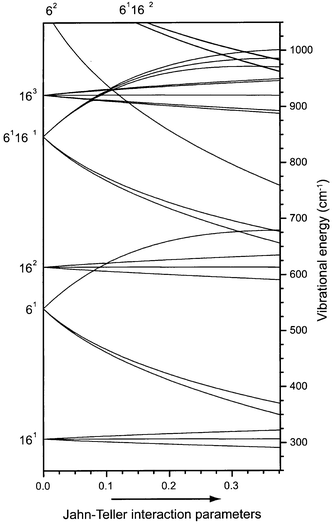Fig. 1 Correlation diagram, linking the energy levels in the benzene cation with Jahn–Teller interaction (right axis) to those expected in the absence of Jahn–Teller interaction (left axis). In the two-mode interaction model that is used, only the ν₆ and ν₁₆ vibrations have been included. From left to right the Jahn–Teller interaction parameters are linearly increased to their experimentally determined values.¹³

Table 1 Observed vibrational levels for the C₆H₆ and C₆D₆ cations (in cm⁻¹), with symmetry and mode assignments

C6H6^+							C6D6^+
Assignment		Ref. 12	Ref. 24	Ref. 13	Ref. 14	This work	Assignment		Ref. 23	Ref. 24	Ref. 13	This work
a Fermi resonance of ν11 mode with two ν6ν16 combination modes. b Fermi multiplet of ν6ν11, ν6ν6ν16, ν6ν16 and ν17 modes.
16^1	B1u	285	289	292			16^1	B1u	245	249	245
16^1	E1u	303	306	306		305	16^1	E1u	262	265	262
16^1	B2u		328				16^1	B2u	286	289	285
6^1	B1g	343	347	350			6^1	B1g	336	338	335
6^1	B2g	363	367	370			4^1	E2g	340	344
4^1	E2g	416	418	422			6^1	B2g	353	357	356
16^2	E2g		586				11^1^a	E1u		488	488	485
16^2	A1g, A2g		611				16^2	Eg		505		506
6^116^1/11^1^a	E1u	626	630	629		629	16^2	Ag		540		538
16^2	E1g					635	16^2	Eg		562
11^1/6^116^1^a	E1u	659	660	663		660	4^116^1	A2u	588			590
6^1	E1g	674	677	680	677	678	4^116^1,6^116^1^a	E2u, E1u	601	604	603	605
6^116^1/11^1^a	E1u		696	700		697	6^116^1^a	E1u		622	620	621
4^116^1	A2u		724				4^116^1	A1u				626
6^2			763				6^1	E1g	633	636	634
^b	B1u					958
^b	B2u					968
1^1	E1g	967	969		969
^b	B2u					998
^b	B2u					1017
^b	B1u					1018
^b	B2u					1085
^b	B1u					1091

---

3 Experiment

The molecular beam setup used in this work, schematically shown in Fig. 2, was described previously,^15,18,25,26 and only a brief description is given here. A mixture of approximately 1% benzene vapor in a rare gas (Ne or Ar) at a backing pressure of 3 atm is expanded through a 0.5 mm diameter nozzle into vacuum. Gas pulses of about 50 µs duration are released at a repetition rate of 10 Hz. In the adiabatic expansion the molecules are vibrationally and rotationally cooled to about 5 K. The expansion conditions allow the formation of weakly bonded Van der Waals complexes of benzene with rare gas atoms, and these complexes are internally cooled as well. About 4 cm downstream the molecular beam is skimmed upon entering a differentially pumped Wiley–McLaren type linear time-of-flight (TOF) mass spectrometer. The molecules in the beam interact with incoming UV laser beams as well as with the IR laser beam at the crossing point of the mutually perpendicular molecular beam axis, laser beam axis and TOF tube axis. Ions are produced in this region under field free conditions and subsequently pulse extracted and accelerated towards a micro channel plate (MCP) detector, yielding mass spectra with a resolution of M/ΔM ≈ 200. The signal from the MCP detector is amplified and fed into a 10 bit, 100 Msample s⁻¹ digital oscilloscope that is read out by a PC. A four-channel digital delay/pulse generator is used to synchronize the molecular beam to the various laser sources.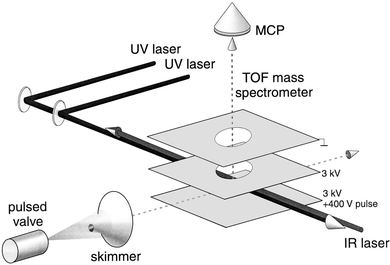

Fig. 2 Experimental set-up used for the IR photodissociation experiments of benzene–Ne, Ar complex cations.

For the measurement of the IR absorption spectrum of the jet-cooled benzene–Ne cation the UV-IR double-resonance scheme indicated in Fig. 3 is used. The first UV laser, later referred to as the excitation laser, excites the neutral benzene–Ne complexes to the ν₆ vibrationally excited level in the first electronically excited (S₁) state. The single photon excitation spectrum for this, as well as that for the other Van der Waals complexes studied in this work, is well-characterized in rotationally resolved high-resolution UV spectroscopy.^27–29 In our case, the excitation light is produced via frequency doubling a Nd:YAG laser pumped pulsed dye laser (5 ns pulses). The spectral width of the excitation laser is around 0.1 cm⁻¹, and the laser is tuned to the center of the (unresolved) rotational envelope. The electronically excited complexes are subsequently ionized with a second tunable UV laser (spectral width around 0.4 cm⁻¹), pumped by the same Nd:YAG laser but optically delayed relative to the excitation laser by a few ns. The ions are produced in zero electric field, and the photon energy of the ionization laser is chosen to bring the Van der Waals complexes just barely above their ionization threshold.³⁰ With an excess energy of less than 5 cm⁻¹ even the lowest Van der Waals mode of the complex ion cannot be excited. Therefore, ions will only be produced in the ground vibrational level, and will be about as cold as the neutral benzene–Ne complexes that they originate from. Shortly after being produced, the complex ions are irradiated with tunable pulsed IR laser light. If a vibrational transition is induced by the IR light in the complex cation, dissociation can occur, leading to the appearance of bare benzene cations and a simultaneous decrease in the number of complex cations. After the IR pulse is over, all ions are pulse-extracted, and mass-selectively detected. The IR absorption spectrum is thus obtained through recording the dissociation yield as a function of IR wavelength, i.e., through recording the ratio of the bare benzene cation signal intensity to the sum of the benzene cation and the complex cation intensity.

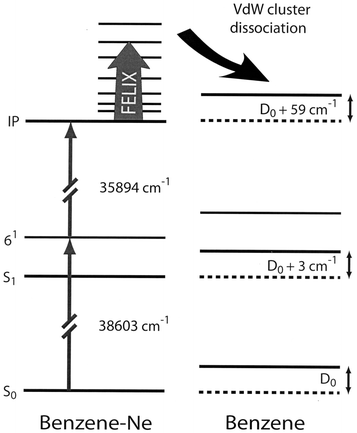Fig. 3 Energy level scheme for benzene and benzene–Ne, indicating the UV-IR double resonance method used to measure the IR spectrum of the benzene–Ne cation. Benzene–Ne ions are produced in their vibrational ground-state in zero electric field via two-color (1+1′) REMPI of benzene–Ne. IR laser induced dissociation of the ionic complex is detected via the appearance of the bare benzene cation, which is pulse-extracted to the detector shortly after the end of the IR laser pulse. The redshifts of the transitions used to prepare the vibrationally cold benzene–Ne complex ions relative to the transitions in the bare benzene molecules correspond to an increased binding energy of the complex of 3 cm⁻¹ upon excitation to the S₁ state and of 59 cm⁻¹ upon ionization.^27,30

The IR radiation is produced at the Free Electron Laser for Infrared eXperiments (FELIX) user facility at our institute.³¹ The output consists of a few μs long burst (macropulse) of micropulses. The micropulse spacing within the burst is set to 1 ns, while the macropulses are repeated at 10 Hz. The micropulse duration is set to about 100 cycles, which results in a bandwidth of approximately 0.5% (fwhm) of the central frequency. The wavelength range that can be covered extends from 40 cm⁻¹ to 2000 cm⁻¹. Energies of up to 100 mJ can be reached in the macropulse. While the linear accelerators and the undulators that are currently used at the FELIX facility are designed and optimized for the 5–250 μm range, shorter wavelength radiation is also produced in the FEL optical cavity in the form of the odd higher harmonics. By installing dielectric mirrors in the FEL cavity with almost no reflectivity at the fundamental wavelength and with a maximum reflectivity at the wavelength of the third harmonic, stable laser operation on the third harmonic can be obtained. In this way, we can routinely produce pulsed IR light tunable throughout the 2700–3300 cm⁻¹ range, with approximately 20 mJ of energy in the macropulse in a bandwidth of about 10 cm⁻¹.

4 Results and discussion

4.1 Benzene–Ne

The IR absorption spectrum of the benzene–Ne cation is displayed in Fig. 4. The observed frequencies of a total of thirteen spectral lines are indicated in the figure. The absolute frequency accuracy is about 1 cm⁻¹ at the low frequency end of the spectrum, gradually deteriorating to 5 cm⁻¹ at the high frequency end. The linewidth observed in the spectrum is almost exclusively determined by the bandwidth of the laser. As we have covered more than a factor of 10 in wavelength in this study, it is rather difficult to accurately determine relative intensities of widely separated lines in the spectrum. Within a limited spectral region, for instance in the 600–800 cm⁻¹ region, relative intensities are accurate to within 20%. The relative intensity between the two outermost lines in the spectrum, however, might be off by as much as a factor five.

Fig. 4 IR absorption spectrum of the benzene–Ne complex cation. In inset A the spectral region from 600–750 cm⁻¹ is shown on an expanded scale together with a simulation (dashed curve) of the Fermi resonance between the IR active ν₁₁ mode and the ν₆ν₁₆ combination modes. In inset B the highest frequency resonance is shown on an expanded scale, together with a decomposition into two 11 cm⁻¹ wide resonances (dashed curves).

As already discussed in Section 2, a maximum of sixteen fundamental modes of the benzene cation are expected in the IR spectrum. The lowest frequency mode is the E_1u central one of the quadratically Jahn–Teller split triad of ν₁₆ modes. This mode, already known from MATI spectroscopy to lie near 306 cm⁻¹, is observed at 305 cm⁻¹ in our spectrum. This mode could not be observed in the IR photodissociation study of the benzene–Ar cation, as it is located significantly below the dissociation limit of the ionic complex in that case.¹⁸ From the observation of the resonance in the present spectrum, it is evident that the dissociation limit of the ionic benzene–Ne complex is below 305 cm⁻¹. This implies an upper value for the dissociation limit D₀ for the neutral benzene–Ne complex in its electronic ground state of D₀ = 305 − 59 = 246 cm⁻¹ (see Fig. 3). The actual value for the dissociation limit is expected to be significantly lower than this, however; theoretically a value of D₀ = 99 cm⁻¹ is found.³²

The spectrum is dominated by intense resonances in the 600–700 cm⁻¹ region. As mentioned in Section 2, the IR active ν₁₁ mode (out-of-plane C–H bending) of vibronic E_1u symmetry is expected in this region, but no other fundamental IR active modes are. In our previous study on the benzene–Ar cation we have already indicated that the three strongest resonances in this spectral region can be attributed to the occurrence of a Fermi resonance.¹⁸ It is seen from Fig. 1 that the two lowest frequency ν₆ν₁₆ combination modes, both of E_1u symmetry as well, are expected to be very close in energy to the ν₁₁ mode. Interaction of these three modes leads to a textbook example of Fermi resonance, an interaction between different, accidentally degenerate, vibrations of the same symmetry.²⁰ This Fermi resonance is shown on an expanded scale in inset A in Fig. 4.

In the most simplified model of the Fermi resonance, it is assumed that both ν₆ν₁₆ combination modes couple only to the ν₁₁ mode with the same coupling parameter, and that only the ν₁₁ mode carries IR intensity. In this model we have therefore four parameters (three unperturbed line positions and one coupling parameter α) whereas we have five observables from the experimental spectrum (three line positions and two relative line intensities). The best fit to the experimentally observed spectrum is shown as the lower (dashed) trace in the inset in Fig. 4; the calculated stick spectrum is convoluted with a lineshape function representing the laser linewidth. As can be seen, fairly good agreement is obtained, and a coupling parameter α of 22 cm⁻¹ is found. The unperturbed line position for the ν₁₁ mode is 668 cm⁻¹, whereas the two ν₆ν₁₆ combination modes are found at 650 cm⁻¹ and 669 cm⁻¹. The latter values are in good agreement with the expected unperturbed frequencies as depicted in Fig. 1.

In the high-frequency C–H stretching region the e_1uν₂₀ vibration, resulting in A_1u, A_2u and E_2u modes, as well as the b_1uν₁₃ vibration, resulting in an IR active mode of E_2u vibronic symmetry, are expected. In Fig. 4 a single absorption feature centered at 3097 cm⁻¹ is observed. The full width at half maximum (FWHM) of this absorption is approximately 14 cm⁻¹, mainly determined by the spectral profile of the IR radiation. As shown more clearly in inset B, a slight asymmetry can be recognized in the line shape, hinting at a possible overlap of more absorption lines. The absorption can be deconvoluted into two 11 cm⁻¹ wide components centered at 3089 cm⁻¹ and 3098 cm⁻¹ with a 1∶3 intensity ratio, as shown by the dashed curves in the inset. For the benzene–Ar cation, a significantly wider absorption feature centered at 3094 cm⁻¹ was recently reported by Dopfer et al.¹⁷ In their experiment, Van der Waals complex ions are produced after electron impact ionization of neutral benzene in the expansion region of a pulsed gas jet. The complex ions that are thus produced can be at relatively high internal temperatures, leading to a broadening of the absorption lines.

Based on the known vibrational frequencies in the ground state of neutral benzene,²⁰ the ten remaining IR active fundamental modes in the cation are all expected to lie in the 800–1600 cm⁻¹ spectral region. In this region of the spectrum, the peak absorption frequency of eight recognizable absorption lines is indicated in Fig. 4. To obtain a better understanding of the observed spectral structure in this region, density functional theory calculations are performed using the BeckeLYP method with the 6-31G* basis set, as implemented in GAUSSIAN 98.³³ Starting with the two D_2h benzene cation structures that were calculated by Raghavachari et al.² the results obtained earlier by Müller-Dethlefs and Peel were reproduced;²¹ for a more detailed discussion on the methods used and the interpretation of the D_2h calculations the reader is referred to ref. 21. The calculated IR spectra for these two structures are displayed in Fig. 5. As is clearly visible, the four resonances in the 900–1200 region cm⁻¹ are well reproduced in both calculated spectra and can be attributed to four fundamental vibrational modes of the benzene cation.

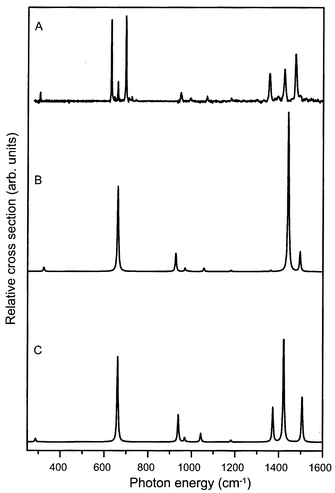Fig. 5 Density functional calculations of the IR absorption spectrum of the benzene cation. The experimentally obtained spectrum is given in trace A. Traces B and C represent the calculated spectra for the elongated benzene structure of electronic B_2g symmetry and for the compressed structure of B_3g symmetry, respectively.

4.2 Van der Waals sidebands

In the IR absorption spectrum shown in Fig. 4, additional weak absorption lines are seen at the high frequency side of the strong resonance at 697 cm⁻¹. This is shown more clearly on an expanded scale in the upper part of Fig. 6. As no IR active fundamental modes are expected in the 700–750 cm⁻¹ spectral region, these weak additional lines are attributed to Van der Waals sidebands, i.e., combination modes of the IR active mode at 697 cm⁻¹ with low-frequency intermolecular benzene–Ne modes. The frequency shift of these sidebands relative to the 697 cm⁻¹ mode, directly indicating the frequency of the corresponding Van der Waals mode, is given in the spectrum. It is noted that no Van der Waals sidebands are visible at the low-frequency side of the 697 cm⁻¹ resonance, confirming that the complex ions are originally only present in their vibrational ground state. The lowest frequency Van der Waals mode also appears as a distinct sideband at the next strongest IR active mode at 629 cm⁻¹.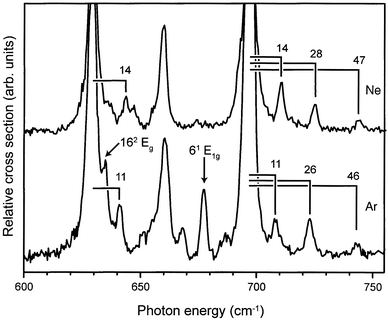

Fig. 6 Expanded view of the 600–750 cm⁻¹ region of the IR absorption spectrum of benzene–Ne (upper trace) and benzene–Ar (lower trace) complex cations. In both spectra distinct Van der Waals sidebands are observed, and the Van der Waals frequencies, i.e., the frequency shift of the sidebands relative to the IR active mode of the benzene cation chromophore, are indicated. In the benzene–Ar spectrum the ν₆ mode and the ν₁₆ overtone mode are observed (indicated by arrows); both modes are of gerade symmetry, and therefore not IR allowed, for the bare benzene cation.

Another possible assignment for these weak additional lines is that they originate from the three ν₄ν₁₆ combination modes. These combination modes are IR allowed, although it is a priori not clear what their intensity would be; normally combination modes are at least an order of magnitude weaker than the fundamental modes, and the ν₁₆ fundamental mode is already rather weak. Nevertheless, these combination modes are expected to nearly coincide, depending on their (unknown) cross-anharmonicity, with the presently found lines (see Table 1). We therefore decided to perform a similar study on the benzene–Ar cation, the result of which is shown in the lower part of Fig. 6. For this complex, a similar pattern of weak additional lines is observed, but the lines are significantly shifted relative to the strong peak at 697 cm⁻¹. This is consistent with an interpretation of these additional lines as Van der Waals sidebands as a significant shift in absolute frequency would not be expected if these lines originated from the ν₄ν₁₆ combination modes. Also for the benzene–Ar complex cation, the lowest frequency Van der Waals mode can be recognized on the high frequency side of the 629 cm⁻¹ mode. The corresponding Van der Waals frequencies are therefore again indicated in the figure. The frequencies of the benzene–Ar cation are slightly smaller than those of the Ne complex and are—with frequencies of 11 cm⁻¹, 26 cm⁻¹ and 46 cm⁻¹—considerably lower than the Van der Waals frequencies in the neutral benzene–Ar complex.³⁴

IR selection rules are not very helpful in trying to identify the observed Van der Waals modes. In the complex, the mirror symmetry in the plane of the benzene molecule is no longer present, lowering the symmetry from D_6h to C_6v. The IR active ν₁₁ mode of a_2u symmetry in D_6h is of a₁ symmetry in C_6v. Motion of the noble gas atom in the plane of the benzene chromophore is of e₁ symmetry, while motion perpendicular to the plane is of a₁ symmetry. Character multiplication then reveals that both bending and stretching modes are IR allowed as Van der Waals sidebands. One can speculate that the vibration at 46 cm⁻¹ represents the stretching mode; this value compares well to an earlier experimentally determined value of 48 cm⁻¹.³⁵ The values for the Van der Waals frequencies for the benzene–Ar cation are in remarkably good agreement with preliminary calculations of Lotrich and Van der Avoird.³⁶

4.3 Symmetry breaking effects

As already mentioned above, the mirror symmetry in the plane of the benzene molecule is no longer present in the benzene–Ne and benzene–Ar complex, lowering the symmetry in the complex from D_6h to C_6v. The most important consequence of this is that all modes of vibronic A and E symmetry in D_6h, both gerade and ungerade, in principle become IR allowed in the complex cation. Interestingly, this clearly manifests itself in the spectrum of the benzene–Ar cation as shown by the appearance of the two peaks indicated with an arrow in Fig. 6. The relatively strong resonance at 678 cm⁻¹ is assigned to the high-frequency mode of the Jahn–Teller active ν₆ vibration (see Fig. 1). In the bare benzene cation, this mode has E_1g vibronic symmetry and is not IR allowed. This mode has, however, unambiguously been assigned in other experimental studies on bare benzene and its various complexes.^11–14 The second manifestation of the symmetry breaking in the benzene–Ar complex is the shoulder on the high-energy side of the strong resonance at 629 cm⁻¹. From Fig. 1 it can be seen that in this region the ν₁₆ overtone modes, obviously of gerade character in D_6h, are expected. The shoulder is assigned to the highest frequency, doubly degenerate, ν₁₆ overtone mode, which is thus found at 635 cm⁻¹. In the ZEKE spectrum shown by Lindner et al.,¹¹ three small features are discernible at 586, 611 and 638 cm⁻¹, which have not been assigned thus far. We here propose to assign these three features to the ν₁₆ overtone modes, as indicated in Table 1.

Both resonances that appear due to symmetry breaking in the benzene–Ar complex are almost absent in the case of benzene–Ne, even though the formal breaking of symmetry is, of course, the same. The effect of the symmetry breaking on the IR intensity of lines that only become allowed in the complex is expected to be significantly less for the neon complex, however, due to its lower atomic mass and in particular due to its substantially lower polarizability (0.3956 ų for Ne versus 1.6411 ų for Ar).³⁷ Therefore, the clear difference in the spectrum of benzene–Ar compared to benzene–Ne with respect to these two lines is the best evidence for their assignments.

To study these symmetry breaking effects somewhat further, we have also performed measurements on the benzene–Kr complex (not shown). Here one would expect an even more pronounced appearance of the two E_g modes of the benzene cation in the IR spectrum of the Van der Waals complex. The interpretation of relative line intensities in the spectrum of the benzene–Kr complex in the 600–700 cm⁻¹ spectral region is complicated, however, as the vibrational levels in this region are very close to the dissociation limit of the benzene–Kr cation.¹⁶

It is now also interesting to study a benzene–Ar_n Van der Waals complex in which the original D_6h symmetry is retained. The obvious candidate for such a study is the benzene–Ar₂ complex, for which two different conformers exist.^29,38 In one conformer, denoted as the (1|1) complex, the argon atoms are centered on the axis above and below the benzene plane. In the other conformer, denoted as the (2|0) complex, both argon atoms are located on the same side of the benzene plane. The (1|1) complex has D_6h symmetry, and it is expected that modes of gerade symmetry are rigorously absent from its IR absorption spectrum. To selectively prepare the (1|1) complex cation, the excitation laser is tuned to 38564.2 cm⁻¹, which is the center of the S₁(6¹)←S₀ transition in the neutral benzene–Ar₂ complex.²⁹ From the rotationally resolved spectrum as recorded and analyzed by Weber et al. it has been concluded that this transition is that of a symmetric top molecule, and that the rotational constants obtained are consistent with the (1|1) structure of the complex.²⁹ Moreover, this transition is red-shifted by some 20 cm⁻¹ with respect to the corresponding transition in benzene–Ar, a shift that is almost identical to the 21 cm⁻¹ red-shift observed in going from the benzene monomer to the benzene–Ar complex. The latter is strong evidence that both argon atoms are in identical positions relative to the benzene plane, and that there is relatively little interaction between the two argon atoms. Therefore, it is believed that the (1|1) complex is selectively excited in this transition. For completeness it should be mentioned that there is another transition of the benzene–Ar₂ complex that is found to be blue-shifted by 4 cm⁻¹ with respect to the same transition in benzene–Ar, which has consequently been assigned to the S₁(6¹)←S₀ transition in the (2|0) conformer.³⁸

After preparing the (1|1) complex in the electronically excited state, ionization is performed by tuning the second UV laser just slightly above the ionization threshold, which is some 160 cm⁻¹ lower than that of the benzene–Ar complex;³⁹ an almost identical lowering of the ionization threshold is found in going from the benzene monomer to the benzene–Ar complex, again supporting the selective preparation of the (1|1) complex cation.

The IR absorption spectrum of the benzene–Ar₂ (1|1) complex cation throughout the 600–750 cm⁻¹ region is depicted in Fig. 7, together with the spectrum of the benzene–Ar cation already shown earlier. The IR spectrum of the benzene–Ar₂ cation is deduced through recording the appearance of the benzene–Ar ionic dissociation product as a function of IR wavelength; single photon dissociation of the benzene–Ar₂ cation into a bare benzene ion and two argon atoms is energetically not possible, and indeed not observed, in this frequency range.

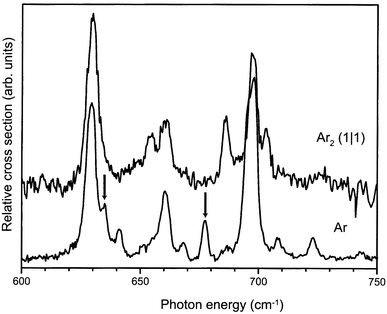Fig. 7 Part of the IR absorption spectrum of the benzene–Ar₂ complex cation in the symmetric (1∣1) configuration (upper trace), compared to the spectrum of the benzene–Ar complex cation (lower trace) already shown in Fig. 6.

In the spectrum of the benzene–Ar₂ complex the Fermi-resonance structure of the ν₁₁ and ν₆ν₁₆ modes discussed earlier can still be recognized. The two gerade modes of the benzene cation, indicated by arrows in the spectrum of the benzene–Ar cation, appear to be absent in the higher symmetry benzene–Ar₂ ionic complex. Due to the lower signal-to-noise ratio in the spectrum of the benzene–Ar₂ complex, Van der Waals sidebands cannot be recognized as such in the spectrum. However, there is rather strong additional structure in the spectrum of the benzene–Ar₂ cation; the central peak of the Fermi triad appears to be split in the benzene–Ar₂ complex, whereas the highest frequency peak of the triad has distinct additional structure on either side. It is clear that as long as this additional structure is not understood, no firm conclusions on the absence of gerade modes in this spectrum can be drawn.

The additional structure observed in the spectrum of the benzene–Ar₂ cation is quite intriguing. From the experimental preparation procedure detailed above, we are quite confident to originally have had the (1|1) complex ions in their vibrational ground state with even no Van der Waals modes excited; Van der Waals sidebands would not be expected to occur with significant intensity anyway. The apparent absence of the gerade modes in the spectrum of the benzene–Ar₂ cations seems to confirm that there is indeed inversion symmetry in the complex ion. Nevertheless, there is no straightforward explanation for the occurrence of the three distinct additional lines in the spectrum if the symmetry of the complex ion is indeed D_6h. One could speculate on possible other, lower symmetry, arrangements of the Ar atoms in the ionic complex. An interesting structure is one in which the Ar atoms are positioned away from the symmetry axis, but in such a way as to retain inversion symmetry of the complex. Such a structure, which would have C_2h symmetry, would formally not even be Jahn–Teller unstable. It might therefore be energetically favorable for the system to partially lift the Jahn–Teller instability by displacement of the Ar atoms, instead of by distortion of the benzene nuclear framework. In reducing the symmetry from D_6h to C_2h the degeneracy of the E_1u modes is lifted, yielding a total of six modes of B_u symmetry in this spectral region which would couple in an IR active Fermi multiplet, and which might explain the observed spectra.

5 Deuterated benzene

To get more insight into the vibrational structure of the benzene cation and to confirm some of the vibrational assignments made, IR photodissociation studies on complexes of fully deuterated benzene (C₆D₆) with Ar have been performed as well. A preliminary version of the spectrum covering the 450–1500 cm⁻¹ range has been published before.¹⁸

It would also have been interesting to study the C–D stretching vibrations, but unfortunately, the region around 2200 cm⁻¹ is not (yet) accessible with our IR source. Therefore, in the present study, we particularly focused on the low frequency range from 450–650 cm⁻¹, which we investigated with an improved spectral resolution. Ground state C₆D₆–Ar cations are produced after laser excitation (38765 cm⁻¹) and subsequent ionization (35650 cm⁻¹) of the jet-cooled neutral complexes.^28,40

The resulting IR absorption spectrum is shown in Fig. 8. The dominant IR absorption peak observed at 485 cm⁻¹ can unambiguously be assigned to the ν₁₁ (out-of-plane C–H bending) mode, found in neutral C₆D₆ at 496 cm⁻¹.²⁰ The peak positions of four resonances in the 600 cm⁻¹ region are indicated in the figure as well. The resonances at 621 cm⁻¹ and 626 cm⁻¹ could not be resolved as separate ones in our earlier study.¹⁸ In addition, the line shape of the 605 cm⁻¹ resonance suggests that it might be composed of more than one mode. In trying to assign all these observed modes, it has to be realized that the two lowest ν₆ν₁₆ combination modes are expected in this region, borrowing intensity from the ν₁₁ mode via a Fermi resonance, just as in the protonated benzene cation. Apart from these modes, the three ν₄ν₁₆ combination modes fall in this region. A consistent picture is obtained when the modes at 605 cm⁻¹ and 621 cm⁻¹ are assigned as ν₆ν₁₆ combination modes. In the Fermi-resonance model described earlier, now with a slightly increased coupling parameter α of 23 cm⁻¹, unperturbed values of 494 cm⁻¹ for the ν₁₁ mode and 601 cm⁻¹ and 616 cm⁻¹ for the ν₆ν₁₆ combination modes are obtained. The latter values are in good agreement with the values expected from a two-mode Jahn–Teller simulation.¹³ The absorption at 590 cm⁻¹, the (blended) absorption at 605 cm⁻¹ and the absorption at 626 cm⁻¹ are then assigned to the ν₄ν₁₆ combination modes, having A_2u, E_2u and A_1u symmetry, respectively. All these assignments are indicated in Table 1.

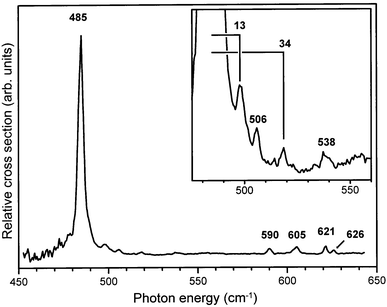Fig. 8 Part of the IR absorption spectrum of the C₆D₆–Ar cation. In the inset, weak additional resonances on the high frequency side of the strong IR active ν₁₁ mode at 485 cm⁻¹ are shown, and the frequencies of two Van der Waals modes are indicated.

On the high-frequency side of the 485 cm⁻¹ resonance, additional structure is observed as shown on an expanded scale in the inset to Fig. 8. This structure could be the Van der Waals sidebands of the strong ν₁₁ mode. However, the resonances at 506 cm⁻¹ and 538 cm⁻¹ have also been reported in ZEKE studies on the bare deuterated benzene cation.²⁴ There, the only vibrational modes that can occur in this spectral region are the ν₁₆ overtone modes. Although these modes are of gerade symmetry in the bare benzene cation, we already know from our work on protonated benzene–Ar complex cations that such modes can appear in the IR spectrum due to symmetry breaking in the complex. We therefore attribute these two absorptions to the two lowest ν₁₆ overtone modes; an additional mode observed by Lindner et al. at 562 cm⁻¹ is most likely the highest frequency ν₁₆ overtone mode (see Table 1). The remaining two resonances in our spectrum are attributed to intermolecular Van der Waals vibrations, and their frequency offset relative to the 485 cm⁻¹ peak is given in the figure, indicating Van der Waals modes at 13 cm⁻¹ and at 34 cm⁻¹. These values are higher than those of protonated benzene, which is contrary to expectation as the reduced mass is increased.³⁶ It is noted, however, that the character of the intra-molecular mode (pure out-of-plane C–D bending) to which the Van der Waals modes appear as sidebands is rather different than the character of the intra-molecular modes for which sidebands are observed in protonated benzene (the ν₆ν₁₆–ν₁₁ Fermi triad). This difference may lead to the appearance of different Van der Waals modes as sidebands.

6 Hot band spectroscopy of benzene–Ar

The combined experimental work on the C₆H₆ cation has resulted in the assignment of all modes below 800 cm⁻¹, as well as in the assignment of some additional strong resonances like the ν₁ mode of E_1g symmetry at 969 cm⁻¹ (see Table 1). Many more resonances have been observed, but a further unambiguous identification has proven to be difficult. IR absorption spectroscopy has the obvious advantage that it has rigorous selection rules, as opposed to ZEKE and MATI spectroscopy, where the appearance of lines in the spectra is governed by Franck–Condon overlap of the wavefunctions of the corresponding vibronic levels.

To further exploit the possibilities offered by IR photodissociation spectroscopy, vibronic levels of different symmetry can be used as initial states in the IR absorption process. Obviously, the initially excited vibrational state for such an experiment should lie below the dissociation limit of the complex to prevent dissociation before the actual IR transition can be induced. The preparation of a pure sample of ions in one selected vibrationally excited state, i.e., without any population in the vibrational ground state of the ion, is experimentally difficult. It is relatively straightforward, however, to produce a sample of ions with a known distribution over a selected set of vibrational levels. By measuring the IR absorption spectrum of this sample, a type of ‘hot-band’ spectroscopy is performed.

In our experiment, we resonantly excite neutral benzene–Ar complexes as described earlier, but then tune the ionization laser to an energy several hundred cm⁻¹ above the ionization threshold. Specifically, the frequency of the ionization laser is tuned slightly above that required to produce ionic complexes in a selected vibrationally excited state. In this way, ions are produced in a mixture of vibrational states; ground state ions are produced when the electron carries away the maximum possible excess energy, whereas vibrationally excited ions in the targeted state are prepared when electrons with zero kinetic energy are produced. The vibrational population distribution that is thus created is completely governed by Franck–Condon factors, which are well known from, e.g., ZEKE spectroscopy measurements.¹¹

In the first experiment of this type, the ionization laser is tuned some 350 cm⁻¹ above the ionization threshold for the benzene–Ar complex. As can be seen from Table 1, ions can then be prepared in the lowest energy ν₆ mode of B_1g symmetry. Obviously, it is energetically also possible to produce ions in any of the lower lying vibrational levels, e.g., in the vibrational ground state as well as in the three ν₁₆ modes around 300 cm⁻¹. Based on the results of ZEKE-measurements¹¹ it is expected that both the vibrational ground state and the lowest energy ν₆ mode will be almost equally populated with only a few percent of the total population residing in the ν₁₆ modes in this case. The IR photodissociation spectrum of this sample of ions in which a mixture of vibrational states is populated is thus expected to show all the resonances observed before for the vibrational ground state of the benzene–Ar cation together with additional resonances. These additional resonances then most likely originate from the ν₆ mode of B_1g symmetry, obeying the corresponding selection rules.

The 580–770 cm⁻¹ range of the IR absorption spectrum of benzene–Ar cations prepared in this mixture of vibrational states is shown as the upper trace in Fig. 9. For comparison, the IR absorption spectrum of the vibrationally cold benzene–Ar cations is displayed in the lower trace of the figure. As expected, all vibrational structure present in the lower trace is also discernible in the upper spectrum. In addition, however, four distinct new resonances appear in the so-called hot-band spectrum at photon energies of 621 cm⁻¹, 651 cm⁻¹, 670 cm⁻¹ and 738 cm⁻¹. These four resonances disappear if the ionization laser is even only slightly red-detuned (on the order of only 10 cm⁻¹), confirming that these four transitions indeed originate from the vibrationally excited ν₆ mode at 347 cm⁻¹ in the ion.

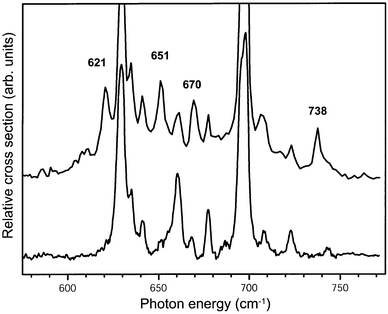Fig. 9 IR absorption spectrum of benzene–Ar complex cations recorded with the ionization laser tuned to some 350 cm⁻¹ above the ionization threshold (upper trace). IR absorption occurs both from the ground vibrational state as well as from the ν₆ vibrationally excited state of the cation. For comparison the IR spectrum of the benzene–Ar complex cation recorded when only the vibrational ground state is initially populated, and which has already been shown in Fig. 6, is included as well (lower trace). The frequencies of the four distinct new resonances originating from the ν₆ mode of B_1g symmetry at 347 cm⁻¹ are indicated.

One has to realize that it is not a priori expected that clearly separated, distinct additional resonances appear in our hot-band spectrum. In the typical hot-band spectra of molecules of the size of the benzene molecule, one most often only observes a gradual broadening and red-shift of IR absorption lines compared to the spectra of the vibrationally cold molecules.²⁰ This is explained by the fact that modes that are IR active from the vibrational ground state are always IR active from the vibrationally excited levels as well; the cross-anharmonicities between the vibrationally excited modes and the IR active modes in general leads to a gradual red-shift of the IR transitions with increasing vibrational excitation. Of course, transitions to other fundamental modes might become IR allowed from the vibrationally excited levels as well, but these then necessarily appear as combination modes, e.g., decreasing one quantum in the originally vibrationally excited mode and increasing one quantum in another mode, and are therefore expected to be rather weak. In our case it is the Fermi resonance of the IR active ν₁₁ mode with all other nearby modes of the same vibronic symmetry, widely shifting lines in position and distributing IR intensity over many lines, which leads to the appearance of distinct new lines in the hot-band spectrum.

Selection rules dictate that only states of vibronic B_2u and E_2u symmetry can be reached via IR allowed transitions originating from a state of vibronic B_1g symmetry. Starting from the lowest frequency ν₆ mode, the IR active transition to the ν₆ν₁₁ combination mode of vibronic B_2u symmetry is expected to be dominant in the spectral region shown in Fig. 9. It therefore appears likely that all four modes are of B_2u symmetry, and are observable due to coupling to the ν₆ν₁₁ combination mode. The ν₆ν₁₁ combination mode will again have a Fermi-resonance with the (single) B_2uν₆ν₆ν₁₆ combination mode as well as with the (single) ν₆ν₁₆ combination mode of the same symmetry (see Fig. 1). The only other mode of vibronic B_2u symmetry that is expected in this region is the ν₁₇ (C–H out-of-plane bending) mode. This mode is quadratically Jahn–Teller active and has never been experimentally identified in the benzene cation, but is found at 970 cm⁻¹ in neutral benzene.²⁰ The four extra modes observed can thus be interpreted as this Fermi quartet.

In a second measurement of a hot-band spectrum, the ionization laser is tuned some 370 cm⁻¹ above the ionization threshold for the benzene–Ar complex. In this case vibrationally excited ions are prepared in both low frequency ν₆ modes as well as in the vibrational ground state with almost equal probability.¹¹ The resulting hot-band spectrum is shown in the upper trace of Fig. 10, where it is compared to the hot-band spectrum that we already discussed above (lower trace). It is evident from these spectra that three new resonances, originating from the ν₆ mode of B_2g symmetry at 367 cm⁻¹, now appear in the spectrum. Again, the IR active transition to the ν₆ν₁₁ combination mode, which now is of vibronic B_1u symmetry, is expected to give IR intensity to the three modes observed in the spectrum, which consequently all have to be of B_1u symmetry. The absolute frequencies of the additional resonances observed in the hot-band spectra as well as their symmetry assignments are listed in Table 1. As all these modes are most likely mixtures of the ν₆ν₁₁, ν₆ν₆ν₁₆, ν₆ν₁₆ and the ν₁₇ mode, no more definite assignment has been made.

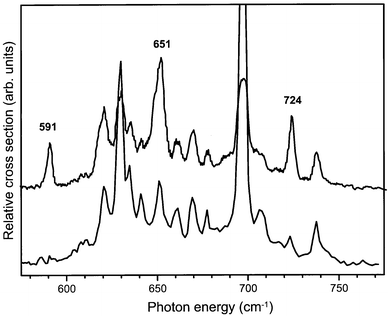Fig. 10 IR absorption spectrum of benzene–Ar complex cations recorded with the ionization laser tuned to some 370 cm⁻¹ above the ionization threshold (upper trace). IR absorption occurs both from the ground vibrational state as well as from the two ν₆ vibrationally excited states of the cation. For comparison the IR spectrum of the benzene–Ar complex cation recorded when only the vibrational ground state and the lowest vibrationally excited ν₆ state are initially populated (see Fig. 9), is included as well (lower trace). The frequencies of the three distinct new resonances originating from the ν₆ mode of B_2g symmetry at 367 cm⁻¹ are indicated.

7 Conclusions

The infrared (IR) absorption spectra of the jet-cooled benzene cation complexed with Ne and Ar have been recorded throughout the 275–1600 cm⁻¹ and the 2800–3200 cm⁻¹ range via IR-laser induced vibrational dissociation spectroscopy. By starting the IR photodissociation process from vibrationally excited complex cations, additional information on the vibrational structure has been obtained. The combined results from the work presented here and previous ZEKE and MATI studies on benzene cations have made a complete assignment of all observed vibrational modes below 800 cm⁻¹ possible. A detailed comparison between the IR absorption spectra of benzene–Ne and benzene–Ar in selected spectral regions convincingly demonstrates that the spectrum of the benzene–Ne cation indeed represents the IR absorption spectrum of the bare benzene cation. In using Ne as a messenger atom in the IR photodissociation technique, Van der Waals sidebands can appear in the spectrum, but no effects of the formal symmetry breaking in the complex due to the presence of the messenger atom have been observed. We therefore conclude that, to within our present spectral resolution, the spectrum of the benzene–Ne cation as shown in Fig. 4 is the true and complete IR spectrum of the benzene cation, and should serve as a benchmark for future analyses of the vibrational properties of this important species.

Acknowledgements

We gratefully acknowledge support by the ‘Stichting voor Fundamenteel Onderzoek der Materie (FOM)’ in providing the required beam time on FELIX, and highly appreciate the skillful assistance of the FELIX staff, in particular of Dr A. F. G. van der Meer. This work is part of the research programme of FOM, and it is in part financially supported by the Council for Chemical Sciences (CW) both of which are financially supported by the ‘Nederlandse Organisatie voor Wetenschappelijk Onderzoek’ (NWO).

References

1. H. Jahn and E. Teller, Proc. R. Soc. London, Ser. A, 1937, 161, 220.
2. K. Raghavachari, R. Haddon, T. A. Miller and V. Bondybey, J. Chem. Phys., 1983, 79, 1387.
3. J. Cernicharo, A. M. Heras, A. G. G. M. Tielens, J. R. Pardo, F. Herpin, M. Guélin and L. B. F. M. Waters, Astrophys. J., 2001, 546, L123.
4. A. Leger and J. L. Puget, Astron. Astrophys., 1984, 137, L5.
5. L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., 1985, 290, L25.
6. O. Braltbart, E. Castellucci, G. Dujardin and S. Leach, J. Phys. Chem., 1983, 87, 4799.
7. T. A. Miller and V. Bondybey, in Molecular Ions: Spectroscopy, Structure and Chemistry, ed. T. A. Miller and V. Bondybey, North-Holland Publishing Company, Amsterdam, 1983, ch. The Jahn–Teller Effect in Benzenoid Cations: Theory and Experiment, p. 201.
8. S. R. Long, J. T. Meek and J. P. Reilly, J. Chem. Phys., 1983, 79, 3206.
9. G. Müller, J. Y. Fan, J. L. Lyman, W. E. Schmidt and K. L. Kompa, J. Chem. Phys., 1989, 90, 3490.
10. J. Le Calvé, M. Schmidt and M. Mons, J. Phys. Chem., 1992, 96, 4131.
11. R. Lindner, K. Müller-Dethlefs, E. Wedum, K. Haber and E. Grant, Science, 1996, 271, 1698.
12. H. Krause and H. J. Neusser, J. Chem. Phys., 1992, 97, 5923.
13. J. G. Goode, J. D. Hofstein and P. M. Johnson, J. Chem. Phys., 1997, 107, 1703.
14. K. Siglow and H. J. Neusser, J. Electron Spectrosc. Relat. Phenom., 2000, 112, 199.
15. J. A. (Hans) Piest, G. von Helden and G. Meijer, J. Chem. Phys., 1999, 110, 2010.
16. H. Krause and H. Neusser, J. Chem. Phys., 1993, 99, 6278.
17. O. Dopfer, R. V. Olkhov and J. P. Maier, J. Chem. Phys., 1999, 111, 10754.
18. R. G. Satink, J. A. (Hans) Piest, G. von Helden and G. Meijer, J. Chem. Phys., 1999, 111, 10750.
19. E. B. Wilson, J. Decius and P. C. Cross, Molecular Vibrations, McGraw-Hill, New York, NY, 1955.
20. G. Herzberg, Molecular Spectra and Molecular Structure, Krieger, Malabar, FL, 2nd edn., 1991.
21. K. Müller-Dethlefs and J. B. Peel, J. Chem. Phys., 1999, 111, 10550.
22. H. Longuet-Higgins, Adv. Spectrosc., 1961, 2, 429.
23. H. Krause, Mehr-Photonen-Massenspektrometrie und massenselektive gepulste Feldionisation langlebiger Rydbergzustände: Zustandsselektive Anregung und Dissoziation von Molekül- und Clusterionen, PhD Thesis, Technische Universität München, 1993.
24. R. Lindner, Rotationsaufgelöste Zero Kinetic Energy Spektroskopie Am Benzol: Die Geometrie Des Kations und der Jahn–Teller Effekt, PhD Thesis, Technische Universität München, 1996.
25. J. A. (Hans) Piest, G. von Helden and G. Meijer, Astrophys. J., 1999, 520, L75.
26. J. A. (Hans) Piest, J. Oomens, J. M. Bakker, G. von Helden and G. Meijer, Spectrochim. Acta, Part A, 57, 717.
27. T. Weber, E. Riedle, H. J. Neusser and E. Schlag, J. Mol. Struct., 1991, 249, 69.
28. T. Weber, A. von Bargen, E. Riedle and H. J. Neusser, J. Chem. Phys., 1990, 92, 90.
29. T. Weber and H. J. Neusser, J. Chem. Phys., 1991, 94, 7689.
30. K. Siglow, R. Neuhauser and H. J. Neusser, Chem. Phys. Lett., 1998, 293, 19.
31. D. Oepts, A. F. G. van der Meer and P. van Amersfoort, Infrared Phys. Technol., 1995, 36, 297.
32. P. Hobza, O. Bludsky, K. Selzle and E. Schlag, J. Chem. Phys., 1992, 97, 335.
33. Gaussian 98, revision A.7. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, R. E. S. J. A. Montgomery, Jr., J. C. Burant, S. Dapprich, A. D. D. J. M. Millam, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, A. G. Baboul, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, W. C. P. M. W. Gill, B. Johnson, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople; Pittsburgh, PA, 1998.
34. R. Neuhauser, J. Braun, H. J. Neusser and A. van der Avoird, J. Chem. Phys., 1998, 108, 8408.
35. R. Neuhauser, K. Siglow and H. J. Neusser, Phys. Rev. Lett., 1998, 80, 5089.
36. V. F. Lotrich and A. van der Avoird, J. Chem. Phys., in preparation.
37. Handbook of Chemistry and Physics, CRC Press, Boca Raton, FL, 74th edn., 1993–1994.
38. M. Schmidt, M. Mons and J. le Calvé, Chem. Phys. Lett., 1991, 177, 371.
39. H. J. Neusser and H. Krause, Chem. Rev., 1994, 94, 1829.
40. K. Siglow, R. Neuhauser and H. J. Neusser, J. Chem. Phys., 1999, 110(12), 5589.

---