The photochemistry of 1,4-cyclohexadiene in solution and in the gas phase: conical intersections and the origin of the ‘helicopter-type’ motion of H₂ photo-generated in the isolated molecule

Abstract

The complex photochemistry of 1,4-cyclohexadiene (CHDN) in solution and in the gas phase is analyzed using a model postulating the involvement of conical intersections. Several conical intersections are found for this system, using a method based on the Longuet–Higgins phase-change rule. The energies and structures of the conical intersections and of some key intermediates are calculated using quantum chemical methods. A single conical intersection, the H/allyl one, is shown to account qualitatively for all the products observed in solution, and also for the cleavage of a H-atom observed in the gas phase. The model is also consistent with the isotopic distribution in the products of deuterated CHDN. The helicopter-type motion of the H₂ product observed in the collision-free photolysis of CHDN by E. V. Cromwell, D.-J. Liu, M. J. J. Vrakking, A. H. Kung and Y. T. Lee (J. Chem. Phys., 1991, 95, 297 [ref. 9]), is not compatible with the properties of this conical intersection. A different one, which is shown to lead naturally to such motion is proposed, and its properties are calculated.

---

I. Introduction

The photochemistry of 1,4-cyclohexadiene (CHDN) has been extensively studied in the gas phase^1–3 and in solution.¹ In this paper we discuss primarily products formed upon direct irradiation (i.e. singlet state products), rather than by Hg sensitization (triplet state products). Several products have been found in solution, their relative yields determined, and the isotopic distribution of the hydrogen atoms established for 3,3,6,6-tetradeuteroCHDN.¹ The data, summarized in Scheme 1, provide a wealth of information that has not yet been fully accounted for. In the gas phase, the dominant reaction is H-atom or H₂ elimination to form benzene either by a two step process or by a concerted reaction. Ultrafast experiments by Zewail and coworkers⁴ revealed rapid formation of atomic hydrogen, and no detectable production of H₂. The ultrafast formation of atomic hydrogen and the complete absence of fluorescence in this system, indicate an efficient non-radiative transition to the ground state. A reaction via a conical intersection (CI), which is an efficient funnel for this process was therefore proposed.^4,5 The concerted elimination of H₂ is symmetry allowed in the ground state, and is readily observed upon heating. The measured activation energy for this process is 43.8 kcal mol⁻¹.⁶ The H₂ concerted photochemical elimination from CHDN is apparently too slow to be observed in the ultrafast experiments,⁴ leading the authors to suggest that it is controlled by IVR (intramolecular vibrational relaxation).

Scheme 1 The products of CHDN photolysis reactions in solution (ref. 1).

Some 10 years ago, Lee and coworkers^7–9 reported an exciting finding concerning CHDN photolysis. From the vector correlation between the rotational angular momentum and the recoil velocity of the H₂ fragment, they concluded that H₂ departs from benzene with a helicopter-type motion. This process took place relatively slowly (on the nanosecond time scale) and was probably below the detection limit of the more recent femtosecond experiments.⁴ In the original work, no mechanistic explanation for the origin of this unique motion was offered. Several theoretical papers reported extensive investigations of this system.^5,10 It was established that the reaction probably takes place on the ground state, after rapid internal conversion from the initially excited state. The structure of the ground state transition state was calculated, but revealed nothing about the origin of the helicopter-type motion.¹⁰ Most recently, the structure and relative energies of two conical intersections were calculated for this system.⁵ They were found to be low enough in energy to provide a rapid funnel from the excited state to the ground state. However, nothing in their structure indicated the concerted formation of benzene and H₂ and the cause of the helicopter-type motion.

In this paper we propose that all available data on CHDN photolysis may be explained by the presence of several different conical intersections (CIs). For this purpose we utilize a recently developed chemically oriented method for locating conical intersections.^11,12 The method is based on the phase change rule¹³ that states that a conical intersection necessarily arises within a region enclosed by a loop along which the total electronic wave function changes sign. We have shown that such loops can be constructed on the ground state potential surface, using three elementary reactions of the system as a guide. These reactions involve not only the reactant and the desired product, but also a third species, since the loop encloses a two dimensional surface, and therefore two independent coordinates are required to define it. We use the term ‘anchors’ for the three species defining the loop. The coordinates chosen are reaction coordinates connecting the three anchors, of which only two are independent. In order for the total electronic wave function to change sign, either one or all three of the reactions must be phase inverting (see ref. 11 for details). Such reactions are usually thermally forbidden (using the Woodward–Hoffmann nomenclature¹⁴), and are not easily experimentally detectable in thermal reactions. However, they can be readily found computationally. For pericyclic reactions, which is the case in hand, a phase inverting reaction has an antiaromatic transition (AATS) state, and a phase preserving one—an aromatic transition state (ATS).¹⁵ Bornemann and Klessinger¹⁶ used this approach in the analysis of the photo-reactions of 2H-azirines. They implemented the method by calculating the ground and excited-state geometries using the CASSCF method, starting from previous MNDOC-CI results.¹⁷ The coordinates along which the conical intersection was searched for were determined by the phase change rule.

The two CIs previously discussed for CHDN (ref. 5) are easily located using the loop method. However, they alone cannot account for all experimental findings. In this paper we show that the method can be used to locate an additional conical intersection of the CHDN system, that leads naturally to the observed helicopter-type reaction. Others are also found and discussed. The model presented provides a unified view of both the solution-phase and the collision-free photochemistry of 1,4-cyclohexadiene.

This paper is the first detailed description of the application of the phase change rule method for the quantitative calculation of conical intersections in a polyatomic system and computing their properties. The energies and geometries of all conical intersections are computed by ab-initio quantum chemical methods. It is shown that for this molecule, a large number of conical intersections connect the first excited singlet state with the ground state.

The structure of the paper is as follows: Section II details the principles of our method, which is based on the phase change rule and Section III, the computational realization. In Section IV the results are compared with experiment, Section V discussed the results and the impact on other organic photochemical systems and Section VI summarizes the work.

II. Method

In this section the systematic search for conical intersections based on the Longuet–Higgins (LH) phase change rule is described. Several computational methods are currently available for finding conical intersections in polyatomic systems and calculating their properties. The basic difficulty encountered in the course of such searches has been summarized by Worth and Cederbaum:¹⁸ ‘The complete evaluation of potential energy surfaces is an impossible task for systems comprising more than a few atoms’. Thus, some simplifying assumptions have to be made. Here, we limit the discussion to Hückel-type systems only, unless specifically noted otherwise,^19–21 extension to Möbius-type ones is straight-forward. For Hückel-type reactions, a phase preserving reaction path involves an aromatic transition state, and a phase inverting reaction an antiaromatic transition state²² (see ref. 15 for the definition and discussion of these transition states). In the former, an odd number of electron pairs is involved (3, 5, ...), and in the latter, an even number (2, 4, ...). The first step in the analysis is the determination of the LH loops^11–13 containing a conical intersection for the reaction of interest. CHDN and one of the observed products serve as two anchors, the third anchor is chosen so that the loop will be a phase inverting one. The choice is not necessarily unique, since in principle a given pair of anchors may be part of several loops, containing different conical intersections. A systematic search for the third anchor may be conducted by considering the electrons that are to be re-paired (i.e. that form chemical bonds that change in the reaction). A convenient systematic way of doing this is by considering first the re-pairing of the smallest possible number of electrons that change their pairing under the energy constraints of the reaction. In closed shell systems, four electrons must be involved since at least one phase inverting reaction is required. Next, reactions involving six electrons are considered, etc.

The simplest loops would be the i³ loops^11,12 in which all three reactions exchange two electron pairs. We begin by considering valence electrons (neglecting core electrons) in order of increasing energy: π electrons first, then combinations of π and σ electrons, and finally two pairs of σ electrons.

We illustrate the method by constructing the loops relevant to the CHDN molecule. There are four π electrons in this system. They may be paired in three different ways, leading to the anchors shown in Fig. 1. The loop is phase inverting (type i³), as each reaction is phase-inverting, and therefore contains a conical intersection; since the products are highly strained, the energy of this conical intersection is expected to be high. Indeed, neither of the two expected products was observed experimentally so far. We defer the discussion of this issue to Section IV.

Fig. 1 The loop formed by CHDN and the two possible products made up by the re-pairing of the four π electrons in CHDN. The bonds formed by the electrons that are exchanged in the reactions are highlighted by bold-face lines.

Next, we consider one pair of π electrons and one pair of σ electrons. The σ electrons may form a CH or a CC bond. As seen from Fig. 2, both resulting loops are phase inverting (i³-type), and enclose, in the case of a CH bond an H/allyl conical intersection, and when a CC bond is involved, a vinyl/allyl conical intersection. Both were reported in ref. 5. The BCE (cf. Scheme 1) isotopomer formed from the H/allyl loop is seen to agree with that found by Srinivasan et al.¹ at 60% yield of the total. We designate this type as BCE(I). The isomers forming the loop encircling the vinyl/allyl CI were not observed experimentally. One of them, BCE(III), is the isotopomer expected from the di-π methane rearrangement.²³

Fig. 2 The loops leading to the H/allyl (bottom) and vinyl/allyl (top) conical intersections for CHDN. The methylene hydrogen atoms are labeled (as in the case of 3,3,6,6-d₄-CHDN), in order to facilitate comparison with experiment. The isotope distribution obtained for BCE formed in the H/allyl case (BCE(I)) is different from that of BCE formed in the vinyl/allyl case (BCE(III)). The bonds formed by the electrons that are exchanged in the reactions are highlighted by bold-face lines. Neither one of the two products expected from the vinyl/allyl CI was experimentally observed.

The exchange of two pairs of σ electrons is expected to lead to a high lying conical intersection that is not likely to be important in the UV photochemistry of CHDN.

This winds up the possibilities of loops involving two-electron pair exchanges only. The next simplest loop would contain at least one reaction in which three electron pairs are re-paired. Inspection of the possible combinations of 2 four-electron reactions and one six-electron reaction starting with CHDN reveals that they all lead to phase preserving i²p loops that do not contain a conical intersection. It is therefore necessary to examine loops in which one leg results in a two electron-pair exchange, and the other two legs involve three electron-pair exchanges. Several such possibilities exist; the one shown in Fig. 3 leads to the desired isotopomer (which we label as BCE(II)). We designate the conical intersection encircled by this loop as the CP-H/allyl CI. Srinivasan et al.¹ found that 40% of the BCE formed from CHDN-d₄ had this structure.

Fig. 3 A Longuet–Higgins loop leading to BCE(II), in which two reactions are phase preserving (an ip² loop). Two different isomers of BCE(II) are shown as anchors. The isotope distribution of this BCE isotopomer is different than both BCE molecules shown in Fig. 2.

The concerted CHDN → benzene + H₂ reaction (Fig. 4a) has an aromatic transition state^10,15 and is phase preserving. Three electron pairs are re-paired in the reaction. In order to construct a conical intersection containing Longuet–Higgins loop that has this reaction as one of the legs, we must look for another reaction of CHDN (or benzene + H₂) that is phase inverting. The reaction must involve the two hydrogen atoms (that are eliminated in the benzene-forming reaction), so that all four electrons of the two CH bonds must participate in the reaction. Obviously, other bonds must also change, so that in order for the reaction to be phase inverting,^11,12 at least two more electron pair exchanges are required. Thus the simplest loop that contains a CI and leads to benzene and H₂ in a concerted reaction is of ip² type, in which the phase inverting leg involves eight electrons. A reaction that suggests itself is the isomerization CHDN(I) → CHDN(II), in which a shift of the two double bonds (Fig. 4b) takes place. Being a thermally ‘forbidden’ reaction, it is likely to have a high barrier. The loop encircling the conical intersection which is defined by these three reactions is shown in Fig. 4c.

Fig. 4 (a) The electron spin re-pairing scheme for the H₂ elimination reaction. Benzene is depicted as the in-phase combination of two Kekulé structures. The reaction involves the re-pairing of three electron pairs (shown schematically below the structures), and is thus phase preserving (p) and allowed thermally. There are two possible re-pairing schemes, corresponding to the two Kekulé forms. Orbitals whose electron are not changed are highlighted in bold-style. (b) The electron spin re-pairing scheme for the isomerization reaction CHDN(I) → CHDN(II). Four electron pairs are involved in the re-pairing, the reaction is therefore phase inverting (i). (c) A Longuet–Higgins loop constructed from the reactions between CHDN(I), CHDN(II) and the benzene + H₂ pair. It is a phase inverting loop and thus contains a conical intersection. The helicopter-type motion arises naturally from the isomerization reaction of CHDN(I) to CHDN(II). By symmetry, the conical intersection is found along the coordinate leading from the transition state between CHDN(I) and CHDN(II), and the final products.

Another possible outcome of CHDN photolysis is bond cleavage to form an H atom and the cyclohexadienyl radical (CHDR), which appears to be the major route under collision-free conditions. It was also observed directly in bulk gas experiments,² and may lead to the formation of benzene by a consecutive H-atom loss. Inspection of the loops presented in Fig. 2 (bottom) and 3, shows that a C–H bond is lengthened in the CI enclosed by them, so that a C–H bond cleavage is likely to occur. The singlet radical pair that is formed, CHDR and a H-atom has the same spin pairing scheme as the intact molecule from which it is formed. CHDR may be formed in an excited state, and then decay via a conical intersection to the ground state. We have included these reactions in the computations.

III. Computational procedure and results

The calculations were performed using the GAMESS program suite.²⁴ The MCSCF complete active space (CAS) method²⁵ was used, with an appropriate active space, using the DZV basis set. The computational search for the conical intersection is conducted in the following way. The Longuet–Higgins phase change rule requires that in order for a conical intersection to be enclosed in the loop, at least one of the reaction coordinates forming it is phase inverting.^11–13 Motion along this coordinate leads to an antiaromatic transition state (AATS).^22,26 The coordinate connecting this transition state and the third anchor is phase preserving.²⁷ Thus, the conical intersection lying within the region encircled by the three anchors, may be found by moving first along the phase inverting reaction coordinate from CHDN to the AATS and then along the phase preserving coordinate to the third anchor. In practice, the geometry of the AATS is calculated and the system is transported vertically to the first electronically excited state surface. From this point it is allowed to follow the steepest gradient downwards from the electronically excited state under two constraints: the phase inverting reaction coordinate is kept at the same symmetry it had at the AATS geometry, and the molecule is directed along the phase preserving reaction coordinate in the direction of the third anchor. All other coordinates are optimized for minimum energy—this is a constrained minimum energy path (MEP) leading to the product. The point at which the system reaches the ground state potential lies on the conical intersection. It is not necessarily the minimum energy point on the CI; rather, the spot reached by this process is obtained upon moving along the shortest path to the product from the excited state surface (at the AATS geometry). In all cases, this procedure did result in locating a conical intersection, as confirmed by calculating the energy separation between the two electronic states. The calculation was discontinued when that energy gap was smaller then 1 kcal mol⁻¹. The numerical data given below are for these points on the CI.

Let us demonstrate this procedure by an explicit example—finding the H/allyl CI shown in Fig. 2. The system is propagated along the reaction coordinate from CHDN to 1,3-CHDN, and the geometry and energy of the AATS of this reaction is computed. In order to locate the exact position of this point, we search for the minimum energy difference between S_t and S₀ along this coordinate. The system is excited to the Franck–Condon region above the AATS yielding the energy of the first excited singlet state (S₁) lying vertically above this AATS. The system is now propelled along the phase-preserving coordinate connecting this point on S₁ and the third anchor, BCE in this example (which lies on S₀). Motion along this trajectory, carried out under the constraints mentioned above, is bound to lead the system to the conical intersection enclosed in the loop.²⁷

As a check on the effectiveness of the procedure, the formation of the three possible products on the ground state potential surface was verified at the conclusion of the search for the conical intersection. After traversing the conical intersection, the system was allowed to relax to an energy minimum on the S₀ surface. Removing all constraints led to one of the three anchors, while the other two were looked for by nudging the atoms slightly in the direction of their geometry, and then letting the system find a minimum energy. The nudging is equivalent to allowing some redistribution of energy on the ground state surface. Recovery of the three anchors without encountering a barrier confirms the location of the CI in the loop and the validity of the process.

The H/allyl conical intersection discussed by Wilsey and Houk⁵ was thus recovered by using the Longuet–Higgins loop shown in Fig. 2. Since re-pairing of only two electron pairs is involved, a four electron active space suffices. The conical intersection leading to the benzene + H₂ reaction requires, in contrast, a minimum of eight electrons (Section II). In order to allow proper comparison between the different reaction routes, all calculations were performed with eight electrons in eight orbitals (except those of the CHDR radical, in which seven electrons were used).

We have calculated the properties of the H/allyl CI and some others using the procedure sketched above, and found a structure very similar to that reported in ref. 5. The energies of this CI and of the other ones calculated in this work are listed in Table 1. The calculated CASSCF values of the energies of the two lowest electronically states are 9.0 eV (S₁, vertical) and 10.3 eV (S₂, vertical).^28,29 They are considerably higher than the experimental ones, as noted for this method by other workers.⁵ In all cases, the computed conical intersections lie at much lower energies than the excited states, and are easily accessible upon excitation to S₁. Our calculated energy for the H/allyl CI is slightly (0.15 eV) lower than that of ref. 5 in which the CASSCF method was used at the (4,4)/6-31G level.

Table 1 The CASSCF(8,8)/DZV energies of some stable molecules and conical intersections relevant to 1,4-cyclohexadiene (CHDN) photochemistry (kcal mol⁻¹ relative to 1,4-CHDN)

a In Hartree units, Eh.
Molecule	1,4-CHDN	1,3-CHDN	BCE	Benzene + H2	CHDR + H	BCE/allyl biradical
Energy	−231.84363^a	−8.1	18.9	13.7	73.0	39.6
Conical Intersection	H/allyl	CP-H/allyl	Helicopter-type	CHDR1	CHDR2
Energy	103.2	144.1	148.1	135.5	136.5

---

In the case of the H/allyl CI, the validity confirmation process recovered the CHDN and 1,3-CHDN anchors. An attempt to approach the third anchor (BCE(I)) resulted instead in a biradical, shown in Scheme 2. The biradical may be regarded as allyl-type resonance hybrid of two biradicals. As discussed in ref. 30, the combination in allyl radicals is an out-of-phase one. This biradical was calculated to be at an energy of 39.6 kcal mol⁻¹ above CHDN (Table 1), and to lie in a real local minimum on the S₀ potential energy surface. A normal mode analysis showed that all frequencies were real. The properties of this biradical, which we term a BCE biradical, and its role in the photochemistry of CHDN, are discussed in the next section.

Scheme 2 Top: The electronic resonance structure of the BCE/allyl biradical. The radical is the out-of-phase combination of the two resonance hybrids. Bottom: The calculated (CAS(8,8)/DZV) structure of the biradical.

The CP-H/allyl conical intersection enclosed in the loop shown in Fig. 3, leading to BCE(II), was computed to lie at an energy significantly higher than the H/allyl one. Its structure is shown in Fig. 5, which also shows the geometry of the H/allyl CI, for comparison. It is seen that the structures of the two CIs are similar in the part near the methylene hydrogen atom that moves away from the carbon atom to which it was originally bonded. In both CIs, this atom is found at a similar distances from the three nearest carbon atoms. In contrast, the other part of the system has a different structure. In the H/allyl CI, one of the double bonds retains its character, while in the CP-H/allyl CI, both former double bonds extend to almost single C–C bond distance, and the cyclopropane ring begins to form.

Fig. 5 The calculated structures of the H/allyl and the CP-H/allyl conical intersections.

The search for the conical intersection leading to the concerted ejection of H₂ (the ‘helicopter-type’ reaction) was facilitated by the fact that the AATS between CHDN(I) and CHDN(II) has an added nuclear symmetry element with respect to the reactant: the molecule has a C_2v symmetry, which distorts to C₂ on the way to the transition state. When the system reaches the AATS, the symmetry becomes again C_2v (with different symmetry elements). The ground state electronic wave function of this AATS (of A₂ symmetry) is formed by an out-of-phase combination of the electronic wave functions of the two VB structures having the same geometry but different spin pairing schemes. A similar instance is that of the transition state between the two rectangular forms of cyclobutadiene, which is an out-of-phase combination of two Kekulé VB structures.²² The electronic wave functions of such transition states transform as one of the non-totally symmetric irreducible representations of the group. In the case at hand, as the A₂ representation of C_2v. From Fig. 4 it is clear, that the (1¹A₁/1¹A₂) conical intersection, by symmetry, is to be found on the coordinate connecting the AATS between the two isomeric hexadienes and the third anchor—benzene and H₂ (A₁ symmetry in C_2v).

The potential surfaces of the ground and excited states in the vicinity of the conical intersection were calculated point by point, along the trajectory leading from the antiaromatic transition state to the benzene and H₂ products. In this calculation, the HH distance was varied, and all other coordinates were optimized to obtain the minimum energy of the system in the excited electronic state (¹A₁). The energy of the ground state was calculated at the geometry optimized for the excited state. In the calculation of the conical intersection locality, the system was constrained to C_2v symmetry, that is the rotational motion of the two hydrogen atoms forming the H₂ molecules was frozen. It was found that the two surfaces (¹A₁ and ¹A₂, cf. Fig. 6) did cross at a certain geometry, representing a conical intersection, as expected from the phase-change rule. Some numerical results are shown in Fig. 6. The approach to the conical intersection from the hexadiene side is much more gradual than from the benzene and H₂ side. The geometry of this conical intersection, shown in Fig. 7, is found to be similar to that of the AATS. In both, the CC bonds have very similar values. The HH distance is much larger in the AATS, while the H₂ center-of-mass distance to the carbon ring is larger in the conical intersection. The angle between the line connecting the two H atoms and the line connecting the two carbon atoms to which they were originally bonded changes due to the rotational motion of two H atoms with respect to the C₆H₆ fragment. It is 30° at both the AATS and at the conical intersection.

Fig. 6 Energetics of the ‘helicopter-type’ conical intersection. Bottom: A cartoon of the overall energy level diagram. X₁ is the reaction coordinate leading from CHDN(I) to CHDN(II) (see Fig. 4b). The transition state between them (AATS) is of A₂ symmetry in C_2v. X₂ is the coordinate leading from this transition state to benzene and H₂. The aromatic transition states (ATS) between the two CHDNs and benzene + H₂ are also shown. The conical intersection region is enclosed by a dashed rectangle. A detailed view of this region is shown in the top part. Top: A cut of the calculated potential surface near the conical intersection along the coordinate connecting the two hydrogen atoms that eventually form the H₂ molecule. The solid line represents the A₂ state (it is the ground state at large HH separations) and the dashed line—the A₁ state, which is the ground state at short HH separations. In this calculation the energy of the system was minimized for the ground state potential with respect to all other nuclear degrees of freedom, while the system was constrained to C_2v symmetry. The energies in this presentation are relative to that of the conical intersection. The rotational motion of the two hydrogens (the ‘helicopter’ motion) was frozen at that symmetry.

Fig. 7 The structure of the conical intersection leading to the helicopter-type motion, calculated at the CASSCF(8,8)/DZV level. (a) Top view, showing the motion of the two hydrogen atoms from their initial position to their location in the conical intersection. (b) Some geometrical parameters of the system at the conical intersection geometry. The structure is slightly boat-shaped (not shown), with an angle of 161°.

The two departing hydrogen atoms perform a complex motion from their initial positions to the conical intersection: contracting of the distance between them, rotation that brings them to the position above the center of the ring and increasing the distance between the center of mass (CM) of the H₂ fragment and the carbon ring. The angular momentum created in this motion is the origin of the observed helicopter-type one. It may be traced to the participation of the isomerization reaction in the Longuet–Higgins loop encircling the conical intersection which induces the necessary angular momentum.

The excitation energy used in the experiments, is large enough to form the CHDR radical in an electronically excited state, and also to dissociate the radical to form benzene. Thus, this radical can also dissociate via a conical intersection. We found two such conical intersections that lie at low enough energies, and may therefore play a role in the photochemistry of CHDN. The energies and geometries of these two conical intersections were calculated, their structures are shown in Fig. 8.

Fig. 8 The calculated structures of two conical intersections involved in the dissociation of the CHDR radicals.

IV. Comparison with experiment

IVa. Gas phase

The main reaction channel in the photochemistry of CHDN in the gas phase under collision free conditions is the detachment of a hydrogen atom. A second one, the formation of H₂ molecules by the helicopter-type channel, is much slower. As seen from Fig. 5, the H atom that migrates on the way to a conical intersection is driven a long way from the heavy atoms skeleton, and under collision free conditions is likely to dissociate. H-atom elimination is favored from the entropy point of view, and is a ubiquitous process³¹ observed upon UV irradiation of many organic molecules in the gas phase. The reaction takes place indirectly, in the sense that the C–H chromophore need not absorb the photolyzing radiation. It was determined that the dissociation often took place from a very hot ground state;³¹ this indicates a rapid internal conversion process. Under the experimental conditions reported in ref. 1 and 4, the formation of H atoms can take place either on the excited state or after crossing to the ground state.

The slow formation of H₂ might appear to be in contradiction with the participation of a conical intersection, as the transition from the excited state to the ground state via this channel is very rapid. However, in this case the relatively long rise time of the product may be determined by the IVR (intramolecular vibrational relaxation) rate. The excited molecule samples the complete phase space rapidly, without net loss of energy (in the absence of collisions). IVR opens the way to all energetically possible reaction channels. The probability of a given channel depends, statistically, on the density of states for the transition state (or conical intersection) leading to it. Since the H₂ elimination is statistically less likely than H atom elimination, the latter dominates. The less probable elimination of H₂ is only observed at longer time intervals.

Experimentally, in the nanosecond experiments^7–9 at 193 nm (148 kcal mol⁻¹) no signal was observed at m/z = 79 u (cyclohexadienyl radical cation, CHDR⁺). Analysis showed, however, that the m/z = 78 u species (benzene cation) was due in part to consecutive elimination of H atoms. It was suggested that a CHDR radical was formed with enough excess energy to further dissociate before it could be detected. In the ultrafast experiments,⁴ the available energy was 186 kcal mol⁻¹ (two photons at 307 nm). In this case, in spite of the much larger available energy, the 79 u signal was observed. Its decay time was 110 fs, explaining the failure to observe it in the nanosecond experiments.

IVb. Solution photochemistry

In solution, the H-atom elimination reaction may be suppressed due to the cage effect and rapid vibrational relaxation, leading to the dominance of isomerization reaction channels. Srinivasan's extensive study¹ of CHDN photolysis in solution is summarized in Scheme 1. The H/allyl conical intersection can lead to the two major isomerization products (1,3-CHDN and BCE(I)), as shown in Fig. 2. Hexatriene and benzene can also be produced, if a step-wise mechanism beginning with the anchors shown in Fig. 2 is allowed. This option is elucidated in more detail in Fig. 9.

Fig. 9 An expanded version of the loop containing the H/allyl CI, showing how different products are related to it. Hexatriene can be formed by an allowed thermal reaction from 1,3-CHDN. This process is energetically possible since the conical intersection lies above the barrier for this reaction. The cyclohexadienyl (CHDR1) radical + H atom pair formed upon C–H bond fission has the same spin pairing as CHDN, and thus belongs to the same anchor. Bond dissociation can take place either on the ground state or on the excited state (in the latter case the CHDR radical is formed in an electronically excited state). Loss of another H atom leads to the formation of benzene. The upper part shows how para-dideuterobenzene (the major product, ref. 1) is formed from 3,3,6,6-d₄-CHDN. In the lower part, the route to the minor benzene isomer product (benzene-d₃) is shown, via the radical CHDR2, which belongs to the same anchor as 1,3-CHDN.

In the figure, the loop encircling the H/allyl CI is shown in the center. The main route to benzene can be by consecutive D atom eliminations from the hot CHDN molecule formed on the ground state upon crossing the conical intersection. A CHDR radical, CHDR1, is an intermediate, yielding para-dideuterobenzene upon a further D atom loss—the main isotopomer found in the CHDN-d₄ experiments. The 1,3-CHDN anchor, also formed with a large excess energy may isomerize in a thermally allowed reaction to hexatriene. On the other hand, it may also lose a hydrogen atom, forming an isotopomer of CHDR1, CHDR2. The latter, by losing another H atom, may form either para-dideuterobenzene (if a D atom is released), or the minor product observed in ref. 1, 1,2,4-trideuterobenzene (shown in Fig. 9) if a H atom is lost.

These routes may be experimentally observed under collision free conditions, using isotopically labeled CHDN molecules.

The notion that 1,3-CHDN and hexatriene formation are related was discussed in ref. 1. It was found experimentally that a longer wavelengths, the [1,3-CHDN]/[hexatriene] concentration ratio increased. This is compatible with the assignment of both products to the same reaction channel (same conical intersection and same anchor), and with the requirement for higher energy in the production of hexatriene.

However, only a fraction (60%) of the BCE product is formed with an isotopic distribution that is compatible with the loop as shown in Fig. 2. The CP–H/allyl CI encircled by the loop shown in Fig. 3 (structure shown in Fig. 5) is a possible funnel leading to the BCE(II) isotopomer. The high energy of that CI makes this proposition rather doubtful.

Another option for explaining the experimental isotope distribution suggests itself by considering the properties of the BCE/allyl biradical that was computed to be formed on the ground state from the H/allyl CI (Scheme 2). In most cases, a biradical formed by the cleavage of a single bond has the same spin pairing as the parent molecule, and thus lies in the same anchor. Most such biradicals collapse to a more stable molecule without encountering a barrier. The BCE biradical is different, due to the presence of a double bond adjacent to an un-paired p electron: as shown in Scheme 2, the biradical formally formed from BCE(I) is in fact one component of a resonance hybrid that may be termed a BCE/allyl biradical. The biradical is expected to be more stable than either component due to the resonance energy of the allyl structure. A computation confirmed the extra stability of this biradical (Section III), and also the expected form of an allyl-type species: as shown in Scheme 2, it has C_2v symmetry.

Once formed, the BCE/allyl biradical can react to form BCE(I) or BCE(II), as shown in Scheme 3. Thus, if the third anchor in the loop encircling the H/allyl CI is the BCE/allyl radical, both BCE(I) and BCE(II) may be formed from a single CI (the H/allyl one). This point is further discussed in the next section.

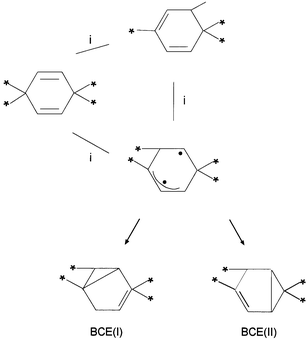Scheme 3 A modified version of the loop encircling the H/allyl conical intersection, using the BCE/allyl biradical as an anchor. Both BCE(I) and BCE(II) can be formed from this intermediate.

In solution, the ‘helicopter-type’ elimination of H₂ may be suppressed, since the strong interaction with the solvent tends to vibrationally relax the system, and to move to lower lying conical intersections. Nonetheless, Srinivasan et al.¹ reported that about 85% of the benzene molecules formed upon 185 nm irradiation of 3,3,6,6-d₄-CHDN in solution were found with two deuterium atoms positioned para to each other (Scheme 1). This isotopomer is the one expected from the conical intersection proposed in this paper, through the intermediate cyclohexadienyl radicals CHDR1 and CHDR2, as outlined in Fig. 9; the minor benzene isotopomer product, 1,2,4-trideuterobenzene, may be produced by consecutive elimination of one D atom and one H atom from CHDR2.

V. Discussion

In this paper we presented a general method for locating conical intersections in a polyatomic system. Several different CIs were identified and their energies and structures calculated. The complex photochemistry of CHDN in solution may be explained by assuming the involvement of a single conical intersection (the H/allyl CI), which was found to be located at a lower energy than all others. Srinivasan¹ proposed that the isotopic labeling experiments could be explained by assuming a 1,2-hydrogen shift reaction, through the intermediacy of a BCE/allyl biradical. He also suggested a 1,3-hydrogen shift to explain the formation of 1,3-CHDN and left open the mechanism of benzene formation. According to our model, all these products may be traced to a single primary process via one conical intersection.

The BCE/allyl biradical shown in Scheme 2 owes its stability to the resonance energy of the allyl radical. Similar allyl stabilized biradicals are expected in other systems, for instance in the photochemistry of benzene, leading to the formation of fulvene and benzvalene (ref. 32, p. 358). In the present case, it is proposed to provide the pathway to both BCE(I) and BCE(II) products, Scheme 3 and Fig. 9.

A noteworthy result is the fact that the entire complex photochemistry of CHDN may be explained by reactions in which the decisive step is the cleavage of H–C bonds. No primary reaction involving C–C bond rupture seems to be important. Other possible conical intersections, in which C–C bonds are broken or exchanged, lead to products that have not yet been experimentally observed. In particular, products expected from the di-π methane rearrangement, a ubiquitous photochemical reaction,^1,23 were not found experimentally. We have shown that the di-π methane rearrangement product, BCE(III), could form from the vinyl/allyl conical intersection, discussed in ref. 5 (see Fig. 2). We did not repeat their computations, since the possible products are not experimentally observed by a singlet state route. This isotopomer is formed photochemically only by Hg sensitization.¹

Other products arising from reactions dominated by C–C bond exchange, such as those expected from the CI enclosed by the loop shown in Fig. 1, were also not detected experimentally upon direct irradiation.

1,3-hydrogen atom shift reactions are frequently encountered in molecular photochemistry (ref. 32, p. 241). Their widespread occurrence may be due to H/allyl conical intersections that serve as efficient funnels for this pathway. In the CHDN system the calculated structure of the CI (Fig. 5) indicates that the migrating hydrogen atom moves to a relatively large distance from the carbon atoms. The H atom can therefore be cleaved to form a CHDR radical, which may undergo a secondary H atom dissociation to form benzene, as observed in the gas phase. It follows that both gas phase and liquid solution data are consistent with the proposed model.

The reasons for the absence of products due to C–C bond cleavage or exchange are not clear at this time. The energy of the vinyl/allyl CI, as calculated by ref. 5, is about 0.7 eV higher than that of the H/allyl CI. In solution, this energy difference may be large enough to make the route through the H/allyl CI entirely dominant. The di-π methane reaction is ubiquitous, but a survey of available data²³ shows that in all cases the methylene group connecting the two double bonds is substituted by methyl groups (or other substituents via a carbon atom). When substituted by hydrogen atoms, different reactions take place preferentially. The notion that reactions involving the migration of H atoms are preferred over those requiring the migration of an alkyl or heavier group is strongly supported by these observations.

Yet, the fact that many of the expected products are rather strained calls for another possible explanation. The cyclobutane derivative (Fig. 1), for instance, would most likely convert rapidly to the more stable isomers under ambient conditions. Strained species may be observed in cryogenic matrices, as shown for example in the case of butadiene photochemistry.³³ We are not aware of a matrix isolation study of CHDN photochemistry.

In order to account for more subtle data, such as the helicopter-type departure of H₂ under collision-free conditions, a different conical intersection must be implicated. We have demonstrated the existence of a possible candidate, that lies at a much higher energy than the H/allyl CI. If the ‘helicopter-type’ CI is operative under collision-free conditions, it follows that the system does not necessarily remain on the excited state surface until it reaches the lowest energy point before the curve crossing takes place. A crossing may take place at any point on the conical intersection hyper-surface. The details of these dynamic processes depend on the initial conditions, coupling constants and surface morphology. This issue is beyond the scope of this paper.

Finally, a remark concerning the number of conical intersections connecting the S₀ and S₁ potential surfaces is in order. Due to symmetry, each of the several conical intersections connecting the S₁ and S₀ surfaces of CHDN discussed in this paper represents, in fact, a number of CIs. For instance, the H/allyl CI is 8-fold degenerate—there are four H atoms that may move on the two sides of the carbon atoms ring. A similar degeneracy holds for the other conical intersections. The picture that emerges is that many funnels connect the excited energy potential surface to the ground state one.

VI. Summary

A general method for calculating the properties of all conical intersection in a given system is presented. The Longuet–Higgins loop method^11,12,26 is a useful guide for approximately locating the active conical intersection for a desired reaction. The structure of the locus on the conical intersection surface reached by the system after excitation can be calculated using quantum chemical methods. The method is shown to provide a unified account for the rather complex CHDN photochemistry.

All solution phase products can be accounted for by the involvement of a single conical intersection—the H/allyl one. A common feature of the reactions is the weakening of C–H bonds in the decisive primary steps. Conical intersections in which the prolongation of carbon–carbon bond distances is the major chemical change exist, but do not appear to yield products. A conical intersection leading to the helicopter-type motion observed under collision-free conditions is proposed and computationally demonstrated.

The course of a photochemical reaction does not necessarily match the thermal pattern that follows the lowest lying route. The actual pathway selected by the system may depend on experimental conditions: high-lying conical intersections are likely to be revealed under collision-free conditions. Dynamical information, such as obtained by vector correlation methods^7–9,34 is a sensitive indicator for the course of a photochemical reaction, and can be used to identify the active conical intersection from among several possibilities.

Acknowledgements

This research was supported by The Israel Science Foundation founded by The Israel Academy of Sciences and Humanities. The Farkas Center for Light Induced Processes is supported by Minerva Gesellschaft mbH.

References

1. R. Srinivasan, L. S. White, A. R. Rossi and G. A. Epling, J. Am. Chem. Soc., 1981, 103, 7299.
2. A. Kumar, P. K. Chowdhury, K. V. S. R. Rao and J. P. Mittal, Chem. Phys. Lett., 1991, 182, 165.
3. A. Kumar, P. D. Naik, R. D. Sainy and J. P. Mittal, Chem. Phys. Lett., 1999, 309, 191.
4. S. De Feyter, E. W.-G. Diau and A. H. Zewail, Phys. Chem. Chem. Phys., 2000, 2, 877.
5. S. Wilsey and K. N. Houk, J. Am. Chem. Soc., 2000, 122, 2651.
6. S. W. Benson and R. Shaw, J. Am. Chem. Soc., 1967, 89, 5351.
7. X. Zhao, R. E. Continetti, A. Yokoyama, E. J. Hintsa and Y. T. Lee, J. Chem. Phys., 1989, 91, 4118.
8. E. V. Cromwell, D.-J. Liu, M. J. J. Vrakking, A. H, Kung and Y. T. Lee, J. Chem. Phys., 1990, 92, 3230.
9. E. V. Cromwell, D.-J. Liu, M. J. J. Vrakking, A. H. Kung and Y. T. Lee, J. Chem. Phys., 1991, 95, 297.
10. R. J. Rico, M. Page and C. Doubleday, Jr., J. Am. Chem. Soc., 1992, 114, 1131.
11. S. Zilberg and Y. Haas, Eur. J. Chem., 1999, 5, 1755.
12. S. Zilberg and Y. Haas, Chem. Phys., 2000, 259, 249.
13. H. C. Longuet-Higgins, Proc. R. Soc. London, A, 1975, 344, 147.
14. R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1969, 7, 227.
15. M. J. S. Dewar, Adv. Chem. Phys., 1965, 8, 121.
16. C. Bornemann and M. Klessinger, Chem. Phys., 2000, 259, 263.
17. R. Izzo and M. Klessinger, J. Comput. Chem., 2000, 21, 52.
18. G. A. Worth and L. S. Cederbaum, Chem. Phys. Lett., 2001, 338, 219.
19. In Hückel-type reactions the phase of each atomic electronic orbital is preserved with respect to that of its neighbor. In Möbius-type reactions the phase of one atomic orbital is inverted. Only orbitals of odd symmetry are capable of Möbius inversion–examples are 2p and 4f orbitals, as well as hybrid orbitals of spⁿ type. Examples of such reactions are the conrotatory ring closure of butadiene and hexatriene. See ref. 25, 26..
20. M. J. S. Dewar, Tetrahedron Suppl., 1966, 8(Part 1), 75..
21. H. E. Zimmerman, Acc. Chem. Res., 1972, 4, 272.
22. S. Zilberg and Y. Haas, Int. J. Quantum Chem., 1999, 71, 133.
23. S. S. Hixson, P. S. Mariano and H. E. Zimmermann, Chem. Rev., 1973, 75, 531.
24. M. W. Schmidt, K. K. Baldrige, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, GAMESS, 4th of March 1993 ver., Iowa State University (ISUQCG), IA..
25. B. O. Roos, Adv. Chem. Phys., 1987, 69, 399.
26. S. Zilberg and Y. Haas, J. Photochem. Photobiol., 2001, 144, 221.
27. By the Longuet-Higgins theorem, the conical intersection lies within the loop enclosed by the three anchors A, B and C. One of the two coordinates spanning the plane defined by these anchors is phase preserving and the other phase inverting.^11,13 Without loss of generality, assume that the AATS lies on the phase inverting coordinate. Its electronic wave function may be written as the out-of-phase combination ∣A〉 − ∣B〉. Its twin excited state is the in-phase combination ∣A〉 + ∣B〉,²⁶ and has the same nuclear geometry as the AATS. The electronic wave function of the ground state of C is may also be written as an in-phase linear combination of ∣A〉 and ∣B〉, as there are only two independent wave-function spanning this two dimensional space. The nuclear geometry of C (at the minimum energy) is of course different than that of the AATS. Therefore, the electronic wave functions of S₁ of the AATS and of C have the same phase, and are connected by a phase preserving coordinate (the ‘reaction coordinate’ leading from the AATS between A and B, to C). Motion along this coordinate leads directly from the excited state surface to the ground state one, and is thus bound to reach the seam between the two at the conical intersection. The energy at which this will happen can be minimized by optimizing all other nuclear coordinates of the system..
28. The energies of the excited states are found to be considerably lower at the CASPT2(8,8)/DZV level: 6.86 eV (S₁, vertical) and 7.8 eV (S₂, vertical). For a recent CASPT2 calculation of CHDN energy levels with ANO-type basis set, see ref. 29. This calculation resulted in good agreement with experiment..
29. M. Merchan, L. Serrano-Andres, L. S. Slater, B. O. Roos, R. McDiarmid and X. Xing, J. Phys. Chem., 1999, 103, 5468.
30. L. Salem,Electrons in Chemical Reactions: First Principles, Wiley, New York, 1982..
31. Z. Min, T.-H. Wong and R. Bersohn, J. Chem. Phys., 1999, 110, 9956 and references therein..
32. A. Gilbert and J. Baggott, Essentials of Molecular Photochemistry, Blackwell, London, 1991..
33. M. Squillacote and T. C. Semple, J. Am. Chem. Soc., 1990, 112, 554.
34. G. E. Hall, N. Sivakumar, D. Chawla, P. L. Houston and I. Burak, J. Chem. Phys., 1988, 88, 3682.

---