Activity coefficients of lanthanum salts at 298.15 K†
Received
5th September 2001
, Accepted 1st November 2001
First published on 13th December 2001
Abstract
Activity coefficients of La(NO3)3, La(ClO4)3, and La2(SO4)3 are determined using the method of liquid membrane cells, which allows us to study high dilution levels previously unattainable (10−4 to 10−5 mol kg−1 depending on the salt). Literature values are found to be correct for La(ClO4)3, moderately biased for La(NO3)3 and completely incorrect for La2(SO4)3. This last salt in the diluted regions displays dramatic negative deviations—not recognised earlier because the measurements terminated at ca. 10−3 mol kg−1, where a Debye–Hückel-like misleading trend occurs. Numerical integration of the Poisson–Boltzmann equation and Bjerrum's
theory of ion pairing show an astounding ability to reproduce the trend of La2(SO4)3; however, there is evidence of short-range interactions that add to long-range interactions for lanthanum and bivalent metal sulfates, as if sulfate ions were displacing water from the hydration shells of the cations. Pitzer's equation parameters that reproduce the activity and osmotic coefficients of the three salts and those (recalculated) of LaCl3 are reported.
Introduction
Activity coefficients have an obvious importance for anyone interested in reactions involving ionic species; unfortunately, the level of insight on this matter is still unsatisfactory, excluding low-charge electrolytes that are faithfully covered by theory and experiments. For high-charge electrolytes the data have generally been available so far only in concentrated or poorly diluted solutions, in the form of relative activity coefficients not liable to transformation into activity coefficients. This fact has also had a negative influence on the theoretical developments, since the models concerned with high charge electrolytes lacked precise experimental verification. In recent years, however, emf measurements relying on liquid-membrane potentiometric cells (thermodynamically equivalent to cells without transfer) have made chemical potentials accessible for an unlimited variety of electrolytes down to 10−4 or 10−5 mol kg−1
and beyond.1 These low concentrations generally suffice for ion-interaction treatments to provide unequivocal extrapolation to infinite dilution also for multivalent electrolytes, thus turning the relative activity coefficients into activity coefficients. Moreover, the liquid-membrane cells (like classic cells without transport when available) allow the activity coefficient of a solution of, e.g., a 3 : 2 salt, in this case La2(SO4)3, to be identified by a thermodynamic cycle matching the relevant emf E3 : 2 with emf values E3 : 1, E1 : 2, and E1 : 1 of auxiliary salts 3 : 1 (here LaCl3), 1 : 2 (K2SO4) and 1 : 1 (KCl), whose activity coefficients have been determined previously (absolute point method).1(h,i)
Thus, the activity coefficient of a n : n′
(n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, n′
1, n′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) salt may generally be evaluated by both direct extrapolation and the absolute point method—i.e., extrapolation to zero performed for simpler salts—with a possible mutual check.
1) salt may generally be evaluated by both direct extrapolation and the absolute point method—i.e., extrapolation to zero performed for simpler salts—with a possible mutual check.
Unlike LaCl3 that has been studied by isopiestic measurements,2 concentration cells,3 Harned's method,4 and liquid membrane cells,1c La(NO3)3 and La(ClO4)3 have so far been submitted only to isopiestic measurements of very high quality,5,6 but unable to reach concentration levels lower than 0.1 mol kg−1 and therefore insufficient for the absolute values of the activity coefficients to be unequivocally identified (the values still depend on the theory used to guide the extrapolation to zero). For lanthanum sulfate, osmotic and activity coefficients have not been revised since earlier measurements7 that were quoted to agree with the Debye–Hückel theory.8
We suspected, like Pitzer,9 that the interpretation of past results for La2(SO4)3 was a mistake. The measurements performed more recently in the dilute regions for bivalent metal sulfates, tris(ethylenediamine)cobalt (III) sulfate, alkaline-earth hexacyanoferrate (III) and hexacyanocobaltate (III) salts, as well as 3 : 3 salts,1(b–j) have all shown negative deviations from the limiting law. Typically, ln γ± of a n : n′ electrolyte (n, n′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) presents a negative slope steeper than the limiting law (DHLL) at 10−4 mol kg−1, and a less steep negative slope, or positive slope, in
concentrated solutions. The inversion usually occurs in the neighbourhood of 10−3 mol kg−1; thus a high-charge salt that has been studied only at m
1) presents a negative slope steeper than the limiting law (DHLL) at 10−4 mol kg−1, and a less steep negative slope, or positive slope, in
concentrated solutions. The inversion usually occurs in the neighbourhood of 10−3 mol kg−1; thus a high-charge salt that has been studied only at m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≥
≥![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 mol kg−1 may misleadingly, seem to conform to the Debye–Hückel law.
10−3 mol kg−1 may misleadingly, seem to conform to the Debye–Hückel law.
The results obtained when studying La(NO3)3, La(ClO4)3, and La2(SO4)3 down to the highest dilution levels permitted by our cells are reported.
Experimental
Apparatus
The cells used were | | 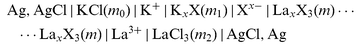 | (cell 1) |
(Xx−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NO3− or ClO4− or SO42− as appropriate), and
NO3− or ClO4− or SO42− as appropriate), and | | 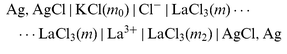 | (cell 2) |
| | 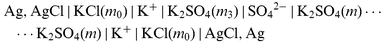 | (cell 3) |
| | 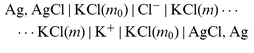 | (cell 4) |
for the three auxiliary salts LaCl3, K2SO4, and KCl. Sections |K+|, |Xx−|,..., |Cl−| denote liquid-membranes permeable to the corresponding ions. Each membrane is made of a salt of the quoted ion with a large organic hydrophobic and lipophilic counterion yielding extreme insolubility in water, dissolved (if not liquid itself)
in an organic solvent, also insoluble in water. The counterion is tetrakis[3,5-bis(trifluoromethyl)phenyl] borate anion (C8H3F6)4B−, TFPB− for brevity, in the cation-responsive membranes, and the tetradodecylammonium cation (C12H25)4N+, TDA+, in the anion-responsive membranes. The preparation and purification of these salts—except for TDANO3 that does not differ, however, from TDACl or TDAClO4—are described elsewhere.1 Membrane compositions were, for |La3+| and |K+| membranes, La(TFPB)3
(12.4%) or KTFPB (17%) dissolved in 2-nitrophenyl octyl ether; for |NO3−|, TDANO3
(11.5%)
in oleyl alcohol; for |Cl−| and |ClO4−|, 4.5% TDACl or saturated (ca. 0.5%) TDAClO4 in 3,4 dichlorotoluene. The |SO42−| membrane is made of (TDA)2SO4(H2O)x, a thick liquid, insoluble in water, not needing any solvents, and obtained by soaking (TDA)2SO4 in water for a few weeks; there are indications that sulfate ions contained here are [SO4(H2O)8]2−.1f Filtering septa of PTFE soaked in the relevant membrane phases are used to separate membrane and aqueous sections.
The two chains of phases (Ag, AgCl, aqueous solutions, and membranes) lying to the left and right of the test solution are assembled inside two PTFE tubes, to form two composite electrodes, for the anion and cation respectively. These electrodes are inserted in a larger vessel also made of PTFE, containing the test solution, ca. 15 cm3. A small magnetic bar (ca. 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mm2, usually at a rotation rate of ca. 1–3 rps) ensures moderate stirring conditions if desired. The details of the cells and electrode assemblage have been described in previous papers (see in particular Fig. 1 of ref. 1d showing the cell, and Fig. 1 of ref. 1f and Fig. 1 of ref.
1j showing the most recent assemblage details of the cation-responsive and anion-responsive electrodes). The entire assembly is contained in an air bath thermostat at 298.15
2 mm2, usually at a rotation rate of ca. 1–3 rps) ensures moderate stirring conditions if desired. The details of the cells and electrode assemblage have been described in previous papers (see in particular Fig. 1 of ref. 1d showing the cell, and Fig. 1 of ref. 1f and Fig. 1 of ref.
1j showing the most recent assemblage details of the cation-responsive and anion-responsive electrodes). The entire assembly is contained in an air bath thermostat at 298.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.02 K. A platinum resistance thermometer (±0.001 K) is used for temperature monitoring. The electrical resistance of the cells generally ranges between 104 and 105
Ω. Emf measurements were performed using a Digital Adret Electronique 103A DC-current and voltage standard as supplier for potentials (±0.001 mV) and a Keithley 614 Electrometer (input impedance
0.02 K. A platinum resistance thermometer (±0.001 K) is used for temperature monitoring. The electrical resistance of the cells generally ranges between 104 and 105
Ω. Emf measurements were performed using a Digital Adret Electronique 103A DC-current and voltage standard as supplier for potentials (±0.001 mV) and a Keithley 614 Electrometer (input impedance![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1014
Ω) as null point (±0.01 mV) detector. The measurements take approximately 90 min per solution, 60 min being waiting time, and 30 for the emf readings—one every 5 min—whose average values and standard deviations are reported in Tables S1–S3.†
1014
Ω) as null point (±0.01 mV) detector. The measurements take approximately 90 min per solution, 60 min being waiting time, and 30 for the emf readings—one every 5 min—whose average values and standard deviations are reported in Tables S1–S3.†
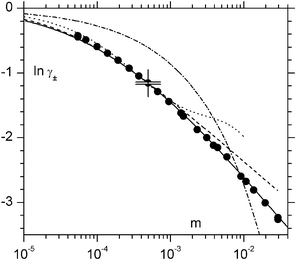 |
| | Fig. 1 Activity coefficients of La2(SO4)3 compared with the limiting law DHLL (dash-dot line) and primitive model approximations DHLL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2
(a B2
(a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.43 nm; dotted line), BT (a 0.43 nm; dotted line), BT (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.38 nm; dashed line) and IPBE (a 0.38 nm; dashed line) and IPBE (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.355 nm; full line). The double cross marks the reference point and its range of uncertainty. 0.355 nm; full line). The double cross marks the reference point and its range of uncertainty. | |
Reagents
The salts La(ClO4)3
(available commercially in the form of a stock solution of ca. 40 wt.%), La(NO3)3, and La2(SO4)3, were Aldrich 99.999% certified products and were used without further purification, while the auxiliary salts KCl, LaCl3, and K2SO4 came from earlier stocks used for the determinations of volumetric properties10 and activity coefficients,1(a–c,g) originally crystallised at least twice from conductivity water. Standard solutions for K2SO4 and KCl were prepared by weighing the salts dried in a furnace at 500 and 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. Stock solutions of La(NO3)3, La(ClO4)3, La2(SO4)3,
and LaCl3, were standardised by acidimetric titration, via cation exchange (Dowex 50W
°C. Stock solutions of La(NO3)3, La(ClO4)3, La2(SO4)3,
and LaCl3, were standardised by acidimetric titration, via cation exchange (Dowex 50W![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 resin in the hydrogen form), dropping the resulting acid on a weighed excess of Na2CO3, then back-titrating with HCl (relative standard deviation, 0.03 to 0.1%). All further solutions were then prepared by weight.
8 resin in the hydrogen form), dropping the resulting acid on a weighed excess of Na2CO3, then back-titrating with HCl (relative standard deviation, 0.03 to 0.1%). All further solutions were then prepared by weight.
Principle and procedures
If the free-energy variations of the isothermal, isobaric, virtual transfer of charge throughout the cell, at constant composition, are all considered, including the contributions of water molecules carried by the ions into the membranes, it is easily established that, in the absence of interfering amounts of foreign ions able to enter the membranes, the emf of cells like cell 1–cell 4 obey the relationship,1| | 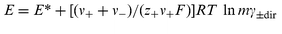 | (1) |
where z+ is the charge of the cation, ν+ and ν− are the number of cations and anions in the electrolyte, and where1g| | 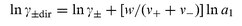 | (2) |
where a1 is the activity of water in the test solutions and w the number of molecules
of water that follow one “molecule” of the electrolyte when its ions leave the test solution and enter the neighbouring membranes.‡ The difference between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±
and ln
γ±
and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±dir can be neglected if m
γ±dir can be neglected if m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 mol kg−1; at higher concentrations, correction of ln
0.01 mol kg−1; at higher concentrations, correction of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±dir into ln
γ±dir into ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± needs either knowledge of w, or knowledge of the osmotic coefficients (ϕ) or relative activity coefficients referring to the non-hydrated electrolyte, obtained from e.g. isopiestic measurements. E* depends on the choice for m0, m1, etc. inside the invariant sections of the cell, and also includes the numeric constant allowing for our use of m
(instead of m±) in eqn. (1).
γ± needs either knowledge of w, or knowledge of the osmotic coefficients (ϕ) or relative activity coefficients referring to the non-hydrated electrolyte, obtained from e.g. isopiestic measurements. E* depends on the choice for m0, m1, etc. inside the invariant sections of the cell, and also includes the numeric constant allowing for our use of m
(instead of m±) in eqn. (1).
E*
(like E° in a classic cell without transport) is generally identified by an extrapolation to ionic strength zero, with the aid of a “guide-line” such as the Debye–Hückel theory (DHT) or higher-order limiting laws. No problems are reasonably expected for low-charge electrolytes (including 1 : 3 and 3 : 1), as the different theories lead to the same extrapolation values when applied to the very diluted solutions permitted by the liquid membrane cells. However, for a 3 : 2 electrolyte the extrapolation process may be critical, even starting from high dilution levels. Fortunately, the absolute point method provides an independent solution to the problem. As the electrodes used in cell 1–cell 4 are always the same although differently matched, by developing the expressions for E* of cell
1–cell 4
(E*3 : 2, E*3 : 1, E*1 : 2, and E*1 : 1), not reported as cumbersome, one finds the relationship:
| | 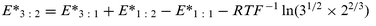 | (3) |
Eqn. (3)
(the absolute point equation) makes it possible to calculate the unknown value
E* of the 3 : 2 salt as a combination of those, much easier to determine, of 3 : 1, 1 : 2, and 1 : 1 auxiliary salts.
§ In particular, for LaCl
3, K
2SO
4, and KCl, the activity coefficients are already known.
1a,c,g,11 Hence, four emf measurements, for La
2(SO
4)
3, LaCl
3, K
2SO
4, and KCl, can be sufficient to obtain
E* for La
2(SO
4)
3. The determination is of course repeated several times (Table S4
†). As the value of
E*
is liable to change, the relevant information is more conveniently stored in the form of the value of the activity coefficient,
γ±(ref), of the reference solution.
Results
Experimental emf and activity coefficients for lanthanum perchlorate, nitrate, and sulfate are reported in Tables S1–S3.† Measurements were stable and reproducible except for the extreme dilution levels near the breakdown of the method (see lanthanum sulfate at 5.424![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 mol kg−1 in Table S3†), where drifts and some dependence of cell potential on the stirring rate became perceptible and increased dramatically on further diluting the solutions, owing to the interference from H+, OH−, and possibly HCO3−. Some drifts, memory effects, and lack of reproducibility were also observed in the concentrated solutions of lanthanum perchlorate (m
10−5 mol kg−1 in Table S3†), where drifts and some dependence of cell potential on the stirring rate became perceptible and increased dramatically on further diluting the solutions, owing to the interference from H+, OH−, and possibly HCO3−. Some drifts, memory effects, and lack of reproducibility were also observed in the concentrated solutions of lanthanum perchlorate (m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8 mol kg−1), indicating that equilibrium conditions were no longer met. The data reported in Tables
S1–S3† are grouped in series, in the same order in which they were determined; each series begins and ends with the reference solution (mref, Eref) to correct some minor shifts (increasing run by run when loading and reloading the cell many times a day) arising from membrane surface leaching.¶ Since the relative activity coefficients γ±′
0.8 mol kg−1), indicating that equilibrium conditions were no longer met. The data reported in Tables
S1–S3† are grouped in series, in the same order in which they were determined; each series begins and ends with the reference solution (mref, Eref) to correct some minor shifts (increasing run by run when loading and reloading the cell many times a day) arising from membrane surface leaching.¶ Since the relative activity coefficients γ±′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±/γ±(ref) are obtained from the difference between E and Eref
(RTF−1 ln
γ±/γ±(ref) are obtained from the difference between E and Eref
(RTF−1 ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mγ±′/mref
mγ±′/mref![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Eref), the disturbing effect is empirically corrected by interpolating Eref throughout the daily series of measurements. The γ±(ref) values were then determined using the following methods.
Eref), the disturbing effect is empirically corrected by interpolating Eref throughout the daily series of measurements. The γ±(ref) values were then determined using the following methods.
La(ClO4)3
(mref![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1.002
1.002![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 10−3 mol kg−1)
10−3 mol kg−1)
Experimental ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±′ for 2
γ±′ for 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2
1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2 extrapolated to zero by DHT provide ln
10−2 extrapolated to zero by DHT provide ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.229
−0.229![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.003 (best value for the distance of closest approach, a, about 0.67 nm).|| The results do not change appreciably if extrapolation
methods based on higher-order approximations are used. IPBE (a numerical integration of the exponential Poisson–Boltzmann equation)12 applied to points between 2
0.003 (best value for the distance of closest approach, a, about 0.67 nm).|| The results do not change appreciably if extrapolation
methods based on higher-order approximations are used. IPBE (a numerical integration of the exponential Poisson–Boltzmann equation)12 applied to points between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 and 3.5
10−4 and 3.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2 mol kg−1 extrapolates ln
10−2 mol kg−1 extrapolates ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.221
−0.221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005 (best value for a, 0.64 nm). Bjerrum's theory of ion pairing (BT)13 suggests ln
0.005 (best value for a, 0.64 nm). Bjerrum's theory of ion pairing (BT)13 suggests ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.231
−0.231![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.004 (2
0.004 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2
1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2; a
10−2; a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.72 nm), or −0.224
0.72 nm), or −0.224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006 (2
0.006 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol
kg−1
m/mol
kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.5
3.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2; a
10−2; a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.78 nm). The DHLL
0.78 nm). The DHLL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2 approximation of the Mayer theory14 provides −0.225
B2 approximation of the Mayer theory14 provides −0.225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005 (a++
0.005 (a++![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a−−
a−−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a±
a±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.65 nm) between 2
0.65 nm) between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 and 8
10−4 and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 mol kg−1, or −
10−3 mol kg−1, or −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.222
0.222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±0.008 (a++
±0.008 (a++![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a−−
a−−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a±
a±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.70 nm) between 2
0.70 nm) between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 and 1.2
10−4 and 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2 mol kg−1. We selected −0.225
10−2 mol kg−1. We selected −0.225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006,
an average estimate, as the best value of ln γ±(ref).
0.006,
an average estimate, as the best value of ln γ±(ref).
![Activity coefficients of La(ClO4)3
(filled diamonds) LaCl3
(open circles) and La(NO3)3
(filled circles) prolonged in the isopiestic range (Pitzer's equation, parameters from Table S8). For comparison, the limiting law DHLL, dash-dot line; [Co(en)3]Cl3, dashed line;1b K3[Fe(CN)6] and K3[Co(CN)6]
(indistinguishable), dotted line.1c,h](/image/article/2002/CP/b108053a/b108053a-f2.gif) |
| | Fig. 2 Activity coefficients of La(ClO4)3
(filled diamonds) LaCl3
(open circles) and La(NO3)3
(filled circles) prolonged in the isopiestic range (Pitzer's equation, parameters from Table S8†). For comparison, the limiting law DHLL, dash-dot line; [Co(en)3]Cl3, dashed line;1b K3[Fe(CN)6] and K3[Co(CN)6]
(indistinguishable), dotted line.1c,h | |
![The deviations from the limiting law, ln γ±−ln γ±(DHLL), of the activity coefficients of 3 : 2 electrolytes: La2(SO4)3, filled circles; [Co(en)3]2(SO4)3,1b open circles, compared with Mg3[Co(CN)6]21h
(thick line), IPBE (thin lines, a = 0.355 nm the lower, a = 0.38 nm the upper) and DHLL + B2
(dashed line, a = 0.43 nm).](/image/article/2002/CP/b108053a/b108053a-f3.gif) |
| | Fig. 3 The deviations from the limiting law, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±−ln γ±−ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(DHLL), of the activity coefficients of 3 : 2 electrolytes: La2(SO4)3, filled circles; [Co(en)3]2(SO4)3,1b open circles, compared with Mg3[Co(CN)6]21h
(thick line), IPBE (thin lines, a γ±(DHLL), of the activity coefficients of 3 : 2 electrolytes: La2(SO4)3, filled circles; [Co(en)3]2(SO4)3,1b open circles, compared with Mg3[Co(CN)6]21h
(thick line), IPBE (thin lines, a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.355 nm the lower, a 0.355 nm the lower, a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.38 nm the upper) and DHLL 0.38 nm the upper) and DHLL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2
(dashed line, a B2
(dashed line, a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.43 nm). 0.43 nm). | |
La(NO3)3
(mref![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 7.495
7.495![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 10−4 mol kg−1)
10−4 mol kg−1)
BT extrapolates ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.224
−0.224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.004 (3
0.004 (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.3
3.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2 mol kg−1; best value for a, 0.435 nm). IPBE provides −0.216
10−2 mol kg−1; best value for a, 0.435 nm). IPBE provides −0.216![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006 (3
0.006 (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.11; best value for a, 0.425 nm). DHT no longer reproduces the experimental data with sufficient precision if m
0.11; best value for a, 0.425 nm). DHT no longer reproduces the experimental data with sufficient precision if m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 mol kg−1, moreover it requires unreasonably low values of a of ca. 0.3 nm; however, the extrapolated value it finds from values ranging between 3
10−3 mol kg−1, moreover it requires unreasonably low values of a of ca. 0.3 nm; however, the extrapolated value it finds from values ranging between 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
and 5
10−4
and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 mol kg−1 is the same as for BT, −0.224
10−3 mol kg−1 is the same as for BT, −0.224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.004 (a
0.004 (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.30 nm). DHLL
0.30 nm). DHLL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2 needs high dilution levels like DHT and suggests −0.227
B2 needs high dilution levels like DHT and suggests −0.227![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.003 (3
0.003 (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.9
5.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3; best value for a, 0.39 nm). We selected ln
10−3; best value for a, 0.39 nm). We selected ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.222
−0.222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006 as the most probable value.
0.006 as the most probable value.
La2(SO4)3
(mref![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 4.929
4.929![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 10−4 mol kg−1)
10−4 mol kg−1)
The absolute point method yields ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1.158
−1.158![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006 that becomes −1.158
0.006 that becomes −1.158![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.016 if allowance is made for the propagation of the possible error already present in the activity coefficients of K2SO4,1g LaCl3,1c and KCl1a,11
(Table S4†). Extrapolation methods were not successful for La2(SO4)3. DHT is unusable because of the negative deviations in the dilute regions. BT, IPBE, and DHLL
0.016 if allowance is made for the propagation of the possible error already present in the activity coefficients of K2SO4,1g LaCl3,1c and KCl1a,11
(Table S4†). Extrapolation methods were not successful for La2(SO4)3. DHT is unusable because of the negative deviations in the dilute regions. BT, IPBE, and DHLL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2, are able to reproduce the experimental trend with its negative deviations from the limiting law (in particular, IPBE for a between 0.35 and 0.36 nm predicts a trend very similar to the
one in the experimental region; Fig. 1); however, as reassuring as such trends may seem, when trying to use IPBE or Bjerrum treatments as a tool to extrapolate ln
B2, are able to reproduce the experimental trend with its negative deviations from the limiting law (in particular, IPBE for a between 0.35 and 0.36 nm predicts a trend very similar to the
one in the experimental region; Fig. 1); however, as reassuring as such trends may seem, when trying to use IPBE or Bjerrum treatments as a tool to extrapolate ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref), the latter is predicted to lie at ca. 0.1–0.2 units below the absolute point with a large range of uncertainty; conversely, the Mayer theory suggests that ln
γ±(ref), the latter is predicted to lie at ca. 0.1–0.2 units below the absolute point with a large range of uncertainty; conversely, the Mayer theory suggests that ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref) lies 0.1 to 0.2 units above the absolute point. The conclusion to be drawn is that intrinsic approximations prevent these theories from identifying how exactly the salt, as well as the primitive model, should behave. More sophisticated theoretical treatments and even higher dilution levels would be necessary to make extrapolation to zero possible.
γ±(ref) lies 0.1 to 0.2 units above the absolute point. The conclusion to be drawn is that intrinsic approximations prevent these theories from identifying how exactly the salt, as well as the primitive model, should behave. More sophisticated theoretical treatments and even higher dilution levels would be necessary to make extrapolation to zero possible.
Owing to the high dilution levels, the distinction between γ± and γ±dir does not matter when determining γ±(ref). At higher concentrations, γ±dir are turned into the usual activity coefficients γ±
(last column in Tables S1–S3†) using the methods of ref. 1(f) and 1(g). The hydration numbers are known to be twelve for lanthanum ions in |La3+|,1c zero or perhaps one (0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5) for ClO4− in |ClO4−|,1g and eight for SO42− in |SO42−|;1f thus the values of w
[eqn. (2)] have to be 12 (or possibly 15) for La(ClO4)3,** and 48 for La2(SO4)3. No previous data for NO3− in |NO3−| were available; the method of ref. 1f
(which relies on the osmotic and relative
activity coefficients from literature, here ref. 5, and on E values measured in the concentrated regions)
††
yields w
0.5) for ClO4− in |ClO4−|,1g and eight for SO42− in |SO42−|;1f thus the values of w
[eqn. (2)] have to be 12 (or possibly 15) for La(ClO4)3,** and 48 for La2(SO4)3. No previous data for NO3− in |NO3−| were available; the method of ref. 1f
(which relies on the osmotic and relative
activity coefficients from literature, here ref. 5, and on E values measured in the concentrated regions)
††
yields w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 (24.02), hence identifying a hydration number of 4 (not very logical, we agree) for NO3− in |NO3−|.‡‡ Since a hydration number of three, or six, is more appeasing to chemical intuition, calculations were also performed for w
24 (24.02), hence identifying a hydration number of 4 (not very logical, we agree) for NO3− in |NO3−|.‡‡ Since a hydration number of three, or six, is more appeasing to chemical intuition, calculations were also performed for w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 and w
21 and w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30; however, the results agree less well with Rard's.5b Differences between ln
30; however, the results agree less well with Rard's.5b Differences between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± values corrected for w
γ± values corrected for w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 and w
24 and w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 or 30 are negligible except for the three most concentrated solutions, 0.5762, 0.2549, and 0.1100 mol kg−1, where w
21 or 30 are negligible except for the three most concentrated solutions, 0.5762, 0.2549, and 0.1100 mol kg−1, where w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 (30) provides ln
21 (30) provides ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±
0.025 (0.051), 0.011 (0.021), and 0.004 (0.009) units lower (higher). The ranges of uncertainty associated with the ln
γ±
0.025 (0.051), 0.011 (0.021), and 0.004 (0.009) units lower (higher). The ranges of uncertainty associated with the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± values in Tables S1–S3† include the contribution of the uncertain values of w.
γ± values in Tables S1–S3† include the contribution of the uncertain values of w.
Discussion
La(NO3)3 and La(ClO4)3
Comparison of literature data5,6 with ours reveals a perfect agreement of relative activity coefficient values for both La(NO3)3 and La(ClO4)3. Our experimental data extend to much higher dilution orders, ca. 10−4 mol kg−1 instead of 0.1 mol kg−1, and hence extrapolation to zero and the absolute activity coefficients should be preferred. However, La(ClO4)3 in ref. 6 needs no corrections. As for La(NO3)3, γ± values reported at even concentrations in ref. 5 should be multiplied by 0.927![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006 (i.e., the corresponding ln
0.006 (i.e., the corresponding ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± should be shifted by −0.073
γ± should be shifted by −0.073![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006)
for m
0.006)
for m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol kg−1; values reported for m
0.1 mol kg−1; values reported for m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol kg−1
(i.e., beyond the experimental range of the isopiestic measurements) should be discarded. Pitzer's empirical equations,15 in the form devised for high-charge electrolytes,16 can be used as a source of interpolated values for osmotic and activity coefficients; a set of selected parameters fitting both ln
0.1 mol kg−1
(i.e., beyond the experimental range of the isopiestic measurements) should be discarded. Pitzer's empirical equations,15 in the form devised for high-charge electrolytes,16 can be used as a source of interpolated values for osmotic and activity coefficients; a set of selected parameters fitting both ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± and ϕ within ±0.01 is reported in Table 1. Calculations are extended to lanthanum chloride (whose activity coefficients have been reconsidered: Table S5†).
γ± and ϕ within ±0.01 is reported in Table 1. Calculations are extended to lanthanum chloride (whose activity coefficients have been reconsidered: Table S5†).
Table 1 Pitzer's equation best fit parameters for activity and osmotic coefficients of lanthanum salts at 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C in watera
°C in watera
| Anion |
α
1
|
α
2
|
β
(0)
|
β
(1)
|
β
(2)
|
C
γ
MX
b
|
m
1, m2c |
Expt. |
σ
d
|
| |
Equations and parameter symbols from ref. 16.
C
γ
MX![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 CϕMX.
m
1, m2, the experimental range where the parameters have been fitted to ln 1.5 CϕMX.
m
1, m2, the experimental range where the parameters have been fitted to ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± or ϕ
(column Expt.).
Standard deviation of ln γ± or ϕ
(column Expt.).
Standard deviation of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± or ϕ
(column Expt) between m1 and m2.
ln γ± or ϕ
(column Expt) between m1 and m2.
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± from ref. 1(c) corrected for the ion hydration, ref.
3(a) lowered by −0.012, ref. 3(b) lowered by −0.007.
ϕ from ref. 2.
ϕ from ref. 6; points at high concentrations (2.562 γ± from ref. 1(c) corrected for the ion hydration, ref.
3(a) lowered by −0.012, ref. 3(b) lowered by −0.007.
ϕ from ref. 2.
ϕ from ref. 6; points at high concentrations (2.562![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) < <![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1 m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) < <![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.775) not included.
ϕ from ref. 5; points at high concentrations (2.537 4.775) not included.
ϕ from ref. 5; points at high concentrations (2.537![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) < <![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1 m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) < <![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.459) not included. 8.459) not included.
|
| Cl− |
1.96 |
— |
0.584 |
5.37 |
— |
−0.034 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4, 0.9 10−4, 0.9 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±e γ±e |
0.006 |
| (.01) |
— |
(.003) |
(.03) |
— |
(.001) |
0.23, 3.89 |
ϕ
f
|
0.009 |
| ClO4− |
2.05 |
— |
0.757 |
6.74 |
— |
0.010 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4, 0.4 10−4, 0.4 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± γ± |
0.010 |
| (.01) |
— |
(.004) |
(.04) |
— |
(.009) |
0.28, 2.56 |
ϕ
g
|
0.009 |
| NO3− |
1.40 |
— |
0.320 |
3.29 |
— |
−0.031 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4, 0.6 10−4, 0.6 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± γ± |
0.010 |
| (.04) |
— |
(.002) |
(.005) |
— |
(.002) |
0.39, 2.54 |
ϕ
h
|
0.003 |
| SO42− |
18.6 |
54.5 |
5.27 |
−593 |
−1775 |
−16.8 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) × ×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5, 0.03 10−5, 0.03 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± γ± |
0.013 |
| (1.3) |
(9.6) |
(.44) |
(129) |
(230) |
(10.9) |
— |
— |
— |
Pictorial comparison of the activity coefficients of lanthanum nitrate, chloride, and perchlorate (Fig. 2) shows that nitrate and perchlorate behave as if the ionic interactions were respectively stronger and weaker than in lanthanum chloride. Other 1 : 3 and 3 : 1 salts whose activity coefficients are also accurately known since determined down to sufficiently high dilution levels—[Co(en)]3Cl3,1b K3[Fe(CN)6]1c and K3[Co(CN)6]1h—are characterized by still higher ionic interactions, corresponding to a lower value for a in the restricted primitive model. Referring to e.g. the IPBE approximation, the values of a that better fit the experimental curves in the diluted
regions (m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol kg−1) are 0.37 nm for [Co(en)]3Cl3, 0.42 nm for both K3[Fe(CN)6] and K3[Co(CN)6], 0.43 nm for La(NO3)3, 0.51 nm for LaCl3, and 0.64 nm for La(ClO4)3. These differences in a are probably associated with the hydrophobic–hydrophilic character and not only with ion sizes.
0.1 mol kg−1) are 0.37 nm for [Co(en)]3Cl3, 0.42 nm for both K3[Fe(CN)6] and K3[Co(CN)6], 0.43 nm for La(NO3)3, 0.51 nm for LaCl3, and 0.64 nm for La(ClO4)3. These differences in a are probably associated with the hydrophobic–hydrophilic character and not only with ion sizes.
La2(SO4)3
As is shown in Fig. 3, La2(SO4)3 presents much greater negative deviations from the limiting law than those observed for M3[Fe(CN)6]2
(M![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) Mg, Ca, Sr, Ba)1e and M3[Co(CN)6]2
(M
Mg, Ca, Sr, Ba)1e and M3[Co(CN)6]2
(M![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) Mg, Ca),1h hence rather resembling [Co(en)3]2(SO4)3. Strangely, however, La2(SO4)3 displays larger deviations than [Co(en)3]2(SO4)3; this does not occur between La[Fe(CN)6] and [Co(en)3][Fe(CN)6], or between La[Co(CN)6]
and [Co(en)3][Co(CN)6], where the order is opposite and the differences are higher.1j This finding and the values of a required by the primitive model for lanthanum and bivalent metal sulfates—lower compared with those needed for lanthanum and bivalent metal perchlorates—deserve some consideration.
Mg, Ca),1h hence rather resembling [Co(en)3]2(SO4)3. Strangely, however, La2(SO4)3 displays larger deviations than [Co(en)3]2(SO4)3; this does not occur between La[Fe(CN)6] and [Co(en)3][Fe(CN)6], or between La[Co(CN)6]
and [Co(en)3][Co(CN)6], where the order is opposite and the differences are higher.1j This finding and the values of a required by the primitive model for lanthanum and bivalent metal sulfates—lower compared with those needed for lanthanum and bivalent metal perchlorates—deserve some consideration.
Mathematical approaches to the primitive model which, unlike DHT, do not linearise the Poisson–Boltzmann equation (e.g., Gronwall–La Mer–Sandwed theory,17 Mayer theory,14 HNC,18 IPBE,12 and the more modern SPB and MPB19) are able to predict the negative deviations of the high-charge electrolytes as mere effect of electrostatic interactions of each ion with all the ions of the solution cumulatively, independent of ion association. This principle also applies to BT which, in spite of the “ion pairs” quoted, is a legitimate approximation of the primitive model in the absence of real ion pairs (Bjerrum's ion pair is a mathematical device to short-cut the refractory problem of ion distribution in the closer neighbourhoods of each ion, not a chemical species).20 Thus, negative deviations do not represent sufficient evidence for association when high charge electrolytes are involved. However, the ion–ion cloud interactions and ion association can, in some cases, co-operate, yielding higher negative deviations. An indication of such a concurrence of long-range interactions and chemical associations, can be found in the need to introduce unexpectedly low values for a when trying to reproduce the data using the primitive model. This does not occur with 2 : 3 salts like M3[Co(CN)6]2
(M![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) Mg, Ca)1h and M3[Fe(CN)6]2
(M
Mg, Ca)1h and M3[Fe(CN)6]2
(M![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) Mg, Ca, Sr, Ba),1e where the values of a
(ranging between 0.67 and 0.56 nm in the IPBE approximation of the primitive model) are consistent with those
of both K3[Fe(CN)6]1c and K3[Co(CN)6]1h
(ca. 0.42 nm, IPBE). This is not the case for La[Fe(CN)6] and La[Co(CN)6] either, both having a
Mg, Ca, Sr, Ba),1e where the values of a
(ranging between 0.67 and 0.56 nm in the IPBE approximation of the primitive model) are consistent with those
of both K3[Fe(CN)6]1c and K3[Co(CN)6]1h
(ca. 0.42 nm, IPBE). This is not the case for La[Fe(CN)6] and La[Co(CN)6] either, both having a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.66 nm (IPBE).1j Doubts arise for [Co(en)3][Fe(CN)6] and [Co(en)3][Co(CN)6], where a
(0.46 nm, IPBE)1j is exceedingly low compared to corresponding lanthanum salts; however, [Co(en)3]Cl3 also needs an a value lower than LaCl3, 0.37 instead of 0.51 nm (IPBE), and hence the low values of a of [Co(en)3][Fe(CN)6]
and [Co(en)3][Co(CN)6], and also of [Co(en)3]2
(SO4)3
(0.38 nm),1b are possibly regular. On the contrary, chemical associations added to long-range interactions are evident in La2(SO4)3; sulfate ions cannot be smaller than perchlorate ions, thus one would expect a to be ca. 0.64 nm, not 0.35 nm. Therefore, the ion association is mainly responsible for the negative deviations of La2(SO4)3 being so much greater than in M3[Co(CN)6]2 and M3
[Fe(CN)6]2. This kind of behaviour probably means that SO42−, unlike [Fe(CN)6]3−
and [Co(CN)6]3−, displaces water from the hydration shells of lanthanum ion when approaching it sufficiently. The same considerations apply to MSO4 salts (M
0.66 nm (IPBE).1j Doubts arise for [Co(en)3][Fe(CN)6] and [Co(en)3][Co(CN)6], where a
(0.46 nm, IPBE)1j is exceedingly low compared to corresponding lanthanum salts; however, [Co(en)3]Cl3 also needs an a value lower than LaCl3, 0.37 instead of 0.51 nm (IPBE), and hence the low values of a of [Co(en)3][Fe(CN)6]
and [Co(en)3][Co(CN)6], and also of [Co(en)3]2
(SO4)3
(0.38 nm),1b are possibly regular. On the contrary, chemical associations added to long-range interactions are evident in La2(SO4)3; sulfate ions cannot be smaller than perchlorate ions, thus one would expect a to be ca. 0.64 nm, not 0.35 nm. Therefore, the ion association is mainly responsible for the negative deviations of La2(SO4)3 being so much greater than in M3[Co(CN)6]2 and M3
[Fe(CN)6]2. This kind of behaviour probably means that SO42−, unlike [Fe(CN)6]3−
and [Co(CN)6]3−, displaces water from the hydration shells of lanthanum ion when approaching it sufficiently. The same considerations apply to MSO4 salts (M![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) Mg, Ca, Sr, Mn, Co, Ni, Zn, and Cd); their solutions behave as a population of charged hard spheres with a between 0.36 and 0.38 nm, much lower than the values found appropriate in a recent revision for Mn(ClO4)2, Co(ClO4)2, and Ni(ClO4)2, 0.66–0.68 nm.1i
Mg, Ca, Sr, Mn, Co, Ni, Zn, and Cd); their solutions behave as a population of charged hard spheres with a between 0.36 and 0.38 nm, much lower than the values found appropriate in a recent revision for Mn(ClO4)2, Co(ClO4)2, and Ni(ClO4)2, 0.66–0.68 nm.1i
Similar comparisons can be diagnostic for chemical associations in high-charge electrolyte solutions. Table 2 provides examples for several anion–cation combinations. Unfortunately, reliable data are not yet available for many electrolytes (past literature does not satisfactorily cover the dilute regions required for meaningful comparisons of theoretical predictions and experimental data). Therefore more accurate considerations will be possible only when the activity coefficients of a larger number of salts are made available in the dilute regions—first, alkaline earth and tris(ethylenediamine) cobalt(III) perchlorates and nitrates—thus making homogeneous systematic recalculations feasible.
Table 2 Distance of closest approach a for the indicated electrolytesa
| Ions |
Cl− |
NO3− |
ClO4− |
SO42− |
[Fe(CN)6]3− |
[Co(CN)6]3− |
| |
|
Values of a in nm, all pertaining to the IPBE approximation of the primitive model; γ± values processed, from ref. 1(b)–(j) if not otherwise specified. In italics, values relying on literature data lacking in corroboration in the dilute regions. The question marks refer to the salts whose relative activity coefficients although determined are not available in dilute solutions.
γ
± from ref. 11.
γ
±
(on molar scale) from ref. 21.
γ
± from ref. 22.
γ
± from ref. 23.
γ
± from ref. 24.
γ
± from ref. 25.
γ
± from ref. 26.
γ
± values referring to 273.15 not 298.15 K, from ref. 27.
|
| K+ |
0.42b |
0.28b |
1.02c |
0.34 |
0.42 |
0.42 |
| Mg2+ |
0.55
d
|
? |
? |
0.41 |
0.64 |
0.67 |
| Ca2+ |
0.51e |
? |
? |
0.39 |
0.64 |
0.67 |
| Sr2+ |
0.48
d
|
? |
? |
0.39 |
0.64 |
? |
| Ba2+ |
0.46
d
|
? |
? |
— |
0.56 |
? |
| Mn2+ |
0.49
f
|
— |
0.68 |
0.38 |
— |
— |
| Co2+ |
0.54
g
|
0.50
g
|
0.66 |
0.38 |
— |
— |
| Ni2+ |
0.53
g
|
0.51
g
|
0.66 |
0.35 |
— |
— |
| Zn2+ |
0.44
h
|
0.54
h
|
0.59
h
|
0.36 |
— |
— |
| Cd2+ |
— |
0.50
h
|
0.60
h
|
0.34 |
— |
— |
| La3+ |
0.51 |
0.43 |
0.64 |
0.35 |
0.66 |
0.66 |
| [Co(en)3]3+ |
0.37 |
(0.26)i |
(0.32)i |
0.38 |
0.46 |
0.46 |
Conclusions
Modern literature concerned with electrolyte solutions tends to disregard the problem of high charge electrolytes. These are probably considered as a trivial application of principles and methods that, although checked mainly on low-charge electrolytes or on Monte Carlo simulations, should be valid in all cases. This is not necessarily true, however. In a past analysis,18 Rasaiah found that when dealing with high charge electrolytes several high-level theoretical treatments developed in the 70s did not allow the correct sign of deviation from the limiting law even in the limit of infinite dilution. The situation is likely to have changed completely, but until very recent times no suitable experimental information on high charge electrolytes has been available for comparison with the theory predictions. At present, alongside the lanthanum nitrate, lanthanum perchlorate and lanthanum sulfate of the present study, we have precise data at least
down to ca. 10−4 mol kg−1, and sometimes 10−5 mol kg−1 and beyond, for several 1 : 3 and 3 : 1, 2 : 2, 2 : 3 and 3 : 2, and 3 : 3 electrolytes.1b–j The data have so far been treated only in terms of very crude theoretical approximations like IPBE, Bjerrum's ion-pairs, and Mayer's DHLL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2 approach, all based on the restricted primitive model, or using empirical equations like Pitzer's. The application of more sophisticated and modern theoretical treatments would be advisable in order to solve, if possible, chemical problems such as distinguishing between association reactions and long-range interaction effects, and, perhaps more important, to test and corroborate theory features in a somewhat more critical and realistic fashion than using Monte Carlo simulations.
B2 approach, all based on the restricted primitive model, or using empirical equations like Pitzer's. The application of more sophisticated and modern theoretical treatments would be advisable in order to solve, if possible, chemical problems such as distinguishing between association reactions and long-range interaction effects, and, perhaps more important, to test and corroborate theory features in a somewhat more critical and realistic fashion than using Monte Carlo simulations.
We are planning to study, as soon as possible, multivalent ions bearing two or more separate charges (e.g., anions of bi- and trisulfonic acids) rather than a localized multiple charge, to outline possible differences in behaviour.
Supplementary materials available as ESI†
Experimental emf and activity coefficients of La(ClO4)3, La(NO3)3, and La2(SO4)3
(Tables S1–S3). Determination of E* and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref) for La2(SO4)3 using the absolute point method (Table S4). Recalculated activity coefficients of LaCl3
(Table S5). Best-fit treatments of the activity and osmotic coefficients of LaCl3, La(ClO4)3 and La(NO3)3 using the Pitzer theory: discussion, deviation plots (Figs. S1–S5), and alternative parameter sets (Tables S6–S9).
γ±(ref) for La2(SO4)3 using the absolute point method (Table S4). Recalculated activity coefficients of LaCl3
(Table S5). Best-fit treatments of the activity and osmotic coefficients of LaCl3, La(ClO4)3 and La(NO3)3 using the Pitzer theory: discussion, deviation plots (Figs. S1–S5), and alternative parameter sets (Tables S6–S9).
Acknowledgements
The authors dedicate the paper to the memory of Prof. Paolo Papoff. The research was supported by the MURST/MIUR (COFIN 2000) and the Italian National Council of Research (CNR).
References
-
(a) F. Malatesta and G. Carrara, J. Solution Chem., 1992, 21, 1251 Search PubMed;
(b) F. Malatesta, G. Carrara, M. P. Colombini and A. Giacomelli, J. Solution Chem., 1993, 22, 733 Search PubMed;
(c) F. Malatesta, A. Giacomelli and R. Zamboni, J. Solution Chem., 1994, 23, 11 Search PubMed;
(d) F. Malatesta, J. Solution Chem, 1995, 24, 241 Search PubMed;
(e) F. Malatesta, A. Giacomelli and R. Zamboni, J. Solution Chem., 1996, 25, 61 Search PubMed;
(f) F. Malatesta and R. Zamboni, J. Solution Chem., 1997, 26, 791 Search PubMed;
(g) F. Malatesta, L. Carbonaro, N. Fanelli, S. Ferrini and A. Giacomelli, J. Solution Chem., 1999, 28, 597 Search PubMed;
(h) F. Malatesta, F. Bruni, N. Fanelli, S. Trombella and R. Zamboni, J. Solution Chem., 2000, 29, 449 Search PubMed;
(i) F. Malatesta, S. Trombella and N. Fanelli, J. Solution Chem., 2000, 29, 685 Search PubMed;
(j) F. Malatesta, S. Trombella, A. Giacomelli and M. Onor, Polyhedron, 2000, 19, 2493 CrossRef CAS.
- F. H. Spedding, H. O. Weber, V. W. Saeger, H. H. Petheram, J. A. Rard and A. Habenschuss, J. Chem. Eng. Data, 1976, 21, 341 CrossRef CAS.
-
(a) T. Shedlovsky, J. Am. Chem. Soc., 1950, 72, 3680 CrossRef CAS;
(b) F. H. Spedding, P. E. Porter and J. M. Wright, J. Am. Chem. Soc., 1952, 74, 2781 CrossRef CAS.
-
(a) H. S. Harned, Proc. Natl. Acad. Sci. U.S.A., 1954, 40, 551 CAS;
(b) H. S. Harned, The Structure of the Electrolytic Solutions, Wiley, New York, 3rd edn., 1963, Ch.10. Although Harned thought his own results were imprecise for LaCl3, the same values have independently been obtained using the liquid membrane cells (ref. 1(c)).
-
(a) J. A. Rard, L. E. Shiers, D. J. Heiser, F. M. Spedding, J. Chem. Eng. Data, 1977, 22, 337; J. A. Rard, D. G. Miller and F. M. Spedding, J. Chem. Eng. Data, 1979, 24, 348;
(b) J. A. Rard, J. Chem. Eng. Data, 1987, 32, 92 CrossRef CAS.
- J. A. Rard, H. O. Weber and F. H. Spedding, J. Chem. Eng. Data, 1977, 22, 187 CrossRef CAS.
- F. Hovorka and W. H. Rodebush, J. Am. Chem. Soc., 1925, 47, 1614 CrossRef CAS.
-
E. A. Guggenheim,Thermodynamics: An Advanced Treatment for Chemists and Physicists, North Holland, Amsterdam, 1st edn., 1949, ch. 9, p. 320 Search PubMed.
- K. S. Pitzer and L. F. Silvester, J. Phys. Chem., 1978, 82, 1239 CrossRef CAS.
- L. Lepori and F. Malatesta, J. Solution Chem., 1990, 19, 957 Search PubMed.
- W. J. Hamer and Yung-Chi Wu, J. Phys. Chem. Ref. Data, 1972, 1, 1047 CAS.
- E. A. Guggenheim, Trans. Faraday Soc., 1960, 56, 1152; E. A. Guggenheim, Trans. Faraday Soc., 1962, 58,
86. Suitable modified algorithms are described in F. Malatesta and T. Rotunno, Gazz. Chim. Ital., 1983, 11, 783..
- N. Bjerrum, Kgl. Danske Vidensk. Selsk., Mat. Fys., Medd., 1926, 7, No. 9; C. W. Davies, Ion Association, Butterworths, London, 1962..
- E. Mayer, J. Chem. Phys., 1950, 18, 1426 CrossRef CAS.
- K. S. Pitzer, in Activity Coefficients in Electrolyte Solutions, ed. K. S. Pitzer, CRC Press, Boca Raton, FL, 2nd edn., 1991, ch. 3..
- K. S. Pitzer and G. Mayorga, J. Solution. Chem., 1974, 3, 539 Search PubMed.
- T. H. Gronwall, V. K. La Mer and H. Sandved, Phys. Z, 1928, 29, 358 Search PubMed.
- J. C. Rasaiah, J. Chem. Phys., 1972, 56, 3071 CrossRef CAS.
- C. W. Outhwaite, M. Molero and L. B. Bhuiyan, J. Chem. Soc., Faraday Trans., I, 1993, 89, 1315 Search PubMed.
-
(a) H. L. Friedman and B. Larson, Pure Appl. Chem., 1979, 51, 2147 CAS;
(b) H. L. Friedman, J. Solution Chem., 1980, 9, 371 Search PubMed.
- H. S. Harned and J. A. Shropshire, J. Am. Chem. Soc., 1958, 80, 2976 CrossRef.
- R. N. Goldberg and R. N. Nuttal, J. Phys.
Chem. Ref. Data, 1978, 7, 263 CAS.
- B. R. Staples and R. L. Nuttal, J. Phys. Chem. Ref. Data, 1977, 6, 385 CAS.
- R. N. Goldberg, J. Phys. Chem. Ref. Data, 1979, 8, 1005 CAS.
- R. N. Goldberg, R. L. Nuttall and B. R. Staples, J. Phys. Chem. Ref. Data, 1979, 8, 923 CAS.
- R. N. Goldberg, J. Phys. Chem. Ref. Data, 1981, 10, 1.
-
(a) J. M. Arsuaga, A. Martin, M. Caceres and J. Nunez, J. Chem. Eng. Data, 1990, 35, 137 CrossRef CAS;
(b) J. M. Arsuaga Ferreras, Doctoral thesis, Universidad Complutense de Madrid, Spain, 1994..
Footnotes |
| † Electronic Supplementary Information available. See http://www.rsc.org/suppdata/cp/b1/b108053a/ |
| ‡ Eqn. (1) relies on the fact that only one ionic species (and the relevant molecules of hydration water, if any) is able to go through a specific membrane; no interfering amounts of other species able to enter the same membrane are permitted. (Owing to the presence of H+ and OH−, equilibrium conditions are no longer met in very dilute solutions, and emf drifts. However, interference is often less important than expected—probably due to the hydrophilic characteristics of H+ and OH−—thus permitting many electrolytes to be studied down to 10−5 mol kg−1 and beyond.) |
§ The absolute point equation for E*1 of AaBb
(Az+, Bx−), using the auxiliary cells for AYz
(E*2), MxB (E*3), and MY (E*4),
is E*1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E*2 E*2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E*3 E*3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E*4 E*4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RT(azF)−1 ln(aabb) RT(azF)−1 ln(aabb)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RTF−1 ln(xz). RTF−1 ln(xz). |
| ¶ Immediately after a new solution is loaded, the cell potential presents perceptible drifts that quickly decrease, yielding (usually, within 20–40 min) a rather flat “definitive” value for E. If the cell is loaded repeatedly using the same solution, such E values are found to differ increasingly (typically, 0.02 to 0.1 mV for any new run) as if the original composition of membrane surfaces were not perfectly restored (relaxation is slow in the pores of the PTFE filter). At least 12 to 24
h are usually needed to restore the original conditions. |
|| The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref) we provide is the mean value of the extrapolation function y γ±(ref) we provide is the mean value of the extrapolation function y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ln [ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±calc γ±calc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±′] in the concentration range considered, using for a the value with which the standard deviation of y reaches its minimum. Experimental
errors that increase with dilution, and theories whose failures enhance with concentration, circumscribe the range of concentrations to be considered. Since personal considerations play an important role when selecting this range of concentrations, the extrapolated value ln γ±′] in the concentration range considered, using for a the value with which the standard deviation of y reaches its minimum. Experimental
errors that increase with dilution, and theories whose failures enhance with concentration, circumscribe the range of concentrations to be considered. Since personal considerations play an important role when selecting this range of concentrations, the extrapolated value ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref) and its associated range of uncertainty contain a slight unavoidable arbitrariness that, however, in many cases is not so great. For instance, if one includes four further points in the DHT treatment of La(ClO4)3 thus reaching m γ±(ref) and its associated range of uncertainty contain a slight unavoidable arbitrariness that, however, in many cases is not so great. For instance, if one includes four further points in the DHT treatment of La(ClO4)3 thus reaching m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.035 mol kg−1, the best value for a changes from 0.67 to 0.68 nm, and the mean value of y from −0.2288 0.035 mol kg−1, the best value for a changes from 0.67 to 0.68 nm, and the mean value of y from −0.2288![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0032 to −0.2289 0.0032 to −0.2289![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0040, quite a negligible difference of ln 0.0040, quite a negligible difference of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref). γ±(ref). |
** Unlike values corrected for w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12, those corrected for w 12, those corrected for w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 do not fit well with the results of the isopiestic measurements of ref. 6, thus corroborating the supposition that the hydration number of ClO4− is zero in |ClO4−|. 15 do not fit well with the results of the isopiestic measurements of ref. 6, thus corroborating the supposition that the hydration number of ClO4− is zero in |ClO4−|. |
†† Eqn. (5) of ref. 1f applies to 2 : 2 electrolytes only. For AaBb(Az+, Bx−), we have w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 {Δln(mγ±) 1000 {Δln(mγ±)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ(E Δ(E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) − −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Eref)/[(a Eref)/[(a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b)RT/(zF)]}/[18.015 Δ(mϕ)], each Δ denoting a difference between two solutions, at m1 and m2. b)RT/(zF)]}/[18.015 Δ(mϕ)], each Δ denoting a difference between two solutions, at m1 and m2. |
‡‡ The calculation only relies on two points, m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5762 and m 0.5762 and m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2549 mol kg−1; the empirical equations of ref. 5(a) provide ϕ and γ±′ to be matched with γ±dir. Error propagation (in particular, from osmotic coefficients to relative activity coefficients) does not favour the point at m 0.2549 mol kg−1; the empirical equations of ref. 5(a) provide ϕ and γ±′ to be matched with γ±dir. Error propagation (in particular, from osmotic coefficients to relative activity coefficients) does not favour the point at m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1100 mol kg−1. The latter would suggest w 0.1100 mol kg−1. The latter would suggest w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25.4 if matched to m 25.4 if matched to m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5762, or
28.7 if matched to m 0.5762, or
28.7 if matched to m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2549 mol kg−1. Using the empirical equations of ref. 5b the values become 23.4 (instead of 24.02), 24.7 (instead of 25.4), and 28.4 (instead of 28.7). 0.2549 mol kg−1. Using the empirical equations of ref. 5b the values become 23.4 (instead of 24.02), 24.7 (instead of 25.4), and 28.4 (instead of 28.7). |
|
| This journal is © the Owner Societies 2002 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, n′
1, n′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) salt may generally be evaluated by both direct extrapolation and the absolute point method—i.e., extrapolation to zero performed for simpler salts—with a possible mutual check.
1) salt may generally be evaluated by both direct extrapolation and the absolute point method—i.e., extrapolation to zero performed for simpler salts—with a possible mutual check.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) presents a negative slope steeper than the limiting law (DHLL) at 10−4 mol kg−1, and a less steep negative slope, or positive slope, in
concentrated solutions. The inversion usually occurs in the neighbourhood of 10−3 mol kg−1; thus a high-charge salt that has been studied only at m
1) presents a negative slope steeper than the limiting law (DHLL) at 10−4 mol kg−1, and a less steep negative slope, or positive slope, in
concentrated solutions. The inversion usually occurs in the neighbourhood of 10−3 mol kg−1; thus a high-charge salt that has been studied only at m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ≥
≥![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 mol kg−1 may misleadingly, seem to conform to the Debye–Hückel law.
10−3 mol kg−1 may misleadingly, seem to conform to the Debye–Hückel law.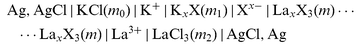
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NO3− or ClO4− or SO42− as appropriate), and
NO3− or ClO4− or SO42− as appropriate), and 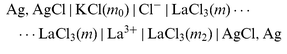
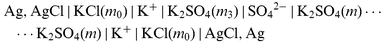
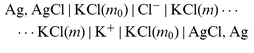
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 mm2, usually at a rotation rate of ca. 1–3 rps) ensures moderate stirring conditions if desired. The details of the cells and electrode assemblage have been described in previous papers (see in particular Fig. 1 of ref. 1d showing the cell, and Fig. 1 of ref. 1f and Fig. 1 of ref.
1j showing the most recent assemblage details of the cation-responsive and anion-responsive electrodes). The entire assembly is contained in an air bath thermostat at 298.15
2 mm2, usually at a rotation rate of ca. 1–3 rps) ensures moderate stirring conditions if desired. The details of the cells and electrode assemblage have been described in previous papers (see in particular Fig. 1 of ref. 1d showing the cell, and Fig. 1 of ref. 1f and Fig. 1 of ref.
1j showing the most recent assemblage details of the cation-responsive and anion-responsive electrodes). The entire assembly is contained in an air bath thermostat at 298.15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.02 K. A platinum resistance thermometer (±0.001 K) is used for temperature monitoring. The electrical resistance of the cells generally ranges between 104 and 105
Ω. Emf measurements were performed using a Digital Adret Electronique 103A DC-current and voltage standard as supplier for potentials (±0.001 mV) and a Keithley 614 Electrometer (input impedance
0.02 K. A platinum resistance thermometer (±0.001 K) is used for temperature monitoring. The electrical resistance of the cells generally ranges between 104 and 105
Ω. Emf measurements were performed using a Digital Adret Electronique 103A DC-current and voltage standard as supplier for potentials (±0.001 mV) and a Keithley 614 Electrometer (input impedance![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1014
Ω) as null point (±0.01 mV) detector. The measurements take approximately 90 min per solution, 60 min being waiting time, and 30 for the emf readings—one every 5 min—whose average values and standard deviations are reported in Tables S1–S3.†
1014
Ω) as null point (±0.01 mV) detector. The measurements take approximately 90 min per solution, 60 min being waiting time, and 30 for the emf readings—one every 5 min—whose average values and standard deviations are reported in Tables S1–S3.†
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2
(a
B2
(a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.43 nm; dotted line), BT (a
0.43 nm; dotted line), BT (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.38 nm; dashed line) and IPBE (a
0.38 nm; dashed line) and IPBE (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.355 nm; full line). The double cross marks the reference point and its range of uncertainty.
0.355 nm; full line). The double cross marks the reference point and its range of uncertainty.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. Stock solutions of La(NO3)3, La(ClO4)3, La2(SO4)3,
and LaCl3, were standardised by acidimetric titration, via cation exchange (Dowex 50W
°C. Stock solutions of La(NO3)3, La(ClO4)3, La2(SO4)3,
and LaCl3, were standardised by acidimetric titration, via cation exchange (Dowex 50W![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 resin in the hydrogen form), dropping the resulting acid on a weighed excess of Na2CO3, then back-titrating with HCl (relative standard deviation, 0.03 to 0.1%). All further solutions were then prepared by weight.
8 resin in the hydrogen form), dropping the resulting acid on a weighed excess of Na2CO3, then back-titrating with HCl (relative standard deviation, 0.03 to 0.1%). All further solutions were then prepared by weight.
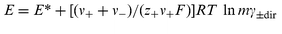
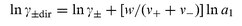
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±
and ln
γ±
and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±dir can be neglected if m
γ±dir can be neglected if m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 mol kg−1; at higher concentrations, correction of ln
0.01 mol kg−1; at higher concentrations, correction of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±dir into ln
γ±dir into ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± needs either knowledge of w, or knowledge of the osmotic coefficients (ϕ) or relative activity coefficients referring to the non-hydrated electrolyte, obtained from e.g. isopiestic measurements. E* depends on the choice for m0, m1, etc. inside the invariant sections of the cell, and also includes the numeric constant allowing for our use of m
(instead of m±) in eqn. (1).
γ± needs either knowledge of w, or knowledge of the osmotic coefficients (ϕ) or relative activity coefficients referring to the non-hydrated electrolyte, obtained from e.g. isopiestic measurements. E* depends on the choice for m0, m1, etc. inside the invariant sections of the cell, and also includes the numeric constant allowing for our use of m
(instead of m±) in eqn. (1).
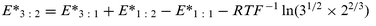
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5 mol kg−1 in Table S3†), where drifts and some dependence of cell potential on the stirring rate became perceptible and increased dramatically on further diluting the solutions, owing to the interference from H+, OH−, and possibly HCO3−. Some drifts, memory effects, and lack of reproducibility were also observed in the concentrated solutions of lanthanum perchlorate (m
10−5 mol kg−1 in Table S3†), where drifts and some dependence of cell potential on the stirring rate became perceptible and increased dramatically on further diluting the solutions, owing to the interference from H+, OH−, and possibly HCO3−. Some drifts, memory effects, and lack of reproducibility were also observed in the concentrated solutions of lanthanum perchlorate (m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8 mol kg−1), indicating that equilibrium conditions were no longer met. The data reported in Tables
S1–S3† are grouped in series, in the same order in which they were determined; each series begins and ends with the reference solution (mref, Eref) to correct some minor shifts (increasing run by run when loading and reloading the cell many times a day) arising from membrane surface leaching.¶ Since the relative activity coefficients γ±′
0.8 mol kg−1), indicating that equilibrium conditions were no longer met. The data reported in Tables
S1–S3† are grouped in series, in the same order in which they were determined; each series begins and ends with the reference solution (mref, Eref) to correct some minor shifts (increasing run by run when loading and reloading the cell many times a day) arising from membrane surface leaching.¶ Since the relative activity coefficients γ±′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±/γ±(ref) are obtained from the difference between E and Eref
(RTF−1 ln
γ±/γ±(ref) are obtained from the difference between E and Eref
(RTF−1 ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mγ±′/mref
mγ±′/mref![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Eref), the disturbing effect is empirically corrected by interpolating Eref throughout the daily series of measurements. The γ±(ref) values were then determined using the following methods.
Eref), the disturbing effect is empirically corrected by interpolating Eref throughout the daily series of measurements. The γ±(ref) values were then determined using the following methods.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1.002
1.002![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 10−3 mol kg−1)
10−3 mol kg−1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±′ for 2
γ±′ for 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2
1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2 extrapolated to zero by DHT provide ln
10−2 extrapolated to zero by DHT provide ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.229
−0.229![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.003 (best value for the distance of closest approach, a, about 0.67 nm).|| The results do not change appreciably if extrapolation
methods based on higher-order approximations are used. IPBE (a numerical integration of the exponential Poisson–Boltzmann equation)12 applied to points between 2
0.003 (best value for the distance of closest approach, a, about 0.67 nm).|| The results do not change appreciably if extrapolation
methods based on higher-order approximations are used. IPBE (a numerical integration of the exponential Poisson–Boltzmann equation)12 applied to points between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 and 3.5
10−4 and 3.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2 mol kg−1 extrapolates ln
10−2 mol kg−1 extrapolates ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.221
−0.221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005 (best value for a, 0.64 nm). Bjerrum's theory of ion pairing (BT)13 suggests ln
0.005 (best value for a, 0.64 nm). Bjerrum's theory of ion pairing (BT)13 suggests ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.231
−0.231![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.004 (2
0.004 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2
1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2; a
10−2; a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.72 nm), or −0.224
0.72 nm), or −0.224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006 (2
0.006 (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol
kg−1
m/mol
kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.5
3.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2; a
10−2; a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.78 nm). The DHLL
0.78 nm). The DHLL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2 approximation of the Mayer theory14 provides −0.225
B2 approximation of the Mayer theory14 provides −0.225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.005 (a++
0.005 (a++![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a−−
a−−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a±
a±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.65 nm) between 2
0.65 nm) between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 and 8
10−4 and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 mol kg−1, or −
10−3 mol kg−1, or −![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.222
0.222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±0.008 (a++
±0.008 (a++![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a−−
a−−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a±
a±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.70 nm) between 2
0.70 nm) between 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4 and 1.2
10−4 and 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2 mol kg−1. We selected −0.225
10−2 mol kg−1. We selected −0.225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006,
an average estimate, as the best value of ln γ±(ref).
0.006,
an average estimate, as the best value of ln γ±(ref).
![Activity coefficients of La(ClO4)3
(filled diamonds) LaCl3
(open circles) and La(NO3)3
(filled circles) prolonged in the isopiestic range (Pitzer's equation, parameters from Table S8). For comparison, the limiting law DHLL, dash-dot line; [Co(en)3]Cl3, dashed line;1b K3[Fe(CN)6] and K3[Co(CN)6]
(indistinguishable), dotted line.1c,h](/image/article/2002/CP/b108053a/b108053a-f2.gif)
![The deviations from the limiting law, ln γ±−ln γ±(DHLL), of the activity coefficients of 3 : 2 electrolytes: La2(SO4)3, filled circles; [Co(en)3]2(SO4)3,1b open circles, compared with Mg3[Co(CN)6]21h
(thick line), IPBE (thin lines, a = 0.355 nm the lower, a = 0.38 nm the upper) and DHLL + B2
(dashed line, a = 0.43 nm).](/image/article/2002/CP/b108053a/b108053a-f3.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±−ln
γ±−ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(DHLL), of the activity coefficients of 3 : 2 electrolytes: La2(SO4)3, filled circles; [Co(en)3]2(SO4)3,1b open circles, compared with Mg3[Co(CN)6]21h
(thick line), IPBE (thin lines, a
γ±(DHLL), of the activity coefficients of 3 : 2 electrolytes: La2(SO4)3, filled circles; [Co(en)3]2(SO4)3,1b open circles, compared with Mg3[Co(CN)6]21h
(thick line), IPBE (thin lines, a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.355 nm the lower, a
0.355 nm the lower, a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.38 nm the upper) and DHLL
0.38 nm the upper) and DHLL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2
(dashed line, a
B2
(dashed line, a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.43 nm).
0.43 nm).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 7.495
7.495![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 10−4 mol kg−1)
10−4 mol kg−1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.224
−0.224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.004 (3
0.004 (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.3
3.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−2 mol kg−1; best value for a, 0.435 nm). IPBE provides −0.216
10−2 mol kg−1; best value for a, 0.435 nm). IPBE provides −0.216![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006 (3
0.006 (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.11; best value for a, 0.425 nm). DHT no longer reproduces the experimental data with sufficient precision if m
0.11; best value for a, 0.425 nm). DHT no longer reproduces the experimental data with sufficient precision if m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 mol kg−1, moreover it requires unreasonably low values of a of ca. 0.3 nm; however, the extrapolated value it finds from values ranging between 3
10−3 mol kg−1, moreover it requires unreasonably low values of a of ca. 0.3 nm; however, the extrapolated value it finds from values ranging between 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
and 5
10−4
and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3 mol kg−1 is the same as for BT, −0.224
10−3 mol kg−1 is the same as for BT, −0.224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.004 (a
0.004 (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.30 nm). DHLL
0.30 nm). DHLL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2 needs high dilution levels like DHT and suggests −0.227
B2 needs high dilution levels like DHT and suggests −0.227![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.003 (3
0.003 (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4
10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5.9
5.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−3; best value for a, 0.39 nm). We selected ln
10−3; best value for a, 0.39 nm). We selected ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −0.222
−0.222![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006 as the most probable value.
0.006 as the most probable value.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 4.929
4.929![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 10−4 mol kg−1)
10−4 mol kg−1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref)
γ±(ref)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −1.158
−1.158![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006 that becomes −1.158
0.006 that becomes −1.158![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.016 if allowance is made for the propagation of the possible error already present in the activity coefficients of K2SO4,1g LaCl3,1c and KCl1a,11
(Table S4†). Extrapolation methods were not successful for La2(SO4)3. DHT is unusable because of the negative deviations in the dilute regions. BT, IPBE, and DHLL
0.016 if allowance is made for the propagation of the possible error already present in the activity coefficients of K2SO4,1g LaCl3,1c and KCl1a,11
(Table S4†). Extrapolation methods were not successful for La2(SO4)3. DHT is unusable because of the negative deviations in the dilute regions. BT, IPBE, and DHLL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2, are able to reproduce the experimental trend with its negative deviations from the limiting law (in particular, IPBE for a between 0.35 and 0.36 nm predicts a trend very similar to the
one in the experimental region; Fig. 1); however, as reassuring as such trends may seem, when trying to use IPBE or Bjerrum treatments as a tool to extrapolate ln
B2, are able to reproduce the experimental trend with its negative deviations from the limiting law (in particular, IPBE for a between 0.35 and 0.36 nm predicts a trend very similar to the
one in the experimental region; Fig. 1); however, as reassuring as such trends may seem, when trying to use IPBE or Bjerrum treatments as a tool to extrapolate ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref), the latter is predicted to lie at ca. 0.1–0.2 units below the absolute point with a large range of uncertainty; conversely, the Mayer theory suggests that ln
γ±(ref), the latter is predicted to lie at ca. 0.1–0.2 units below the absolute point with a large range of uncertainty; conversely, the Mayer theory suggests that ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref) lies 0.1 to 0.2 units above the absolute point. The conclusion to be drawn is that intrinsic approximations prevent these theories from identifying how exactly the salt, as well as the primitive model, should behave. More sophisticated theoretical treatments and even higher dilution levels would be necessary to make extrapolation to zero possible.
γ±(ref) lies 0.1 to 0.2 units above the absolute point. The conclusion to be drawn is that intrinsic approximations prevent these theories from identifying how exactly the salt, as well as the primitive model, should behave. More sophisticated theoretical treatments and even higher dilution levels would be necessary to make extrapolation to zero possible.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5) for ClO4− in |ClO4−|,1g and eight for SO42− in |SO42−|;1f thus the values of w
[eqn. (2)] have to be 12 (or possibly 15) for La(ClO4)3,** and 48 for La2(SO4)3. No previous data for NO3− in |NO3−| were available; the method of ref. 1f
(which relies on the osmotic and relative
activity coefficients from literature, here ref. 5, and on E values measured in the concentrated regions)
††
yields w
0.5) for ClO4− in |ClO4−|,1g and eight for SO42− in |SO42−|;1f thus the values of w
[eqn. (2)] have to be 12 (or possibly 15) for La(ClO4)3,** and 48 for La2(SO4)3. No previous data for NO3− in |NO3−| were available; the method of ref. 1f
(which relies on the osmotic and relative
activity coefficients from literature, here ref. 5, and on E values measured in the concentrated regions)
††
yields w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 (24.02), hence identifying a hydration number of 4 (not very logical, we agree) for NO3− in |NO3−|.‡‡ Since a hydration number of three, or six, is more appeasing to chemical intuition, calculations were also performed for w
24 (24.02), hence identifying a hydration number of 4 (not very logical, we agree) for NO3− in |NO3−|.‡‡ Since a hydration number of three, or six, is more appeasing to chemical intuition, calculations were also performed for w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 and w
21 and w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30; however, the results agree less well with Rard's.5b Differences between ln
30; however, the results agree less well with Rard's.5b Differences between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± values corrected for w
γ± values corrected for w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24 and w
24 and w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 or 30 are negligible except for the three most concentrated solutions, 0.5762, 0.2549, and 0.1100 mol kg−1, where w
21 or 30 are negligible except for the three most concentrated solutions, 0.5762, 0.2549, and 0.1100 mol kg−1, where w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 (30) provides ln
21 (30) provides ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±
0.025 (0.051), 0.011 (0.021), and 0.004 (0.009) units lower (higher). The ranges of uncertainty associated with the ln
γ±
0.025 (0.051), 0.011 (0.021), and 0.004 (0.009) units lower (higher). The ranges of uncertainty associated with the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± values in Tables S1–S3† include the contribution of the uncertain values of w.
γ± values in Tables S1–S3† include the contribution of the uncertain values of w.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006 (i.e., the corresponding ln
0.006 (i.e., the corresponding ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± should be shifted by −0.073
γ± should be shifted by −0.073![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.006)
for m
0.006)
for m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) >
>![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol kg−1; values reported for m
0.1 mol kg−1; values reported for m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol kg−1
(i.e., beyond the experimental range of the isopiestic measurements) should be discarded. Pitzer's empirical equations,15 in the form devised for high-charge electrolytes,16 can be used as a source of interpolated values for osmotic and activity coefficients; a set of selected parameters fitting both ln
0.1 mol kg−1
(i.e., beyond the experimental range of the isopiestic measurements) should be discarded. Pitzer's empirical equations,15 in the form devised for high-charge electrolytes,16 can be used as a source of interpolated values for osmotic and activity coefficients; a set of selected parameters fitting both ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± and ϕ within ±0.01 is reported in Table 1. Calculations are extended to lanthanum chloride (whose activity coefficients have been reconsidered: Table S5†).
γ± and ϕ within ±0.01 is reported in Table 1. Calculations are extended to lanthanum chloride (whose activity coefficients have been reconsidered: Table S5†).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C in watera
°C in watera
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 CϕMX.
c
m
1, m2, the experimental range where the parameters have been fitted to ln
1.5 CϕMX.
c
m
1, m2, the experimental range where the parameters have been fitted to ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± or ϕ
(column Expt.).
d Standard deviation of ln
γ± or ϕ
(column Expt.).
d Standard deviation of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± or ϕ
(column Expt) between m1 and m2.
e ln
γ± or ϕ
(column Expt) between m1 and m2.
e ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ± from ref. 1(c) corrected for the ion hydration, ref.
3(a) lowered by −0.012, ref. 3(b) lowered by −0.007.
f
ϕ from ref. 2.
g
ϕ from ref. 6; points at high concentrations (2.562
γ± from ref. 1(c) corrected for the ion hydration, ref.
3(a) lowered by −0.012, ref. 3(b) lowered by −0.007.
f
ϕ from ref. 2.
g
ϕ from ref. 6; points at high concentrations (2.562![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.775) not included.
h
ϕ from ref. 5; points at high concentrations (2.537
4.775) not included.
h
ϕ from ref. 5; points at high concentrations (2.537![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m/mol kg−1
m/mol kg−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8.459) not included.
8.459) not included.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4, 0.9
10−4, 0.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±e
γ±e![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4, 0.4
10−4, 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±
γ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−4, 0.6
10−4, 0.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±
γ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ×
×![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10−5, 0.03
10−5, 0.03![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±
γ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) <
<![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 mol kg−1) are 0.37 nm for [Co(en)]3Cl3, 0.42 nm for both K3[Fe(CN)6] and K3[Co(CN)6], 0.43 nm for La(NO3)3, 0.51 nm for LaCl3, and 0.64 nm for La(ClO4)3. These differences in a are probably associated with the hydrophobic–hydrophilic character and not only with ion sizes.
0.1 mol kg−1) are 0.37 nm for [Co(en)]3Cl3, 0.42 nm for both K3[Fe(CN)6] and K3[Co(CN)6], 0.43 nm for La(NO3)3, 0.51 nm for LaCl3, and 0.64 nm for La(ClO4)3. These differences in a are probably associated with the hydrophobic–hydrophilic character and not only with ion sizes.![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) Mg, Ca, Sr, Ba)1e and M3[Co(CN)6]2
(M
Mg, Ca, Sr, Ba)1e and M3[Co(CN)6]2
(M![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) Mg, Ca),1h hence rather resembling [Co(en)3]2(SO4)3. Strangely, however, La2(SO4)3 displays larger deviations than [Co(en)3]2(SO4)3; this does not occur between La[Fe(CN)6] and [Co(en)3][Fe(CN)6], or between La[Co(CN)6]
and [Co(en)3][Co(CN)6], where the order is opposite and the differences are higher.1j This finding and the values of a required by the primitive model for lanthanum and bivalent metal sulfates—lower compared with those needed for lanthanum and bivalent metal perchlorates—deserve some consideration.
Mg, Ca),1h hence rather resembling [Co(en)3]2(SO4)3. Strangely, however, La2(SO4)3 displays larger deviations than [Co(en)3]2(SO4)3; this does not occur between La[Fe(CN)6] and [Co(en)3][Fe(CN)6], or between La[Co(CN)6]
and [Co(en)3][Co(CN)6], where the order is opposite and the differences are higher.1j This finding and the values of a required by the primitive model for lanthanum and bivalent metal sulfates—lower compared with those needed for lanthanum and bivalent metal perchlorates—deserve some consideration.
![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) Mg, Ca)1h and M3[Fe(CN)6]2
(M
Mg, Ca)1h and M3[Fe(CN)6]2
(M![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) Mg, Ca, Sr, Ba),1e where the values of a
(ranging between 0.67 and 0.56 nm in the IPBE approximation of the primitive model) are consistent with those
of both K3[Fe(CN)6]1c and K3[Co(CN)6]1h
(ca. 0.42 nm, IPBE). This is not the case for La[Fe(CN)6] and La[Co(CN)6] either, both having a
Mg, Ca, Sr, Ba),1e where the values of a
(ranging between 0.67 and 0.56 nm in the IPBE approximation of the primitive model) are consistent with those
of both K3[Fe(CN)6]1c and K3[Co(CN)6]1h
(ca. 0.42 nm, IPBE). This is not the case for La[Fe(CN)6] and La[Co(CN)6] either, both having a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.66 nm (IPBE).1j Doubts arise for [Co(en)3][Fe(CN)6] and [Co(en)3][Co(CN)6], where a
(0.46 nm, IPBE)1j is exceedingly low compared to corresponding lanthanum salts; however, [Co(en)3]Cl3 also needs an a value lower than LaCl3, 0.37 instead of 0.51 nm (IPBE), and hence the low values of a of [Co(en)3][Fe(CN)6]
and [Co(en)3][Co(CN)6], and also of [Co(en)3]2
(SO4)3
(0.38 nm),1b are possibly regular. On the contrary, chemical associations added to long-range interactions are evident in La2(SO4)3; sulfate ions cannot be smaller than perchlorate ions, thus one would expect a to be ca. 0.64 nm, not 0.35 nm. Therefore, the ion association is mainly responsible for the negative deviations of La2(SO4)3 being so much greater than in M3[Co(CN)6]2 and M3
[Fe(CN)6]2. This kind of behaviour probably means that SO42−, unlike [Fe(CN)6]3−
and [Co(CN)6]3−, displaces water from the hydration shells of lanthanum ion when approaching it sufficiently. The same considerations apply to MSO4 salts (M
0.66 nm (IPBE).1j Doubts arise for [Co(en)3][Fe(CN)6] and [Co(en)3][Co(CN)6], where a
(0.46 nm, IPBE)1j is exceedingly low compared to corresponding lanthanum salts; however, [Co(en)3]Cl3 also needs an a value lower than LaCl3, 0.37 instead of 0.51 nm (IPBE), and hence the low values of a of [Co(en)3][Fe(CN)6]
and [Co(en)3][Co(CN)6], and also of [Co(en)3]2
(SO4)3
(0.38 nm),1b are possibly regular. On the contrary, chemical associations added to long-range interactions are evident in La2(SO4)3; sulfate ions cannot be smaller than perchlorate ions, thus one would expect a to be ca. 0.64 nm, not 0.35 nm. Therefore, the ion association is mainly responsible for the negative deviations of La2(SO4)3 being so much greater than in M3[Co(CN)6]2 and M3
[Fe(CN)6]2. This kind of behaviour probably means that SO42−, unlike [Fe(CN)6]3−
and [Co(CN)6]3−, displaces water from the hydration shells of lanthanum ion when approaching it sufficiently. The same considerations apply to MSO4 salts (M![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) Mg, Ca, Sr, Mn, Co, Ni, Zn, and Cd); their solutions behave as a population of charged hard spheres with a between 0.36 and 0.38 nm, much lower than the values found appropriate in a recent revision for Mn(ClO4)2, Co(ClO4)2, and Ni(ClO4)2, 0.66–0.68 nm.1i
Mg, Ca, Sr, Mn, Co, Ni, Zn, and Cd); their solutions behave as a population of charged hard spheres with a between 0.36 and 0.38 nm, much lower than the values found appropriate in a recent revision for Mn(ClO4)2, Co(ClO4)2, and Ni(ClO4)2, 0.66–0.68 nm.1i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B2 approach, all based on the restricted primitive model, or using empirical equations like Pitzer's. The application of more sophisticated and modern theoretical treatments would be advisable in order to solve, if possible, chemical problems such as distinguishing between association reactions and long-range interaction effects, and, perhaps more important, to test and corroborate theory features in a somewhat more critical and realistic fashion than using Monte Carlo simulations.
B2 approach, all based on the restricted primitive model, or using empirical equations like Pitzer's. The application of more sophisticated and modern theoretical treatments would be advisable in order to solve, if possible, chemical problems such as distinguishing between association reactions and long-range interaction effects, and, perhaps more important, to test and corroborate theory features in a somewhat more critical and realistic fashion than using Monte Carlo simulations.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref) for La2(SO4)3 using the absolute point method (Table S4). Recalculated activity coefficients of LaCl3
(Table S5). Best-fit treatments of the activity and osmotic coefficients of LaCl3, La(ClO4)3 and La(NO3)3 using the Pitzer theory: discussion, deviation plots (Figs. S1–S5), and alternative parameter sets (Tables S6–S9).
γ±(ref) for La2(SO4)3 using the absolute point method (Table S4). Recalculated activity coefficients of LaCl3
(Table S5). Best-fit treatments of the activity and osmotic coefficients of LaCl3, La(ClO4)3 and La(NO3)3 using the Pitzer theory: discussion, deviation plots (Figs. S1–S5), and alternative parameter sets (Tables S6–S9).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E*2
E*2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E*3
E*3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E*4
E*4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RT(azF)−1 ln(aabb)
RT(azF)−1 ln(aabb)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) RTF−1 ln(xz).
RTF−1 ln(xz).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref) we provide is the mean value of the extrapolation function y
γ±(ref) we provide is the mean value of the extrapolation function y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [ln
[ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±calc
γ±calc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±′] in the concentration range considered, using for a the value with which the standard deviation of y reaches its minimum. Experimental
errors that increase with dilution, and theories whose failures enhance with concentration, circumscribe the range of concentrations to be considered. Since personal considerations play an important role when selecting this range of concentrations, the extrapolated value ln
γ±′] in the concentration range considered, using for a the value with which the standard deviation of y reaches its minimum. Experimental
errors that increase with dilution, and theories whose failures enhance with concentration, circumscribe the range of concentrations to be considered. Since personal considerations play an important role when selecting this range of concentrations, the extrapolated value ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref) and its associated range of uncertainty contain a slight unavoidable arbitrariness that, however, in many cases is not so great. For instance, if one includes four further points in the DHT treatment of La(ClO4)3 thus reaching m
γ±(ref) and its associated range of uncertainty contain a slight unavoidable arbitrariness that, however, in many cases is not so great. For instance, if one includes four further points in the DHT treatment of La(ClO4)3 thus reaching m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.035 mol kg−1, the best value for a changes from 0.67 to 0.68 nm, and the mean value of y from −0.2288
0.035 mol kg−1, the best value for a changes from 0.67 to 0.68 nm, and the mean value of y from −0.2288![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0032 to −0.2289
0.0032 to −0.2289![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.0040, quite a negligible difference of ln
0.0040, quite a negligible difference of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ±(ref).
γ±(ref).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12, those corrected for w
12, those corrected for w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 do not fit well with the results of the isopiestic measurements of ref. 6, thus corroborating the supposition that the hydration number of ClO4− is zero in |ClO4−|.
15 do not fit well with the results of the isopiestic measurements of ref. 6, thus corroborating the supposition that the hydration number of ClO4− is zero in |ClO4−|.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 {Δln(mγ±)
1000 {Δln(mγ±)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ(E
Δ(E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −
−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Eref)/[(a
Eref)/[(a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b)RT/(zF)]}/[18.015 Δ(mϕ)], each Δ denoting a difference between two solutions, at m1 and m2.
b)RT/(zF)]}/[18.015 Δ(mϕ)], each Δ denoting a difference between two solutions, at m1 and m2.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5762 and m
0.5762 and m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2549 mol kg−1; the empirical equations of ref. 5(a) provide ϕ and γ±′ to be matched with γ±dir. Error propagation (in particular, from osmotic coefficients to relative activity coefficients) does not favour the point at m
0.2549 mol kg−1; the empirical equations of ref. 5(a) provide ϕ and γ±′ to be matched with γ±dir. Error propagation (in particular, from osmotic coefficients to relative activity coefficients) does not favour the point at m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1100 mol kg−1. The latter would suggest w
0.1100 mol kg−1. The latter would suggest w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25.4 if matched to m
25.4 if matched to m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5762, or
28.7 if matched to m
0.5762, or
28.7 if matched to m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2549 mol kg−1. Using the empirical equations of ref. 5b the values become 23.4 (instead of 24.02), 24.7 (instead of 25.4), and 28.4 (instead of 28.7).
0.2549 mol kg−1. Using the empirical equations of ref. 5b the values become 23.4 (instead of 24.02), 24.7 (instead of 25.4), and 28.4 (instead of 28.7).