Femtosecond spectroscopy of fragment–cage dynamics: I2 in Kr
M.
Bargheer
,
M.
Gühr
,
P.
Dietrich
and
N.
Schwentner
Institut für Experimentalphysik, Freie Universität Berlin, Arnimallee 14, 14195, Berlin, Germany. E-mail: bargheer@physik.fu-berlin.de
First published on 21st November 2001
Abstract
We report femtosecond pump–probe spectra for the B state of I2 in solid Kr with systematic variation of both pump and probe wavelength. The observed oscillations strongly depend on the probe wavelength and we show that it must be tuned together with the pump pulses to obtain the correct vibrational frequencies. We construct an RKR potential for the B state that includes the solvent response. The ionic E state surface is directly constructed from the measurements. Both are compared to DIM potentials. We report rates for vibrational energy relaxation in the B state that increase by three orders of magnitude on going from low excitation to excitation beyond the gas phase dissociation limit. By systematic variation of the probe window we record snapshots of a mean trajectory at the dissociation limit that clearly displays the strong interaction with the cage.
I Introduction
The wave packet dynamics of I2 molecules in the A and B electronic states has been studied in great detail. A series of pioneering publications of the Zewail group1–3 investigated the influence of rare gas environments on the free molecule, in clusters and in the gas phase for increasing rare gas pressures up to liquid phase densities. The observed number of oscillations decreases with increasing rare gas density and this was in part attributed to a rapid loss of B state population due to predissociation. Surprisingly strongly modulated wave packet oscillations extending up to several ps with up to 20 periods were observed in the ordered crystalline phase of Ar, Kr and Xe matrices by the Apkarian group. A wealth of information on energy relaxation and predissociation dynamics induced by the cage was derived from the experimental data in combination with classical trajectory calculations.4–13 Semi quantum mechanical calculations on DIM surfaces14–17 corroborate essential features. The connections between pump–probe, Raman and fluorescence spectroscopy were illustrated and exploited for a further characterization of the dynamics.11,12,18,19 Even focusing of wave packets in the B state after several ps was achieved by linearly chirped pump pulses.20,21 Ground state wave packet dynamics become accessible by fs-CARS data.22 The spectroscopic information on valence and ionic states which can be used in probe transitions extends from the IR with the I**→I* and A→X transitions, to the visible and UV with the I*I*→X, B→X, β→A and D′→A′ transitions. The A and B states in matrices show a peculiarity. While the vibrational dynamics in pump–probe spectra are well resolved it is not possible to derive the essential spectroscopic constants like Te, ωe and ωexe from absorption spectra because only a structureless Franck–Condon envelope is observed. It is explained by long lasting I–I correlation functions and quickly damped I2–matrix and matrix–matrix correlation functions.12This situation provides a challenge and a test bed to derive spectroscopic properties from pump–probe spectra. While for free molecules it was demonstrated in the I2 case23 that the Fourier transformation of fs and ps data is equivalent to analyzing rotationally resolved vibrational progressions,24 this method requires modifications for the strong interactions in condensed phases which in many cases leads to fast vibrational relaxation. A wave packet started at high vibrational levels falls down within few oscillations in the potential well, thus passing quickly through regions of rather different ωe which prohibits a standard Fourier transformation. Just for this case it was shown21 that by following the decrease in duration of the vibrational periods along the time course of a pump–probe spectrum and by systematically varying the pump photon energy, i.e. the starting point in the potential well, it is possible to derive both the spectroscopic constants and the vibrational relaxation rates.
In this contribution we work out this concept in more detail, and we show especially that accurate spectroscopic constants require also a systematic variation of the probe photon energy. The determination of vibrational relaxation rates relies on the anharmonicity which becomes small near the bottom of a bound potential energy surface. We demonstrate how accurately the periods have to be measured depending on the anharmonicity and the energy relaxation rate. An improved B state energy surface up to the dissociation limit is presented that includes the dynamics of the solvent cage. Shifting the spatial position of the probe window near the dissociation limit directly yields snapshots of an experimental R(t) trajectory at large I–I elongation R. The trajectories and the derived kinetic energies display the details of the caging of the I atoms by the matrix atoms.
II Experimental
The samples consisting of 30 µm thick clear crack-free films of Kr doped with I2 in a ratio of 1500∶1 were prepared in the same way as described in ref. 21. The fluorescence around 420 nm consists of two contributions25 belonging to the D′→A′ and the β→A or δ→A transitions and both bands were detected together. The pump beam used to excite the B state was tuned from 600 to 480 nm, and the probe wavelength was varied between 550 and 456 nm. This necessary tunability of both beams required a significant upgrade of the laser system. In short, a commercial amplified Ti:Sa system (CPA 2001 from Clark-MXR) delivering pulses with 800 µJ energy and 150 fs pulse duration was used to pump two non-collinearly pumped optical parametric amplifiers (NOPA) designed by the group of Riedle26,27 and distributed also by Clark-MXR. The low pump energy requirements (200 µJ per NOPA) allowed a simultaneous operation of both NOPA's. The tunability range of the NOPA's was 720 to 450 nm, the pulse energy around 550 nm was 10 µJ and a pulse length of typical 30 fs was used without attempts to shorten it by further alignment. A more detailed description with an improvement in the NOPA pumping optics is presented in ref. 28. The pulses are characterized by auto- and cross-correlation and in addition by polarization-gate frequency-resolved optical gating (FROG) as described in ref. 21.III Results
A B state characterization
The scheme in Fig. 1 shows the X→B transition induced by the pump beam and the B→E transition from the probe beam. Nonradiative relaxation to the states D′(2u) and δ or β(1u) results in the radiative transitions which are recorded. Different X, B and E state surfaces of I2 in the Kr matrix as derived and explained in the following are plotted. The emitting states are not shown.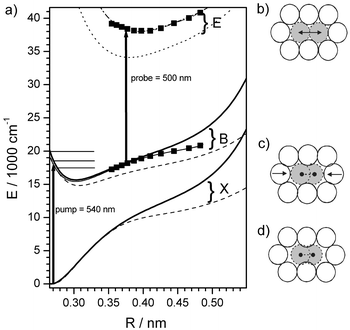 | ||
| Fig. 1 (a) Potential energy diagram of I2 in Kr including the ground state X, the valence B state and the ionic E state relevant for the pump–probe spectra. The arrows depict pump and probe transitions. The horizontal lines indicate pump energies corresponding to λpump = 570, 540 and 500 nm, respectively. The squares indicate the shape of the potentials as derived from the experiment. Dashed lines correspond to DIM calculations in the fixed Kr fcc lattice (see text and Fig. 1b and d) and solid lines to a relaxed cage geometry (see Fig. 1c). The dotted line reproduces the E state from ref. 35 for a fixed fcc lattice (see Fig. 1b) and the dash-dotted line includes a shift by 0.01 nm outwards and 3900 cm−1 up in energy. (d) shows I2 in the ground state surrounded by a fixed fcc lattice. Note the space between I and Kr along the internuclear axis is responsible for the soft potential in this geometry. In (c) the Kr atoms have relaxed around the molecule, bending the outer limb of the potential up. (b) shows the I2 at a bond distance R = 0.4 nm typical for a probe transition. Here the fixed fcc lattice approximates a geometry relaxed around the extended I–I bond. | ||
Pump–probe spectra for excitation ranging from deep in the B state well at 570 nm, going up to the gas phase dissociation limit at 500 nm and even above the dissociation limit (490 and 480 nm) are collected in Fig. 2a for a typical probe wavelength λprobe = 500 nm. In essence, the first complete oscillation period T1(E) in Fig. 2a is the round trip time of the wave packet at the energy Epump prepared by the pump beam and can be converted to ν(E) = 1/T1(E) as shown in Fig. 3. The wave packet passes the probe window two times in each complete period which gives an additional splitting indicated by the inward and outward pointing arrows in Fig. 2a. The energies Epump for λpump = 570, 540 and 500 nm are shown in Fig. 1 together with the spatial position of the probe window for λprobe = 500 nm at Rwin = 0.376 nm. The condition for the probe window Rwin according to the classical Franck principle29 is ΔV = hνpump with the potential energy difference ΔV between the B state and the upper E state. If the energy Epump lies above the B state energy of the probe window Ewin, the wave packet passes the window on the outward motion for the first time, on the inward motion for the second time and, after one full period, it shows up a third time in the outward and a fourth time on the inward motion. Obviously one full period corresponds to the time difference between two outward or two inward passes which are connected in Fig. 2a by dotted lines as a guide to the eye. For λpump = 540 nm the wave packet is excited slightly above the window. Qualitatively it is immediately evident from Fig. 2a that the difference between the first two outward passes indicated by T1 increases with pump energy Epump as expected by the anharmonicity in a Morse-like potential. The origin of the inward/outward splitting can be confirmed by tuning λprobe and keeping λpump fixed at, for example, 540 nm (Fig. 4a). Taking λprobe = 540 nm we catch the wave packet just at the turning point, and the splitting disappears. Shortening λprobe means shifting Rwin inward according to the B–E difference potential. Now the wave packet passes the window twice; it spends a longer and longer time in the region from the window to the outer turning point and back which results in the increased splitting in Fig. 4a.
 | ||
| Fig. 2 Pump–probe spectra for (a) λprobe = 500 nm and λpump = 570 to 480 nm and (b) λpump = 500 and λprobe = 540 to 480 nm. Dashed lines connect the times for passage through the respective probe windows and the arrows indicate → outward and ← inward motion. T1: First round trip time. Note that strikingly similar trends are observed for variation of (a) probe wavelength and (b) pump wavelength. | ||
 | ||
| Fig. 3 First round trip time T1 and frequency ν as a function of energy Epump. The solid circles are the correct values determined by the wave packet at the turning point via an adjustment of the probe wavelength (see text). Deviations occur if the probe wavelength is kept fixed at 520 nm (squares) or 480 nm (triangles). Dashed line: Round trip time in the gas phase corrected for the vertical solvation shift. | ||
 | ||
| Fig. 4 Pump–probe spectra with fixed pump wavelength to demonstrate the effect of the probe window. (a) λpump = 540 nm: decreasing λprobe from 540 to 480 nm yields an increased splitting between probing the inward and outward motion of the wave packet indicated by the arrows. The time between two outward passes (Δt1) and two inward passes (Δt2) seems to be constant at first sight. (b) λpump = 570 nm: The lines indicate the decrease of the measured period T1 with decreasing probe wavelength. After 3 periods the difference for λprobe = 510 and 456 nm has accumulated to 70 fs. | ||
Naively one would assume that the differences Δt1 or Δt2 between the parallel lines for inward or outward motion always correspond to the correct round trip time T1. However, this is not the case, and a systematic deviation of T1 or ν values is obtained in Fig. 3 if, for example, probe wavelengths of 480 nm (triangles) or 520 nm (squares) are used. For an explanation consider the pump wavelength of 570 nm and Figs. 1 and 4b. With λprobe = 480 nm the wave packet will be recorded just at the turning point. In order to form a wave packet it is necessary to coherently excite a superposition of several vibrational levels which inevitably gives amplitude to several levels according to the energetic width of the wave packet. If we reduce λprobe then the probe window moves spatially inward to a lower energy Ewin. Thus the less energetic parts of the wave packet, which have a shorter period according to the anharmonicity, gain in weight and the measured T1 is reduced. This effect can be clearly seen in the experimental spectra shown in Fig. 4b. Although the spatial shift is not large enough to yield a resolved splitting, the differences between the maxima give a smaller T1. The part of the wave packet for which the probe window is at the turning point gains the highest detection efficiency. Classically this is easily understood.8 If the wave packet lies higher above the window it moves with more kinetic energy and larger velocity through the window. Since it spends less time in the window the detection efficiency goes down. Thus the low energy parts with too short periods T1 dominate the experimental spectrum. If the average energy of the wave packet lies below the window only the high energy part is recorded, and the apparent T1 is too long. These classical arguments are in full accord with a quantum mechanical Franck–Condon picture. Since the effect accumulates we show three periods in Fig. 4b to make it clearly visible. The time difference 3T1 for λprobe = 456 nm corresponds to 990 fs and to 1060 fs for λprobe = 510 nm. This results in a variation of T1 from 353 fs for probing above the turning point with 510 nm to 330 fs for probing too deep with 456 nm. This error of 7% fully explains the systematic difference between the results with probe wavelength fixed at 480 or 520 nm probe in Fig. 3. A correct determination of T1 requires a tuning of λprobe just to the turning point for each λpump. The criterion is to choose a λprobe that maximizes the detection efficiency or equivalently the λprobe for which the splitting for probing inward and outward motion disappears. An error of the order of 7% is serious because the anharmonicity itself is typically only of the order of 1% as will be shown later. Therefore the correct T1 values given by the circles in Fig. 3 were derived by an optimization of λprobe for each value of Epump.
From the improved values for the periods T1 given in Fig. 3 we construct a potential that yields the corresponding classical frequencies ν. For resolved quantized vibrational levels one would use the RKR (Rydberg–Klein–Rees)30–32 scheme and here we use the classical continuum analogue.33 The potential is constructed successively by going from the potential minimum to higher energies. Unfortunately the Franck–Condon envelope of the X→B transition does not allow to reach the bottom of the B state expected around 640 nm and from 600 nm on already the X→A transition dominates. Near the minimum the potential should only be weakly influenced by the matrix and well described by a Morse potential. We extrapolate the square of the experimental frequencies ν2(E) linearly to
estimate Te, since for a Morse potential the frequency is  . The matrix shifts of ωe and Te should be on the order 1 to 2% for valence states and under these constraints the extrapolation yields ωe
= 125.9 cm−1 and Te
= 15
. The matrix shifts of ωe and Te should be on the order 1 to 2% for valence states and under these constraints the extrapolation yields ωe
= 125.9 cm−1 and Te
= 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 cm−1, with the corresponding uncertainties. The potential is integrated from Te to higher energies using the fitting function ν2(E) which consists of the Morse-term, ωe(1 +
E/De), and an empirical exponential term that is negligible below 19
420 cm−1, with the corresponding uncertainties. The potential is integrated from Te to higher energies using the fitting function ν2(E) which consists of the Morse-term, ωe(1 +
E/De), and an empirical exponential term that is negligible below 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and describes the deviation of ν2(E) from the Morse value at high energies E
(solid line
in Fig. 3). For the construction of the potential by the RKR method, rotational information is needed to find the absolute position of the inner and outer turning point. In the matrix I2 does not rotate and thus we keep the gas phase Morse potential as the repulsive inner wing of the B state, since the matrix interaction near the inner turning point is expected to be minimal. Alternatively one could adopt the inner wing of the DIM potential, which would shift the outer wing only marginally by less than 0.003 nm to larger elongations. In essence the outer wing was determined from ν(E) and the result of the integration is presented in Fig. 1 as a solid line with solid squares indicating energies for which experimental points have been measured.
500 cm−1 and describes the deviation of ν2(E) from the Morse value at high energies E
(solid line
in Fig. 3). For the construction of the potential by the RKR method, rotational information is needed to find the absolute position of the inner and outer turning point. In the matrix I2 does not rotate and thus we keep the gas phase Morse potential as the repulsive inner wing of the B state, since the matrix interaction near the inner turning point is expected to be minimal. Alternatively one could adopt the inner wing of the DIM potential, which would shift the outer wing only marginally by less than 0.003 nm to larger elongations. In essence the outer wing was determined from ν(E) and the result of the integration is presented in Fig. 1 as a solid line with solid squares indicating energies for which experimental points have been measured.
B E state determination
In deriving ν(E) in section IIIA we fixed the energy EB = Epump in the B state by the pump photon energy, and we looked for the optimal probe photon energy hνprobe which records the wave packet just at the outer turning point Rwin. Again the second criterion for probing at the turning point is the fact that the double splitting of the oscillation due to probing inward and outward motion just disappears. Thus hνprobe corresponds to the difference potential hνprobe = ΔV = EE(R) − EB(R) in the Franck approximation. Since we already know EB(R) we obtain EE(R) just by adding hνprobe to the B state energy in Fig. 1. The experimentally determined points (squares) are compared to the surfaces given by Batista and Coker.16,17,35C Vibrational relaxation in the B state
A careful inspection of successive periods in a pump–probe spectrum shows that the period length Tn decreases systematically from the first to the nth oscillation. A wave packet prepared high up in the B state with a long T1 falls down in energy by vibrational relaxation. In the time course of relaxation it passes regions in the B state with increasingly shorter Tn due to the anharmonicity displayed in Fig. 3. Thus the change of Tn with delay time can be directly traced to a change of energy E of the wave packet with delay time. The various schemes to derive the energy relaxation rate were applied in the same way as described in ref. 21. The resulting rates krel = dE/dt in cm−1 per ps and per period are displayed in Fig. 5. Due to the larger data set we now cover a significantly broader range of energies in the B state. A nearly exponential increase is observed, from very low rates with dissipation of only a fraction of a vibrational quantum per period deep in the well over energy losses of about one quantum per period at λpump = 540 nm and to losses of more than 10 quanta per period at the gas phase dissociation limit and above. The smooth change over three orders of magnitude hides something exceptional happening in the region of the dissociation limit. Therefore we also display in Fig. 5 the energy E1 after the first round trip versus the initial excitation energy Epump. The rise of E1 with Epump is sublinear which reflects that the losses per round trip increase with Epump. Around the dissociation limit the smooth rise is interrupted, and E1 falls with Epump. Thus a wave packet started with a lower energy Epump returns with a larger energy E1 than a packet started with initially higher energy. This is not compatible with simple energy and momentum conservation in an elastic scattering event with a cage atom. It indicates that the tremendous losses above the dissociation limit of up to 30 vibrational energies in the first collision are also connected with severe distortions of the cage which will now be imaged by recording the trajectories. | ||
Fig. 5 Energy relaxation rate krel
= dE/dt in the first oscillation as a function of energy in the B state measured in units of cm−1 per ps (solid squares) and cm−1 per period (solid circles). For comparison we show the values from ref. 7 as open symbols. To demonstrate that near the dissociation limit the behavior of the system qualitatively changes we plot the energy E1 of the wave packet after the first collision (dashed line) as a function of the initial excitation energy Epump. It shows a maximum around E
= 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1. 500 cm−1. | ||
D Trajectory near the dissociation limit
The spectra in Fig. 2a show that the time spent between the first outward and inward passage for the fixed probe window (λprobe = 500 nm, Rwin = 0.376 nm) increases dramatically from 120 fs for λpump = 540 nm up to 350 fs for λpump = 490 nm whereas that for the second outward/inward passage stays essentially constant at 120 fs. Obviously the interaction of an essentially free I atom with the cage atoms around the outer turning point occurs on a long time scale and is connected with such a high energy loss that this region is not reached any more in the second round trip. Snapshots of this interaction are displayed now in Fig. 2b by scanning the probe wavelength λprobe from 540 nm to 480 nm and thus the probe position Rwin from 0.36 nm to 0.45 nm for an excitation at the dissociation limit (λpump = 500 nm). The maxima versus time at these positions are displayed as the time course R(t) of a mean trajectory in Fig. 6 for the first three excursions I to III. Only in the first excursion the wave packet reaches out to 0.43 nm, and already in the second one it does not go beyond 0.39 nm. This most interesting first excursion is rather asymmetric. The outward motion is still rather sinusoidal, and from the window at 0.36 nm to the turning point it takes about 100 fs. The return is extremely delayed, and especially around 300 fs the wave packet is not accelerated on the way back to the potential minimum as expected, but on the contrary it is further slowed down. The return from the turning point to the 0.36 nm window takes more than 250 fs. Differentiation of R(t) with respect to time yields the local velocity, and it is presented as kinetic energy Ekin(t) in Fig. 6. The mild undulations may be artefacts due to the differentiation and scatter in the data points. The smoothed Ekin(t) (dashed) shows a deceleration on the way to the turning point as expected for a Morse potential, but the acceleration on the way back is completely different. The trajectory moves extremely slowly for a long time of 200 fs and at 400 fs it has only about Ekin = 200 cm−1 while on a Morse potential it should have already 2000 cm−1 at 300 fs. It looks as if the I atom sticks to the cage wall and as if it moves back very slowly together with the cage. This peculiar behavior is demonstrated in Fig. 7a on a potential surface. A wave packet excited with λpump = 520 nm reaches out and returns with an energy loss of 455 cm−1. A wave packet pumped with 500 nm lies significantly higher in energy and reaches much farther out on the soft wing of the potential, then it sticks to the potential energy surface and does not gain kinetic energy. It slides down along the potential surface far below the energy of the 520 nm wave packet until it finally leaves the potential energy surface and gains kinetic energy.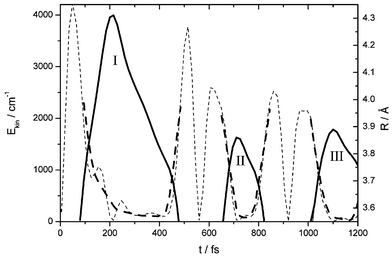 | ||
| Fig. 6 Trajectory R(t) (solid line) showing I–I separation Rversus time t as derived from the maxima in the pump–probe spectra for λpump = 500 nm. (Fig. 2b). Only the outer bow between 0.355 nm and 0.43 nm is covered by probe windows and I–III indicate the first three excursions. The kinetic energy Ekin(t) is obtained from differentiation (weak dashed line) and smoothing (fat dashed line). | ||
 | ||
| Fig. 7 (a) Sketch of potential and kinetic energy showing the peculiar dynamics of the I2 molecule for strong fragment cage interaction: In the first collision a wave packet started near the dissociation limit (λpump = 500 nm) is scattered below a wave packet that was started at lower energy (i.e.λpump = 520 nm). During the interaction the kinetic energy is very small (Fig. 6). The energy after the collision is given (Fig. 5) by the energy relaxation rate. (b) Two cage modes according to ref. 36 illustrate the intuitive breathing of the cage and the belt mode that slows down the I fragments in the recombination event (see text). | ||
IV Discussion
A B and E state spectroscopy
The results of a rather weak red shift of 2% in Te for the B state and a stronger red shift for the E state are typical for the valence character of the B state and the stronger solvation of the ionic E state (Table 1). Concerning the calculation on the E state by Batista and Coker, we find a weaker solvation intermediate between the gas phase and this calculation which may originate from the fixed fcc Kr structure used in the calculation (see below). The blue shift of less than 0.2% in ωe for the B state is negligible. We compare the ν(E) curve in Kr with the gas phase (Fig. 3) shifted by the 350 cm−1 in Te due to solvation. We find a systematically smaller anharmonicity. The repulsive interaction with the cage atoms increases with the elongation R, i.e. with energy E, which bends in the outer wing. This is expressed in a smaller slope of ν(E), keeping ν higher for large E. A Morse-like approximation works well only deep in the well where the interaction is still relatively weak. Near the dissociation limit the cage walls confine the I fragments, even yielding a curvature of ν(E) with the opposite sign.| State | I2 gas phase | I2/Kr RKR | I2/Kr DIM | ||
|---|---|---|---|---|---|
| Dynamic lattice | Relaxed lattice | Fixed fcc lattice | |||
| B | ω e/cm−1 | 125.69 | 125.9 | 125.9 | 116.5 |
| ω e x e/cm−1 | 0.764 | 0.702 | 0.721 | 0.783 | |
| T e/cm−1 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 770 770 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 420 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 644 644 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 816 816 |
|
| E | T e/cm−1 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411 411 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
— | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101 101 |
It has to be kept in mind that this I–I potential reflects a multidimensional potential which includes the cage dynamics. The frequencies ν(E) and the derived RKR potential are obtained from the round-trip time T1 directly after excitation and thus they are precisely valid only for the initial condition of a wave packet prepared on the B state with the surrounding Kr atoms thermally equilibrated around an I2 molecule in its ground state—which is the typical situation in pump–probe spectroscopy. Since the periods are measured for relaxing wave packets, the potential already includes the solvent response in the sense that a classical one dimensional trajectory started on this potential will give the right periods of the multidimensional system. Such a potential is very helpful for quick and precise estimates of the dynamics and to develop an intuitive picture of the multidimensional problem. It also helps to design pump–probe experiments, because the potentials can be directly used to estimate the needed wavelengths and time-resolution.
In trajectory calculations, i.e. using DIM potentials (diatomics in molecules),34 similar to simulations by Batista and Coker16 the potential felt by the I2 including all Kr atoms is calculated (eigenvalues of the Hamiltonian) at each time step for each trajectory. Thus the potential averaged over many trajectories should correspond to the measured RKR potential because the deformation of the surrounding atoms is taken into account. It may be interesting to derive such an average potential and to judge it by comparison with the potential determined from the pump–probe data. The potential allows a deeper understanding of the ultrafast many body dynamics since a detailed theoretical modeling of the probe process to the ionic surfaces is circumvented and the simulations are compared to experiment at an earlier stage.
To give an intuition of the one-dimensional representation of the multidimensional potential and to have a first comparison with experiment we calculated the DIM potential surface for I2 in Kr following refs. 16 and 17 and including their correct diagonalization of the Hamiltonian matrix. The results are shown in Fig. 1a. The dashed lines correspond to calculations of the X and B states where the Kr atoms are kept fixed at the fcc lattice positions (Fig. 1d). This is the geometry for which potentials are shown in refs. 16 and 17. For the solid lines we let the Kr atoms relax around an I2 atom in the X state. In the relaxed geometry the two Kr atoms that are in line with the I2 axis move closer to the I atoms (Fig. 1c). We kept the Kr atoms fixed at this position. Stretching the molecular bond of I2 against this solvent cage induces a steeper outer limb in the potential. Comparison of the DIM potentials with the experimental RKR potential shows that, not surprisingly, the relaxed cage geometry gives much better agreement. However close to the dissociation limit the RKR potential which includes the cage dynamics is softer. In the course of the I–I stretching motion, the Kr atoms are pushed out, which bends the outer limb of the potential towards the loose fcc cage. This is the phenomenon that we expect to be accurately reproduced by the above mentioned averaged trajectory calculation. Note that the repulsive interaction between I and Kr shifts the potential minimum of the B state up by 600 cm−1 upon cage relaxation.
The spectroscopic constants that reflect the situation near the minimum are collected in Table 1. The fixed fcc lattice yields significantly lower Te and ωe and an anharmonicity ωexe closer to the gas-phase value. At higher excitation the anharmonicities change and higher orders are needed for description. However at high excitation energies the RKR potential includes the cage dynamics and the DIM potential does not, hence we only compare the “constants” near the minimum. Concerning the shape EE(R) of the ionic E state surface, the results obtained by Batista and Coker35 in the fcc cage agree very well with our experimentally determined potential if we shift it by 0.01 nm outward and 3900 cm−1 up in energy. (Table 1) Here the experiment probes the potential at I–I elongations around 0.4 nm which is exactly the nearest neighbor distance in Kr (Fig. 1b) rendering the fcc lattice a good approximation.
The effect that the probe wavelength changes the measured oscillation period has already been seen in trajectory simulations.7 There it has been used to fix the probe window since the window position could not be deduced from the systematic variation of probe wavelengths. We would like to remark that the position of the probe window has a dramatic influence on the decay of the envelope of the pump–probe spectra in these simulations and thus also on the predissociation time deduced from the simulations. Our approach has the advantage of separating the processes of vibrational energy relaxation and predissociation whereas in simulations of the observed signal they are inevitably convoluted. Thus tuning both pump and probe wavelength proves to be helpful even when a high level simulation is at hand, i.e. to judge the systematic errors introduced by the simulation of the probe process.
B Vibrational relaxation and I atom trajectories
The comparison of pump–probe spectra with classical simulations indicated already a strong variation of the vibrational relaxation rate with E, but it was also convoluted with losses by predissociation.7 Now in Fig. 5 we have extracted the vibrational relaxation rate versusE and present its systematic variation over three orders of magnitude. Our results are in excellent agreement with the values of the classical simulation in ref. 7 for krel in Kr which are shown as hollow symbols in Fig. 5. We read the values from the graphs in Fig. 6 of ref. 7, because the values given in the text correspond to a rate krel averaged over 1 ps and our results are averaged over one period only. The small rates near the bottom show up also in the calculations. The dynamics at the dissociation limit determined by us for λpump = 500 nm can be qualitatively compared to the classical calculation (λpump = 510 nm) in ref. 7. It is clear that the simulations catch the very strong I–cage interaction that allows only one large excursion beyond R = 0.4 nm. The simulations deliver a swarm of trajectories. Unfortunately only an “anecdotal” trajectory is presented 7 instead of an averaged trajectory with a distribution. Similar to the averaged potential discussed above, a comparison of an averaged trajectory with our experimentally derived trajectory could improve the value of the comparisons and would yield a deeper analysis.The explanation for the apparent sticking of the I atom to the cage is most evident from a simulation of Cl2 in Ar near the dissociation limit.36 Three modes of deformation are excited with large amplitudes. An expansion of the cage along the Cl–Cl axis which is intuitively convincing and two modes which correspond to an inward motion of a belt of 4 matrix atoms just in the middle of the Cl–Cl bond. The expansion and one belt mode are displayed in Fig. 7b. The expansion of the Cl–Cl bond displaces matrix atoms along this direction but creates space just around the center of the bond. The atoms in the belt can move in and thus compensate the volume change from the Cl–Cl expansion. This picture is valid also for the I2-in-Kr case5 in accord with the discussion in ref. 36 and with essential features of the simulations on the A state of I2 in an Ar matrix.13 Now when the I atoms are stopped at the turning point and try to return they have to displace first the matrix atoms in the belt which delays recombination. The acceleration of these belt atoms takes out kinetic energy from the I–I coordinate. It reduces the I velocity as seen in the sliding down on the potential surface in Fig 7a and explains the extremely large energy loss. Only after the belt atoms have been expelled around 400 fs in Fig. 6 then the usual Morse-like rise in kinetic energy appears. The experimental trajectory in Fig. 6 directly displays this peculiar process.
V Conclusion
For the case of I2 in Kr matrix we demonstrated that detailed information on potentials and dynamics of a condensed phase system with strong relaxation may be obtained directly from femtosecond pump–probe spectra. The required accuracy for measuring the round trip time changes considerably with the energy in the B state. Near the bottom of the potential, i.e. for λpump = 580 nm, the round trip time changes by only 4 fs between successive vibrational levels. It takes about 5 periods to dissipate the energy of one vibrational quantum due to the low relaxation rate. Thus a variation of 4 fs distributed over 5 round trips has to be resolved and this limits the applicability of the method in this range. However for the interesting case of strong fragment–cage interaction around λpump = 500 nm the energy loss per round trip exceeds 1000 cm−1. The related change of the period on the order of 100 fs is easily resolved. Using a classical analog of the RKR method we constructed a one dimensional potential for the valence B state that includes the dynamical response of the solvent and thus contains the multidimensional nature of the system. We believe that this access to ultrafast dynamics of systems with several degrees of freedom will help to generate and improve methods for theoretical simulations. Not only averaged potentials but also averaged trajectories may be directly compared to the experiment. It will be helpful to check the agreement of experiment and theory not only by comparing the simulated with the observed signal but also by verifying different output parameters of the simulation, like trajectory positions. The relative simplicity of the system I2 in Kr provides a good test ground for new models and should train intuition for tackling more complicated problems.Using the known B state potential we measured the ionic E state potential in a straightforward way. By tuning the probe wavelength we were able to take snapshots of a trajectory on the B state that is started at the dissociation limit and displays a very strong inelastic collision with the matrix cage. The recombination dynamics were observed on the femtosecond timescale. As a general conclusion we showed that both pump and probe wavelength have to be taken into account when oscillational frequencies are deduced from femtosecond pump–probe spectra. While it is obvious that the pump wavelength determines the oscillation period of the wave packet it is sometimes neglected that the probe window reflects the vibrational levels that are sampled. In the case of I2 in Kr matrix where well modulated signals are observed, indicating that the wave packet is not destroyed by the vibrational relaxation, the error introduced by neglecting the effect of probe window can exceed 7%. In systems with stronger interactions where the wave packet is substantially broadened in energy space (e.g. in liquids with large fluctuations) the question which part of the wave packet is probed will gain importance.
VI Acknowledgements
Extensive discussions with Profs. V. A. Apkarian, D. Coker and Dr C. Margulis are gratefully acknowledged. This work was supported by the Deutsche Forschungsgemeinschaft via SfB 450.References
- C. Lienau and A. H. Zewail, Chem. Phys. Lett., 1994, 222, 224 CrossRef CAS.
- Q. Liu, C. Wan and A. H. Zewail, J. Chem. Phys., 1996, 105, 5294 CrossRef CAS.
- C. Lienau, J. C. Williamson and A. H. Zewail, Chem. Phys. Lett., 1993, 213, 289 CrossRef CAS.
- R. Zadoyan, N. Schwentner and V. A. Apkarian, Chem. Phys., 1998, 233, 353 CrossRef CAS.
- R. Zadoyan, J. Almy and V. A. Apkarian, Faraday Discuss., 1997, 108, 255 RSC.
- R. Zadoyan, M. Sterling, M. Ovchinnikov and V. A. Apkarian, J. Chem. Phys., 1997, 107, 8446 CrossRef CAS.
- R. Zadoyan, M. Sterling and V. A. Apkarian, J. Chem. Soc., Faraday Trans., 1996, 92, 1821 RSC.
- R. Zadoyan, Z. Li, C. C. Martens and V. A. Apkarian, J. Chem. Phys., 1994, 101, 6648 CrossRef.
- R. Zadoyan, Z. Li, P. Ashjian, C. C. Martens and V. A. Apkarian, Chem. Phys. Lett., 1994, 218, 504 CrossRef CAS.
- M. Sterling, R. Zadoyan and V. A. Apkarian, J. Chem. Phys., 1996, 104, 6497 CrossRef CAS.
- M. Ovchinnikov and V. A. Apkarian, J. Chem. Phys., 1997, 106, 5775 CrossRef CAS.
- M. Ovchinnikov and V. A. Apkarian, J. Chem. Phys., 1996, 105, 10312 CrossRef CAS.
- Z. Li, R. Zadoyan, A. V. Apkarian and C. C. Martens, J. Phys. Chem., 1995, 99, 7453 CrossRef CAS.
- V. S. Batista and D. F. Coker, J. Chem. Phys., 1999, 110, 6583 CrossRef CAS.
- (a) V. S. Batista and D. F. Coker, J. Chem. Phys., 1997, 106, 7102 CrossRef CAS; (b) erratum: J. Chem. Phys., 1999, 110, 6583.
- V. S. Batista and D. F. Coker, J. Chem. Phys., 1997, 106, 6923 CrossRef CAS.
- V. S. Batista and D. F. Coker, J. Chem. Phys., 1996, 105, 4033 CrossRef CAS.
- J. Xu, N. Schwentner, S. Hennig and M. Chergui, J. Raman Spectrosc., 1997, 28, 433 CrossRef CAS.
- I. Almy, K. Kitzer, R. Zadoyan and V. Apkarian, J. Phys. Chem. A, 2000, 104, 3508 CrossRef.
- C. F. Bardeen, J. Che, K. R. Wilson, V. V. Yakovlev, V. A. Apkarian, C. C. Martens, R. Zadoyan, B. Kohler and M. Messina, J. Chem. Phys., 1997, 106, 8486 CrossRef CAS.
- M. Bargheer, K. Donovang, P. Dietrich and N. Schwentner, J. Chem. Phys., 1999, 111, 8556 CrossRef CAS.
- M. Karavitis, R. Zadoyan and V. Apkarian, J. Chem. Phys., 2001, 114, 4131 CrossRef CAS.
- M. Gruebele, G. Roberts, M. Dantus, R. M. Bowman and A. H. Zewail, Chem. Phys. Lett., 1990, 166, 459 CrossRef CAS.
- E. Schreiber, Femtosecond real-time spectroscopy of small molecules and clusters, Springer Tr. Mod. Phys. 143, Springer Verlag, Berlin, 1998.
- J. Helbing and M. Chergui, J. Chem. Phys., 2001, 115, 6158 CrossRef CAS.
- T. Wilhelm, J. Piel and E. Riedle, Opt. Lett., 1997, 22, 1494 Search PubMed.
- E. Riedle, M. Beutter, S. Lochbrunner, J. Piel, S. Schenkl, S. Sporlein and W. Zinth, Appl. Phys. B, 2000, 71, 457 CAS.
- M. Bargheer, J. Pietzner, P. Dietrich and N. Schwentner, J. Chem. Phys., 2001, 115, in press Search PubMed.
- J. Franck, Trans. Faraday Soc., 1925, 21, 536 RSC.
- R. Rydberg, Z. Phys., 1931, 73, 376 Search PubMed.
- O. Klein, Z. Phys., 1932, 76, 226 Search PubMed.
- A. Rees, Proc. Phys. Soc. London, Sect. A, 1947, 59, 998 Search PubMed.
- L. D. Landau and E. M. Lifschitz, Lehrbuch der theoretischen Physik, vol. I: Mechanik, Akademie-Verlag, Berlin, 1979.
- F. O. Ellison, J. Am. Chem. Soc., 1963, 69, 3540 CrossRef.
- V. S. Batista, C. Margulis and D. Coker, private communication.
- M. Ovchinikov and V. Apkarian, J. Chem. Phys., 1998, 108, 2277 CrossRef.
| This journal is © the Owner Societies 2002 |
