View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/B106072B (Paper) Phys. Chem. Chem. Phys., 2002, 4, 82-85

Explicit internal signal stochastic resonance in a chemical model

Rui Zhu a and Qian Shu Li *ab
aSchool of Chemical Engineering and Materials Science, Beijing Institute of Technology, Beijing 100081, People's Republic of China. E-mail: qsli@mh.bit.edu.cn
bNational Key Laboratory of Theoretical and Computational Chemistry, Jilin University, Changchun, Jilin 130023, People's Republic of China

Received 9th July 2001 , Accepted 1st November 2001

First published on 13th December 2001

Abstract

A Belousov–Zhabotinsky (BZ) reaction model subject to additive Gaussian white noise is investigated as the model system is located in the dynamical region of period-1 oscillation. The model is composed of three ordinary differential equations representing the time evolutions of HBrO2[thin space (1/6-em)], Ce(IV), and BrCH(COOH)2[thin space (1/6-em)], respectively. Noise is separately added to the three equations. In all three cases the change in the Ce(IV) variable's output signal-to-noise ratio (SNR) as a function of the noise intensity shows non-monotonic behavior, indicating the occurrence of explicit internal signal stochastic resonance. However, its strength is quite different in each case, implying that the three reacting species play different roles in determining the dynamical behavior in the BZ reaction. The change in the peak height of the Ce(IV) variable's output frequency spectrum and the shift of the peak's central frequency with increasing noise intensity are also examined.

1. Introduction

Stochastic resonance (SR) is a phenomenon wherein the response of a nonlinear system to a weak coherent input signal is optimized by the presence of a particular, non-zero, level of noise.1–3 Though SR was originally introduced to account for the periodic oscillations of the Earth's ice ages,4–6 it is now known to occur in a wide range of physical,7–10 chemical11–21 and biological systems.22–26

In 1996, Schneider et al. first investigated chemical SR experimentally with input signal and noise in three nonlinear reaction systems, which are all in a steady state close to a Hopf bifurcation.11–13 Numerical simulations demonstrate that SR with input signal and noise can also occur in bistable chemical systems. However, contrary to the bistable state for the overdamped oscillator that is often used to explain the mechanism of SR, the chemical bistable state corresponds to a stable node and a stable limit cycle, respectively.16 In the numerical work on the photosensitive Belousov–Zhabotinsky reaction, two-parameter SR was found,20,21i.e., when one parameter is modulated by signal and the other by noise, the signal-to-noise ratio (SNR) goes through a maximum with increasing noise intensity. In the earlier studies of SR, as in the cases shown above, it was realized that the occurrence of SR needs three basic ingredients: (i) a threshold nonlinear system, (ii) a weak coherent input, and (iii) a noise input. With the development in SR studies, however, one is convinced that this is not the case. One example is the noise-free SR,27 where the role of noise is played by the chaos generated through the inherent dynamics of a deterministic chaotic system. Another more interesting example is the internal signal stochastic resonance (ISSR), which was first discovered when investigating numerically a two-dimensional autonomous model system in a state near a saddle-node bifurcation.28 When the control parameter is randomly modulated near the saddle-node bifurcation point, noise-induced coherent oscillation (NICO) occurs, the strength of which passes through a maximum with increasing noise intensity. Thereafter, Xin's group studied ISSR numerically in several chemical reaction models, which, however, are in a steady state near a Hopf bifurcation.14–18 Their simulations also showed that ISSR could occur in the two-parameter photosensitive Belousov–Zhabotinsky reaction.18 Very recently, they first presented the experimental observation of ISSR in the Belousov–Zhabotinsky reaction.19

To our knowledge, the systems studied in the previous chemical ISSR are single-threshold systems associated with Hopf bifurcation; and the occurrences of ISSR are closely related to NICO generated by crossing bifurcation. Recently, however, we found a new type of ISSR by simulating the Belousov–Zhabotinsky reaction system in the period-1 oscillatory state with only random modulation of the control parameter.29 It can occur without involving crossing bifurcation. Since in this new type of ISSR the signal comes from the intrinsic period-1 oscillation of a nonlinear system, we called this SR explicit ISSR. The internal signal investigated in the previous ISSR comes from NICO, which is not shown without external noise, so we called the previous type of ISSR implicit ISSR. Contrary to implicit ISSR, no sudden change of state is involved in explicit ISSR. In our previous work, we have compared their characteristics, and concluded that they have different underlying mechanisms.

Our previous studies on explicit ISSR were conducted with parametric perturbation, representing the effect of external noise on the system. In the present work, however, we will use additive perturbation, representing the effect of internal fluctuations on the system. We will use the same system as has been used in our previous work, i.e., the three-variable Belousov–Zhabotinsky reaction model developed by Gyorgyi and Field.30 Noise is added separately in the three equations, thus, there are three cases. Based on the signal to noise ratio variation with noise intensity obtained from the frequency spectrum, numerical simulations demonstrate that explicit ISSR can occur in all three cases, but its strength is significantly different in each case. The variation in frequency spectrum peak height and the shift of the peak's central frequency with noise intensity are examined for the three cases.

2. Model

A. Modified Oregonator model

We here use the three-variable model equations of Gyorgyi and Field together with the numerical parameters for the case of low CSTR flow rates.30 In the following descriptions, x, z, and ν will denote respectively the concentrations of HBrO2[thin space (1/6-em)], Ce(IV), and BrCH(COOH)2[thin space (1/6-em)], dx/dτ, dz/dτ, and dν/dτ represent their time evolutions, and kf the flow rate. See ref. 30 for further details about the model.

B. Random perturbation of one equation

The first case that we will study here is the one where a term Np(τ) is added to dx/dτ. Np(τ)[thin space (1/6-em)]=[thin space (1/6-em)]∑j=0∞[thin space (1/6-em)]Nj[thin space (1/6-em)]Γ(τ[thin space (1/6-em)]−[thin space (1/6-em)]jp), where j is an integer, and Γ(u)[thin space (1/6-em)]=[thin space (1/6-em)]1 for 0[thin space (1/6-em)]⩽[thin space (1/6-em)]u[thin space (1/6-em)]<[thin space (1/6-em)]p or 0 otherwise, Nj is a Gaussian white noise with 〈[thin space (1/6-em)]Nj[thin space (1/6-em)]〉[thin space (1/6-em)]=[thin space (1/6-em)]0 and 〈[thin space (1/6-em)]NiNj[thin space (1/6-em)]〉[thin space (1/6-em)]=[thin space (1/6-em)]2Dδij in which D measures the intensity of the additive noise Np(τ), and p is the noise pulse length, which is set to 0.01 s throughout this work. In the second and third cases the term Np(τ) is added to dz/dτ and dν/dτ, respectively.

In all the three cases, we will examine the output behavior of the z variable, i.e., the Ce(IV) concentration, with increase in the intensity (D) of the additive noise. The choice of the Ce(IV) concentration variable here is based on the consideration of its role in determining the electric potential in the BZ reaction system. This is easily measured by a redox electrode in the real reaction system. Since our studies are conducted with additive perturbation of variables, they in fact investigate the effect of internal fluctuations of the variables on the BZ system.

C. Calculational methods

In each of the above three cases, the original three-variable equations with the addition of noise to one of the three equations are solved numerically using the Gear method. To quantify the SR effect, 16[thin space (1/6-em)]384 output points of the variable z at intervals of 0.001 s are used to obtain the frequency spectrum by fast Fourier transformation. Based on the frequency spectrum, SNR is defined as the ratio of the height of the spectrum of the output signal at the fundamental frequency ωf to the average amplitude of the background noise spectrum in the vicinity of ωf[thin space (1/6-em)].31 Here, we take the surrounding noise signals with the frequency range ωf[thin space (1/6-em)]±[thin space (1/6-em)]0.6 Hz. Each plot of SNR versus noise intensity is obtained by averaging 30 runs.

3. Results

When kf is selected as the control parameter, this unperturbed model can show various types of dynamic behavior. Steady states appear at kf[thin space (1/6-em)]⩽[thin space (1/6-em)]2.350[thin space (1/6-em)]×[thin space (1/6-em)]10−4 s−1. Small-amplitude, sinusoidal period-1 oscillations develop as kf is increased to 3.163[thin space (1/6-em)]×[thin space (1/6-em)]10−4 s−1. The sequence of period-doubling bifurcations follows and results in chaos at kf[thin space (1/6-em)]≈[thin space (1/6-em)]3.230[thin space (1/6-em)]×[thin space (1/6-em)]10−4 s−1. Fig. 1 shows the bifurcation diagram, which agrees with the results of Gyorgyi and Field.30 In this work, we chose the period-1 oscillatory state at kf[thin space (1/6-em)]=[thin space (1/6-em)]3.100[thin space (1/6-em)]×[thin space (1/6-em)]10−4 s−1, indicated by the arrow in Fig. 1, as the state perturbed by noise. Its time traces are shown in Fig. 2. In the next section, we will investigate the SNR behavior with the variation of noise intensity at the fundamental frequency of the time series of variable z for the above three cases.
Bifurcation diagram obtained from numerical simulations for the BZ reaction model of Gyorgyi and Field. Notations used: p1, period-1 oscillations; p2, period-2 oscillations; ch, a chaotic regime. The arrow indicates the period-1 oscillatory state at kf = 3.100 × 10−4 s−1, as studied in this work.
Fig. 1 Bifurcation diagram obtained from numerical simulations for the BZ reaction model of Gyorgyi and Field. Notations used: p1, period-1 oscillations; p2, period-2 oscillations; ch, a chaotic regime. The arrow indicates the period-1 oscillatory state at kf[thin space (1/6-em)]=[thin space (1/6-em)]3.100[thin space (1/6-em)]×[thin space (1/6-em)]10−4 s−1, as studied in this work.

log(z) versus reduced time for the period-1 oscillation at kf = 3.100 × 10−4 s−1 indicated by the arrow in Fig. 1.
Fig. 2 log(z) versus reduced time for the period-1 oscillation at kf[thin space (1/6-em)]=[thin space (1/6-em)]3.100[thin space (1/6-em)]×[thin space (1/6-em)]10−4 s−1 indicated by the arrow in Fig. 1.

A. SNR variation with the noise intensity

Considering now the first case mentioned in section 2.B, i.e., Gaussian white noise added to dx/dτ. Fig. 3(a) shows the SNR as a function of noise intensity D. With increasing noise intensity, the SNR repeatedly increases, then decreases, causing a series of peaks called the resonance peaks, on the SNR curve. However, only the first two resonance peaks at (SNR[thin space (1/6-em)]≈[thin space (1/6-em)]3343, D[thin space (1/6-em)]≈[thin space (1/6-em)]4.094[thin space (1/6-em)]×[thin space (1/6-em)]10−8) and (SNR[thin space (1/6-em)]≈[thin space (1/6-em)]511, D[thin space (1/6-em)]≈[thin space (1/6-em)]1.206[thin space (1/6-em)]×[thin space (1/6-em)]10−7), respectively are clear. For the second and third cases with Gaussian white noise added to dz/dτ and dν/dτ respectively, the plots of SNR against noise intensity are shown in Fig. 3(b) and (c), respectively. As in the first case, there are two clear resonance peaks, (SNR[thin space (1/6-em)]≈[thin space (1/6-em)]5198, D[thin space (1/6-em)]≈[thin space (1/6-em)]2.465[thin space (1/6-em)]×[thin space (1/6-em)]10−7) and (SNR[thin space (1/6-em)]≈[thin space (1/6-em)]623, D[thin space (1/6-em)]≈[thin space (1/6-em)]7.340[thin space (1/6-em)]×[thin space (1/6-em)]10−7) for the second case, and (SNR[thin space (1/6-em)]≈[thin space (1/6-em)]489, D[thin space (1/6-em)]≈[thin space (1/6-em)]1.880[thin space (1/6-em)]×[thin space (1/6-em)]10−8) and (SNR[thin space (1/6-em)]≈[thin space (1/6-em)]94, D[thin space (1/6-em)]≈[thin space (1/6-em)]7.400[thin space (1/6-em)]×[thin space (1/6-em)]10−8) for the third case. What is common to all three cases is that their SNR curves all show non-monotonic behavior, indicating the occurrence of explicit ISSR.
SNR as evaluated from the frequency spectra of time series of log(z) versus noise intensity. Gaussian white noise added to (a) dx/dτ (b) dz/dτ and (c) dv/dτ.
Fig. 3 SNR as evaluated from the frequency spectra of time series of log(z) versus noise intensity. Gaussian white noise added to (a) dx/dτ (b) dz/dτ and (c) dv/dτ.

The presence of such resonance peaks shows that the addition of noise with proper intensity can make the distribution of signals more centralized at the fundamental signals, indicating the constructive role of noise. However, it ought to be noted that the resonance peaks on the SNR curve tend to weaken with increasing noise intensity, indicating that the destructive role of noise still exists. We will see more clearly the two-fold role played by noise in the next section.

B. Variations in peak heights and central frequencies with the noise intensity

It is interesting to study the dependence of the strength of the fundamental signal in the time series upon the noise intensity in the three cases. Fig. 4 plots the frequency spectrum peak height against noise intensity, corresponding to the SNR curves in Fig. 3. The three cases all show more than one peak, which become gradually weaker with increasing noise intensity. Case 1 has three main peaks, case 2 has four, and case 3 has two. Comparing Fig. 4 and Fig. 3, it is seen that the differences between the heights of the main peaks in Fig. 4 for any case are much less than those between their corresponding resonance peaks' SNR in Fig. 3. For example, the difference between the heights of the first and the second main peaks in Fig. 4(b) is 46[thin space (1/6-em)]−[thin space (1/6-em)]45[thin space (1/6-em)]=[thin space (1/6-em)]1, while that between their corresponding resonance peaks' SNR in Fig. 3(b) is 5198[thin space (1/6-em)]−[thin space (1/6-em)]623[thin space (1/6-em)]=[thin space (1/6-em)]4575. This obviously indicates that the noise level surrounding the fundamental frequency in the frequency spectrum for the first resonance peak is much less than that for the second resonance peak. This also implies the existence of contributions from both the constructive and destructive effects of the noise. The constructive role of noise dominates in the first resonance peak, after which the destructive role of noise quickly dominates.
Spectrum peak height plotted against noise intensity. Gaussian white noise added to (a) dx/dτ (b) dz/dτ and (c) dv/dτ.
Fig. 4 Spectrum peak height plotted against noise intensity. Gaussian white noise added to (a) dx/dτ (b) dz/dτ and (c) dv/dτ.

A characteristic of implicit ISSR called the noise-induced frequency shift, in which the spectrum peak's central frequency is significantly shifted with the noise intensity, was reported in ref. 28. Thus, we will next examine the shift of the spectrum peak's central frequency in our three cases. As shown in Fig. 5, the all shift very little, and their values increase with increasing noise intensity except for several plateaus. Comparing Fig. 5 and Fig. 4, we see that the number of plateaus in Fig. 5 for any case is almost equal to the number of main peaks in Fig. 4 for the same case.


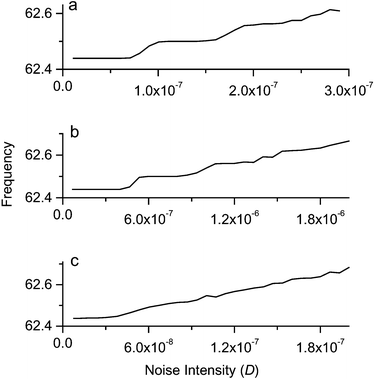Central frequency of the spectrum peak versus noise intensity. Gaussian white noise added to (a) dx/dτ (b) dz/dτ and (c) dv/dτ.
Fig. 5 Central frequency of the spectrum peak versus noise intensity. Gaussian white noise added to (a) dx/dτ (b) dz/dτ and (c) dv/dτ.

4. Discussion

We have investigated the variations of SNR, spectrum peak height, and spectrum peak's central frequency with noise intensity for the three cases, when white noise is added to each of the three ordinary differential equations in turn, leaving the other two equations untouched. We have observed 3 attributes common to the three cases: that the SNR curve has more than one peak; that the differences between the heights of the main peaks on the spectrum peak height curve are much less than those between the corresponding resonance peaks' SNR; and that the number of plateaus on the frequency curve is almost equal to the number of main peaks on the spectrum peak height curve. On the other hand, it is also of interest to examine the differences between the three cases. As shown in Fig. 3, the maximal SNR is 3343 for case 1, 5189 for case 2, and 489 for case 3, indicating that explicit ISSR is significantly different in strength in each case.

dx/dτ, dz/dτ, and dν/dτ represent in the BZ reaction the time evolutions of HBrO2[thin space (1/6-em)], Ce(IV), and BrCH(COOH)2[thin space (1/6-em)], respectively; and the BZ system is investigated with added perturbations representing the effect of internal fluctuations on the system. Thus, the different values of the maximal SNR for the three cases indicate that, among HBrO2[thin space (1/6-em)], Ce(IV), and BrCH(COOH)2 in the BZ reaction, the internal fluctuation of Ce(IV) demonstrates the strongest effect on the system's output electric potential, while that of BrCH(COOH)2 demonstrates the weakest effect. In addition, comparing the three cases in Fig. 3–5, we can easily conclude that the larger the number of the main peaks on the spectrum peak height curve (or the number of plateaus on the frequency curve) the stronger the obtained explicit ISSR.

Besides HBrO2[thin space (1/6-em)], Ce(IV), and BrCH(COOH)2[thin space (1/6-em)], Br− is another important control intermediate to determine the dynamic behavior in the BZ reaction. However, the evolution equation of Br− is deleted for simplicity in the model of the present work. It can be argued that the additive perturbation of Br− should show explicit ISSR yet different in strength from the other three cases. This could be confirmed by doing the same work on the four-dimensional model32 of the BZ reaction (including the evolution equation of Br−).

In a real BZ reaction experiment all variables and even the parameters always fluctuate. According to our previous work on parametric perturbations29 and the present work on additive perturbations, we find that explicit ISSR could occur in both cases, i.e., external noises and internal fluctuations can cause the same effect. For the latter, the strengths of explicit ISSR for different variables could not only give the order of their sensitivities towards internal fluctuations but also examine their roles in determining the dynamic behavior in the BZ reaction from the viewpoint of perturbations.

5. Conclusion

Explicit internal signal stochastic resonance is numerically investigated in a Belousov–Zhabotinsky (BZ) reaction model, which is composed of three ordinary differential equations representing the time evolutions of HBrO2[thin space (1/6-em)], Ce(IV), and BrCH(COOH)2[thin space (1/6-em)], respectively. Noise is added separately to the three equations. It is found that the explicit ISSR obtained from perturbation of the evolution equation of Ce(IV) is the strongest among the 3, while that from perturbation of the evolution of BrCH(COOH)2 is the weakest. The results imply, from the viewpoint of perturbations, that the three species play different important roles in determining the dynamical behavior in the BZ reaction.

Acknowledgements

The authors are grateful to Dr Hong Li Wang for valuable comments and Prof Pei Ran Yan for critically reading the manuscript. This work is supported by the National Natural Science Foundation of China (29873006).

References

  1. L. P. Gammaitoni, P. Hanggi, P. Jung and F. Marchesoni, Rev. Mod. Phys., 1998, 70, 223 CrossRef CAS.
  2. K. Wiesenfeld and F. Jaramillo, Chaos, 1998, 8, 539 CrossRef.
  3. K. Wiesenfeld and F. Moss, Nature (London), 1995, 373, 33 CrossRef CAS.
  4. R. Benzi, S. Sutera and A. Vulpiani, J. Phys. A, 1981, 14, L453 Search PubMed.
  5. C. Nicolis, Tellus, 1982, 34, 1 Search PubMed.
  6. R. Benzi, G. Parisi, A. Sutera and A. Vulpiani, Tellus, 1982, 34, 10 Search PubMed.
  7. S. Fauve and F. Heslot, Phys. Lett. A, 1983, 97, 5 CrossRef.
  8. A. N. Grigorenko, P. I. Nikitin, A. N. Slavin and P. Y. Zhou, J. Appl. Phys., 1994, 76, 6335 CrossRef CAS.
  9. P. Jung and K. Wiesenfeld, Nature (London), 1997, 385, 291 CrossRef CAS.
  10. M. Misono, T. Kohmoto, Y. Fukuda and M. Kunitomo, Opt. Commun., 1998, 152, 255 CrossRef CAS.
  11. A. Guderian, G. Dechert, K. P. Zeyer and F. W. Schneider, J. Phys. Chem., 1996, 100, 4437 CrossRef CAS.
  12. A. Foster, M. Merget and F. W. Schneider, J. Phys. Chem., 1996, 100, 4442 CrossRef.
  13. W. Hohmann, J. Müller and F. W. Schneider, J. Phys. Chem., 1996, 100, 5338.
  14. S. Zhong, Y. J. Jiang and H. W. Xin, J. Chem. Phys., 1999, 111, 9720 CrossRef CAS.
  15. Z. H. Hou and H. W. Xin, J. Chem. Phys., 1999, 111, 721 CrossRef CAS.
  16. L. F. Yang, Z. H. Hou and H. W. Xin, J. Chem. Phys., 1999, 110, 3591 CrossRef CAS.
  17. Z. H. Hou and H. W. Xin, J. Phys. Chem. A, 1999, 103, 6181 CrossRef CAS.
  18. S. Zhong and H. W. Xin, J. Phys. Chem. A, 2000, 104, 297 CrossRef CAS.
  19. Y. J. Jiang, S. Zhong and H. W. Xin, J. Phys. Chem. A, 2000, 104, 8521 CrossRef CAS.
  20. T. Amemiya, T. Ohmori, M. Nakaiwa and T. Yamaguchi, J. Phys. Chem. A, 1998, 102, 4537 CrossRef CAS.
  21. T. Amemiya, T. Ohmori, T. Yamamoto and T. Yamaguchi, J. Phys. Chem. A, 1999, 103, 3451 CrossRef CAS.
  22. J. K. Douglass, L. Wilkens, E. Pantazelou and F. Moss, Nature (London), 1993, 365, 337 CrossRef CAS.
  23. D. F. Russell, L. A. Wilkens and F. Moss, Nature (London), 1999, 402, 291 CrossRef CAS.
  24. D. Petracchi, I. C. Gebeshubr, L. J. DeFelice and A. V. Holden, Chaos, Solitons Fractals, 2000, 11, 1819 CrossRef.
  25. G. Balazsi and L. B. Kish, Phys. Lett. A, 2000, 265, 304 CrossRef CAS.
  26. I. Hidaka, D. Nozaki and Y. Yamamoto, Phys. Rev. Lett., 2000, 85, 3740 CrossRef CAS.
  27. K. Wiesenfeld and F. Jaramillo, Chaos, 1998, 8, 539 CrossRef.
  28. G. Hu, T. Ditzinger, C. Z. Ning and H. Haken, Phys. Rev. Lett., 1993, 71, 807 CrossRef.
  29. Q. S. Li and R. Zhu, J. Chem. Phys., 2001, 115, 6590 CrossRef CAS.
  30. L. Gyorgyi and R. J. Field, Nature (London), 1992, 355, 808 CrossRef CAS.and references therein.
  31. D. Gong, G. Hu, X. Wen, C. Yang, G. Qin, R. Li and D. Ding, Phys. Rev. A, 1992, 46, 3423 CrossRef.
  32. L. Gyorgyi and R. J. Field, J. Phys. Chem., 1991, 95, 6594 CrossRef CAS.
This journal is © the Owner Societies 2002
Click here to see how this site uses Cookies. View our privacy policy here.