View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/B105514N (Paper) Phys. Chem. Chem. Phys., 2002, 4, 68-74

Ar scattering on Ru (0001): a comparison to the washboard model†

B. Berenbak abc, S. Zboray a, B. Riedmuller a, D. C. Papageorgopoulos a, S. Stolte b and A. W. Kleyn *ac
aFOM-Institute for Atomic and Molecular Physics, Kruislaan 407, 1098 SJ Amsterdam, The Netherlands
bDepartment of Physical Chemistry, Faculty of Exact Sciences, Vrije Universiteit Amsterdam, De Boelelaan 1083, 1081 HV Amsterdam, The Netherlands
cLeiden Institute of Chemistry, Gorlaeus Laboratories Leiden University, Einsteinweg 55, P.O. Box 9502, 2300 RA Leiden, The Netherlands. E-mail: a.kleyn@chem.leidenuniv.nl

Received 22nd June 2001 , Accepted 22nd October 2001

First published on 14th December 2001

Abstract

The scattering of Ar atoms on a Ru (0001) surface has been studied by applying supersonic molecular beam techniques. Variation of the incidence energy (Ei) results in a rich variety of angular and energy distributions. At a low energy, clear zero-order diffraction has been identified. At higher energies (≥1 eV), argon scattering of Ru (0001), however, seems to be dominated by a totally different mechanism, which appears to be almost quantitatively reproduced by the washboard model, developed by Tully (J. C. Tully, J. Chem. Phys., 1990, 92, 680, ref. 1). This is surprising since his comparison of the washboard model to a reference of classical trajectory calculations for the Ar/Pt (111) system showed essential deviations. Our attempt to reproduce the experimental Ar/Ru (0001) data by similar simulations was unsuccessful, most likely due to shortcomings in the description of the solid state.

I. Introduction

Scattering atoms from surfaces with the help of molecular beam techniques has been successfully applied to a study of the fundamentals of gas–surface interaction. Though a lot has been achieved over the last decades, simple systems with noble gases scattering from crystalline metallic surfaces are still non-trivial to analyse. (Semi-) classical trajectory calculations have proven to yield substantial insight but are obviously limited due to simplifications of the (pair) potentials as well as the large number of surface atoms necessary to generate a realistic phonon bath.2,3 Even if the simulation reproduces the data set, a full understanding of the essential mechanisms is not directly obtained. Furthermore the quantized phonon can have a large influence on the character of the interaction. For instance, the diffraction of argon on W (100)-2H, observed by Schweizer et al.,4,5 has been found to occur without phonon excitation. A wide variety of scattering effects has been explained by them in terms of classical and quantum models. We report a similar zero order diffraction peak for the scattering of thermal argon from the Ru (0001) surface.

Basic models are desirable in order to rationalize and feed intuition on basic trends in gas–surface interaction. A combination of the simplest models, the binary collision model for sub-specular and the hard cube model for super-specular deflection angles often suffices for qualitative analyses. The washboard model, the simplest corrugated extension to the flat hard cube model, developed by Tully,1 serves as a useful tool to elucidate trends in the scattering from corrugated surfaces. In this model a ripple is introduced to allow off-normal momentum transfer to the surface. This simple corrugated extension to the flat hard cube model permits (double) rainbow structures to emerge in the angular distributions. When applying the washboard model to argon scattering from various crystal faces of platinum, almost quantitative agreement with stochastic trajectory calculations was reported by Tully.1 Only the smooth (111) surface gave rise to some remarkable deviations in the velocity distribution. Tully attributed this malfunction to an overestimated corrugation parameter αm.

In this paper we present angular and velocity distributions of argon scattered from Ru (0001) for a range of beam energies. Energy distributions for relatively high incidence energies (≥2 eV) show exactly those washboard features that Tully found to be doubtful for the (111) face of platinum. Two solutions seem possible: either the Ru (0001) surface possesses a larger surface corrugation than Pt (111), or Tully's trajectory calculations do not accurately represent the real system. The second option should be considered since our similar trajectory calculations on the Ar/Ru (0001) system failed to reproduce the experimental data. Especially the competition between energy transfer to the surface through (binary) collisions and energy uptake from the warm surface from phonons seems subtle.

II. Scattering experiments

A. Experimental set-up

The experiments were carried out in a UHV scattering chamber described in detail in a number of earlier studies.6 It consists of a main chamber with a base pressure of 1[thin space (1/6-em)]×[thin space (1/6-em)]10−10 mbar, which contains the sample, mounted on a 3-axis goniometer7 enabling the study of azimuthal dependences. To this chamber is attached a 3-stage supersonic molecular beam source with an 80 mm alumina (Al2O3) nozzle. A rotating disc chopper, positioned in the second stage, provides pulses of 0.5 to 50% duty cycle duration at up to 500 Hz. The translational energy of the Ar was varied between 0.1 and 2.5 eV by changing the seeding ratio of Ar in either H2 or He and heating the nozzle; this was done by electron bombardment (500 V) of a tungsten tube around the nozzle. For the H2-seeded beam the nozzle temperature was restricted to ∼1300 K, since a higher temperature would allow the H2 to reduce the Al2O3 nozzle.

Beam energies were determined by measuring the time-of-flight (TOF) of a short pulse (10 ms) of gas from the chopper to a differentially pumped rotatable quadrupole mass spectrometer (QMS) in the scattering chamber. The final energy of the scattered molecules was obtained by deconvolution of their TOF signals with the direct beam profiles, as described elsewhere.6,8 Angular resolved scattered beam intensities were measured using a 50∶50 modulated beam fitting the output of the multi-channel scaler (MCS) with a modified square wavefunction in order to obtain directly the background corrected signal (Signl): MCSi[thin space (1/6-em)]=[thin space (1/6-em)]Backgr[thin space (1/6-em)]+[thin space (1/6-em)](Signl[thin space (1/6-em)]−[thin space (1/6-em)]Backgr)/(e[(Δ−i)/τ][thin space (1/6-em)]×[thin space (1/6-em)]e−[(Δ+Topen−i)/τ]), with Topen the open time of the chopper. The quadrupole mass spectrometer used for these measurements (Extranuclear Labs.) is mounted on a doubly differentially pumped rotatable cover in order to provide angular resolution.

The Ru sample was aligned and polished to within 0.1° of the (0001) crystal face. It could be heated by electron bombardment (600 V, 80 mA) at up to 25 K s−1, regulated by a programmable controller (Eurotherm 900 EPC) and cooled to ∼100 K with liquid nitrogen. The sample temperature was measured with a type C thermocouple. This was calibrated against a type K thermocouple for temperatures below 273 K. Cleaning was performed in situ by repeated cycles of flashing in a background pressure of oxygen (2[thin space (1/6-em)]×[thin space (1/6-em)]10−8 mbar) to 1500 K. An oxygen free surface could be obtained by a single flash to 1600 K in ultra-high vacuum (UHV). Helium thermal energy atom scattering (TEAS) was found to be an extremely sensitive probe of the surface cleanliness and order. This proved to be particularly useful because the main contaminant (C) is difficult to detect in small concentrations by Auger electron spectroscopy (AES) due to overlap with the ruthenium peaks.9,10 Low energy electron diffraction is available for calibration of the azimuthal orientation of the crystal surface.

B. Angular distributions

Depending on the incidence energy and surface temperature, the angular distributions of argon scattered from the (0001)-face of ruthenium show scattering phenomena qualitatively similar to those observed for the Ar/W (100)-2H system by Schweizer et al.5 For the 140 K Ru surface, scattering the lowest energy beam (80 meV) revealed a diffraction peak positioned on top of a broad background of collision events in which phonons are excited (see Fig. 1). For this energy, the higher order diffraction peaks are expected at θspec[thin space (1/6-em)]±[thin space (1/6-em)]1.6° n (n[thin space (1/6-em)]=[thin space (1/6-em)]1, 2, 3, ...). This separation is smaller than the experimental resolution of ≈2° but might explain the repeatedly observed shoulders around the zero-order diffraction peak (inset of Fig. 1). A liquid-nitrogen cooled nozzle, as used by Schweizer et al.5 will produce a slower Ar beam with a sharper velocity distribution which will result in more pronounced diffraction peaks with larger angular separation. Upon increasing the beam energy the diffraction peak disappears. The broad background sharpens from a FWHM of about 22° at 0.08 eV to 15° at Ei[thin space (1/6-em)]=[thin space (1/6-em)]0.56 eV. At this energy the surface corrugation experienced at this surface temperature causes a double rainbow structure to develop which is absent for the comparable Ts[thin space (1/6-em)]=[thin space (1/6-em)]550 K data of Fig. 2, the origin of which will become clear in Section III. At even higher energies, 1.40 eV, a single peak with a FWHM of 8.5° is formed. Note the presence of a super specular shift of the distributions increasing the incoming collision energy, indicative of an increasing amount of normal momentum being transferred to the surface.
Argon reflectivity of the 140 K Ru (0001) surface at θi = 60°: Ei = 0.08 eV (■) shows a zero-order diffraction peak, Ei = 0.56 eV (•) shows a rainbow-like double structure and Ei = 1.40 eV (▲) shows a single peak. The vertical arrow indicates the specular scattering direction (θf = θi). The inset shows a zoom in on the specular diffraction region.
Fig. 1 Argon reflectivity of the 140 K Ru (0001) surface at θi[thin space (1/6-em)]=[thin space (1/6-em)]60°: Ei[thin space (1/6-em)]=[thin space (1/6-em)]0.08 eV (■) shows a zero-order diffraction peak, Ei[thin space (1/6-em)]=[thin space (1/6-em)]0.56 eV (•) shows a rainbow-like double structure and Ei[thin space (1/6-em)]=[thin space (1/6-em)]1.40 eV (▲) shows a single peak. The vertical arrow indicates the specular scattering direction (θf[thin space (1/6-em)]=[thin space (1/6-em)]θi). The inset shows a zoom in on the specular diffraction region.

Argon scattering from the Ts = 550 K Ru (0001) surface, θi = 50°, for three different incident energies Ei = 0.44, 1.05 and 1.56 eV. The solid lines (left panel) are drawn to guide the eye only. Dashed lines in the right panel represent the energy losses for binary collisions of Ar (m = 40 u) from various masses (M/u = 202, 505 and infinite). The solid line holds for parallel momentum conservation. While the angular distributions narrow and shift super-specular with increasing Ei , the energy distributions develop features which no longer resemble the binary collision or hard cube model.
Fig. 2 Argon scattering from the Ts[thin space (1/6-em)]=[thin space (1/6-em)]550 K Ru (0001) surface, θi[thin space (1/6-em)]=[thin space (1/6-em)]50°, for three different incident energies Ei[thin space (1/6-em)]=[thin space (1/6-em)]0.44, 1.05 and 1.56 eV. The solid lines (left panel) are drawn to guide the eye only. Dashed lines in the right panel represent the energy losses for binary collisions of Ar (m[thin space (1/6-em)]=[thin space (1/6-em)]40 u) from various masses (M/u[thin space (1/6-em)]=[thin space (1/6-em)]202, 505 and infinite). The solid line holds for parallel momentum conservation. While the angular distributions narrow and shift super-specular with increasing Ei[thin space (1/6-em)], the energy distributions develop features which no longer resemble the binary collision or hard cube model.

C. Time of flight distributions

The most surprising part of the data set consists of the final energy distributions obtained by TOF measurements of argon scattered from the Ru (0001) surface. This energy distribution (Fig. 2) shows a peculiar pattern for the highest incoming energy of 1.56 eV. A remarkable transition on scattering mechanisms is clearly observed for energies in the range 0.44[thin space (1/6-em)]≤[thin space (1/6-em)]Ei eV[thin space (1/6-em)]≤[thin space (1/6-em)]1.56. The lower incidence energy results in an energy distribution which can qualitatively be understood by combining the binary collision model for the sub-specular (θf[thin space (1/6-em)]<[thin space (1/6-em)]θi), and the parallel momentum conservation for super-specular scattering (θf[thin space (1/6-em)]>[thin space (1/6-em)]θi). Upon increasing the beam energy this simple trend no longer holds and other mechanisms seem to dominate energy transfer and uptake.

Sub-specular (θf[thin space (1/6-em)]=[thin space (1/6-em)]35°), nearly elastic collisions are observed for both the lowest and the highest energy, while the intermediate shows substantial energy loss. The broadness of thermal Ar TOF spectra caused severe problems with the analysis for low energies, and only spectra for Ei[thin space (1/6-em)]≥[thin space (1/6-em)]0.2 eV could be deconvoluted. The raw TOF data presented in Fig. 3 however clearly illustrates momentum gain of the Ar atoms from hot surface phonons. The bending down of the sub-specular scattering for the intermediate energy (Ei[thin space (1/6-em)]=[thin space (1/6-em)]1.05 eV) is probably due to relatively hard collisions with a turning point closer to the surface. This allows more momentum transfer to individual atoms instead of a heavier surface cluster, as is the case for softer super-specular scattering where generally the momentum transfer only takes place in the direction normal to the surface while leaving the parallel component conserved. These are common trends, but apparently do not hold for the higher energy particles of the 1.56 eV curve, where effective energy uptake from surface phonons seems to compensate for the expected momentum transfer. The super-specular scattering again shows remarkable deviations, while the low and intermediate energy curves follow the parallel momentum conservation curve nicely.


Raw TOF data showing the shorter flight time for low energy (≈0.08 eV) argon scattered off the Ru (0001) surface (θi = 40°, θf = 20°) at different temperatures (Ts).
Fig. 3 Raw TOF data showing the shorter flight time for low energy (≈0.08 eV) argon scattered off the Ru (0001) surface (θi[thin space (1/6-em)]=[thin space (1/6-em)]40°, θf[thin space (1/6-em)]=[thin space (1/6-em)]20°) at different temperatures (Ts).

When considering the coupling to phonons, the interaction time could be the crucial parameter. The influence of surface temperature at high energy is shown in Fig. 4. Surprisingly the lowest temperature curves Ts[thin space (1/6-em)]=[thin space (1/6-em)]140 K (H-covered surface) and 300 K follow the binary collision trend fairly well over the entire angular region. The resemblance over these two curves might be due to partial hydrogen coverage at Ts[thin space (1/6-em)]=[thin space (1/6-em)]300 K from the H2/Ar mixed beam. Above the hydrogen desorption temperature, the Ts[thin space (1/6-em)]=[thin space (1/6-em)]450, 550 and 850 K curves appear within the expected error bars.


Argon reflectivity of the Ru (0001) surface, θi = 40°, Ei = 2.2 eV for different surface temperatures (Ts). Vertical arrows indicate the specular scattering direction (θi = θf).
Fig. 4 Argon reflectivity of the Ru (0001) surface, θi[thin space (1/6-em)]=[thin space (1/6-em)]40°, Ei[thin space (1/6-em)]=[thin space (1/6-em)]2.2 eV for different surface temperatures (Ts). Vertical arrows indicate the specular scattering direction (θi[thin space (1/6-em)]=[thin space (1/6-em)]θf).

III. Comparison to the washboard model

As mentioned in the Introduction, the washboard model is a simple extension of the hard cube model which allows off-normal momentum transfer. Diffraction will not be observed since quantized energy transfer to surface phonons is not included. The appearance of the double peak structure in the 0.56 eV curve of Fig. 1 however can clearly be understood by the introduction of the surface corrugation, as can be observed in the top-right panel of Fig. 5. When focusing on the energy distribution measured for the highest beam energy (2.32 eV) presented in Fig. 6, quite surprisingly, almost quantitative correspondence of the washboard model to the experimental data is achieved, with very reasonable input parameters (αm[thin space (1/6-em)]=[thin space (1/6-em)]6° and mAr/Mcube[thin space (1/6-em)]=[thin space (1/6-em)]40/303). However this agreement is not accompanied by optimum correspondence in the angular distribution. We choose however to focus on the qualitative analysis of the unconventional energy distribution.
Variation of three input parameters of the washboard model, developed by Tully et al.:1,3 the maximum angle in the washboard angle in the washboard ripple αm (top panel), the cube mass Mcube (middle panel) and the surface temperature Ts (bottom panel). The increased effect of surface temperature on lower energy scattering is also shown in this panel (Ei = 0.5 eV, Ts = 10 K.) Fixed parameters are the well depth (W = 0.1 eV) and the incoming angle (θi = 40°).
Fig. 5 Variation of three input parameters of the washboard model, developed by Tully et al.:1,3 the maximum angle in the washboard angle in the washboard ripple αm (top panel), the cube mass Mcube (middle panel) and the surface temperature Ts (bottom panel). The increased effect of surface temperature on lower energy scattering is also shown in this panel (Ei[thin space (1/6-em)]=[thin space (1/6-em)]0.5 eV, Ts[thin space (1/6-em)]=[thin space (1/6-em)]10 K.) Fixed parameters are the well depth (W[thin space (1/6-em)]=[thin space (1/6-em)]0.1 eV) and the incoming angle (θi[thin space (1/6-em)]=[thin space (1/6-em)]40°).

Comparison of the washboard model with the actual data for 3 beam energies (at θi = 40°, Ts = 550 K). Dashed lines in the right panel represent the energy losses for binary collisions of Ar (m = 40 u) from various masses (M/u = 303 and infinite). Vertical arrows indicate the specular scattering direction (θi = θf). Optimum agreement is achieved for the highest beam energy of 2.32 eV. Lower incidence energies result in large deviations in the specular region of the angular distributions.
Fig. 6 Comparison of the washboard model with the actual data for 3 beam energies (at θi[thin space (1/6-em)]=[thin space (1/6-em)]40°, Ts[thin space (1/6-em)]=[thin space (1/6-em)]550 K). Dashed lines in the right panel represent the energy losses for binary collisions of Ar (m[thin space (1/6-em)]=[thin space (1/6-em)]40 u) from various masses (M/u[thin space (1/6-em)]=[thin space (1/6-em)]303 and infinite). Vertical arrows indicate the specular scattering direction (θi[thin space (1/6-em)]=[thin space (1/6-em)]θf). Optimum agreement is achieved for the highest beam energy of 2.32 eV. Lower incidence energies result in large deviations in the specular region of the angular distributions.

Fig. 5 shows the response of the output of the washboard model upon variation of the essential input parameters. In the specular region Ef/Ei follows the binary collision curve. Scattering to outgoing angles beyond the sub- and super specular rainbow maxima (θf,[thin space (1/6-em)]sub[thin space (1/6-em)]=[thin space (1/6-em)]35.8° and θf,[thin space (1/6-em)]sup[thin space (1/6-em)]=[thin space (1/6-em)]61.2°) is prohibited for the 0 K surface. Only specific thermal fluctuations of the washboard can result in these scattering angles (bottom row Fig. 5). Outgoing angles of θf[thin space (1/6-em)]<[thin space (1/6-em)]θf,[thin space (1/6-em)]sub can be achieved by scattering off a maximum backwards tilted rising cube. Similarly θf[thin space (1/6-em)]>[thin space (1/6-em)]θf,[thin space (1/6-em)]sup is possible when scattering off a maximum forward tilted dropping cube. The subsequent energy gain or loss with respect to the binary collision result is clearly reflected in the left column of Fig. 5. For sub-specular angles the final energy is determined by competing mechanisms. The balance between energy uptake from the surface phonons vs. the transfer of momentum to the surface due to binary collisions is largely determined by the velocity and mass of the surface cube. Furthermore, larger deflection angles, i.e. harder collisions, are generally concomitant with turning points to the trajectories closer to the surface, leading to interaction with less surface atoms simultaneously and thus relatively light cube masses. A dependence of the cube mass on the deflection angle is not invoked in the cube model which therefore overemphasizes the influence of the surface vibrations. Moreover, it must be noted that the temperature invoked in the washboard model makes the entire ripple vibrate as a whole. In reality the coupling between the surface atoms will allow thermal vibrations, causing the shape of the unit cell to be distorted. Also, differences in the Debye temperatures are not included.

IV. Classical trajectory calculations

A. Computational method

The computational code used to simulate the Ar/Ru (0001) system has been described in great detail elsewhere.2 In short the classical trajectory calculations consist of solving the classical molecular dynamics by integrating the Newtonian mechanical equations using the Verlet algorithm. The pair potential describing the forces between the nearest neighbours in the solid is of the following form: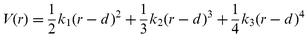
 
ugraphic, filename = b105514n-t1.gif(1)
 
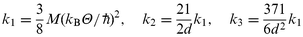ugraphic, filename = b105514n-t2.gif(2)
with the anharmonic force constants k2 and k3 determined from a Taylor expansion of a Lennard-Jones potential. The surface Debye temperature is accounted for by an additional set of force constants for all atoms connected to a surface atom according to the same eqns. (1) and (2). A finite surface temperature is introduced by initially imposing a Maxwell–Boltzmann velocity distribution on the crystal atoms in their equilibrium position. With evolving time, half of the kinetic energy is transferred to potential energy. The potential of the gas–solid interaction is a combined repulsive Born–Mayer pair potential and an attractive van der Waals-like z-dependent interaction:
 
ugraphic, filename = b105514n-t3.gif(3)
 
ugraphic, filename = b105514n-t4.gif(4)
With R, the position of the Ar atom and ri the position of each ith crystal atom, {C} and {S} denote the ensemble of crystal and surface atoms, respectively.

In the fitting the potential energy data, as calculated by standard LDA-techniques, to the form of eqn. (3), emphasis has been put on the agreement for the atop position. The resulting parameters are: A[thin space (1/6-em)]=[thin space (1/6-em)]120[thin space (1/6-em)]664 eV, α[thin space (1/6-em)]=[thin space (1/6-em)]3.80363 Å−1, B[thin space (1/6-em)]=[thin space (1/6-em)]2.520 eV Å−1, z0[thin space (1/6-em)]=[thin space (1/6-em)]2.514 Å and γ[thin space (1/6-em)]=[thin space (1/6-em)]0.0304 Å−4. The range of the attractive potential is set to be about 10 surface atoms (σ[thin space (1/6-em)]=[thin space (1/6-em)]0.149 Å−2).

B. Results of simulation

Running classical trajectory calculations for the best known set of input parameters (see Table 1) did not result in quantitative correspondence with the experimental data. As can be seen in Fig. 7(△), even qualitative washboard-like similarities are mostly absent. In order to gain insight into the mechanisms responsible for the malfunctioning of the simulation code, various input parameters have been tested. A more accurately calculated pair potential of the Ar/Ru pair potential appeared to have minor influence on the results. Increasing the bulk and surface Debye temperatures of ruthenium (415 and 216 K respectively) turned out to be more effective. As shown in Fig. 8 a trend similar to the washboard model develops when increasing both the Debye temperatures of the crystal by a factor of 1.5–2.0. The increased lattice stiffness invoked by the stronger links between the crystal atoms increases the effective surface mass, explaining the reduced average energy transfer in the collisions. Furthermore, double rainbow structures appear in the angular distributions due to the lesser thermal disordering of the crystal. This trend can also be observed when comparing the scattering data on the Ts[thin space (1/6-em)]=[thin space (1/6-em)]140 and 550 K surfaces shown in Fig. 1 and 2.
The output of the classical trajectory using the TACO code for 4 different sets of bulk and surface Debye temperatures (0.7, 1.0, 1.5 and 2.0 times the default Debye temperatures θbulk = 415 K and θsurf = 216 K), for a fixed surface temperature of Ts = 550 K compared to the experimental data (θi = 40°, Ei = 2.32 eV).
Fig. 7 The output of the classical trajectory using the TACO code for 4 different sets of bulk and surface Debye temperatures (0.7, 1.0, 1.5 and 2.0 times the default Debye temperatures θbulk[thin space (1/6-em)]=[thin space (1/6-em)]415 K and θsurf[thin space (1/6-em)]=[thin space (1/6-em)]216 K), for a fixed surface temperature of Ts[thin space (1/6-em)]=[thin space (1/6-em)]550 K compared to the experimental data (θi[thin space (1/6-em)]=[thin space (1/6-em)]40°, Ei[thin space (1/6-em)]=[thin space (1/6-em)]2.32 eV).

The effect of limiting the impact to the atop string vs. the entire unit cell for Ei = 2.32 eV scattering at θi = 40° and Ts = 550 K. Clearly the string impacts resemble the washboard results in the specular region (see Fig. 6 and 7), contrary to scattering from the whole unit cell.
Fig. 8 The effect of limiting the impact to the atop string vs. the entire unit cell for Ei[thin space (1/6-em)]=[thin space (1/6-em)]2.32 eV scattering at θi[thin space (1/6-em)]=[thin space (1/6-em)]40° and Ts[thin space (1/6-em)]=[thin space (1/6-em)]550 K. Clearly the string impacts resemble the washboard results in the specular region (see Fig. 6 and 7), contrary to scattering from the whole unit cell.
Table 1 Comparison of the main parameters depicting the interaction between argon and the Ru (0001) and the Pt (111) crystal faces
Parameter Ru (0001) Ref. Pt (111) Ref.
 
Mass/u 101   195  
Lattice structure HCP   FCC  
Nearest-neighbour distance/Å 2.669 12 2.77 2
Bulk Debye temperature/K 415 12 230 2
Surface Debye temperature/K 216 12 110 2
Argon physisorption well/meV 62 12 78 11

A significantly better correspondence to the data is obtained when limiting the impact parameters to a string over the atop sites, as shown in Fig. 8. In this way the scattering is mostly in-plane, excluding chattering between rows of surface atoms. This especially affects the behaviour of the specular region. The overlapping curves in the wings indicate that the more extreme sub- and super-specular angular regions are hardly reached by particles with impact parameters lying outside the atop string.

V. Discussion

Highest incoming energies yield the most surprising result: the washboard model reproduces the peculiar experimentally obtained energy distributions, while both Tully's trajectory calculations for the Ar/Pt (111) as well as ours for the Ar/Ru (0001) system failed to do so. Comparison of the experimental data, washboard model and classical trajectory calculations raises several questions. Could the washboard model, despite its simplicity, contain all the essential physics on energy transfer processes, or is the agreement more a coincidence? Though Tully showed the washboard model to work surprisingly well (almost quantitatively) for various corrugated faces of platinum, the model is meant only to elucidate simple trends in gas–surface scattering. When comparing the washboard model to the calculations for the relatively smooth Pt (111) system, Tully observed effects in the energy distribution that did not seem to have any physical meaning1 (similar to Fig. 6). Much to our surprise, the Ar/Ru (0001) measurements show exactly those unexpected washboard features that seemed erroneous for the Ar/Pt (111) system.

Direct comparison of the trajectory calculations with the washboard is facilitated by limiting the impact parameters to the atop string; thus performing pseudo-2-dimensional calculations. A sinusoidal approximation of the washboard ripple seems valid in this situation. The results, depicted in Fig. 8, clearly show different trends in the specular region for the 2 and 3-dimensional simulations, probably caused by a substantial amount of multiple collisions and scattering from the heavy hollow sites. Surface phonons are treated fundamentally differently by the washboard model and our simulation code TACO. The washboard oscillates as a whole maintaining the sinusoid shape, whereas the more realistic trajectory calculations include thermal distortion of the lattice. Furthermore, the Debye temperature is not accounted for in the washboard model; a conventional Maxwellian distribution of vibration frequencies and amplitudes is assumed. Other possible sources of discrepancies are the hard collisions and the constant cube mass for all scattering angles (Section 3). Especially for the larger scattering angles (sub-specular scattering), the closer approach of the surface causes the argon atom to interact with less surface atoms simultaneously, i.e. a lower cube mass. Note that extending the washboard model for such details could improve quantitative agreement with experiments but at the expense of the accessibility for intuition. Deducing the crucial problem in the simulation method could lead us to the difference between the Ar/Ru (0001) and the Ar/ Pt (111) systems. The observed effective tuning of the Debye temperature suggests that the main reason why our trajectory simulations fail to reproduce the experiment lies in the implementation of the interactions in the solid state. The oscillation amplitude and frequency of (real) surface atoms is likely to result in an interaction-time-dependent coupling to the surface phonons. In this way changes made in the incidence energy will affect the balance between energy loss or uptake.

This raises the question: why does Ru (0001) scatter argon in a qualitatively different way than Pt (111), behaving so much like a washboard? In order to facilitate comparison, the most important parameters describing the two crystals are presented in Table 1. Both the atomic masses and the Debye temperatures differ by a factor of two. Our trajectory calculations showed the effect of the Debye temperatures on the energy distributions (Fig. 7) which could account for the difference in the observed sub-specular energy distributions.

VI. Conclusions

As simple as scattering of a noble gas atom from a single crystalline surface might seem, we observe multiple scattering mechanisms for Ar/Ru (0001). Zero-order diffraction at the lowest incidence energy, rainbow scattering at intermediate and washboard-like energy transfers for the highest attainable energy. In particular, these peculiar energy distributions, qualitatively different from the Ar/Pt (111)-system, are nicely reproduced by the washboard model. While not too much significance should be attached to the quantitative aspect of the output, this simple model does prove to be a powerful tool in the straightforward analysis of the competing mechanisms behind the energy exchange of gases and surfaces.

Comparison of pseudo-2-d and full 3-d classical trajectory simulations show the 1-d washboard ripple to be clearly insufficient to describe the Ru (0001) surface corrugation. Satisfactory correspondence to the experimentally determined energy distributions was however not obtained, most likely due to shortcomings in the representation of the phonon bath in our simulation code (TACO).

Acknowledgements

The authors would like to thank Francois Giskes, Richard Schaafsma and Hans Alberde for their extensive technical support, Rene Koper for preparing the ruthenium crystal, and for his critical reading of the manuscript. This work is part of the research program of the “Stichting voor Fundamenteel Onderzoek der Materie (FOM)”, which is financially supported by the “Nederlandse Organisatie voor Wetenschappelijk Onderzoek (N.W.O.)”.

References

  1. J. C. Tully, J. Chem. Phys., 1990, 92, 680 CrossRef CAS.
  2. R. J. W. E. Lahaye, PhD Thesis, Vrije University of Amsterdam, 1995..
  3. G.-Q. Xu, S. L. Bernased and J. C. Tully, J. Chem. Phys., 1988, 88, 3376 CrossRef CAS.
  4. E. K. Schweizer and C. T. Rettner, Phys. Rev. Lett., 1989, 62, 3085 CrossRef CAS.
  5. E. K. Schweizer, C. T. Rettner and S. Holloway, Surf. Sci., 1991, 249, 335 CrossRef CAS.
  6. A. Raukema, R. J. Dirksen and A. W. Kleyn, J. Chem. Phys., 1995, 103, 6217 CrossRef CAS.
  7. A. Raukema, A. P. de Jongh, H. P. Alberda, R. Boddenberf, E. de Haas, A. W. Kleyn, H. Neerings, R. Schaafsma and H. Veerman, Meas. Sci. Technol., 1997, 8, 253 CrossRef CAS.
  8. A. Raukema, PhD Thesis, University of Amsterdam, 1995..
  9. J. T. Grant and T. W. Haas, Surf. Sci., 1970, 21, 76 CrossRef CAS.
  10. P. D. Reed, C. M. Comrie and R. M. Lambert, Surf. Sci., 1976, 59, 33 CrossRef CAS.
  11. Martin Head-Gordon, C. T. Rettner, B. C. Mullins, D. J. Auerbach and J. C. Tully, J. Chem. Phys., 1991, 94, 1516 CrossRef CAS.
  12. Martin Head-Gordon, H. Schlichtling, D. Menzel and J. C. Tully, J. Chem. Phys., 1991, 95, 9266 CrossRef CAS.

Footnote

† Presented at the Stereodynamics 2000 Conference on Dynamics and Stereodynamics of Chemical Reactions, El Escorial, Madrid, December 1–5, 2000.
This journal is © the Owner Societies 2002
Click here to see how this site uses Cookies. View our privacy policy here.