On the mechanism of skeletal rearrangements in the acid catalysed acetylation of isodrin 

Abstract

1,8,9,10,11,11-Hexachlorotetracyclo[6.2.1.1^3,6.0^2,7]dodec-9-en-4-exo-yl acetate, tetracyclic1; 1,2,2,3,10,11-hexachloropentacyclo[5.4.1.0^3,10.0^4,12.0^5,9]dodecan-8-exo-yl acetate, half-cage2; 1,2,2,3,10,11-hexachloropentacyclo[5.4.1.0^3,10.0^4,12.0^5,9]dodecan-8-endo-yl acetate, half-cage3 and 1,9,10,11,11,12-hexachlorohexacyclo[5.4.1.0^2,6.0^3,10.0^4,8.0^9,12]dodecane, birdcage4 were obtained from acid catalysed acetylation of isodrin. It was observed that the intramolecular rearrangement control is highly dependent on reaction time. The equilibria involved in these rearrangements were determined by gas chromatography. Semiempirical calculations at the PM3-MNDO, AM1 and MNDO levels have been performed to obtain the optimized geometry of the reagent, products, intermediates and transition states for the rearrangement mechanism. The results of the calculations are in good agreement with the experimental data. On the basis of the theoretical and experimental investigations we propose a revised mechanism which involves a new transition state and a new non-classical reaction intermediate.

---

Introduction

The synthesis of hexachlorinated polycyclic systems such as the insecticides isodrin, endrin and their derivatives was reported in the early 1950s.¹ Soloway et al.² verified that chlorinated compounds with the 1,4∶5,8-dimethanonaphthalene nucleus undergo unusual skeletal rearrangements in their reactions. Winstein et al.³ observed Wagner–Meerwein rearrangements in solvolysis reactions of polycyclic derivatives by mechanisms that involve the formation of non-classical ions. These pioneering studies established the basis for numerous works involving several aspects of modern chemistry, such as investigation of carbocations and intramolecular rearrangements,^4–8 steric compression, long-range and short-range interactions ^9–13 as well as NMR spectroscopy.^14–17 Recently our group has demonstrated that the pentacyclo[5.4.1.0^3,10.0^4,12.0^5,9]dodecane derivatives, known as half-cage compounds, are interesting models for the development of methodologies for enantiomeric analysis in NMR spectroscopy using a mixture of chiral and achiral shift reagents,^18,19 and for the development of an approach to determine the optimal position of a lanthanide ion in complexes formed by shift reagents with a substrate using the pseudocontact model ²⁰ and the kinetic resolution of very hindered secondary alcohol that uses lipase from Candida rugosa.²¹

Serious limitations in the studies of these strained systems are the low yields and the difficult purification of compounds. In general, these structures are obtained by complex rearrangements which occur when isodrin is treated with acid.²² In particular, the reaction of isodrin with acetic acid containing sulfuric acid represents a good example for observation of these rearrangements that produce a mixture of four products (Scheme 1): tetracyclic 1, half-cage 2, half-cage 3 and birdcage 4. However, in spite of the various efforts of mechanistic investigations of the solvolysis of the methanesulfonate derivatives,^22–25 most details on the pathway that determines how half-cages 2 and 3 are formed by rearrangement of isodrin are still to be clarified.

Scheme 1

In order to clarify the behavior of isodrin and its products in acidic media, and to establish parameters describing the dependences between reagents and products, we decided to reinvestigate the mechanism of this reaction. In this paper, we describe the empirical methods used to optimize the yield of half-cage 3 and to minimize the yield of birdcage 4. The evolution of this reaction in relation to temperature and time is used to monitor their effects on the control of formation of the products. Computational analyses of reagent, products, intermediates and transition states involved in this mechanism by semiempirical methods PM3-MNDO, AM1, and MNDO have been undertaken in order to confirm experimental findings. From these data we propose a revised mechanism of these complex rearrangements which involves new transition states and non-classical reaction intermediates.

Results and discussion

Empirical optimization methods

Complete factorial.²⁶. This method required four experiments for two variables and permits an estimate of the effect that each one exerts on the formation of each reaction product. The areas of interest for the reaction are the variable temperature (x₁) (105 and 125 °C) and the variable time (x₂) (10 and 25 min). These conditions were defined because it was observed that for temperatures below 105 °C the reaction does not occur. Also, the variation in products is more significant between 10–25 min. The initial amount of isodrin and volumes of acetic acid and sulfuric acid were held constant. All the data from this method are presented in Table 1.

Table 1 Results from 2² factorial design

	Matrix		Variables		Response factors (% products)
Exper.	x 1	x 2	T/°C	t/min	1	2	3	4
1	−	−	105	10	18.0	27.5	28.0	18.0
2	+	−	125	10	7.7	47.0	19.7	18.0
3	−	+	105	25	8.5	40.0	16.6	20.0
4	+	+	125	25	0.0	53.0	7.5	23.0

---

The response factors obtained for each compound are shown in Table 1. The data indicate that the optimal reaction conditions for getting tetracyclic 1 and half-cage 3 are short times and low temperatures, and for obtaining half-cage 2 and birdcage 4, it is necessary to use long times and high temperatures. Here, it is important to point out the strong control that temperature has over the formation of half-cage 2 and that time has over the formation of half-cage 3 and birdcage 4 (Table 2).

Table 2 Estimated effects from factorial design

Variables	Tetracyclic 1	Half-cage 2	Half-cage 3	Birdcage 4
Temperature	−4.7	+8.1	−4.3	+1.5
Time	−4.3	+4.6	−5.9	+3.5

---

Modified simplex method.^27–29. In this methodology the goal was to optimize half-cage 3 and to minimize birdcage 4. The conditions of interest for both compounds were 105–125 °C and 0–30 min. The initial simplex (represented by A, B and C points) was chosen randomly within the dominion. The evaluation of the responses (% yields) pointed to the direction in which to move the simplex. Nine experiments were carried out for both compounds and they are described in Table 3.

Table 3 Results and evolution of the modified simplex method

	Half-cage 3				Birdcage 4
Exper.	T/°C	t/min	Yield (%)	Exper.	T/°C	t/min	Yield (%)
A	125	10	19.7	A′	125	15	24.2
B	115	19	18.9	B′	115	30	32.7
C	115	10	31.4	C′	115	15	14.8
D	125	1	33.0	D′	125	0	50.0
E	115	1	23.0	E′	117	22	15.0
F	117	3	37.0	F′	107	22	14.0
G	118	6	31.0	G′	105	15	16.0
H	121	2	38.6	H′	114	21	24.0
I	116	6	32.0	I′	115	10	11.2

---

The evolution of the simplex for half-cage 3 contains a sequence of two reflections, three contractions and one expansion; on the other hand, the evolution of the simplex of birdcage 4 contains a sequence of one reflection, one contraction, two reflections, one contraction and one expansion. An unexpected result was obtained by the reflection of the points A′, B′ and C′ to get the point D′ of the birdcage 4 simplex (t = 0). As it is impossible to have chemical reactions in zero time, it is necessary to provoke the back of the simplex to the dominion of interest, and this is only possible by the introduction of a bad response. With several points for both compounds, it was possible to obtain the reaction surfaces ³⁰ represented in Figs. 1 and 2 respectively.

Fig. 1 Reaction surface for minimization of birdcage 4 by the modified simplex method.

Fig. 2 Reaction surface for optimization of half-cage 3 by the modified simplex method.

In Fig. 1, it is possible to observe that the maximum of the birdcage 4 falls outside the dominion of interest and the parameter time has a strong influence on its formation. Similarly, the parameter time for half-cage 3 (Fig. 2) is more important than the temperature, in accordance with the results obtained by the complete factorial procedure. Perhaps the most important result of this study was to verify that the region of the maximum for half-cage 3 does not coincide with the region of the minimum for birdcage 4, and, consequently, it is impossible to separate half-cage 3 from birdcage 4 using only the variables of temperature and time.

In fact, all experiments showed the formation of the four reaction products in different proportions. These observations suggest that the mechanism for this reaction is sensitive to variations of time and temperature.

Evolution reaction curves

From three fixed temperatures (105, 115 and 125 °C), three evolution reaction curves (Figs. 3a, 3b, and 3c) were obtained. The reaction conditions were the same as in the empirical optimization procedures. At each time interval, samples were taken that, by means of gas chromatography, gave the respective proportions of reagents and products.

Fig. 3 Reaction evolution curves: a) reaction at 105 °C; b) reaction at 115 °C; c) reaction at 125 °C.

The three curves presented the same overall behavior. This observation shows that the effect of temperature is to increase significantly the isodrin disappearance and the product formation rate. However, their relative proportions remained constant. Consequently, the temperature does not have an important influence on the pathway of reaction. On the other hand, the reaction curves show that the control of these rearrangements is determined by time.

The effect of time exhibits two intervals with different behavior. At short times, with a significant amount of isodrin in the reaction medium, the concentrations of the products increase at different rates. An interesting aspect in this interval is that the half-cage 3 was formed faster than the other compounds, followed by tetracyclic 1, half-cage 2 and birdcage 4. At longer times, an intramolecular rearrangement promotes the conversion of the tetracyclic 1 and half-cage 3 into half-cage 2 and birdcage 4.

In order to elucidate the real pathway for these rearrangements, the isolated compounds (1, 2, 3, and 4) were submitted to the same reaction conditions as for isodrin at a temperature of 125 °C (Scheme 2). The methodology to obtain pure tetracyclic 1, half-cage 2, half-cage 3, and birdcage 4 from isodrin was recently reported by our group.²¹ From these data, it is possible to observe the rearrangements of tetracyclic 1 and half-cage 2 and 3 to other products (Figs. 4a, 4b, and 4c), but for birdcage 4, after two hours under the same reaction conditions, no rearrangement was observed.

Scheme 2

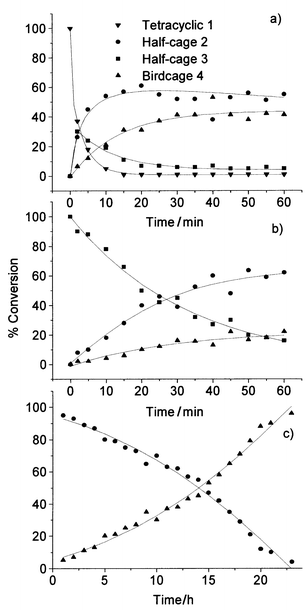Fig. 4 Evolution of the reaction curves at 125 °C for: a) tetracyclic 1; b) half-cage 3; c) half-cage 2.

The reaction of tetracyclic 1 (Fig. 4a) yielded half-cage 2, half-cage 3 and birdcage 4 with a similar profile to that of the isodrin reaction (Fig. 3c), although the formation rate of half-cage 2 is practically the same as that of half-cage 3. The reaction of half-cage 3 (Fig. 4b) produced half-cage 2 and birdcage 4, and the reaction of half-cage 2 gave only the birdcage 4 (Fig. 4c) with a very low rate of conversion.

Computational analysis

In order to determine the pathway involved in the rearrangements, we propose computational analysis for comparison with experimental data. Because ab initio studies of these structures are very difficult due to the large number of electrons, PM3-MNDO, AM1, and MNDO semiempirical methods have been used with the UNICHEM 4.1-MNDO94 program ³¹ for the optimized geometry of the reagents, products, intermediates, and transition states. Combined with experimental data, it is thus possible to propose a mechanism for the observed rearrangements (Scheme 3).

Scheme 3

The results for isodrin show that the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) calculated by PM3-MNDO, AM1, and MNDO possess a similar symmetry to the molecular orbital diagram of the cyclobutane dication obtained by ab initio STO-3G theory.^32,33 Molecular geometries converged rapidly due to the high rigidity of the carbon skeleton. Only transition states with a single imaginary frequency in the vibrational analysis were considered in the possible pathway (Table 4).

Table 4 Enthalpies of formation (ΔH_f /kcal mol⁻¹) and imaginary frequencies (IF/cm⁻¹) calculated by PM3-MNDO, AM1, and MNDO semiempirical methods

	PM3-MNDO		AM1		MNDO
Structure	ΔHf	IF	ΔHf	IF	ΔHf	IF
Transition state 6	254.19	−1099.30	261.35	−1072.41	291.96	−1152.60
Transition state 5	245.55	−129.80	273.54	−903.27	317.51	−1160.65
Intermediate 8	224.56		237.58		267.56
Intermediate 9	224.52		235.44		263.43
Intermediate 7	222.43		249.89		284.81
Isodrin	47.28		57.05		65.87
Birdcage 4	−1.50		14.37		12.96
Tetracyclic 1	−66.79		−55.83		−33.06
Half-cage 3	−72.73		−52.84		−34.28
Half-cage 2	−76.86		−58.45		−33.39

---

Table 4 lists the enthalpies of formation for all the structures and imaginary frequencies of the transition states. It is possible to observe that the enthalpy of formation obtained by PM3-MNDO is smaller than those obtained by the AM1 and MNDO methods, respectively, for the majority of the structures. Only for birdcage 4 is there an inversion between the AM1 and MNDO methods.

The computational data exhibit two possible transition states 5 and 6 for the protonation of isodrin (Fig. 5). The formation of the transition state 6 is not surprising, but special attention is given to transition state 5 and its geometry. For the formation of 5, the LUMO of the proton is mixed with the HOMO of the double-bond system of isodrin,^24,34,35 and a similar structure was postulated by Winstein and de Vries ³ in the early 1960s as an intermediate in the formation of tetracyclic 1 and half-cage 2 from endo-exo tetracyclo[6.2.1.3^3,6.0^2,7]dodec-9-en-4-exo-p-bromobenzenesulfonate.

Fig. 5 Optimized geometries of the transition states calculated by the PM3-MNDO method.

The difference in enthalpy of formation between transition states 5 and 6 is 8.64 kcal mol⁻¹ for PM3-MNDO, −12.19 kcal mol⁻¹ for AM1, and −25.55 kcal mol⁻¹ for MNDO (Table 4). These differences suggest that both transition states could be concomitantly formed. On the other hand, when the geometries of the intermediates from both transition states were calculated, the transition state 6 converged to intermediate 8 and the transition state 5 also converged to intermediate 8, but, predominantly, to intermediate 7. The stability of cation 7 might be explained by the capacity of the chlorine atom to accommodate the positive charge by back-donation (p–p interaction) of the nonbonded electron pairs involving several resonance strutures.^36,37 On the other hand the 8 is stabilized by the pair of electrons delocalized over C4, C9, and C10.

The rearrangement of half-cage 2 and 3 to birdcage 4 involves the elimination of acetic acid to give the cationic intermediate 9 that, by elimination of a proton, induces the cyclization. Support for this pathway can be obtained from the interatomic nonbonded distances between C4 and C10 that are involved in the cyclization. It becomes evident from the data summarized in Table 5, that the short distance between C4 and C10 in structure 9 causes a steric compression effect, which results in an increase of the strain in the pentacyclic carbon skeleton. This effect can be observed in the decreasing C4–C10 distance in relation to half-cages 2 and 3, and intermediate 9. In fact, the mechanism of cyclization for the formation of birdcage 4 follows a reaction coordinate with the proton receding from the half-cage cation 9 at the same time as C4 and C10 become closer and form the bond.

Table 5 Comparison of the nonbonded distances between the carbon atoms involved in the cyclization

Structures	Nonbonded distances between C4 and C10/Å
Half-cage 3	2.80
Half-cage 2	2.71
Cation 9	2.29
Birdcage 4	1.55

---

Conclusions

Some aspects of the results reported here are new. Firstly, our results show that the calculations are in good agreement with the experimental data with a revised mechanism suggesting, in contrast to the literature,²² that the protonation of isodrin occurs by two pathways characterized by transition states 6 and 5. The second path represents a new kind of protonation in a double-bond system like isodrin, with the intermediate 7 being responsible for the formation of the pentacyclic system. On the other hand, the experimental data confirm all of the steps for the formation of the products. Another aspect noted in this study is that the rearrangements observed depend significantly on reaction time and that temperature only influences the reaction rate.

Experimental

Melting points were measured on an Electrothermal IA 9100 digital Melting Point apparatus. NMR spectra were recorded on a Varian VXR-200 spectrometer at a magnetic field of 4.7 T and a temperature of 22 °C. Chemical shifts are expressed in δ (ppm) relative to TMS as an internal standard. Elemental analysis was recorded on a Perkin-Elmer 2400 CHN Elemental Analyzer apparatus. Products were analyzed by GC using capillary columns (25 m × 0.2 mm (id) × 0.11 μm) packed with SE-30 and a Varian Model star 3400 CX equipped with FID.

Acetylation of isodrin

Concentrated sulfuric acid (1 mL) was added to a solution of isodrin (3.0 g, 8.2 mmol) in acetic acid (12 mL) at a temperature of 125 °C under magnetic stirring. After 5 minutes, the system was cooled down and neutralized with a 10% NaHCO₃ solution. A precipitate was formed and separated. An additional extraction with chloroform was undertaken. The extract was combined with the precipitate. This solution was dried with MgSO₄, and after solvent evaporation from the filtrates, a white solid was obtained as a mixture of four compounds. These products were chromatographed on a silica gel column (hexane–ethyl acetate: 0 to 20%). Tetracyclic 1, birdcage 4 and a mixture of the half-cages 2 and 3 were obtained. A small amount of pure half-cage 3 could be separated manually from its half-cage 2 isomer, since on slow crystallization from chloroform 2 forms thin needles, while 3 forms fine platelets.³⁸ Tetracyclic 1: mp 195–196 °C (lit.¹² 194–195 °C). FTIR (film, CHCl₃) ν/cm⁻¹ 1725 (C[double bond, length half m-dash]O). ¹H NMR (200 MHz, CDCl₃) δ 1.9 (s, 3H, methyl), 4.8 (d, 1H, H α-O). ¹³C NMR (50 MHz, CDCl₃) δ 21.1 (CH₃), 34.0 (CH), 37.9 (CH), 41.1 (CH₂), 44.0 (CH), 52.9 (CH), 53.6 (CH), 72.0 (CH), 79.3 (C), 79.9 (C), 109.0 (C), 132.0 (C), 132.2 (C), 179.0 (C[double bond, length half m-dash]O). Half-cage 2: mp 193–194 °C (lit.²⁰ 194–195 °C). FTIR (film, CHCl₃) ν/cm⁻¹ 1735 (C[double bond, length half m-dash]O). ¹H NMR (200 MHz, CDCl₃) δ 2.1 (s, 3H, methyl), 5.5 (s, 1H, H α-Cl), 5.8 (s, 1H, H α-O). ¹³C NMR (50 MHz, CDCl₃) δ 21.1 (CH₃), 36.5 (CH₂), 41.6 (CH), 43.4 (CH), 55.6 (CH), 58.8 (CH), 60.0 (CH), 64.7 (CH), 74.0 (C), 76.4 (CH), 79.6 (C), 84.8 (C), 99.5 (C), 169.8 (C[double bond, length half m-dash]O). Half-cage 3: mp 153–154 °C. FTIR (KBr) ν/cm⁻¹ 1731 (C[double bond, length half m-dash]O). ¹H NMR (200 MHz, CDCl₃) δ 2.19 (s, 3H, CH₃), 4.92 (d, J = 6.05 Hz, 1H, H α-OAc), 6.57 (s, 1H, H α-Cl). ¹³C NMR (50 MHz, CDCl₃) δ 21.0 (CH₃), 37.4 (CH₂), 42.5 (CH), 43.1 (CH), 54.8 (CH), 56.1 (CH), 58.6 (CH), 64.8 (CH), 72.4 (C), 79.5 (CH), 80.6 (C), 83.4 (C), 99.0 (C), 169.4 (C[double bond, length half m-dash]O). Anal. calcd: C, 39.53; H, 2.82. Found: C, 39.77; H, 2.79%. Birdcage 4: mp 290 °C (lit.² 287–289 °C). ¹³C NMR (50 MHz, CDCl₃) δ 39.8 (CH₂), 43.4 (2CH), 54.4 (2CH), 58.4 (2CH), 78.2 (2C), 83.5 (2C), 97.5 (C).

General procedures for obtaining the points of the factorial, simplex and evolution curves for the reaction

Concentrated sulfuric acid (1 mL) was added to a solution of isodrin (3.0 g, 8.2 mmol) (or tetracyclic 1, half-cages 2 and 3, and birdcage 4) and acetic acid (12 mL) at a temperature of 105, 115 or 125 °C under magnetic stirring. Small samples were taken for each temperature at the appropriate intervals of time and neutralized with a 10% NaHCO₃ solution after extraction with chloroform. The samples of the isodrin, tetracyclic 1, half-cages 2 and 3, and birdcage 4 were analyzed by gas chromatography using the conditions: det. temp. = 300 °C; inj. temp. = 250 °C; flow = 20 psi; isotherm of 200 °C (5 min), slope of 10 °C min⁻¹ to 300 °C, isotherm 300 °C (5 min). Under these conditions the retention times are 3.28 min for isodrin, 6.10 min for tetracyclic 1, 9.06 min for half-cage 2, 8.39 min for half-cage 3 and 4.59 min for birdcage 4.

Molecular orbital calculations

The calculations by the MNDO-PM3, AM1, and MNDO semiempirical methods were performed using the UNICHEM 4.1-MNDO94 program ³¹ package on a GRAY-YMP computer system.

Acknowledgements

The authors are grateful for financial support from Conselho Nacional de Pesquisa Científica e Tecnologica (CNPq), Coordenação de Aperfeiçoamento de Pessoal de Ensino Superior (CAPES) and Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul (FAPERGS). The Centro Nacional de Supercomputação (CESUP) is acknowledged for CPU time on the GRAY-YMP computer system.

References

1. R. E. Lidov , US Patent 2717851, 1955;; H. Bluestone , US Patent 2676132, 1954..
2. S. B. Soloway, A. M. Damiana, J. W. Sims, H. Bluestone and R. E. Lidov, J. Am. Chem. Soc., 1960, 82, 5377.
3. L. de Vries and S. Winstein, J. Am. Chem. Soc., 1960, 82, 5363.
4. T. Svensson and S. Winstein, J. Am. Chem. Soc., 1972, 94, 2336.
5. R. K. Howe, P. Carter and S. Winstein, J. Org. Chem., 1972, 37, 1473.
6. R. K. Howe and S. Winstein, J. Org. Chem., 1973, 38, 2797.
7. K. A. Mead, K. Mackenzie and P. Woodward, J. Chem. Soc., Perkin Trans. 2, 1982, 571.
8. M. N. Paddon-Row, J. Chem. Soc., Perkin Trans. 2, 1985, 257.
9. P. Carter and S. Winstein, J. Am. Chem. Soc., 1972, 94, 2171.
10. D. Lenoir and R. M. Frank, Chem. Ber., 1981, 114, 3336.
11. O. Ermer, S. A. Mason, F. A. L. Anet and S. S. Miura, J. Am. Chem. Soc., 1985, 107, 2330.
12. T. A. Robbins, V. V. Toan, J. W. Givens III and D. A. Lightner, J. Am. Chem. Soc., 1992, 114, 10799.
13. K. D. Jordan and M. N. Paddon-Row, Chem. Rev., 1992, 92, 395.
14. P. R. Seidl, K. Z. Leal, V. E. U. Costa and M. E. S. Mollmann, Magn. Reson. Chem., 1993, 31, 241.
15. P. R. Seidl, K. Z. Leal, V. E. U. Costa and N. D. Poli, Magn. Reson. Chem., 1990, 28, 869.
16. P. R. Seidl, K. Z. Leal, V. E. U. Costa and M. E. S. Mollmann, Magn. Reson. Chem., 1998, 36, 261.
17. V. E. U. Costa, J. Alifantes, M. Axt, M. E. S. Mollmann and P. R. Seidl, J. Braz. Chem. Soc., 1999, 10, 341.
18. V. E. U. Costa and M. Axt, Magn. Reson. Chem., 1996, 34, 929.
19. M. Axt, J. Alifantes and V. E. U. Costa, J. Chem. Soc., Perkin Trans. 2, 1999, 2783.
20. P. F. B. Gonçalves, M. Axt, V. E. U. Costa and P. R. Livotto, Comput. Chem., 1998, 22, 399.
21. V. E. U. Costa, J. Alifantes and J. E. D. Martins, Tetrahedron: Asymmetry, 1998, 9, 2579.
22. C. W. Bird, R. C. Cookson and E. Crundwell, J. Chem. Soc., 1961, 4809.
23. E. Osawa, K. Aigami and Y. Inamoto, Tetrahedron, 1978, 34, 509.
24. K. B. Astin, A. V. Fletcher, K. Mackenzie, A. S. Miller, N. M. Ratcliffe, A. A. Frew and K. W. Muir, J. Chem. Soc., Perkin Trans. 2, 1982, 111.
25. C. Y. A. Yeung, C. W. Bird, S. C. Nyburg and N. H. Rama, Tetrahedron, 1998, 54, 5983.
26. G. E. P. Box , S. J. Hunter and W. G. Gordon , Statistics for Experimenters, John Wiley, New York, 1978..
27. S. N. Deming and S. L. Morgan, Anal. Chem., 1973, 45, 278a.
28. G. L. Ritter, S. R. Lowry, C. L. Wilkins and T. L. Isenhour, Anal. Chem., 1975, 47, 1952.
29. C. L. Shavers, M. L. Persons and S. N. Deming, J. Chem. Educ., 1979, 56, 307.
30. StatSoft, Inc. (1997) Statistica for Windows [Computer Program Manual], Tulsa, OK: StatSoft, Inc. Licensed by Professor Ricardo Baumhardt Neto..
31. UNICHEM 4.1, Oxford Molecular Ltd., Beaverton, USA, 1996. W. Thiel , MNDO94 Program, Organisch-Chemisches Institut, Universität Zürich, Zürich, Switzerland, 1994..
32. G. K. S. Prakash, V. V. Krishnamurthy, R. Herges, R. Bau, H. Yuan, G. A. Olah, W.-D. Fessner and H. Prinzbach, J. Am. Chem. Soc., 1988, 110, 7764.
33. J. S. Binkler, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939; M. S. Gordon, J. S. Binkler, J. A. Pople, W. J. Pietro and W. Hehre, J. Am. Chem. Soc., 1982, 104, 2797; J. S. Binkler, R. A. Whiteside, R. Krishnan, R. Seeger, D. J. DeFrees, H. R. Schlegel, S. Topiol, L. R. Kahn and J. A. Pople, QCPE Bull., 1981, 13, 406; P. N. Van Kamper, G. F. Smiths, F. A. M. De Leeuw and C. Altona, QCPE Bull., 1982, 14, 437.
34. S. Inagaki, H. Fujimoto and K. Fukui, J. Am. Chem. Soc., 1976, 98, 4693.
35. S. Inagaki, H. Fujimoto and K. Fukui, J. Am. Chem. Soc., 1975, 97, 4054.
36. G. A. Olah, L. Heiliger and G. K. S. Prakash, J. Am. Chem. Soc., 1989, 111, 8020.
37. G. A. Olah, G. Rasul, L. Heiliger and G. K. S. Prakash, J. Am. Chem. Soc., 1996, 118, 3580.
38. V. E. U. Costa, J. Alifantes, Y. P. Mascarenhas, C. H. T. de Paula e Silva and P. R. Seidl, J. Mol. Struct., 2000, 519, 37.

---

Footnote

† IUPAC name for isodrin is 1,8,9,10,11,11-hexachlorotetracyclo[6.2.1.1^3,6.0^2,7]dodeca-4,9-diene.

---