Partial molar volume study of the complexes of calix[4]naphthalenes with [60]fullerene in different solvents

Abstract

Calix[4]naphthalenes are a class of cavitands or container molecules that possess deeper cavities than those of analogous calix[4]arenes. Earlier studies of the complexation of [60]fullerene (C₆₀) with the C₄-symmetrical endo-calix[4]naphthalene (1) and its tert-butyl-substituted derivative (2) show that they form supramolecular 1∶1 complexes with C₆₀ in benzene, toluene or CS₂ solution with relatively high association equilibrium constants (K_assoc). Reported herein are densitometer-derived standard partial molar volume changes for the complexation, in these respective solvents, of C₆₀ and the calix[4]naphthalenes 1 and 2. In the case of the C₆₀⊂2 complexes, the results are consistent with a solvophobic effect postulated previously. The results obtained for the C₆₀⊂1 complexes however suggest that in addition to a solvophobic effect, other factors may be operating.

---

Introduction

Solution volume studies of the inclusion complex formed between [60]fullerene (C₆₀) and p-benzylcalix[5]arene were reported in 1997 by Isaacs et al.¹ These authors measured the changes in partial molar volumes (Δ_rV̄) upon complexation using high-precision densitometry. This technique was used earlier by Ruelle et al.² to measure the standard partial molar volumes of C₆₀ itself in different solvents. Their densitometric analyses were based upon Liron and Cohen’s method ^3,4 for determining limiting partial molar volumes of various solutes at infinite dilutions. The inclusion properties of container molecules (cavitands) with guest molecules in general is a subject of considerable current interest ⁵ and there have been many recent studies reported concerned with the inclusion complexes of C₆₀ with various host molecules, such as the calixarenes, resorcinarenes and cyclotriveratrylene.⁶ Volumetric studies using high-precision densitometry provide a potentially general and simple experimental method to probe the nature of these “host–guest” interactions in solution;^1,7 however, to date no other studies have been reported.

We have shown previously ^8,9 that the endo-calix[4]naphthalene (1) and its tert-butylated derivative (2) form stable inclusion complexes with C₆₀. These calix[4]naphthalenes,^10,11 which are the subject of ongoing investigations by our group, are a class of cavitands possessing deeper cavities than those of analogous calixarenes, and so their complexation properties are of interest. It was found that the respective association equilibrium constants (K_assoc), of the 1∶1 supramolecular complexes in benzene, toluene or CS₂ increased in the order benzene, toluene, CS₂, and the hypothesis was presented that this trend could be due to a solvophobic effect.⁵ The results obtained from a thermodynamic study ⁹ on the above systems were consistent with this hypothesis. In order to ascertain whether standard partial molar volume changes could provide further insights into the nature of the inclusion complexation observed, we have employed high-precision densitometry. Our results and their interpretation are presented herein.

Results and discussion

The partial molar volume of a solute (V̄₂) [eqn. (1)] is the differential change in volume of its solution (V ) as a function of the change in the number of moles of the solute (n₂) for a given temperature (T ), pressure ( p) and number of moles of solvent (n₁).

V̄ ₂ = (∂V/∂n₂)_T,p,n1 (1)

By definition, the standard partial molar volume, V ₂^{[circle, cut, short horiz bar]}, is the limiting value of V ₂^{[circle, cut, short horiz bar]} at infinite dilution. Experimental values of V ₂^{[circle, cut, short horiz bar]} can be obtained from eqn. (2) by measuring V_ϕ,2, the apparent molar volume of the solute,¹² and extrapolating the results to m₂ = 0, i.e.V ₂^{[circle, cut, short horiz bar]} = lim_m2→0 (V_ϕ,2); here m₂ is the molality of the solute, component 2; M₂ is its molar mass; ρ and ρ₁ are the densities of the solution and the solvent, respectively.

V _ϕ,2 = 1/m₂ [{(1000 + m₂M₂)/ρ} − (1000/ρ₁)] (2)

Since the solutions employed in our work were very dilute (m₂ ≈ 10⁻⁴ mol kg⁻¹), there was no need to extrapolate V_ϕ,2 to infinite dilution, as was done by Isaacs and Young ⁷ in their study. At these low molalities, the average of the V_ϕ,2 values obtained could be shown to represent very closely the standard partial molar volume at infinite dilution. The standard partial molar volumes calculated from the average V_ϕ,2 values derived from eqn. (2) (method A) for the cavitands and C₆₀ are shown in Tables 1 and 2.

Table 1 Solute standard partial molar volumes (V ₂^{[circle, cut, short horiz bar]}/cm³ mol⁻¹) of C₆₀, 1 and the C₆₀∶1 complex (C₆₀⊂1) in different solvents and the calculated reaction volumes (Δ_rV ₂^{[circle, cut, short horiz bar]}/cm³ mol⁻¹) ^a

			V 2^[circle, cut, short horiz bar]
Solvent	Run	Method	C60	10^4c2	1	10^4c2	C60∶1	10^4c2	ΔrV ^[circle, cut, short horiz bar]
a c 2 = mass fraction; italic figures in parentheses are the number of data points. ± values are standard deviations, derived (for method A) from the statistical treatment (Sigmaplot v 3.0) and (for method B) from a non-linear least-squares analysis (Sigmaplot v 3.0).
Toluene	1	A	370 ± 14	4.0–7.3 (5)	548 ± 21	4.6–11.2 (4)	1064 ± 59	5.0–10.5 (4)
	2	A	366 ± 10	4.7–7.3 (5)	521 ± 19	2.3–6.7 (4)	1083 ± 23	1.2–8.5 (4)
		Mean values	368 ± 12		535 ± 20		1074 ± 45		171 ± 51
	1	B	361 ± 23	4.0–7.3 (5)	580 ± 15	4.6–11.2 (4)	1110 ± 38	5.0–10.5 (4)
	2	B	367 ± 13	4.7–7.3 (4)	528 ± 35	2.3–5.5 (4)	1075 ± 22	1.2–8.5 (4)
		Mean values	364 ± 19		554 ± 27		1092 ± 31		174 ± 45
Benzene	1	A	363 ± 3	4.0–9.0 (4)	560 ± 30	2.7–4.7 (5)	837 ± 40	3.0–5.7 (5)
	2	A	355 ± 18	1.7–3.0 (5)	545 ± 25	3.0–8.0 (5)	857 ± 26	3.0–9.4 (5)
		Mean values	359 ± 13		552 ± 28		847 ± 34		−64 ± 46
	1	B	371 ± 2	4.0–9.0 (4)	542 ± 39	2.7–4.7 (5)	841 ± 54	3.0–5.7 (5)
	2	B	349 ± 48	1.7–3.0 (5)	559 ± 9	3.0–8.0 (5)	879 ± 40	3.0–9.4 (5)
		Mean values	360 ± 34		551 ± 28		860 ± 48		−62 ± 56
CS2	1	A	345 ± 12	2.0–2.8 (3)	458 ± 28	1.4–4.0 (4)	784 ± 15	0.80–1.6 (4)
	2	A	348 ± 8	1.6–3.0 (3)	480 ± 20	1.0–2.0 (6)	813 ± 12	2.7–4.0 (4)
	3	A	342 ± 8	7.0–16.0 (5)	491 ± 5	6.0–12.0(6)	812 ± 10	6.0–16.0 (6)
		Mean values	345 ± 10		476 ± 20		803 ± 13		−18 ± 21
	1	B	348 ± 11	2.0–2.8 (3)	446 ± 26	1.4–4.0 (4)	800 ± 36	0.80–1.6 (4)
	2	B	370 ± 9	1.6–3.0 (3)	458 ± 18	1.0–2.0 (6)	851 ± 22	2.7–4.0 (4)
	3	B	341 ± 18	7.0–16.0 (6)	489 ± 11	6.0–12.0 (7)	817 ± 14	6.0–16.0 (4)
		Mean values	353 ± 13		464 ± 19		823 ± 26		−10 ± 34

---

Table 2 Solute standard partial molar volumes (V ₂^{[circle, cut, short horiz bar]}/cm³ mol⁻¹) of C₆₀, 2 and the C₆₀∶2 complex (C₆₀⊂2) in different solvents and the calculated reaction volumes (Δ_rV ₂^{[circle, cut, short horiz bar]}/cm³ mol⁻¹) ^a

			V 2^[circle, cut, short horiz bar]
Solvent	Run	Method	C60	10^4c2	2	10^4c2	C60∶2	10^4c2	ΔrV ^[circle, cut, short horiz bar]
a See Table 1.
Toluene	1	A	370 ± 14	4.0–7.3 (5)	746 ± 15	4.2–15 (5)	1178 ± 40	6.0–13 (5)
	2	A	366 ± 10	4.7–7.3 (4)	753 ± 48	4.0–12 (4)	1139 ± 19	2.0–6.0 (4)
		Mean values	368 ± 12		749 ± 36		1158 ± 31		41 ± 49
	1	B	361 ± 23	4.0–7.3 (5)	748 ± 12	4.2–15 (5)	1187 ± 36	6.0–13 (5)
	2	B	367 ± 13	4.7–7.3 (4)	729 ± 40	4.0–12 (4)	1194 ± 26	2.0–6.0 (4)
		Mean values	364 ± 19		739 ± 29		1190 ± 31		87 ± 46
Benzene	1	A	363 ± 3	4.0–9.0 (4)	777 ± 44	4.0–5.5 (3)	1196 ± 19	3.2–4.6 (4)
	2	A	355 ± 18	1.6–3.0 (5)	786 ± 2	3.5–5.5 (4)	1190 ± 30	2.5–4.3 (5)
		Mean values	359 ± 13		782 ± 31		1193 ± 25		52 ± 42
	1	B	371 ± 2	4.0–9.0 (4)	798 ± 47	4.0–5.5 (3)	1229 ± 28	3.2–4.6 (4)
	2	B	349 ± 48	1.6–3.0 (5)	812 ± 7	3.5–5.5 (4)	1168 ± 44	2.5–4.3 (5)
		Mean values	360 ± 34		805 ± 34		1198 ± 37		22 ± 50
CS2	1	A	345 ± 12	2.0–2.8 (3)	630 ± 20	1.0–1.5 (4)	1115 ± 38	1.0–3.0 (4)
	2	A	348 ± 8	1.6–3.0 (4)	655 ± 18	1.6–3.3 (3)	1104 ± 28	1.0–2.0 (4)
	3	A	342 ± 8	7.0–16.0 (5)	640 ± 9	6.5–16.0 (6)	1073 ± 33	6.0–16 (4)
		Mean values	345 ± 10		642 ± 16		1097 ± 33		110 ± 39
	1	B	370 ± 9	1.6–3.0 (4)	654 ± 38	1.6–3.3 (3)	1101 ± 70	1.0–2.0 (4)
	2	B	341 ± 18	7.0–16.0 (6)	617 ± 6	6.5–16.0 (6)	1035 ± 8	6.0–16 (4)
	3	B	348 ± 11	2.0–2.8 (3)	630 ± 36	1.0–1.5 (4)	1095 ± 44	1.0–3.0 (4)
		Mean values	353 ± 13		634 ± 30		1077 ± 48		98 ± 69

---

The solutions of the complexes contained a small excess of either the cavitand or C₆₀. Values of the overall apparent molar volume, V_ϕ, were obtained from the general form of eqn. (2) for n solutes.¹² Young’s rule ¹³ [eqn. (3)] was then applied to calculate V_ϕ,2:

V _ϕ,2 = Σ F_nV_ϕ,n (3)

In eqn. (3), F_n is the molar fraction of each solute in a multicomponent solution of n solutes, for example F₂ = n₂/(n₂ + n₃), and V_ϕ,n is the apparent molar volume of each individual solute. The apparent molar volumes of the 1∶1 complexes of C₆₀ with 1 and 2 are listed in Tables 1 and 2, respectively. Fig. 1 shows the plots of V_ϕ,2versus molality for the solutions in benzene, of C₆₀, 2 and the C₆₀∶2 (1∶1) complex, respectively, from which the V ₂^{[circle, cut, short horiz bar]} values in Table 2 were derived. Table 1 contains the corresponding data for the volumetric studies on the complex formation between C₆₀ and 1.

Fig. 1 Apparent molar volume (V_ϕ,2) of solutes (■, C₆₀; △, 2; ✦, C₆₀⊂2) vs. their molality in benzene.

V ₂^{[circle, cut, short horiz bar]} may also be derived from the limiting partial specific volume v_s,2 of the solute, which can be calculated (method B) from a plot of the specific volume of the solution, v_s = 1/ρ, versus the mass fraction of solute (c₂).^2,3V ₂^{[circle, cut, short horiz bar]} is related to v_s,2 by eqn. (4).^2,3

V ₂^{[circle, cut, short horiz bar]} = M₂·v_s,2 (4)

We employed the same data points used to calculate the partial molar volumes from eqn. (2) above, to calculate V ₂^{[circle, cut, short horiz bar]} (method B) from eqn. (4). The standard partial molar volumes calculated by both methods show good agreement within experimental error. The experimental curves shown in Fig. 2 (which are typical), were obtained directly from the density measurements of benzene solutions having known mass fractions respectively, of each of the solutes C₆₀, 2, and the C₆₀∶2 (1∶1) complex.

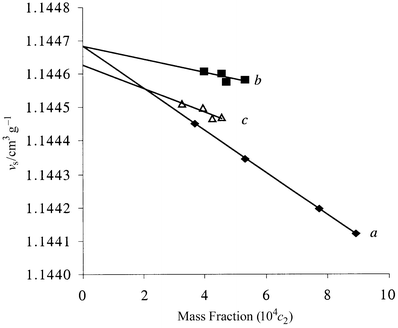Fig. 2 Specific volume (ν_s) of solutions in benzene of solutes (✦, C₆₀; ■, 2; △, C₆₀⊂2) vs. their mass fraction (c₂).

The following discussion is based upon the results calculated using method A since they contain corrections for the excess, presumably uncomplexed, solute in the respective solutions, although the results obtained using both methods are in close agreement. When the error limits for the mean values obtained from our assays are taken into account, our data for the partial molar volume of C₆₀ itself in each of the three solvents are basically in agreement with those reported by Ruelle et al.² and with the values obtained in toluene by Isaacs et al.¹

Using the mean values obtained from method A, a trend can be seen in the partial molar volumes of tert-butylcalix[4]naphthalene (2) (Table 2), being largest in benzene (782 ± 31), followed by toluene (749 ± 36) and CS₂ (642 ± 16) cm³ mol⁻¹. A similar trend can be seen in the partial molar volumes of calix[4]naphthalene (1) (Table 1) measured in the same respective solvents, being 552 ± 28 in benzene, 535 ± 20 in toluene and 476 ± 20 cm³ mol⁻¹ in CS₂.

Handa and Benson ¹⁴ have noted that the volume changes observed on mixing two liquids can be the result of any of several factors, such as (i) differences in sizes and shapes of the component molecules, (ii) structural changes, (iii) differences in the intermolecular interaction energy between like and unlike molecules, and/or (iv) formation of new chemical species. Using these considerations, as well as observations noted by Ruelle et al. and others,^15–17 it is possible to rationalize the changes that we observed for 1 or 2 with the different solvents, as follows.

Firstly, the trend in the solubilities (mg cm⁻³) of 1 and 2 in each of the three solvents decreases in the following order: CS₂ (>10) > toluene (1.8) > benzene (1.7) for 1 and CS₂ (>10) > toluene (3.5) > benzene (2.6) for 2. Increases in the limiting partial molar volume changes of solutes in various solvents are known to be roughly inversely proportional to their solubilities in the respective solvents.^15–17 This is indeed the trend that we noted above, with the smallest partial molar volumes of either 1 or 2 being in CS₂, the solvent in which both calixnaphthalenes have the highest solubilities.

A second factor to consider is the difference in size and shape of the component molecules in each case, outlined as factor (i) above, and which Ruelle et al. considered in their intensive study of C₆₀ itself in different solvents. These authors determined a good correlation between the solvent molar volume and the variation in the size of C₆₀ in solution. For our calixnaphthalene compounds, however, this does not appear to be the case since, whilst CS₂ has the smallest reported molar volume, followed by benzene, then toluene, the trend in partial molar volumes in these solvents follows a different order: benzene > toluene > CS₂. An additional factor, outlined as factor (iv) above, could account for this apparent anomaly between benzene and toluene as solvents of either 1 or 2. This could be the intermolecular π ⋯ methyl interaction that might occur between the naphthalene rings and the methyl group of toluene, but would not be present when benzene is the solvent. This supposition is supported by the well-known fact that a stable toluene∶tert-butylcalixarene clathrate forms, as first reported by Andreetti et al.¹⁸

The partial molar volumes of the 1∶1 complexes C₆₀⊂1 and C₆₀⊂2 in the respective solvents were also determined in the same way, and calculated using method A. However, it should be noted that the sparing solubilities of the calixnaphthalenes in benzene or toluene limited the concentration ranges that could be employed and resulted in uncertainties of the order of 3–6%, which are nevertheless comparable to the findings reported by Isaacs et al.¹

The calculated reaction volumes (Δ_rV ₂^{[circle, cut, short horiz bar]}) ⁷ for the C₆₀∶2 complex formation are +110 in CS₂, +52 in benzene and +41 cm³ mol⁻¹ in toluene. Based on the molar volumes of each of the solvents, these reaction volumes are roughly equivalent to the partial molar volumes of 2, 0.6 and 0.4 molecules of the respective solvents which, as interpreted by Isaacs et al.,¹ are displaced upon complex formation. The trend is consistent with our earlier hypothesis ⁸ that a solvophobic effect (i.e. that a larger number of molecules of CS₂ are displaced from the cavitand cavity upon complex formation) is a driving force in the complex formation processes studied.

For C₆₀∶1 complex formation, the calculated reaction volumes (Δ_rV ₂^{[circle, cut, short horiz bar]}_,calc) are −18 in CS₂, −64 in benzene and +171 cm³ mol⁻¹ in toluene. These values do not support the solvophobic effect hypothesis, since in CS₂ and in benzene they are lower than expected when compared with the corresponding values obtained for the C₆₀⊂2 complex. Thus, for the C₆₀⊂1 complex, for which a deeper penetration of C₆₀ into the cavity is possible relative to the C₆₀⊂2 complex, solvation of the complex by CS₂ and benzene could therefore be stronger, thus negating a possible solvophobic effect. For toluene as the solvent, approximately two molecules of toluene are displaced upon complex formation, similar to the finding observed by Isaacs et al.¹ in their system.

When the toluene data for the two complexation processes are compared, more solvent molecules are displaced on formation of the C₆₀⊂1 complex than the C₆₀⊂2 complex. This is also consistent with our earlier rationalization ⁹ that, in the case of C₆₀⊂1 we have deep-cavity inclusion. By contrast, a shallower penetration of the C₆₀ guest molecule may be occurring in the case of the C₆₀⊂2 complex, since the tert-butylmethyl ⋯ C₆₀π interactions may sterically inhibit the potentially more effective interactions between C₆₀ and the naphthalene rings.

There appears to be no simple direct correlation between the stability constants, K_assoc, which we determined earlier,⁹ and the reaction volume changes. On the other hand, a positive correlation is found for the volume changes and Δ_r S ^{[circle, cut, short horiz bar]} values determined earlier for the formation of the C₆₀⊂1 complex and a negative correlation for the formation of the C₆₀⊂2 complex.

Connors published an extensive review in 1997 on cyclodextrin complexes in solution.¹⁹ In this review he points out that interpretations based upon small calculated molar volume changes having relatively large uncertainties should be considered with care and that only after the collection of very many experimental results for a wide range of substrate types will accurate patterns emerge. This holds true for calixarene-based host–guest complexation processes, and we are continuing to design and study other calixnaphthalenes.

In conclusion, the results presented herein show that apparent molar volume measurements can be employed to study host–guest complexation processes and can provide some information as to how deep the inclusion of a guest into the substrate can occur. However, it is important to also take into account additional information, such as the solvation of all of the individual species concerned, solvent molar volumes and other factors identified by Handa and Benson,¹⁴ which may require additional physical methodologies.

Experimental

Toluene (BDH, Scintillation Grade) was distilled over sodium metal with benzophenone prior to use. Benzene (ACP Chemicals Inc., A.C.S. grade, 99%) and CS₂ (Aldrich Chemical Company, Inc., Spectrophotometric Grade, 99+%) and anhydrous ethanol (Commercial Alcohols Inc.) were used without further purification. C₆₀ (99.5%) was purchased from Aldrich. Calix[4]naphthalenes 1 and 2 were prepared according to methods previously described.^10,11 For all the solvents tested 4–6 solution samples with decreasing mass fraction were prepared from a specific amount of a pre-prepared stock solution of known mass fraction by dilution with a known mass of solvent. In the case of the complex mixtures, an exact mass of the stock solution of 1 or 2 was mixed with the exact mass of C₆₀ stock solution to give a 1∶1 molar ratio, then this mixture was diluted with a known mass of solvent. All solutions were weighed with a precision of ±10⁻⁵ g. The high-precision density measurements were carried out at 25.00 ± 0.01 °C using a vibrating-tube densitometer (Sodev Model D03), capable of measuring relative densities (ρ − ρ₁) to a precision of ±5 × 10⁻⁶ g cm⁻³. Before each series of measurements, the instrument was calibrated with absolute ethanol and the solvent system used in the experiment, whose densities (g cm⁻³) at 25.00 °C were taken from published data:²⁰ρ₁ (ethanol) = 0.78509, ρ₁ (toluene) = 0.86222, ρ₁ (benzene) = 0.87366, ρ₁ (CS₂) = 1.25585. In a typical experiment, approximately 2.0 cm³ of the tested solution was injected into the densitometer using a glass syringe. The apparent molar volume, V_ϕ, at each molality was calculated using the general form of eqn. (2), then V_ϕ,2 was determined by applying Young’s rule. The standard partial molar volume, V ₂^{[circle, cut, short horiz bar]}, was calculated from the average of all the data points in that experiment (method A). The same data points were analyzed by plotting the specific volume (1/ρ) of a series of solutions against the mass fractions. From these plots, the partial molar volumes could also be calculated using eqn. (4) (method B). Measurements in each solvent were conducted in duplicate or triplicate. Statistical analyses were conducted using Sigmaplot v 3.0 and curve fitting was conducted using Excel 97.

Acknowledgements

This research was supported by the Natural Sciences and Research Council of Canada and the Department of Chemistry, Memorial University of Newfoundland.

References

1. N. S. Isaacs, P. J. Nichols, C. L. Raston, C. A. Sandoval and D. J. Young, Chem. Commun., 1997, 1839.
2. P. Ruelle, A. Farina-Cuendet and U. W. Kesselring, J. Am. Chem. Soc., 1996, 118, 1777.
3. Z. Liron and S. Cohen, J. Pharm. Sci., 1983, 72, 499.
4. A. Martin, Z. Liron and S. Cohen, J. Pharm. Sci., 1985, 74, 638.
5. D. J. Cram and J. M. Cram , Container Molecules and Their Guests, Royal Society of Chemistry, Cambridge, 1994..
6. For a recent bibliography see F. C. Tucci, D. M Rudkevich and J. Rebek, Jr., J. Org. Chem., 1999, 64, 4555 and references cited therein..
7. N. S. Isaacs and D. J. Young, Tetrahedron Lett., 1999, 40, 3953 The notation ΔV_c→0 in ref. 7 = Δ_rV ^{[circle, cut, short horiz bar]} in this work; similarly, V = V ₂^{[circle, cut, short horiz bar]}..
8. P. E. Georghiou, S. Mizyed and S. Chowdhury, Tetrahedron Lett., 1999, 40, 611.
9. S. Mizyed, P. E. Georghiou and M. Ashram, J. Chem. Soc., Perkin Trans. 2, 2000, 277.
10. P. E. Georghiou and Z.-P. Li, Tetrahedron Lett., 1993, 34, 2887.
11. P. E. Georghiou, M. Ashram, Z.-P. Li and S. Chaulk, J. Org. Chem., 1995, 60, 7284.
12. (a) I. M. Klotz and R. M. Rosenberg , Chemical Thermodynamics: Basic Theory and Methods, 5th Edn., Wiley, New York, 1994, ch. 17;; (b) C. Collins, J. Tobin, D. Shvedov, R. Palepu and P. R. Tremaine, Can. J. Chem., 2000, 78, 151and references cited therein..
13. T. F. Young and M. B. Smith, J. Phys. Chem., 1954, 58, 716.
14. Y. P. Handa and G. C. Benson, Fluid Phase Equilib., 1979, 3, 185.
15. K. Shinoda and J. H. Hildebrand, J. Phys. Chem., 1958, 62, 295.
16. W. B. Jepson and J. S. Rowlinson, J. Chem. Soc., 1956, 261, 1278.
17. E. B. Smith, J. Walkely and J. H. Hildebrand, J. Phys. Chem., 1959, 63, 703.
18. (a) G. D. Andreetti, R. Ungaro and A. Pochini, J. Chem. Soc., Chem. Commun., 1979, 1005; (b) M. Coruzzi, G. D. Andreetti, V. Bocchi and A. Pochini, J. Chem. Soc., Perkin Trans. 2, 1982, 1133; (c) G. D. Andreetti, A. Pochini and R. Ungaro, J. Chem. Soc., Perkin Trans. 2, 1983, 1773; (d) C. Rizzoli, G. D. Andreetti, R. Ungaro and A. Pochini, J. Mol. Struct., 1982, 82, 133.
19. K. A. Connors, Chem. Rev., 1997, 97, 1325.
20. J. Timmermans , Physico-chemical Constants of Pure Organic Compounds, Elsevier, New York, 1950..

---