Leapfrog fullerenes, Hückel bond order and Kekulé structures

Abstract

Investigation of a sample of 5436 fullerene isomers indicates a relationship between Kekulé structures and the molecular orbital theory of these trivalent cages. In leapfrog fullerenes (those constructed by omnicapping and dualising a fullerene parent), the edges of maximal Hückel π bond order define the Kekulé structure with the maximum number of benzenoid hexagons (the Fries structure). For general fullerenes, the bond orders rarely correspond exactly to a Kekulé structure: of 1812 C₆₀ fullerene isomers, for example, only 23 have a Hückel Kekulé structure.

---

Introduction

Fullerenes embrace a wide variety of potential shapes, symmetries and electronic configurations,¹ of which some are systematically preferred according to experimental observation. The present note explores one aspect of the connection between fullerene molecular graphs and electronic structure: the definition of bond order in leapfrog fullerenes. Our aim is to shed some light on the links between Hückel theory and Kekulé structures for these prototypical closed-shell fullerenes.

Several regularities linking electronic structure and topology have been identified for fullerenes, of which the most direct is the leapfrog construction ² of closed-shell ³ isomers C_60 + 6k in one-to-one correspondence with general fullerene parents (C_20 + 2k (k ≠ 1). The leapfrog isomer is obtained formally by omnicapping the parent and then taking the dual, and the class of leapfrogs has been shown to be identical with those obeying the Fries stability criterion,^4,5i.e. leapfrog fullerenes C_n are those that support a unique ⁶ Kekulé structure that achieves the maximal number of benzenoid hexagons.^7,8

The formal double bonds of this particular (Fries) Kekulé structure play a special role in the proof of the closed-shell property ³ and of the various symmetry theorems for leapfrog polyhedra ^9,10 from which, for example, the general tendency of fullerenes to electron deficiency is rationalised.¹¹ These bonds lie along the n/2 edges of the leapfrog that cut the parent edges transversely. Indeed, an alternative construction of leapfrogs is: cross every edge of the parent with a new edge and join the ends of all the new edges on each parent r-gonal face to form an inset cycle of the same size rotated through π/r. In the Fries Kekulé structure, all transverse edges are formally double, all inset edges formally single, and so the leapfrog construction gives a well defined ‘topological’ criterion for bond order based on a localised model.

On the other hand, Hückel molecular orbital theory provides an independent criterion based on the delocalised eigenvectors of the fullerene adjacency matrix: the ‘double’ bonds can be assigned to the n/2 edges of maximal π bond orderp_rs, which is given by eqn. (1).

p _rs  = ^Σ_i n_ic_irc_is (1)

The sum runs over the partial mobile bond orders contributed by all molecular orbitals i with occupation number n_i and coefficients c_ir and c_is on the σ-bonded pair of atoms r and s.

The main question addressed in this note is simply: do the localised and delocalised choices of double bonds for leapfrog fullerenes agree?

Hückel and Fries leapfrog bond orders

An exact numerical match between the integral bond orders of a Kekulé structure and the real numbers of Hückel theory is not to be expected. However, if the Fries structure is indeed the dominant resonance contribution to the Hückel ground state for a leapfrog C_n molecule, it may fairly be expected to predict the n/2 bonds of highest Hückel bond order. The Fries structure for the smallest leapfrog, I_h C₆₀, supports this claim: the 30 formally double hexagon–hexagon edges have simple Hückel π bond order p₆₆ = 0.6010 and the 60 formally single pentagon edges have p₅₆ = 0.4758. The X-ray structural determination of a C₆₀ derivative confirms the implied alternation in the hexagonal rings, with average bond lengths r̄₅₆ = 1.432 Å and r̄₆₆ = 1.388 Å.¹²

To provide more extensive numerical evidence, calculations of bond order and other Hückel properties were made for two test sets of isomers, those obtained by leapfrogging once (L) and then a second time (L²) the 1812 fullerene isomers of C₆₀. The parent isomers (P) span a wide range of structures and relative stabilities, from the spherical isolated-pentagon I_h cage to the fivefold symmetric D_5d cylinder with 20 pentagon–pentagon fusions that lies much higher in energy (e.g. by 2400 kJ mol⁻¹ according to the QCFF/PI model ¹³). 1508 of the 1812 isomers have no symmetry at all, 189 have only C₂ symmetry and 67 have only mirror symmetry. Isomers of C₆₀ have Kekulé counts K varying from 8562 to 16501, with the most stable isomer ranking only 21st, at K = 12500.¹⁴

The isomers are constructed from their spiral codes which lead directly to fullerene adjacency matrices from which the matrices for the leapfrogs can be derived with a simple computer program. Diagonalisation then yields the Hückel eigenvectors and the related bond orders. The Fries double bonds are easily identifiable in the labelling scheme used to construct the leapfrog expansion of the parent. Leapfrogging preserves molecular symmetry and, by the eigenvalue theorem,³ all C₁₈₀ and C₅₄₀ structures considered here have fully symmetric closed-shell electronic configurations. The configurations of the 1812 parents include five open shells, 1806 pseudo-closed shells and just one properly closed shell (I_h C₆₀, which is itself a leapfrog of C₂₀). In fact, three of the five open-shell isomers are amongst the 20 that have higher Kekulé counts than icosahedral C₆₀.¹⁴

The main result of the survey is simply stated: for all 3625 leapfrog isomers in the sample, the n/2 strongest bonds according to their Hückel π bond orders are exactly the formal double bonds of the Fries structure. Thus, there is a ‘Hückel’ Kekulé structure for all of these cases, and it is identical with the Fries Kekulé structure. All 3625 leapfrog structures have a well defined gap between the lowest ‘double’ and highest ‘single’ bond orders and the match is therefore unambiguous. Hückel theory thus predicts the dominance of the localised Fries Kekulé structure, and this is consistent with the known lack of correlation between raw Kekulé count, K, and overall stability for fullerenes; ¹⁴ it appears that it is not necessary to have many Kekulé structures to achieve low energy, but simply to have one ‘good’ structure that coincides with the requirement of avoiding double bonds in pentagons and maximising the number of benzenoid hexagons.

Table 1 shows the ranges for the various Hückel quantities within and across the three sets. A general trend is that, after the first application of the leapfrog operation, successive leapfrogs have smaller band gaps. This is an illustration of the tendency towards the semi-metallic configuration of the graphite sheet with the falling proportion of non-hexagonal faces. Any leapfrog fullerene, no matter how large, can have at most one Fries structure, but the perturbing effects of the pentagons are expected to become less important at large n. This is illustrated for repeated leapfrogging by a marked decrease in the average order of formal double bonds, an increase in the average order of single bonds and a smaller difference between the orders of the weakest formal double and strongest formal single bond (see Table 1). In the infinite graphite limit, we could expect the distinction between single and double bonds of the Fries structure to vanish as the structure becomes fully delocalised. As an alternant framework, graphite has three disjoint Fries structures and every bond is formally double in precisely one of them.

Table 1 Hückel parameters for the fullerene isomers of C₆₀, their leapfrogs (C₁₈₀) and double leapfrogs (C₅₄₀). The delocalisation energy per atom (E_π) and HOMO–LUMO gap (Δ) are in units of |β|. p_j denotes the order of the jth π bond when the bonds of each isomer are arranged in non-increasing order (p₁ and p_3n/2 are the orders of the strongest and weakest π bonds, respectively). Δp_d is the range of values for the n/2 strongest bonds and Δp_s for the n weakest. Δp_d−s is the difference between bond orders p_n/2 and p_n/2 + 1. p̄_d and p̄p_s are the average values for the n/2 strongest and n weakest π bonds within an isomer. The values for the I_h isomers are compared with the maximum and minimum of the other 1811 isomers of each set and the mean taken over all 1812.

	Parent (C60)				Leapfrog (C180)				Double leapfrog (C540)
	I h	Max	Min	Mean	I h	Max	Min	Mean	I h	Max	Min	Mean
E π/|β|	0.5527	0.5490	0.5270	0.5406	0.5670	0.5672	0.5668	0.5670	0.5721	0.5721	0.5720	0.5721
Δ/|β|	0.7566	0.4140	0.0000	0.1049	0.5795	0.5330	0.2445	0.4459	0.3578	0.3348	0.1706	0.2808
p 1	0.6010	0.6956	0.5210	0.6256	0.5609	0.6006	0.5749	0.5878	0.5488	0.5603	0.5500	0.5547
p n/2	0.6010	0.5708	0.5153	0.5356	0.5554	0.5462	0.5323	0.5396	0.5344	0.5329	0.5285	0.5305
p n/2 + 1	0.4758	0.5548	0.5095	0.5337	0.5071	0.5227	0.5147	0.5198	0.5213	0.5232	0.5214	0.5224
p 3n/2	0.4758	0.4643	0.2924	0.3839	0.4976	0.4907	0.4696	0.4792	0.5042	0.5033	0.4978	0.5006
Δpd	0.0000	0.1721	0.0010	0.0900	0.0055	0.0649	0.0297	0.0483	0.0144	0.0314	0.0175	0.0242
Δps	0.0000	0.2377	0.0507	0.1498	0.0095	0.0517	0.0248	0.0406	0.0170	0.0251	0.0183	0.0218
Δpd − s	0.1252	0.0600	0.0000	0.0019	0.0483	0.0300	0.0113	0.0198	0.0132	0.0114	0.0054	0.0081
p̄ d	0.6010	0.5929	0.5204	0.5659	0.5591	0.5589	0.5557	0.5577	0.5387	0.5386	0.5379	0.5384
p̄ s	0.4758	0.5033	0.4749	0.4873	0.5040	0.5057	0.5041	0.5047	0.5167	0.5171	0.5167	0.5168

---

It is notable that almost all quantities in Table 1 have a prominent outlier which corresponds to the icosahedral isomer and its leapfrogs. Apart from any special considerations of symmetry, this may simply reflect the fact that I_h C₆₀ is already a leapfrog and so it and its descendants are one leapfrog order ⁶ ahead of the rest of their generation.

Hückel bond orders in general fullerenes

The successful match between Hückel and Fries bond orders in leapfrog fullerenes suggests that a more subtle graph-theoretical/valence-bond relationship may exist for general fullerene isomers. Unlike leapfrogs, general fullerenes do not have a simple ‘topological recipe’ that describes a dominant valence-bond structure. As trivalent graphs, fullerenes have at least three Kekulé structures,¹⁵ although it has been shown that typical fullerenes, such as the isomers of C₆₀, have Kekulé counts of several thousand.¹⁴

There is no reason why any particular valence-bond structure should dominate for an individual cage, although a clear link exists between the calculated and pictorial bond-order properties for some isomers. For example, isomer 60∶1809 has been identified as the only cage approaching I_h C₆₀ in stability according to the Fries criterion.¹⁴ This isomer is the unique product of Stone–Wales rotation ¹⁶ of one of the hexagon–hexagon bonds of the icosahedral cage and has a reduced symmetry of C_2v, two pentagon adjacencies and a maximum of 18 benzenoid hexagons. The Stone–Wales bond is formally double in the Fries structure of the I_h cage and its four neighbouring bonds are all single. Intuition suggests that rotation of this bond will cause only a small perturbation of the overall Fries structure of the original cage, with the positions of the 29 other formal double bonds remaining the same in isomer 1809 (Fig. 1). This turns out to be the case: the Hückel model generates a distinct set of 30 double bonds that correspond to the 29 bonds that remain from the icosahedral Fries structure, plus the rotated Stone–Wales bond.

Fig. 1 Local effects on the π system around the Stone–Wales bond transformation on going from 60∶1812 (I_h) to 60∶1809 (C_2v).

The pictorial valence-bond structure also agrees with the calculated bond orders for several other isomers that can be obtained from I_h C₆₀ by Stone–Wales transformations via isomer 1809. Rotation of a second Stone–Wales bond that was antipodal to the first in the original cage generates a D_2h isomer (60∶1810 in the spiral sequence) in which the 28 remaining bonds from the Fries structure plus the two rotated bonds account for the 30 strongest π bonds from the Hückel model. The same is true for isomer 1811 of D₃ symmetry that is obtained by three simultaneous Stone–Wales transformations around a threefold axis of the icosahedral cage. In all three examples, each Stone–Wales transformation generates two adjacent pentagons with one of each pair containing two double bonds. Hence isomers 1809, 1810 and 1811 contain two, four and six pentagon adjacencies and cyclopentadienoid rings, respectively.

Despite the success of the ‘bond-rotation’ method for some isomers, cages that are only two Stone–Wales steps away from I_h C₆₀ provide examples where the simple rotated π-bond pattern does not match the calculated bond orders, either because the n/2 strongest bonds do not yield a Kekulé structure at all (e.g. isomer 60∶1807, C₂ symmetry (Fig. 2)), or produce one that differs from that predicted by Stone–Wales rotation of the I_h Fries structure (e.g. isomer 60∶1804, C_s symmetry).

Fig. 2 Valence-bond electronic structure of the C₂ isomer 60∶1807. The 28 solid-line double bonds are predicted by both the Hückel and bond-rotation models. The dotted lines indicate the positions of the final two bonds that would complete the pictorial Kekulé structure but are, in fact, outside the set of 30 strongest bonds in the Hückel model (the two bonds that complete this set are circled).

In order to investigate whether a general relationship exists between geometric structure and bond order for fullerenes, the bond orders of all 1812 isomers of C₆₀ were calculated. The size of the gap between the values of p_n/2 and p_n/2 + 1 when the orders of the 3n/2 bonds are arranged in non-increasing order varies between parent isomers, ranging from 0.1252 for 60∶1812 (I_h) to effectively zero for 60∶1510. Hence, many general fullerene isomers have no clear distinction between the sets of n/2 ‘double’ and n ‘single’ bonds, e.g. in 130 of the 1812 isomers of C₆₀p_n/2 and p_n/2 + 1 are separated by less than 1.0 × 10⁻⁵.

A total of just 23 of the isomers were found to have calculated bond-order patterns rigorously corresponding to a Kekulé structure, i.e. with the n/2 strongest bonds forming a vertex-spanning set of 30 edges in which each of the 60 atoms is common to one formally double and two formally single bonds. This comparative scarcity of Hückel Kekulé structures is rationalisable to an extent on symmetry grounds. Hückel bond orders of a closed-shell or half-open state of a molecule are necessarily equal for symmetry-equivalent bonds. A Hückel Kekulé structure, if one exists, must therefore have the full symmetry of the molecule. For a general fullerene that has some non-trivial symmetry, the totally symmetric Kekulé structures constitute a small minority of the total set or may not exist at all, as e.g. for C₂₀, C₂₆ and T_d C₂₈ (see ref. 17 for a tabulation). In leapfrog fullerenes, however, the existence of at least one totally symmetric Kekulé structure is guaranteed by the method of their construction, making the Hückel/Fries identification possible. In other classes of fullerene, the Hückel bond orders may perhaps correspond to a totally symmetric superposition of Kekulé structures, as they do in benzene, but matching to a single structure is unlikely. This argument is clearly only indicative, as the majority of the larger fullerenes in fact belong to the trivial point group C₁.

The 23 Hückel Kekulé isomers of C₆₀ are illustrated in Fig. 3 and their bond-order properties are summarised in Table 2 using data taken from ref. 13, in particular the Fries numbers, F, and Taylor numbers T_H(a), T_H(b), T_P and T_P2. For fullerenes, a Fries number can be defined for an individual Kekulé structure as the number of benzenoid hexagons that it contains; F is then the maximum number of such hexagons taken over all possible Kekulé structures. The Taylor number T_H(a) is the maximum number of benzenoid hexagons taken over all those Kekulé structures that have the minimum number of double bonds in pentagons, T_P. T_H(b) is the maximum number of benzenoid hexagons taken over all the minimal-T_P structures that also have the minimum number (T_P2) of cyclopentadienoid rings. Use of the numbers T_H(a) and T_H(b) is motivated by Taylor’s argument that minimisation of π bond order in pentagons should take priority over maximisation of the number of benzenoid hexagons in isolated-pentagon fullerenes.¹⁸T_H(b) recognises the additional steric strain in pentagonal rings containing two double bonds. The values H, H_P and H_P2 in Table 2 are respectively the numbers of benzenoid hexagons, double bonds in pentagons and cyclopentadienoid rings in the Hückel-derived Kekulé structure.

Table 2 Bond-order properties of the 23 isomers of C₆₀ in which the calculated bond orders rigorously correspond to a Kekulé structure (see Fig. 3). Isomers are identified by their sequence number in the lexicographic list of ring spirals. F is the Fries number and T_P, T_H(a), T_H(b) and T_P2 are the Taylor numbers for each cage (see text and ref. 14 for definitions). H is the number of benzenoid hexagons in the Kekulé structure described by the Hückel bond orders. H_P and H_P2 are the number of double bonds in pentagons and number of cyclopentadienoid rings, respectively, in the same structure. Δp_d−s is the gap between the orders of the weakest formal double and strongest formal single bonds.

Isomer	F	T P	T H(a)	T H(b)	T P2	H	H P	H P2	Δpd−s
60∶44	16	10	16	16	4	16	10	4	2.56 × 10^−2
60∶220	16	10	16	16	4	16	10	4	2.87 × 10^−2
60∶356	12	9	12	12	3	12	9	3	3.64 × 10^−4
60∶993	13	8	13	13	2	13	8	2	4.10 × 10^−3
60∶1079	9	10	8	8	6	6	12	4	1.60 × 10^−2
60∶1123	16	8	16	16	0	16	8	0	6.00 × 10^−2
60∶1124	14	10	14	14	0	14	10	0	3.00 × 10^−3
60∶1286	12	12	12	12	4	12	12	4	1.89 × 10^−2
60∶1547	14	10	14	14	2	14	10	2	1.40 × 10^−2
60∶1548	12	10	12	12	1	12	10	1	1.84 × 10^−3
60∶1756	14	9	14	14	1	14	9	1	2.50 × 10^−3
60∶1757	16	7	15	15	2	15	7	2	3.97 × 10^−3
60∶1761	16	9	16	16	0	16	9	0	4.07 × 10^−2
60∶1793	12	12	8	8	0	8	12	0	1.17 × 10^−2
60∶1798	12	10	10	10	4	10	11	2	4.13 × 10^−3
60∶1803	14	6	14	14	0	14	6	0	3.08 × 10^−2
60∶1804	16	6	15	15	1	15	6	1	3.43 × 10^−2
60∶1805	16	8	16	16	0	16	8	0	3.65 × 10^−2
60∶1808	14	8	12	12	4	12	8	4	3.07 × 10^−2
60∶1809	18	4	18	18	2	18	4	2	2.71 × 10^−2
60∶1810	16	8	16	16	4	16	8	4	2.53 × 10^−2
60∶1811	14	10	10	8	1	14	12	6	1.05 × 10^−3
60∶1812	20	0	20	20	0	20	0	0	1.25 × 10^−1

---

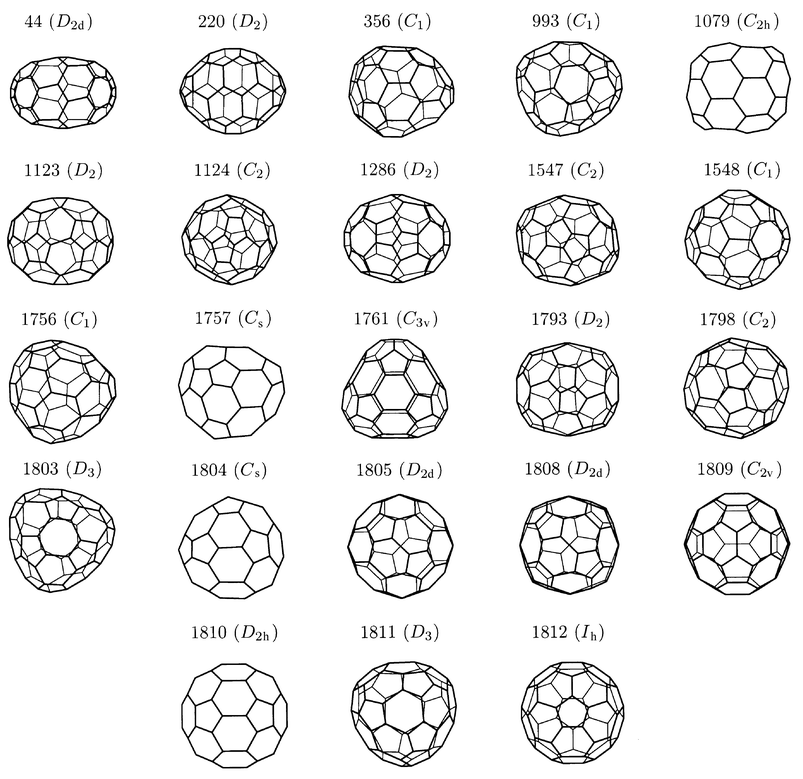Fig. 3 The 23 fullerene isomers of C₆₀ (labelled by spiral number and maximal point-group symmetry) in which the n/2 strongest bonds according to the equal-α, equal-β Hückel model rigorously correspond to a Kekulé structure. See Table 2 for a list of bond-order properties of these cages.

The results summarised in Table 2 give support to the Taylor criterion of stability and demonstrate that the graph-theoretical Hückel model reflects the preference for minimisation of double bonds in pentagons over unrestrained maximisation of benzenoid hexagons. Sixteen of the isomers in the table have F = T_H(a) = T_H(b), indicating that the maximum number of benzenoid hexagons over all Kekulé structures is achievable simultaneously with minimal values of T_P and T_P2. In all sixteen cases, the values H, H_P and H_P2 match their counterpart Fries and Taylor numbers, confirming the dominance of the maximal-benzenoid Kekulé pattern in the Hückel-derived electronic structure.

Of the other seven isomers, six have bond-order patterns that correspond with fewer than the Fries number of benzenoid hexagons, but the Hückel results still follow the Taylor criterion in most cases, i.e. minimising T_P2 (H_P2) for a given minimal value of T_P (H_P). For two isomers (1079 and 1798) the Hückel model exceeds the Taylor numbers, generating a bond-order pattern that has more double bonds in pentagons than the minimum but at the same time allows a smaller number of cyclopentadienoid rings than T_P2.

In conclusion, the Hückel bond orders appear to provide a realistic interpretation of the π-electronic distribution in general fullerene isomers. Although only a small subset of isomers have calculated bond orders that rigorously correspond to a Kekulé structure, the Hückel model gives a reliable graph-theory based illustration of the bond-order pattern for the vast majority of isomers. The Hückel model supports the energetic criterion of strain minimisation by reduction of bond orders in pentagonal rings and stresses avoidance of cyclopentadienoid rings in π-electronic structures.

Acknowledgements

K. M. R. thanks EPSRC for financial support, and both authors acknowledge the EU TMR network contracts FMRX-CT97-0126 and FMRX-CT98-0192.

References

1. P. W. Fowler and D. E. Manolopoulos , An Atlas of Fullerenes, Oxford University Press, Oxford, UK, 1995..
2. P. W. Fowler and J. I. Steer, J. Chem. Soc., Chem. Commun., 1987, 1403.
3. D. E. Manolopoulos, D. R. Woodall and P. W. Fowler, J. Chem. Soc., Faraday Trans., 1992, 88, 2427.
4. K. Fries, Justus Liebigs Ann. Chem., 1927, 454, 121.
5. K. Fries, R. Walter and K. Schilling, Justus Liebigs Ann. Chem., 1935, 516, 248.
6. P. W. Fowler and T. Pisanski, J. Chem. Soc., Faraday Trans., 1994, 90, 2865.
7. P. W. Fowler, J. Chem. Soc., Perkin Trans. 2, 1992, 145.
8. P. W. Fowler, M. Fujita and M. Yoshida, J. Chem. Soc., Faraday Trans., 1996, 92, 3673.
9. P. W. Fowler and D. B. Redmond, Theor. Chim. Acta, 1992, 83, 367.
10. P. W. Fowler and D. B. Redmond, MATCH, 1996, 33, 101.
11. P. W. Fowler and A. Ceulemans, J. Phys. Chem., 1995, 99, 508.
12. J. M. Hawkins, A. Meyer, T. A. Lewis, S. Loren and F. J. Hollander, Science, 1991, 252, 312.
13. E. E. B. Campbell, P. W. Fowler, D. Mitchell and F. Zerbetto, Chem. Phys. Lett., 1996, 250, 544.
14. S. J. Austin, P. W. Fowler, P. Hansen, D. E. Manolopoulos and M. Zheng, Chem. Phys. Lett., 1994, 228, 478.
15. D. J. Klein and X. Liu, J. Math. Chem., 1992, 11, 199.
16. A. J. Stone and D. J. Wales, Chem. Phys. Lett., 1986, 128, 501.
17. S. J. Austin, J. Baker, P. W. Fowler and D. E. Manolopoulos, J. Chem. Soc., Perkin Trans. 2, 1994, 2319.
18. R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1992, 3.

---