Theoretical studies of nonenzymatic reaction pathways for the three reaction stages of the carboxylation of ribulose-1,5-bisphosphate

Abstract

Alternative reaction pathways of the nonenzymatic carboxylation of D-ribulose-1,5-bisphosphate (RuBP) have been theoretically deduced by carrying out a series of first-principle calculations on two model systems. Several favorable competing reaction pathways have been found. The optimized geometries of the transition states and intermediates and the calculated relative energies are employed to explore the nature of transition-state stabilizing factors. It has been shown that hydrogen bonding plays a key role in the transition state stabilization in the competing reaction pathways for addition of CO₂ and H₂O. Substituent effects on the calculated energy barriers are also very large for the addition of CO₂, but less important for the subsequent reaction stages. Including solvent effects, the energy barriers calculated for the addition of CO₂ become significantly lower, while the energy barriers calculated for the addition of H₂O and for the C–C bond cleavage step become significantly and slightly higher, respectively.

---

Introduction

The world’s most abundant enzyme, D-ribulose-1,5-bisphosphate carboxylase/oxygenase (Rubisco), is of great biotechnological interest because of its significance to agriculture and in the greenhouse effect.¹ This enzyme catalyzes both the carboxylation of D-ribulose-1,5-bisphosphate (RuBP) and the metabolically wasteful oxygenation of RuBP (reactions 1a and 1b), which are the initial steps in the reductive pentose phosphate pathway of photosynthesis and in the photorespiration pathway, respectively.

Recently, various kinds of Rubisco structures have been characterized by the determination of high resolution X-ray structures and multidisciplinary studies.^1a,2 Based on numerous experimental studies, possible mechanisms of Rubisco have been proposed.^1a So far, the widely accepted mechanism for carboxylation of RuBP includes the addition of CO₂ (1) and H₂O to enolized RuBP, followed by C–C bond cleavage to the ene-2,3-diol(ate) as shown in Scheme 1. King et al. recently examined the enolization of RuBP by carrying out ab initio second-order Møller–Plesset (MP2) calculations and density functional theory (DFT) calculations.³ Their results suggest that the transition state for proton abstraction in the enolization step may be stabilized by an active site acidic Lys side chain. For the case of Rubisco from Synechococcus, (L₂S₂)₄·^ACO₂·Mg^II·2CABP,^2e this is Lys-175. Unless stated otherwise, we will refer to other key residues whose numbering is based on this structure.

Scheme 1

Reaction pathways for the subsequent Rubisco-catalyzed carboxylation of RuBP were proposed to be related to the reaction pathways for the nonenzymatic carboxylation of RuBP.⁴ In any case, it is interesting to know the fundamental pathways of both the enzymatic and nonenzymatic reactions for the purpose of understanding the function of the enzyme: How does the enzyme change the reaction pathway for carboxylation of RuBP? How much lower is the energy barrier for the enzymatic reaction than that for the corresponding nonenzymatic reaction? So, our first step towards understanding the complicated Rubisco mechanism is to study possible pathways for the nonenzymatic carboxylation of RuBP.

The possible transition states and intermediates of carbon dioxide fixation in the nonenzymatic carboxylation mechanism of RuBP were initially investigated by Tapia and co-workers ⁴ using the ab initio Hartree–Fock (HF ) level of theory. According to their recently reported results,^4a,h the carboxylation step has a very high energy barrier. Although they assumed that the transition state structures may be stabilized by the ‘O’ of the Lys-201 carbamino group through hydrogen bonding, possible intramolecular hydrogen bonding, substituent effect, and solvent effects have not been considered in their ab initio studies of the model system.

To better understand the fundamental pathways for the nonenzymatic carboxylation of RuBP, we have undertaken a more detailed examination of the possible transition state structures and intermediates of differently substituted model systems for the carboxylation of RuBP by carrying out first-principle calculations. Then, by combining the calculated structures, energies, substituent and solvent effects, we deduce the role of the various potential stabilizing factors in lowering the activation energy for the carboxylation and carbon–carbon cleavage steps.

Calculation methods

Two substituted model systems for the carboxylation of RuBP were investigated in this study. In one model system the substituents R′ and R′′ (indicated in Scheme 1) are all simplified as hydrogen atoms, and in the other model system R′ and R′′ are all simplified as methyl groups. Similar simplifications were made by Tapia and co-workers,⁴ who considered R′ = CH₃ and R′′ = H. We expect that this simplification does not change the fundamental reaction pathways, but only affects the calculated energy barriers.

Previous theoretical studies ⁵ of the fundamental reaction pathways for ester hydrolysis indicate that electron correlation effects are not important in the geometry optimizations, but are important in the final energy calculations, for studying the energy profiles of those organic reactions. With a given basis set, the energy barriers evaluated by performing second-order Møller–Plesset (MP2) energy calculations using MP2 geometries are all very close to those evaluated by MP2 calculations using geometries optimized with Hartree–Fock (HF ) and density functional theory (DFT) methods. The energy barriers calculated with the MP2 method are all very close to those calculated with MP4SDQ, QCISD and QCISD(T) methods, indicating that the MP2 method is sufficiently accurate for recovery of the electron correlation.⁵ It should be mentioned that so far, we have considered only the dynamic correlation effects. Non-dynamic correlation effects are sometimes important, particularly for the structure whose lowest electronic excited state is very close to the ground state in energy. Multi-reference configuration interaction calculations are expected to better account for non-dynamic correlation effects. Nevertheless, we checked the energy gaps between HOMO and LUMO for all the optimized structures, and found no obviously small HOMO–LUMO gap. It is expected from the large HOMO–LUMO gap that the first electronic excitation energies should not be very small and, therefore, we feel that non-dynamic correlation effects are not important for the systems considered in this study. Hence, the geometries of all the species considered in this study were optimized by the DFT method,⁶ using Becke’s three parameter hybrid exchange functional ^7a and the Lee–Yang–Parr correlation functional (B3LYP) ^7b with the 6-31+G* basis set.⁸ To further examine the basis set dependence of the optimized geometries, geometry optimizations were also carried out at the B3LYP/6-31G level of theory for some species.⁸ The optimized geometries were employed to carry out MP2 energy calculations with two different basis sets, 6-31+G* and 6-31++G**.⁸ Our results indicate that the 6-31+G* basis set is sufficiently large for both the B3LYP geometry optimizations and the MP2 energy evaluations of the systems considered in this work (see below). Vibrational frequencies were evaluated at the optimized geometries to confirm all the first-order saddle points and local minima found on the potential energy surfaces, and to evaluate zero-point vibration (ZPV) energies.⁹ Intrinsic reaction coordinate (IRC) calculations were also performed to verify the expected connections of the first-order saddle points with local minima found on the potential energy surfaces.¹⁰ Unless indicated otherwise, the Gaussian 98 program ⁸ was used to obtain the present results.

Solvent shifts of energies from gas phase to aqueous solution were evaluated using a self-consistent reaction field (SCRF ) procedure,¹¹ in which the solvent surrounding a solute is considered as a polarizable continuum dielectric medium.¹² The solute–solvent interaction can be divided into a long-range electrostatic interaction and short-range non-electrostatic interaction (such as cavitation, dispersion and Pauli repulsion). While the electrostatic interaction is usually dominant, the non-electrostatic interaction should also have significant contributions to the total energy of the solvated solute.¹² Our previous calculations ⁵ in aqueous solution with the polarizable continuum model (PCM),¹³ implemented in the Gaussian98 program, indicate that the total contributions of the short-range non-electrostatic interaction to the energy changes for all the reaction steps are very small. The largest total contribution of the non-electrostatic interaction to the calculated energy barriers is ≈1 kcal mol⁻¹, while the largest total contribution of the electrostatic interaction to the calculated energy barriers is over 20 kcal mol⁻¹ for the ester hydrolysis.^5b More detailed comparison can be found in literature.^5c Hence, in the present work we completely ignored the non-electrostatic interaction and considered only the electrostatic interaction in the SCRF calculations. In the present study, we used the recently developed GAMESS ¹⁴ implementation of the surface and volume polarization for electrostatic interactions (SVPE).¹¹ The SVPE model is sometimes also called the fully polarizable continuum model (FPCM) ^5b,15 because it fully accounts for both surface and volume polarization effects in the SCRF calculation.¹¹ Previous SVPE calculations indicate that electron correlation effects of the solvent shifts of the calculated energy barriers are nearly negligible; the largest difference between the solvent shifts of the energy barriers for methyl acetate hydrolysis evaluated with the MP2 and HF methods is only ≈0.2 kcal mol⁻¹.^5b Hence, we elected to evaluate the solvent shifts of the energy changes by carrying out the SVPE calculations at the HF/6-31+G* level. The calculated energy change in solution, ΔE_sol, is taken as the sum of the energy change calculated at the MP2/6-31++G** level in the gas phase, ΔE_gas, and the corresponding solvent shift calculated at the HF/6-31+G* level, ΔΔE_sol; i.e. we have ΔE_sol = ΔE_gas + ΔΔE_sol.

All the computations in this work were performed on Silicon Graphics Inc. Origin 200 multiprocessor computers.

Results and discussion

The reaction pathways determined for the addition of CO₂, the addition of H₂O and the C–C bond cleavage are briefly illustrated in Schemes 2, 3 and 4, respectively. The results, including optimized geometries of the reactants (1 and 2a,b), transition states (3a,b, 5a,b, 7a,b, 9a,b, 11a,b, 13a,b, 15a,b, 17a,b, 18a,b, and 19a,b), intermediates (4a,b, 6a,b8a,b, 10a,b, 12a,b, 14a,b, and 16a,b), and products (20a,b and 21a,b) and calculated energy profiles, are depicted in Figs. 1 to 9 and summarized in Tables 1 and 2. A survey of the relative energies listed in Tables 1 and 2 reveals that the relative energies calculated with the B3LYP functional are usually different from those calculated with the MP2 method by a few kcal mol⁻¹. The results of the MP2 energy calculations with two basis sets, 6-31+G* and 6-31++G**, are very close to each other. The largest difference between the two kinds of results associated with the two basis sets is ≈1.5 kcal mol⁻¹. So, the 6-31+G* basis set is indeed sufficient for studying the problem at hand. Below, we will first discuss the results calculated in gas phase for the addition of CO₂, the addition of H₂O, and the C–C bond cleavage. The solvent/environmental effects on the energy profiles will be discussed subsequently.

Table 1 Relative energies (in kcal mol⁻¹) calculated for R′ = R′′ = H with two different basis sets (BS1 = 6-31+G*; BS2 = 6-31++G**). ZPV energies are included

	ΔEgas
	B3LYP/BS1	MP2/BS1	MP2/BS2	ΔΔEsol	ΔEsol
A: Addition of CO2
1 + 2a + H2O	0.0	0.0	0.0	0.0	0.0
3a + H2O (TS2a-4a)	33.1	36.8	37.0	−6.5	30.5
4a + H2O	1.6	0.2	1.0	1.1	2.2
5a + H2O (TS2a-6a)	30.0	31.1	31.8	−6.7	25.1
6a + H2O	0.6	−1.2	−0.2	−0.2	−0.4
7a + H2O (TS2a-8a)	33.3	35.9	37.4	−11.9	25.4
8a + H2O	14.8	13.3	13.8	−1.5	12.3
B: Addition of H2O
9a + H2O (TS4a-10a)	11.0	9.0	9.7	0.4	10.1
10a + H2O	2.2	0.4	1.2	−1.0	0.2
11a (TS10a-12a)	36.9	34.1	35.1	5.9	41.0
12a	−1.8	−5.7	−4.7	5.6	0.9
13a (TS4a-14a)	34.1	31.4	32.5	5.9	38.4
14a	−4.8	−8.6	−7.4	7.5	0.1
15a (TS6a-16a)	33.9	31.2	32.7	8.9	41.6
16a	−2.7	−6.6	−5.4	6.6	1.2
C: C–C bond cleavage
17a (TS12a-20,21a)	27.8	32.2	31.8	7.0	38.9
18a (TS14a-20,21a)	27.0	30.7	31.4	8.0	39.5
19a (TS16a-20,21a)	26.8	30.0	30.8	8.7	39.5
20a + 21a	18.8	23.5	24.2	0.0	24.2

---

Table 2 Relative energies (in kcal mol⁻¹) calculated for R′ = R′′ = CH₃ with two different basis sets (BS1 = 6-31+G*; BS2 = 6-31++G**). ZPV energies are included

	ΔEgas
	B3LYP/BS1	MP2/BS1	MP2/BS2	ΔΔEsol	ΔEsol
D: Addition of CO2
1 + 2b + H2O	0.0	0.0	0.0	0.0	0.0
3b + H2O (TS2b-4b)	27.9	28.0	29.2	−6.1	23.1
4b + H2O	−1.3	−5.8	−4.5	2.1	−2.3
5b + H2O (TS2b-6b)	21.7	19.4	19.9	−4.7	15.2
6b + H2O	−2.2	−7.0	−6.0	1.2	−4.8
7b + H2O (TS2b-8b)	28.2	27.2	28.8	−9.7	19.1
8b + H2O	14.4	8.5	9.0	−0.6	8.4
E: Addition of H2O
10b + H2O	1.4	−4.2	−3.3	−3.9	−7.2
11b (TS10b-12b)	38.1	29.6	30.4	7.1	37.5
12b	2.5	−7.2	−6.3	6.1	−0.2
13b (TS4b-14b)	34.3	25.7	26.7	8.8	35.5
14b	−2.1	−11.9	−10.7	8.1	−2.6
15b (TS4b-16b)	34.4	25.8	27.0	10.0	37.0
16b	0.6	−9.3	−8.2	7.2	−1.0
F: C–C bond cleavage
17b (TS12b-20,21b)	28.2	28.2	28.0	7.7	35.7
18b (TS14b-20,21b)	28.5	26.4	26.4	8.2	34.6
19b (TS16b-20,21b)	29.5	27.2	27.6	9.1	36.6
20b + 21b	13.2	18.4	19.3	2.2	21.5

---

Scheme 2

Scheme 3

Scheme 4

Reaction pathways for addition of CO₂

One can see from Figs. 1 and 2 that the reactants 2a and 2b have a weak intramolecular hydrogen bond between the two hydroxy groups. Upon the substituent change from 2a to 2b, this hydrogen bond becomes stronger, where the H ⋯ OH distance of 2b is shorter by 0.20 Å than that of 2a. So, the methyl group indirectly enhances this hydrogen bonding interaction. CO₂ may attack the C2-center of the enediol in three ways, denoted as A, B, and C in Scheme 2. In the A- and B-types of CO₂ attack, two different kinds of hydrogen bond can be formed: (i) one CO₂ oxygen acts as a nucleophilic center interacting with the hydrogen atom of the –OH group of the C3-center (A-type), which may lead to proton transfer from the –OH to CO₂ during the new C–C bond formation process (4); and (ii) a CO₂ oxygen acts as a nucleophilic center interacting with the hydrogen atom of the –OH group of the C2-center (B-type), which may lead to simultaneous proton transfers from the –OH of the C2-center to CO₂ and from the –OH of the C3-center to the –OH of the C2-center, during the new C–C bond formation process (6). Since no hydrogen bond is formed in the third type of CO₂ attack (C-type), one might expect the formation of the structure with a four-membered ring (8).

Fig. 1 Optimized geometries of CO₂ (1) and 2a–8a involved in the addition of CO₂ for R′ = R′′ = H.

Fig. 2 Optimized geometries of CO₂ (1) and 2b–8b involved in the addition of CO₂ for R′ = R′′ = CH₃.

Fig. 3 Optimized geometries of 9a–16a involved in the addition of H₂O for R′ = R′′ = H.

Fig. 4 Optimized geometries of 9b–16b involved in the addition of H₂O for R′ = R′′ = CH₃.

Fig. 5 Optimized geometries of 17a–21a involved in the C–C bond cleavage for R′ = R′′ = H.

Fig. 6 Optimized geometries of 17b–21b involved in the C–C bond cleavage for R′ = R′′ = CH₃.

Fig. 7 Energy profiles determined in gas phase and in aqueous solution for R′ = R′′ = H. Indicated in parentheses are the corresponding results determined for R′ = R′′ = CH₃. The gas phase energies, ΔE_gas, were calculated at MP2/6-31++G**//B3LYP/6-31+G* level. ΔE_sol = ΔE_gas (MP2/6-31++G**//B3LYP/6-31+G*, including ZPV energy correction) + ΔΔE_sol (HF/6-31G+G*//B3LYP/6-31+G*).

Fig. 8 Energy profiles determined in gas phase and in aqueous solution for R′ = R′′ = H. Indicated in parentheses are the corresponding results determined for R′ = R′′ = CH₃. The gas phase energies, ΔE_gas, were calculated at MP2/6-31++G**//B3LYP/6-31+G* level. ΔE_sol = ΔE_gas (MP2/6-31++G**//B3LYP/6-31+G*, including ZPV energy correction) + ΔΔE_sol (HF/6-31G+G*//B3LYP/6-31+G*).

Fig. 9 Energy profiles determined in gas phase and in aqueous solution for R′ = R′′ = H. Indicated in parentheses are the corresponding results determined for R′ = R′′ = CH₃. The gas phase energies, ΔE_gas, were calculated at MP2/6-31++G**//B3LYP/6-31+G* level. ΔE_sol = ΔE_gas (MP2/6-31++G**//B3LYP/6-31+G*, including ZPV energy correction) + ΔΔE_sol (HF/6-31G+G*//B3LYP/6-31+G*).

The A-, B- and C-types of CO₂ attack lead to transition states 3, 5, and 7, respectively, as shown in Figs. 1 and 2. Our optimized geometry of 3 is similar to the “TS1” structure reported by Safont et al.,^4a where those authors obtained a significantly higher energy barrier, ≈59 kcal mol⁻¹, with their HF calculations. The transition states 5 and 7 are reported here for the first time. In 3a, the strong hydrogen bonding leads to a pseudo six-membered ring structure, while the strong hydrogen bonding in 5a leads to a structure with two pseudo five-membered rings. Compared with the proton transfer in 3a, the greater extent of proton transfer in 5a results in a shorter partial C–C bond between C2 and CO₂ and a stronger C[double bond, length half m-dash]O double bond at C3. It is also noteworthy that the methyl group leads to shortening of the length of the new partial C–C bond. Thus, the addition of CO₂ is sensitive to both substituent and hydrogen bonding effects. A similar substituent effect can also be observed in 7, where the length of the partial C–C bond in 7B is shorter than that in 7a. Clearly, 7 is different from 3 and 5 in that an additional weak interaction between C3 and one oxygen of CO₂ exists in 7, rather than a hydrogen bond between the hydroxy hydrogen and an oxygen of CO₂. It is interesting to note that the further change from 3 to 4 leads to a trans conformation for the two hydroxy oxygen atoms at C2 and C3, while the further change from 5 to 6 leads to a cis conformation for the hydroxy oxygen atoms at C2 and C3. As seen from the energy profiles indicated in Figs. 7 to 9 and Tables 1 and 2, the B-type of CO₂ attack, assisted by double-proton transfer through 5 to 6, is slightly exothermic with a relatively lower energy barrier compared to the A-type, assisted by one-proton, and C-type, without proton transfer. In addition, the effect of methyl groups significantly reduces the barrier by about 7 ≈ 10 kcal mol⁻¹ and increases the stability of 4b, 6b, and 8b.

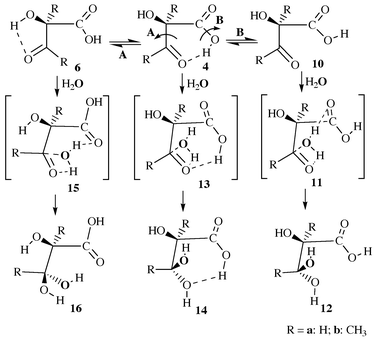
Reaction pathways for addition of H₂O

Once CO₂ has been added to C2 of the substrate, the stage is set for reaction with H₂O starting from intermediate 4, 6 or 8. Of the choices of the starting structure for reaction with H₂O, 6 and 8 each have a cis conformation as discussed above, while 4 has a trans conformation. Of the two cis intermediates, only 6 is further considered here, since it is about 14 kcal mol⁻¹ more stable than 8. The trans intermediate 4 is also further considered below.

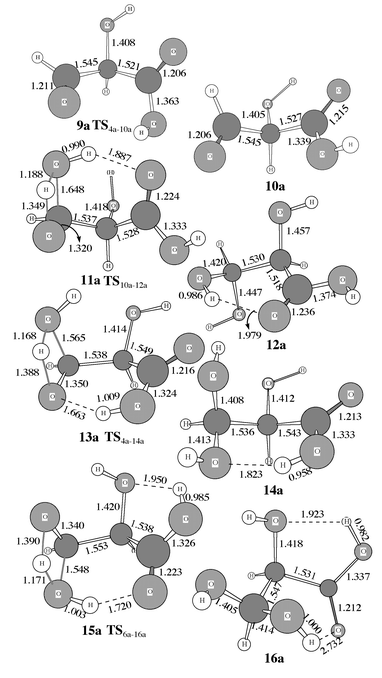
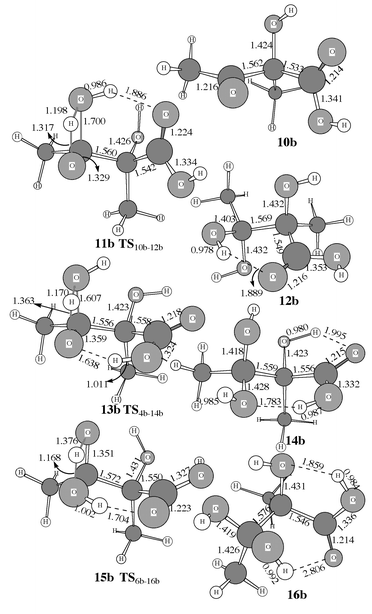
As shown in Scheme 3, the reaction of intermediate 6 with H₂O takes place by attack of H₂O on C3. While the H₂O oxygen gradually approaches C3, one H₂O hydrogen gradually approaches the oxygen atom of the C3-center. However, the H₂O oxygen could approach C3 from two directions. H₂O addition from one direction goes to intermediate 16via transition state 15. In the transition state structure 15 depicted in Figs. 3 and 4, the carbonyl oxygen in the carboxy group is strongly hydrogen bonded with the H₂O hydrogen that is not being transferred to the oxygen of the C3-center. H₂O attack from the other direction can not form a hydrogen bond in the transition state structure; since the energy must be significantly higher than that of 15, we will not further consider this possibility. For the same reason, we also do not consider any obviously unfavorable directions of H₂O attack on intermediate 4.

Direct H₂O attack on intermediate 4 goes to intermediate 14via transition state 13, in which the carboxy hydrogen is strongly hydrogen bonded with the oxygen of the C3-center, as shown in Figs. 3 and 4. Besides direct H₂O attack on intermediate 4, it is also possible that intermediate 4 first changes its configuration into that of intermediate 10 through rotation of the single C–O bond in the carboxy group before H₂O attack (Scheme 3, reaction B). In both intermediates 4 and 10, the four carboxy atoms are all nearly on a plane. The notable configuration difference between 4 and 10 is that their carboxy O–C–O–H dihedral angles are ≈180 and ≈0°, respectively. The C–O bond could rotate in two directions, and thus is associated with two parallel transition states. It is not surprising that the calculated energy barriers with respect to the two rotational transition states are much lower than the energy barriers calculated for other reaction steps. Hence we only show the one, which is the transition state 9a in Fig. 3, with the lowest energy barrier for the case R′ = R′′ = H. The energy of the other transition state (not shown here) is about 3 kcal mol⁻¹ higher than 9a. The addition of H₂O to intermediate 10 produces intermediate 12 through transition state 11, in which the carbonyl oxygen in the carboxy group is hydrogen bonded with the non-transferring hydrogen of H₂O. Comparison between the results calculated for R′ = R′′ = H and for R′ = R′′ = CH₃ indicates that the substituent effects on the energy barriers are not important for the addition of H₂O.

Safont et al.^4a also reported a transition state (“TS2”) for the H₂O addition with a very high energy barrier of ≈66 kcal mol⁻¹ calculated at the HF level. Compared to their reported transition state structure “TS2”, the transition state structures 11, 13, and 15 found in this study all have an additional hydrogen bond between the H₂O hydrogen and the carbonyl oxygen in the carboxy group or between the carboxy hydrogen and the oxygen of the C3-center. Obviously, these hydrogen bonds should significantly stabilize the corresponding transition states. It is noteworthy that the calculated energy barrier becomes lower (Figs. 7 to 9) with R′ = R′′ = H and R′ = R′′ = CH₃ on going from transition state structure 11 to transition state structure 15 and to transition state structure 13. This is completely consistent with the order of the optimized O ⋯ H distance within the hydrogen bond as seen in Figs. 3 and 4. So, the stronger the hydrogen bonding in the transition state, the lower the energy barrier.

Reaction pathways for C–C bond cleavage

After the hydrated ketone intermediates, 12, 14, and 16, are formed, the stage is set for C–C bond cleavage between C2 and C3 as illustrated in Scheme 4. All of the three intermediates go to the same products, 20 and 21, through slightly different transition state structures, 17, 18 and 19, depicted in Figs. 5 and 6. According to the three reaction pathways examined here, the C–C bond cleavage always involves the hydroxy hydrogen of the C3-center attacking the carbonyl oxygen of the carboxy group. In the absence of enzyme, C–C bond cleavage requires direct proton transfer within the molecule. The attacking hydrogen is finally transferred to the receptor oxygen, while the C–C bond is broken. Since the transition states 17, 18 and 19 are all associated with the same kind of proton transfer and same type of hydrogen bonding, the calculated energy barriers corresponding to these transition states are close to each other. The substituent effect is rather small for this reaction stage.

Solvent effects

The calculated solvent shifts of the relative energies and the corresponding relative energies in aqueous solution are listed in the last two columns in Tables 1 and 2. The profiles of the relative energies are also depicted in Figs. 7 to 9. The numerical results reveal that the solvent effects on the energy barriers are significant. The largest solvent shift of an energy barrier is ≈12 kcal mol⁻¹ for the CO₂ addition from 2 to 8. Including the solvent effects, the calculated energy barriers for the addition of CO₂ all become significantly lower by 7–12 kcal mol⁻¹, the calculated energy barriers for the addition of H₂O all become significantly higher by 4–11 kcal mol⁻¹, and the calculated energy barriers for the C–C bond cleavage all become slightly higher by 1–2 kcal mol⁻¹. The solvent shifts of the energy barriers calculated are qualitatively consistent with the corresponding molecular polarity changes from reactants/intermediates to transition states. The polarity, which may be characterized by molecular dipole and multipole moments, of the transition state structures for CO₂ addition is significantly stronger than that of the corresponding reactants, while the polarity of the transition state structures for H₂O addition is significantly weaker than that of the corresponding reactants. The changes in polarity are very small for the C–C bond cleavage reaction stage. It is notable that for each of the reaction pathways depicted in Figs. 7 and 8, the order of the relative magnitudes of the energy barriers for the three major reaction stages are changed by solvent effects.

Finally, it should be mentioned that the solvent effects have been computed with geometries optimized in vacuum without any attempt to explicitly include some additional solvent water molecules in the model for quantum mechanical calculations. By analogy with similar systems studied previously by others it may be assumed that re-optimization of the geometry including solvent effects will not introduce important changes, although the inclusion of one or more water molecules could perhaps modify some transition state structures and make the reaction easier.

Conclusion

A series of first-principle calculations have been carried out on two simplified RuBP model systems to study the reaction mechanism of the nonenzymatic carboxylation of RuBP. Several favorable competing reaction pathways have been found and analyzed. The optimized geometries of the transition states and intermediates and the calculated relative energies are employed to explore the potential importance of stabilizing factors, including hydrogen bonding, substituent and solvent effects. It has been shown that hydrogen bonding plays a key role in transition state stabilization. For the competing reaction pathways in a given reaction stage, the lowest energy barrier is usually associated with the transition state structure with the strongest hydrogen bonding, which is evident in the addition of CO₂ and H₂O. Substituent effects on the calculated energy barriers are also very large for the addition of CO₂, but less important for the subsequent reaction stages. Including solvent effects, the energy barriers calculated for the addition of CO₂ all become significantly lower, the energy barriers calculated for the addition of H₂O all become significantly higher, and the energy barriers calculated for the C–C bond cleavage all become slightly higher.

Acknowledgements

This work was supported partially by the Environmental Technology Division at the Pacific Northwest National Laboratory (R. L. O.). Pacific Northwest National Laboratory is a multiprogram national laboratory operated for the US Department of Energy by Battelle Memorial Institute under contract DE-AC06-76RLO 1830. S. N. has a postdoctoral fellowship administrated by Associated Western Universities.

References

1. (a) W. W. Cleland, T. J. Andrews, S. Gutteridge, F. C. Hartman and G. H. Lorimer, Chem. Rev., 1998, 98, 549; (b) L. Stryer , Biochemistry, W. H. Freeman and Company, New York, 1988;; (c) T. J. Andrews and G. H. Lorimer , in The Biochemistry of Plants, A Comprehensive Treatise, Vol. 10, Photosynthesis, eds. M. D. Hatch and N. K. Boardman, Academic Press, New York, 1987, p. 131;; (d) F. C. Hartman and M. R. Harpel, Annu. Rev. Biochem., 1994, 63, 197; (e) S. Gutteridge and A. A. Gatenby, Plant Cell, 1997, 7, 809; (f) F. C. Hartman and M. R. Harpel, Adv. Enzymol., 1993, 67, 1.
2. (a) T. Lundqvist and G. Schneider, Biochemistry, 1991, 30, 904; (b) T. C. Taylor and I. Andersson, Nat. Struct. Biol., 1996, 3, 95; (c) T. C. Taylor and I. Andersson, J. Mol. Biol., 1997, 265, 432; (d) T. Lundqvist and G. Schneider, J. Biol. Chem., 1991, 226, 12604; (e) J. Newman and S. Gutteridge, J. Biol. Chem., 1993, 268, 25876.
3. W. A. King, J. E. Gready and T. J. Andrews, Biochemistry, 1998, 37, 15414.
4. (a) V. S. Safont, M. Oliva, J. Andres and O. Tapia, Chem. Phys. Lett., 1997, 278, 291; (b) M. Oliva, V. S. Safont, J. Andres and O. Tapia, Chem. Phys. Lett., 1998, 294, 87; (c) O. Tapia, J. Andres and V. S. Safont, THEOCHEM, 1995, 342, 131; (d) O. Tapia, J. Andres and V. S. Safont, J. Phys. Chem., 1994, 98, 4821; (e) J. Andres, V. S. Safont, J. Queralt and O. Tapia, J. Phys. Chem., 1993, 97, 7888; (f) J. Andres, V. S. Safont and O. Tapia, Chem. Phys. Lett., 1992, 198, 515; (g) V. Moliner, J. Andres, M. Oliva, V. S. Safont and O. Tapia, Theor. Chim. Acta, 1999, 101, 228; (h) J. Andres, M. Oliva, V. S. Safont, V. Moliner and O. Tapia, Theor. Chim. Acta., 1999, 101, 234.
5. (a) C.-G. Zhan, D. W. Landry and R. L. Ornstein, J. Am. Chem. Soc., 2000, 122, 1522; (b) C.-G. Zhan, D. W. Landry and R. L. Ornstein, J. Am. Chem. Soc., 2000, 122, 2621; (c) C.-G. Zhan, D. W. Landry and R. L. Ornstein, J. Phys. Chem. A, 2000, 104, 7672.
6. R. G. Parr and W. Yang , Density-Functional Theory of Atoms and Molecules, Oxford University Press, Oxford, 1989..
7. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
8. M. J. Frisch , G. W. Trucks , H. B. Schlegel , G. E. Scuseria , M. A. Robb , J. R. Cheeseman , V. G. Zakrzewski , J. A. Montgomery, Jr. , R. E. Stratmann , J. C. Burant , S. Dapprich , J. M. Millam , A. D. Daniels , K. N. Kudin , M. C. Strain , O. Farkas , J. Tomasi , V. Barone , M. Cossi , R. Cammi , B. Mennucci , C. Pomelli , C. Adamo , S. Clifford , J. Ochterski , G. A. Petersson , P. Y. Ayala , Q. Cui , K. Morokuma , D. K. Malick , A. D. Rabuck , K. Raghavachari , J. B. Foresman , J. Cioslowski , J. V. Ortiz , B. B. Stefanov , G. Liu , A. Liashenko , P. Piskorz , I. Komaromi , R. Gomperts , R. L. Martin , D. J. Fox , T. Keith , M. A. Al-Laham , C. Y. Peng , A. Nanayakkara , C. Gonzalez , M. Challacombe , P. M. W. Gill , B. Johnson , W. Chen , M. W. Wong , J. L. Andres , M. Head-Gordon , E. S. Replogle and J. A. Pople , Gaussian 98, Revision A.6, Gaussian, Inc., Pittsburgh, PA, 1998..
9. (a) H. B. Schlegel, Theor. Chim. Acta, 1984, 66, 33; (b) J. B. Foresman and Æ. Frisch , Exploring Chemistry with Electronic Structure Methods, Gaussian, Inc., 1993..
10. (a) C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154; (b) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523.
11. (a) C.-G. Zhan, J. Bentley and D. M. Chipman, J. Chem. Phys., 1998, 108, 177; (b) C.-G. Zhan and D. M. Chipman, J. Chem. Phys., 1998, 109, 10543; (c) C.-G. Zhan and D. M. Chipman, J. Chem. Phys., 1999, 110, 1611the solute cavity surface is defined as a solute electron charge isodensity contour determined self-consistently during the FPCM iteration process. The contour value has been calibrated as 0.001 a. u. in ref. 11(b). Regarding the detail of the FPCM computation on a given solute under a given quantum mechanical approximation level, once the solute cavity is defined and the relative permittivity is known, the accuracy of the FPCM numerical computation depends only on the number of surface nodes (N ) representing the cavity surface and number of layers (M ) describing the volume polarization charge distribution within a certain, sufficiently large three-dimensional space outside the solute cavity. If one could use an infinite number of nodes and an infinite number of layers, then the numerical results obtained from the FPCM computation would be exactly the same as those determined by the exact solution of the Poisson’s equation for describing the solvent polarization potential. We have shown that the accuracy of the FPCM numerical computations employed in this study with N = 590 and M = 40 (for a step of 0.2 Å) is higher than that required for listing Tables 1 and 2 in this paper. The relative permittivity of water used for the FPCM calculations is 78.5..
12. (a) J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027; (b) C. J. Cramer and D. G. Truhlar , in Solvent Effects and Chemical Reactions, ed. O. Tapia and J. Bertran, Kluwer, Dordrecht, 1996, p. 1..
13. (a) S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117; (b) S. Miertus and J. Tomasi, Chem. Phys., 1982, 65, 239; (c) V. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327.
14. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347.
15. C.-G. Zhan, O. Norberto de Souza, R. Rittenhouse and R. L. Ornstein, J. Am. Chem. Soc., 1999, 121, 7279.

---

Footnote

† Currently visiting the Pacific Northwest National Laboratory. E-mail: Chang-Guo.Zhan@pnl.gov.

---