The role of heteroatom substitution in the rigidity and curvature of buckybowls. A theoretical study

Abstract

Ab initio (Hartree Fock), hybrid density functional (B3LYP), and semiempirical SCF (MNDO and AM1) calculations on sumanene (2), trioxa-sumanene (3) and trithia-sumanene (4) show that the C_3v-bowl structure is a minimum in all cases, but show dramatic variations in bowl depths and inversion barriers. Calculations on monosubstituted corannulenes C₁₉XH₁₀ (X = N⁺, B⁻, P⁺ and Si) at various levels predict that isoelectronic substituents possessing large atomic size increase the bowl-to-bowl inversion barrier at the hub position and decrease it at the rim position. Strain is a guiding factor, which accounts for the relative stability of positional isomers, curvature and bowl rigidity. The most stable positional isomer for a given substituent shows the minimum bowl-to-bowl inversion barrier in all cases. Calculations are performed on monosubstituted sumanenes derived by replacing skeletal C by isoelectronic atoms on sumanene (2), C₂₀XH₁₂ for X = N⁺ and Si. The general strategy of substituting larger atoms at rim positions flattens the bowl, and at the hub position it makes the bowl deeper. The strategy seems to work well. HF/3-21G and B3LYP/6-31G* computations are in very good agreement with each other, both qualitatively and quantitatively, and the central results are reproducible even at semiempirical levels. The performance of MNDO is consistently better than AM1 and becomes the method of choice when ab initio and DFT methods are not practical. Homodesmic equations, used to ascertain the thermodynamic stabilities of the monosubstitutions on corannulenes and sumanenes, show that substitution at appropriate sites imparts stability to the buckybowl framework. Linear correlation is obtained between the curvature, as estimated by the pyramidalization angle (Φ), and the inversion barrier. It is shown that bowl rigidity, curvature and the relative stabilities of positional isomers are controlled by the strain energy build up, which depends on the size of the substituent and the site of substitution.

---

Introduction

The discovery of fullerenes gave a tremendous boost to the research on curved polycyclic aromatic hydrocarbons, and consequently the planarity of polycyclic aromatic hydrocarbons can no longer be taken for granted.¹ Buckybowls, substructures of fullerenes, with an inbuilt curvature exhibit properties which are unique and much different from their planar counterparts.^2–7 Corannulene, 1 (Scheme 1), the leading buckybowl discovered much before the fullerene era,⁸ has drawn renewed attention in the post-fullerene era. Owing to much recent attention to this class of compounds, synthesis of a large number of buckybowls has been accomplished, and many synthetic attempts have been made towards larger buckybowls which form sub-units of fullerenes.^2–12 The other key member of the buckybowl family that is still elusive for experimental synthesis, is 1a,3a,4,4a,6a,7-hexahydro-1H-tricyclopenta[def,jkl,pqr]triphenylene known as sumanene (2) and it is expected to show a rigid bowl according to previous MNDO calculations.^13,14 In terms of symmetry corannulene (1) and sumanene (2) represent basic fullerene fragments possessing five- and three-fold axes respectively.^14a While a large number of theoretical studies of high sophistication have appeared on corannulene,¹⁵ to our knowledge only semiempirical calculations have been done on sumanene and directed synthetic attempts towards this fascinating molecule by Mehta and co-workers did not meet with success.^7,13 The syntheses of many other higher buckybowls, including the three semibuckminsterfullerenes (C₃₀ units) have been accomplished.^9,10 All these higher buckybowls are rigid. In contrast, corannulene is a highly fluxional molecule, which experiences rapid bowl-to-bowl inversion, despite the presence of substantial curvature. Previous strategies to arrest the bowl-to-bowl inversion involve construction of a cyclophane bridge ¹⁶ and fusing of at least one more five-membered ring.¹⁷ Although substitution of a limited number of alkyl or halo groups on the corannulene skeleton does not have a noticeable impact on the bowl rigidity, permethyl substitution substantially reduces the inversion barrier, according to the theoretical calculations of Seigel et al., and this reduction in bowl depth and rigidity is traced to the steric repulsions in the bowl structure.¹⁸ Thus, the strategies employed so far in rigidifying or flattening the bowl geometry of corannulene involve augmenting the molecule with more atoms.

Scheme 1 The structures of corannulene (1), sumanene (2), trioxa-sumanene (3) and trithia-sumanene (4).

As reported in our preliminary communication,¹⁹ the simplest of the strategies to regulate curvature and bowl rigidity involve the replacement of skeletal carbon atoms by isoelectronic substituents. The possible resemblance of deeply curved bowl shaped molecules to the fullerene molecules is an interesting incentive for exploring this chemistry. Despite the tremendous attention directed towards the chemistry of curved carbon networks, as well as some progress in heterofullerene chemistry,^20–23 surprisingly, until recently, very little attention has been paid to hetero-buckybowls. Theoretical calculations on pentasubstituted heterocorannulenes reveal that substitution can greatly affect the inversion barrier.^19,21 Replacement of the three unique methylene groups at the vertex position (Scheme 2) in sumanene (2), by isovalent O and S gives trioxa-sumanene (3) and trithia-sumanene (4).† Incidentally, trithia-sumanene (4) is the first heterobowl molecule to be synthesized; its X-ray structure shows that it is much flatter than corannulene (1).²² Analysing the underlying reasons for the flattening of the bowl on trithia substitution is important, and a comparative study on trioxa-sumanene will shed more light on the problem.

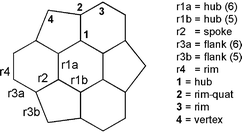Scheme 2 The definition of various unique atom centres and bonds in C_3v sumanene.

The present study reports the first ab initio and DFT calculations on sumanene (2), trioxa-sumanene (3) and trithia-sumanene (4) and compares their bowl rigidity and curvature with that of corannulene. Efforts to understand the structural and electronic perturbations and their consequences on bowl rigidity and curvature by heteroatom substitution on buckybowl are made next by introducing monosubstitutions on corannulenes, at the hub (5), rim-quat (6) and rim (7) positions, and sumanenes at the hub (8), rim-quat (9), rim (10), and vertex (11) positions (Schemes 3 and 4). Skeletal replacements are made with isoelectronic groups. Employing reliable computational methods to get correct trends to understand the general principle is our main concern. Therefore, computational methods were carefully chosen and tested with previous calculations to assess their suitability.

Scheme 3 The structures of monosubstituted corannulenes at the hub (5), rim-quat (6) and rim (7) positions.

Scheme 4 The structures of monosubstituted sumanenes at the hub (8), rim-quat (9), rim (10) and vertex (11) positions.

Computational details

The geometries of all the structures considered in this study were initially fully optimized within symmetry constraints using semiempirical AM1 ²⁴ and MNDO ²⁵ procedures and the stationary points were obtained. Then, the geometries were further refined with standard ab initio techniques by using the HF method with the split valence 3-21G basis set.²⁶ The geometries of C₁₈H₆X₃ are optimized also at the B3LYP ²⁷ level using the 6-31G* basis set, in order to see the effect of electron correlation and a higher basis set on the geometries of the sumanenes. Frequency calculations to characterise the nature of the stationary points were carried out at both semiempirical and HF/3-21G levels for all the monosubstituted corannulenes and C₁₈H₆X₃. Obtaining all real frequencies designates a minimum and one imaginary frequency designates a transition state structure. In most cases, the bowl structures are characterized as minima and the planar structures are characterized as transition states. However, in some cases (7P⁺++ and 8Si) ‡ the planar stationary point possesses two out-of-plane imaginary frequencies, technically designating it as a second-order saddle point. Thus, the true bowl-to-bowl inversion transition in these cases will not be planar. The imaginary frequency for the planar structures corresponds to the normal mode describing the bowl-to-bowl inversion motion. In all cases the designation of the nature of the stationary points is identical both at the semiempirical levels and with the ab initio methods, except for 5P⁺+ which shows two imaginary frequencies at the semiempirical levels and only one at the HF/3-21G level. For the substituted sumanenes only semiempirical methods were used to characterize the stationary point, but geometry optimizations were carried out at the HF level. The inclusion of electron correlation and the effect of adding a set of polarization functions to the basis sets were evaluated by doing B3LYP single point calculations on the HF optimized geometries. All the calculations were done using the Gaussian 94 suite of programs.²⁸ The central idea of the study is to assess the effects of replacing the skeletal C atoms by isoelectronic atoms and to examine the effect on structure, inversion barrier and other properties at intermediate levels of theory. Although we do not claim quantitative accuracy, the trends obtained at this level are unlikely to change at higher levels.

Results and discussion

In this section first the structures, curvature and energetics of sumanene (2), trioxa-sumanene (3) and trithia-sumanene (4) are compared among themselves as well as to those of corannulene (1). This is followed by the study of structural and energetic perturbations on the replacement of C by an isoelectronic group (X = N⁺, B⁻, P⁺ and Si) on the corannulene skeleton. Finally, monosubstituted sumanenes are discussed, where we consider the effect of only two substituents N⁺ and Si, which represent smaller and larger atoms. In this paper, the C–X bond length is taken as a measure for estimating the size of X; thus X = O and N⁺ are smaller substituents, as the C–X bond lengths are shorter than C–C, and similarly X = B⁻, P⁺, S and Si are taken as larger substituents.²⁹

C₁₈H₆X₃ (X = CH₂, O and S): sumanene and related structures

Selected geometrical parameters for the bowl geometry as well as for the corresponding planar transition state structure for bowl-to-bowl inversion are given in Table 1. Bowl depth is defined as the inter-planar distance between the best planes formed by the hub and rim atoms. Clearly, sumanene (2), which possesses a much higher bowl depth, consistently at all levels of theory employed here, is a much deeper bowl than corannulene (1), which is in agreement with a previous study.¹⁴ A substantial increase in the curvature is seen in going from 2 to 3, as reflected in the bowl depths and pyramidalization angles (Table 1 and Fig. 1). In contrast, 4, trithia-sumanene is computed to be a very shallow bowl and exhibits the least curvature among all the structures considered in this section. At the HF/3-21G level the equilibrium structure of 4 is computed to be virtually flat, while some substantial curvature is observed at all other levels. The result of substituting all three of the vertex positions in sumanene by a smaller O atom, which makes the bowl much deeper, and by a larger S atom, which makes it much flatter, is reproduced at all levels of theory. Fig. 1 depicts the B3LYP/6-31G* optimized structures 1–4, which clearly illustrate that sumanene (2) is much more curved than corannulene (1). Also drastic variations in the curvatures of 3 and 4 upon replacing the vertex methylene groups by O and S groups respectively, compared to parent sumanene (2) are clearly illustrated. Let us explore the underlying reasons for this dramatic alteration in the curvature of buckybowls upon skeletal replacements with atoms with different sizes and electronegativity.

Table 1 Selected geometric parameters, total energies at the HF/3-21G and B3LYP/6-31G* levels for corannulene (1) and sumanenes (2–4). Total energies in hartrees, bond lengths in Å and pyramidalization angle (Φ) in degrees. B3LYP/6-31G* optimized values are given in parentheses

	1		2		3		4
Parameter	Bowl	Planar	Bowl	Planar	Bowl	Planar	Bowl	Planar
a The pyramidalization angle (Φ) is defined as Φ = 360 − (θ1 + θ2 + θ3), where, θ1, θ2 and θ3 are the bond angles around the unique hub atom. b Bowl depth is defined as the inter-planar distances between the best planes formed by the hub and rim atoms respectively. c Corresponds to values for HF/3-21G optimized geometries. d Corresponds to B3LYP/6-31G* optimized geometries.
Hub (6): r1a	1.415 (1.417)	1.393 (1.397)	1.364 (1.387)	1.346 (1.366)	1.375 (1.399)	1.330 (1.349)	1.365 (1.391)	1.365 (1.383)
Hub (5): r1b	—	—	1.435 (1.433)	1.398 (1.399)	1.433 (1.428)	1.369 (1.369)	1.409 (1.414)	1.409 (1.403)
Spoke: r2	1.359 (1.385)	1.343 (1.368)	1.389 (1.399)	1.365 (1.376)	1.373 (1.389)	1.339 (1.351)	1.369 (1.391)	1.369 (1.384)
Flank (6): r3a	1.449 (1.448)	1.467 (1.462)	1.382 (1.400)	1.403 (1.417)	1.392 (1.409)	1.425 (1.439)	1.390 (1.410)	1.390 (1.414)
Flank (5): r3b	—	—	1.567 (1.556)	1.617 (1.597)	1.426 (1.408)	1.495 (1.482)	1.876 (1.813)	1.875 (1.827)
Rim: r4	1.368 (1.390)	1.383 (1.404)	1.426 (1.432)	1.446 (1.455)	1.407 (1.417)	1.460 (1.474)	1.417 (1.419)	1.417 (1.428)
Φ ^a	6.4 (7.0)	—	6.9 (6.7)	—	11.5 (12.5)	—	0.0 (0.3)	—
Bowl depth ^b	0.879 (0.863)	—	1.122 (1.120)	—	1.424 (1.486)	—	0.001 (0.643)	—
E HF	−758.90818	−758.89143	−797.69900	−797.66986	−904.49414	−904.39310	−1867.98997	−1867.98996
E B3LYP	−768.14269 ^c (−768.14933) ^d	−768.12964 (−768.13562)	−807.42523 (−807.43128)	−807.39847 (−807.40445)	−915.07506 (−915.08203)	−914.96855 (−914.97325)	−1884.10301 (−1884.11528)	−1884.10318 (−1884.11242)

---

Fig. 1 B3LYP/6-31G* optimized structures of corannulene (1), sumanene (2), trioxa-sumanene (3), and trithia-sumanene (4).

Curvature is an important feature and the pyramidalization at the hub atoms will give a quantitative measure of this. However, in all the substitutional isomers, except for the parent compounds, the hub has no local symmetry and thus pyramidalizations at various hub positions are different. The variation in pyramidalization is of course very drastic in the hub-substituted isomers. Several measures were previously put forward for the pyramidalization at the tricoordinate carbon and the curvature in polycyclic systems.^30–33 The most straight-forward and simplest of these is the deficiency angle, ϕ = 360 − (θ₁ + θ₂ + θ₃), where θ₁, θ₂, θ₃ are angles around a given hub atom. The sum of these angles in a plane-faced surface will yield the Gaussian curvature for the structure. Thus, the sum of the deficiency angles at the hub position will provide the Gaussian curvature for the buckybowls. Then, the average of the ϕ values in the hub position is taken as the pyramidalization angle (Φ), which is nothing but the curvature per peri-fused hub atom. Therefore, the pyramidalization angle (Φ) will act as a uniform measure to gauge the curvature of the structures considered in the study.

The driving force for a polycyclic aromatic hydrocarbon containing an admixture of five- and six-membered rings to adopt curved geometry is strain relief from the planar form. Naturally, higher strain in the planar structure leads to a greater tendency to pucker. Therefore, the structures, which experience maximum strain in the planar form, have a greater tendency to pucker and eventually their equilibrium bowl structures will be more curved. The build-up of strain in both planar and bowl forms is clearly reflected in the bond lengths of their planar forms; the inner bond lengths, which represent the hub for the buckybowl, are shorter than normal and the outer bond lengths, which represent the rim of the buckybowl, are elongated in this class of compound. The release of strain in going from planar to bowl structures can be seen in the increase of hub and spoke bond lengths and decrease of rim and flank bond lengths. Maximum changes in bond length are seen for 3 and the minimum for 4, in going from the bowl to transition state structure. The optimized geometries of 1–4 are depicted in Fig. 1, which helps in correlating the bowl depths of these structures.

Bowl-to-bowl inversion barriers computed at various levels for 1–4 are given in Table 2. The bowl-to-bowl inversion barrier of sumanene (2) is almost double that of corannulene (1). While MNDO underestimates the barrier of corannulene, AM1 overestimates it. Both semiempirical methods, MNDO and AM1, significantly overestimate the barrier for sumanene (2) compared to higher levels. Interestingly, trithia-sumanene (2) shows no barrier at the HF/3-21G level, as expected from its virtually flat structure at this level (Table 1). However, reoptimization at the B3LYP level shows some curvature, but the inversion barrier is just 1.8 kcal mol⁻¹, indicating an extremely soft potential for bowl-to-bowl inversion and high flexibility of the structure. Single point calculations at the B3LYP level show very similar results to that of the B3LYP optimized structure. Therefore, for all the unsymmetrical structures only single point calculations at B3LYP level are performed and the expensive optimizations are avoided. One particular imposing qualitative observation is that O substitution at vertex positions increases the barrier while S substitution decreases the inversion barrier by an order of magnitude, a feature that is maintained at all levels of theory (Table 2).

Table 2 Bowl-to-bowl inversion barriers of corannulene (1), sumanene (2), trioxa-sumanene (3) and trithia-sumanene (4) calculated at AM1, MNDO, HF/3-21G and B3LYP levels. All values are given in kcal mol⁻¹

Method	1	2	3	4
AM1	16.9	35.0	96.6	7.8
MNDO	8.0	24.4	97.8	7.6
HF/3-21G	10.5	18.3	63.4	0.0
B3LYP/6-31G*//HF/3-21G	8.2	16.8	66.8	−0.1
B3LYP/6-31G*	8.6	16.8	68.3	1.8

---

Monosubstituted corannulenes, C₁₉XH₁₀ (X = N⁺, B⁻, P⁺ and Si)

In this as well as the following sections only the equilibrium geometries at the HF/3-21G level and the energetics of B3LYP/6-31G* on HF/3-21G geometries are discussed unless otherwise specified.

Table 3 gives the important skeletal parameters of the mono hub-substituted corannulenes (5) at the HF/3-21G level along with the total energies for both minima and transition states for bowl-to-bowl inversion. The numbering scheme is given in Scheme 5. In the planar form, the bond lengths are already substantially shrunk in the parent corannulene (1) as well as in other buckybowls. Therefore, substitution at the hub position by a larger atom demanding longer bond lengths, increases the strain, while the smaller substituents decrease the bond lengths as can be clearly seen from Table 1. Comparison of relative sizes is done by taking C as the reference atom, and in this regard N is classified as the smaller atom and B, P and Si as larger atoms in increasing order of the size. Thus a smaller substituent at a hub position will naturally fit into the site and decrease strain in the planar form, while a larger substituent increases the strain. Accordingly, the strain energy in the planar form, which is a driving force for ring puckering and manifests itself in a bowl-to-bowl inversion barrier, is controlled by the size of the substituent. The pyramidalization angle, which is lower for 5N⁺+, compared to the parent corannulene (1) and higher for 5B⁻−, 5P⁺+ and 5Si nicely correlates with the fact that a larger substituent at the rim positions makes the surface more curved.

Table 3 Selected geometric parameters, total energies at HF/3-21G and B3LYP/6-31G* of the corannulenes substituted at the hub position. Total energies, ZPE in hartrees, bond lengths in Å and angles (ϕ and Φ) in degrees

	5N^++		5B^−−		5P^++		5Si
Parameter	Bowl	Planar	Bowl	Planar	Bowl	Planar	Bowl	Planar
a ϕ1 is defined as the pyramidalization angle ϕ1 = 360 − (θ1 + θ2 + θ3), where, θ1, θ2 and θ3 are the angles around centre 1 (Scheme 4). Similarly ϕ2 and ϕ3 represent pyramidalization angles at centres 2 and 3, respectively. b Φ is defined as the average of the pyramidalization angles at the hub position (Φ = (ϕ1 + ϕ2 + ϕ3 + ϕ4 + ϕ5)/5). c NIMG stands for number of imaginary frequencies. d Single point energies of HF/3-21G optimized geometries.
Hub: r1a	1.376	1.363	1.513	1.468	1.815	1.641	1.852	1.692
Hub: r1b	1.388	1.375	1.427	1.393	1.393	1.391	1.420	1.391
Hub: r1c	1.396	1.378	1.445	1.419	1.448	1.422	1.456	1.443
Spoke: r2a	1.331	1.323	1.457	1.420	1.812	1.606	1.816	1.645
Spoke: r2b	1.352	1.343	1.369	1.343	1.366	1.339	1.369	1.336
Flank: r3a	1.432	1.440	1.448	1.473	1.414	1.534	1.440	1.546
Flank: r3b	1.442	1.451	1.463	1.493	1.456	1.525	1.465	1.552
Rim: r4	1.374	1.383	1.376	1.402	1.387	1.418	1.374	1.425
ϕ1 ^a	2.5	—	13.5	—	78.0	—	78.1	—
ϕ2	3.2	—	10.5	—	4.2	—	6.1	—
ϕ3	5.1	—	6.1	—	6.2	—	6.5	—
Φ ^b	3.8	—	9.3	—	19.8	—	20.7	—
E HF	−775.21444	−775.20918	−745.80417	−745.76783	−1059.97337	−1059.83262	−1008.55907	−1008.41530
ZPE (NIMG) ^c	0.25206	0.25282	0.24431	0.24446	0.24346	0.24383	0.24177	0.23978
E B3LYP ^d	−784.58523	−784.57828	−754.91705	−754.88194	−1071.10510	−1070.99742	−1019.43484	−1019.31638

---

Scheme 5 The numbering scheme employed in Tables 3–5 for the monosubstituted corannulenes.

Variations in skeletal geometric parameters and pyramidalization angles for the rim-quat substituted corannulenes (6) are given in Table 4. A glance through Table 4 does not show any unusual build up of strain in any of the isomers compared to the parent corannulene. The variations of bond lengths in going from bowl to planar forms are comparable to those in the parent corannulene. Importantly, the variation in the pyramidalization angle is much smaller in the rim-quat substituted isomers and comparable to that of corannulene. However, there is a slight preference for a larger atom to occupy the rim-quat position as reflected in the lower pyramidalization angles for larger substituents.

Table 4 Selected geometric parameters, total energies at HF/3-21G and B3LYP/6-31G* of the corannulenes substituted at the rim-quat position. Total energies, ZPE in hartrees, bond lengths in Å and angles (ϕ and Φ) in degrees

	6N^++		6B^−−		6P^++		6Si
Parameter	Bowl	Planar	Bowl	Planar	Bowl	Planar	Bowl	Planar
a Single point energies of HF/3-21G optimized geometries.
Hub: r1a	1.406	1.387	1.415	1.394	1.412	1.396	1.415	1.398
Hub: r1b	1.411	1.386	1.420	1.402	1.416	1.396	1.420	1.405
Hub: r1c	1.416	1.391	1.411	1.393	1.411	1.392	1.407	1.392
Spoke: r2a	1.313	1.296	1.469	1.446	1.707	1.658	1.734	1.716
Spoke: r2b	1.358	1.341	1.371	1.355	1.369	1.353	1.370	1.357
Flank: r3a	1.418	1.433	1.579	1.604	1.821	1.824	1.858	1.882
Flank: r3b	1.455	1.474	1.462	1.475	1.453	1.459	1.453	1.461
Rim: r4	1.354	1.368	1.368	1.382	1.354	1.370	1.370	1.379
ϕ1	3.5	—	9.3	—	2.7	—	6.6	—
ϕ2	7.3	—	4.6	—	5.5	—	3.6	—
ϕ3	7.2	—	5.1	—	5.7	—	4.4	—
Φ	6.5	—	5.7	—	5.0	—	4.5	—
E HF	−775.18984	−775.17319	−745.83628	−745.82306	−1059.99700	−1059.98294	−1008.63101	−1008.62211
ZPE (NIMG)	0.25145	0.25214	0.24449	0.24496	0.24453	0.24525	0.24330	0.24379
E B3LYP ^a	−784.55954	−784.54347	−754.94614	−754.93525	−1071.12811	−1071.11252	−1019.49751	−1019.48830

---

Table 5 gives the variation in the geometric parameters in the rim-substituted corannulenes along with the total energies. The maximum changes in the bond length variations are seen for 7N⁺+, and they are much smaller in 7Si. More importantly, the variations in 7Si and 7P⁺++ are much smaller even compared to the parent corannulene (Table 1). Pyramidalization angles (Φ) give key information on how curved these bowls are. Larger Φ values represent higher curvature and greater bowl depths. The geometric form of 7Si is much shallower. Clearly, larger substituents at this position make the structures much flatter and smaller substituents make the structure more curved.

Table 5 Selected geometric parameters, total energies at HF/3-21G and B3LYP/6-31G* of the corannulenes substituted at the rim position. Total energies, ZPE in hartrees, bond lengths in Å and angles (ϕ and Φ) in degrees

	7N^++		7B^−−		7P^+++		7Si
Parameter	Bowl	Planar	Bowl	Planar	Bowl	Planar	Bowl	Planar
a Single point energies of HF/3-21G optimized geometries.
Hub: r1a	1.407	1.383	1.419	1.405	1.439	1.422	1.437	1.433
Hub: r1b	1.408	1.387	1.407	1.388	1.397	1.398	1.411	1.403
Hub: r1c	1.417	1.390	1.414	1.399	1.407	1.389	1.400	1.392
Hub: r1d	1.417	1.392	1.408	1.391	1.405	1.388	1.397	1.389
Hub: r1e	1.411	1.384	1.420	1.406	1.409	1.402	1.418	1.412
Spoke: r2a	1.351	1.333	1.372	1.360	1.355	1.358	1.370	1.367
Spoke: r2b	1.371	1.353	1.382	1.366	1.400	1.369	1.370	1.365
Flank: r3a	1.396	1.408	1.581	1.604	1.859	1.799	1.860	1.868
Flank: r3b	1.408	1.425	1.422	1.434	1.368	1.414	1.436	1.439
Rim: r4	1.343	1.361	1.513	1.527	1.860	1.742	1.778	1.784
ϕ1	7.2	—	4.0	—	3.0	—	1.5	—
ϕ2	5.1	—	6.4	—	2.5	—	1.9	—
ϕ3	8.1	—	3.8	—	4.7	—	2.0	—
Φ	7.0	—	4.7	—	3.7	—	2.0	—
E HF	−775.19243	−775.17174	−745.83180	−745.82334	−1060.00690	−1059.99355	−1008.64519	−1008.64385
ZPE (NIMG)	0.25189	0.25259	0.24283	0.24325	0.24179	0.24233	0.24076	0.24109
E B3LYP ^a	−784.56424	−784.54568	−754.94950	−754.94268	−1071.13567	−1071.12852	−1019.51789	−1019.51676

---

Fig. 2 depicts the optimized structures of all the monosubstituted corannulenes studied here. Clearly, one can see that in going from hub-substitution to rim-substitution the bowl becomes flatter for B⁻, P⁺ and Si and gets somewhat deeper for the N⁺ case. However, the energetics of these isomers and the inversion barriers for each of these isomers are good indicators for the rigidity of the individual isomers.

Fig. 2 HF/3-21G optimized structures of monosubstituted corannulenes C₁₉XH₁₀ (X = N⁺, B⁻, P⁺, and Si) at the hub (5), rim-quat (6) and rim (7) positions.

Table 6 gives the relative energies of the positional isomers as well as the inversion barriers for each of the isomers. The relative stabilities of the positional isomers show interesting trends. For N⁺, which is a smaller substituent the hub position gives maximum thermodynamic stability. However, for other substituents (B⁻, P⁺ and Si), which are larger in size, the rim substituted compound (7) is expectedly the most stable positional isomer and possesses the least strain. The rule of topological charge stabilization ^34,35 fails to predict the correct relative stability orderings of corannulenes following monosubstitution. Thus, the relative stabilities of the positional isomers are solely controlled by the size of the substituents and largely independent of other properties such as electronegativity of the substituent.^19,35 The positional isomer that is the least stable possesses the highest inversion barrier in all cases. This clearly indicates that strain plays a decisive role in determining the thermodynamic stability and curvature of the buckybowls. Thus, a smaller substituent (N⁺) prefers to occupy the rim position with consequently lower strain, while the larger substituents (B⁻, P⁺ and Si) prefer to occupy the rim position.

Table 6 The relative energies (ΔE) and the bowl-to-bowl inversion barriers (ΔE^‡) of monosubstituted corannulenes at the HF/3-21G and B3LYP/6-31G* levels. All values are given in kcal mol⁻¹

	HF		B3LYP ^a
Structure	ΔE	ΔE ^‡	ΔE	ΔE ^‡
a Single point energies of HF/3-21G optimized geometries.
5N^++	0.0	3.3	0.0	4.4
6N^++	15.4	10.5	16.1	10.1
7N^++	13.8	13.0	13.2	11.6
5B^−−	0.0	22.8	0.0	22.0
6B^−−	−20.2	8.3	−18.3	6.9
7B^−−	−17.3	5.3	−20.4	4.3
5P^++	0.0	88.3	0.0	67.6
6P^++	−14.8	8.8	−14.4	9.7
7P^+++	−21.0	8.3	−19.2	4.5
5Si	0.0	90.2	0.0	74.3
6Si	−45.1	5.5	−39.3	5.8
7Si	−54.0	0.8	−52.1	0.7

---

Monosubstituted sumanenes, C₂₀YH₁₂ (Y = N⁺ and Si)

The HF/3-21G optimized skeletal parameters for molecules monosubstituted at the hub (8), rim-quat (9), rim (10) and vertex (11) substituted sumanenes are given in Tables 7, 8, 9 and 10 respectively. Fig. 3 depicts the optimized minimum energy bowl structures of all the positional isomers. Here only N⁺ and Si substitutions are chosen, which will effectively represent the effect of smaller and larger substitutions. Expectedly at a rim position, Si substitution leads to a more curved network with a large pyramidalization angle, which necessitates greater variations in the skeletal parameters in going from bowl to planar forms. Surprisingly Si substitution at the rim-quat (9Si) and rim (10Si) positions leads to shallower bowl structures with much reduced curvature, which gets further reduced in going to the vertex position (11Si). Thus, 8Si is the most strained positional isomer with the highest Φ. Clearly, the system strain energy estimated through Φ accounts for the thermodynamic stability, which then increases in the following order: 8Si < 9Si < 10Si < 11Si. Exactly the opposite trends are seen for the smaller substituent N⁺. Thus, the hub-substituted sumanene (8N⁺+) yields the most shallow bowl, and the bowl depth increases as we go to rim-quat, rim and vertex substitutions as reflected in the pyramidalization angles. The changes in the skeletal parameters in going from bowl to planar forms are more in cases where the pyramidalization angle is more (Tables 7–10). Therefore, for sumanenes skeletal replacement of a C atom by an isoelectronic larger substituent at the hub position increases the strain, thus triggering higher puckering, and replacement by smaller substituents reduces strain, which gives flatter equilibrium structures. Substitution at the vertex position has exactly the opposite effect, i.e., larger substituents decrease strain and smaller substituents increase strain.

Table 7 Selected geometric parameters, total energies at HF/3-21G and B3LYP/6-31G* of the sumanenes substituted at the hub position. Total energies in hartrees, bond lengths in Å and angles (ϕ and Φ) in degrees. The numbering convention is as illustrated

	8N^++		8Si
Parameter	Bowl	Planar	Bowl	Planar
a Single point energies of HF/3-21G optimized geometries.
Hub (6): r1a	1.319	1.310	1.833	1.653
Hub (5): r1b	1.405	1.378	1.894	1.686
Spoke: r2	1.367	1.354	1.884	1.663
Flank (6): r3a	1.363	1.374	1.348	1.466
Flank (5): r3b	1.561	1.595	1.555	1.765
Rim: r4	1.438	1.453	1.467	1.508
ϕ1	3.7	—	88.1	—
ϕ2	4.5	—	5.0	—
ϕ3	6.2	—	6.9	—
ϕ4	5.7	—	7.6	—
Φ	5.1	—	19.7	—
E HF	−814.00331	−813.98932	−1047.35702	−1047.18174
E B3LYP ^a	−823.86429	−823.84769	−1058.72130	−1058.57460

---

Table 8 Selected geometric parameters, total energies at HF/3-21G and B3LYP/6-31G* of the sumanenes substituted at the rim-quat position. Total energies in hartrees, bond lengths in Å and angles (ϕ and Φ) in degrees. The number convention is as illustrated

	9N^++		9Si
Parameter	Bowl	Planar	Bowl	Planar
a Single point energies of HF/3-21G optimized geometries.
Hub (6): r1a	1.363	1.347	1.366	1.353
Hub (5): r1b	1.415	1.382	1.439	1.413
Spoke: r2	1.338	1.314	1.769	1.744
Flank (6): r3a	1.355	1.374	1.796	1.821
Flank (5): r3b	1.552	1.611	1.974	2.039
Rim: r4	1.391	1.409	1.428	1.437
ϕ1	4.4	—	6.4	—
ϕ2	8.5	—	3.8	—
ϕ3	6.5	—	4.9	—
ϕ4	7.4	—	5.1	—
Φ	7.1	—	4.8	—
E HF	−813.99296	−813.96346	−1047.42797	−1047.41362
E B3LYP ^a	−823.85486	−823.82436	−1058.78584	−1058.77067

---

Table 9 Selected geometric parameters, total energies at HF/3-21G and B3LYP/6-31G* of the sumanenes substituted at the rim position. Total energies in hartrees, bond lengths in Å and angles (φ and Φ) in degrees. The number convention is as illustrated

	10N^++		10Si
Parameter	Bowl	Planar	Bowl	Planar
a Single point energies of HF/3-21G optimized geometries.
Hub (6): r1a	1.366	1.346	1.385	1.379
Hub (5): r1b	1.432	1.389	1.443	1.426
Spoke: r2	1.372	1.348	1.398	1.392
Flank (6): r3a	1.337	1.356	1.794	1.806
Flank (5): r3b	1.561	1.624	1.566	1.585
Rim: r4	1.403	1.425	1.828	1.844
ϕ1	8.7	—	2.3	—
ϕ2	7.9	—	3.9	—
ϕ3	7.5	—	4.4	—
ϕ4	6.4	—	4.8	—
Φ	7.3	—	3.8	—
E HF	−813.99137	−813.95904	−1047.43346	−1047.42573
E B3LYP ^a	−823.85347	−823.82206	−1058.79961	−1058.79211

---

Table 10 Selected geometric parameters, total energies at HF/3-21G and B3LYP/6-31G* of the sumanenes substituted at the vertex position. Total energies in hartrees, bond lengths in Å and angles (ϕ and Φ) in degrees. The number convention is as illustrated

	11N^++		11Si
Parameter	Bowl	Planar	Bowl	Planar
a Single point energies of HF/3-21G optimized geometries.
Hub (6): r1a	1.363	1.342	1.370	1.363
Hub (5): r1b	1.428	1.387	1.457	1.445
Spoke: r2	1.376	1.348	1.398	1.390
Flank (6): r3a	1.373	1.394	1.388	1.396
Flank (5): r3b	1.554	1.610	1.943	1.965
Rim: r4	1.426	1.449	1.421	1.429
ϕ1	7.9	—	2.4	—
ϕ2	7.2	—	3.5	—
ϕ3	7.6	—	4.4	—
Φ	7.6	—	3.4	—
E HF	−813.96108	−813.92421	−1047.47969	−1047.47364
E B3LYP ^a	−823.81691	−823.78113	−1058.83947	−1058.83329

---

Fig. 3 HF/3-21G optimized structures of monosubstituted sumanenes C₂₀XH₁₂ (X = N⁺ and Si) at the hub (8), rim-quat (9), rim (10) and vertex (11) positions.

The relative energetics of the monosubstituted corannulenes and the bowl-to-bowl inversion barriers of all the positional isomers for N⁺ and Si substituted sumanenes are given in Table 11. The HF and B3LYP levels exhibit excellent qualitative agreement with each other and thus the principal conclusions obtained using any of the methods should be the same. Firstly, the relative stabilities of the positional isomers show trends, which are essentially similar to what is observed for monosubstituted corannulenes and the stabilities of the positional isomers are in the order 11Si > 10Si > 9Si > 8Si. Following the same trend for the substitution by a smaller atom (N⁺) the hub substitution (8N⁺+) leads to the most stable isomer, and the isomer stability decreases as we go to rim-quat, rim and vertex substitutions, with the following relative stability ordering: 8N⁺+ > 9N⁺+ > 10N⁺+ > 11N⁺+. Thus clearly the thermodynamic stabilities of the positional isomers are controlled by the strain factor.

Table 11 The relative energies (ΔE) and the bowl-to-bowl inversion barriers (ΔE^‡) of monosubstituted sumanenes at the HF/3-21G and B3LYP/6-31G* levels. All values are given in kcal mol⁻¹

	HF		B3LYP ^a
Structure	ΔE	ΔE ^‡	ΔE	ΔE ^‡
a Single point energies of HF/3-21G optimized geometries.
8N^++	0.0	8.8	0.0	10.4
9N^++	6.5	18.5	5.9	19.2
10N^++	7.5	20.3	6.8	19.7
11N^++	26.5	23.1	29.7	22.5
8Si	0.0	110.0	0.0	92.1
9Si	−44.5	9.0	−40.5	9.5
10Si	−48.0	4.9	−49.1	4.7
11Si	−77.0	3.8	−74.2	3.9

---

The bowl-to-bowl inversion barriers for N⁺ substituted sumanenes show that the hub-substituted isomer has a significantly lower barrier compared to the parent sumanene (2). But 9N⁺+, 10N⁺+, and 11N⁺+ where N⁺ is substituted at the rim-quat, rim, and vertex positions respectively have much higher barriers than both 8N⁺+ and sumanene (see Table 2). In contrast for Si substitution, the barrier shoots up to more than 90 kcal mol⁻¹ for hub substitution. However, the bowl-to-bowl inversion barriers for 9Si and 11Si are much less compared to that for 2. Therefore, in sumanenes, the rim-quat (9) position also mimics the periphery rather than the base of the bowl in a similar fashion to the rim (10) and vertex (11) positions.

The other important observation is that the least stable positional isomer exhibits the maximum bowl-to-bowl inversion barrier in both cases, which is a diagnostic feature clearly establishing the link between the strain energy, thermodynamic stability, curvature and bowl rigidity. In other words, the isomer that is more strained will be the least stable positional isomer for a given substituent and will experience maximum strain. Therefore, a greater reorganization of the skeleton is necessary to relieve strain, which makes the structure a deeper bowl. Thus, the key feature that controls the relative stability and bowl-to-bowl inversion barrier in these hetero-buckybowls is strain, which in turn is controlled by the size and site of substitution.

Suitability of theoretical methods

The energetics of the substituted corannulenes and sumanenes are evaluated at semiempirical (AM1 and MNDO), ab initio and DFT levels. In this study, B3LYP/6-31G* energetics are taken as a reference and the performances of other methods are evaluated with respect to it. Fig. 4 gives the relative energies of monosubstituted corannulenes. The B3LYP and HF levels are in good agreement with each other, albeit with small differences between 4B⁻− and 5B⁻−. The qualitative trends are reproducible at all levels, except in the case of the P⁺ substituent where both semiempirical methods fail to reproduce the correct trends. The deviation of AM1 in giving the relative stabilities is very significant, making it quite unsuitable, and the performance of MNDO is slightly better for the rest of the isomers.

Fig. 4 Relative energies of positional isomers of monosubstituted corannulenes C₁₉XH₁₀ (X = N⁺, B⁻, P⁺, and Si) at various levels of theory. (a) X = N⁺; (b) X = B⁻; (c) X = P⁺ and (d) X = Si.

Fig. 5 gives the comparative performances of various methods for the substituted sumanenes. Here also the trends as well as absolute values at the HF and B3LYP levels are comparable and MNDO was found to be good for N⁺ substitution. Again, the performance of the AM1 level is bad, making it a poor choice to study this class of compounds. MNDO performs extremely well for N⁺ substituted isomers and the deviations are significant for Si isomers.

Fig. 5 Relative energies of positional isomers of monosubstituted sumanenes C₂₀XH₁₂ (X = N⁺ and Si) at various levels of theory. (a) X = N⁺; (b) X = Si.

Fig. 6 gives the inversion barriers of all the isomers studied in the paper at all the theoretical levels. The variations of the bowl-to-bowl inversion barriers cover a wide range from nothing (0 kcal mol⁻¹) to more than 100 kcal mol⁻¹. The graph clearly indicates that HF and B3LYP are in excellent agreement with each other, especially in cases where the inversion barrier heights are lower than 25 kcal mol⁻¹. Although the trends as well as the quantities obtained are essentially similar at the HF and B3LYP levels in most cases, some significant deviations are seen for isomers with high inversion barriers. Of the two semiempirical methods, the performance of MNDO is consistently better than that of AM1 in essentially all cases, and the former makes a better choice for predicting the energetics for this class of compounds. In all cases, the barrier height is computed to be higher at the AM1 level compared to MNDO. For monosubstituted corannulenes the barrier height at the MNDO level is either underestimated or comparable to that at higher levels, which is similar to that of the parent molecule. In contrast, for the substituted sumanenes (except for 6Si) as well as for 2, 3 and 4, the barrier is consistently overestimated by both MNDO and AM1 levels.

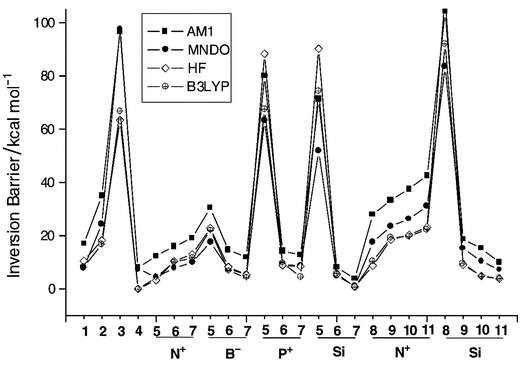Fig. 6 Plot of the barrier heights for the bowl-to-bowl inversion at various levels of theory for all the isomers considered in the study.

Thus, the intermediate levels of ab initio and DFT calculations are expected to yield reliable trends in predicting the relative stabilities of the positional isomers as well as the bowl-to-bowl inversion barriers. Although higher levels may be required for quantitative accuracy, the trends obtained at this level are unlikely to be altered at higher levels of theory.

Homodesmic equations

The thermodynamic stabilities of the heteroaromatic species compared to their parent unsubstituted molecules are evaluated by using the following homodesmic equation [eqn. (1)] for 3 and 4. The B3LYP energies of HF optimized geometries are used to obtain the ΔE values. From a thermodynamic point of view, both 3 and 4 seem to be less stable compared to their unsubstituted analogue. The stability of trithia-sumanene (4) is more or less comparable to that of sumanene, whereas its oxa analogue 3 is significantly less stable.

C₂₁H₁₂ (2) + 3(CH)₄X → C₁₈X₃H₆ + 3(CH)₄CH₂ (1)

(ΔE/kcal mol⁻¹ = 67.8 (X = O); 11.5 (X = S))

To gauge the effect of monosubstitution on the thermodynamic stability compared to pristine systems the following homodesmic equations, eqn. (2) and eqn. (3) are used for corannulenes and sumanenes respectively. For comparison, only the energetics of the most stable isomer are given. Thus, for a larger substituent the substitutions at the rim and vertex position are given for corannulene and sumanene respectively. Similarly, for the smaller substituent, N⁺, the hub-substituted isomer is given.

C₂₀H₁₀ (1) + (CH)₅XH → C₁₉XH₁₀ + (CH)₆ (2)

(ΔE/kcal mol⁻¹ = −21.5 (5N⁺+); −27.7 (7B⁻−); −26.5 (7P⁺++); −17.9 (7Si))

C₂₁H₁₂ (2) + (CH)₅XH → C₂₀XH₁₂ + (CH)₆ (3)

(ΔE/kcal mol⁻¹ = −19.3 (8N⁺+); −42.4 (11Si))

(CH)₅XH corresponds to the skeletally monosubstituted benzene.

The above homodesmic equations indicate that monosubstitutions do not confer any instability and in contrast they impart stability to the curved networks when placed at a suitable position that decreases the strain. The comparable stability of these hetero-buckybowls and the possibility to tailor and modulate the curvature, inversion dynamics, and the consequent physical and chemical properties make them attractive synthetic targets and expand the scope of the chemistry of buckybowls in this direction.

Curvature vs. bowl-to-bowl inversion

The pyramidalization angle (Φ), which gauges the curvature of a given buckybowl, is plotted against the bowl-to-bowl inversion barrier (Fig. 7). Although there is a reasonably good overall correlation, the correlation within the subsets divided into corannulenes [Fig. 7 inset (a)] and sumanenes [inset (b)] is much better. This plot clearly confirms the general feature that more curved buckybowls will have higher inversion barriers and vice versa. The other inference that can be made is that our pyramidalization angle (Φ) seems to be a good quantitative measure for curvature in this class of compounds.

Fig. 7 Plot of the inversion barrier (ΔE ^‡ ) versus the pyramidalization angle (Φ) of all the isomers considered in the study; the insets (a) and (b) depict the individual plots for corannulenes and sumanenes respectively.

Concluding remarks

This study provides the first higher level calculations on sumanene (2), trioxa-sumanene (3) and the recently synthesized trithia-sumanene (4). Their curvature, bowl depths and inversion barriers are compared with those of the well studied buckybowl, corannulene (1). Calculations were performed to gauge the effect of monosubstitutions at each of the unique sites in corannulene (1) and sumanene (2), which result in three isomers for the former and four for the latter. Theoretical methods starting from semiempirical (AM1 and MNDO), ab initio (HF/3-21G) and hybrid density functional methods (B3LYP/6-31G*) are employed. While the central result of the paper can be obtained using any of the above methods, the performance of semiempirical methods, particularly AM1 is not impressive. MNDO seems to be consistently better than AM1. In compounds where a larger substituent replaces the C atom at a hub position the curvature increases, which further results in a higher bowl-to-bowl inversion barrier. Smaller substituents at a hub position have exactly the opposite effect: a decrease in the curvature and the inversion barrier. The effect of substitution is not very dramatic at the rim-quat site in corannulene and at the rim-quat and rim sites in sumanene, and only smaller variations in curvature and inversion barriers are computed. However, substitution at the rim position in corannulene and the vertex position in sumanene causes dramatic changes in curvature and bowl depths depending on the size of the substituent. Thus, larger substituents at the peripheral position flatten the bowl structure with much lower bowl-to-bowl inversion barriers, and smaller substituents make the bowl deeper with higher inversion barriers. Rabideau and co-workers have reported the synthesis of 12, the first crystallographically characterized transition metal buckybowl, which was found to be much flatter than 13.³⁶ This flattening, which results from expansion of the rim of the semibuckminsterfullerene, is readily explained by using the arguments put forward in this study. Thus, the present study provides a simple mechanical model that in a bowl, stretching the rim leads to flattening and stretching the hub leads to bowl depth enhancement. A linear correlation between the curvature and the pyramidalization angle (Φ) and bowl-to-bowl inversion barrier is obtained. The synthetic realization of these hetero-buckybowls should also be controlled by the strain, which is solely governed by the size and site of substitution.³⁷ The possibility of tailoring and modulating the curvature and rigidity and the consequent physical and chemical properties of buckybowls by suitable heteroatom substitutions at appropriate positions is expected to unfold many exciting aspects of hetero-buckybowl chemistry.

Acknowledgements

G. N. S. thanks Professor Thomas Bally for his support and for extending computational facilities during his stay at the University of Fribourg, Switzerland. U. D. P. thanks UGC, New Delhi for a Junior Research Fellowship. This work is funded by a research grant from AICTE (8017/RDII/R&D/TAP (868)/98-99). Professor E. D. Jemmis is thanked for his encouragement and for extending computational facilities. Dr G. Madhavi Sastry and Professor H. Surya Prakash Rao are thanked for helpful discussions. Professor D. J. Klein and Professor T. P. Radhakrishnan are thanked for sending relevant works on pyramidalization.

References

1. (a) R. F. Curl, Angew. Chem., Int. Ed. Engl., 1997, 36, 1566; (b) R. Kroto, Angew. Chem., Int. Ed. Engl., 1997, 36, 1578; (c) R. E. Smalley, Angew. Chem., Int. Ed. Engl., 1997, 36, 1594.
2. P. W. Rabideau and A. Sygula, Acc. Chem. Res., 1996, 29, 235.
3. R. Faust, Angew. Chem., Int. Ed. Engl., 1995, 34, 1429.
4. (a) G. Mehta and H. S. P. Rao, Tetrahedron, 1998, 54, 13325; (b) G. Mehta and H. S. P. Rao , in Advances in Strain in Organic Chemistry, ed. B. Halton, JAI Press, London, 1997, vol. 6, pp. 139–187..
5. P. W. Rabideau and A. Sygula, Adv. Theor. Interesting Mol., 1995, 3, 1.
6. L. T. Scott, H. E. Bronstein, D. V. Preda, R. B. M. Ansems, M. S. Bratcher and S. Hagen, Pure Appl. Chem., 1999, 71, 209.
7. G. Mehta and G. Panda, PINSA–A: Proc. Indian Natl. Sci. Acad., Part A, 1998, 64, 587.
8. (a) W. E. Barth and R. G. Lawton, J. Am. Chem. Soc., 1966, 88, 380; (b) W. E. Barth and R. G. Lawton, J. Am. Chem. Soc., 1971, 93, 1730.
9. (a) P. W. Rabideau, A. H. Abdourazak, H. E. Folsom, Z. Mareinow, A. Sygula and R. Sygula, J. Am. Chem. Soc., 1994, 116, 7891; (b) A. H. Abdourazak, Z. Mareinow, A. Sygula and P. W. Rabideau, J. Am. Chem. Soc., 1995, 117, 6410; (c) S. Hagen, M. S. Bratcher, M. S. Erickson, G. Zimmermann and L. T. Scott, Angew. Chem., Int. Ed. Engl., 1997, 36, 406; (d) G. Mehta and G. Panda, Chem. Commun., 1997, 2081.
10. (a) L. T. Scott, M. S. Bratcher and S. Hagen, J. Am. Chem. Soc., 1996, 118, 8743; (b) R. B. M. Ansems and L. T. Scott, J. Am. Chem. Soc., 2000, 122, 2719.
11. (a) G. Mehta and P. V. V. S. Sarma, Chem. Commun., 2000, 19; (b) E. D. Jemmis, G. N. Sastry and G. Mehta, J. Chem. Soc., Perkin Trans. 2, 1994, 437; (c) G. Mehta, G. Panda and P. V. V. S. Sarma, Tetrahedron Lett., 1998, 39, 5835.
12. (a) L. T. Scott, M. M. Hashemi and M. S. Bratcher, J. Am. Chem. Soc., 1992, 114, 1920; (b) L. T. Scott, P.-C. Cheng, M. M. Hashemi, M. S. Bratcher, D. T. Meyer and H. B. Warren, J. Am. Chem. Soc., 1997, 119, 10963.
13. G. Mehta, S. R. Shah and K. Ravikumar, J. Chem. Soc., Chem. Commun., 1993, 1006.
14. (a) G. N. Sastry, E. D. Jemmis, G. Mehta and S. R. Shah, J. Chem. Soc., Perkin Trans. 2, 1993, 1867A detailed computational study of sumanene will be published separately, U. D. Priyakumar and G. N. Sastry , J. Phys. Chem. A, submitted. .
15. (a) P. U. Biedermann, S. Pogodin and I. Agranat, J. Org. Chem., 1999, 64, 3655; (b) K. K. Baldridge and J. S. Siegel, Theor. Chem. Acc., 1997, 97, 67; (c) A. Sygula and P. W. Rabideau, THEOCHEM, 1995, 333, 215.
16. T. J. Seiders, K. K Baldridge and J. S. Seigel, J. Am. Chem. Soc., 1996, 118, 2734.
17. (a) A. Sygula and P. W. Rabideau, J. Am. Chem. Soc., 1999, 121, 7800; (b) A. H. Abdourazak, A. Sygula and P. W. Rabideau, J. Am. Chem. Soc., 1993, 115, 3010; (c) A. Sygula, A. H. Abdourazak and P. W. Rabideau, J. Am. Chem. Soc., 1996, 118, 339.
18. (a) T. J. Seiders, K. K. Baldridge, E. L. Elliot, G. H. Grube and J. S. Seigel, J. Am. Chem. Soc., 1999, 121, 7439; (b) T. J. Seiders, E. L. Elliot, G. H. Grube and J. S. Seigel, J. Am. Chem. Soc., 1999, 121, 7804; (c) T. C. Dinadayalane , U. D. Priyakumar and G. N. Sastry , THEOCHEM, in the press..
19. G. N. Sastry, H. S. P. Rao, P. Bednarek and U. D. Priyakumar, Chem. Commun., 2000, 843.
20. (a) A. Hirsch , The Chemistry of the Fullerenes, Georg Thieme Verlag, Stuttgart, New York, 1994, p. 196;; (b) N. Kurita, K. Kobayashi, H. Kumahora, K. Tago and K. Ozawa, Chem. Phys. Lett., 1992, 198, 95.
21. R. L. Disch and J. M. Schulman, J. Am. Chem. Soc., 1994, 116, 1533.
22. K. Imamura, K. Takimiya, Y. Aso and T. Otsubo, Chem. Commun., 1999, 1859.
23. (a) T. Otsubo, Synlett, 1997, 544; (b) K. Imamura, D. Hirayama, H. Yoshimura, K. Takimiya, Y. Aso and T. Otsubo, Tetrahedron Lett., 1999, 40, 2789.
24. M. J. S. Dewar, Z. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902.
25. M. J. S. Dewar and W. Theil, J. Am. Chem. Soc., 1977, 99, 4899.
26. W. J. Hehre , L. Radom , P. v. R. Schleyer and J. A. Pople , Ab initio molecular orbital theory, Wiley, New York, 1986..
27. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
28. M. J. Frisch , G. W. Trucks , H. B. Schlegel , P. M. W. Gill , B. G. Johnson , M. A. Robb , J. R. Cheeseman , T. Keith , G. A. Patersson , J. A. Montgomery , K. Raghavachari , M. A. Al-Laham , V. G. Zakrzewski , J. V. Ortiz , J. B. Foresman , J. Cioslowski , B. B. Stefanov , A. Nanayakkara , M. Challacombe , C. Y. Peng , P. Y. Ayala , W. Chen , M. W. Wong , J. L. Andres , E. S. Replogle , R. Gomperts , R. L. Martin , D. J. Fox , J. S. Binkley , D. J. Defrees , J. Baker , J. J. P. Stewart , M. Head-Gordon , C. Gonzalez and J. A. Pople , Gaussian 94, Gaussian, Inc, Pittsburgh, PA, 1995..
29. W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1984, 23, 272.
30. (a) T. G. Schmalz, W. A. Seitz, D. J. Klein and G. E. Hite, J. Am. Chem. Soc., 1988, 110, 1113; (b) D. J. Klein , in Chemical Topology, ed. D. Bonchev and D. H. Rouvray, Gordon & Breach, Amsterdam, 1999, p. 39;; (c) D. J. Klein and H. Zhu , in From Chemical Topology to Three-Dimensional Geometry, ed. Balaban, Plenum, New York, 1997, p. 297;; (d) D. J. Klein and X. Liu, Int. J. Quantum Chem., 1994, S28, 501.
31. (a) W. T. Borden, Chem. Rev., 1989, 89, 1095; (b) L. A. Paquette, C.-C. Shen and J. A. Krause, J. Am. Chem. Soc., 1989, 111, 2351.
32. T. P. Radhakrishnan and I. Agranat, Struct. Chem., 1991, 2, 107.
33. (a) R. C. Haddon, J. Am. Chem. Soc., 1990, 112, 3385; (b) R. C. Haddon, J. Am. Chem. Soc., 1987, 109, 1676; (c) R. C. Haddon, J. Phys. Chem., 1987, 91, 3719.
34. B. M. Gimarc, J. Am. Chem. Soc., 1983, 105, 1979.
35. Mulliken population analysis shows that, in general, the rim position bears greater negative charge compared to the hub position. Thus, according to the rule of topological charge stabilization, the more electronegative substituent should prefer the rim position, which is exactly contrary to the computed results. For charge analysis on corannulene see: S. Tsuzuki, T. Uchimaru and K. Tanabe, J. Phys. Chem. A, 1998, 102, 740.
36. R. M. Shaltout, R. Sygula, A. Sygula, F. R. Fronczek, G. G. Stanley and P. W. Rabideau, J. Am. Chem. Soc., 1998, 120, 835.
37. (a) U. D. Priyakumar and G. N. Sastry , J. Mol. Graphics Modell., 2000, in the press;; (b) U. D. Priyakumar and G. N. Sastry , Tetrahedron Lett., in the press. .

---

Footnotes

† In this paper we use the common names trioxa-sumanene (3) and trithia-sumanene (4) where the three vertex methylene groups are replaced by isovalent O and S groups respectively.

‡ The planar structure of 7P⁺++ shows two imaginary frequencies (127.9i, 69.1i). The planar forms of all the monosubstituted sumanenes give only one imaginary frequency, which corresponds to bowl-to-bowl inversion except for 8Si. The planar form of 8Si shows two imaginary frequencies at both the MNDO (189.3i, 27.9i) and AM1 (207.4i, 116.4i) levels. The first frequency corresponds to the bowl-to-bowl inversion, and as the magnitude of the second frequency is very low in all cases, the planar structure can be designated as a true transition state for all cases. Although it is not certain that all the planar structures are transition states for bowl-to-bowl inversion, the characterization and energetics of the planar form are strategically important in this study.

---