View PDF VersionNext Article
 
DOI: 10.1039/B008808K (Communication) J. Chem. Soc., Perkin Trans. 2, 2001, 1-2

A comparison of the Cieplak model and the cation complexation model as applied to selected 2,3-disubstituted norbornan-7-ones[hair space]†

Veejendra K. Yadav * and Rengarajan Balamurugan
Department of Chemistry, Indian Institute of Technology, Kanpur, 208 016, India. Fax: 91-512-597436; E-mail: vijendra@iitk.ac.in

Received (in Cambridge, UK) 1st November 2000 , Accepted 14th November 2000

First published on 7th December 2000

Abstract

Compared with the Cieplak model, which is totally inadequate for predicting the π-selectivities of 1a–1c, the antiperiplanar effects in suitably cation-complexed species predict carbonyl pyramidalizations that lead to the observed selectivities.

Norbornan-7-ones (1, Fig. 1) have been the subject of intense experimental studies for their facial selectivities caused by endo-substituents at positions 2 and 3. The impetus arose particularly because, unlike cyclohexanones, norbornan-7-ones are rigid and devoid of significant geometrical distortions around the carbonyl function.1 2,3-Bis(methoxymethyl)norbornan-7-one, 1a, and 2,3-divinylnorbornan-7-one, 1b, show anti-preference for addition of nucleophiles. These substituents are electron-withdrawing and thus Cieplak’s hyperconjugation model[hair space]2 predicts syn-addition. Mehta[hair space]1 and le Noble[hair space]3 have attributed the observed anti-selectivities to through space donations from these substituents in rigid conformers such as 2 for the divinyl species. In 2, the vinyl π bonds are held parallel to the C1–C2 and C3–C4 bonds. Though this geometrical assumption may appear logical,4 it nevertheless prompted us to employ our cation complexation model[hair space]5 to see whether or not the right facial preference is predicted and also to test the merits of the above rigid conformer contribution. In the present paper, we demonstrate that (a) the cation complexation model performs well and predicts only the experimental selectivity; (b) the explanation advanced earlier to explain the anti-selectivity of 1a within the ambit of the Cieplak model is inappropriate; and, most important of all, (c) the Cieplak model is inadequate for explaining the syn-selectivity of 2,3-bis(methoxycarbonyl)norbornan-7-one, 1c.
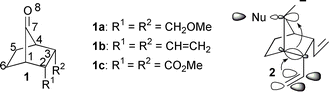The structures of species 1 and the proposed rigid conformer of 2.
Fig. 1 The structures of species 1 and the proposed rigid conformer of 2.

The Cieplak model requires a nucleophile to approach the carbonyl carbon from a direction that is antiperiplanar (app) to the more electron-donating σ bond at the α-carbon. From the transition structures for LiH additions to a series of 2,3-disubstituted norbornan-7-ones, Houk and co-workers have concluded that the hyperconjugative effects are unimportant and that the electrostatic effects constitute the sole control.6 Electron-withdrawing substituents induce positive charges at C2 and C3 and syn-addition is favored. On the other hand, electron-donating substituents induce negative charges at C2 and C3 and anti-addition becomes favorable. If so, why do 1a and 1b favor anti-addition and 1c the syn-addition when the substituents in all are electron-withdrawing? Houk has considered electrostatic repulsion between a nucleophile and the substituents in 1a and 1b and electrostatic attraction in 1c. This differential treatment of similar substituents may, at best, be considered an anomaly.

In application of the cation complexation model to norbornan-7-ones, we have calculated[hair space]7 the torsion angles D1 = O8–C7–C1–C2, D2 = O8–C7–C1–C6, D3 = O8–C7–C4–C3 and D4 = O8–C7–C4–C5, both before and after complexation, to assess the direction of carbonyl pyramidalization. We call the pyramidalization ‘anti’ when D1 and D3 are smaller than D2 and D4 and ‘syn’ when D1 and D3 are larger than D2 and D4, respectively. The ‘anti-pyramidalization’ leads to anti-addition and the ‘syn-pyramidalization’ leads to syn-addition. The directional changes in the torsion angles D5 = H–C1–C7–O8 and D6 = H–C4–C7–O8 can also provide information about the direction of pyramidalization. These geometrical data are collected in Table 1, the relevant app-effects in Table 2 and the 3D geometries of 1a–1c in Fig. 2.

Table 1 Selected B3LYP/6-31G* geometrical parameters of 1a–1c and their complexes. D1 = O8–C7–C1–C2; D2 = O8–C7–C1–C6; D3 = O8–C7–C4–C3; D4 = O8–C7–C4–C5; D5 = H9–C1–C7–O8; D6 = H14–C4–C7–O8
Substrate D1 D2 D3 D4 D5 D6
1 124.56 −124.56 −124.56 124.56 −0.00 −0.00
1a 122.29 −124.50 −121.49 125.08 −0.63 +1.06
1a–H+ 115.56 −132.55 −114.70 132.56 −5.54 +7.12
1a–Li+ 119.50 −127.88 −119.66 127.33 −2.52 +2.93
1b 121.31 −125.33 −121.31 125.33 −1.01 +1.01
1b–H+ 112.13 −135.90 −112.85 135.20 −8.82 +8.08
1b–Li+ 119.16 −128.15 −119.13 128.19 −3.02 +3.03
1b–BH3 120.48 −126.71 −120.42 126.46 −1.95 +1.84
1c 125.10 −121.76 −122.35 124.79 +2.49 −0.39
1c–H+ 127.39 −120.03 −123.95 123.96 +3.52 −1.32
1c–2H+ 133.32 −111.84 −132.66 115.05 +10.2 −8.33
1c–2Li+ 127.12 −119.98 −126.78 120.15 +4.64 −4.51

Table 2 The B3LYP/6-31G*  app-effects from second order perturbation theory analysis of the Fock matrix in NBO basis for 1a–1c and their complexes
  E/kcal mol−1
  σC1–C2– σC1–C6– σC3–C4– σC4–C5–
Substrate π*C7–O8 π*C7–O8 π*C7–O8 π*C7–O8
1a 3.46 3.41 3.38 3.15
1a–H+ 9.65 5.76 7.95 5.44
1a–Li+ 6.36 4.56 5.61 4.48
1b 3.64 3.08 3.64 3.08
1b–H+ 10.0 4.67 10.1 4.75
1b–Li+ 6.27 4.31 6.28 4.30
1b–BH3 4.93 3.94 4.81 3.78
1c 3.13 3.44 3.76 3.08
1c–H+ 6.21 7.40 8.02 6.38
1c–2H+ 4.60 6.92 5.91 7.57
1c–2Li+ 4.37 4.89 4.45 4.82


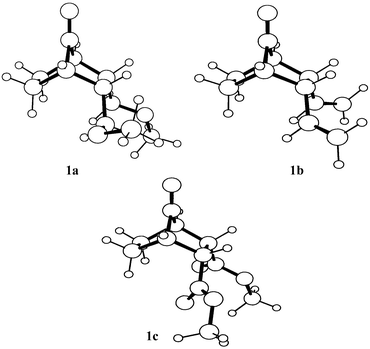Computed 3D structures of 1a–1c.
Fig. 2 Computed 3D structures of 1a–1c.

The torsion angle changes in 1a and 1b on carbonyl protonation suggest anti-addition for both. This is in accordance with experimental observations.1 From reactions with NaBH4 in MeOH and MeLi in Et2O, 40∶60 and 34∶66 and 36∶64 and 27∶73 selectivities in favor of anti-addition were observed for 1a and 1b, respectively. We sought a rationale for this anti-preference in the orientations of the substituents and their app-interactions[hair space]8 with σ*C1–C2 and σ*C3–C4. Whereas the CH2–O bond on C2 is app to C2–C3 (O–C–C2–C3 = 170.99–175.00°), the CH2–O bond on C3 is app to C3–C4 (O–C–C3–C4 = 168.97–171.97°). The sums of the σC1–C2–π*C[double bond, length half m-dash]O and σC3–C4–π*C[double bond, length half m-dash]O and of the σC1–C6–π*C[double bond, length half m-dash]O and σC4–C5–π*C[double bond, length half m-dash]O interactions are, respectively, 6.84 and 6.56 kcal mol−1 in 1a, 17.60 and 11.20 kcal mol−1 in 1a–H+, and 11.97 and 9.04 kcal mol−1 in 1a–Li+. The better interactions of π*C[double bond, length half m-dash]O with σC1–C2 and σC3–C4 in comparison to the interactions with σC1–C6 and σC4–C5 are set to favor anti-pyramidalization and, hence, the observed anti-addition. It is interesting to note that one of the two C–H bonds of the methylene on C2 is app to C1–C2 (H–C–C2–C1 = 171.07–174.43°) and the σC–H–σ*C1–C2 interaction energy is 3.61, 4.02 and 3.98 kcal mol−1 in 1a, 1a–H+ and 1a–Li+, respectively. The most interesting feature is the observation that in contradiction to the hypotheses of Mehta and le Noble neither the σC–O on C2 nor any of the two electron pair orbitals on this oxygen is in interaction with σ*C1–C2.

The sums of the σC1–C2–π*C[double bond, length half m-dash]O and σC3–C4–π*C[double bond, length half m-dash]O and of the σC1–C6–π*C[double bond, length half m-dash]O and σC4–C5–π*C[double bond, length half m-dash]O interactions are 7.28 and 6.16, 20.1 and 9.42, 12.55 and 8.61, and 9.74 and 7.72 kcal mol−1 in 1b, 1b–H+, 1b–Li+ and 1b–BH3, respectively. The larger interactions of π*C[double bond, length half m-dash]O with σC1–C2 and σC3–C4 in comparison to its interactions with σC1–C6 and σC4–C5 favor anti-pyramidalization. Both the vinyl groups are in an eclipsing orientation with the exo-hydrogens on C2 and C3. The πC[double bond, length half m-dash]C–σ*C1–C2/πC[double bond, length half m-dash]C–σ*C3–C4 interaction energy is 3.50, 5.20, 4.42, and 3.84 kcal mol−1 in 1b, 1b–H+, 1b–Li+ and 1b–BH3, respectively. These interactions raise the electron densities of the C1–C2 and C3–C4 bonds in support of the earlier speculations.1,3

From the absolute values of D1 vs. D2 and D3 vs. D4 in 1c, one experiences great difficulty in predicting the facial selection. While D1 is larger than D2 by 3.34°, D3 is smaller than D4 by 2.44°. Since the sum of the σC1–C2–π*C[double bond, length half m-dash]O and σC3–C4–π*C[double bond, length half m-dash]O interactions (6.89 kcal mol−1) is superior by 0.37 kcal mol−1 to the sum of σC1–C6–π*C[double bond, length half m-dash]O and σC4–C5–π*C[double bond, length half m-dash]O interactions (6.52 kcal mol−1), one is led to predict anti-addition. This, however, is in contrast to the Cieplak model which predicts σC1–C2 and σC3–C4 to be inferior to σC1–C6 and σC4–C5 in their electron-donating abilities due to the −I effects of the ester functions. This reversal is due to orientation effects arising from the ester functions that allow πC[double bond, length half m-dash]O–σ*C1–C2 (1.59 kcal mol−1 on C2) and σC–O–σ*C3–C4 (1.42 kcal mol−1 on C3) interactions. These relative electron-donating abilities were reconfirmed in 1c–H+ in which the C7-ketone was protonated; the sum of σC1–C2–π*C[double bond, length half m-dash]O and σC3–C4–π*C[double bond, length half m-dash]O interactions (14.23 kcal mol−1) was superior to the sum of the σC1–C6–π*C[double bond, length half m-dash]O and σC4–C5–π*C[double bond, length half m-dash]O interactions (13.78 kcal mol−1). The app-effects, therefore, predicted anti-addition, which is in clear violation of the experimental selectivities that varied from 77∶23 to 90∶10 in favor of syn-addition in reactions with various nucleophiles.1a

The above discrepancy is not without good reason. Why must only the 7-keto oxygen undergo cation complexation when the carbonyl oxygen of the ester function bears a similar or even better charge? The NBO analysis indicated the carbonyl oxygen on C2 to be the most negative of all the oxygen atoms and more negative (0.61 units) than the oxygen of the C7-keto group (0.51 units). This also necessitates cation complexation of the ester oxygen. Both the D1 and D2 and D3 and D4 differences in 1c–2H+ are now unambiguously in favor of syn-addition, supported by the app-effects. The sum of the σC1–C2–π*C[double bond, length half m-dash]O and σC3–C4–π*C[double bond, length half m-dash]O interactions (10.51 kcal mol−1) is inferior to the sum of σC1–C6–π*C[double bond, length half m-dash]O and σC4–C5–π*C[double bond, length half m-dash]O interactions (14.49 kcal mol−1). A similar conclusion is drawn from the 1c–2Li+ variant of 1c–2H+.

We conclude that while the rigid conformer concept for 1b is valid in explaining its anti-selectivity, it is not so for 1a. In 1a, it is rather the electron-donating interaction of one of the two methylene C–H bonds with σ*C1–C2 that plays the key role in promoting anti-pyramidalization. Further, the Cieplak selectivity of 1c on account of its ground state structure and the hyperconjugation effects in it meets with failure. However, the geometry resulting from the allowance of a suitable level of cation complexation possesses all the features of the observed syn-selectivity.

Acknowledgements

The author thanks the Council of Scientific and Industrial Research, New Delhi for financial support and the Computer Center, IIT Kanpur for generous allocation of computer time on a Silicon Graphics series of minisupercomputers.

References

  1. (a) G. Mehta and F. A. Khan, J. Am. Chem. Soc., 1990, 112, 6140 CrossRef CAS; (b) G. Mehta and F. A. Khan, J. Chem. Soc., Chem. Commun., 1991, 18 RSC.
  2. A. S. Cieplak, J. Am. Chem. Soc., 1981, 103, 4540 CrossRef CAS; A. S. Cieplak, B. D. Tait and C. R. Johnson, J. Am. Chem. Soc., 1989, 111, 8447 CrossRef CAS.
  3. H. Li, G. Mehta, S. Padma and W. J. le Noble, J. Org. Chem., 1991, 56, 2006 CrossRef CAS.
  4. For other examples, see: T. Laube and T.-K. Ha, J. Am. Chem. Soc., 1988, 110, 3511; D. Kost and H. Egozy, J. Org. Chem., 1989, 54, 409.
  5. D. A. Jeyaraj, A. Yadav and V. K. Yadav, Tetrahedron Lett., 1987, 38, 4483 CrossRef CAS; D. A. Jeyaraj and V. K. Yadav, Tetrahedron Lett., 1997, 38, 6095 CrossRef CAS; V. K. Yadav and D. A. Jeyaraj, J. Org. Chem., 1998, 63, 3474 CrossRef CAS; V. K. Yadav, G. Senthil and D. A. Jeyaraj, Tetrahedron, 1999, 55, 14211 CrossRef CAS; V. K. Yadav, D. A. Jeyaraj and R. Balamurugan, Tetrahedron, 2000, 56, 7581 CrossRef CAS.
  6. M. N. Paddon-Row, Y.-D. Wu and K. N. Houk, J. Am. Chem. Soc., 1992, 114, 10638 CrossRef CAS For related work, see: S. S. Wong and M. N. Paddon-Row, J. Chem. Soc., Chem. Commun., 1990, 456 RSC; S. S. Wong and M. N. Paddon-Row, J. Chem. Soc., Chem. Commun., 1991, 327 RSC; Y.-D. Wu, J. A. Tucker and K. N. Houk, J. Am. Chem. Soc., 1991, 113, 5018 CrossRef CAS.
  7. All the geometry optimizations and the calculations of NBO charges were performed at the Becke3LYP/6-31G* level using the program Gaussian 94, Revision C.2 M. J. Frisch , G. W. Trucks , H. B. Schlegel , P. M. W. Jones , B. G. Johnson , M. A. Robb , J. R. Cheeseman , T. Keith , G. A. Petersson , J. A. Montgomery , K. Raghavachari , M. A. Al-Laham , V. G. Zakrzewski , J. V. Ortiz , J. B. Foresman , J. Cioslowski , B. B. Stefanov , A. Nanayakkara , M. Challacombe , C. Y. Peng , P. Y. Ayala , W. Chen , M. W. Wong , J. L. Andres , E. S. Replogle , R. Gomperts , R. L. Martin , D. J. Fox , J. S. Binkley , D. J. Defrees , J. Baker , J. P. Stewart , M. Head-Gordon , C. Gonzalez and J. A. Pople , Gaussian, Inc., Pittsburgh, PA, 1995. .
  8. P. Deslongchamps , Stereoelectronic Effects in Organic Chemistry, Pergamon Press, New York, 1983.  Search PubMed.

Footnote

† The Cartesian coordinates of species 1a–1c and their complexes are available as supplementary data. For direct electronic access see http://www.rsc.org/suppdata/p2/b0/b008808k/
This journal is © The Royal Society of Chemistry 2001
Click here to see how this site uses Cookies. View our privacy policy here.