A coupled dual hydrogen bridge system—solution dynamics and crystal structure of 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine![[hair space]](https://www.rsc.org/images/entities/h2_char_200a.gif) †
†
Peter
Fischer
*a,
Achim
Fettig
a,
Wolfgang U.
Frey
a,
Sonja
Henkel
a,
Helga
Hoier
a,
Horst E. A.
Kramer
*b,
Manfred
Roessler
b and
Jean-Luc
Birbaum
c
aInstitut für Organische Chemie, Universität Stuttgart, Pfaffenwaldring 55, D-70569, Stuttgart, Germany
bInstitut für Physikalische Chemie, Universität Stuttgart
cCiba Specialty Chemicals Inc., Basel, Switzerland
First published on 11th December 2000
Abstract
Detailed NMR analysis (CD2Cl2, 183 K) shows the two intramolecular hydrogen bridges of 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine to be directed either towards N-1 and N-3 (S conformer; both hydrogen bonds to an aza nitrogen ortho to the N(CH3)2 group) or towards N-1/N-3, respectively, and N-5 (A conformer; one ortho and one para hydrogen bond each), with the ratio S∶A = 1∶2.65. The conformational equilibrium has been probed by dynamic NMR spectroscopy. For 180° rotation of one 2-hydroxyphenyl moiety, i.e. the mutual interconversion of A and S, ΔG![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡ ≅ 47 kJ mol−1 is determined by complete line shape analysis (range 213–243 K). The activation barrier for simultaneous rotation of both 2-hydroxyphenyl groups is higher by only ≅ 0.5 kJ mol−1; this process thence contributes substantially to the overall dynamic process. For the crystalline state, X-ray diffraction shows only the A conformer. The C–O–H bond angles appear compressed towards 90° for both the ortho and the para bridge. In the para bridge, O(15)–H(15)
‡ ≅ 47 kJ mol−1 is determined by complete line shape analysis (range 213–243 K). The activation barrier for simultaneous rotation of both 2-hydroxyphenyl groups is higher by only ≅ 0.5 kJ mol−1; this process thence contributes substantially to the overall dynamic process. For the crystalline state, X-ray diffraction shows only the A conformer. The C–O–H bond angles appear compressed towards 90° for both the ortho and the para bridge. In the para bridge, O(15)–H(15)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N(5), the bonding hydrogen is located close to symmetrically between the donor O and the acceptor N (bond angle ≈165°).
N(5), the bonding hydrogen is located close to symmetrically between the donor O and the acceptor N (bond angle ≈165°).
Introduction
UV Absorbers with a strong intramolecular hydrogen bond (IMHB) are among the most effective additives for protecting synthetic polymers against photodegradation.1,2 Photoexcitation of these molecules is followed by an excited state intramolecular proton transfer (ESIPT) and subsequent rapid radiationless deactivation (which may also be a competitive mode).3,4 The ESIPT process itself constitutes no absolute prerequisite for effective energy transformation. The proviso rather is conservation of the IMHB in the excited state to offer a sufficiently wide range of vibrational modes for triggering radiationless deactivation;5 the strength of the hydrogen bond therefore is of crucial importance.A comparative X-ray structure analysis as well as IR and NMR spectral evidence have demonstrated that the IMHB in 2-hydroxyaryltriazines is far stronger than that in the corresponding 2-hydroxyarylbenzotriazoles (e.g. Tinuvin P®).6 Breaking the hydrogen bridge in 2,4-bis(2,4-dimethylphenyl)-6-(2-hydroxy-4-methoxyphenyl)-1,3,5-triazine, for instance, requires an enthalpy of activation ΔH![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) † = 50 kJ mol−1 as we have determined by dynamic NMR spectroscopy.7 Yet even these strong, chelate-type bonds can be opened in the excited state by sufficiently polar matrices such as polymethacrylate coatings.8 It seemed conceivable, though, that in a triazine with a second IMHB, this would stay intact even under these conditions and furnish the requisite vibrational modes.
† = 50 kJ mol−1 as we have determined by dynamic NMR spectroscopy.7 Yet even these strong, chelate-type bonds can be opened in the excited state by sufficiently polar matrices such as polymethacrylate coatings.8 It seemed conceivable, though, that in a triazine with a second IMHB, this would stay intact even under these conditions and furnish the requisite vibrational modes.
We now report on assessing, both quantitatively and individually, the strength of the two hydrogen bonds in such a dual-bridge triazine system.
Results and discussion
NMR Study of solution dynamics
2-Dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine, a new representative in the class of (2-hydroxyaryl)triazines, indeed forms two intramolecular hydrogen bridges at the same time. With the reasonable assumption that none of the aza nitrogen atoms in the triazine ring may function as an acceptor for two bridges simultaneously, three arrangements are possible for these two hydrogen bonds: one conformation with C2 symmetry (S in Fig. 1), and two asymmetrical conformations (A′, A′′) which are transformed into one other by 180° rotation around the C2 axis, and thence are structurally identical and energetically degenerate. | ||
Fig. 1 Reaction scheme for the interconversion of the two O–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N hydrogen bridges in 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine, based on the “three site exchange” model, for the phenolic proton of the left-hand 2-hydroxyphenyl ring. N hydrogen bridges in 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine, based on the “three site exchange” model, for the phenolic proton of the left-hand 2-hydroxyphenyl ring.
| ||
The two asymmetrical conformations A′ and A′′ are converted, by 180° rotation around the C-4–C-1′ or C-6–C-1′′ bond, respectively, into the symmetrical structure S which in turn is transformed, by a 180° rotation around the C-6–C-1′′ or C-4–C-1′ bond, into the respective other asymmetrical conformer. Simultaneous rotation, finally, around both the C-4–C-1′ and the C-6–C-1′′ bond directly interconverts A′ and A′′. All these transformations constitute equilibria with first order forward and back reactions which are characterized by six rate constants as assigned in Fig. 1.
 | ||
Fig. 2
1H NMR spectrum of 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine at 183 K (11.74 T, CD2Cl2); expansions for a) the O–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N bridging protons, b) 6′,6′′-H, c) the syn and antiN-CH3 groups of the dimethylamino function. N bridging protons, b) 6′,6′′-H, c) the syn and antiN-CH3 groups of the dimethylamino function.
| ||
Two singlets with different chemical shifts, though equal intensity, are expected for the ortho and the para bridge, respectively, of the symmetry-equivalent conformers A′ and A′′. The two more intense (37%) resonances thence can be unequivocally assigned to the asymmetrical form. The bridging protons in the symmetrical S conformer are in chemically identical environments and so give rise to the remaining, less intense (26%) singlet. The same arguments hold for all atom positions in this triazine. The aryl protons 6′,6′′-H, for instance, in the ortho position opposite to the bridging hydroxy groups, are set off to low field due to the combined −M and anisotropy effect of the triazine ring. The expansion in Fig. 2b shows that their resonances are likewise split into three multiplets (relative intensity 36/36/28%; 3J![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) (6′-H,5′-H) = 7.9 Hz, 4J
(6′-H,5′-H) = 7.9 Hz, 4J![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) (6′-H,4′-H) = 1.2 Hz).
(6′-H,4′-H) = 1.2 Hz).
Three singlets, with once more the same intensity ratio, also appear for the N(CH3)2 protons (cf.Fig. 2c; relative intensity again 28/36/36%). The C–N bond, by which the +M substituent N(CH3)2 is joined to the triazine ring, has considerable partial double bond character. At 183 K, rotation around this bond is completely frozen out as we have unequivocally established for the homologous 2-dimethylamino-4-(2-hydroxyphenyl)-6-phenyl-1,3,5-triazine.9 This holds up to >323 K,9i.e. the barrier of rotation for the N(CH3)2 moiety in 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine has the same order of magnitude as in dimethylformamide.10 For both asymmetrical conformers A′ and A′′, two signals therefore are expected, at all temperatures investigated here, for the two N-CH3 groups, oriented syn and anti, respectively, to the ortho hydrogen bridge, and mutually isochronous for the two forms. The third, less intense singlet arises from the symmetry-equivalent N-CH3 groups of the S conformer.
On this compound NMR evidence, the two structures with both an ortho and a para bridge appear favoured over the conformer with two ortho bridges by 2.65∶1. Since a (partial) positive charge is stabilized by a +M substituent in the para better than in the ortho position, the slight preference for an O–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N bridge to the aza nitrogen para to the N(CH3)2 group appears quite reasonable. The somewhat greater strength of this O–H
N bridge to the aza nitrogen para to the N(CH3)2 group appears quite reasonable. The somewhat greater strength of this O–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N bridge also implies a higher energy of activation for breaking a para than for disrupting an ortho hydrogen bond. The schematic energy diagram in Fig. 3 rests on this reasonable assumption.
N bridge also implies a higher energy of activation for breaking a para than for disrupting an ortho hydrogen bond. The schematic energy diagram in Fig. 3 rests on this reasonable assumption.
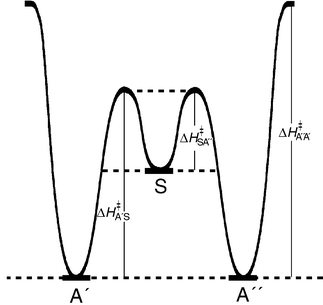 | ||
| Fig. 3 Schematic energy diagram for the interconversion of the A′, S and A′′ conformers. | ||
 | ||
| Fig. 4 N-CH31H resonances of 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine at 183, 213, and 233 K (11.74 T, CD2Cl2). | ||
With such a complex pattern, coalescence points can no longer be acccurately fixed as for the other (2-hydroxyaryl)triazines studied so far.7,9 Rate constants for the individual transformations rather must be determined by complete line shape analysis![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 14,15 requiring, besides precise frequency position and half-height width of the individual signals at a given temperature, the molar fraction(s) p of the corresponding conformer(s). These were determined by separate integration over the 6′,6′′-H signals for the individual conformers, and remain constant, within the NMR integration error limit, between 183 and 213 K when increasing signal overlap thwarts sufficiently precise separate integration.
14,15 requiring, besides precise frequency position and half-height width of the individual signals at a given temperature, the molar fraction(s) p of the corresponding conformer(s). These were determined by separate integration over the 6′,6′′-H signals for the individual conformers, and remain constant, within the NMR integration error limit, between 183 and 213 K when increasing signal overlap thwarts sufficiently precise separate integration.
| p A′ = pA′′ = 0.357 |
| p S = 0.286 |
The individual transformation rates, as assigned in Fig. 1, are intercorrelated by these molar fractions as shown in eqn. (1) and (2):
k
A′/S = (![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) pS/pA′)·kS/A′ = kA′′/S = (pS/pA′′)·kS/A′′ pS/pA′)·kS/A′ = kA′′/S = (pS/pA′′)·kS/A′′
| (1) |
| k A′/A′′ = kA′′/A′ | (2) |
The six principal rate constants of the “three-site exchange” model (cf.Fig. 1) in practice thus are reduced to two; these we have varied, systematically, for a best fit between calculated and experimental line shape. Rotation around the (C-2)–N(CH3)2 bond is frozen out in the temperature range in question,9 as stated above, and thence need not be considered for the exchange. Fig. 5a shows, exemplarily, the close to perfect fit for the N-CH3 resonances at 213 and 228 K, i.e. at temperatures somewhat below coalescence: the experimental spectral trace always lies centered in the grey-shaded band which represents the calculated spectrum. The 6′,6′′-H resonances have only one third the relative intensity of the N-CH3 signal, and are further split by 1H,1H coupling. Despite the far lower signal to noise ratio, especially above 223 K, an excellent fit is still obtained as demonstrated in Fig. 5b. For the bridging proton signals, on the other hand, a line shape analysis is not practical. Due perhaps to increasing alignment of CD2Cl2 solvent dipoles with the hydrogen bridge dipoles at lower temperatures, the line width of these resonances is itself strongly temperature-dependent. The half-height width, determined from a slow-exchange spectrum, thus cannot be used for simulations at higher temperatures.
 | ||
| Fig. 5 Line shape analysis for the 1H resonances (11.74 T, CD2Cl2) of 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine: black trace—experimental spectrum, grey-shaded band—calculated line shape for the best fit of the two iterated rate constants. a) N-CH3 signals at 213 and 228 K, b) 6′,6′′-H signals at 223 and 238 K. | ||
![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ) in an Eyring, or as ln k in an Arrhenius diagram (Fig. 6),10 linear regression analysis yields individual activation parameters for each hydrogen bridge re-orientation. The values for energy and enthalpy of activation appear as identical, though, for all transformations within the rather wide error limits (Table 2).
) in an Eyring, or as ln k in an Arrhenius diagram (Fig. 6),10 linear regression analysis yields individual activation parameters for each hydrogen bridge re-orientation. The values for energy and enthalpy of activation appear as identical, though, for all transformations within the rather wide error limits (Table 2).

|
![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ) vs. 1/T correlation
) vs. 1/T correlation
| Interconversion | E A/kJ mol−1 | ΔH![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡/kJ mol−1 ‡/kJ mol−1 |
|---|---|---|
| S→A′/S→A′′ | 48 ± 3 | 47 ± 3 |
| A′→S/A′′→S | 47 ± 3 | 46 ± 3 |
| A′→A′′/A′′→AS | 47 ± 3 | 45 ± 3 |
 | ||
| Fig. 6 Arrhenius plot for the individual hydrogen bridge interconversions in 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine (for data cf. Table 1). | ||
Alternatively, ΔG![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡ values can be calculated directly from the k values for each temperature (cf.Table 1). If these are plotted vs. T in a Gibbs–Helmholtz diagram, the error in the k/T or, respectively, ΔG
‡ values can be calculated directly from the k values for each temperature (cf.Table 1). If these are plotted vs. T in a Gibbs–Helmholtz diagram, the error in the k/T or, respectively, ΔG![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡/T correlations is smaller by more than an order of magnitude within the temperature range for which the individual k values were determined experimentally by line shape analysis (213–243 K). This is demonstrated strikingly in Fig. 7 for the two interconversions S→A′/S→A′′. The 6′,6′′-H and N-CH3 signals have been evaluated jointly for this correlation; still, over a range of 30 K, the correlation straight line lies well within the error bars for the individual ΔG
‡/T correlations is smaller by more than an order of magnitude within the temperature range for which the individual k values were determined experimentally by line shape analysis (213–243 K). This is demonstrated strikingly in Fig. 7 for the two interconversions S→A′/S→A′′. The 6′,6′′-H and N-CH3 signals have been evaluated jointly for this correlation; still, over a range of 30 K, the correlation straight line lies well within the error bars for the individual ΔG![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡ values, with purely statistical deviations.
‡ values, with purely statistical deviations.
 | ||
Fig. 7 ΔG![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡/T Correlation for the transformations S→A′ and S→A′′. ‡/T Correlation for the transformations S→A′ and S→A′′.
| ||
Closer inspection of the ΔG![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡/T correlation plot in fact reveals a delicate gradation (cf. the blow-up in Fig. 8) which is already apparent in the Arrhenius diagram (see Fig. 6). Conformational changes, by which the more stable para hydrogen bridge is formed, as expected require a slightly lower activation energy than processes during which such a para bridge is broken, i.e. the correlation straight line for the transformations A′→S/A′′→S is set off by ≈0.5 kJ mol−1 from that for the reverse processes. The free enthalpy difference between symmetrical and asymmetrical conformer at e.g. 238 K is calculated from the A/S ratio at this temperature as ΔΔG = 0.67 kJ mol−1. The free enthalpies of activation ΔG
‡/T correlation plot in fact reveals a delicate gradation (cf. the blow-up in Fig. 8) which is already apparent in the Arrhenius diagram (see Fig. 6). Conformational changes, by which the more stable para hydrogen bridge is formed, as expected require a slightly lower activation energy than processes during which such a para bridge is broken, i.e. the correlation straight line for the transformations A′→S/A′′→S is set off by ≈0.5 kJ mol−1 from that for the reverse processes. The free enthalpy difference between symmetrical and asymmetrical conformer at e.g. 238 K is calculated from the A/S ratio at this temperature as ΔΔG = 0.67 kJ mol−1. The free enthalpies of activation ΔG![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡ for the forward and back reaction, i.e. the transformations A′→S and S→A′ and likewise and A′→S and S→A′′ must differ by the same value independent of how high the activation barrier is (cf. Fig. 3). Agreement between the values for ΔΔG, derived from thermodynamic, and ΔΔG
‡ for the forward and back reaction, i.e. the transformations A′→S and S→A′ and likewise and A′→S and S→A′′ must differ by the same value independent of how high the activation barrier is (cf. Fig. 3). Agreement between the values for ΔΔG, derived from thermodynamic, and ΔΔG![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡, derived from kinetic data, is more than satisfactory.
‡, derived from kinetic data, is more than satisfactory.
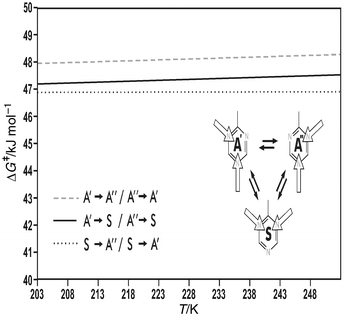 | ||
Fig. 8 ΔG![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡/T Correlation straight lines for the individual hydrogen bridge interconversions in 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine. ‡/T Correlation straight lines for the individual hydrogen bridge interconversions in 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine. | ||
Direct interconversion of A′ and A′′ requires sacrificing both hydrogen bonds at the same time, and therefore appears a priori rather unlikely. The perfect line shape fit, as is demonstrated exemplarily in Figs. 5a,b, can be obtained, however, only when the two rate constants for this process, kA′,A′′ and kA′′,A′, are included in the simulation. Even more surprisingly, the double bridge exchange is barely slower than the other two re-orientation processes where only one hydrogen bridge needs to be broken, and thence contributes significantly and substantially to the dynamic process. The activation barrier, determined by DNMR, for the A′⇌A′′ interconversion as a matter of fact again lies only ≈0.5 kJ mol−1 higher than that for the para→ortho rearrangement (A′→S/A′′→S; cf.Figs. 6 and 8).
X-Ray crystal structure determination![[hair space]](https://www.rsc.org/images/entities/h3_char_200a.gif) ‡
‡
2-Dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine crystallizes in the monoclinic space group P21/c, with one molecule per asymmetric unit (for selected bond lengths and angles, see Table 3; fractional atomic coordinates, stereoscopic projections of crystal packing, and other relevant crystallographic data are available as supplementary data![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ‡). The arrangement in the unit cell (Z = 4) is much like that for an analogue without an IMHB, 2-(4-methoxy)-4,6-diphenyl-1,3,5-triazine.6
‡). The arrangement in the unit cell (Z = 4) is much like that for an analogue without an IMHB, 2-(4-methoxy)-4,6-diphenyl-1,3,5-triazine.6
| C(2)–N(1) | 1.350(4) | C(2)–N(7) | 1.332(4) |
| C(2)–N(3) | 1.351(4) | N(7)–C(8) | 1.457(4) |
| N(1)–C(6) | 1.333(4) | N(7)–C(9) | 1.457(4) |
| N(3)–C(4) | 1.330(4) | ||
| N(5)–C(6) | 1.343(4) | ||
| N(5)–C(4) | 1.346(4) | ||
| C(4)–C(10) | 1.480(4) | C(6)–C(16) | 1.469(4) |
| C(10)–C(15) | 1.395(5) | C(16)–C(21) | 1.406(4) |
| C(15)–O(15) | 1.304(4) | C(21)–O(21) | 1.334(4) |
| O(15)–H(15) | 1.25(7) | O(21)–H(21) | 0.97(6) |
H(15)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N(5) N(5) |
1.35(7) | H(21)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N(1) N(1) |
1.66(6) |
O(15)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N(5) N(5) |
2.561(4) | O(21)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N(1) N(1) |
2.574(3) |
| N(5)–C(4)–C(10) | 117.1(3) | N(1)–C(6)–C(16) | 117.9(3) |
| C(4)–C(10)–C(15) | 122.2(3) | C(6)–C(16)–C(21) | 121.9(3) |
| C(10)–C(15)–O(15) | 122.5(3) | C(16)–O(21)–H(21) | 122.8(3) |
| C(15)–O(15)–H(15) | 97(3) | C(21)–O(21)–H(21) | 103(3) |
| O(15)–H(15)–N(5) | 160(5) | O(21)–H(21)–N(1) | 154(5) |
The packing diagram (Fig. 9a) shows perfectly planar bis(hydroxyphenyl)triazines, arranged in oblique stacks which are tilted relative to each other by ≈30° in a herring-bone-like arrangement. The crystal structure gives no indication, either of interaction between the individual stacks or of intermolecular hydrogen bridging, orthogonal to the plane of the triazines, within the stacks. Charge-transfer between two adjacent layers is likewise precluded by the vertical separation of the molecules within a stack (3.6–3.8 Å) as well as by their relative orientation. For an effective charge-transfer, the electron-deficient triazine core would have to be oriented face to face over one of the electron-rich hydroxyphenyl rings in an adjacent layer; as the projection in Fig. 9b clearly shows, this is not the case. Another cooperative effect becomes apparent, though, from this representation of the crystal ordering: within the stacks, the triazines are arranged pairwise, with the strong N(CH3)2 donors diametrically opposite, and the overall molecular dipole moments thus compensating each other for any such pair. The two triazines of a pair are displaced sidewise by only half a triazine diameter to minimize steric interactions; the triazine in the next layer, however, which belongs to another dipole-compensated pair, is displaced by one and a half triazine diameters.
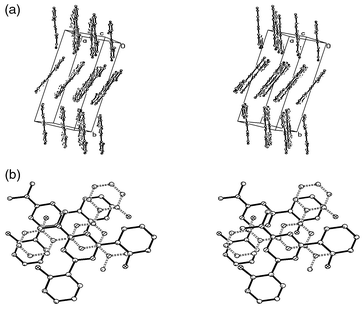 | ||
| Fig. 9 3D Packing diagram with unit cell dimensions for 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine: a) viewed along the triazine σ plane, b) three successive molecules within a stack (the middle one drawn with dashed lines). | ||
The structure gives no indication of disorder: only the slightly more stable asymmetrical conformer A, with one ortho and para hydrogen bridge each, is represented in the crystal (A′ and A′′ are of course crystallographically symmetry-equivalent). The Boltzmann energy, available at the (ambient) temperature at which the structure was determined, is insufficient for reorientation of these intramolecular hydrogen bonds. Another striking element of order becomes apparent, though, if one assigns the acceptor site for the ortho hydrogen bridge as N-3, and that for the para bridge as N-5: all triazines in the crystal show the same sense of rotation.
A strong molecular dipole moment had been invoked above to rationalize the pairwise head-to-tail alignment of the triazine moieties within the vertical stacks. The attenuated bond length between C-2 and the dimethylamino nitrogen N-7 and also the negligible torsional angle (1.332 Å and 0.5°, respectively; cf.Table 3 and Fig. 10) likewise prove an exceptionally strong mesomeric interaction between the (CH3)2N group as +M donor and the triazine π system as acceptor. This manifests itself most strikingly in the fact that the formal single bond N(7)–C(2) has the same length, within the standard deviation of the X-ray analysis, as the two aromatic N(1)–C(6) and N(3)–C(4) bonds (1.332 vs. 1.333 and 1.330 Å). Since the six C–N bonds within the triazine core, on the other hand, all have more or less identical length (1.34 ± 0.01 Å), this must be interpreted in terms of a (charge-transfer) polarization of the π-electron cloud as a whole,16 apparently a class characteristic of these aryltriazines,17 rather than in terms of a para-quinoid structure which would require strictly alternating bond lengths. The crystal structure data thus present a perfect rationale for why rotation around the C(2)–N(7) bond is frozen out even in ambient temperature NMR spectra (see above).
 | ||
| Fig. 10 X-Ray crystal structure for 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine (A conformer only) with atom labelling. | ||
The position of the bridging hydrogen could be refined for both the ortho and the para bridge (cf. Experimental section). Compared to the single bridge in 2-(2-hydroxy-4-methoxyphenyl)-4,6-diphenyl-1,3,5-triazine (M–OH–P),6 the O–H bond of the ortho hydrogen bridge, O(21)–H(21)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N(1), in 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine (NMe2) appears even more elongated (0.97 vs. 0.898 Å, see Table 4), with a concomitant reduction in the N
N(1), in 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine (NMe2) appears even more elongated (0.97 vs. 0.898 Å, see Table 4), with a concomitant reduction in the N![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) H distance, and the C(21)–O(21) bond even more compressed. The O–H
H distance, and the C(21)–O(21) bond even more compressed. The O–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N inter-hydrogen-bond angle, though, deviates markedly further from linear than in M–OH–P.
N inter-hydrogen-bond angle, though, deviates markedly further from linear than in M–OH–P.
| r/Å | C–O | O–H | H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N N |
O–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N N |
O–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N/° N/° |
〈O–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯ ⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N/° N/° |
|
|---|---|---|---|---|---|---|---|
M–OH–P![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 6 6 |
Single bridge | 1.368 | 0.898 | 1.733 | 2.594 | 159.6 | |
| NMe2 | ortho bridge | 1.334 | 0.97 | 1.66 | 2.574 | 154 | |
| para bridge | 1.304 | 1.25 | 1.35 | 2.561 | 160 |
The C(15)–O(15) bond and the overall O–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N distance of the para bridge both are shortened still further, and the O–H
N distance of the para bridge both are shortened still further, and the O–H![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N inter-hydrogen-bond angle is flattened out again (160°). The striking difference, though, is in the position of the bridging hydrogen which is located almost intermediate between O(15) and N(5): at least in the crystalline state, the hydrogen bridge O(15)–H(15)
N inter-hydrogen-bond angle is flattened out again (160°). The striking difference, though, is in the position of the bridging hydrogen which is located almost intermediate between O(15) and N(5): at least in the crystalline state, the hydrogen bridge O(15)–H(15)![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ⋯
⋯![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) N(5) seems to approach the symmetrical (Table 4).
N(5) seems to approach the symmetrical (Table 4).
Conclusion
In conjunction, the NMR and crystal structure, i.e. solution and solid state data presented here constitute clear proof that both hydrogen bridges of a bis(2-hydroxyaryl)triazine are at least comparable in strength, individually, to the single hydrogen bond in analogous (2-hydroxyaryl)triazines, and thence definitely stronger than the hydrogen bridge in any corresponding benzotriazole.6,8It has been clearly demonstrated, on the other hand, that the intramolecular hydrogen bond (IMHB) in e.g. 2-(2-hydroxy-4-methoxyphenyl)-4,6-diphenyl-1,3,5-triazine must be opened upon irradiation, under formation of an intermolecular hydrogen bond to the solvent lattice, before the triplet state will be populated, with concomitant evolution of phosphorescence.18 A comparative study of 2-hydroxyaryl- and the corresponding 2-methoxyaryl-triazines, with two, one, and no IMHB, respectively, has furthermore shown that all intramolecular bridges must be opened for these molecules to exhibit phosphorescence.19 With the strength of both bridges now definitely established as comparable, it becomes readily apparent why bis(2-hydroxyaryl)-1,3,5-triazines are distinctly more resistant to photodegradation than structurally corresponding triazines with only one IMHB.
Experimental
DNMR measurements and spectral analysis
1H NMR spectra were recorded on a Bruker ARX-500 spectrometer (11.74 T, nominal frequency 500.13 MHz, 0.1 M solution in CD2Cl2) with the following standard parameters for the individual measurements at a given temperature:7,9 pulse width (90°) 11.3 μs, 30° flip angle, 32K FID, digital resolution ±0.16 Hz per point. Temperature was adjusted and controlled by a Bruker BVT-2000 variable temperature unit calibrated according to van Geet.20 To ensure maximum homogeneity after resetting the temperature, the sample was held for 20 min at this temperature in the probehead before acquisition was started.Complete line shape analyses were performed with a program based on DNMR5.15 The source program used![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 21 was modified for a direct on-screen fit of calculated to experimental trace.9 In the range of incipient coalescence, the effective resonance frequency was determined by extrapolation from a Δν/T plot for each signal. The highest field resonance within each set was taken as reference, and assigned 0 Hz relative frequency for each temperature. Since the slope in the Δν/T plot for a given signal may be positive, negative, or close to zero,7,9 the relative Δν values for a given set show no regular trend. The following relative line positions were used for the simulations: N-CH3—0, 90, 250 Hz (218 K); 0, 90, 249 Hz (223 K); 0, 88, 245 Hz (228 K); 0, 85, 237 Hz (233 K); 0, 84, 235 Hz (238 K); 0, 84, 233 Hz (243 K); 6′,6′′-H—0, 81, 92 Hz (213 K); 0, 70, 83 Hz (223 K); 0, 69, 81 Hz (228 K). A line width of 5 Hz was employed for the N-CH3 resonances. For the ortho-aryl protons 6′,6′′-H, this value was incremented by the sum of the two coupling constants, 3Jortho + 4Jmeta, giving an effective line width of 14 Hz.
21 was modified for a direct on-screen fit of calculated to experimental trace.9 In the range of incipient coalescence, the effective resonance frequency was determined by extrapolation from a Δν/T plot for each signal. The highest field resonance within each set was taken as reference, and assigned 0 Hz relative frequency for each temperature. Since the slope in the Δν/T plot for a given signal may be positive, negative, or close to zero,7,9 the relative Δν values for a given set show no regular trend. The following relative line positions were used for the simulations: N-CH3—0, 90, 250 Hz (218 K); 0, 90, 249 Hz (223 K); 0, 88, 245 Hz (228 K); 0, 85, 237 Hz (233 K); 0, 84, 235 Hz (238 K); 0, 84, 233 Hz (243 K); 6′,6′′-H—0, 81, 92 Hz (213 K); 0, 70, 83 Hz (223 K); 0, 69, 81 Hz (228 K). A line width of 5 Hz was employed for the N-CH3 resonances. For the ortho-aryl protons 6′,6′′-H, this value was incremented by the sum of the two coupling constants, 3Jortho + 4Jmeta, giving an effective line width of 14 Hz.
X-Ray analysis
2-Dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine was purified by repeated recrystallization from anhydrous cyclohexane. Yellow crystals were grown from chloroform at ambient temperature by slow solvent evaporation within ten months; residual solvent was removed in vacuo. A single crystal (1.2 × 0.45 × 0.2 mm3, mounted in a thin-walled capillary) was used for X-ray data collection on a Nicolet/Siemens P3 four-cycle diffractometer with graphite-monochromatized Mo-Kα radiation (λ = 0.71069 Å). Reflection data were collected to a resolution of 2θmax = 50°, and subjected to a full-matrix least-square refinement without any constraints.![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ) (>2σ(I
) (>2σ(I![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) )) = 0.0816 and for ωR2(F
)) = 0.0816 and for ωR2(F![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 2) (>2σ(I
2) (>2σ(I![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) )) = 0.2326.
)) = 0.2326.
References
- J. F. Rabek, Photostabilization of Polymers. Principles and Applications, Elsevier Applied Science Publishers, London, 1990. Search PubMed.
- H. J. Heller and H. R. Blattmann, Pure Appl. Chem., 1972, 30, 145 CrossRef CAS; H. J. Heller and H. R. Blattmann, Pure Appl. Chem., 1974, 36, 141.
- Th. Förster, Z. Elektrochem., 1950, 54, 42, 531 Search PubMed.
- (a) G. Goeller, J. Rieker, A. Maier, J. J. Stezowski, E. Daltrozzo, M. Neureiter, H. Port, M. Wiechmann and H. E. A. Kramer, J. Phys. Chem., 1988, 92, 1452 CrossRef CAS; (b) C. Chudoba, E. Riedle, M. Pfeiffer and T. Elsaesser, Chem. Phys. Lett., 1996, 263, 622 CrossRef CAS; (c) M. Moriyama, Y. Kawakami, S. Tobita and H. Shizuka, Chem. Phys., 1998, 231, 205 CrossRef CAS, and references cited therein; (d) J. Catalán, J. L. G. de Paz, M. R. Torres and J. D. Tornero, J. Chem. Soc., Faraday Trans., 1997, 1691 RSC, and references cited therein..
- J. Keck, M. Roessler, C. Schroeder, G. J. Stueber, F. Waiblinger, M. Stein, D. LeGourriérec, H. E. A. Kramer, H. Hoier, S. Henkel, P. Fischer, H. Port, T. Hirsch, G. Rytz and P. Hayoz, J. Phys. Chem. B, 1998, 102, 6975 CrossRef CAS.
- G. J. Stueber, M. Kieninger, H. Schettler, W. Busch, B. Goeller, J. Franke, H. E. A. Kramer, H. Hoier, S. Henkel, P. Fischer, H. Port, T. Hirsch, G. Rytz and J.-L. Birbaum, J. Phys. Chem., 1995, 99, 10097 CrossRef CAS.
- P. Fischer and A. Fettig, Magn. Reson. Chem., 1997, 35, 839 CrossRef.
- F. Waiblinger, J. Keck, M. Stein, A. P. Fluegge and H. E. A. Kramer, J. Phys. Chem. A, 2000, 104, 1100 CrossRef CAS.
- A. Fettig, Dissertation, Universität Stuttgart, 1999. Search PubMed.
- H. Günther, NMR-Spektroskopie, 3rd edn., Thieme Verlag, Stuttgart, New York, 1992, p. 307–312. Search PubMed.
- J. Sandström, Dynamic NMR-Spectroscopy, Academic Press, New York, 1982. Search PubMed.
- G. Binsch and H. Kessler, Angew. Chem., 1980, 92, 237.
- Dynamic Nuclear Magnetic Resonance Spectroscopy, ed. L. M. Jackman and F. A. Cotton, Academic Press, New York, 1975. Search PubMed.
- H. S. Gutowsky, “Time-dependent Magnetic Perturbations”, in Dynamic Nuclear Magnetic Resonance Spectroscopy, ed. L. M. Jackman and F. A. Cotton, Academic Press, New York, 1975, ch. 1. Search PubMed.
- G. Binsch, “Band Shape Analysis”, in Dynamic Nuclear Magnetic Resonance Spectroscopy, ed. L. M. Jackman and F. A. Cotton, Academic Press, New York, 1975, ch. 3. Search PubMed.
- A. R. Katritzky and R. D. Topsom, Angew. Chem., Int. Ed. Engl., 1970, 9, 87 CrossRef CAS; A. R. Katritzky and R. D. Topsom, J. Chem. Educ., 1971, 48, 427 Search PubMed; R. D. Topsom, Progr. Phys. Org. Chem., 1976, 12, 1 Search PubMed.
- F. Elbe, J. Keck, A. P. Fluegge, H. E. A. Kramer, P. Fischer, P. Hayoz, D. Leppard, G. Rytz, W. Kaim and M. Ketterle, J. Phys. Chem. A, 2000, 104, 8296 CrossRef CAS.
- F. Waiblinger, J. Keck, M. Stein, A. P. Fluegge, H. E. A. Kramer and D. Leppard, J. Phys. Chem. A, 2000, 104, 1100 CrossRef CAS.
- F. Waiblinger, A. P. Fluegge, J. Keck, M. Stein, H. E. A. Kramer and D. Leppard, Res. Chem. Intermed., 2000, 26, in the press Search PubMed.
- A. L. van Geet, Anal. Chem., 1970, 42, 679 CrossRef CAS.
- G. Hägele, DNMR-SIM, 1994. Search PubMed.
Footnotes |
| † A stereoscopic projection of the packing of the crystal structure of 2-dimethylamino-4,6-bis(2-hydroxyphenyl)-1,3,5-triazine is available as supplementary data. For direct electronic access see http://www.rsc.org/suppdata/p2/b0/b005956k/ |
| ‡ CCDC reference number 188/280. See http://www.rsc.org/suppdata/p2/b0/b005956k/ for crystallographic files in .cif format. |
| This journal is © The Royal Society of Chemistry 2001 |
