Comparative spectroscopic and theoretical studies on the conformation of some α-diethoxyphosphoryl carbonyl compounds and their α-ethylsulfonyl analogues 

Abstract

Comparative ν_CO IR analysis of β-carbonylphosphonates [XC(O)CH₂P(O)(OR)₂: X = Me 1, Ph 2, OEt 3, NEt₂4 and SEt 5; R = Et] (series I) and β-carbonylsulfones [XC(O)CH₂SO₂R: X = Me 6, Ph 7, OEt 8, NEt₂9 and SEt 10; R = Et] (series II) along with ab initio 6-31G** calculations on 1a and 6a (R = Me) suggest the existence of only a single gauche conformer for series I. The negative carbonyl frequency shifts for both series follow approximately the electron-affinities of the π*_CO orbital of the parent compounds MeC(O)X 11–15. The less positive asymmetric sulfonyl frequency shifts (Δν_SO2) for II in relation to the phosphoryl frequency shifts (Δν_PO) for I and the larger negative carbonyl frequency shifts for II with respect to the corresponding values for I are in line with the upfield ¹³C NMR chemical shifts of the carbonyl carbon for II compared to I. These trends agree with the shorter O_(SO2) ⋯ C_(CO) contact in comparison with the O_(PO) ⋯ C_(CO) one and are discussed in terms of O_lp→π*_CO charge transfer and electrostatic interactions, which are stronger for series II than for I, indicating that the sulfonyl oxygen atom is a better electron donor than the phosphoryl oxygen atom. Intrinsic geometrical parameters of O[double bond, length half m-dash]S–CH₂ and O[double bond, length half m-dash]P–CH₂ moieties seem to be responsible for this behaviour as indicated by X-ray study and ab initio calculations of dialkyl (methylsulfonyl)methylphosphonate MeSO₂CH₂P(O)(OR)₂ (R = Et 18, Me 18a).

---

Our previous spectroscopic (IR, ¹³C NMR, UV and UPS), X-ray diffraction and theoretical studies of some β-carbonyl-sulfides and -sulfones XC(O)CH₂SO_nR ^2–13 (X = Me, Ar, NR₂, OR and SR; R = Me, Ar; n = 0 and 2) indicated that these compounds in the gas phase, in solution and in the solid state (for the β-carbonylsulfones) prefer a gauche conformation between the C[double bond, length half m-dash]O and CH₂–S bonds. For the corresponding β-carbonylsulfoxides XC(O)CH₂S(O)R ^{2,5,9,13–15} the gauche rotamer is also the more stable, but the cis one prevails for some X or R substituents due to electronic ^16,17 or steric ¹⁷ factors.

In general, the stability of the gauche rotamers of β-carbonyl-sulfides, -sulfoxides and -sulfones has been ascribed to π*_CO/σ_C–S and π_CO/σ*_C–S orbital interactions. However, in the case of β-carbonyl-sulfones ^10,11 and -sulfoxides,^14,15 additional stabilisation of the gauche (or cis) rotamer derives from crossed electrostatic and charge transfer interactions between oppositely charged atoms i.e. O_(SO2)→C_(CO) and (or) O_(CO)→S_(SOn) (n = 1 and 2).

The relevant electronic properties of closely related molecules differing only in the nature of their third row element, such as P or S, are quite similar. In fact, the ionisation energies of the outermost MO (oxygen lone pair) for dimethyl sulfone Me₂SO₂ (10.65 eV) ^18–20 and dimethyl methylphosphonate (MeO)₂P(O)Me (10.71 eV) ²¹ are almost identical. Similarly, the field-inductive parameters for the ethylsulfonyl EtSO₂– and diethoxyphosphoryl (EtO)₂P(O)– groups are equal (F ≡ 0.55).²² In addition, the attachment energy (i.e. the negative of the electron affinity) values for electron capture into the σ*_C–S and σ*_C–P orbitals of Me₂S (3.25 eV) ⁸ and Me₃P (3.10) ^23,24 are similar, and the σ_C–S and σ_C–P ionisation energies (12.7 ⁸ and 11.3 ²⁵ eV, respectively) are not very different. Therefore, it was interesting to study the α-diethoxyphosphoryl carbonyl compounds (EtO)₂P(O)CH₂C(O)X (X = Me 1, Ph 2, OEt 3, NEt₂4 and SEt 5) by means of IR and ¹³C NMR spectroscopies and ab initio calculations in order to compare these data with those previously reported for the corresponding α-ethylsulfonyl carbonyl compounds ^2,9,11 EtSO₂CH₂C(O)X (X = Me 6, Ph 7, OEt 8, NEt₂9 and SEt 10). This paper also reports the X-ray diffraction data and the results of ab initio calculations on dialkyl (methylsulfonyl)methylphosphonates (EtO)₂P(O)CH₂SO₂R (R = Et 18, Me 18a), necessary to obtain the experimental geometric parameters of the (EtO)₂P(O)CH₂– group which cannot be easily obtained from the liquid compounds 1–5. Moreover, compound 18 allows a comparison of the relative electron-donor abilities of the sulfonyl and phosphoryl oxygen atoms.

Experimental

Materials

All solvents for IR measurements were spectrograde and were used without further purification. The already known α-diethoxyphosphoryl carbonyl compounds (EtO)₂P(O)CH₂C(O)X (X = Me 1,²⁶ Ph 2,²⁷ OEt 3,²⁸ NEt₂4 ^28,29 and SEt 5 ³⁰) were prepared by an adaptation of the method described for 5, i.e., by reacting equimolar quantities of triethyl phosphite with the corresponding α-bromocarbonyl compound in benzene at room temperature, followed by reflux for 8 hours. The α-diethoxyphosphoryl carbonyl compound was chromatographically separated from isomeric diethyl 1-substituted-vinyl phosphate H₂C[double bond, length half m-dash]C[X][OP(O)(OEt)₂] through a silica gel column using hexane–acetone as eluent. After solvent evaporation, the liquid α-diethoxyphosphoryl carbonyl compounds 1–5 were obtained in a pure form by distillation under reduced pressure. Diethyl (methylsulfonyl)methylphosphonate 18 (mp 92–93 °C, colourless crystals from chloroform) was synthesised following a literature procedure.³¹

IR measurements

The IR spectra were obtained using an FT-IR Nicolet Magna 550 Spectrometer with 1.0 cm⁻¹ resolution. For the carbonyl phosphonates 1–5 the carbonyl stretching region (1800–1600 cm⁻¹) was recorded in 2.0 × 10⁻² mol dm⁻³ carbon tetrachloride, chloroform and acetonitrile solution, using a 0.519 mm sodium chloride cell. The phosphoryl (P[double bond, length half m-dash]O) stretching region (1300–1100 cm⁻¹) was analysed in carbon tetrachloride solution. The existence of a single symmetric carbonyl stretching band for the series 1–5, in all solvents, was confirmed by Fourier Self Deconvolution (FSD) and second derivative analysis performed on each carbonyl band using the OMNIC Version 1.0 FT-IR software of the Nicolet instrument.

NMR measurements

¹H and ¹³C NMR spectra of 0.5 mol dm⁻³ solutions in chloroform with TMS as an internal standard were recorded at 200 and 50 MHz, respectively, using a Bruker AC-200 spectrometer in the FT mode. The conditions for recording ¹H and ¹³C NMR spectra have been described elsewhere.¹²

Calculations

The most stable conformation, the geometric parameters and the electron charge distribution at the various atoms of α-dimethoxyphosphorylacetone 1a, dimethyl (methylsulfonylmethyl)phosphonate 18a, α-methylsulfonylacetone 6a, dimethyl sulfone 19 and dimethyl methylphosphonate 20 were computed at the HF/6-31G** level using the Gaussian 98 series of programs.³² To save computer time, the ethyl groups were replaced by methyl groups. C_2v and C_s symmetry was used for 19 and 20, respectively, while several (gauche and cis) starting geometries were used for the other compounds.

Crystal data

C₆H₁₅O₅PS, M = 230.21, monoclinic, space group P2₁/a, a = 10.074(1), b = 8.3570(9), c = 13.991(2) Å, β = 108.46(1)°, V = 1117.3(2) ų, Z = 4, D_x = 1.369 Mg m⁻³, λ(Mo-Kα) = 0.71073 Å, μ = 0.423 mm⁻¹, R = 0.0453.†

Data collection and processing

X-Ray diffraction data were collected on a CAD4 Mach3 diffractometer with the θ/2θ scan technique at 293 K; solution by direct methods (SIR92),³³ full-matrix least-squares refinement on F ². 2040 measured reflections (2θ_max = 50°) yielded 1958 unique and 1463 with F_o² ⩾ 4σF_o². Anisotropic displacement parameters for all non-H atoms were applied. H atoms were located on stereochemical grounds and refined with fixed geometry, each riding on a carrier atom, with an isotropic displacement parameter amounting to 1.5 (for methyl H atoms) or 1.2 (for the other H atoms) times the value of the equivalent isotropic displacement parameter of the atom to which they are attached. 121 parameters were refined and the final conventional R was 0.0453. Structure refinement, final geometrical calculations were carried out with SHELXL97,³⁴ PARST-95 ³⁵ and WinGX.³⁶Fig. 1 was produced using ZORTEP.³⁷

Fig. 1 ZORTEP view of compound 18 showing the thermal ellipsoid at 50% probability and the heavy atom labelling.

Results and discussion

Table 1 collects the carbonyl stretching frequencies for the α-diethoxyphosphoryl carbonyl compounds 1–5, in carbon tetrachloride, chloroform and acetonitrile. This table also includes the carbonyl stretching frequencies of the predominant gauche conformer of the α-ethylsulfonyl carbonyl compounds ^2,5,96–10 and the corresponding data for the parent carbonyl compounds ⁹11–15. Only a symmetrical carbonyl band is observed for the whole series 1–5 in all solvents. The existence of a good linear correlation between the carbonyl frequencies of 6–10 and 1–5 in carbon tetrachloride [r = 0.990; s = 5.8 cm⁻¹] suggests that the latter compounds also exist in solution in the gauche conformation.³⁸

Table 1 Frequencies of the carbonyl stretching bands ^a in the IR spectra of α-diethoxyphosphoryl carbonyl compounds (EtO)₂P(O)CH₂C(O)X 1–5, for the gauche conformer ^b of the α-ethylsulfonyl carbonyl compounds EtSO₂CH₂C(O)–X 6–10 and of the parent carbonyl compounds ^c CH₃C(O)–X 11–15

		ν/cm^−1
Compound	X	CCl4	CHCl3	CH3CN
a Each carbonyl frequency corresponds to the maximum of a single symmetrical band (see Experimental section). b The gauche conformer is the more abundant one (conc. >80%). c From ref. 9. d From refs. 2,5 and 9, respectively. e From refs. 2,5 and 9, respectively. f From refs. 2,5 and 9, respectively.
1	Me	1719.3	1714.7	1716.1
6 ^d		1720.5	1720.0	1723.0
11		1718.5	1711.5	1714.5
2	Ph	1685.0	1681.9	1683.4
7 ^e		1680.0	1679.0	1682.0
12		1691.0	1683.0	1693.0
3	OEt	1740.8	1735.0	1736.6
8 ^f		1738.0	1739.0	1743.0
13		1742.0	1732.5	1736.6
4	NEt2	1646.5	1636.8	1637.4
9 ^f		1650.0	1644.0	1645.0
14		1650.0	1640.0	1644.0
5	SEt	1687.2	1680.6	1683.7
10 ^f		1678.0	1677.5	1681.0
15		1695.0	1687.0	1690.0

---

Table 2 lists the carbonyl frequency shifts (Δν_CO/cm⁻¹) for 1–5 and 6–10 in relation to the parent compounds 11–15 together with the attachment energy value for the latter compounds. The Δν_CO values for both series are negative, or slightly positive for the methyl derivatives 1 and 6. The two series are reasonably well correlated (r = 0.912) and follow approximately the electron affinity trend of the parent carbonyl compounds ^8,39 (except in the case of the methyl derivatives 1 and 6). These data suggest that the geometry of the α-phosphoryl carbonyl compounds (structure I) is similar to that of the gauche conformer of the α-sulfonyl carbonyl compounds (structure II), whose geometry was previously determined by theoretical calculations and X-ray diffraction analysis. The trends of Table 2 are in line with previous propositions ^2,9,12,13 on β-keto sulfones and suggest that the O_(PO)→π*_CO and O_(SO2)→π*_CO charge transfer and π*_CO/σ_C–Het hyperconjugative ^2,40 interactions are the main factors which stabilise the gauche conformation (structures I and II).

Table 2 Carbonyl frequency shifts (Δν_CO) ^a for the α-diethoxyphosphoryl (EtO)₂P(O)CH₂C(O)–X 1–5 and for the α-ethylsulfonyl EtSO₂CH₂C(O)–X 6–10 carbonyl compounds, in CCl₄, and the attachment energy values (E_A) ^b for the π*_C(O)X orbital of the parent carbonyl compounds CH₃C(O)–X 11–15

Compound	X	ΔνCO/cm^−1	Compound	ΔνCO/cm^−1	E A/eV
a ΔνCO refers to the difference: νsubstituted carbonyl compound − νparent compound. b From ref. 8. c The value for acetophenone is not detectable by ETS, from ref. 39.
1–11	Me	+0.8	6–11	+2.0	1.26
2–12	Ph	−6.0	7–12	−11.0	<0 ^c
3–13	OEt	−1.2	8–13	−4.0	2.09
4–14	NEt2	−3.5	9–14	0.0	2.26
5–15	SEt	−7.8	10–15	−17.0	0.95

---

The frequencies of the phosphoryl (ν_PO) and asymmetric sulfonyl (ν_SO2) stretching bands of 1–5 and 6–10 in carbon tetrachloride, and the corresponding frequency shifts with respect to their respective parent compounds 16 and 17 are collected in Table 3. All the frequency shifts are positive and the Δν_SO2 values are ca. 1.7 times smaller than the corresponding Δν_PO ones. This behaviour is in line with the absolute carbonyl gauche shifts for 6–10 being larger than the corresponding values for 1–5 (Table 2) and strongly suggests that the O_lp→π*_CO charge transfer interaction in the gauche rotamer of β-carbonyl sulfones is stronger than the corresponding interaction for β-carbonyl phosphonates. In fact, a stronger O_(SO2)→π*_CO charge transfer than the O_(PO)→π*_CO one should lead to a large decrease in the bond order of both C[double bond, length half m-dash]O and O[double bond, length half m-dash]S[double bond, length half m-dash]O oscillators in compounds 6–10 and, therefore, in their frequencies, compared to the C[double bond, length half m-dash]O and P[double bond, length half m-dash]O oscillators for compounds 1–5.

Table 3 Frequencies of the phosphoryl (ν_PO) and sulfonyl asymmetric (ν_SO2) stretching bands in the IR spectra of the α-diethoxyphosphoryl (EtO)₂P(O)CH₂C(O)–X 1–5 and α-ethylsulfonyl EtSO₂CH₂C(O)–X 6–10 carbonyl compounds, in CCl₄, and the corresponding frequency shifts (Δν) ^a in relation to the parent compounds 16 and 17

Compound	X	ν PO/cm^−1	ΔνPO/cm^−1	Compound	ν SO2(as)/cm^−1 ^b	ΔνSO2(as)/cm^−1
a Refers to the difference: να-phosphoryl or νsulfonyl compound − νparent compound. b From ref. 9. c Refers to the parent compounds (EtO)2P(O)Me and Et2SO2, respectively. d Refers to the parent compounds (EtO)2P(O)Me and Et2SO2, respectively.
1	Me	1261	+15	6	1331	+10
2	Ph	1267	+21	7	1332	+11
3	OEt	1270	+24	8	1335	+14
4	NEt2	1253	+7	9	1325	+4
5	SEt	1265	+19	10	1335	+14
16 ^c	—	1246	—	17 ^d	1321	—

---

Table 4 shows the carbonyl ¹³C chemical shifts in deuterochloroform for 1–5 and 6–10 together with the differences (Δ δ) between the chemical shift of each α-substituted carbonyl compound and the chemical shift of the corresponding parent compound 11–15. The smaller carbonyl upfield shifts (Δ δ) of ca. 2.0 ppm for the α-phosphoryl derivatives compared to the α-sulfonyl derivatives, in spite of the quasi equal field-inductive effect ²² for the diethylphosphoryl and the ethylsulfonyl groups, indicate that the O_(PO)→π*_CO CT interaction in the gauche rotamers of series 1–5 is weaker than the O_(SO2)→π*_CO CT in the corresponding rotamers of series 6–10, supporting the IR frequency shift analysis.

Table 4 Carbonyl carbon chemical shifts (δ_C, ppm) in the ¹³C NMR spectra of the α-diethoxyphosphoryl carbonyl compounds (EtO)₂P(O)CH₂C(O)–X 1–5, α-ethylsulfonylcarbonyl compounds EtSO₂CH₂C(O)–X 6–10 and of the parent carbonyl compounds CH₃C(O)X 11–15, in CDCl₃–Me₄Si

X	Compound	δ CO	Compound	δ CO	ΔδCO ^a	Compound	δ CO	ΔδCO ^a
a ΔδCO refers to the difference: δsubstituted carbonyl compound − δreference compound.
Me	11	203.7	1	200.0	−3.7	6	198.0	−5.7
Ph	12	196.7	2	192.0	−4.7	7	189.1	−7.6
OEt	13	169.8	3	165.8	−4.0	8	163.1	−6.7
NEt2	14	164.8	4	162.5	−2.3	9	161.4	−3.4
SEt	15	193.6	5	190.4	−3.2	10	188.2	−5.4

---

In order to confirm the gauche conformer assignment of the single carbonyl band of the diethoxyphosphoryl carbonyl compounds 1–5, and to have precise geometries for the gauche rotamer of these compounds, ab initio calculations on α-dimethoxyphosphorylacetone 1a (chosen as a representative compound for the whole series) were carried out. The relevant data are presented in Table 5 along with the corresponding data for the gauche rotamer of α-methylsulfonylacetone 6a. The two most stable minima of 1a have the gauche conformation (Structures III and IV). It seems reasonable, therefore, to decide that the single carbonyl band observed in solution for the whole α-diethoxyphosphoryl carbonyl series 1–5 should correspond to the more abundant g₁ rotamer of 1a in the gas phase.

Table 5 Relative energy, conformer concentration, dipole moment, selected dihedral angles and interatomic distances of selected non-bonded atoms for the gauche (g) conformers of (MeO)₂P(O)CH₂C(O)Me 1a and MeC(O)CH₂SO₂Me 6a, at the HF/6-31G** level, and the sum of the relevant van der Waals radii

					Dihedral angles ^d/°
Compound	Conf. ^a	E/kJ mol^−1^b	p (%) ^c	μ/D	α	β	γ	γ′	O(5) ⋯ C(2)/Å ^f	O(1) ⋯ P(4)/Å ^g	O(7) ⋯ C(2)/Å ^f	O(6) ⋯ C(2)/Å ^f
1a	g 1	0.0	87.1	2.28	82.2	45.6	171.6	−81.8	3.128	3.331	3.976	3.416
	g 2	4.78	12.9	2.41	88.2	−165.3	−37.6	68.4	4.057	3.459	3.065	3.234

---

					Dihedral angles ^e/°
				μ/D	α	β	γ	γ′	O(6) ⋯ C(2)/Å ^f	O(1) ⋯ S(4)/Å ^g
a Refers to the gauche conformation. b Relative energy. c Molar fraction of each rotamer as a percentage. d α = O(1)–C(2)–C(3)–P(4); β = C(2)–C(3)–P(4)–O(5); γ = C(2)–C(3)–P(4)–O(7); γ′ = C(2)–C(3)–P(4)–O(6). e α = O(1)–C(2)–C(3)–S(4); β = C(2)–C(3)–S(4)–C(5); γ = C(2)–C(3)–S(4)–O(6); γ′ = C(2)–C(3)–S(4)–O(7). f Sum of van der Waals radii = 3.22 Å. g Sum of van der Waals radii = 3.32 Å. h The second minimum energy conformation corresponds to another gauche rotamer whose concentration is less than 1%.
6a ^h	g	0.0	>99	3.03	78.8	−70.3	44.9	174.5	2.973	3.298

---

The higher stability of the g₁ with respect to the g₂ rotamer is in line with a propitious geometry (structure III) giving an intramolecular distance (3.128 Å) between the negatively charged phosphoryl oxygen (q_O = −0.740 e) and the positively charged carbonyl carbon (q_C = +0.498 e), which is shorter than the sum of the van der Waals radii (3.22 Å) (see Table 5). This close contact produces significant O^δ−_PO→C^δ+_CO Coulombic and charge transfer interactions. Further stabilisation derives from the distance (3.331 Å) between the carbonyl oxygen (q_O = −0.523 e) and the phosphoryl phosphorus (q_P = +1.577 e) which is very close to the sum of the van der Waals radii (3.32 Å).

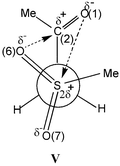
The geometry of the gauche conformer of 6a (see Table 5 and structure V) is very close to that of the g₁ conformer of 1a (structure III). However, the O(6) ⋯ C(2) and O(1) ⋯ S(4) contacts between pairs of oppositely charged atoms are shorter than the corresponding distances for 1a (g₁) (see Tables 5 and 6). Thus, the HF/6-31G** calculations for 1a and 6a corroborate the IR and ¹³C NMR data for 1–5 and 6–10, indicating that both series of compounds exist, in the gas phase and in solution, in the gauche conformation and that the O^δ−_SO2→C^δ+_CO charge transfer and Coulombic interactions in β-carbonyl sulfones are stronger than the O^δ−_PO→C^δ+_CO CT and Coulombic interactions in β-carbonyl phosphonates.

Table 6 Charges (e) at selected atoms for gauche conformers of MeC(O)CH₂X: X = P(O)(OMe)₂1a and X = SO₂Me 6a by ab initio 6-31G** computations (a minus sign indicates an excess of negative charge)

		e/C
Compound	Conf.	O(5)[PO]	O(6)[OR]	O(7)[OR]	P(4)[PO]	C(2)[CO]	O(1)[CO]	O(6)[SO2]	O(7)[SO2]	S(4)[SO2]
1a	g 1	−0.740	−0.718	−0.700	+1.577	+0.498	−0.523
	g 2	−0.714	−0.716	−0.717	+1.574	+0.512	−0.520
6a	g					+0.513	−0.514	−0.690	−0.672	+1.457

---

In the less stable g₂ conformer of 1a the alkoxy oxygens O(6) and O(7) are the donor atoms (structure IV). Their interatomic distances from the oppositely charged carbonyl carbon atom C(2) are close to and shorter than, respectively, the sum of the van der Waals radii and shorter than the corresponding distances in the g₁ conformer (see Tables 5 and 6). The lower stability of the g₂ with respect to the g₁ rotamer is probably related to the oxygen lone pair IE values which are higher for the methoxy than for the phosphoryl oxygen (12.0 and 10.71 eV, respectively ²⁴ for dimethyl methylphosphonate taken as a reference compound).

The existence of only the g₁ conformer for 1–5 in a low permittivity solvent such as carbon tetrachloride (Table 1) can hardly be justified by the small (0.1 D) dipole moment difference between the two gauche rotamers of 1a. However, a close inspection of structures III and IV shows that the P[double bond, length half m-dash]O and C[double bond, length half m-dash]O dipoles are relatively close to each other in g₁ and practically directly opposite each other in g₂. Therefore, even the low relative permittivity but polarizable nature of carbon tetrachloride as solvent would stabilise the g₁ to a greater extent than the g₂ conformer.

Direct information about the relative donor/acceptor ability of the PO and SO₂ groups has been obtained from an X-ray single crystal analysis of diethyl (methylsulfonyl)methyl phosphonate 18. Fig. 1 and Table 7 show that in the solid state 18 assumes a syn-clinal or quasi-gauche geometry with respect to both the α (−41.8°) and γ (−42.5°) dihedral angles. Moreover, the O(1) ⋯ P contact (3.18 Å) is significantly shorter than the sum of the relevant van der Waals radii (3.32 Å), while the O(3) ⋯ S contact (3.295 Å) is only slightly smaller. The most stable conformer of 18a from HF/6-31G** calculations has practically the same geometrical parameters as those obtained by X-ray diffraction for 18. In conclusion, this model compound shows that the O_(SO2)→P_(PO) charge transfer interaction between the sulfonyl oxygen (q_O = −0.700 e) and the phosphoryl phosphorus (q_P = 1.601 e) occurs over a shorter distance and is likely to be more pronounced than the interaction between the phosphoryl oxygen (q_O = −0.743 e) and the sulfonyl sulfur (q_s = 1.459 e), giving some support to the fact that O_(SO2) in 6–10 is a better electron donor toward the π*_CO orbital than O_(PO) in 1–5.

Table 7 Selected dihedral angles and non-bonded distances for the minimum energy conformation of (MeO)₂P(O)CH₂SO₂Me 18a at the HF/6-31G** level, and the corresponding X-ray data for (EtO)₂P(O)CH₂SO₂Me 18, and the sum of the relevant van der Waals radii

			Dihedral angles ^a/°
Compound	Conf. ^b		α	β	γ	γ′	P ⋯ O(1)/Å ^c	P ⋯ O(2)/Å ^c	S ⋯ O(3)/Å ^c
a α = O(3)–P–C(2)–S; β = P–C(2)–S–C(1); γ = P–C(2)–S–O(1); γ′ = P–C(2)–S–O(2). b Refers to the quasi-gauche conformation. c Sum of van der Waals radii = 3.32 Å.
18	q-g	X-Ray	−41.8(2)	74.4(2)	−42.5(2)	−170.3(2)	3.180(2)	4.203(2)	3.295(2)
18a	q-g	HF/6-31G**	−47.5	69.3	−46.2	−175.5	3.243	4.242	3.417

---

The better electron-donor ability of the sulfonyl oxygen lone pair n_O(SO2) than the phosphoryl oxygen lone pair n_O(PO) towards the π*_CO orbital would appear to be unexpected. In fact, the basicity of the oxygen atom of the phosphoryl group evaluated from the ν_OH frequency shift in the diethyl ethylphosphonate–phenol complex with respect to phenol (CCl₄, Δν_OH = 398 cm⁻¹) ⁴¹ is more than twice the basicity of the oxygen of the sulfonyl group estimated for the dimethyl sulfone–p-fluorophenol complex (Δν_OH = 154 cm⁻¹),⁴² and the basicity trend is in line with the larger negative charge at O_(PO) in 19 (−0.743 e) than at O_(SO2) in 20 (−0.678 e). However, in the model compound 18/18a (structure VI), the CH₂–S[double bond, length half m-dash]O angle and the S[double bond, length half m-dash]O bond length are smaller, respectively, than the CH₂–P[double bond, length half m-dash]O angle and the P[double bond, length half m-dash]O bond length. Moreover, the corresponding parameters O[double bond, length half m-dash]P–CH₃ (118.0°) and the P[double bond, length half m-dash]O (1.459 Å) for MeP(O)(OMe)₂19, and O[double bond, length half m-dash]S–CH₃ (107.8°) and S[double bond, length half m-dash]O (1.435 Å) for Me₂SO₂20 are very close to those computed for 18a. Thus, these intrinsic geometrical parameters, which allow close contact between oppositely charged atoms in 18, seem to be responsible for the abnormally stronger electron-donor ability of the sulfonyl oxygen lone pair n_O(SO2) in 6–10 than the phosphoryl oxygen lone pair in 1–5.

Conclusions

The IR frequency of the single ν_CO band of the β-carbonylphosphonates [XC(O)CH₂P(O)(OEt)₂: X = Me 1, Ph 2, OEt 3, NEt₂4 and SEt 5] (series I), which correlates well with the ν_CO frequencies of the gauche rotamer of the corresponding β-carbonyl sulfones [XC(O)CH₂SO₂Et: X = Me 6, Ph 7, OEt 8, NEt₂9 and SEt 10] (series II) along with ab initio 6-31G** computations for 1a and 6a (X = Me) indicate the existence of a single gauche conformer (g₁) for series I in solution.

The abnormal negative carbonyl frequency shifts (Δν_CO) for both series approximately follow the electron affinities of the π*_CO orbital of the parent carbonyl compounds MeC(O)X 11–15. These data suggest that the gauche conformations of series I and II should have similar geometries.

The less positive asymmetric sulfonyl frequency shifts (Δν_SO2) in comparison with the phosphoryl frequency shifts (Δν_PO) and the larger negative carbonyl gauche conformer shifts of β-carbonyl sulfones 6–10 in relation to the corresponding values of the β-carbonyl phosphonates 1–5 are in line with the greater upfield carbonyl ¹³C chemical shifts for series II with respect to series I. These trends are in agreement with their O_(SO2) ⋯ C_(CO) distances which are shorter than O_(PO) ⋯ C_(CO) in compounds 6a and 1a, respectively, and are discussed in terms of the O_lp→π*_CO charge transfer and electrostatic interactions, which are stronger for series II than for I. This unexpected behaviour indicates that the sulfonyl oxygen atom of the SO₂R group is a better electron donor than the phosphoryl oxygen atom of the P(O)(OR)₂ group. The intrinsic geometric parameters of the O[double bond, length half m-dash]S–CH₂ and O[double bond, length half m-dash]P–CH₂ moieties seem to be responsible for this behaviour. In fact, X-ray and ab initio calculations of dialkyl (methylsulfonyl)methylphosphonate MeSO₂CH₂P(O)(OR)₂ (R = Et, 18, Me 18a) support this analysis.

Acknowledgements

The Brazilian authors thank Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) for financial support and the concession of the CAD4-Mach 3 X-ray diffractometer, and the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for a grant (to P. R. O. and J. Z.-S.) and a scholarship (to R. R. F.). The Italian authors thank the Ministero della Ricerca Scientifica e Tecnologica for financial support.

References

1. Presented in part at the 18th International Symposium on the Organic Chemistry of Sulfur, Florence, Italy, 1998; summary in: Phosphorus, Sulfur Silicon Relat. Elem., 1999, 153–154, 353.
2. P. R. Olivato and M. G. Mondino, Phosphorus, Sulfur Silicon Relat. Elem., 1991, 59, 219.
3. P. R. Olivato, S. A. Guerrero and E. A. Martins, Phosphorus, Sulfur Silicon Relat. Elem., 1989, 44, 9.
4. P. R. Olivato, B. Wladislaw and S. A. Guerrero, Phosphorus, Sulfur Relat. Elem., 1987, 33, 135.
5. P. R. Olivato, E. Bonfada and R. Rittner, Magn. Reson. Chem., 1992, 30, 81.
6. P. R. Olivato, B. Wladislaw, S. A. Guerrero and D. Russowsky, Phosphorus, Sulfur Relat. Elem., 1985, 24, 225.
7. P. R. Olivato, F. Oike and J. C. D. Lopes, Phosphorus, Sulfur Silicon Relat. Elem., 1990, 47, 391.
8. D. Jones, A. Modelli, P. R. Olivato, M. Dal Colle, M. de Palo and G. Distefano, J. Chem. Soc., Perkin Trans. 2, 1994, 1651.
9. P. R. Olivato , M. G. Mondino and M. Sakuragi , unpublished results. .
10. G. Distefano, M. Dal Colle, V. Bertolasi, P. R. Olivato, E. Bonfada and M. G. Mondino, J. Chem. Soc., Perkin Trans. 2, 1991, 1195.
11. M. Dal Colle, V. Bertolasi, M. de Palo, G. Distefano, D. Jones and P. R. Olivato, J. Phys. Chem., 1995, 99, 15011.
12. P. R. Olivato, S. A. Guerrero and R. Rittner, Phosphorus, Sulfur Silicon Relat. Elem., 1997, 130, 155.
13. P. R. Olivato , E. Bueno , S. A. Guerrero and J. Zukerman-Schpector , 18th International Symposium on the Organic Chemistry of Sulfur, Florence, Italy, 1998, Abstract Book, p. 214..
14. P. R. Olivato, S. A. Guerrero and R. Rittner, Phosphorus, Sulfur Silicon Relat. Elem., 2000, 156, 255.
15. P. R. Olivato, S. A. Guerrero and J. Zukerman-Schpector, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 112.
16. G. Distefano, M. Dal Colle, M. de Palo, D. Jones, G. Bombieri, A. Del Pra, P. R. Olivato and M. G. Mondino, J. Chem. Soc., Perkin Trans. 2, 1996, 1661.
17. P. R. Olivato, M. G. Mondino, M. H. Yreijo, B. Wladislaw, L. Marzorati, M. B. Bjorklund, G. Distefano, M. Dal Colle, G. Bombieri and A. Del Pra, J. Chem. Soc., Perkin Trans. 2, 1998, 109.
18. B. Solouki, H. Bock and R. Appel, Chem. Ber., 1975, 108, 897.
19. C. Müller and A. Schweig, Tetrahedron, 1973, 29, 3973.
20. H. D. Martin, R. Iden, H. Landen, B. Mayer, G. Distefano, A. Modelli and R. Gleiter, J. Electron Spectrosc. Relat. Phenom., 1986, 41, 385.
21. S. Chattopadway, G. Findley and S. P. McGlyn, J. Electron Spectrosc. Relat. Phenom., 1981, 24, 27.
22. C. Hansh , A. Leo and D. Hoekman , Exploring QSAR Hydrophobic, Electronic and Steric Constants, ACS Professional Reference Book, American Chemical Society, Washington, DC, 1995..
23. J. A. Tossell, J. H. Moore and J. C. Giordan, Inorg. Chem., 1985, 24, 1100.
24. J. C. Giordan, J. H. Moore, J. A. Tossell and W. Kaim, J. Am. Chem. Soc., 1985, 107, 5600.
25. H. Schmidt, A. Schweig, F. Mathey and G. Mueller, Tetrahedron, 1975, 31, 1287.
26. A. N. Pudovik and V. P. Avery’anova, Zh. Obshch. Khim., 1956, 26, 1431 ( Chem. Abstr. , 1956 , 50 , 14513 ).
27. I. J. Borowitz, M. Anschel and S. Firstenberg, J. Org. Chem., 1967, 32, 1723.
28. A. J. Speziale and R. C. Freeman, J. Org. Chem., 1958, 23, 1883.
29. R. W. Balsiger, D. G. Jones and J. A. Montgomery, J. Org. Chem., 1959, 24, 434.
30. H. J. Liu, P. A. Rose and D. J. Sasaki, Can. J. Chem., 1991, 69, 934.
31. G. H. Posner and D. J. Brunelle, J. Org. Chem., 1972, 37, 3547.
32. Gaussian 98, Revision A.6, M. J. Frisch , G. W. Trucks , H. B. Schlegel , G. E. Scuseria , M. A. Robb , J. R. Cheeseman , V. G. Zakrzewski , J. A. Montgomery, Jr. , R. E. Stratmann , J. C. Burant , S. Dapprich , J. M. Millam , A. D. Daniels , K. N. Kudin , M. C. Strain , O. Farkas , J. Tomasi , V. Barone , M. Cossi , R. Cammi , B. Mennucci , C. Pomelli , C. Adamo , S. Clifford , J. Ochterski , G. A. Petersson , P. Y. Ayala , Q. Cui , K. Morokuma , D. K. Malick , A. D. Rabuck , K. Raghavachari , J. B. Foresman , J. Cioslowski , J. V. Ortiz , B. B. Stefanov , G. Liu , A. Liashenko , P. Piskorz , I. Komaromi , R. Gomperts , R. L. Martin , D. J. Fox , T. Keith , M. A. Al-Laham , C. Y. Peng , A. Nanayakkara , C. Gonzalez , M. Challacombe , P. M. W. Gill , B. Johnson , W. Chen , M. W. Wong , J. L. Andres , M. Head-Gordon , E. S. Replogle and J. A. Pople , Gaussian Inc., Pittsburgh PA, 1998..
33. A. Altomare, G. Cascarano, C. Giacovazzo and A. Guagliardi, J. Appl. Crystallogr., 1993, 26, 343.
34. G. M. Sheldrick , SHELXL97. Program for the Refinement of Crystal Structures, University of Göttingen, Germany, 1997..
35. M. Nardelli, J. Appl. Crystallogr., 1995, 28, 659.
36. L. J. Farrugia , WinGX. A Windows Program Package for Crystal Structure Analysis, University of Glasgow, Scotland, 2000..
37. L. Zsonai , ZORTEP, Molecular Graphics Program, University of Heidelberg, Germany, 1995..
38. In our experience, in fact, a good linear correlation is not obtained when the frequencies of the gauche rotamers of a series of compounds are plotted against the frequencies of the cis conformers of a different series..
39. G. Distefano , A. Modelli and D. Jones , unpublished results. .
40. P. R. Olivato and R. Rittner, Rev. Heteroat. Chem., 1996, 15, 115.
41. J. E. Oliveira , MSc Thesis, Instituto de Quimica, Universidade de São Paulo, Brazil, 1980..
42. A. Chardin, C. Laurence, M. Berthelot and D. G. Morris, J. Chem. Soc., Perkin Trans. 2, 1996, 1047.

---

Footnote

† CCDC reference number 188/279. See http://www.rsc.org/suppdata/p2/b0/b005501h/ for crystallographic files in .cif format.

---