Molecular dynamics study of 21C7 crown ether derivatives and their alkali cation complexes. Comparison with 1,3-alt-calix[4]arene-crown-6 compounds

Abstract

A molecular dynamics study in vacuo and in an explicit water phase was undertaken on 21C7 benzo and cyclohexano crown ether derivatives, in order to better understand the differences between these compounds and calixarene-crown-6 compounds regarding the complexation of alkali cations. Whatever the number and the position of the benzo or cyclohexano groups on the crown ether, this crown ether remains highly flexible when it is simulated in the gas phase. The most notable differences appear in simulations in an explicit aqueous phase and are discussed in terms of hydrophobicity of the free ligands and instability of non hydrated complexes in water. Calixarene-crown-6 compounds appear to be much better preorganized, with a smaller and less mobile ether loop due to its grafting onto the calixarene cavity. In contrast to the 21C7s, the crown can adapt perfectly only around caesium and penalises sodium particularly. Moreover, the calixarenes isolate better the cations from the bulk aqueous phase. These differences of preorganisation and cation accessibility to the solvent can explain the superior extracting properties and the stronger selectivity of calixcrowns.

---

Introduction

In the field of nuclear waste treatment, the achievement of the separation of caesium with a high selectivity from solutions containing other alkali cations, especially sodium, is a major goal. To date, 1,3-alt-calix[4]crown-6s have proven to be the best extractants to reach this goal in solvent extraction experiments.^1–3 The Cs⁺/Na⁺ selectivity is enhanced when benzo groups are grafted onto the crown ether loop, due to a lower extraction of sodium whatever the composition of the aqueous phase, and to a higher extraction of caesium in the presence of nitric acid.^4,5

Other macrocyclic extractants, like 18C6, 21C7 and 24C8 crown ether derivatives, were also experimentally studied for caesium removal. Their extracting properties and selectivity in the alkali and alkaline earth series were discussed, focusing on the size of the crown ether and on the influence of benzo and cyclohexano substituents on the loop.^6,7 The most efficient compounds are found in the 21C7 series, with a Cs⁺/Na⁺ selectivity enhanced for the benzo derivatives whereas cyclohexano derivatives are better extractants.⁸

This efficiency for caesium extraction depends on the number and location of the benzo groups on the crown: [2,5]dibenzo21C7 is a better extractant of caesium than the n-decylbenzo derivative,² which is better than [3,4]dibenzo21C7.^4,9 The Cs⁺/Na⁺ selectivity order is a little bit different with [2,5]DB21C7 > [3,4]DB21C7 ≥ n-decylB21C7.

The selectivity of extraction by 21C7 derivatives towards larger alkali cations (caesium, rubidium, potassium) was studied in competitive extraction conditions, with either a mixture of nitrate salts ¹⁰ or a mixture of picrate salts.¹¹ In these experiments, the distribution coefficients of alkali cations to dichloroethane or chloroform are very low (about 10⁻² or 10⁻³), as is the selectivity, which depends on the counter-ion and extraction conditions. [3,4]Dibenzo21C7 is able to show a weak Cs⁺/Rb⁺ selectivity while [3,4]dicyclohexano21C7 shows no selectivity between these cations. [3,4]Tricyclohexano21C7 shows a light selectivity peak for Rb⁺, while tribenzo21C7 is truly Rb⁺ selective.

Many structural and simulation data can be found on the 18C6 derivatives, but those on the 21C7 and 24C8 series are scarce. X-Ray data were recently published on tribenzo21C7 and tetrabenzo24C8 caesium and rubidium complexes and the selectivity for Rb⁺ (tribenzo21C7) or Cs⁺ (tetrabenzo24C8) in solvent extraction experiments was related to ligand strain energy in the complexes by means of molecular mechanics simulations in the gas phase.^12,13 Hay developed this method to rationally evaluate from structural criteria the selectivity of a ligand with respect to a series of cations or related ligands, and tested it on crown ethers.¹⁴ The strain energy, defined as the difference in steric energy between the conformations of lowest energy of the uncomplexed ligand and the steric energy of the complexed conformation, is thus quantified. Improvements on a ligand should result in the minimization of its strain energy upon complexation of a given cation, and the selectivity for a cation should result from the lowest strain energy for the ligand. Although qualitative, this method takes into account precisely the ligand preorganization and complementarity towards the cation. It can also be applied through ab initio quantum mechanical calculations, and results on the Cs⁺/Rb⁺ selectivity of benzo21C7 and tribenzo21C7 in the gas phase will soon be reported.¹⁵

The study reported here is partially related to strain energy, but instead of working on isolated molecular mechanics (MM) structures, we chose to work on molecular dynamics (MD) samplings at 300 K, which give a set of equilibrated conformations coexisting in the same energy minimum, thus giving additional insights into the actual ligand flexibility. The other main advantage is to be able to take into account the influence of solvation on the ligand structure and evaluate its hydrophobicity through interactions with the closest water molecules. Moreover, water molecules may reinforce the cationic complex but may also compete with the ligand and lead to cation decomplexation.

Molecular dynamics simulations on alkali complexes with calixcrowns were previously reported.¹⁶ To demonstrate the similarities and differences between calixcrowns and crown ethers, we report new MD simulations on benzo and cyclohexano derivatives of 21C7 crown ether (Fig. 1), and their complexes with Cs⁺, Rb⁺, K⁺ and Na⁺in vacuo and in a water phase.

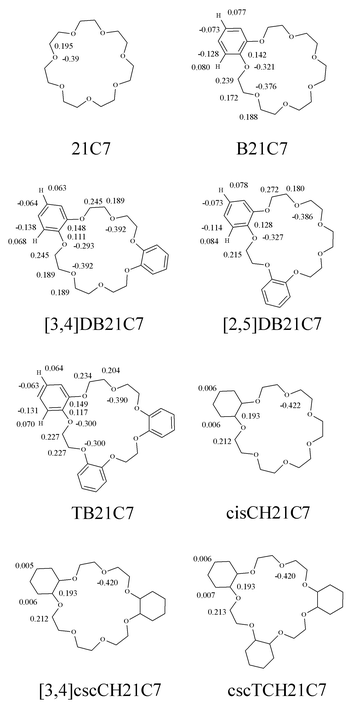Fig. 1 21C7 benzo and cyclohexano derivatives, and atomic charges used in calculations.

Computational methods

All calculations were carried out on an SG INDIGO 2 R8000 workstation with AMBER 4.1 software,¹⁷ using, as a force field, the all-atom parameters and eqn. (1) as a representation of the potential energy,¹⁸ where r, θ and φ represent, respectively, the bond length, the bond angle and the dihedral angle. R_ij is the distance between atoms i and j, q_i is the atomic charge on atom i and ε is the relative permittivity.

As a starting point for our calculations we used caesium structures model built with SYBYL 6.1 software.¹⁹ The other complexes were generated by changing the parameters of the cation.

The atomic charges on the crown ethers (Fig. 1) were calculated with the MNDO semiempirical method and scaled up with a 1.26 scaling factor to allow a nice fit with 6-31G*/ESP values commonly used for crown ether moieties.²⁰ With these charges, the electrostatic term thus compensates the absence of an explicit polarization term in the force field equation. The charge on H atoms belonging to methylene or methine groups was incorporated into the charge of the corresponding carbon atom. The ion parameters came from Aqvist ²¹ and were adapted to the AMBER force field (TIP3P water model and periodic boundary conditions, PBC). The 1–4 non bonded contributions were scaled down by a factor of 0.5.

In vacuo, the alkali complexes were submitted to minimization with 50 steepest descent iterations followed by conjugate gradient iterations until convergence with an RMS at 0.01 kcal mol⁻¹ Å⁻¹ on the gradient of energy. Then MD simulations were performed at constant temperature (300 K) and energy for 500 ps with a 1.0 fs time step, a relative permittivity set at 1.0 and a sharp 10 Å residue-based cut-off. One conformation was saved on each picosecond calculation and the trajectories, constituted by the collection of these conformations, were visualized on a graphic screen by MD/DRAW software ²² and analyzed by MDS software.²³ The first ten picoseconds, corresponding to the system thermal equilibration, were not taken into account in the structural and energetic analysis and averages were calculated over 490 ps of MD.

In water, the Molecular Dynamics simulations used a time step of 2.0 fs, and a 12 Å cut-off. The SHAKE procedure was used to constrain bonds involving hydrogen atoms. We used PBC and an isothermal–isobaric ensemble of 300 K and 1 atm through coupling to temperature and pressure baths. All the starting structures were complexes minimized at the end of the MD run in vacuo, and immersed in a TIP3P cubic box, removing water molecules within 2 Å of the solute. These systems were energy minimized and submitted to Molecular Dynamics. For the alkali complexes, if no decomplexation occurred, MD in water was performed for at least 100 ps. The free crown ethers were submitted to 200 ps of MD in water, and the structural and energetic data were calculated between 100 and 200 ps, after full equilibration of the system.

Free energy calculations in water were performed with the Thermodynamic Integration procedure (TI),²⁴ with the protocol previously described.⁵

Results and discussion

Evolution of crown size and flexibility from the free crown to the alkali complexes

MD simulations at 300 K allow a sampling of conformations at room temperature, in order to get average structural and energetic data. The visualisation of the trajectories is also of importance to get insight into the flexibility of the free and complexed ligands. In the absence of a solvent phase or a counter-ion, these simulated data allow a characterization of the intrinsic affinity between cations and ligands.

In vacuo, for the uncomplexed crowns, most of the time averaged distances between the oxygen atoms and their centroid, dC–O_C, have fluctuations ranging between 0.4 and 0.7 Å during the MD sampling at 300 K. The radial distribution functions (rdf_vac) of the oxygen atoms around their mass center show, in many cases, a very broad peak, without a well defined maximum (Fig. 2). This illustrates the very high flexibility of these crown ethers.

Fig. 2 Radial distribution function rdfC–O_C of the crown oxygen atoms around their centroid, collected during 500 ps of MD in vacuo (rdf_vac) and from 100 to 200 ps of MD in water (rdf_wat).

In an explicit water phase, one or two water molecules are in interaction with up to five oxygen atoms of the crown, through hydrogen bonds. This organizes only a part of the crown for complexation, with these oxygen atoms converging towards the center of the crown. As a consequence, the dC–O_C distances show smaller variations than in vacuo (ranging between 0.2 and 0.3 Å). The best organization is found for B21C7 where all the oxygen atoms are at the same distance from their mass center. For the DCH and TCH derivatives, two maxima can be found on the rdfC–O_C curve in water, due to two oxygen atoms not converging on the mass center (Figs. 2 and 3).

Fig. 3 Crown ethers after 100 ps of MD simulation at 300 K in an explicit water phase, and the closest water molecules.

The most hydrated crowns are 21C7, its monosubstituted cyclohexano and benzo derivatives and [3,4]DB21C7, for which rdfC–O_w, the radial distribution function of the water oxygen atoms around C, the mass center of the crown oxygen atoms, shows an average of 2.5 O_w located within a radius of 3.5 Å around C. The other crowns are much more hydrophobic with about 1.2 O_w around C.

For the sake of simplicity, in the free ligand, cavity size can be characterized with the parameter <dC–O_C> corresponding to the average of the seven individual dC–O_C time averages. The crown flexibility can be deduced from direct comparison between <dC–O_C> for the free and complexed crown, where the crown tries to adapt its size to the size of the cation, in order to optimize the electrostatic interactions with the oxygen donors. The average size of the uncomplexed crowns presents a close fit to that of the caesium complexes, with a slight divergence for TB and TCH derivatives (Fig. 4). The average size of the hydrated crowns is smaller, TB21C7 having a size closer to that of its rubidium complex, which can be related to its Rb⁺ selectivity with respect to the caesium selectivity of the other benzo compounds.⁸ Indeed, the selectivity is a balance between the intrinsic preference for a cation corrected by the relative desolvation energy of the cations considered. Optimizing the interactions and preorganization for Rb⁺ can overcome the dehydration energy which favours Cs⁺.

Fig. 4 Evolution of the size of the crown cavity for the alkali complexes from MD simulations in vacuo and for the free crown ethers in vacuo and in a water phase. Visualization of individual dC–O_C minimum and maximum time averaged distances only for the uncomplexed crowns in vacuo. For alkali complexes, the average distances show less variation (±0.05 Å for 21C7, B21C7 and CH21C7, ±0.10 Å for the other complexes with the exception of ±0.25 Å for TB21C7–Rb⁺ and [2,5]DB21C7–K⁺).

In vacuo the size of the complexed crown cavity follows the size of the cation. Whatever the crown or the cation, all the distances d(M⁺–O_C)_vac between the cation and the crown oxygen atoms are close to the optimal cation–water oxygen distances calculated in our conditions from simulations in water i.e. 3.2 Å for Cs⁺, 2.9 Å for Rb⁺, 2.8 Å for K⁺ and 2.5 Å for Na⁺.⁵ So, these benzo and cyclohexano 21C7 derivatives, even with several substituents, are flexible enough to adapt their size to the cation complexed, showing in any case a good structural complementarity.

Energetic data

The good structural complementarity observed for all cations is to the detriment of the internal ligand energy, especially in the sodium complexes. As demonstrated in available X-ray data, the crown ether wraps around the smallest cations, an example of the ether deformation being illustrated in Fig. 5. The energetic penalty is mainly for the sodium cation, and is more pronounced for the cyclohexano derivatives.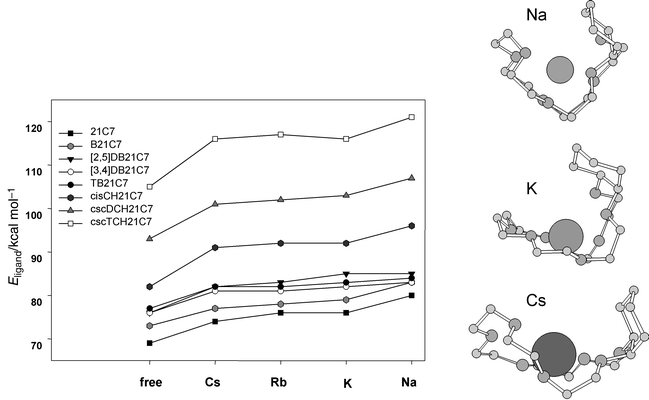

Fig. 5 Evolution of the average internal energy for the crown ethers uncomplexed and in the geometry of their alkali complexes during 500 ps of molecular dynamics at 300 K in vacuo. Minimized structures of the Cs⁺, K⁺ and Na⁺ CH21C7 complexes. Variation: ±4 kcal mol⁻¹ for 21C7 and benzo derivatives, ±5 kcal mol⁻¹ for cyclohexano derivatives.

In vacuo, the total energy of the complex is the sum of the energy of the ligand and the interaction energy between the ligand and the cation. These latter data, in any case, strongly favor the smallest cation, due to the main electrostatic interactions, giving a selectivity for sodium, whatever the crown size and deformation. This has been evidenced in ESI MS experiments on crown ethers.²⁵

The calculated interaction energy is very sensitive to the point charges set, and one must be very careful when comparing simulation data for a series of molecules, where the point charges were calculated independently for each compound. Indeed, when increasing the number of benzo substituents on the crown, the charges on the oxygen atoms are delocalized and then decrease, with a subsequent decrease of the interaction energy (Fig. 6). An exception was found for [2,5]DB21C7, in which the atomic charges on the oxygen atoms are intermediate between those of B21C7 and [3,4]DB21C7. This may be due to a better structural complementarity for the caesium cation, point charges being calculated for the geometry of a caesium complex (convergent orientation of all oxygen atoms towards the inside of the crown). Nevertheless, it should be observed that in solvent extraction experiments, [2,5]DB21C7 extracts caesium better than B21C7 and [3,4]DB21C7. On the other hand, in the cyclohexano series and for the same cation, no significant differences are found in the interaction energy which is much more important than in the benzo series. This can be related to more polarized point charges which are not influenced by the number of cyclohexano groups. According to this criterion, one should expect the same behavior towards alkali cations for the cyclohexano compounds, with stronger complexes than in the benzo series. This result must be confirmed by simulations in water, giving insights into the cation solvation and the actual complex stability.

Fig. 6 Interaction energy between the alkali cations and the crown ethers during 500 ps of molecular dynamics at 300 K in vacuo. Variation: ±2 kcal mol⁻¹ for all complexes.

Evolution of complexes during simulations in an explicit water phase

Minimized structures of complexes after MD in vacuo were submitted to MD simulations in an explicit water phase, in order to check their stability when the solvent is competing with the crown ether. Water molecules are always present in solvent extraction experiments and the hydration of the cation in the complex is also a key feature of the selectivity towards competing cations.⁵

For all the 21C7 derivatives studied here, contact between the cation initially in the complex and bulk water occurred rapidly. In the case of 21C7, only the sodium remained complexed during the MD run, with two water molecules stabilizing the cation in the complex. In the benzo series, none of the complexes remained stable in water, with in most of the cases a very rapid decomplexation, occurring at less than 20 ps of MD run. Following the observations drawn from simulations in vacuo, [2,5]DB21C7 gave the most stable complexes in that series, with decomplexation occurring at 41, 72 and 76 ps of MD run respectively for Cs⁺, K⁺ and Na⁺. In the cyclohexano series, decomplexations were observed only for the monocyclohexano derivative (at 66, 63 and 90 ps respectively for Cs⁺, Rb⁺ and Na⁺), DCH and TCH giving stable hydrated complexes for the four cations, with at least two water molecules coordinated to the cation. Thus, the evolution of these complexes to decomplexation or hydrated species depends not only on the strength of the complexes in vacuo but also on the limitation of the contact between the cation and water, due to the presence of bulk hydrophobic substituents or a folded conformation.

Some additional selectivity calculations were performed on TCH21C7 complexes in water, with the thermodynamic cycle method ²⁴ and gave the expected result of values under the uncertainty of the calculation. To our knowledge, there is not a complete set of data for these eight crown ethers and four alkali cations. In most of the cases, the experimental possible selectivity is so weak that it cannot be reasonably illustrated by these simulations.

From crown size considerations in water, we have retrieved the rubidium selectivity of TB21C7 and a likely caesium selectivity of DB21C7 derivatives. These MD simulations have also highlighted why di- and tricyclohexano compounds should not be selective and, in spite of stronger oxygen donors, should not be much better extractants due to their bad organization in water. MD simulations in water are thus able to give some additional help to understand the behavior of such highly flexible compounds, with many conformations of low energy, when pure structural data (X-ray, MM, or MD in vacuo) fail to account for the actual experimental selectivities.

Comparison between crown ethers and calixcrowns

Calixcrown-6s, in the 1,3-alternate conformation, are much better extractants for caesium than the 21C7 derivatives but, above all, present an exceptional Cs⁺/Na⁺ selectivity. In this calixcrowns series, BC6 is the least lipophilic and selective compound (Cs⁺/Na⁺ selectivity of 1500 compared with 300 for n-decylB21C7 under the same experimental conditions ²), while BC6B2 is the most selective one, which was attributed to greater difficulty in complexing a hydrated sodium cation in solvent extraction experiments.⁵

Our aim is to compare these calixcrowns to their closest crown ethers, namely 21C7, [2,5]DB21C7 and TB21C7, with respect to the organization of their empty or complexed crown, and solvation effects.

Simulations on the alkali complexes of these calixcrowns have been reported elsewhere. For the free compounds, the MD sampling was performed in vacuo during 1 ns, to gain similar results on both crowns.⁵

In contrast to those of the crown ethers, the rdfC–O_C curves in vacuo and in water show two peaks, centered at 2.5 and 3.7 Å, whose integral corresponds to the two oxygen atoms at the top of the crown for the first peak, and the four others for the second one (Fig. 7). The minimum dC–O_C distances are larger than those observed in simulations on benzo crown ethers, suggesting a better preorganization for complexation of large cations. In vacuo, the value of the <dC–O_C> parameter is 3.50 ± 0.50 Å for BC6, and 3.26 ± 0.50 Å for BC6B2 (this important variation corresponds to the presence of the two peaks; for crown ethers, that variation ranges from 0.10 Å for [2,5]DB21C7 to 0.28 Å for CH21C7). Thus, BC6 has the larger crown in both the calixcrown-6s and 21C7s series, and will need an important reorganization to fit even the caesium cation. The average crown size of the free BC6B2 is much closer to that of its caesium complex, and individual dCs⁺–O_C distances are very homogeneous (<dCs⁺–O_C> = 3.15 ± 0.09 Å in vacuo and 3.19 ± 0.03 Å in water). So, in spite of the presence of the two peaks on the rdfC–O_C curves, the reorganization of these oxygen atoms to an average peak centred at 3.1 Å around their mass center and 3.2 Å around caesium will occur easily.

Fig. 7 Calixcrown6s. Radial distribution function rdfC–O_C of the crown oxygen atoms around their centroid, collected during 1 ns of MD in vacuo (rdf_vac) and from 100 to 200 ps of MD in water (rdf_wat).

In water, important differences appeared between these calixarenes. For BC6, crown hydration occurred for both crowns, at 1 ps for one crown and 174 ps for the second one. The rdf_wat given in Fig. 7 comes from the hydrated crown, where two water molecules are statistically distributed within a radius of 3.5 Å around the centroid C, which corresponds to an intermediate value in comparison to the simulations on crown ethers reported above. It may be noted that the rdf_wat of the second crown, although not hydrated during the whole simulation, does not show significant differences. None of the crowns of BC6B2 became hydrated during the 200 ps of MD run. They gave the same rdf_wat curves, one crown remaining in the conformation g⁻0g⁻0g⁻, the other one showing some g⁺g⁻ transitions. Thus BC6B2 appears much more hydrophobic and preorganized than BC6 or benzo-21-crown-7.

Another difference of primary importance between these calixcrowns and benzo crown ethers arises from the ligand flexibility and its consequences for cation–crown complementarity. Indeed, these crown ethers are sufficiently flexible to adapt to the cation, whatever its size, from sodium to caesium. The rigid calixarene structure, onto which the crown is grafted, does not allow this adaptation to the cation. The crown size is more or less fitted for caesium, depending on the substituents on the crown, but that fit decreases when the cation size diminishes, giving a very bad structural complementarity for sodium whatever the environment considered for the cation (presence of water or counter-ion).

Finally, the potassium to caesium complexes formed with BC6 and BC6B2 are stable in water for more than 100 ps, which was encountered only in simulations on di- and tricyclohexano21C7s. The calixarene cavity in the 1,3-alternate conformation is thus able to shield enough the cation from the bulk solvent phase, preventing rapid decomplexation, and this may be related to a higher extracting power compared to benzocrown ethers.

Conclusion

This molecular dynamics study on 21C7 crown ether derivatives was undertaken to better understand the differences between these compounds and calixarene-crown-6 compounds regarding the complexation of alkali cations.

The first striking result drawn from these simulations is the very high flexibility of these crown ethers, whatever the number and the position of the benzo or cyclohexano groups. Notable differences in hydrophobicity and complex stability appear in simulations in an explicit aqueous phase. Thus the monosubstituted derivatives are definitely less hydrophobic than the di- and trisubstituted derivatives. Benzo derivatives are well preorganized in water for complexation but form weak complexes in which the cation is not sufficiently shielded from the water phase. According to preorganization and complementarity considerations, these compounds should easily form complexes with the larger cations, giving a weak selectivity for caesium (both B21C7 and DB21C7) or rubidium (TB21C7) cations. CH21C7 shows the same behavior as the benzo derivatives. DCH21C7 and TCH21C7, with a more pronounced lack of preorganization due to a larger and more flexible crown but also bad reorganization in presence of water, should present an entropic penalty upon complexation but give strong hydrated complexes, without selectivity amongst alkali cations.

Calixarene-crown-6 compounds appear to be much better preorganized, due to the calixarene cavity. Here, the crown can only fit perfectly to caesium and the rigid calixarene cavity penalizes sodium particularly. Moreover, the calixarenes isolate better cations from the bulk aqueous phase, preventing rapid decomplexations. These differences of preorganisation and cation accessibility to the solvent can explain the superior extracting properties and the stronger selectivity of calixcrowns although 21C7 crown ethers show comparable characteristics in terms of complementarity with respect to the caesium cation.

References

1. R. Ungaro, A. Casnati, F. Ugozzoli, A. Pochini, J. F. Dozol, C. Hill and H. Rouquette, Angew. Chem., Int. Ed. Engl., 1994, 33, 1506.
2. Z. Asfari, C. Bressot, J. Vicens, C. Hill, J. F. Dozol, H. Rouquette, S. Eymard, V. Lamare and B. Tournois, Anal. Chem., 1995, 67, 3133.
3. T. J. Haverlock, P. V. Bonnesen, R. A. Sachleben and B. A. Moyer, Radiochim. Acta, 1997, 76, 103.
4. J.-F. Dozol , V. Lamare , N. Simon , R. Ungaro and A. Casnati , in Calixarene Molecules for Separations, ed. G. Lumetta, R. D. Rogers and A. S. Gopalan, ACS Symposium Series 757, ch. 2, American Chemical Society, Washington DC, 2000, p. 12..
5. V. Lamare, J.-F. Dozol, S. Fuangswasdi, F. Arnaud-Neu, P. Thuery, M. Nierlich, Z. Asfari and J. Vicens, J. Chem. Soc., Perkin Trans. 2, 1999, 271.
6. W. J. McDowell, B. A. Moyer, G. N. Case and F. I. Case, Solvent Extr. Ion Exch., 1986, 4, 217.
7. R. A. Sachleben, Y. P. Deng and B. A. Moyer, Sep. Sci. Technol., 1997, 32, 275.
8. B. A. Moyer, Y. P. Deng, Y. F. Sun, R. A. Sachleben, A. K. Batra and R. B. Robinson, Solvent Extr. Ion Exch., 1997, 15, 791.
9. J. F. Dozol, J. Casas and A. M. Sastre, Sep. Sci. Technol., 1995, 30, 435.
10. R. A. Sachleben , Y. Deng , D. A. Palmer and B. A. Moyer , Value Adding Through Solvent Extraction, ed. D. C. Shallcross, R. Paimin and L. M. Prvcic, International Solvent Extraction Conference, Melbourne (Australia), University of Melbourne, Dep. of Chemical Engineering, Parkville, Australia, 1996, p. 377..
11. G. G. Talanova, N. S. A. Elkarim, R. E. Hanes, H. S. Hwang, R. D. Rogers and R. A. Bartsch, Anal. Chem., 1999, 71, 672.
12. J. C. Bryan, R. A. Sachleben, J. M. Lavis, M. C. Davis, J. H. Burns and B. P. Hay, Inorg. Chem., 1998, 37, 2749.
13. J. C. Bryan, R. A. Sachleben and B. P. Hay, Inorg. Chim. Acta, 1999, 290, 86.
14. B. P. Hay, D. L. Zhang and J. R. Rustad, Inorg. Chem., 1996, 35, 2650.
15. J. Golebiowski , V. Lamare , J. F. Dozol and M. F. Ruiz-Lopez , manuscript in preparation. .
16. P. Thuery, M. Nierlich, V. Lamare, J. F. Dozol, Z. Asfari and J. Vicens, J. Inclusion Phenom., 2000, 36, 375 and references therein..
17. D. A. Pearlman , D. A. Case , J. W. Caldwell , W. S. Ross , T. E. Cheatham III , D. M. Ferguson , G. L. Seibel , U. C. Singh , P. Weiner and P. A. Kollman , AMBER 4.1, San Francisco, 1995..
18. S. J. Weiner, P. A. Kollman, D. T. Nguyen and D. A. Case, J. Comput. Chem., 1986, 7, 230.
19. SYBYL 6.1, Molecular Modeling Software, 1994..
20. T. J. Marrone, D. S. Hartsough and K. M. J. Merz, J. Phys. Chem., 1994, 98, 1341.
21. J. Aqvist, J. Phys. Chem., 1990, 94, 8021.
22. E. Engler and G. Wipff , in Crystallography of Supramolecular Compounds, ed. G. Tsoucaris, Kluwer, Dordrecht, 1996, p. 471..
23. E. Engler and G. Wipff , MDS, Strasbourg, 1992. .
24. P. Kollman, Chem. Rev., 1993, 93, 2395.
25. H. Abdoul-Carime, J. Chem. Soc., Faraday Trans., 1998, 94, 2407.

---