Fast oxygen ion conductors—from doped to ordered systems†
Truls
Norby
*
Department of Chemistry, University
of Oslo, Centre for Materials Science, Gaustadalleen 21, Oslo, Norway N-0349. E-mail: trulsn@kjemi.uio.no; Fax: +47-22958749
First published on 10th October 2000
Abstract
This contribution briefly introduces the traditional acceptor doping of oxides, charge compensated by oxygen vacancies to bring about the oxygen ion conduction utilised in solid oxide electrolytes. It is next shown how a simple defect–chemical approach to defect–defect interactions is a useful first-approximation tool in the interpretation of data and design of improved materials, e.g. by optimising dopants. Moreover, it is shown how the trapping of vacancies at acceptor defects can be avoided altogether if the cation sublattice can be made to order completely. This is realised in a few known systems and we illustrate the principle using the oxygen deficient complex perovskite Sr4(Sr2Nb2)O11 as an example, in which the Sr and Nb on the B-site sublattice can be perfectly ordered into a NaCl-structure-type arrangement, leaving all oxygen ion sites equivalent, without trapping sites. The design of new materials should thus aim at cation order, and the possibility of achieving this is discussed also for pyrochlore type oxides. A Kröger–Vink type notation for an inherently deficient sublattice without defects in the other sublattices is proposed.
Introduction
Since the discoveries of solid state oxygen ion conductors, e.g., in the form of Y-substituted ZrO2, the principle of substituting in a lower valent cation to form charge compensating oxygen vacancies has become the standard route to oxygen ion conducting electrolytes. Many systems have since been investigated, and several oxides with superior oxygen ion conduction have been and are being identified, both electrolytes (e.g. Gd-doped CeO2 and Sr + Mg-doped LaGaO3) and mixed conductors (e.g. Sr-doped LaCoO3 and Fe-doped SrTiO3). We will look at the principles behind this doping strategy in very simple ways and see how oxygen vacancy conductivity normally is suppressed at large defect concentrations, caused by defect interactions and ordering. However, by following the behaviour of an untypical example, we will show that order can be turned to our advantage if we are able to order the charge deficient cation sublattice without ordering the accompanying anion defects.The ideal, acceptor substituted oxide
In an acceptor substituted oxide, where the acceptors are compensated by oxygen vacancies, V˙˙O, the electroneutrality requires that the effective charges of the vacancies correspond to those of the acceptors, and in terms of concentration it reads: | (1) |
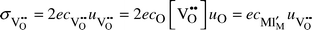 | (2) |
The mobility of vacancies is in principle proportional to the probability that a neighbouring site is occupied, and thus the mobility contains the factor 1 − [V˙˙O].1 This will in itself give a maximum in the conductivity vs. acceptor doping content at a level corresponding to [V˙˙O] = 1/2, although this is not reached in practice in oxygen ion conducting oxides. For small dopant and defect levels, this term can be neglected, and the mobility considered independent of vacancy concentration.
In the case we have described, the temperature dependence of the conductivity only reflects that of the mobility of vacancies:
 | (3) |
 is
the pre-exponential of the mobility (at [V˙˙O] = 0) and the 1/T
term arises through the Nernst–Einstein relation between mobility and
random diffusion. Thus, for an acceptor-dominated, pure oxygen vacancy
conductor, ΔHm is typically reported from the slope
of the (ideally) straight line of a plot of ln(σT)
vs.
1/T. It can also be obtained from an Arrhenius plot of the oxygen
diffusivity (ln DOvs. 1/T).
It can not be obtained from a plot of ln σ
(or
log σ)
vs. 1/T, which should not
be a fully straight line and typically would give a value of ΔHm
which is around 10 kJ mol−1
(0.1 eV)
too small. Nevertheless, the presentation of the conductivity can
be done well in a log σvs. 1/T
plot, as this is more intelligible than ln(σT) or
log(σT) plots in terms of the actual value of the
conductivity.
is
the pre-exponential of the mobility (at [V˙˙O] = 0) and the 1/T
term arises through the Nernst–Einstein relation between mobility and
random diffusion. Thus, for an acceptor-dominated, pure oxygen vacancy
conductor, ΔHm is typically reported from the slope
of the (ideally) straight line of a plot of ln(σT)
vs.
1/T. It can also be obtained from an Arrhenius plot of the oxygen
diffusivity (ln DOvs. 1/T).
It can not be obtained from a plot of ln σ
(or
log σ)
vs. 1/T, which should not
be a fully straight line and typically would give a value of ΔHm
which is around 10 kJ mol−1
(0.1 eV)
too small. Nevertheless, the presentation of the conductivity can
be done well in a log σvs. 1/T
plot, as this is more intelligible than ln(σT) or
log(σT) plots in terms of the actual value of the
conductivity.
Defect interactions
At increasing levels of dopants and charge compensating point defects, one may expect non-idealities, and it was soon found for most systems that the conductivity goes through a maximum as a function of dopant content (at levels far below that predicted from the 1 − [V˙˙O] term). Furthermore, the conductivity usually deviates from the Arrhenius-like behaviour of eqn. (3) and exhibits an increasing activation enthalpy with decreasing temperature. This behaviour has been given various physical interpretations including changes in the lattice parameter and other variations in the structure, defect structure changes, trapping and other defect–defect interactions, and defect ordering. These are, in turn, described mathematically with various degrees of sophistication, ultimately only approachable by computer simulation techniques.In a simple approach, each vacancy can be considered to be attracted by and trapped at a site neighbouring or at least close to an acceptor. This is often conceived as due to coulomb attraction, but it is probably more correct to view it simply as an overall decrease in the lattice energy (as this will not preclude the possibility of, e.g., vacancy–vacancy association which is the basis for many types of ordering).
The diffusion of the vacancy trapped to an immobile acceptor dopant will now have to include an extra activation enthalpy each time the vacancy is to get freed from its captor. One can approach this by analysing the diffusion in terms of normal jumps and de-trapping jumps, with different activation energies.
An alternative approach, probably to be considered as even simpler, is based on defect chemistry. In this we consider all trapped (associated) vacancies as immobile, all un-associated vacancies as mobile, and the concentration of the two types a matter of a simple defect–chemical reaction:
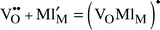 | (4) |
 | (5) |
 | (6) |
 | (7) |
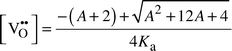 | (8) |
Eqn. (8) has two limiting cases: at relatively high temperatures and low dopant concentrations, practically all vacancies are free; their concentration is almost independent of temperature, given only by the dopant level. At relatively low temperatures and high dopant levels, on the other hand, practically all vacancies are trapped. The concentration of free vacancies then decreases with decreasing temperature and becomes independent of dopant level.
Fig. 1 shows [V˙˙O] from eqn. (8) plotted vs. 1/T in an arbitrary case, with three different negative values of ΔHa. Fig. 2 shows the same for three different values of ΔSa. While ΔHa is often considered the parameter of prime importance, it is noteworthy that a modest value of ΔSa also makes a difference. If positive it may cause substantial association even at very high temperatures or small ΔHa values. Conversely, a negative ΔSa may shift association to lower temperatures and help maintain a high vacancy mobility.
 | ||
| Fig. 1 Fraction of free oxygen vacancies (over all oxygen sites) vs. inverse temperature (500–∞ K) for an oxide MO2 doped with 10% Ml3+ for ΔSa = 0and at three different values of ΔHa. | ||
 | ||
| Fig. 2 Fraction of free oxygen vacancies (over all oxygen sites) vs. inverse temperature (500–∞ K) for an oxide MO2 doped with 10% Ml3+ for ΔHa = −50 kJ mol−1 and at three different values of ΔSa. | ||
Fig. 3 shows a plot of [V˙˙O] vs. the dopant concentration (from 1 to 100%) according to eqn. (8). It shows that the association causes the concentration of free vacancies to level out at a plateau given by temperature, ΔHa, and ΔSa.
 | ||
| Fig. 3 Fraction of free oxygen vacancies (over all oxygen sites) for an oxide MO2vs. content of Ml3+ acceptor for ΔSa = 0 and at three different values of ΔHa. T = 440 K. | ||
The fraction of unassociated, mobile vacancies from eqn. (8) can be inserted into the factor [V˙˙O] in eqn. (3) above for the conductivity, whereas the factor 1 − [V˙˙O] (if not neglected) should contain not only the free, but all vacancies, and can thus be conveniently replaced by a term 1 − [V˙˙O]0 = 1 − [MlM]0cM/cO:
 | (9) |
Fig. 4 shows an example of the temperature dependence of the conductivity (as log(σT) vs. 1/T) according to eqns. (8) and (9), obviously showing a bend as association effectively sets in, so that the activation enthalpy at low temperatures is the sum of ΔHm and ΔHa. (Note that it is necessary to plot log(σT) rather than log σ in order to obtain anything near linear parts of the curves above and below the association changeovers.)
 | ||
| Fig. 4 Log(σT) vs. 1/T (500–∞ K) for an oxide MO2 doped with 10% Ml3+ for ΔHm = 50kJ mol−1, ΔSa = 0, and at three different values of ΔHa. | ||
Fig. 5 shows the conductivity isotherm vs. dopant concentration. Now, the 1 − [MlM]0cM/cO term causes the case with heavy association to go through a maximum.
 | ||
| Fig. 5 Log σvs. content of Ml3+ acceptor for ΔSa = 0 and at three different values of ΔHa. T = 440 K, ΔHm = 50 kJ mol−1, ΔSa = 0. | ||
The fitting of experimental data to this simple kind of model works reasonably well in many cases, especially when the defect concentrations are not too large and the temperatures not too low. Fig. 6 shows results from our own laboratory2 of the ac conductivity of three compositions of Sr + Mg-doped LaGaO3 fitted to a model like the one we have described here. The results are in perfect agreement with SIMS 18O diffusivity measurements on one of the compositions and do not differ much from the results of others on similar compositions. The fit results for the three compositions fell within ΔHm = 50 ± 5kJ mol−1, ΔHa = −65 ± 5 kJ mol−1, and ΔSa = −40 ± 10 J mol K−1 for the simple model used. It is important to emphasise that this is but one, and the simplest, of several possible models. (Alternative models comprise structural changes and vacancy clustering.)3 Thus, the fit parameters obtained should not be given too much weight at this stage. Nevertheless, with the fairly large association enthalpy it is tempting to consider the possibility that it is actually the considerable negative entropy obtained here that may be responsible for the high conductivity of this material, cf.Fig. 2.
 | ||
| Fig. 6 Log(σT) vs. 1/T for La1 − xSrxGa1 − xMgxO3 − x/2 for x = 0.01, 0.05 and 0.1. Lines are fits to a model for association as described in the text. Reprinted with permission from ref. 2. | ||
Fig. 7 shows conductivities of rare-earth doped CeO2vs. dopant contents. (The measured data are taken at low temperatures where the effect of dopants is pronounced, and where bulk resistance is easily delineated from grain boundary resistance by impedance spectroscopy). The characteristic maxima and curve shapes in Fig. 7 resemble the curves predicted from our model (Fig. 5). However, the real dependencies are typically stronger upon dopant content at both sides of the maxima. On the low-content side, this may be attributed to activation energies decreasing with doping. This is common and may reflect lattice parameter and other structural changes and also a changeover from intrinsic to extrinsic defect dominance. On the high-content side of the maximum, the large dependency may reflect more severe defect–defect interactions and ordering phenomena than accounted for in our simple model. It appears that the simple model we have excercised thus works best at intermediate dopant contents (and high temperatures), i.e., where the conductivities and research efforts are highest.
 | ||
| Fig. 7 Log(σT) vs. dopant content in rare-earth-doped CeO2. Gd-doped sample data taken at 500 K, La- and Yb-doped samples data taken at 440 K. Reprinted with permission from ref. 1. | ||
In order to take into account larger defect clusters and defect interactions on longer length-scales one will generally need to use computer simulation techniques. These show that in ZrO2 (see Fig. 8)4 and CeO25 the binding energies between acceptor and vacancy are highest for nearest-neighbour positions for small rare earth dopants and next-nearest neighbour positions for the largest rare earths. The smallest activation energy and highest value for the oxygen vacancy mobility appears at the crossover. These and other investigators' calculations6 also show a higher binding energy for double associates (MlMVOMlM)x which helps explain how the conductivity and phase stability is reduced beyond that predicted by the simple model at high dopant contents. For recent reviews with various focii on these and related aspects of oxygen ion conduction in oxides in general and ceria in particular, see, for instance, refs. 1,7,8,9.
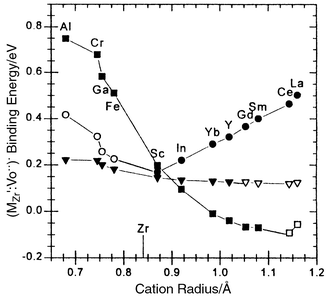 | ||
| Fig. 8 Atomistic simulation of binding (association) energy between vacancy and acceptor in ZrO2 as a function of acceptor radius. Nearest-neighbour binding (■) largest for small acceptors, next-nearest neighbour (●) largest for big acceptors. Optimum dopant is expected to be at the minimum. Next-next-neighbour positions are also included (▽). Open symbols represent artificially stabilised configurations. Reprinted with permission from ref. 4. | ||
In order to successfully delineate the diffusivity into terms of trapping and free defect migration (at the least) one has to be able to monitor the bulk ionic transport process over a fairly large span of temperature and/or doping. If this is not possible, it is still useful to realise that association effects may be in operation, in order to ensure constructive interpretation of transport data. The author would like to encourage the use of a simple model such as the one above rather than to neglect association altogether in fear of the full complexity involved.
As we gain better control of the concentration of mobile vacancies it is getting clear that the mobility (or diffusivity) and its activation energy for these vacancies vary little between different compounds within the same structural group. For instance, a number of LaMO3 perovskites with different dopings all have vacancy diffusivities less than an order of magnitude apart, and with comparable activation energies.10 Similar behaviour, but with other values, is found within fluorite-related structures. One route to higher ionic conductivity thus clearly lies in the concentration of mobile vacancies through acceptor doping and the optimisation of dopants in order to minimize association. Examples are found in the optimisation of rare earth dopants in fluorite oxides (Sc3+ in ZrO24 and Gd3+ in CeO25,7,8) and the development of Sr2+ + Mg2+-doping for LaGaO3 and later on the replacement of Mg2+ by Co2+.11
Inherently defective, disordered systems
Some compounds without dopants at all, and with inherently defective disordered structures, are found to have considerably lower activation energies of diffusion and conduction than doped systems. For example, the classical material δ-Bi2O3, with a fluorite-type structure, has only around 0.3 eV of activation energy for vacancy transport, the same, by the way, as the disordered proton conductor CsHSO4, and mainly the same as activation energies in liquid electrolytes.Similarly, disordered oxygen vacancies with high diffusivities and correspondingly low activation energies of around 0.5 eV are found in the high-temperature perovskite phases of Sr2Fe2O512 and Ba2In2O5.13
If we wish, the disordered and highly oxygen ion conducting phases of Bi2O3, Sr2Fe2O5, and Ba2In2O5 mentioned above may be seen as, for instance, ZrO2, SrZrO3, and BaZrO3 in which Zr is substituted 100% with, respectively, Bi, Fe, and In, and compensated by oxygen vacancies. From this we get a hint that while acceptors in large concentrations trap vacancies, the trapping may disappear if we are able to reach a compound where the acceptors are no longer foreign to their sublattice. Nevertheless, all the mentioned compounds still undergo disorder–order phase transitions upon cooling from high temperatures, whereby they lose their high ionic conductivities.
Order and disorder
In both classes of oxide ion conductors described above (doped and inherently defective systems) we associate high vacancy mobility with disorder: A disordered, random solution of acceptor substituents to be compensated by unassociated oxygen vacancies, or, a disordered amount of originally ordered inherent oxygen vacancies.No doubt, in our quest for high oxygen transport, the desire for a disordered oxygen sublattice remains. But this is often taken to carry over to the cation sublattice(s). We shall see that this needs not be the case, that order and disorder in the cation and anion sublattices can be independent of each other, and that cation disorder is mainly a disadvantage if we can have oxygen disorder without it. We shall use perovskite-related and pyrochlore systems in our examples in the following.
Order/disorder in the perovskite-related system Sr3(Sr1 + xNb2 − x)O9 − 3x/2 (0 ≤ x ≤ 0.5)
The compound Sr3(SrNb2)O9 is related to many similarly composed complex perovskite-related electroceramics, but is remarkable in that the large Sr2+ ion here occupies part of the small, octahedrally coordinated B-sites in the perovskite structure. In the stoichiometric composition, all oxygen sites are occupied, and the B-site cations are ordered into the so-called 2∶1 structure which may be seen as two Sr + Nb layers alternating with one Nb-only layer. As we increase the Sr content, the Sr∶Nb ratio on the B-site increases. Thus, the average charge on the B-site decreases, and oxygen vacancies are introduced for charge compensation. The electroneutrality condition can be approximated as 2[V˙˙O] = 3[Sr‴Nb] = 2[Sr″B], where the two acceptor defect representations arise from different choices of host site (Nb5+ sites or average B4+ sites).The material becomes an oxygen vacancy conductor, and the ionic conductivity
increases with Sr excess. At moderate temperatures, the material picks up
water and becomes a protonic conductor,14
but that will not be our concern here. During our studies mainly of protonic
conduction in the system, however, it was established that the oxygen ion
conduction not only increased with Sr excess, it increased much more than
expected. At low Sr excesses it was approximately proportional to the Sr content,
but then increased exponentially towards the end-member Sr3(Sr1.5Nb1.5)O8.25,
as evident from the plot in Fig. 9.
There was thus in this sense little resemblance to the acceptor–vacancy
associations or vacancy–vacancy ordering commonly seen in most other
doped systems. The end-member has 1 out of 12 oxygen ions missing and
is more conveniently written Sr4(Sr2Nb2)O11;
after proper high temperature annealing it exhibits a very high ionic conduction
with a small activation energy of around 0.4 eV down as low as 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C
and thus no sign of association, see Fig. 10. (By
annealing at intermediate temperatures the conductivity nevertheless slowly
degrades as the situation that sustains the high conductivity breaks down
in some way.)
°C
and thus no sign of association, see Fig. 10. (By
annealing at intermediate temperatures the conductivity nevertheless slowly
degrades as the situation that sustains the high conductivity breaks down
in some way.)
 | ||
| Fig. 9 Total conductivity of Sr3(Sr1 + xNb2 − x)O9 − 3x72vs. vacancy fraction at different temperatures in wet air. Filled symbols represent conductivity of end composition (=Sr4(Sr2Nb2)O11) without proper annealing (and include a high proportion of proton conduction at the lowest temperatures). Slopes indicated for comparison. Reprinted with permission from ref. 14. | ||
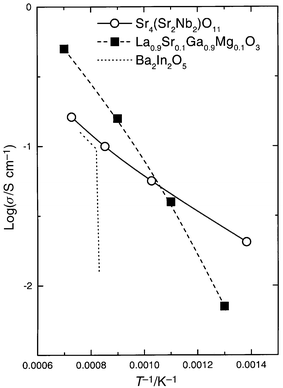 | ||
| Fig. 10 Total (mainly ionic) conductivity of Sr4(Sr2Nb2)O11(extracted from the previous figure) in comparison with 10% Sr,Mg-doped LaGaO32 and Ba2In2O5.13 Values for Sr4(Sr2Nb2)O11 and Ba2In2O5 may be on the low side due to use of the two-point technique as compared to the four-point technique used for LaGaO3. | ||
What goes on in this system to give such a high mobility of the vacancies as the acceptor concentration increases? The pseudo-cubic lattice constant increases linearly, from around 8.265 Å to around 8.31 Å, not a sufficiently large effect to rationalise the dramatic increase in conductivity. In their study of proton conduction in Ba3(Ca1 + xNb2 − x)O9 − 3x/2 (“BCN”) and related materials, Du and Nowick15 found that BCN materials had undergone a change from the 2∶1 to the 1∶1 type of ordering in the B-site cations when the Ca excess had reached 18%, and the samples with this and higher Ca contents exhibited a higher proton mobility than those with lower Ca contents. We assume that the same goes on in our system; neutron diffraction, X-ray diffraction, and electron diffraction on the Sr4(Sr2Nb2)O11 end member are all in agreement with this (although neither method can unambiguously position all cations in the structure).
Irrespective of details, the system starts out at x = 0 with some Sr–O–Nb and some Nb–O–Nb configurations. As the Sr excess, x, increases, there are more Sr–O–Nb configurations, but also Sr–O–Sr in the disordered B-site cation planes. As we approach x = 0.5 the structure takes on the 1∶1 ordering in which Sr and Nb occur in such a way that the B-site lattice can be seen as a NaCl structure-type arrangement. Now, we only have Sr–O–Nb arrangements.
We have thus a lattice of alternating SrO6 and NbO6 octahedra; very different in bond-lengths and size, but this can otherwise be well accommodated in the 1∶1 ordering, as depicted two-dimensionally in Fig. 11.
 | ||
| Fig. 11 Schematic illustration of the 1∶1 ordering in Sr4(Sr2Nb2)O11, with alternating small Nb and large Sr octahedra (exaggerated size difference). Oxygen ions (and vacancies) are not shown, but occupy all line crosspoints (which are all equivalent). | ||
However, the oxygen vacancies, by all landmarks, remain disordered. As all positions are now equivalent, there are no traps (as in normal acceptor doped cases) and the vacancy mobility and the conductivity become very high.
One can imagine that annealing at the right temperature is essential to obtain the high conductivity: Insufficient annealing or too high a temperature may render the cations disordered, thereby creating Sr–O–Sr vacancy traps and Nb–O–Nb vacancy migration obstacles. On the other hand, too low a temperature may order the oxygen vacancies (probably requiring a rearrangement of cations as well). It is thus, in retrospect, not surprising that the x = 0.5 end member first turned out to have a disappointingly low conductivity (included in Fig. 9) until we learned to anneal it properly.
With x close to, but still below 0.5, there will be occasional Nb–O–Nb configurations; these will impose distortions to the lattice and traps and hinder oxygen vacancy migration, and the conductivity drops sharply as the Sr excess falls below 0.5.
We would like to add that much the same behaviour and dependency on the Sr content is found also for the Sr3(Sr1 + xTa2 − x)O9 − 3x/2 system.16 These systems have limited practical interest due to their high basicity and poor thermochemical stability towards CO2 and H2O, but they are instructive and inspiring as they exemplify high oxygen ion conduction along new routes.
Are we able to devise new perovskite-related oxides with high oxygen vacancy concentration and possibly high mobility as a result of ordering of the charge deficient cation sublattice? The example above has shown the utilisation of pentavalent B-site cations. If we instead consider uses of a tetravalent cation, like Ti4+, we may for instance try to formulate an A4(B2Ti2)O11 phase, where A is an alkaline earth cation and B is a trivalent cation, and where we would hope for B∶Ti ordering in a NaCl manner like in the Sr–Nb-case above. In order to do this we would want a large B3+ cation. Candidates are the larger lanthanoids, e.g., Gd or Nd. The compound would be similar to Ba2YSnO5.5 recently reported to be a proton conductor in wet atmospheres.17 The use of Ti may allow us to use a smaller A-site cation; possibly Ca, which is beneficial for the CO2 tolerance.
Order and disorder in fluorite and pyrochlore systems
Consider adding an increasing amount of a fairly large trivalent cation like Nd3+ or Gd3+ to the oxide of a somewhat smaller tetravalent cation like Zr4+ in ZrO2. The structure attains the cubic, fluorite structure at high temperature, randomly distributing both the acceptor dopant and oxygen vacancies. Oxygen vacancy conductivity first increases with doping. However, the vacancies and the acceptors eventually associate, and conductivity decreases and phase separation occurs.If the trivalent rare earth is added in as much as a 1∶1 ratio a new phase is formed, with the pyrochlore structure, e.g., Gd2Zr2O7 in which the cations are ordered. Furthermore, the anion sites of the fluorite-related structure are ordered into three different sites; 6 equivalent oxygen sites, denoted O(1), one differing oxygen site, denoted O(2), and one structurally empty site, denoted O(3).
The stoichiometric pyrochlore is at best a mediocre ionic conductor, relying on thermal creation of anion Frenkel defects (vacancies mainly on the 6 equivalent sites and interstices in the structural vacancies). The pyrochlores may be acceptor- or donor-doped to give a rich variety of conductivity enhancements (n- or p-type electronic or ionic)18 but that is not our prime concern here.
However, if we heat the ordered, stoichiometric pyrochlores to sufficiently
high temperatures, they may disorder. The ease with which they disorder depends
mainly on the size difference, i.e., the bigger the A∶B size
ratio, the less easily they disorder. La2Zr2O7
does not disorder at any temperature, Nd2Zr2O7
disorders to a defective fluorite only at around 2300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C while
Gd2Zr2O7, with A and B cations much more
similar in size, disorders at around 1500
°C while
Gd2Zr2O7, with A and B cations much more
similar in size, disorders at around 1500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. Ordering is sluggish,
so the disordered states can often be quenched and characterised at ambient
temperatures.
°C. Ordering is sluggish,
so the disordered states can often be quenched and characterised at ambient
temperatures.
Those which disorder may then be viewed as 50% acceptor-doped fluorites. They exhibit high oxygen ion conductivities, but generally not higher than those of the same system with smaller contents of the acceptor (dilute solution range). This is as expected as we now have a very large concentration of disordered acceptors and vacancies which may associate extensively.
The interesting question is whether we can have partial order/disorder, as recently discussed by Wuensch et al..19 Upon heating the ordered system it appears that the 6 equivalent oxygen ions at O(1) positions and the vacant site O(3) may disorder first (by formation of anion Frenkel pairs) while the 7th ion at O(2) takes part first at a somewhat higher temperature. A similar behaviour is shown in Fig. 12 which summarises results from neutron diffraction studies of Heremans et al.20 of the system Y2(ZryTi1 − y)2O7. As one increases the Zr content y the structure disorders, and the occupancy of O(1) decreases and that of the formerly empty O(3) increases somewhat before O(2) begins to participate.
 | ||
| Fig. 12 Occupancies of different oxygen sites in the Y2(ZryTi1 − y)2O7 pyrochlore vs. Zr content y as determined by neutron diffraction. Reprinted with permission from ref. 20. | ||
Now to the important question of whether the cations at this stage have disordered or not. If they have, we are back at the heavily doped fluorite. But if they have not, we may see a higher vacancy mobility due to the regularity of the lattice and the equivalency of all sites. Fig. 12 indicates that cation disordering (A and B mixing) is relatively closely connected with anion disorder in the Y2(ZryTi1 − y)2O7 system.
A pyrochlore with ordered cations and disordered anions has to the author's knowledge not been reported. However, various sublattices within one structure may disorder independently, possibly as we have seen also in the pyrochlores, and the matter deserves further investigation. Keeping the cations ordered will require a relatively large size difference, while we also want to use rather large cations for polarisability and anion mobility. It might thus be of interest to investigate further III–IV pyrochlores with La, Pr, and Nd as A-site cations with various tetravalent anions at high temperatures. And it is certainly of interest to investigate II–V pyrochlores with Ca or Sr as A-site cations.
Defect notation in inherently deficient systems
We have described above the likely and possible settings where we have a deficiency in the oxygen sublattice but an ordered and therefore non-defective situation in the cation sublattice. Examples we have mentioned comprise the anion-disordered phases of Sr2Fe2O5, Ba2In2O5 (perovskites), Sr4(Sr2Nb2)O11 (complex perovskite) and δ-Bi2O3 (fluorite). If we were to describe the situation in these compounds in terms of defects, what would the formalism look like? There are basically three possibilities:In the anion-Frenkel approach, we may see the disordered oxygen sublattice as a number of interstices on what used to be structurally empty sites and a corresponding number of vacancies on the structurally occupied sites. The electroneutrality would be cV˙˙O = cO″i, and we would have such a large anion-Frenkel constant that the lattice would be saturated with defects and the defect concentrations would be fairly constant with temperature. However, one may not feel comfortable having to appoint interstitial and normal oxygen sites in a system now believed to contain equivalent sites.
In the fully-acceptor-doped approach, one considers that the compound is 100% substituted with an acceptor. Thus, SrFeO2.5 might be seen as 100% Sr-substituted LaFeO3 or 100% Fe-substituted SrTiO3. Likewise, δ-Bi2O3 might be seen as 100% Bi-substituted ZrO2. Sr3(Sr1.5Nb1.5)O8.25 may be seen as Sr-substituted Sr3(SrNb2)O9. and the electroneutrality then reads, for instance, 2cV˙˙O = 3cSr‴Nb = constant. Again, one may feel uncomfortable operating with an effectively charged acceptor defect in a perfect cation sublattice.
A third approach, applicable to disordered inherently deficient sublattices, has been forwarded lately by the author.21,22,23 Here, one accepts the cation sublattice as perfect, and assigns a partially occupied oxygen site as a perfect one. For instance, the oxygen sites of the disordered δ-Bi2O3 and Sr2Fe2O5 would be, respectively, 3/4 and 5/6 occupied. The oxygen sites in Sr4(Sr2Nb2)O11 would correspondingly be 11/12 occupied, with a real charge of −22/12 (=−11/6). In this framework, both the instantly empty and the instantly occupied sites are defects, and the electroneutrality reads:
 | (10) |
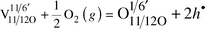 | (11) |
dependency, as usual.
The three approaches above all give basically the same physical result, and one may argue that the third “new” approach does not actually give anything that is new. However, it describes the situation without appointing defects in what really is a perfect cation lattice and without using an anion-Frenkel reaction to explain the anion disorder; the disorder did not arise from a defect reaction, but from a phase transformation.
Concluding remarks
We have pointed at the development of solid oxidic electrolytes by acceptor doping compensated by anion vacancies. In such solid solutions, association between the dopant and vacancy defects depresses the ionic conductivity at practical temperatures. The effect can be counteracted by optimising the acceptor dopant to fit the host lattice and/or be more polarisable, e.g. Gd3+ in CeO2, Sc3+ in ZrO2, and Co2+ in LaGaO3. A simple theoretical treatment of association in terms of defect chemistry has been presented, and its application demonstrated in the analysis of oxygen ion conductivity variations.Several examples are made of oxides which order their acceptors, normally to form new phases, and these are most often accompanied by ordering of the oxygen vacancies. Therefore, order as such is often seen as the thing to avoid in ionic conductors. However, we have also given examples of the occurence of systems with simultaneous cation order and a deficient, disordered anion sublattice, and in these one can avoid the trapping of oxygen vacancies, since there are in principle no cation defects. In binary oxides, this implies very high anion deficiencies, making their disorder highly unlikely, and δ-Bi2O3 with its small stability range is the only known example. Ternary oxides require less vacancies and more systems are known, e.g., BaInO2.5 and SrFeO2.5. As the number of different cation sites increases, we actually get more possibilities of creating anion disorder without cation disorder, as the number of oxygen vacancies decreases to a more bearable level, examples being complex perovskites such as Sr4(Sr2Nb2)O11 and, as it seems, layered structures such as Sr4Fe6O13.22 The pyrochlore structure A2B2O7 seems to offer similar possibilities to perovskites, and there are indications that the different occupied and vacant anion sites in some cases do disorder independently, but a clear cut example with an extraordinary oxygen vacancy conductivity has not been reported.
Anion deficiency and disorder, without cation defects, have been somewhat hard to describe in terms of typical Kröger–Vink defect notation, and an approach to facilitate this has been suggested.
We have suggested the search for new high ionic conductivity candidate systems among certain complex perovskites and among certain III–IV pyrochlores and in general among II–V pyrochlores. Both with respect to new and old systems our improved understanding will require a range of methods, preferably in situ (high temperature) for determination of structure, comprising the standard diffraction techniques (X-ray diffraction, neutron diffraction, and electron diffraction) for long range structure and order, but also e.g. EXAFS, Raman spectroscopy, and HRTEM for complementary information on short range order. Further, transport studies may comprise electrical conductivity measurements and tracer diffusion studies (notably 18O diffusion by SIMS). 17O-NMR can be a useful complementary technique.9 Not least, however, we would like to stress the importance of checking the characteristics of the microstructure of any fast ionic conductor under test by analytical and high resolution electron microscopy and proper impedance spectroscopy. Good ionic conductors are easily missed if their conductance is masked by grain or domain boundary resistances, as has been the case e.g. with the protonic conduction of BaZrO3.24
References
- J. A. Kilner, Solid State Ionics, 2000, 129, 13 Search PubMed.
- E. M. Ottesen, unpublished M.S. thesis, Department of Chemistry, University of Oslo, 1998 (in English)..
- P. R. Slater, J. T. S. Irvine, T. Ishihara and Y. Takita, J. Solid State Chem., 1998, 139, 135 CrossRef CAS.
- M. O. Zacate, L. Minervini, D. J. Bradfield, R. W. Grimes and K. Sickafus, Solid State Ionics, 2000, 128, 243 Search PubMed.
- L. Minervini, M. O. Zacate and R. W. Grimes, Solid State Ionics, 1999, 116, 339 Search PubMed.
- N. Sawaguchi and H. Ogawa, Solid State Ionics, 2000, 128, 183 Search PubMed.
- M. Mogensen, N. M. Sammes and G. A. Tompsett, Solid State Ionics, 2000, 129, 63 Search PubMed.
- B. C. H. Steele, Solid State Ionics, 2000, 129, 95 Search PubMed.
- J. A. Reimer and S. B. Adler, in Solid-state NMR spectroscopy of inorganic materials, ed. J. J. Fitzgerald, American Chemical Society, Washington DC, Symposium Series 717, 1999, p. 156. Search PubMed.
- J. Mizusaki, T. Kawada, Y. Nigara and K. Kawamura, ISSI Lett. (ISSN0937-5961), 1999, 9, 2 Search PubMed.
- T. Ishihara, H. Furutani, M. Honda, T. Yamada, T. Shibayama, T. Akbay, N. Sakai, H. Yokokawa and Y. Takita, Chem. Mater., 1999, 11, 2081 CrossRef CAS.
- A. Holt, T. Norby and R. Glenne, Ionics, 1999, 5, 434 Search PubMed.
- J. B. Goodenough, J. E. Ruiz-Diaz and Y. S. Zhen, Solid State Ionics, 1990, 44, 21 Search PubMed.
- R. Glöckner, A. Neiman, Y. Larring and T. Norby, Solid State Ionics, 1999, 125, 369 Search PubMed.
- Y. Du and A. S. Nowick, Mater. Res. Soc. Symp. Proc., 1995, 369, 289 Search PubMed.
- I. Animitsa, A. Neiman, D. Dildin and S. Nohrin, Solid State Ionics, 2000, in print. Search PubMed.
- P. Murugaraj, K.-D. Kreuer, T. He, T. Schober and J. Maier, Solid State Ionics, 1997, 98, 1 Search PubMed.
- H. Tuller, Solid State Ionics, 1992, 52, 135 Search PubMed.
- B. J. Wuensch, K. W. Eberman, C. Heremans, E. M. Ku, P. Onnerud, E. M. E. Yeo, S. M. Haile, J. K. Stalick and J. D. Jorgensen, Solid State Ionics, 2000, 129, 111 Search PubMed.
- C. Heremans, B. J. Wuensch, J. K. Stalick and E. Prince, J. Solid State Chem., 1995, 117, 108 CrossRef CAS.
- T. Norby, in Diffusion and concentration of mobile species in fuel cell materials, ed. B. Zachau-Christiansen, Proceedings Workshop, Nordic Energy Research Programme, Ås, Norway, March 1998. Search PubMed.
- R. Bredesen, T. Norby, A. Bardal and V. Lynum, Solid State Ionics, 2000, in print. Search PubMed.
- R. Bredesen and T. Norby, Solid State Ionics, 2000, 129, 285 Search PubMed.
- K.-D. Kreuer, Solid State Ionics, 2000, 125, 285 Search PubMed.
Footnote |
| † Basis of a presentation given at Materials Discussion No. 3, 26–29 September, 2000, University of Cambridge, UK. |
| This journal is © The Royal Society of Chemistry 2001 |

