The route to CMR manganites: what about charge ordering and phase separation?

Abstract

The CMR manganites Ln_1 − xA_xMnO₃ with the perovskite structure form a very important family of magnetic oxides, studied for their fascinating colossal magnetotransport properties. In this review, we discuss two phenomena, charge ordering and phase separation, which are crucial for the appearance of CMR in these oxides. We propose a new route to CMR, based on the Mn-site doping of these materials by other cations, such as Cr, Co, Ni and Ru.

---

The discovery of magnetoresistance properties in manganese oxides with the perovskite structure has allowed new features related to charge ordering and electronic phase separation to be evidenced and discussed. The properties of charge ordering in perovskite manganites Ln_1 − xA_xMnO₃ (Ln = lanthanide, A = Ca, Sr) were established a long time ago,^1,2 long before the discovery of colossal magnetoresistance (CMR) effects^3–5 in these oxides.

In these systems, the charge ordered (CO) state is insulating and either antiferromagnetic or paramagnetic, but plays a very important role in the CMR effect: it can be melted into a ferromagnetic (FM) metallic state by application of a magnetic field. This ability to generate a FM metallic state is explained by a double exchange (DE) mechanism,⁶ but the origin of the melting of the CO state under a magnetic field, the relationships between this transformation and the structure and chemical bonding are still matters of discussion. In a similar way, the behavior of orbital ordering and its relation with charge ordering are, so far, not completely understood.

The results obtained by numerous authors clearly show that the CMR effect results from the coexistence of two competing phases, a ferromagnetic metallic (FMM) phase with an antiferromagnetic insulating phase (AFMI).⁷ It has been proposed that the intriguing properties of CMR manganites are due to electronic phase separation, involving the coexistence of regions of different carrier concentrations within the same crystal.⁸ Such a pure electronic phase segregation is difficult to explain over a large length scale. In fact, it will be shown further that this phase separation originates from the coexistence of different structures within the same crystal, in agreement with the numerous structural transitions observed in these oxides.

In this review, we discuss the main features which govern the charge and orbital ordering in manganites in connection with their magnetoresistive properties, and we describe the different results which evidence phase separation in these systems.

Structural evidence for charge ordering

The first evidence for the collapse of a charge ordered state under a magnetic field was shown for Pr_1/2Sr_1/2MnO₃.⁹ Unfortunately, subsequent structural investigations, coupling neutron diffraction and electron microscopy¹⁰ did not confirm the existence of a CO state for this phase at low temperature. Thus, this phenomenon, although it is of particular interest, cannot be attributed to the collapse of charge ordering, but rather to a structural transition of a different nature, implying a transition from A-type AFM^10,11 to FMM upon the application of a magnetic field. In contrast, CO has been observed by structural techniques in several CE-type AFM half doped manganites Ln_0.5Ca_0.5MnO₃ with Ln = La, Nd, Pr, Sm.^12–16 In the CE-type AFM structure, zig-zag FM chains of Mn³⁺/Mn⁴⁺ are AFM coupled with their nearest neighboring chains. In these CO oxides, a doubling of one cell parameter, a, when cooling the material below T_CO is observed. This behavior corresponds to a 1 ∶ 1 ordering of the Mn³⁺ and Mn⁴⁺ species. From the TEM observations, it appears probable that the CO appears as Mn³⁺ and Mn⁴⁺ stripes which alternate along a. In fact, the CO is not limited to the particular composition Ln_0.5Ca_0.5MnO₃. Charge ordered stripes have been evidenced by lattice imaging in electron microscopy for x > 0.50 in La_1 − xCa_xMnO₃¹⁷ and for 0.4 ≤ x ≤ 0.75 in Sm_1 − xCa_xMnO₃.¹⁵ Such phenomena are illustrated by the lattice images of the “SmCa” manganites recorded at 92 K, i.e. below T_CO (Fig. 1). For particular x values, x = 3/4, 2/3 and 1/2, a system of fringes spaced by 22 (Fig. 1a), 16.5 (Fig. 1b) and 11 Å (Fig. 1c) respectively, is observed, corresponding to a quadrupling, a tripling and a doubling of the a = a_p√2 parameter, in agreement with the corresponding electron diffraction patterns. These results can be easily interpreted as the alternation along a of one Mn³⁺ stripe, with three (Fig. 2a), two (Fig. 2b) and one (Fig. 2c) Mn⁴⁺ stripes. For intermediate x values, the situation is more complex, as exemplified by two lattice images (Fig. 3b,c) recorded for x = 0.55, where it is shown that the ordering of the stripes either takes place in a short range manner (Fig. 3b), or in a regular long range sequence, but with a more complex “periodicity” close to 7a_p√2. In fact, whatever the value of x in the range from 0.40 to 0.75, a long range ordering of the Mn³⁺ and Mn⁴⁺ stripes exists, which can be either commensurate for particular x values, or incommensurate for intermediate x values. Such a long range ordering of the stripes can thus be characterized by the wave q vector, which is remarkably found to be roughly equal to the 1 − x value, i.e.q ≈ 1 − x at 92 K, so that the superstructure along a for particular x values is given by a ≈ (1/q)a_p√2.

Fig. 1 [010] ED patterns and [010] lattice images recorded at 92 K for Sm_1 − xCa_xMnO₃ with (a) x = 3/4, (b) x = 2/3 and (c) x = 1/2.

Fig. 2 Examples of structural models for Sm_1 − xCa_xMnO₃ with (a) q = 3/4, (b) q = 2/3 and (c) q = 1/2.

Fig. 3 Sm_0.45Ca_0.55MnO₃ at 92 K: (a) [010] pattern and [010] lattice images of different areas of the corresponding crystallite. They exemplify (b) short range ordering and (c) long range ordering.

The transition from the AFM charge ordered state to the paramagnetic state is clearly evidenced by the evolution of the q value versus temperature, as shown for several x compositions (Fig. 4). After the low temperature plateau which characterizes the CO, the q vector decreases abruptly as T increases, corresponding to the disappearance of charge ordering above T_CO. Note that the T_CO value deduced from the structural evolution is closely connected with the T_peak value observed on the magnetization curves of these oxides (Fig. 5), i.e.T_peak ≈ T_CO, showing that charge ordering plays a prominent role in the appearance of the AFM state at low temperature. This is the reason why many authors assign the M(T) peak of the manganites to charge ordering, but without any crystallographic proof of its existence.

Fig. 4 Evolution of qversusT for the different Sm_1 − xCa_xMnO₃ samples with 0.40 ≤ x ≤ 0.75. For the x = 0.50 sample, arrows indicate two particular temperatures: ↑, temperature at which superlattice spot appears on cooling (T_CO); ↓, temperature at which the q value remains constant (q = q_max).

Fig. 5 T dependence of the magnetization of the series of Sm_1 − xCa_xMnO₃ samples, where T_peak indicates the temperature of the maximum magnetization value.

The effect of A cation size upon CO: influence on CMR properties

The strong influence of the size of the A-site cations upon charge ordering has been evidenced by several authors.^18–20 This phenomenon is easily explained by the fact that the Mn–O–Mn bond angle is significantly affected by the size of the A cations and, consequently, the e_g band width is strongly dependent on 〈r_A〉. A comparison of the magnetic phase diagrams recently established for four Ln_1 − xA_xMnO₃ systems, with Ln = Pr, Sm and A = Ca, Sr,²¹ illustrates the important role of the A cation size upon CO and, consequently, upon the magnetotransport properties of these oxides. The “SmCa” (Fig. 6a) and “PrCa” (Fig. 6b) manganites, which are characterized by smaller 〈r_A〉 values, exhibit both CO domains for a wide range of compositions, from x = 0.40 to 0.80 for Sm and from 0.34 to 0.85 for Pr; their regions coincide in both cases with a large AFMI region. In both systems, T_CO goes through a maximum for x = 0.60. The “SmCa” system exhibits maximum T_CO values significantly larger than those of the “PrCa” system, showing that T_CO is reinforced as 〈r_A〉 decreases when replacing praseodymium by samarium. Such an increase of T_CO by decreasing 〈r_A〉 was also shown for the solid solution Pr_0.5Sr_0.5 − xCa_xMnO₃,²⁰ for which T_CO increases from 180 K for x = 0.25 to 250 K for x = 0.50. Note that the charge ordering temperature may be significantly different from the Néel temperature, as shown for the “PrCa system”, for which T_N < T_CO (Fig. 6b). When 〈r_A〉 increases, the CO is rapidly destabilized, as shown for the "SmSr" manganites (Fig. 6c), for which the CO domain is reduced to x = 0.4–0.66, and finally disappears for higher 〈r_A〉 values, as illustrated by the “PrSr” system (Fig. 6d), for which no CO was evidenced. Note also that the dramatic influence of 〈r_A〉 upon T_CO is confirmed: the “SmSr” manganites show T_CO values ranging from 130 to 200 K (Fig. 6c), to be compared to the “PrCa” system (Fig. 6d), whose smaller 〈r_A〉 values allow T_CO values up to 260 K to be reached.

Fig. 6 Magnetic phase diagrams for the Sm_1 − xCa_xMnO₃ (a), Pr_1 − xCa_xMnO₃ (b), Sm_1 − xSr_xMnO₃ (c) and Pr_1 − xSr_xMnO₃ (d) series. The gray symbols and lines are for the magnetization values at 4.2 K (right y axis). Black symbols: (●) T_C, (■) T_CO, (▲) T_N. FM: ferromagnet, M for metal and I for insulator; AFM: antiferromagnet; CO: charge ordered; CG: cluster glass. The dashed areas are for intermediate regions. The CMR compositions are delimited by arrows in the upper parts.

It is also remarkable, upon comparing these four diagrams, that the reduction of the CO region, which results from the increase of 〈r_A〉 (Ca → Sr), takes place to the benefit of the ferromagnetic domain, which expands from x ≈ 0.04–0.30 for the Ca systems (Fig. 6a,b) to x ≈ 0.1–0.50 for the Sr system (Fig. 6c,d), T_C increasing with 〈r_A〉 and the FMM state replacing progressively the FMI state as 〈r_A〉 increases. Another point concerns the disappearance of the CO state on the Mn⁴⁺ rich side (x > 0.50) for higher 〈r_A〉 values, i.e. in the Sr systems, for which an AFMI state without CO extends over a wide compositional range, from 0.60 to 0.9 for “SmSr” (Fig. 6c) and for 0.5 to 0.90 for “PrSr” (Fig. 6d). In contrast, for smaller 〈r_A〉 values, the CO state persists over a large compositional range in the Mn⁴⁺ region, being replaced by a short range charge ordering around x ≈ 0.8, leading finally to a cluster glass (CG)²² for x ≥ 0.9 (see Fig. 6a,b) in which ferromagnetic clusters coexist within the AFM matrix.

This modification of the CO state versus 〈r_A〉 has a great impact on the magnetotransport properties of the manganites. The resistivity of the manganites is indeed influenced by charge ordering, as illustrated by the ρ(T) curves of several Sm_1 − xCa_xMnO₃ oxides (Fig. 7). For the oxides corresponding to 0.40 ≤ x ≤ 0.85, a transition from a semi-metallic behavior or semi-conducting state to an insulating state as T decreases is indeed observed. All the curves (Fig. 7) show a resistivity jump at a temperature T_R, which coincides in fact with the peak temperature on the M(T) curves (Fig. 5), and corresponds, in fact, to T_CO. Clearly, at low temperature, below T_CO, the antiferromagnetic insulating state is stabilized.

Fig. 7 T dependence of the resistivity for the Sm_1 − xCa_xMnO₃ samples with 0.40 ≤ x ≤ 0.85 (x values are labelled on the graph). The arrow indicates T_R.

From the viewpoint of the CMR effect, the CO state opposes the appearance of a ferromagnetic metallic state, since it is highly insulating, but allows the obtention of the highest resistance ratio. Its destruction, by applying a magnetic field in order to get the FMM state, allows resistivity jumps of several orders of magnitude to be reached. Thus, in order to produce a CMR effect, the manganite should either exhibit a paramagnetic insulating to ferromagnetic metallic transition, or at least present a metastability of its insulating charge ordered state, which can be destroyed by a magnetic field. This viewpoint is strongly supported by comparison of the magnetic phase diagrams in Fig. 6. CMR appears in FMM regions, as shown for “SmSr” (Fig. 6c) and “PrSr” (Fig. 6d), and can extend over the CO region. For small A cations, “SmCa” (Fig. 6a) and “PrCa” (Fig. 6b) systems, CMR is obtained in spite of the absence of a ferromagnetic metallic state (FMM). CMR appears in the electron doped regions at the boundary between the CO and the CG regions. Moreover, in the hole doped region, a CMR effect can also be obtained at the boundary between the FMI and CO regions, for the PrCa system (Fig. 6b). The compositional range where the CMR appears corresponds, then, to the regions where CO is either not well established or, in any case, not yet very stable. For this reason, the CMR compositional ranges that are obtained for the small A cations are rather narrow. Nevertheless, the CMR effects are spectacular, as exemplified for the electron doped manganite²² Sm_0.15Ca_0.85MnO₃ (Fig. 8a), which exhibits a resistance ratio of 10² at 80 K under 7 T and for the oxide Pr_0.7Ca_0.3MnO₃ (Fig. 8b), for which a resistance ratio of 3 × 10² at 80 K under 7 T was reached. In contrast, for large A cations, “SmSr” (Fig. 6c) and “PrSr” (Fig. 6d), the CMR effect appears only in the hole doped region, due to the fact that the metastable charge ordered state has disappeared in the electron rich region close to SrMnO₃, and is replaced by a very stable AFMI state. Then, the CMR effect covers a rather wide composition range involving the adjacent CO and FMM and even FMI domains as shown for the “SmSr” system (Fig. 6c), for which T_CO is smaller than 200 K, so that CO state is certainly more metastable. For the largest 〈r_A〉 values, “PrSr”, the CMR effect also extends over a wide composition range in the hole doped region, but, in that case, it does not result from the destruction of the CO state, but is only due to the PMI–FMM transition, which is strongly modified by the application of a magnetic field.

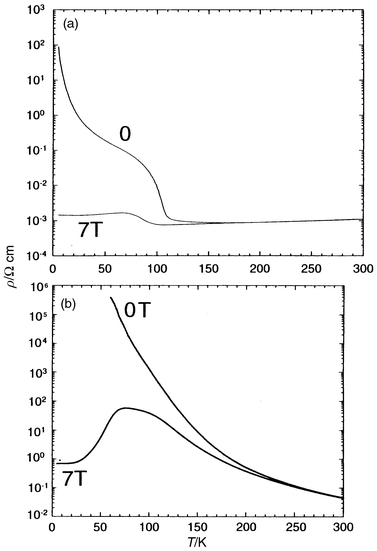Fig. 8 T dependence of the resistivity registered under 0 and 7 T for (a) Sm_0.85Ca_0.15MnO₃ and (b) Pr_0.7Ca_0.3MnO₃.

Phase separation: coexistence of ferromagnetism and charge ordering

The appearance of ferromagnetism at low temperature in manganites is easily explained by the DE model.⁶ However, this model cannot explain the entire phase diagrams. More particularly, the role of charge ordering in the magnetotransport properties is not taken into account in the framework of double exchange. In the same way, magnetization and neutron diffraction studies evidenced weak FM moments which could not be explained by DE alone. In order to explain such features, several theoretical papers^23–25 have proposed the existence of phase separation between hole undoped antiferromagnetic regions and hole rich antiferromagnetic regions at low temperature. Arguments for the coexistence of two phases, supporting the model of phase separation, were also developed in several experimental works on manganites.^26–29 The coexistence of the CO state with the FMM phase was shown, for instance, by in situ observation on heating a Nd_0.5Sr_0.5MnO₃ sample in an electron microscope.³⁰ This was interpreted as microscopic electronic phase separation. In a recent study of manganites, Uhera and Cheong³¹ showed that the coexistence of FM and CO can be dramatically influenced by cooling rate and aging, and suggested that the origin of the phase separation is, in fact, structural.

These results demonstrate that the CO state plays a role in the transition to the FMM state, and strongly suggest that the nature of the transition under a magnetic field is percolative, so that ferromagnetic clusters within the CO-AFM matrix are formed in a first step, the sample going from an AFMI to a FMM behavior.

Mn-site doping: a chemical route to CMR

Bearing in mind the role of charge ordering in the magnetotransport properties of the manganites, it should be possible to enhance the CMR properties of these materials by weakening, or even by suppressing, the CO state using a chemical route. The doping of Mn sites with various foreign cations is, in this respect, a very efficient method, since it introduces disorder on the Mn sites and is susceptible to breaking both orbital and charge ordering.

The Mn-site doping of the charge ordered manganite Pr_0.5Ca_0.5MnO₃ with various M cations (M = Mg²⁺, Fe³⁺, Al³⁺, Ga³⁺, Ti⁴⁺, Sn⁴⁺) leads to destruction of the charge ordering.³² For example, the signatures of the CO on both the ρ(T) (Fig. 9) and χ′(T) curves (Fig. 10) have disappeared with only 3% dopant, and a weak ferromagnetic component is observed at low temperature on the χ′(T) curves (Fig. 10). Consequently, CMR properties are induced by doping, as exemplified for Pr_0.5Ca_0.5Mn_0.97Fe_0.03O₃ (Fig. 11). But the most spectacular effect is obtained by doping the Mn sites with magnetic elements, such as Cr, Co, Ni and Ru. In the series Pr_0.5Ca_0.5Mn_1 − xM_xO₃ with M = Cr, Co, Ni, it is shown^33–35 that a magnetic field is not required to induce insulator to metal transitions. Clear I–M transitions are observed, in the absence of magnetic field in the Cr doped material Pr_0.5Ca_0.5Mn_1 − xCr_xO₃ for x values as low as 0.02 (Fig. 12). Correlatively, the M(T) curves (Fig. 13) show that the metallic state at low temperature is associated with ferromagnetism, large magnetization values of 3 μ_B, close to the theoretical magnetic moment, being reached. The disappearance of charge ordering by chromium doping was clearly evidenced by the electron microscopy study of Sm_0.5Ca_0.5Mn_0.97Cr_0.03O₃. As a consequence of the disappearance of CO, CMR behavior similar to that of the hole doped manganites, without any CO, is restored. This is illustrated in Fig. 14, where the ρ(T) curves recorded at 0 and 7 T allow Pr_0.5Ca_0.5Mn_0.97Cr_0.03O₃ to be compared with Pr_0.7Ca_0.2Sr_0.1MnO₃. Similar results are obtained for cobalt and nickel doping, but chromium is the most efficient cation to induce ferromagnetism.

Fig. 9 ρ(T) curves of Pr_0.5Ca_0.5MnO₃ (pristine compound) and of the corresponding doped manganites Pr_0.5Ca_0.5Mn_0.97M_0.03O₃ (M = Mg²⁺, Al²⁺, Fe³⁺, Ti⁴⁺, Sn⁴⁺).

Fig. 10 Dependence of the real part of the susceptibility (χ′) for Pr_0.5Ca_0.5MnO₃ and 3% doped Pr_0.5Ca_0.5Mn_0.97M_0.03O₃ samples (M = Mg²⁺, Fe³⁺, Ti⁴⁺).

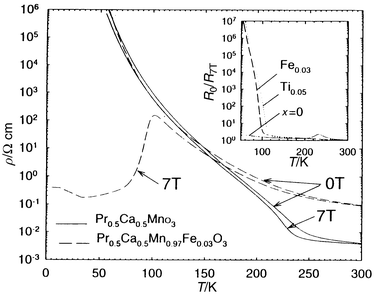Fig. 11 Dependence of the resistivity (ρ) on T for Pr_0.5Ca_0.5MnO₃ and Pr_0.5Ca_0.5Mn_0.97Fe_0.03O₃ recorded at 0 and 7 T. Inset: dependence on T of the R₀/R_7T ratios, demonstrating the CMR induced by doping with M = Fe and Ti.

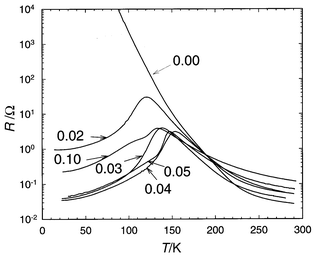Fig. 12 ρ(T) curves of the Pr_0.5Ca_0.5Mn_1 − xCr_xO₃ samples; the solid line corresponds to x = 0.

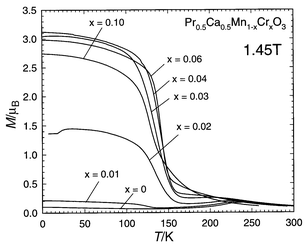Fig. 13 Pr_0.5Ca_0.5Mn_1 − xCr_xO₃: M(T) curves.

Fig. 14 ρ(T) recorded at 0 and 7 T for the Cr doped Pr_0.5Ca_0.5Mn_0.97Cr_0.03O₃ manganite. The same curves for a classical charge delocalized Ln_0.7A_0.3MnO₃ manganite are also given.

In fact, further studies of the Cr doped manganites^36,37 clearly establish that the transformation of the CO state into the FM state takes place by a phase separation mechanism. Coexistence of CO domains with the ferromagnetic metallic phase is clearly evidenced by electron diffraction at low temperature.³⁷ This is illustrated by the ED pattern and lattice image of the manganite Pr_0.5Ca_0.5Mn_0.95Cr_0.05MnO₃ measured at 92 K (Fig. 15). The [010] ED pattern (top Fig. 15) shows that the superlattice reflections are indeed in an incommensurate position (q = 0.42), whereas they were close to the commensurate positions (q ≈ 0.48) in the undoped material. The lattice image (bottom Fig. 15) shows that the order is partly destroyed, i.e. ordered and non-ordered domains with variable sizes coexist throughout the crystal, the first corresponding to CO regions and the second being attributed to ferromagnetic regions.

Fig. 15 [010] ED pattern of Pr_0.5Ca_0.5Mn_0.95Cr_0.05MnO₃ recorded at 92 K. Arrows indicate superlattice reflections.

These results show that magnetic ions, like chromium, not only destroy charge ordering, but also participate in ferromagnetism. In the case of chromium, the following scenario can be proposed:³⁷ as Cr³⁺ replaces the isovalent Mn³⁺ cation it goes with reversed spin, leading to a decrease of the magnetic moment (3.15 μ_B observed instead of 3.45 μ_B without altering the spin direction). Direct evidence of spin reversal was given by a magnetic dichroism study on the same compound.³⁸ The spin configuration before and after chromium doping can be schematized as shown in Fig. 16. Without chromium (top Fig. 16) the antiferromagnetic ordering is of the CE type below 170 K, with two FM zig-zag chains antiferromagnetically coupled in the ac plane, such planes are stacked along b with reversed spins. Thus, in the undoped CE-type phase, metallic conduction along the FM zig-zag chains is inhibited by the strong repulsive Coulombic interaction between the charge carriers and interchain AFM coupling. After chromium doping (bottom Fig. 16), the occupation of some Mn positions by Cr³⁺ with reversed spins breaks the AFM coupling between the chains and forms local ferromagnetic clusters (circled region at the bottom of Fig. 16). Thus, for a very small doping level (x < 0.05), the e_g electron is itinerant within these clusters, but in the regions outside the clusters, charge and AFM ordering are weakened but still preserved. Thus, the insulating state breaks into majority CO domains, with either spins ordered antiferromagnetically or fluctuating within them, and minority ferromagnetic metallic domains. The size of the CO-AFM domains decreases as x increases and then metallicity appears in a percolative way.

Fig. 16 Schematic spin configuration of Pr_0.5Ca_0.5MnO₃ (top) and Pr_0.5Ca_0.5Mn_1 − xCr_xO₃ (bottom). The dashed zig-zag lines are to illustrate interchain ferromagnetic coupling. The region enclosed by the circle represents the ferromagnetic cluster formed by two Cr³⁺ cations. Mn³⁺ e_g orbital ordering is also shown as lobes. Cr substitution weakens orbital ordering, as shown in the lower part of the figure.

The possibility of inducing an I–M transition in a CO manganite, Nd_0.5Ca_0.5MnO₃, by ruthenium doping was shown for the first time by Rao et al.,³⁹ the Curie temperature increasing with the ruthenium content. The doping of the Mn(IV)-rich manganites Ln_0.4Ca_0.6MnO₃⁴⁰ and CaMnO₃⁴¹ with ruthenium shows that the potential of this cation to induce metallicity and ferromagnetism is still superior to Cr, Co and Ni. This is illustrated by the ρ(T) and M(T) curves (Fig. 17) of the Pr_0.4Ca_0.6Mn_1 − xRu_xO₃ series. It can be seen that, starting from an insulating phase (x = 0, upper inset in Fig. 17), the resistivity is lowered in a spectacular way, by several orders of magnitude on doping with ruthenium, showing “double bump” curves (Fig. 17). Correlatively, ferromagnetism is induced in a spectacular way, the magnetic moment reaching a maximum value of 2.8 μ_B at 4 K for x = 0.06 (lower inset in Fig. 17). These results show that Ru weakens charge ordering, but the disappearance of CO is not sufficient to explain the appearance of ferromagnetism and metallicity at low temperature and also the double bump phenomenon on the ρ(T) curves. Again, they can be interpreted on the basis of the phase separation scenario.^23–29 For low doping levels, FM clusters are formed around the Ru cations within the AFM insulating matrix, so that, for x = 0.02, CO coexists with these FM clusters and the resistivity is not affected significantly. For higher doping levels (x ≈ 0.04), metallic FM regions coexist with insulating AFM regions. The first bump at high temperature on the ρ(T) curve (Fig. 17) corresponds to the I–M transition within the FM regions, whereas the second bump at lower temperature characterizes the competitive contribution of both regions, AFM insulating and FM metallic, to the conductivity. Finally, for x = 0.10, the percolation of FM clusters and their large domains can be explained by the ability of this element to exhibit two high oxidation states, Ru(IV) and Ru(V). The t_2g³ configuration of Ru(V) is similar to Mn(IV), whereas the t_2g⁴ configuration of Ru(IV) is different from the t_2g³e_g¹ configuration of Mn(III). Mn(III) can interact with both Ru(V) and Ru(IV) via ferromagnetic superexchange interaction involving overlap of the partly filled e_g orbital of Mn(III) and the empty e_g orbitals of Ru(IV) and Ru(V). Thus, its introduction on the Mn lattice not only tends to destroy the charge ordering, but may contribute to the increased Mn³⁺ content according to the equilibrium Mn⁴⁺ + Ru⁴⁺ ⇋ Mn³⁺ + Ru⁵⁺. Consequently, FM clusters are generated not only by DE between Mn species (Mn³⁺ + Mn⁴⁺ ⇋ Mn⁴⁺ + Mn³⁺), but also by the FM superexchange interactions between Mn³⁺ and both Ru(IV) and Ru(V). Thus, it is most probable that the FM clusters are formed around the Ru atoms, which locally destroy CO and simultaneously favor DE.

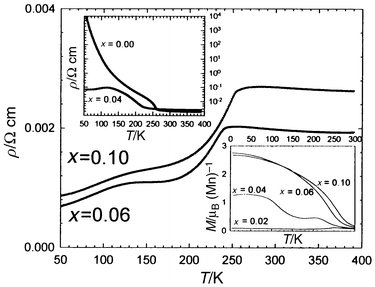Fig. 17 ρ(T) curves of Pr_0.4Ca_0.6Mn_1 − xRu_xO₃. Upper inset: x = 0 and x = 0.04 ρ(T) curves. Lower inset: M(T) curves of Pr_0.4Ca_0.6Mn_1 − xRu_xO₃.

Finally, it should be emphasized that the Ru doped manganites exhibit CMR effects in spite of their metallic conductivity, as shown, for instance, for Pr_0.4Ca_0.6Mn_0.94Ru_0.06O₃ (Fig. 18a). More importantly, CMR is enhanced in a spectacular way for lower doping levels, when smaller FM domains coexist with AFM regions, as illustrated for Pr_0.4Ca_0.6Mn_0.96Ru_0.04O₃ (Fig. 18b) which exhibits a resistance ratio of 40 at 110 K under 7 T, whereas, under the same conditions, the undoped phase is not magnetoresistive. Thus, this shows that the AFM regions shrink under an external magnetic field, extending the FM clusters and eventually leading to percolation.

Fig. 18 ρ(T) curves obtained upon cooling in 0 and 7 T (left y axis) and ρ₀(T)/ρ_7T(T) ratio (right y axis) for Pr_0.4Ca_0.6Mn_1 − xRu_xO₃ with x = 0.06 (a) and x = 0.04 (b).

Concluding remarks

The few results presented in this study show the prime roles of charge ordering and phase separation phenomena in the magnetotransport properties of manganites, allowing us to explain and to discover a route to the generation of new CMR properties. Many questions, however, still need to be answered in order to understand the curious behavior of the manganites. The role of orbital ordering and its interplay with charge and magnetic ordering is one of the most important issues which has been the subject of only a few studies^13,42-43 to date. Some results suggest, for instance, that the incommensurate structure observed by electron microscopy involves the presence of partial orbital disordering and complete charge ordering, and that long range orbital ordering is never achieved so that charge order drives the orbital order at the transition. Further systematic investigations are necessary to understand all these phenomena.

References

1. E. O. Wollan and W. C. Koehler, Phys. Rev., 1955, 100, 545.
2. J. B. Goodenough, Phys. Rev., 1955, 100, 564.
3. R. M. Kusters, J. Singleton, D. A. Keon, R. H. Greddy and N. Hayes, Physica B, 1989, 155, 362.
4. A. Asamitsu, Y. Moritomo, Y. Tomioka and Y. Tokura, Nature, 1995, 373, 407.
5. A. Maignan, Ch. Simon, V. Caignaert and B. Raveau, Solid State Commun., 1995, 96, 623.
6. C. Zener, Phys. Rev., 1951, 82, 403.
7. M. Uhera, S. Mori, C. H. Chen and S. W. Cheong, Nature, 1999, 399, 560.
8. S. Yunoki, J. Hu, A. Malvezzi, A. Moreo, N. Furukawa and E. Dagotto, Phys. Rev. Lett., 1998, 80, 845.
9. Y. Tomioka, A. Asamitsu, Y. Moritomo, H. Kuwahara and Y. Tokura, Phys. Rev. Lett., 1995, 74, 5108.
10. F. Damay, C. Martin, M. Hervieu, A. Maignan, B. Raveau, G. André and F. Bourée, J. Magn. Magn. Mater., 1998, 184, 71.
11. H. Kawano, R. Kajimoto, H. Yoshizawa, Y. Tomioka, H. Kuwahara and Y. Tokura, Phys. Rev. Lett., 1997, 78, 4253.
12. P. M. Woodward, D. E. Cox, T. Vogt, C. N. R. Rao and A. K. Cheetham, Chem. Mater., 1999, 11, 3528.
13. (a) C. H. Chen and S. W. Cheong, Phys. Rev. Lett., 1996, 76, 4042; (b) P. Radaelli, D. E. Cox, M. Marezio and S. W. Cheong, Phys. Rev. B, 1997, 55, 3015.
14. F. Damay, Z. Jirak, M. Hervieu, C. Martin, A. Maignan, B. Raveau, G. André and F. Bourée, J. Magn. Magn. Mater., 1998, 190, 221.
15. (a) M. Hervieu, A. Barnabé, C. Martin, A. Maignan, F. Damay and B. Raveau, Eur. Phys. J. B, 1999, 8, 31; (b) A. Barnabé, M. Hervieu, C. Martin, A. Maignan and B. Raveau, J. Mater. Chem., 1998, 8, 1405.
16. Z. Jirak, S. Krupicka, Z. Simsa, M. Dlouha and S. Vratislav, J. Magn. Magn. Mater., 1985, 53, 153.
17. C. H. Chen, S. W. Cheong and H. Y. Hwang, J. Appl. Phys., 1997, 81, 4326.
18. N. Kumar and C. N. R. Rao, J. Solid State Chem., 1997, 129, 363.
19. A. Barnabé, M. Hervieu, C. Martin, A. Maignan and B. Raveau, J. Appl. Phys., 1998, 84, 5506.
20. F. Damay, C. Martin, A. Maignan, M. Hervieu, B. Raveau, Z. Jirak, G. André and F. Bourée, Chem. Mater., 1999, 11, 536.
21. C. Martin, A. Maignan, M. Hervieu and B. Raveau, Phys. Rev. B, 2000, 60, 12191.
22. (a) C. Martin, A. Maignan, F. Damay, M. Hervieu and B. Raveau, J. Solid State Chem., 1997, 134, 198; (b) A. Maignan, C. Martin, F. Damay and B. Raveau, Chem. Mater., 1998, 10, 1974; (c) A. Maignan, C. Martin, F. Damay B. Raveau and J. Hejtmanek, Phys. Rev. B, 1998, 58, 2578.
23. S. Yunoki, J. Hu, A. Malvezzi, A. Moreo, N. Furukawa and E. Dagotto, Phys. Rev. Lett., 1998, 80, 845.
24. E. Dagotto, S. Yunoki, A. Malvezzi, A. Moreo, J. Hu, S. Capponi, D. Poilblanc and F. Furukawa, Phys. Rev. B, 1998, 58, 6414.
25. S. Yunoki and A. Moreo, Phys. Rev. B, 1998, 58, 6403.
26. P. Schiffer, A. P. Ramirez, W. Bao and S. W. Cheong, Phys. Rev. Lett., 1995, 75, 3336.
27. P. G. Radaelli, D. E. Cox, M. Marezio, S. W. Cheong, P. Schiffer and A. P. Ramirez, Phys. Rev. Lett., 1995, 75, 4488.
28. G. Allodi, R. De Renzi, G. Guidi, F. Licci and M. W. Piepper, Phys. Rev. B, 1997, 56, 6036.
29. G. Allodi, R. De Renzi, F. Licci and M. W. Piepper, Phys. Rev. Lett., 1998, 81, 4736.
30. N. Fukumoto, S. Mori, N. Yamamoto, Y. Moritomo, T. Katsufuji, C. H. Chen and S. W. Cheong, Phys. Rev. B, 1999, 60, 12963.
31. M. Uhera and S. W. Cheong, Relaxation Between Charge Order and Ferromagnetism in Manganites: Indication of Structural Phase Separation, preprint..
32. F. Damay, C. Martin, A. Maignan and B. Raveau, J. Magn. Magn. Mater., 1998, 183, 143.
33. B. Raveau, A. Maignan and C. Martin, J. Solid State Chem., 1997, 130, 162.
34. A. Maignan, F. Damay, C. Martin and B. Raveau, Mater. Res. Bull., 1997, 32, 965.
35. A. Barnabé, A. Maignan, M. Hervieu, F. Damay, C. Martin and B. Raveau, Appl. Phys. Lett., 1997, 71, 3907.
36. Y. Moritomo, A. Machida, S. Mori, N. Yamamoto and A. Nakamura, Phys. Rev. B, 1999, 60, 9220.
37. R. Mahendiran, M. Hervieu, A. Maignan, C. Martin and B. Raveau, Solid State Commun., 2000, 114, 429.
38. (a) F. Studer, O. Toulemonde, J. B. Goedkoop, A. Barnabé and B. Raveau, Jpn. J. Appl. Phys., 1999, 38, 377; (b) O. Toulemonde, F. Studer, A. Barnabé, A. Maignan, C. Martin and B. Raveau, Eur. Phys. J. B, 1998, 4, 159.
39. P. V. Vanitha, A. A. Rulraj, A. R. Raju and C. N. R. Rao, C. R. Acad. Sci., 1999, 2, 595.
40. B. Raveau, A. Maignan, C. Martin, R. Mahendiran and M. Hervieu, J. Solid State Chem., in press..
41. B. Raveau, A. Maignan, C. Martin and M. Hervieu, Mater. Res. Bull., in press..
42. S. Mori, T. Katsufuji, N. Yamamoto, C. H. Chen and S. W. Cheong, Phys. Rev. B, 1999, 59, 13573.
43. M. Zimmermann, J. P. Hill, D. Gibbs, M. Blume, D. Casa, B. Keimer, Y. Murakami and Y. Tomika, Phys. Rev. Lett., 1999, 83, 4872.

---

Footnote

† Basis of a presentation given at Materials Discussion No. 3, 26–29 September, 2000, University of Cambridge, UK.

---