Prediction of high pressure phases in the systems Li3N, Na3N, (Li,Na)3N, Li2S and Na2S†
J. Christian
Schön
,
Marcus A. C.
Wevers
and
Martin
Jansen
Max-Planck-Institut für
Festkörperforschung, Heisenbergstr.
1, D-70569, Stuttgart, Germany. E-mail: schoen@c3serv1.mpi-stuttgart.mpg.de
First published on 3rd October 2000
Abstract
The prediction of high pressure phases of a chemical system is realized as a two-step process: identification of structure candidates through the global exploration of their energy landscapes over a range of different pressures, followed by a limited local optimization using ab initio methods. The application of this recipe is presented for several systems, Li3N, Na3N, LixNa(6 − x)N2 (x = 1,…,5), Li2S and Na2S. We find that at standard pressure, the optimal configurations for the binary end compositions of the alkali nitrides, Li3N and Na3N, exhibit the Li3N and Li3P structures, respectively. Among the ternary compounds, the compositions with x = 2 and x = 4 are preferred, the optimal structures being ternary variations of the Li3N structure type. At moderately high pressures, phase transitions from Li3N to Li3Bi related structures are predicted for all ternary compounds, while Na3N and Li3N exhibit transitions from Li3P to Li3Bi and Li3N via Li3P to Li3Bi, respectively. The analogous study of the landscapes of Li2S and Na2S shows that a sequence of phase transitions from the CaF2 structure via the PbCl2 structure to the Ni2In structure is expected.
1. Introduction
One of the main issues in the field of solid state chemistry is the question: to what extent is it possible to predict which solid compounds are capable of existence in a given chemical system?1,2 Clearly, one can often provide suggestions based on similar compounds in related systems. With the introduction of high-throughput methods, sometimes collectively called combinatorial chemistry,3 it has become possible to perform rather systematic explorations of chemical systems. However, this approach is only feasible if the new compounds one aims for are easily accessible via a fast massively parallel application of traditional solid state chemistry synthesis techniques.In most cases, however, synthesizing a new compound is a very challenging task, with even successful syntheses involving many careful experiments. Thus a priori information, whether a given chemical system admits the existence of stable or metastable compounds, would be very helpful. An important related issue is the question of whether one should expect phase transitions to occur, e.g. due to the application of high pressures or temperatures. Finally, there is the need to determine phase diagrams for ternary or higher compounds. While commonly a few compounds at certain compositions are already known in a given chemical system, there remain large unexplored regions in many phase diagrams.
An obvious alternative to the experimental exploration of a chemical system is the use of theoretical methods, in particular since high-speed computers and more or less robust programs4–6 for ab initio quantum mechanical calculations have become available. Thus, over the past two decades, there have been a number of examples7,8 where a hypothetical compound has been studied by first choosing a few possible structures by analogy to related systems, then calculating their energies using ab initio programs, and finally comparing the results. Depending on the amount of computer time available, the ab initio calculations have also involved some adjustments of the cell constants, yielding an equilibrium volume in the process.
While being very attractive at first sight, this approach still possesses several drawbacks. Most importantly, when guessing the possible structures, one must rely either on one's imagination or on the expectation that nature will repeat itself. Furthermore, these ab initio calculations are usually only feasible in the static limit, i.e. at T = 0 K excluding the zero point vibrations; using ab initio molecular dynamics at non-zero temperatures is very expensive computationally. Even a local optimization (in the static limit) of both the cell constants and the atomic coordinates is often quite difficult. Thus, in most instances, already estimates of the stability of the hypothetical compounds for non-zero temperatures are not possible, and high-temperature modifications that are not even metastable at low temperatures (i.e. that are not associated with a local minimum of the potential energy) are essentially inaccessible.
In order to address these problems, at least to a certain extent, we have developed a multi-stage approach to the prediction of structures of hypothetical compounds.1 In a first step, a simple empirical potential is employed to approximately model the energy landscape of the chemical system of interest. Next, this energy landscape is explored for a fixed chemical composition using global optimization techniques and related search algorithms. This yields a large set of local minima of the system, each corresponding to a different structure candidate, together with estimates of the energetic and entropic barriers stabilizing these structures. In a further step, these minima serve as input to ab initio calculations, where a numerical local optimization of the cell is performed, as far as feasible. Finally, the whole procedure is repeated for many different compositions of the chemical system.
In this paper, we concentrate on the changes of the energy landscape as a function of pressure using lithium nitride as the main example. The results are combined with earlier studies9,10 of the energy landscapes of alkali metal nitrides in the Li/Na/N system at zero pressure to yield an overview of their stable and metastable compounds as a function of pressure. Finally, results of an analogous study of the landscapes of Li2S and Na2S are presented.
2. Methods
2.1. Modeling the landscape
In general, many hundreds of global optimization runs have to be performed, in order to find the most important local minima of the energy landscapes of the systems under investigation. Since each run requires several hundred thousand or millions of energy evaluations, it is not possible to employ ab initio methods or elaborate computationally intensive potentials at this stage of the procedure. Thus, we model the systems as spherical ions that interact via empirical two-body potentials Vij(rij), which only depend on the distances between the ions, rij. The expression for the enthalpy is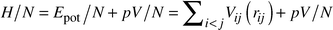 | (1) |
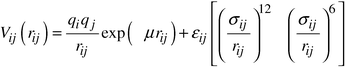 | (2) |
Since we are interested in crystalline compounds, we have applied periodic boundary conditions. Furthermore, the optimizations were performed for simulation cells that contain either two or four formula units of the respective compounds.
The calculations were repeated for a number of pressures, whose contribution to the enthalpy at T = 0 K is given in eqn. (1). Since only a limited number of global optimizations was feasible, we decided to start with a pressure of about one atmosphere, and increase the pressure subsequently by a factor of 10 each time. The reason for this choice of sample pressure was the expectation that at high pressures packing effects would dominate the possible structures, which are controlled by the repulsive terms in the interaction potential (cf.eqn. (2)). Thus changes in the landscape between subsequent “high” values of pressure should occur at considerably larger absolute pressure differences than those at “low” pressure values. Of course, in this way one will not be able to calculate e.g. a transition pressure. But at this stage, the goal is only to find structure candidates. No quantitative predictions of phase transitions or ground state energies etc. are attempted—the potentials used during the global optimization stage clearly lack the necessary accuracy. Instead, such predictions are based on the subsequent ab initio calculations.
2.2. Optimization procedure
The global optimizations were performed using the so-called simulated annealing algorithm,14,15 which is based on random walks on the energy landscapes. Each step from configuration xi to a neighbor xi + 1 is accepted according to the Metropolis criterion, i.e. with probability min(1,exp(−(Ei+1 − Ei)/C). Here C is a control parameter, which is reduced to zero, according to a so-called annealing schedule. For a schedule we used C(n) = C0fn, n = 0,…,nmax. Typical values were C0 = 1.3 eV atom−1, f = 0.99, and nmax = 1000, with 300–1000 (depending on the system size) attempted random walk steps between adjustments of C. Typically, the move class (=rule according to which neighboring configurations are chosen at random) was: 80% movements of individual ions, 5% exchanges of ions, and 15% variations of the simulation cell.One should note that the structure candidates obtained in this way are always slightly distorted from the true structure that usually exhibits at least some symmetry, i.e. they are given in the space group P1. We have determined the higher symmetry of the true structure using the symmetry finding and space group detecting programs SFND16 and RGS,17 respectively.§ The procedure yields idealized structures, which can then be used as input for the cell optimization when performing ab initio calculations. Of course, one would prefer to skip this idealization step by performing a full local optimization on an ab initio level, including the positions of the individual atoms in addition to the cell parameters. However, even now, such a full optimization is still a very difficult and time-consuming task. Thus, we have optimized only some of the cell parameters of the structure candidates, while keeping the symmetry of the structure and the relative atomic positions fixed.
Of course, even for the same structure, the cell constants and the exact locations of the atoms within the cell vary slightly from run to run, and both depend on pressure. Such variations have commonly been observed during all previous investigations of crystalline systems.10,12,13 In order to deal with this aspect of global optimization on energy landscapes, we have introduced the concept of a “minimum basin”.18 Such a basin contains all nearly identical local minima that are associated with minute variations of a given structure candidate. These side minima possess tiny energetic barriers and are stabilized by boundary effects due to the long range Coulomb interactions.¶
Furthermore, it is commonly found that several of the structures belonging to distinct minimum basins are nevertheless very closely related in a topological sense.10,12,13 Their coordination polyhedra and bonding topology are identical, and the configurations can be transformed into each other by very minor changes of the cell parameters together with slight displacements of the atoms. Thus, the structure candidates can be classified according to their topologically different structure types. In most but not all instances, it is obvious which of the several structures associated with the same structure type constitute the best minimum and should be chosen as the representative for the ab initio calculations.
2.3. Ab initio calculations
After performing some preliminary calculations using several ab initio methods, the Hartree–Fock method as implemented in the program CRYSTAL954 was chosen for the calculation of the alkali nitrides. The test calculations showed9 both relatively fast convergence and good agreement with experimental values for the cell constants of Li3N—the only system known in the alkali metal nitrides so far.19–21 Basis sets were taken from the literature.22,23 Similarly, for Li2S and Na2S, we again used CRYSTAL95, employing basis sets given in the literature,24,25 where polarization d functions were included for Na and S.In each system, we calculated the energy as a function of volume for a selected group of structure candidates, varying the volume by ca. 1% at each step. During the limited numerical local optimizations involved, the relative positions of the atoms and the symmetry of the structures were kept fixed. Furthermore, for orthorhombic or monoclinic structures, the ratios of the side lengths of the cells were usually not varied, i.e. only the total volume was changed during the optimization. The curve E(V) was then found by interpolation, where we have used the standard Murnaghan formula26
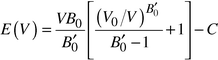 | (3) |
We note that the slope of the E(V) curve for a given structure at some specified volume V′ equals the negative value of precisely that pressure p′ = −∂E/∂V, at which V′ corresponds to the equilibrium volume of the structure at the pressure p′. As a consequence, the enthalpy H(p) = E(V(p)) + pV(p) is given by the intercept of this tangent with the y-axis. Since a pressure-induced phase transition between two structures 1 and 2 implies that both the enthalpies and the pressures are equal in the two phases, H1 = H2 and p1 = p2 = pc, the transition pressure is given by the negative slope of the common tangent of the E(V) curves, E1,2(V), belonging to the two structures. Typically, the error in the computed value of the transition pressure is estimated to be roughly about 20–25%, where three possible sources of error dominate: limitations of the ab initio calculations (neglect of correlation energy, choice of basis sets), use of restricted local optimizations when computing data points, and the dependence of the fit of E(V) on the range and density of these data points. If no common tangent exists, or if the tangent implies negative transition pressures, one of the two structures will be metastable at all pressures. One should note, however, that these calculations only apply to zero temperature. It can very well be that for high temperatures, T ≫ 0, a plot of the respective free energies F1,2(T;V) = E1,2(T;V) − TS1,2(T;V) instead of E1,2(T = 0;V) would show a reverse order of the two structures regarding their thermodynamic stability.
3. Results
3.1. Li3N
For each pressure, about the same number of topologically different structure types was found during the global optimizations (7–10). However, for “low” pressures (p ≤ 1.6 GPa), the number of different local minima determined was considerably larger than for “high” pressures (p ≥ 16 GPa): 11–17 vs. 7–10, respectively (cf.Table 1). Quite generally, p = 16 GPa appears to constitute a “watershed” regarding the types of structures observed. With only one exception (I-Na3N), no structure type was observed both below and above p = 16 GPa.
| Pressure | Li3N | Li2S | Na2S |
|---|---|---|---|
| 0 | 15/8 (22%) | 4/3 (10%) | 5/5 (10%) |
| 0.00001 | 16/9 (32%) | 7/6 (15%) | 8/6 (15%) |
| 0.0001 | 14/7 (26%) | 4/3 (20%) | 10/7 (15%) |
| 0.001 | 16/9 (8%) | 5/4 (30%) | 7/6 (25%) |
| 0.01 | 17/10 (4%) | 6/5 (25%) | 9/8 (35%) |
| 0.1 | 11/8 (6%) | 6/4 (50%) | 2/2 (5%) |
| 1 | 10/7 (0%) | 3/3 (10%) | 2/2 (0%) |
| 10 | 10/8 (0%) | 2/2 (10%) | 3/3 (30%) |
| 100 | 8/7 (0%) | No runs | No runs |
For all pressures, each of the structures exhibited a variation in the enthalpy on the order of 1% from one optimization run to the next. On the other hand, the variability of the unit cell volume for a given structure was much larger at “low” pressures than at “high” pressures (2% vs. 0.01%). This difference in variability was also present when an average over all minima observed at a given pressure was performed: both the average volume and the standard deviation decreased with pressure. The reason for the large spread at “low” pressures is connected to a similarly large spread in coordination number of N by Li, of course (cf.Table 2). For “low” pressures, the structure candidates exhibited local coordination ranging from CN = 8 or 6 to CN = 14, with no well-defined structures occurring with CN = 9 or 10, however. On the other hand, for “high” pressures the coordination varied much less, CN = 12–15. In addition, the fraction of successful optimizations that reached the two most commonly found minimum basins (not always the ones with the lowest energy!) was very high, 65–90%, to be compared with 30–50% at “low” pressures.
| Pressure | Li3N | Li2S | Na2S |
|---|---|---|---|
| 0 | 11.46 (6–14) | 8.00 (8–8) | 8.33 (8–10) |
| 0.00001 | 11.40 (6–14) | 8.07 (8–9) | 8.20 (8–9) |
| 0.0001 | 11.91 (8–14) | 8 (8–8) | 8.35 (8–10) |
| 0.001 | 11.75 (8–14) | 8.07 (8–9) | 8.40 (8–10) |
| 0.01 | 11.60 (8–14) | 8.07 (8–9) | 8.70 (8–11) |
| 0.1 | 12.16 (11–14) | 10.00 (8–11) | 11.75 (11–12) |
| 1 | 12.99 (12–15) | 11.70 (10–12) | 12.00 (12–12) |
| 10 | 13.84 (12–15) | 12.00 (12–12) | 12.00 (12–12) |
| 100 | 13.65 (12–15) | No runs | No runs |
An important observation is the fact that for the landscapes at “low” pressure many local minima with rather high energies were found, in agreement with earlier results10 of global optimizations at p = 0 Pa. This suggests that a) the energetic and entropic barriers separating these minima from the rest of the landscape are quite substantial, and b) that the local densities of states in those high lying minimum basins are large enough to compete successfully with the energetically favored low energy minima.|| In this context, we note that there exists a large low energy region of the landscape at “low” pressures, where over 80% of all the successful optimization runs ended up. All the structure types belonging to this region can be derived from the Li3Bi structure type by moderately large rearrangements of the ions, changing the coordination from 8 + 6 to 11 + 3, 12 + 2 or 13 + 1. Threshold investigations show that these minima are separated by rather small energy barriers that are crossed very quickly, indicating only small entropic contributions to the barriers. Furthermore, their E(V) curves when calculated on an ab initio basis are practically identical near the minimum of E(V) (cf.Fig. 1). In contrast, all other structure types that occur at “low” pressures appear to be separated by relatively large barriers from the remainder of the landscape. Data for selected structure types are found in the appendix.
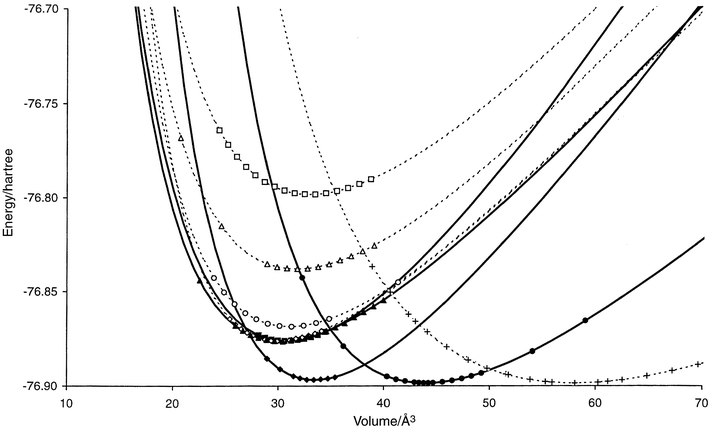 | ||
| Fig. 1 E(V) curves for promising structure candidates (cf.Table A1 in the appendix) in the system Li3N. Li3N: filled circles (solid), Li3P: filled diamonds (solid), ReO3: crosses (dashed), Li3Bi: filled triangles (solid), I-Na3N: filled squares (solid), Al3Ti: hollow diamonds (dashed), Cr3Si: hollow circles (dashed), AuCu3: hollow squares (dashed), A1-Li3N: hollow triangles (dashed). The computed data points used for the Murnaghan fit are shown for each curve. Structures that are found to be stable in some pressure range are shown as solid curves, while the metastable ones are given as dashed lines. | ||
3.2. Na3N and (Li,Na)3N
In earlier work, the energy landscape of Na3N at zero pressure has been studied in detail.10 Quite generally, we note that many of the structure types observed for the Li3N system reappeared for the landscape of Na3N. Again many structure candidates related to the Li3Bi structure were found. Using the threshold algorithm,27 they were shown to be separated by only a small energy barrier (within the empirical potential model, of course). Thus, following the lead of the Li3N system, E(V) curves were calculated only for the Li3N, the Li3P and the Li3Bi structure types9 (cf.Fig. 2). It was found that the structure candidate with the lowest energy at zero pressure is the Li3P structure, closely followed by the Li3N structure. Since the equilibrium volume of the Li3N structure is considerably larger than that of the Li3P structure, it is no surprise that the only pressure induced phase transition found for this system was the one between the Li3P and the Li3Bi structure types at pc = 13.8 ± 3.2 GPa. The Li3N structure is metastable with a relatively small negative transition pressure, pc = −0.3 ± 0.06 GPa, relative to the Li3P structure.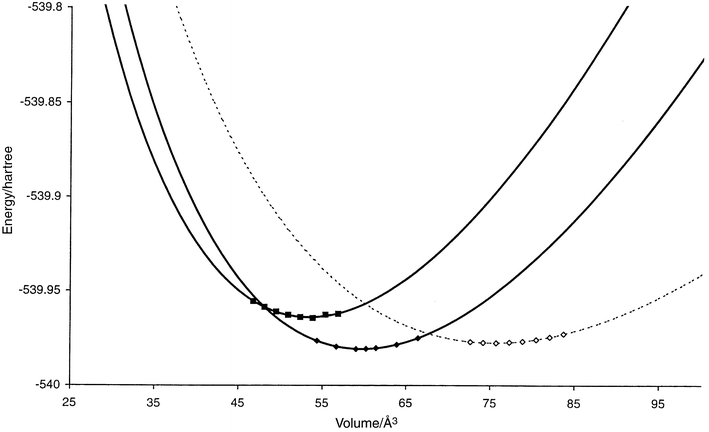 | ||
| Fig. 2 E(V) curves for promising structure candidates (cf.Table A2 in the appendix) in the system Na3N. Li3N: hollow diamonds (dashed), Li3P: filled diamonds (solid), Li3Bi: filled squares (solid). The computed data points used for the Murnaghan fit are shown for each curve. Structures that are found to be stable in some pressure range are shown as solid curves, while the metastable ones are given as dashed lines. | ||
Similarly, the energy landscape of the ternary system (LixNa6 − xN2) (x = 1,…,5) has been studied9 at zero pressure, and the results can be summarized as follows: At standard pressure, the compositions x = 2 and x = 4 are preferred, the optimal structures being ternary variations of the Li3N structure type. Here, several of the possible placements of the cations on the Li positions in the Li3N structure are found to lead to configurations that represent local minima of the energy landscape. In the optimal arrangements, the minority cations are located at the apices of the hexagonal bipyramids around the N ions, connecting the N containing layers. While ternary analogues of the Li3Bi, I-Na3N and Al3Ti structure types are found as additional local minima, no analogues of the Li3P, AuCu3 or Cr3Si structure types have been observed. Ab initio calculations show that at moderately high pressures, phase transitions from Li3N to Li3Bi related structures are predicted for all compositions x. However, the transition pressure is much higher (pc = 7.8 ± 1.8 GPa, pc = 7.2 ± 1.6 GPa) for the compositions x = 2 and 4, respectively, than for the compositions x = 1,3,5 (pc = 0.3 ± 0.06 GPa, pc = 2.9 ± 0.6 GPa and pc = 1.6 ± 0.35 GPa, respectively). This serves as an indication that the preference for the compositions x = 2,4 should persist towards higher pressures. For comparison, the hypothetical transitions from the Li3N to the Li3Bi structure type for the binary end compositions, the Li3N and the Na3N system, would occur at pc = 7.0 ± 1.5 GPa and pc = 3.0 ± 0.6 GPa, respectively.
3.3. Li2S and Na2S
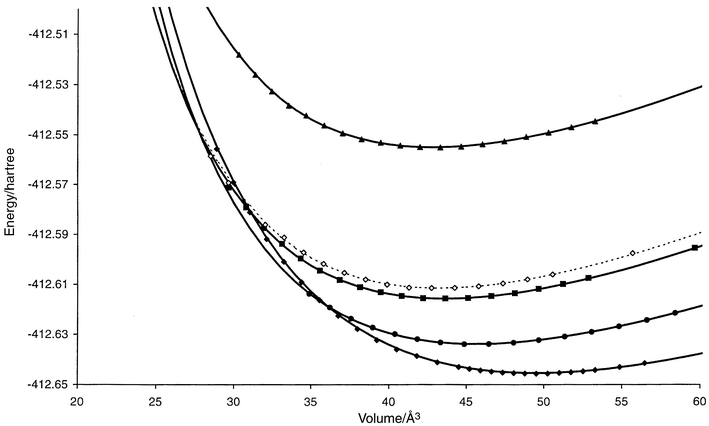 | ||
| Fig. 3 E(V) curves for promising structure candidates (cf.Table A3 in the appendix) in the system Li2S. CaF2: filled diamonds (solid), PbCl2: filled circles (solid), Ni2In: hollow diamonds (dashed), Ni2In-(d) (see Discussion): filled squares (solid), A1-Li2S: filled triangles (solid). The computed data points used for the Murnaghan fit are shown for each curve. Structures that are found to be stable in some pressure range are shown as solid curves, while the metastable ones are given as dashed lines. | ||
Similar to the Li2S system, we have also performed ab initio local optimizations for Na2S. The results available so far indicate that a phase transition should occur between the CaF2 and the Ni2In structure, with a possible appearance of the PbCl2 structure over a short intermediate pressure range. This might be followed by a transition to a 12-fold coordinated structure A1-Na2S (space group I41/amd) at very high pressures. The transition pressure(s) for the transition(s) up to the Ni2In structure are expected to lie in a pressure range around pc = 11 ± 2.5 GPa, while either the A1-Na2S structure or the A2-Na2S structure might be stable above a pressure of pc = 120 GPa.
4. Discussion
Perhaps the most striking result of the landscape investigations is the persistence of major features of the energy landscape when varying the pressure. Many of the important structure types correspond to deep-lying local minima over a wide pressure range, for both alkali metal nitrides and sulfides. The second general observation is the division of the structures into two groups, constituting local minima at either “high” or “low” pressures. This is no great surprise, of course, but it underlines the importance of exploring the energy landscape of a system at many different pressures.When comparing the landscapes for different systems, it appears somewhat surprising that considerably more structure candidates are found for Li3N than for Li2S and Na2S taken together. However, this might well be caused by the larger sample of optimization runs for the Li3N system. Clearly, further optimizations are needed for the sulfides, which might result in a change in the number of distinct structures observed.
As was mentioned earlier, Li3N is the only binary or ternary alkali metal nitride known so far. Its high pressure behavior has been studied in recent years, and the transition to the Li3P structure we have found has been observed at ca. 0.6 GPa28 by experiment. Taking into account experimental and theoretical uncertainties, this agrees well with the value of 0.4 GPa we have computed. Furthermore, there are hints at a transition to a high-symmetry structure like e.g. Li3Bi somewhere in the pressure range from 10 to 35 GPa.28,29 Again, this agrees well with our prediction of a transition to Li3Bi or a closely related structure at pc = 28 GPa. Clearly, more careful experimental investigations are needed to resolve the discrepancy between the experiments and allow a comparison with our calculations. We also note that our results are of the same order of magnitude as those of a recent LDA-based calculation29 for Li3N, where a transition pressure of 38 GPa has been suggested between the Li3P structure (which was computed to be the equilibrium structure at standard pressure, however!) and the Li3Bi structure.
Regarding Na3N and the ternary system (Li,Na)3N, no synthesis has proven to be successful so far, in spite of some claims in the past.30 Thus we can only judge the results by comparing with the most closely related structures. Here, the fact that the energy landscapes of Li3N and Na3N are very similar lends confidence to the prediction of Na3N existing either in the Li3N or the Li3P structure at standard pressure. For the ternary system, we note that in particular the Li3N related structures with minority cations at the apices of the hexagonal bipyramids lead to very well balanced structures for Li ∶ Na ratios of 1 ∶ 2 (x = 2) and 2 ∶ 1 (x = 4). As a consequence, we might find phase separation instead of perfect mixing in the (Li,Na)3N system. The preference for the Li3N related modifications at standard pressure agrees well with the existence of ternary systems31–33 of the composition (Li,M)3N (M = Cu, Ni, Co, Mn, Fe), all exhibiting a Li3N related structure with minority cations between the layers containing N ions.
While this is very encouraging, one needs to recall that in general further phases might be present that do not show the desired composition (Li,Na)3N. In particular, elementary (gaseous) nitrogen and (metallic) sodium together with Li3N might form as an alternative to the desired compounds, e.g. Li2NaN or LiNa2N.
Turning to the sulfides, recent experimental work34 on Li2S has shown that the transition to the PbCl2 structure type does take place at pc = 12 GPa, while the predicted transition to the Ni2In structure at higher pressure has not yet been observed. Regarding experiments on Na2S, transitions from the CaF2 structure via the PbCl2 structure to the Ni2In structure have recently been observed35 at pressures of about 5 GPa, and somewhere between 8 and 20 GPa, respectively, while further transitions at higher pressures have not yet been found.
In this context one needs to address the question of systematic errors in the qualitative and quantitative prediction of transition pressures. Beyond the basic limitations of each ab initio method, we face the requirement of having to use the same basis set and/or effective interaction potential for all volumes, in order to achieve consistency and comparability of the E(V) curves. This can lead to various cut-off problems when computing data points far away from the minimum of the E(V) curve. This is especially critical when starting from structure candidates that were only observed at high pressures, since here the starting point of the local optimization can be far removed from the minimum of the E(V) curve. While this has not been a problem for the sulfides up to now, it has proven to be rather difficult to achieve convergent E(V) calculations for the structure candidates found at very high pressures (p ≥ 160 GPa) in the Li3N system. Thus these data have been excluded from the E(V) diagram in Fig. 1. A further potential source of error is the dependence of the fit on the available computed data points, especially when attempting extrapolations towards low volumes. Tests for e.g. the sulfide systems have shown that the curvature of the fitted E(V) curve can exhibit non-negligible changes upon addition of further data points.
A second concern is the restriction of keeping symmetry and atomic positions fixed during the local optimizations with ab initio methods. As a consequence, the computations produce at best upper bounds on the true E(V) curves of the compound. This caveat applies in particular if the structure under investigation is not highly symmetric or contains many atoms in general positions (x,y,z). Since we are rarely able to optimize all cell parameters and the positions of the atoms at the same time, it is quite likely that in such a case the true E(V) curve will lie somewhat lower than the computed one, resulting e.g. in a lower transition pressure. Directly related to this is the fact that a numerical optimization by hand (CRYSTAL95 has no gradient available) will always lack the precision of a gradient based optimization. An instance where a full optimization might be advisable is the PbCl2 related structure found in Li2S and Na2S, which possesses a relatively low symmetry and contains many atoms in general positions, and is similar in energy to the Ni2In structure in Na2S. Thus, the corresponding E(V) curves computed for Li2S (Fig. 3) and Na2S (Fig. 4) should only be considered as a first approximation as far as quantitative conclusions are concerned.
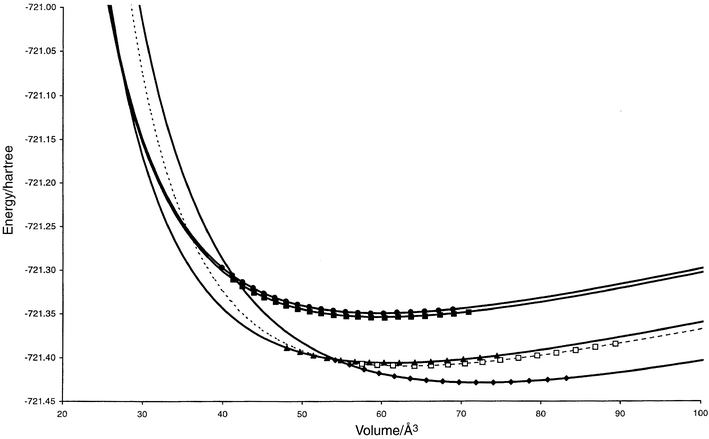 | ||
| Fig. 4 E(V) curves for promising structure candidates (cf.Table A4 in the appendix) in the system Na2S. CaF2: filled diamonds (solid), PbCl2: hollow squares (dashed), Ni2In: filled triangles (solid), A1-Na2S: filled circles (solid), A2-Na2S: filled squares (solid). The computed data points used for the Murnaghan fit are shown for each curve. Structures that are found to be stable in some pressure range are shown as solid curves, while the metastable ones are given as dashed lines. | ||
In order to investigate the possible errors due to an incomplete local optimization, we have computed additional E(V) data points, both for Li2S and Na2S in the Ni2In and the PbCl2 modifications each. We find for most modifications, except for the PbCl2 structure in Li2S, that the data points resulting from the less restricted local optimization lie clearly below the curve obtained from the one-parameter optimization. Furthermore, there appears to be a slight shift to somewhat larger equilibrium volumes at zero pressure. In addition, we also studied the effect of including five more data points at low volumes for the fluorite structure of Na2S. We find that the curvature of the E(V) curve changes significantly, leading to a large change of the transition pressure from 16 GPa to about 11 GPa. In general one should note that the effect of the potential errors appears to be very specific for each system and modification. Furthermore, the changes in the E(V) curve have the greatest impact in the range of very small volumes and extremely high pressures (p > 10 GPa).
Finally, we note that it is quite possible that a slightly distorted structure candidate with somewhat lower symmetry might be energetically preferable within some pressure range. An example is the Ni2In structure type in Li2S, which occurred as a local minimum both as a fully symmetric and a slightly distorted structure, called Ni2In and Ni2In-(d), respectively. For both, the E(V) curves have been computed and are shown in Fig. 3. We note that in this instance, the distorted version appears slightly more favorable at low pressures, while at high pressures both curves are nearly identical.
5. Summary
We have shown how a two-step procedure consisting of an exploration of the energy landscapes of chemical systems at various pressures using global optimization techniques, followed by a local optimization with ab initio methods, leads to successful predictions of pressure induced phase transitions. For those chemical systems where a synthesis has already been successful (Li3N, Li2S, Na2S), the results agree well with experimental observations. But there still remains a challenge to the experimentalist, as additional predicted structures in the Li3N, Na3N, (Li,Na)3N, Li2S and Na2S systems still await their realization. Tables A1–A4:| Li3N Minimum | Space group (number), origin choice, crystal system | Lattice constants a, b, c/Å; α, β, γ/° | Atom (multiplicity, Wyckoff symbol), fractional coordinates | |||
|---|---|---|---|---|---|---|
| Li3N | P6/mmm (191), hexagonal | a = 3.612, c = 3.875 | Li2 (2c) | 1/3 | 2/3 | 0 |
| α = 90.00, β = 90.00, γ = 120.00 | Li1 (1b) | 0 | 0 | 1/2 | ||
| N (1a) | 0 | 0 | 0 | |||
| I-Na3N | Pmmn (59), orthorhombic | a = 3.523, b = 4.929, c = 3.523 | Li1 (4e) | 3/4 | 0.5 | 0.72 |
| α = 90.00, β = 90.00, γ = 90.00 | Li2 (2b) | 3/4 | 1/4 | 0.18 | ||
| N (2a) | 3/4 | 3/4 | 0.78 | |||
| Al3Ti | I4/mmm (139), tetragonal | a = 3.502, c = 4.877 | Li1 (4d) | 1/2 | 0 | 1/4 |
| α = 90.00, β = 90.00, γ = 90.00 | Li2 (2b) | 1/2 | 1/2 | 0 | ||
| N (2a) | 0 | 0 | 0 | |||
| Li3P | P63/mmc (194), origin choice 2, hexagonal | a = 3.509, c = 6.262 | Li1 (4f) | 1/3 | 2/3 | 0.58 |
| α = 90.00, β = 90.00, γ = 120.00 | N (2c) | 1/3 | 2/3 | 1/4 | ||
| Li2 (2b) | 0 | 0 | 0 | |||
| Li3Bi |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
(225), cubic m
(225), cubic |
a = 4.957 | Li (8c) | 1/4 | 1/4 | 1/4 |
| α = 90.00, β = 90.00, γ = 90.00 | N (4b) | 1/2 | 1/2 | 1/2 | ||
| Li (4a) | 0 | 0 | 0 | |||
| AuCu3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
(221), cubic m
(221), cubic |
a = 3.223 | Li (3c) | 1/2 | 1/2 | 0 |
| α = 90.00, β = 90.00, γ = 90.00 | N (1a) | 0 | 0 | 0 | ||
| Cr3Si |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) n
(223), cubic n
(223), cubic |
a = 3.967 | Li (6c) | 1/4 | 0 | 1/2 |
| α = 90.00, β = 90.00, γ = 120.00 | N (2a) | 0 | 0 | 0 | ||
| ReO3 |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
(221), cubic m
(221), cubic |
a = 4.334 | Li (3d) | 1/2 | 0 | 0 |
| α = 90.00, β = 90.00, γ = 90.00 | N (1a) | 0 | 0 | 0 | ||
| A1-Li3N | Cmma (67), orthorhombic | a = 3.972, b = 5.956, c = 5.372 | Li (8m) | 0 | 0.10 | 0.64 |
| α = 90.00, β = 90.00, γ = 90.00 | N (4g) | 1/2 | 1/4 | 0.74 | ||
| Li (4a) | 1/4 | 1/2 | 0 | |||
| Na3N Minimum | Space group (number), origin choice, crystal system | Lattice constants a, b, c/Å; α, β, γ/° | Atom (multiplicity, Wyckoff symbol), fractional coordinates | |||
|---|---|---|---|---|---|---|
| Li3P | P63/mmc (194), origin choice 2, hexagonal | a = 4.257, c = 7.524 | Li1 (4f) | 1/3 | 2/3 | 0.58 |
| α = 90.00, β = 90.00, γ = 120.00 | N (2c) | 1/3 | 2/3 | 1/4 | ||
| Li2 (2b) | 0 | 0 | 0 | |||
| Li3N | P6/mmm (191), hexagonal | a = 4.365, c = 4.590 | Li2 (2c) | 1/3 | 2/3 | 0 |
| α = 90.00, β = 90.00, γ = 120.00 | Li1 (1b) | 0 | 0 | 1/2 | ||
| N (1a) | 0 | 0 | 0 | |||
| Li3Bi |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
(225), cubic m
(225), cubic |
a = 5.995 | Li (8c) | 1/4 | 1/4 | 1/4 |
| α = 90.00, β = 90.00, γ = 90.00 | N (4b) | 1/2 | 1/2 | 1/2 | ||
| Li (4a) | 0 | 0 | 0 | |||
| Li2S Minimum | Space group (number), origin choice, crystal system | Lattice constants a, b, c/Å; α, β, γ/° | Atom (multiplicity, Wyckoff symbol), fractional coordinates | |||
|---|---|---|---|---|---|---|
| CaF2 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
(225), cubic m
(225), cubic |
a = 5.5 | Li (8c) | 1/4 | 1/4 | 1/4 |
| α = 90.00, β = 90.00, γ = 90.00 | S (4a) | 0 | 0 | 0 | ||
| Ni2In-(d) (distorted, see text) | Cmcm (63), orthorhombic | a = 4.065, b = 7.870, c = 5.458 | Na1 (4c) | 0 | 0.67 | 1/4 |
| α = 90.00, β = 90.00, γ = 120.00 | S (4c) | 1/2 | 0.85 | 1/4 | ||
| Na2 (4a) | 0 | 0 | 1/2 | |||
| Ni2In | P63/mmc (194), hexagonal | a = 4.350, c = 5.220 | S (2d) | 1/3 | 2/3 | 3/4 |
| α = 90.00, β = 90.00, γ = 120.00 | Li1 (2c) | 1/3 | 2/3 | 1/4 | ||
| Li2 (2a) | 0 | 0 | 0 | |||
| A1-Li2S | P6/mmm (191), hexagonal | a = 3.824, c = 3.635 | Li (2d) | 2/3 | 1/3 | 1/2 |
| α = 90.00, β = 90.00, γ = 120.00 | S (1a) | 0 | 0 | 0 | ||
| PbCl2 | Pnma (62), orthorhombic | a = 6.278, b = 3.828, c = 7.470 | Li1 (4c) | 0.97 | 3/4 | 0.67 |
| α = 90.00, β = 90.00, γ = 90.00 | Li2 (4c) | 0.64 | 1/4 | 0.57 | ||
| S (4c) | 0.25 | 1/4 | 0.61 | |||
| Na2S Minimum | Space group (number), origin choice, crystal system | Lattice constants a, b, c/Å; α, β, γ/° | Atom (multiplicity, Wyckoff symbol), fractional coordinates | |||
|---|---|---|---|---|---|---|
| CaF2 |
Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m
(225), cubic m
(225), cubic |
a = 6.600 | Na (8c) | 1/4 | 1/4 | 1/4 |
| α = 90.00, β = 90.00, γ = 90.00 | S (4a) | 0 | 0 | 0 | ||
| Ni2In | P63/mmc (194), hexagonal | a = 4.915, c = 5.950 | S (2d) | 1/3 | 2/3 | 3/4 |
| α = 90.00, β = 90.00, γ = 120.00 | Na1 (2c) | 1/3 | 2/3 | 1/4 | ||
| Na2 (2a) | 0 | 0 | 0 | |||
| A1-Na2S | I41/amd (141), origin choice 2, tetragonal | a = 3.755, c = 13.202 | Na (8e) | 1/2 | 1/4 | 0.21 |
| α = 90.00, β = 90.00, γ = 90.00 | S (4b) | 0 | 1/4 | 7/8 | ||
| A2-Na2S | P6/mmm (191), hexagonal | a = 3.816, c = 3.696 | Na (2d) | 2/3 | 1/3 | 1/2 |
| α = 90.00, β = 90.00, γ = 120.00 | S (1a) | 0 | 0 | 0 | ||
| Pb2Cl | Pnma (62), orthorhombic | a = 6.278, b = 3.828, c = 7.470 | Na1 (4c) | 0.71 | 1/4 | 0.42 |
| α = 90.00, β = 90.00, γ = 90.00 | Na2 (4c) | 0.95 | 3/4 | 0.30 | ||
| S (4c) | 0.27 | 3/4 | 0.89 | |||
Acknowledgements
We would like to thank G. Stollhoff, K. Syassen, A. Vegas, and R. Hundt for valuable discussions. This work has been partly funded by the DFG via the Sonderforschungsbereich 408.References
- (a) J. C. Schön and M. Jansen, Angew. Chem., 1996, 108, 1358; (b) J. C. Schön and M. Jansen, Angew. Chem., Int. Ed. Engl., 1996, 35, 4001 CrossRef.
- M. L. Cohen, Science, 1986, 234, 549 CAS.
- (a) B. Jandeleit, D. J. Schaefer, T. S. Powers, H. W. Turner and W. H. Weinberg, Angew. Chem., 1999, 111, 1648 CrossRef; (b) B. Jandeleit, D. J. Schaefer, T. S. Powers, H. W. Turner and W. H. Weinberg, Angew. Chem., Int. Ed., 1999, 38, 2494 CrossRef CAS.
- R. Dovesi, V. R. Saunders, C. Roetti, M. Causa, N. M. Harrison, R. Orlando and E. Apra, CRYSTAL95, University of Torino, 1996..
- P. Blaha, K. Schwarz and J. Luitz, WIEN97, Vienna University of Technology, 1997..
- R. Car and M. Parinello, Phys. Rev. Lett., 1985, 55, 2471 CrossRef CAS.
- A. Y. Liu and M. L. Cohen, Phys. Rev. B, 1990, 41, 10727 CrossRef CAS.
- P. Kroll and R. Hoffmann, Angew. Chem., Int. Ed., 1998, 37, 2527 CrossRef CAS.
- J. C. Schön, M. A. C. Wevers and M. Jansen, Solid State Sci., 2000, in press. Search PubMed.
- M. Jansen and J. C. Schön, Z. Anorg. Allg. Chem., 1998, 624, 533 CrossRef CAS.
- S. W. DeLeeuw, J. W. Perram and E. R. Smith, Proc. R. Soc. London A, 1980, 373, 27 Search PubMed.
- M. A. C. Wevers, J. C. Schön and M. Jansen, J. Solid State Chem., 1998, 136, 233 CrossRef CAS.
- J. C. Schön and M. Jansen, Comput. Math. Sci., 1995, 4, 43 Search PubMed.
- S. Kirkpatrick, C. D. Gelatt, Jr. and M. P. Vecchi, Science, 1983, 220, 671 CrossRef.
- V. Czerny, J. Opt. Theory Appl., 1985, 45, 41 Search PubMed.
- R. Hundt, J. C. Schön, A. Hannemann and M. Jansen, J. Appl. Crystallogr., 1999, 32, 413 CrossRef CAS.
- A. Hannemann, R. Hundt, J. C. Schön and M. Jansen, J. Appl. Crystallogr., 1998, 31, 922 CrossRef CAS.
- M. A. C. Wevers, J. C. Schön and M. Jansen, J. Phys. Condens. Matter, submitted. Search PubMed.
- E. Zintl and G. Brauer, Z. Electrochem., 1935, 41, 102 Search PubMed.
- A. Rabenau and H. Schulz, J. Less-Common Met., 1976, 50, 155 Search PubMed.
- N. E. Brese and M. O'Keefe, Struct. Bonding (Berlin), 1992, 307 Search PubMed.
- M. Prencipe, A. Zupan and R. Dovesi, Phys. Rev. B, 1995, 51, 3391 CrossRef CAS.
- R. Pandey, J. E. Jaffe and N. M. Harrison, J. Phys. Chem. Solids, 1994, 55, 1357 CrossRef CAS.
- A. Lichanot, E. Apra and R. Dovesi, Phys. Status Solidi (b), 1993, 177, 157 Search PubMed.
- R. Dovesi, C. Roetti, C. Freyria-Fava, M. Prencipe and V. R. Saunders, Chem. Phys., 1991, 156, 11 CrossRef CAS.
- F. D. Murnaghan, Proc. Natl. Acad. Sci. USA, 1944, 30, 244.
- J. C. Schön, H. Putz and M. Jansen, J. Phys. Condens. Matter, 1996, 8, 143 CrossRef.
- H. J. Beister, S. Haag, R. Kniep, K. Strößner and K. Syassen, Angew. Chem., 1988, 100, 1116 CAS.
- A. C. Ho, M. K. Granger and A. L. Ruoff, Phys. Rev. B, 1999, 59, 6083 CrossRef CAS.
- H. Wattenberg, Ber. Dtsch. Chem. Ges., 1930, 63, 1667 Search PubMed.
- W. Sachsze and R. Juza, Z. Anorg. Allg. Chem., 1949, 259, 278 CAS.
- J. Klatyk and R. Kniep, Z. Kristallogr. NCS, 1999, 214, 447 Search PubMed.
- J. Klatyk and R. Kniep, Z. Kristallogr. NCS, 1999, 214, 445 Search PubMed.
- A. Grzechnik, A. Vegas, K. Syassen, I. Loa, M. Hanfland and M. Jansen, J. Solid State Chem., 2000, in press. Search PubMed.
- A. Vegas, A. Grzechnik, K. Syassen, I. Loa, M. Hanfland and M. Jansen, Acta Crystallogr., Sect. B, submitted. Search PubMed.
Footnotes |
| † Basis of a presentation given at Materials Discussion No. 3, 26–29 September, 2000, University of Cambridge, UK. |
| ‡ In these studies, ε was varied between 0.1 and 0.5, rs between 1.0 and 1.2, and μ between 0.05 and 0.15. |
| § The structure candidates cluster around the high symmetry structure, with deviations Δϕ/ϕ in angles and ΔL/L in cell lengths ranging from typically less than 1% up to 5% for strongly distorted minima. In some cases, a sequence of space groups may be found as a function of the tolerances employed in SFND and RGS. |
| ¶ These boundary effects are analogous to the surface effects encountered when performing cluster calculations. However, in clusters, these effects can have a physical meaning, while in infinite crystals only an overall dipole moment should survive.18 |
|| Local densities of states gi(E)
refer to the states that belong to the extended region around a minimum i
of the energy landscape, which can be determined using e.g. the threshold
algorithm.27 These influence the outcome of
the global optimization when using e.g. simulated annealing starting
at high temperatures with a moderately fast schedule. While at T = 0 K,
the local free energy Fi = Ei,
where Ei is the potential energy of the local minimum i,
for T > 0 K, the local entropy Si = kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) gi contributes to Fi, Fi = Ei − TSi, and thus minima with large gi will
be sampled frequently during the optimization even for relatively high values
of Ei. gi contributes to Fi, Fi = Ei − TSi, and thus minima with large gi will
be sampled frequently during the optimization even for relatively high values
of Ei. |
| This journal is © The Royal Society of Chemistry 2001 |
