Determination of total and EDTA extractable metal distributions in the colloidal fraction of contaminated soils using SdFFF-ICP-HRMS†
Bailin Chena, Charles A. Shandb and Ronald Beckett*a
aCRC for Freshwater Ecology, Water Studies Centre, School of Chemistry, Monash University, Clayton, Victoria, 3800, Australia. E-mail: Ron.Beckett@sci.monash.edu.au; Fax: (61 3)
9905 4196; Tel: (61 3) 9905 4555
bMacaulay Land Use Research Institute, Aberdeen, UK AB15
8QH
First published on 6th December 2000
Abstract
Newly developed methods involving an on-line combination of sedimentation field-flow fractionation-inductively coupled plasma-high resolution mass spectrometry (SdFFF-ICP-HRMS) have been used to study the distributions of extractable heavy metals in a soil which had been treated with sewage sludge contaminated with Cu or Pb. The relationship of these metals with other elements in the colloidal fraction was also investigated. The colloidal fraction from the soil was obtained by repeated gravitational sedimentation and extracted with 0.11 M acetic acid, 0.1 M hydroxylamine hydrochloride, 0.05 M ethylenediaminetetraacetic acid disodium salt (EDTA) or aqua regia to assess the potential availability of the metals Cu and Pb. Large proportions of the Cu and Pb were extracted by EDTA, approaching that removed by aqua regia, whereas <10% of the aqua regia extractable metals were removed by acetic acid and hydroxylamine chloride. The distributions of the heavy metals, the major mineral forming element (Al) and the elements forming sesquioxides (Fe and Mn) within different size classes (0.05–1 µm) of the colloidal fraction were measured using SdFFF-ICP-HRMS before and after extraction with EDTA. This information provides an insight into the composition of the colloids and the distributions of metal contaminants. In the contaminated soil colloids, the concentration of Fe, Mn and Pb is greatest in the smaller particles (<0.2 µm). In contrast, the Cu concentration is constant over the size range studied. Iron oxide surface coatings probably play a significant role in Pb adsorption on soil particles, but may be less important for Cu. The combination of selective chemical extraction, SdFFF and ICP-HRMS provides a means of determining the distribution of potentially available heavy metals within the colloidal fraction of contaminated soils.
1. Introduction
Heavy metals can enter soil through a variety of natural processes, such as weathering of rocks, and anthropogenic processes, such as atmospheric deposition of particles from industrial emissions and the application of fertilisers. In recent years, the utilisation of sewage sludge as a fertiliser within Europe has increased in response to changes in European Community legislation,1 which has banned the dumping of sewage sludge into the sea. In addition to valuable N, P and C, sewage sludge may contain heavy metals, even in sludge derived from non-industrial areas. When added to soils, heavy metals may be adsorbed, form complexes or coprecipitate. Unlike organic pollutants, heavy metals cannot be decomposed by biological processes and tend to preferentially accumulate in the clay sized fraction because of its large surface area. It is thus of interest to determine more about the distribution and potential availability of metals within this fraction. Metals which bind strongly to the colloidal fraction can in many cases be considered to be largely immobile. However, under certain circumstances, such as when the pH is increased, colloidal transport may become important.2,3This study focuses on an investigation of two biologically important metals Cu and Pb which are often found in sewage sludge. For mineral soils, a typical colloidal particle consists of a silica, silicate or aluminosilicate core which is often coated with hydrous Fe oxides, Mn oxides and natural organic matter. These coatings are thought to have a profound effect on the bioavailability and cycling behaviour of trace elements.4
Colloids can be separated into different sizes by sedimentation field-flow fractionation (SdFFF) with high resolution.5 SdFFF is an elution technique with similarities to liquid chromatography, the main difference being that separation by SdFFF is induced by hydrodynamic processes (physical interactions) rather than by chemical interaction with a stationary phase. The sample of colloidal suspension (typically 50 µL containing up to 50 µg of solid) is injected onto one end of a flat rectangular open channel, which sits within a centrifuge basket [Fig. 1(a)]. Under stop flow, the centrifugal field is applied at right angles to the flat face of the channel and colloidal particles are driven towards the accumulation wall, where an equilibrium cloud is formed [Fig. 1(b)]. After this relaxation period, the carrier liquid flow is turned on, and a parabolic fluid flow profile in the channel is generated. Since flow velocities increase away from the accumulation wall, particles with a lower effective mass are swept along the channel by a higher average flow velocity compared to large particles and are eluted first [Fig. 1(c)].
 | ||
| Fig. 1 Schematic representation of the SdFFF-ICP-MS apparatus and the SdFFF separation mechanism occurring in the channel. | ||
The fractions eluting from SdFFF can be collected and their composition determined off-line by inductively coupled plasma-mass spectrometry (ICP-MS),6 inductively coupled plasma-atomic emission spectrometry (ICP-AES)7 or graphite furnace atomic absorption spectrometry (GFAAS).8 However, when using off-line methods with discrete samples, there is a greater likelihood of contamination problems for trace elements and it is more difficult to obtain high resolution information on changes of chemical composition related to size. Murphy et al.9 overcame this limitation by using SdFFF directly coupled to ICP-MS. A recent improvement employed by Chen et al.10 and Tadjiki7 involved using high resolution magnetic sector mass spectrometry (HRMS). The resulting combination (SdFFF-ICP-HRMS) offers extremely powerful particle size fractionation and multi-element analyses of major and minor elements with low detection limits and little spectroscopic interference.
For dilute suspensions (<0.2% w/v), particles with sizes <5 µm are effectively atomised by the ICP.11 Direct slurry ICP-MS analysis of a range of geological materials has been reported.12,13 The eluent from SdFFF is much more dilute than the suspensions used in the previous studies, and in the normal mode of operation FFF is restricted to particles with sizes <2 µm, which makes ICP-MS a suitable method of analysis.
Changes in chemical composition of the sample particles as a function of particle size can be displayed by plotting the appropriate eluent element concentration ∶ UV signal ratio (which is proportional to the element concentration in the particles) and element atomic ratio versus particle diameter. These data can then be used to interpret changes in mineralogy or surface coatings over the particle size distribution of the sample.
The objective of our study was to identify which size fractions of these soil colloids contain the largest fraction of potentially bioavailable heavy metals. To achieve this, the particle size distributions and elemental composition distributions of the colloid phase were determined within the range 0.05–1 µm. This was performed before and after extraction with EDTA. The colloids were analysed for their major (Al, Fe) and minor (Mg, Ti, Mn) element compositions, including the heavy metals (Cu, Pb).
EDTA is a strong complexing agent and has been used to determine extractable Cu14 and Pb15 contents of soils. EDTA removes more than just the readily available component and has been added to soils as an aid in phytoremediation.16
2. Theory
2.1. Sedimentation field-flow fractionation
The mechanism and theory of SdFFF have been detailed elsewhere.17–20 The sample particles are injected at the inlet end of the channel and are compressed on one of the channel walls (the accumulation wall) under the influence of the applied centrifugal field. The mean thickness of the sample layer (l) determines the migration velocity down the channel. The layer thickness depends on the force on the particles generated by the field (F) and the thermal energy (kT) according to the expression: | (1) |
For SdFFF, the value of F for a given sample depends on the buoyant mass of the particles. Thus particles with larger size and density have longer retention times than smaller or less dense particles. The retention time (tr) is used to determine the equivalent spherical diameter (d) as a function of elution volume. In the case of constant field conditions for well retained samples, the approximate expression is as follows:
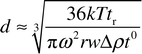 | (2) |
If the sample contains a wide range of particle sizes and a constant field sufficient to separate the smallest particles is applied, the elution time for the separation of the largest particles becomes long. In practice, a high field is initially applied which is then reduced over time. In the case of field decay SdFFF runs, numerical computations can be carried out in a series of short time intervals using eqn. (2) so that the particle diameter at each elution time is calculated.19,21
An effective program for reducing the field with time is known as the power decay approach.22 It involves applying a constant speed ω0 for an initial period t1 after which the speed decays according to the power equation:
 | (3) |
2.2. Fractograms and particle size distributions
The raw data obtained from an SdFFF instrument is a plot of detector signal versus elution time or volume. This is referred to as a fractogram. The equivalent spherical particle diameter corresponding to a given elution time or volume can be computed as indicated above. It has been demonstrated experimentally by Kirkland et al.24 that the particle shape has little or no effect on SdFFF retention until the aspect ratio is larger than 50. Beckett and Giddings20 have concluded from theoretical considerations that shape should not be important unless the major dimension of the particle approaches the cloud thickness value l. Therefore, the equivalent spherical diameter calculated from the above equations is valid for most particles.The equivalent spherical diameter at any given elution time or volume can be calculated if the particle density is known. The UV detector response, which is designated UVi at point i along the elution profile, is assumed to be proportional to the mass concentration of the sample in the eluent (dmci/dVi), which can be converted to the appropriate y-axis for a particle size distribution (dmci/ddi) by eqn. (4):
 | (4) |
2.3. Element content distributions
If the SdFFF eluent is fed into an ICP-HRMS instrument, an ion current IEi is generated for each element E of interest, where IEi is proportional to the mass concentration of the element present in the eluent (dmcEi/dVi). Then the element fractogram is converted to an element-based particle size distribution using eqn. (5): | (5) |
2.4. Element atomic ratio distributions
Element atomic ratio distributions indicate changes in chemical composition across the entire size range of the sample. By selecting two appropriate elements (E(a) and E(b)), the ratios of their molar concentrations can be computed from eqn. (6): | (6) |
2.5. Elemental concentration in particles
The distribution of metal per unit mass of particle (dmcE/dmc) at any point i along the elution time or volume axis is calculated as follows:25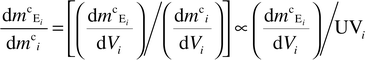 | (7) |
2.6. Surface density distributions of extractable metals
The amount of metal found on the particle surfaces can be calculated by the difference between the extracted and non-extracted samples. These data are then used to calculate the extractable metal surface density distribution (SDD), which is a plot of the amount of extractable metal per unit area of particle surface (dmcEi/dAci, in arbitrary units) as a function of particle size. Assuming a constant spherical shape and density for the particles, the following equation can be used to determine the y-axis of the SDD: | (8) |
3. Materials and methods
3.1. Soil
The soil, located within the grounds of the Macaulay Land Use Research Institute, was an imperfectly drained humus iron podzol developed on a till from granite and granitic gneiss. It is classified under the Soil Survey of Scotland as belonging to the Countesswells Association, Dess series,26 or as a stagnic-podzol.27 The soil in different plots was surface treated in 1989 with sewage contaminated with individual heavy metal salts (i.e. one metal per plot).28 The salts were copper carbonate or lead acetate and the amounts added were designed to increase the Cu or Pb content in the top 25 cm of the soil to near twice the allowed European Community maxima (Table 1). The plots received no further treatments except for occasional cutting, the harvested vegetation being removed. The soil was sampled in 1997 from the top surface to a depth of 25 cm.3.2. Colloidal fraction
Soil was sampled, air-dried and screened (2 mm) to remove stones and large roots. The soil (50 g) was dispersed in 1.2 L of water by sonication (model VCX-600, Sonics & Materials Inc., Danbury, CT, USA) at 650 W for 5 min while cooling. The clay fraction (nominal size <1.4 µm) was isolated by repeated sedimentation under gravity,29 assuming a mineral density of 2.5 g cm−3. The suspensions from six sequential sedimentation cycles were combined, and concentrated by freeze-drying. The mineral composition of the clay fraction was determined quantitatively by a combination of reference intensity ratio methods as described by Cheshire et al.303.3. Extraction
A procedural speciation scheme involving four separate extractants was used (Table 2). The extractants were acetic acid (0.11 M), hydroxylamine hydrochloride (0.1 M) in HCl (pH = 2), EDTA (0.05 M, pH = 6) and aqua regia [3 ∶ 1 v/v concentrated HCl ∶ HNO3]. Extractions were performed on 200 mg air-dried soil clay. For the samples extracted with acetic acid, hydroxylamine hydrochloride or EDTA, the clay was weighed into a 15 mL centrifuge tube. The extractant (8 mL) was added. The mixture was placed in an end-over-end shaker for 16 h at room temperature. For the sample digested with aqua regia, the clay was weighed into a borosilicate glass beaker covered with a watch glass; 10 mL of aqua regia was added. The mixture was gently digested on a hot plate for a few hours. When the volume of the mixture had been reduced to about 1 mL, more aqua regia was added and the digestion repeated. After digestion, the residue was transferred to a 25 mL volumetric flask and the volume was adjusted to the mark with Milli-Q water. All the extractable supernatants were decanted off and retained for analysis of Cu, Pb, Fe and Mn by flame atomic absorption spectrometry (FAAS) (Perkin-Elmer, model 1100). The residue solids were dried for total organic carbon (TOC) measurement using a carbon analyser (Shimadzu, SSM-5000A). Blank samples were analysed in order to monitor contamination from the sample preparation procedure and impurities in the chemical reagents.3.4. Particle analysis by SdFFF-ICP-HRMS
The freeze-dried clay fraction (untreated, Cu treated and Pb treated) and the EDTA extracted pellet (Cu treated and Pb treated) were analysed using SdFFF-ICP-HRMS. The sample was suspended in 0.0005% w/v sodium dodecyl sulfate with 0.0002% w/v sodium azide (50 mg solids in 100 mL solution) and filtered through a glass fibre paper (Whatman, GF/C) to give a nominal particle size of <1.2 µm. SdFFF was performed using a standard instrument as described by Ranville et al.31 (FFFractionation LLC, Utah, USA; model S101). The sample (50 µL containing about 25 µg of solid) was injected directly into the channel. The following power program was used: relaxation 15 min at 700 rpm; t1 5 min; ta 40 min. A Milton Roy ConstaMetricIII metering pump was used to deliver carrier flow at 1.00 mL min−1. Fractograms were obtained by monitoring the absorbance of the eluent at 254 nm using a UV/Vis detector (Spectra 100).The eluent from the SdFFF was fed directly into the ICP torch of an ICP-HRMS (Finnigan, MAT, ELEMENT). By using a T-piece after the UV detector and a peristaltic pump attached to one of the outlets, about 70% of the eluent from the SdFFF flowed into the V-groove nebuliser of the ICP-HRMS. The instrument operated in pulse-counting mode at medium resolution. A mass range of 24–208 u was scanned. The operating conditions of the ICP-HRMS instrument are shown in Table 3. Calibration was achieved using a standard solution containing 100 µg L−1 Mg, 200 µg L−1 Al, 100 µg L−1 Ti, 10 µg L−1 Mn, 200 µg L−1 Fe, 25 µg L−1 Cu and 25 µg L−1 Pb. This standard solution was diluted 2-, 5- and 10-fold to obtain calibration curves for the various elements. In order to correct for noise and drift, the standard solution and the carrier of SdFFF contained 100 µg L−1 Co and 100 µg L−1 Cs. The elemental masses determined were: Mg 23.9850, Al 26.9815, Ti 47.9479, Mn 54.9380, Fe 55.9349, Co 58.9332, Cu 62.9296, Cs 132.9054, Pb 207.9766. The SdFFF carrier solution was analysed before and after each SdFFF run and these signals were used as blanks for subtracting the background signal from the sample run on a sliding linear scale. An in-house QBASIC software program was used to compute the element concentration based on ion currents of standard solutions and to perform element by element drift corrections, noise reduction and data smoothing.
| Forward power/W | 1250 |
| Reflected power/W | <5 |
| Cooling gas flow (Ar)/L min−1 | 13.00 |
| Auxiliary gas flow (Ar)/L min−1 | 1.00 |
| Sample gas flow (Ar)/L min−1 | 0.80 |
| Nebuliser model | Meinhard concentric |
| Measurement mode | Peak jumping |
| Number of sweeps/min−1 | 15 |
| Sample time/s | 0.01 |
4. Results and discussion
4.1. Extractability
The extraction scheme was designed to liberate heavy metals from particular solid phases in the clay fraction.15,32–34 Dilute acetic acid (0.11 M) was used to identify heavy metals associated with acid-soluble phases, such as calcium carbonate, or held on weak adsorption sites. This extractant has been extensively used for the determination of plant available elements in soils from Scotland which tend to be acidic.35 Hydroxylamine hydrochloride (0.1 M) in HCl (pH = 2) identified heavy metals associated with reducible phases. Both procedures were similar to those reported by Davidson et al.36 and Thomas et al.37 for the analysis of river sediments. EDTA (0.05 M, pH = 6) broadly identified metals held in complexed forms or solid phases which dissolve when the cation (e.g., Fe) is strongly complexed. The procedure using EDTA was adapted from Berrow and Reaves.14Aqua regia [3 ∶ 1 v/v concentrated HCl ∶ HNO3] is often used to release most metals in soil and sediment samples, except those in the lattice of very stable silicate and aluminosilicate minerals. The procedure was adapted from Davidson et al.36The effectiveness of various extractants in removing Cu, Pb, Fe, Mn and TOC from the colloidal soil fraction is summarised in Table 4. The soil clay fraction was found to contain quite high Fe and TOC concentrations. The amounts of aqua regia soluble Cu and Pb in the colloidal fraction (<1.4 µm) from the soil treated with those particular metals were 1260 mg kg−1 and 2750 mg kg−1, respectively (see Table 4), whereas the concentrations of these metals in the unfractionated treated soils (i.e., still containing >1.4 µm material) were 280 mg kg−1 and 600 mg kg−1, respectively (Table 1). This demonstrates that the heavy metals added to the soil were concentrated in the clay size fraction.
| Sample | Extractant | Cu | Pb | Mn | Fe | TOC |
|---|---|---|---|---|---|---|
| Untreated | CH3COOH | 4.0 (0.3) | <8 | 300 (12.5) | 0.02 (0.01) | — |
| NH2OH·HCl | 2.0 (0.1) | <8 | 380 (13.5) | 0.29 (0.01) | — | |
| EDTA | 64 (3.0) | 93 (3.0) | 350 (2.3) | 0.52 (0.01) | — | |
| Aqua regia | 108 (1.5) | 170 (7.6) | 1010 (6.5) | 6.5 (0.05) | — | |
| — | — | — | — | — | 14.2 (0.2) | |
| Cu treated | CH3COOH | 105 (4.6) | <8 | 250 (12.2) | 0.02 (0.0) | 0.21 (0.02) |
| NH2OH·HCl | 47 (5.6) | <8 | 440 (24.9) | 0.34 (0.03) | 0.16 (0.01) | |
| EDTA | 1150 (13.0) | 100 (6.6) | 370 (8.5) | 0.54 (0.02) | 2.6 (0.1) | |
| Aqua regia | 1260 (7.6) | 180 (15.9) | 1080 (13.0) | 6.5 (0.1) | 8.3 (0.3) | |
| — | — | — | — | — | 14.2 (0.1) | |
| Pb treated | CH3COOH | 3.2 (0.2) | 91 (5.5) | 310 (2.3) | 0.02 (0.01) | 0.33 (0.03) |
| NH2OH·HCl | 1.6 (0.4) | 220 (8.3) | 410 (6.6) | 0.24 (0.03) | 0.31 (0.02) | |
| EDTA | 70 (11.0) | 2540 (22.7) | 400 (18.0) | 0.54 (0.01) | 2.3 (0.05) | |
| Aqua regia | 108 (1.5) | 2750 (22.5) | 1010 (11.3) | 6.5 (0.2) | 8.6 (0.3) | |
| — | — | — | — | — | 14.1 (0.1) |
The amounts of metals extracted by EDTA were only slightly smaller than those extracted by aqua regia. Up to 91% Cu and 92% Pb were removed by EDTA compared to the values obtained by aqua regia extraction. EDTA removed a much larger proportion of the Cu and Pb from the clay than did acetic acid or hydroxylamine hydrochloride.
Only a small amount of Fe (<10%) was extracted by hydroxylamine hydrochloride and EDTA compared to aqua regia, indicating that most Fe is present in the form of fairly unreactive minerals such as crystalline iron oxides. In contrast, over 30% of the Mn was extracted by acetic acid, hydroxylamine hydrochloride or EDTA compared to aqua regia.
EDTA extracted more Fe than hydroxylamine hydrochloride. It is possible that the strong Fe–EDTA complex causes dissolution of some of the iron hydroxy oxide phases with consequent release of coprecipitated trace metals. Alternatively, EDTA may be more efficient at releasing Fe from strong natural organic matter (NOM) complexes.
In this NOM rich soil sample, EDTA probably extracted a considerable amount of metals complexed with NOM. As indicated above, EDTA would also be expected to extract metals bound within Fe oxides if the EDTA dissolved these phases. However, in this sample, not much Fe was released by EDTA (<10%).
4.2. SdFFF fractograms
The UV detector fractograms of the soil colloids (untreated, Cu treated, Pb treated, Cu treated-EDTA extracted and Pb treated-EDTA extracted) are similar. This indicates that the soil colloid mineral cores were not attacked substantially by the EDTA extraction process, and thus the effect of metal extraction can be readily evaluated by comparing the SdFFF-ICP-HRMS data before and after treatment.4.3. Particle mass- and element-based size distributions
The particle size distribution of the colloidal fraction can be calculated directly from the UV detector fractogram assuming that the UV absorbance is proportional to the particle mass concentration in the eluent [eqn. (4)]. The void peak was removed from the fractogram before calculating the particle size distributions. Element concentration-based size distributions can also be computed using eqn. (5) and the ICP-HRMS ion current data set for each element and each fractogram (normalised, drift corrected, noise reduced and smoothed). The relationship between the particle size distributions and Cu and Pb distributions is shown in Fig. 2. The results indicate that the soil colloids have a smooth monomodal size distribution in the range of about 0.08–0.5 µm with a maximum around 0.2 µm. The Cu- and Pb-based size distributions are similar, although the element and particle distributions are not coincident, showing that there are some changes in composition across the size range of the particles. The metal-based size distributions for the untreated and EDTA extracted metal treated soils are identical showing that all of the added Cu and Pb is stored in a fairly labile form.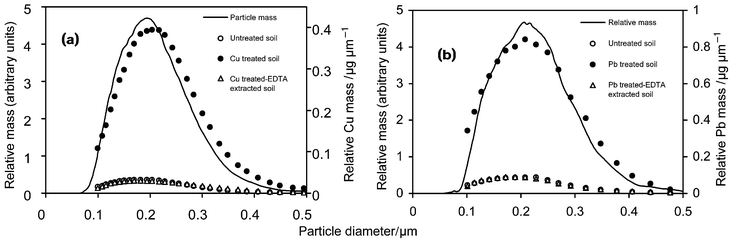 | ||
| Fig. 2 Particle mass-based and element content-based size distributions of soil colloids for (a) Cu treated soil and (b) Pb treated soil. | ||
4.4. Element concentration distributions
The ratio of the element concentrations in the eluent to the UV detector response, which represents the particle concentration in the eluent, gives the composition of a given element in the particles (i.e., mass of element per mass of solid in arbitrary units). The Al, Mg and Ti concentrations plotted against the particle diameter are shown in Fig. 3. The Al/UV ratio distributions for each soil sample are very similar, indicating that EDTA extraction did not remove very much Al from the soil. The trends for Mg/UV and Al/UV are quite similar and show that most of the Mg is in a strongly bound form probably within the mineral lattice. For both Mg/UV and Al/UV there is only a small increase (<15%) over the size range 0.1–0.4 µm. This suggests that there is little change in the major mineral composition with particle size. The slight increase in Al/UV is possibly due to an increase in kaolin which has a relatively high Al content. The X-ray diffraction results show that there is an appreciable amount of kaolin mineral in the clay fraction (Table 5), and kaolin is often found to have a higher concentration in the coarser components of soil clay fractions. There is a much more substantial increase in the Ti/UV concentration distribution, which represents a major change in the proportion of minerals containing Ti. There may be clay minerals containing minor amounts of Ti impurity or small amounts of titanium oxides (e.g., rutile). | ||
| Fig. 3 Element concentration distributions in soil colloids plotted as element concentration from ICP-HRMS/UV detector response versus particle diameter for (a) Al/UV, (b) Mg/UV and (c) Ti/UV. | ||
| All minerals | g kg−1 | Clay minerals | g kg−1 |
|---|---|---|---|
| Quartz | 21 | Illite | 65 |
| Albite | 14 | Kaolin | 104 |
| K-feldspar | 7 | Vermiculite + mica/vermiculite | 468 |
| Goethite | 17 | Chlorite | 13 |
| Dioctahedral clay | 392 | ||
| Trioctahedral clay | 258 | ||
| Total | 709 | 650 |
4.5. Element atomic ratio distributions
Changes in soil colloid chemistry and mineralogy can also be visualised by plotting element atomic ratio distributions. Fig. 4 shows Fe/Al, Mn/Al and Cu/Al atomic ratios from Cu treated soil and the Pb/Al atomic ratio from Pb treated soil plotted against particle size. Since aluminosilicates are a major class of mineral in most soils, Al was chosen as the reference element in the absence of data for Si. | ||
| Fig. 4 Element atomic ratio distributions of soil colloids treated with Cu for (a) Fe/Al, (b) Mn/Al and (c) Cu/Al, and treated with Pb for (d) Pb/Al. | ||
Fig. 4(a) shows how the Fe/Al ratio distributions change with the particle size. The Fe/Al ratio distribution of untreated soil colloids is similar to that of Cu treated soil colloids, whereas the Fe/Al ratios for the EDTA extracted colloids are only slightly lower than those of the untreated soil. This again illustrates that only a very small proportion of iron exists in the form of relatively easily extractable surface coatings of hydrous iron oxides.
The Fe/Al ratios in these soils are higher than those of Australian soil and sediment colloids9,10,38 studied previously, in which Fe/Al atomic ratios were generally between 0.1 and 0.3. The colloidal fraction of the Scottish soil may have contained relatively high concentrations of Fe rich illites and vermiculites. The X-ray diffraction results (Table 5) confirm that there is a high composition of trioctahedral (Fe rich) clay in the sample. The Fe/Al ratio distributions decrease across the entire particle size range. This behaviour probably indicates that there is significant Fe in oxide surface coatings, which leads to an enrichment in the overall Fe concentration in the smaller particles as the surface area increases. However, we cannot discount the possibility that minerals with high Fe/Al ratios, such as illites or vermiculites, may contribute to the trend in Fe content if they are present in larger amounts in the smaller particle size ranges.
The Mn/Al ratio distributions of untreated soil and soils treated with heavy metal salts decrease with an increase in particle size, whereas the Mn/Al ratio for the soil treated with heavy metal with EDTA extraction is almost constant over the whole size range [Fig. 4(b)]. This observation indicates that a part of the Mn present in the colloids is in a surface coating form.
The atomic ratio distributions of Cu/Al and Pb/Al are shown in Fig. 4(c) and Fig. 4(d), respectively. A dramatic increase is observed in the Cu/Al ratio for the Cu treated soil fraction and in the Pb/Al ratio for the Pb treated soil fraction compared to untreated and EDTA extracted soils. This indicates that a significant amount of the added Cu and Pb is still present on the soil particles 8 years after treatment.
4.6. Metal distributions in surface coatings
The ratio of the EDTA extractable metal concentration in the eluent to the UV detector response is directly related to the composition of extractable metal in the particles. The relevant ratio can be calculated by the difference between the extracted and non-extracted samples. The plots of extractable Cu/UV for Cu treated soil and Pb/UV for Pb treated soil are shown in Fig. 5(a). Also plotted is the Fe/UV ratio for the Cu treated soil. The extractable Fe/UV ratio decreases by about a factor of two as the particle size increases from 0.08 to 0.3 µm. The trend of extractable Pb/UV drops from 1.35 to 1.0 (in arbitrary units) as the particle diameter increases from 0.08 to 0.17 µm, then remains nearly constant over the size range 0.17–0.42 µm. These results could indicate that a substantial amount of extractable Fe and Pb is present in surface coatings, most likely as a hydrous oxide or organic complex form. In contrast, an almost constant distribution of extractable Cu/UV is observed over the entire particle size range. | ||
| Fig. 5 (a) EDTA extractable Fe and Cu concentrations in colloids from the soil treated with Cu versus particle diameter; also plotted is the extractable Pb in the Pb treated soil. (b) Corresponding plot of EDTA extractable Fe, Cu and Pb/particle surface area versus particle diameter. (c) Cu and Pb (in coatings)/Fe (in coatings) atomic ratios. “In coatings” corresponds to the EDTA extractable metal content of the soil colloids. | ||
Fig. 5(b) shows the corresponding surface density distributions of the extractable Fe, Cu and Pb calculated by assuming that the particles are spherical. The plots of extractable Fe, Cu and Pb per unit of particle surface area increase substantially as the diameter increases from 0.1 to 0.4 µm. If the particles were spherical, this would suggest that the amount of Fe, Cu and Pb formed denser or thicker coatings around the larger particles than around the smaller particles. Alternatively, the data may indicate that the particle shape deviates dramatically from the spherical model assumed in the calculations. For example, if the dominant shape was a thin plate of constant thickness, then the surface area would increase in proportion to the mass of particles. Thus the metal surface adsorption density distribution would show the same trend as the metal concentration distribution shown in Fig. 5(a).
If we consider the metal to be associated with iron hydroxy oxide coatings, then it is informative to plot the trend in the extractable metal ∶ extractable Fe ratio. This is shown in Fig. 5(c) for both Cu and Pb with the ratios being converted to an atomic (i.e., molar) basis. The metal ∶ Fe atomic ratio increases slightly across the size distribution. Since the Cu ∶ Fe ratio increases to more than 0.5, it seems unlikely that most of the Cu would be coprecipitated with iron hydroxy oxides. It is probably more likely that the Cu is complexed with the large amount of organic matter associated with the particles (TOC = 14.2%). Unfortunately, we could not measure the TOC in the SdFFF eluent and thus could not compute metal ∶ TOC ratio distributions. The Pb ∶ Fe atomic ratio is 0.1–0.2 and it seems feasible that the Pb could be bound in either hydrous iron oxide or organic surface coatings.
5. Conclusions
This study has illustrated the range of information that can be obtained using chemical extraction and SdFFF-ICP-HRMS techniques, and how these methods may be valuable for studying natural soil colloids and their association with metal contaminants. The results show that, even after 8 years, considerable amounts of the added Cu and Pb are still associated with submicrometre sized particles. The hydrous iron oxide and organic matter surface coatings play a significant role in heavy metal adsorption on soil particles. The content of EDTA extractable Pb per unit mass of the particles increases as the particle diameter decreases. However, the amount of EDTA extractable Cu per unit mass of the particles is uniform over the whole size range in this soil. It is likely that Cu is complexed with organic matter, whereas Pb is possibly associated with both organic matter and hydrous oxide iron surface coatings.Acknowledgements
We thank the Scottish Executive Rural Affairs Department (SERAD), the Royal Society, the Australia Research Council and the CRC for Freshwater Ecology for financial support. Bailin Chen received a scholarship from Monash University. We also thank Shona Sellers for isolating the soil clay fractions, Dr Steve Hillier for the X-ray diffraction analysis, Finlay Shanks for assistance with the SdFFF-ICP-HRMS work and Sandra Sdraulig for help with the FAAS determinations.References
- Council of European Communities, Directive Concerning Urban Waste Water Treatment, CEC, Brussels, 1991, Official Journal L135, pp. 40–52. Search PubMed.
- J. F. McCarthy and J. M. Zachara, Environ. Sci. Technol., 1989, 23, 496 CAS.
- R. Kretzschmar, M. Borkovec, D. Grolimund and M. Elimelech, Adv. Agron., 1999, 66, 121 Search PubMed.
- A. Manceau, I. Charlet, M. C. Boisset, B. Didier and L. Spadini, Appl. Clay Sci., 1992, 7, 201 CrossRef CAS.
- J. C. Giddings, Chem. Eng. News, 1988, 66, 33 Search PubMed.
- H. E. Taylor, J. R. Garbarino, D. M. Murphy and R. Beckett, Anal. Chem., 1992, 64, 2036 CrossRef CAS.
- S. Tadjiki, PhD Thesis, Monash University, Clayton, Australia, 2000..
- C. Contado, G. Blo, F. Fagioli, F. Dondi and R. Beckett, Colloids Surf. A, 1997, 120, 47 CrossRef CAS.
- D. M. Murphy, J. R. Garbarino, H. E. Taylor, B. T. Hart and R. Beckett, J. Chromatogr., 1993, 642, 459 CrossRef CAS.
- B. Chen, J. Hulston and R. Beckett, Sci. Total Environ., 2000, 263, 23 CrossRef CAS.
- K. E. Jarvis, A. L. Gray and R. S. Houk, Handbook of Inductively Coupled Plasma Mass Spectrometry, Blackie, London, 1992, p. 380. Search PubMed.
- S. T. Sparkes and L. Ebdon, J. Anal. At. Spectrom., 1988, 3, 563 RSC.
- K.E. Jarvis and J. G. Williams, Chem. Geol., 1989, 77, 53 CrossRef CAS.
- M. L. Berrow and G. A. Reaves, J. Soil Sci., 1985, 36, 31 Search PubMed.
- S. P. McGrath and J. Cegarra, J. Soil Sci., 1992, 43, 313 Search PubMed.
- D. E. Salt, M. Blaylock, N. P. B. A. Kumar, V. Dushenkov, B. D. Ensley, I. Chet and I. Raskin, Bio/Technology, 1995, 13, 468 Search PubMed.
- J. C. Giddings, M. N. Myers, K. D. Caldwell and S. R. Fisher, Methods Biochem. Anal., 1980, 26, 79 Search PubMed.
- J. C. Giddings, Sep. Sci. Technol., 1984, 19, 831 Search PubMed.
- R. Beckett and B. T. Hart, in Environmental Particles, ed. J. Buffle and H. P. van Leeuwen, Lewis Publishers, Boca Raton, FL, 1993, vol. 2, pp. 165–205. Search PubMed.
- R. Beckett and J. C. Giddings, J. Colloid Interface. Sci., 1997, 186, 53 CrossRef CAS.
- P. S. Williams and J. C. Giddings, Anal. Chem., 1994, 66, 4215 CrossRef CAS.
- P. S. Williams and J. C. Giddings, Anal. Chem., 1987, 59, 2038 CrossRef CAS.
- P. S. Williams and J. C. Giddings, J. Chromatogr., 1991, 550, 787 CrossRef CAS.
- J. J. Kirkland, L. E. Schallinger and W. W. Yau, Anal. Chem., 1985, 57, 2271 CrossRef CAS.
- R. Beckett, D. M. Hotchin and B. T. Hart, J. Chromatogr., 1990, 517, 435 CrossRef CAS.
- R. Glentwoth and J. W. Muir, The Soils of the Country Round Aberdeen, Inverurie and Fraserburgh, HMSO, Edinburgh, 1963, p. 371. Search PubMed.
- Food and Agriculture Organisation of the United Nations, World Reference Base for Soil Resources, World Soil Resources Report, 84, International Society of Soil Science, International Soil Reference and Information Centre, and Food and Agriculture Organization of the United Nations, Rome, 1998. Search PubMed.
- E. Filcheva, M. V. Cheshire, C. D. Campbell and D. B. McPhail, Appl. Geochem., 1996, 11, 331 CrossRef CAS.
- C. B. Tanner and M. L. Jackson, Soil Sci. Soc. Am. J., 1947, 12, 60 Search PubMed.
- M. V. Cheshire, C. Dumat, A. R. Fraser, S. Hillier and S. Staunton, Eur. J. Soil Sci., 2000, 51, 497 Search PubMed.
- J. F. Ranville, D. J. Chittleborough, F. Shanks, R. J. S. Morrison, T. Harris, F. Doss and R. Beckett, Anal. Chim. Acta, 1999, 381, 315 CrossRef CAS.
- W. L. Lindsay and W. A. Norvell, Soil Sci. Soc. Am. J., 1978, 42, 421 Search PubMed.
- A. Tessier, P. G. C. Campbell and M. Bisson, Anal. Chem., 1979, 51, 844 CrossRef CAS.
- J. Qian, X. Shan, Z. Wang and Q. Tu, Sci. Total Environ., 1996, 187, 131 CrossRef CAS.
- Bulletin 1, Advisory Soil Analysis and Interpretation, MISR/SAC (Macaulay Institute for Soil Research and Scottish Agricultural Colleges), Aberdeen, 1985, p. 13. Search PubMed.
- C. M. Davidson, R. P. Thomas, S. E. McVey, R. Perala, D. Littlejohn and A. M. Ure, Anal. Chim. Acta, 1994, 291, 277 CrossRef CAS.
- R. P. Thomas, A. M. Ure, C. M. Davidson, D. Littlejohn, G. Rauret, R. Rubio and J. F. López-Sánchez, Anal. Chim. Acta, 1994, 286, 423 CrossRef CAS.
- J. van Berkel and R. Beckett, J. Liq. Chromatogr. Relat. Technol., 1997, 20, 2647 CAS.
Footnote |
| † Presented at the Whistler 2000 Speciation Symposium, Whistler Resort, BC, Canada, June 25–July 1, 2000. |
| This journal is © The Royal Society of Chemistry 2001 |
