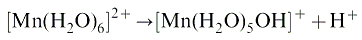Trace element speciation at cell membranes: aqueous, solid and lipid phase effects

Abstract

Biological interest in trace element speciation has tended to be polarised in very different ways according to the concerns of the investigators. Much of the ecological interest has centred on the effects of metal ions in the external environment with the “free metal ion model” dominating discussions of potential toxicity. By way of contrast biochemists have been much more concerned with the stereochemical and kinetic aspects of specificity in metal–protein interactions in the cytoplasm. Separating these two sets of interests are the membrane biophysicists whose studies have concentrated on the channel concept. All three groups have tended to ignore speciation onto the solid phase. In the overall biological context, trace element speciation in the cell is more concerned with kinetics and the evolution of specificity of interaction between diverse ligands than with the conditions for equilibrium.

---

1 Introduction

The relative abundance of the elements, the way that they speciate and the properties of the resultant molecules have largely determined the course of biological evolution. It is clear, however, that unlike the chemical speciations that occur in the inorganic environment those that occur in biological systems are carefully controlled to facilitate some process. Living organisms survive because they direct the type and reactivity of the elements and molecules with which they associate.

In order to appreciate this, imagine a mineral EL₁ that has partly dissolved in an aqueous solution to release the element (E) and its associated ligand (L₁). In this solution is a second ligand L₂ that is also capable of associating with element E. At equilibrium the system would exist as shown in Fig. 1. The free dissociated ion of element E in the environment is shown as E_e.

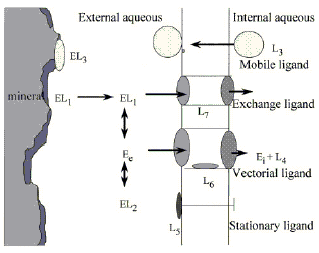Fig. 1 Possible interactions of an element (E) with a variety of ligands (L₁–L₇ ). The element enters the aqueous environment by dissolution of the mineral (EL₁) and dissociates to form a free metal ion (E_e) capable of speciating with other dissolved ligands (EL₂). In the presence of living organisms there may be other ligands released into the system (L₃) that could form biofilms on the mineral, binding the element (EL₃) and potentially removing E from the system by sedimentation. A cell might also produce a membrane bound ligand (L₅) capable of sensing the element E which may also enter the cell through a ion pump (L₆) to be released in the cytoplasm (E_i) where it can speciate onto intracellular ligands (L₄). Alternatively anion transporting channels (L₇) may allow speciated forms of the element (EL₁) direct access into the cell.

Consider what would happen now if an organism that could act as a source of additional ligands (e.g., L₃) resided within this system. Such ligands might be humic acids or bacterial exopolymers and they would raise at least two additional possibilities. First, the biological products might coat the surface of the mineral forming biofilms that interacted with element E resulting in it becoming speciated onto this surface (EL₃). Second, if this particle sedimented out of the aqueous environment there would also be a loss of the surface-bound elements from the system. The system would now have progressed from an equilibrium situation to a kinetically driven state that determined the residence time of the element (E) in the aqueous phase.

This example of the speciation of an element onto a surface and the sedimentation of such an organically coated particle has been used to explain both the composition of the marine environment¹ and the occurrence of geochemical cycling.² It is a powerful argument that when carried to its conclusion provides an explanation for the composition of the extracellular fluids of many organisms since these are thought to reflect the concentrations resulting from such biogeochemical processes.

Let us, therefore, try to complete this model by considering the other speciation effects that a living cell could have on this system. Cells control the type and reactivity of the elements with which they associate. They do this by isolating heterogeneous aqueous compartments within hydrophobic cell membranes. This is achieved by trapping molecules with hydrophilic ligands (L₄) and by synthesizing hydrophobic ligands that become trapped in the membrane itself. These form localised element-sensing molecules (L₅) or vectorial channels containing elaborate structural ligands (L_6, L₇). Various elements become speciated with these ligands and thus segregated from the bulk phase to provide the organisational basis that defines living organisms.

From this brief introduction it will be apparent that the definition of speciation as ‘the occurrence of an element in separate identifiable forms’ effectively requests a review of the whole of inorganic biochemistry and its relationship to biogeochemical cycling. This is an almost impossible remit and in order to introduce some shape into this overview we pose three questions.

(1) Are the laws of inorganic chemistry directly applicable to biological systems? If the operational answer to this question is ‘Yes’ then we have a common starting ground for chemists and biologists. If the answer is ‘No’ then we have to identify how living systems are modified by factors such as nanoscale dimensions or localised energy inputs.

(2) How diverse are the speciation processes that occur in biological systems? This, in effect, questions how many ‘identifiable ligands’ or speciation pathways have to be considered either in the external environment or within the cell. In order to control the types of speciation that have to be discussed we have chosen to base our analysis on a few examples from the different aqueous, mineral and lipid environments that are involved in living systems.

(3) Does this provide a rational context for considering the toxicity of some speciation pathways that might otherwise appear to be disparate phenomena?

2 Are the laws of inorganic chemistry directly applicable to biology?

Speciation refers to the form in which an element is found. It could be in its elemental state, in different oxidation states, as a free ion, an ion pair, a hydrated ion, a covalently bound complex with, e.g., a protein, or it could exist as a crystalline or amorphous solid. In the external environment this speciation will be greatly influenced by random events, such as ligand occurrence or pH changes, but in the cellular environment the process is likely to be much more controlled and specific. In their review of the biological chemistry of the elements da Silva and Williams³ identify a number of factors that are likely to influence the speciation of an element. These are: (1) charge, (2) ion size, (3) donor atom involved, (4) its co-ordination geometry, (5) spin pairing stabilisation and (6) binding in clusters. The interaction of these properties results in a number of general relationships and over the past 50 years biologists have been driven to accept that trace element behaviour in organisms must incorporate these physicochemical approaches. Thus, it is now commonplace for environmentalists to use the classification of metal ions into class “a”, class “b”, and borderline groups⁴ or the grouping of hard, soft and borderline acids and bases.⁵ On this basis they explain their toxicological data.⁶ These two concepts were, however, derived differently and they can not always be applied in a simplistic way especially when steric factors are involved.

The Ahrland, Chatt and Davies basis for class “a” and “b” groups reflects differences in their stability with ligands containing different donor atoms. These increase in the order O > N > S for class “a” and the reverse order for class “b” in accordance with the polarisability of the donor atoms.⁴

The Pearson hard/soft, acid/base theory is based on the concept of a Lewis acid that can accept an electron pair and a Lewis base that can donate an electron pair. A hard acid prefers to bind to a hard base and a soft acid prefers a soft base.⁵

Both systems indicate a relationship between ionic charge (z) and the ionic radius (r), such that z/r relates to the second ionisation potential for the transition of E⁺ to E²⁺.

Like many other biologists we have attempted to test these particular physicochemical approaches to biology by designing experiments intended to question whether these interpretations can be used on living organisms. In such an experiment we have injected pairs of competing metal ions into the blood of the snail (Helix aspersa) and traced the movement of these elements from the blood, across the cell membrane and into the cytoplasm of the digestive gland which is the main site of bioaccumulation. The class “a” metals became attached to pyrophosphate granules in this tissue while the class “b” and borderline metals remained in the cytosol probably associated with metallothionein-like molecules.⁷

Investigating the mineralogy of the phosphatic granules of various invertebrates we discovered that in the crab (Carcinus maenas) these deposits were amorphous calcium phosphate and if moistened with saline they would transform into hydroxyapatite;⁸ a clear example of the Ostwald–Lussac law of sequential solubility.

We have also considered the biological application of the Irving–Williams⁹ series, which is based on the fact that for divalent transition metals the sequence of complex stability is Mn < Fe < Co < Ni < Cu > Zn.

We injected these metals into the haemocoel of the crayfish (Austropotamobius pallipes) and measured the rate at which they were lost from the blood.¹⁰ Plotting the half-lives (t_½ ) for the fast components of this loss gave the series Mn < Fe < Co < Cu > Zn.

This is in keeping with the binding of these metals to some ligand accessible from the blood that reflects the Irving–Williams series.

It appears, therefore, that in all these cases the chemical laws governing the thermodynamic binding of cations are directly applicable to how these elements behave in biological situations. The effects of charge, ion size, and ligand donor group are clearly illustrated and the speciation of these elements follows their interaction with ligands according to the relevant electron structures. This is a sufficient justification for pursuing this analysis further, although as we will see, it may be necessary to reconsider the details when looking at the complexity of some of the events that occur with organic ligands where steric factors may play a dominant role in determining these interactions (Section 3.3.2).

3 How diverse are the speciation processes?

We have already drawn examples from aqueous, mineralogical and membrane-based aspects of biology but it is now worth considering how environmentalists have used these data.

3.1 Speciation in the aqueous environment

The general consensus that has emerged among biologists is that the initial step in the bioaccumulation of elements by an organism in an aqueous environment is dependent upon the speciation of the available elements. There is now an extended set of experimentally determined and computer derived data sets for fresh and seawater samples showing how the presence of extensive speciation of metal ions in these solutions can reduce bioavailability. This is understandable for element E entering a cell according to the scheme shown in Fig. 1 but only if the following assumptions are made.

First, entry of the element into the cell must be proportional to the external activity of the ion [E_e]. It follows from this that other speciated forms of E must be neither lipid soluble (which would give direct entry across the cell membrane), nor associated with any other type of transport of a speciated form (such as EL₁). It is also apparent that [E_e] must not become depleted during the time course of the observations so that the kinetics of speciation, and the rate of diffusion through the unstirred layers on either side of the membrane must not be limiting.

Second, the system shown in Fig. 1 should not be perturbed during the period of observation. In biological systems this condition is commonly violated by the secretion of additional ligands that provide extra speciation pathways (e.g., L₃ could be a siderophore or a mucus secretion produced over the absorbing surface). Alternatively there may be a release of other elements that compete with existing speciation pathways.

Despite all these assumptions there is now an extensive series of experiments with complex saline solutions or hydrophilic chelating agents that provide support for identifying [E_e] as a major factor in determining the uptake of elements from the environment into biological systems. Thus the accepted view of environmentalists is that the biological system is driven by the dissociated free ion (i.e., [E_e] in Fig. 1) and that strong binding or speciation reduces its uptake. This ‘free ion activity model’ (FIAM) has been discussed at length taking specific data from a wide range of biological examples.¹¹ The conclusions are clear. If one ignores lipophilic complexes (such as methyl mercury or tributyl tin¹²) then the driving force in the uptake of metal ions is often the activity of the free ion itself.

The free ion activity model has had a large impact on ecotoxicology and has been very successful at provoking thoughts about the route of uptake of pollutant ions. It is, however, little more than a guideline. Frequently all that it shows is that if you introduce a molecule with very strong thermodynamic binding effects into a sequential series of ligand–ion interactions that strong interaction will dominate the properties of the system.

3.2 Speciation on mineral phases

The mineral phase differs from the aqueous phase by an increase in the way that the ions are ordered in space. In the amorphous state this is limited to short-range effects but in the crystalline form the unit cell is repeated to form structures with long-range order.

Biological minerals are nearly always formed from the aqueous phase and there is often an energy barrier that has to be overcome in order to achieve the ordered packing of ions into the lattice structure. Ions pack best if they are of roughly equal size and the extent to which there is a residual hydration of the ions is determined by the ratio of the radii of the cation and anion. Frequently ions have to lose some of their hydration shells in order to fit into the lattice structure and the initiation of this is facilitated if nucleation sites already exist. Growth is also assisted if these surfaces contain steps in the lattice structure that stabilise the attachment of ions. These step sites are frequently initiated by the speciation of foreign ions that are too large to fit into the regular crystal lattice. Alternatively step dislocations may become blocked by the speciation of foreign ions onto these specific sites of crystal growth. The effects of these interactions are crucial to the appreciation of element speciation into the mineral phase. The use of static simulation of ionic lattices has recently been extended to model a number of phosphate biominerals with good agreement between the calculated and experimental structures.^13,14 Using this method we have calculated the interatomic potentials and lattice energies to determine the effects of ion substitutions. The results rationalise the effects of various ion substitutions on the formation of minerals in biological systems.¹⁵

The Ostwald–Lussac Law states that if minerals can exist in several polymorphic forms then they will tend to precipitate from a solution with the most soluble mineral occurring first and the least soluble last. This is obviously counter-intuitive and it is usually explained in terms of the energetic processes involved with the more soluble phase having a lower solid–solution interfacial tension.¹⁶ Amorphous minerals are often the first type to form from a supersaturated solution. The ions in amorphous solids are irregularly arranged because they may include ions with various degrees of hydration. The transition to more stable (less soluble) crystals involves the subsequent loss of water and interfering ions, as the mineral assumes its more energetically-favourable forms.

Different faces of the crystal may also react to speciating elements in different ways. Thus, if one precipitates calcium carbonate from a simple seawater solution containing sodium and calcium chlorides then the mineral that forms is calcite. If one includes magnesium ions in the solution then aragonite is the mineral that forms. If one uses natural seawater then mineral deposition may be totally inhibited because phosphates block the growth sites.¹⁷ The control over the formation of minerals by speciation of ions onto mineral phases can be crucially important in biology. Many body fluids are supersaturated and there is clearly a need to avoid the precipitation of minerals that would cause kidney stones or ectopic bone.¹⁷

One of the most intriguing examples of the use of the mineral phase in biology is in the excretion of trace elements by incorporating them into amorphous minerals. Virtually all invertebrates possess cells capable of depositing amorphous calcium phosphates of various types.¹⁸ These deposits are effectively phosphate glasses and they obey Zachariesen's rules about the arrangement of cations around the polyhedral anions.¹⁹ Like other glasses they are capable of incorporating a wide range of other elements and the absence of a lattice structure with long-range order clearly facilitates this. Elements that are speciated into these glasses are then expelled from the body as microscopic spheres in the faeces.

3.3 Speciation associated with the membrane phase

3.3.1 Speciation on the membrane surface. Speciation onto the cell membrane may occur in several forms. Free metal ions, of which calcium is the best example, may attach to binding sites and induce a change in cellular behaviour. Two examples will illustrate this. Calcium ions bind to specific proteins in the cell membrane and form cross-links between adjacent cells.²⁰ These intercellular junctions are of different types in different tissues but treatment of many epithelia with chelating agents, such as EDTA, results in a change in the speciation of calcium and a disintegration of the tissue into isolated cells. If calcium ions are returned to the system the cells will re-aggregate and often show specific tissue interactions in the process.

A second type of speciation onto the cell membrane occurs in an even more specific way. In the past few years considerable progress has been made in isolating and cloning an extracellular calcium receptor molecule.²¹ The molecule is most common on cells, such as those of the parathyroid gland, that are intimately involved with calcium metabolism. The bovine protein has a molecular weight of about 120 kDa with an extracellular amino terminal sequence followed by a hydrophobic region which spans the lipid bilayer seven times before terminating with the carboxy end in the cytosol. It is thought that the extracellular sequence contains acidic amino acids capable of folding and thereby forming preferential coordination sites for binding calcium ions. The intracellular region of the protein interacts with regulatory G proteins.²² As a trans-membrane molecule the receptor is able to detect changes in the extracellular fluid and signal these to the intracellular systems. The important feature of this molecule, as far as the present discussion is concerned, is that it is largely specific for calcium and the cell responds to the free ion activity in the extracellular fluid with a directly proportional response.

A final example of metal speciation that occurs onto a cell membrane occurs in the phenomenon of endocytosis. This process involves the uptake of material into a cell by the formation of an invaginated membrane-bound vesicle. The process is facilitated in diverse cells by biofilms or specific opsonins, i.e., substances that bind to the particle surface and induce endocytosis. The significance of this process in the present context is that it introduces the concept of speciation at the solution–solid interface.

We have recently tried to assess the significance of this solid phase interaction by using a phosphatic mineral (hydroxyapatite) and two artificial resin beads. The surface properties of these minerals were characterised using Langmuir adsorption isotherms to measure the adsorption constant (K_L) for ⁶⁵Zn²⁺ and ¹⁰⁹Cd²⁺ ions. These particles were then fed to the mussel (Mytilus edulis) which assimilated them and endocytosed them into the cells of the digestive gland. Animals that were fed particles accumulated more metal than those kept in water-only conditions.²³ In addition they released the contaminant ions into the cytosol of the digestive gland cells according to the log K_L of the particle surfaces.²⁴ These experiments emphasise another feature of importance in speciation onto solid phases in aquatic environments. The speciation in a particle-containing system can clearly be quite different from that occurring in water-only situations and this has major clinical consequences with, for example, the adsorption of ions onto bone minerals. The experiments also highlight the fact that membrane uptake by endocytosis is rapidly followed by the exposure of the particle in the enzyme-rich and low pH conditions of the lysosome and endosome systems. These two processes must involve some of the most extreme speciation conditions in biology.

3.3.2 Speciation and movement across the membrane. If speciation onto the cell membrane appears complex then the events involved in transporting elements through the membrane are even more sophisticated. Most of the cationic channels that have been studied have a high specificity so that it is the free metal ions that can gain access. The specificity is closely regulated in relation to the hydration/dehydration state of the metal ion, its size, and its binding to the channel walls.²⁵ These features are encapsulated in the concept of a channel filter that imposes specificity on the movement of ions through these hydrophilic channels.

A large number of speciation events are involved in these ion movements. The surface of the cell membrane normally carries a negative charge associated with the polar lipids that form the membrane. Consequently there is a diffuse electrical double layer of ions forming the Stern layer for a distance of about 1 nm over the cell surface. The entrance to the channels is often raised above the membrane so that they protrude above the Stern layer and can impose their own ionisation effects upon surrounding ions. This is frequently the first discrimination barrier that determines what enters the channel. Those ions that penetrate further will be hydrated and charged but within the environment of the channel they will be subjected to other speciation effects. Thus, interaction with the walls of these distorted passages can lead to both dehydration and ligand binding. These events are, however, slow compared with the diffusion process and for this reason ions that bind water very tightly (e.g., Ni²⁺, Mg²⁺) could take anywhere between ten and a thousand times longer for the movement through the channel than for diffusion alone. Thus the selectivity process can be a major factor in retarding ion flow and the selectivity process is usually restricted to only a small region of the channel that forms a discriminating filter.²⁶

Mutation of individual amino acids in these structures greatly influences the selectivity of cation movement through the channel and these charged groups are obviously involved in forming the selectivity filter. In the calcium channel the glutamic acid residues are not all in the same state and the pK_a values (7.2–8.0) are dramatically different from most carboxy side chains (pK_a 4.2–4.8). Apparently half the glutamic acid groups in the pore region are not dissociated. Thus, the selectivity filter appears to be a narrow region of the channel (ca. 6 Å diameter) where two of the glutamic acid groups are not ionised and two are deprotonated on each of the four motifs.

The specificity of the channel in permitting calcium ions to move is probably due to: (a) the driving force of a divalent cation coordinated to non-dissociated glutamic acid residues, (b) the possible rotation of the dissociated glutamic acid groups as the ion passes through, and (c) the size of the narrow filter with roughly the same diameter as [Ca(H₂O)₆]²⁺ or [Ca(H₂O)₈]²⁺. Thus both kinetic and thermodynamic properties could be involved with two calcium ions occupying the channel at any one time so that the first is surrounded by ligand oxygen atoms in a heptadentate structure while the second is coordinated by five carboxylate oxygens.²⁷

The calcium channel may change its configuration during voltage-mediated stimulation but many of the other channels in the cell membrane are energised, i.e., they use an energy source (ATP) to pump ions against their electrochemical gradients. This is usually thought to be accomplished by the action of an ATP binding cassette (ABC)²⁸ but the generation of the motive force is still not explained. There are, however, some interesting properties emerging from the study of these systems. Perhaps the most surprising of these is the evidence for some form of co-ordinated interaction²⁹ between cationic and anionic channels, such as Na⁺ and Cl⁻; a phenomenon that if widespread could have some impact on cation–anion interactions.

A second example will make this more explicit. Obligatory, coupled co-transport of sodium, potassium and chloride ions has been reported from nearly every animal cell type. The transport is electrically silent with stoichiometric ratios of 1Na⁺ ∶ 1K⁺ ∶ 2Cl⁻. All of which must coexist simultaneously on the same side of the cell membrane.²⁹ Both binding and release are ordered and must go to completion before transport can occur. This has clear implications in relation to the speciation within the transport protein, i.e., ions that may not be linked in solution need to be involved in these associations during transport.

Metal ions that are bound to various protein species may also initiate very precise responses with the cell membrane. An obvious example of this speciation effect can be seen with the protein transferrin (Tf). This protein is capable of displacing hydroxy ions from their association with ferric ions and therefore solubilizing Fe(OH)₃ that is otherwise extremely insoluble. The transferrin molecule attaches via two metal binding sites onto two ferric ions per molecule.³⁰ Much of the interest in this particular example of speciation relates to the discovery that there is a synergistic binding of bicarbonate ions to form Fe³⁺–CO₃–Tf . It is in this form, where the iron is held between two tyrosines, one histidine, one aspartic acid and a bidentate carbonate, that iron is transported in the plasma of many animals.³¹ Cells access this element by expressing specific transferrin receptors on the cell membrane. The iron–transferrin–receptor complex is then endocytosed into the cell and fused onto an endosome which releases protons into this site. The ensuing loss of the bicarbonate anion causes a release of the iron ion from the ternary complex. Here, therefore we have an example of a protein that is involved in speciation with both a cation metal and an anion radical prior to attaching at specific sites on specific cell membranes. Subsequent destruction of the anion leads to unloading of the transported iron and another change in speciation.

4 Toxicological aspects of speciation at the cell membrane

The examples that have been chosen of speciation of elements in cell biology illustrate the types of information that biochemists use in trying to understand how cells normally function. There are, however, a number of situations where speciation leads to toxic effects and thereby questions our understanding of some of the current concepts.

4.1 The extracellular fluid

The success of the free ion activity model (FIAM) in predicting the way that speciation influences the bioavailability of ions tends to ignore much of the complexity shown in Fig. 1.

As an example consider the elegant work of van Ginneken et al.³² who exposed carp (Cyprinus carpio) to cadmium and zinc in waters that contained a variety of complexing ions. They were able to calculate free ion activities and relate these to the uptake of the contaminating ions into the fish. They found that in the presence of EDTA the uptake was as calculated for the free ion activity but when citrate, glycine or histidine were present the absorption of cadmium was markedly higher than expected. After abandoning the free ion model they suggested that the anions must be transporting the cadmium as a complex. This phenomenon certainly occurs in microbes where there are reports that in a number of bacteria, metals may be carried into the cell as part of a phosphate transport system.³³ This is not a case of counter-ion transport but rather an example of a soluble [MHPO₄] complex being carried through an anionic channel. Clearly speciation of a metal in these circumstances enhances rather than inhibits membrane transport. A similar phenomenon occurs in the green alga Selenastrum capricornutum where the presence of citrate ions facilitates cadmium uptake by apparently transporting the cadmium–citrate complex.³⁴

The question, therefore, arises as to whether such transport of speciated metals could also occur in vertebrates and other extracellular fluids.

If there is evidence for the movement of speciated metals through an anionic channel then the best place to start looking for evidence to support this would be the erythrocyte membrane because of the very dramatic and fast anion exchanges that occur during carbon dioxide transport. In most vertebrates carbon dioxide is not carried in the blood as a dissolved gas. Instead it penetrates into the erythrocyte where the enzyme carbonic anhydrase catalyses its hydration to carbonic acid. The proton from this acid is buffered on the haemoglobin molecule while the bicarbonate ion diffuses rapidly out of the cell in exchange for plasma chloride ions. The bicarbonate/chloride exchange occurs rapidly through an anion exchange channel in the membrane of the red blood cell during its passage around the body and the flux is reversed when it passes through the lungs, releasing carbon dioxide for exhalation.

The concept of ‘anionic cation-transport’ within this system was based on the observation that bicarbonate ions stimulated the passive release of sodium or lithium ions from the human erythrocyte.³⁵ This somewhat curious result took on a more significant status when Wieth³⁶ proposed that it was not the bicarbonate but the [NaCO₃]⁻ ion pair that passed through the anion exchanger of the membrane. There are, of course, only small concentrations of such ion pairs in the blood but such is the capacity of the anion exchanger that it can move ions 10⁶ times faster than normal sodium leakage from the red blood cell.³⁷ Thus it was soon recognised, clinically, that patients with metabolic alkalosis (raised plasma bicarbonate levels) accumulated excess sodium ions in their erythrocytes.³⁸

In order to appreciate the way in which the anionic exchange channel functions in these cases it is necessary to know more about this protein. The anionic exchange protein (also known as band 3 protein) occupies about 25% of the membrane proteins of the red blood cell with about 10⁶ molecules per cell. It is 90–100 kDa in size with 7 membrane spanning domains that act as the HCO₃⁻/Cl⁻ exchange site. The cytosolic domain binds to cytoskeletal proteins and to haemoglobin. The channel appears to act as a ‘ping–pong’ system, i.e., one anion is bound and transported before the other one binds and is transported back. This appears to be the reason why there is an obligatory 1∶1 linkage between the catalytic transfer of the two ions. It is important to note, however, that the exchanger is not regulated by any cell signalling system nor by ATP availability.³⁹ The system has a low specificity so that this channel can also transfer Br⁻, SO₄²⁻ and PO₄³⁻ ions although only when in the form of a single negatively charged complex.

Since the original discovery of the metal transporting ability of the anion exchanger channel there has been considerable interest in the diversity and effectiveness of its activities. The relevant studies have included cadmium, copper, lead and zinc uptake into kidney and red blood cells (Table 1), which are the two tissues with the highest concentrations of the anion exchanger in mammals. With the red blood cell, copper fluxes are driven by increases in the extracellular concentrations of either bicarbonate or chloride ions.⁴⁰ The anion exchanger channel can be blocked by the inhibitor 4,4-diisothiocyanostilbene-2,2-disulfonic acid (DIDS) so that its influence can be separated from those of any other transport systems and this is perhaps the easiest way to assess its significance. It is difficult to interpret the toxicological effects of the uptake of these ions via the anion exchanger. The Cd²⁺ influx into red blood cells is, however, similar in magnitude to the Na⁺ and K⁺ fluxes induced by the Na⁺/K⁺ ion pump and it accumulates in the cell by binding to the metallothionein formed in the erythroblasts.⁴¹ The anion exchange channel is therefore capable of transporting a variety of metal carbonate complexes as monovalent anions so that a variety of pollutant metals enter the cell along this route.

Table 1 Examples of metal transport by the mammalian anion exchange channel^39,40,52,53

Metal	Transported form	Tissue	Uptake by this route (%)
Cd	[Cd(OH)(HCO3)Cl]^−	Kidney	—
	[Cd(OH)(HCO3)2]^−
Cd	As above	Red blood cells	96
Cu	[Cu(OH)2Cl]^−	Red blood cells	80
	[Cu(OH)2HCO3]^−
Pb	[Pb(CO3)Cl]^−	Red blood cells	90
Zn	[Zn(HCO3)2 Cl]^−	Red blood cells	—

---

The anion exchange protein provides a clear example where metal speciation at the cell membrane level may lead to enhanced uptake. There are other examples that suggest other anion transporters may also function to accumulate cationic elements in vertebrate tissues. Thus the monocarboxylate transporter at the blood/brain barrier appears similarly to be involved in transporting aluminium citrate out of the brain across this barrier.⁴²

4.2 Element speciation and the mineral phase

A number of elements, such as cadmium, are known to speciate onto bone mineral and cause diseases³ but here we will concentrate on an unusual phenomenon in which elements speciate into intracellular amorphous minerals and are excreted as encapsulated glasses.⁴³ In studying this phenomenon it was found that manganese became associated with these deposits extremely quickly. Granules extracted from the digestive gland of the snail (H. aspersa), which is the main site of this reaction, showed an unusual rosette structure on their surface.⁴⁴ This was associated with a breakdown in the cellular structure of the associated cells. Electron probe microanalysis and extended X-ray absorption fine structure (EXAFS) studies of the surface rosettes showed that they were composed of manganese phosphate. Elemental analysis of normal and manganese treated granules showed that calcium was displaced by manganese in these deposits. It appears that the hydrated ion [Mn(H₂O)₆]²⁺ enters the cell but dissociates to act as a Bronsted acid:
The proton that is liberated erodes the surface of the granule. This releases phosphates that precipitate on the surface as manganese salts, forming the rosette structures. The calcium that is liberated from the granule overwhelms the calcium regulating system causing cell death. This corrosion of an intracellular granule appears to be a novel biochemical lesion caused by the speciation of an element onto a mineral surface.

4.3 Speciation at the cell membrane

The ability of the lipid bilayer to act as a barrier to hydrophilic molecules is essential to the maintenance of ion gradients within the cell. This is nowhere more important than in the mitochondrion where proton gradients are used to synthesise adenosine triphosphate (ATP) molecules. Thus the speciation of protons in this system can be an extremely important process and underlies one of the best-studied cases of toxicity. The ability of substituted phenols, such as dichlorophenol (DCP), to uncouple electron transport and ATP synthesis has been extensively studied⁴⁵ and is due to the phenoxylate acting as a shuttle to carry protons across the membrane. In the context of the subject of this symposium it is clear that protons can speciate onto the phenoxylate and traverse the membrane as the undissociated complex thereby breaking down the proton gradient. The system is likely to produce toxic effects in two ways either by uncoupling biochemically important gradients (as in this chemiosmotic example) or by providing an access route for other undissociated acids. This latter phenomenon is important in systems, such as the fish gill, where respiratory exchange can cause considerable pH changes in the boundary layer⁴⁶ and where QSAR studies have shown that any change in water pH can have large effects upon the uptake of chlorophenols.⁴⁷

5 Conclusions

To a biologist the chemical principles that affect the speciation of chemicals in inorganic aqueous environments appear to be well understood in terms of element size, charge and types of interactions. Unfortunately such biologists are forced to deal with living non-equilibrium systems that manipulate the concentrations of the reactants using ligands with extremely complex stereochemical properties. Nowhere is this more apparent than in studies on cell membranes.

Three aspects of the manipulation of element speciation in biological systems are worth emphasising. The first is the sophistication of the ligands that are involved. Diatoms can release chelates that stimulate their growth by depressing the availability of toxic metals (e.g., copper) or accessing insoluble iron. Such siderophores can remove iron from artificial chelates, such as EDTA,⁴⁸ and effect their transfer across cell membranes. Clearly organisms that can modify their extracellular sites in such powerful ways are not passive inhabitants and may dominate other free-living cells.^48,49 Interactions with channel proteins show similar precise structural and chemical features that may be further enhanced where phosphorylation also enables allosteric movements. Thus ecotoxicologists should place more emphasis on sequential ligand–ion interaction models (SLIM) rather than the free ion activity model (FIAM) that conceals as much as it reveals. The whole existence of cells depends upon their ability to exist in a different situation from that of their environment and this in turn depends upon some sort of control system. This control of the elements is exercised by manipulating their speciation.⁵⁰ The free ion activity model simply emphasises the chemistry of the elements at one extreme of the data set. Where living systems are involved the cell has utilised a variety of ligands, their stereochemical properties and the barrier of the lipid bilayer to exploit the kinetics of speciation in a structural context.

Structural aspects are also involved in a second aspect of biological systems. Many cellular systems use mineral solid phase changes to manipulate element speciation. Thus cells can both dissolve and induce minerals on either side of the cell membrane with remarkable control over the composition, and crystallographic or amorphous form. The examples of magnetite formation in bacteria, silica deposition in foraminifera or sponges and the secretion of calcareous or phosphatic shells with strict crystallographic orientations are models of sophisticated speciation and nanotechnology.⁵¹ Manipulation of phase changes is, therefore, another aspect of element speciation in biology.

Finally it is worth emphasising the use of vesicles in biological systems. Membrane enclosed spaces often of nanometer size are commonplace in cells. Some, such as the derivatives of the endoplasmic reticulum, can accumulate, store or release calcium ions and act as major signalling systems. Other vesicles, such as the endosomes and lysosomes, are associated with proton pumps capable of changing the pH of the vesicle contents by up to two units within seconds of them being formed. These compartmentalised systems are frequently used to manipulate the speciation of a variety of elements within the cell. It is the stereochemical properties of these interactions that produce the kinetic effects and add so much to the complexity of speciation of elements in biological systems.

References

1. R. D. Cherry, J. J. W. Higgo and S. W. Fowler, Nature, 1978, 274, 246.
2. M. Whitfield, Interdiscip. Sci. Rev., 1981, 6, 12.
3. J. J. R. F. da Silva and R. J. P. Williams, The biological chemistry of the elements: the inorganic chemistry of life, Clarendon Press, Oxford, 1991..
4. S. Ahrland, J. Chatt and N. R. Davies, Q. Rev. Chem. Soc., 1958, 12, 265.
5. R. G. Pearson, J. Am. Chem. Soc., 1963, 25, 3533.
6. (a) E. Nieboer and D. H. S. Richardson, Environ. Pollut. Ser. B, 1980, B1, 3; (b) E. Nieboer, G. G. Fletcher and Y. Thomassen, J. Environ. Monit., 1999, 1, 1.
7. K. Simkiss, J. Exp. Biol., 1981, 94, 317.
8. K. Simkiss and M. G. Taylor, J. Mar. Biol. Assoc. UK, 1994, 74, 459.
9. H. Irving and R. J. P. Williams, J. Chem. Soc., 1953, 3192.
10. R. Lyon, M. G. Taylor and K. Simkiss, J. Exp. Biol., 1984, 113, 19.
11. P. G. C. Campbell, in Metal Speciation and Bioavailability, ed. A. Tessier and D. R. Turner, IUPAC–John Wiley, Chichester, 1995, pp. 45–102..
12. E. Pelletier, in Metal Speciation and Bioavailability, ed. A. Tessier and D. R. Turner, IUPAC–John Wiley, Chichester, 1995, pp. 103–148..
13. M. G. Taylor, K. Simkiss, M. G. Drew, P. C. H. Mitchell and M. Leslie, Mol. Simul., 1992, 9, 129.
14. M. G. Taylor, K. Simkiss and M. Leslie, J. Chem. Soc., Faraday Trans., 1994, 90, 641.
15. K. Simkiss and M. G. Taylor, J. Exp. Biol., 1994, 190, 131.
16. W. Stumm and J. J. Morgan, Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters, John Wiley and Sons, New York, 3rd edn., 1995..
17. (a) K. Simkiss, Nature, 1964, 201, 492; (b) K. Simkiss, Biol. Rev., 1964, 39, 487.
18. K. Simkiss, Bull. Inst. Oceanogr., 1993, 14(Spec), 49.
19. W. H. Zachariasen, J. Am. Chem. Soc., 1932, 54, 3841.
20. R. O. Hynes, Trends Biochem. Sci., 1999, 24, M33.
21. S. C. Herbert and E. M. Brown, Curr. Op. Cell Biol., 1995, 7, 484.
22. D. Riccardi, Cell Calcium, 1999, 26, 77.
23. N. Davies and K. Simkiss, J. Mar. Biol. Assoc. UK, 1996, 76, 1073.
24. N. Davies, M. G. Taylor and K. Simkiss, Environ. Pollut., 1997, 96, 179.
25. B. A. Wallace, BioEssays, 2000, 22, 227.
26. D. A. Doyle, J. M. Cabral, R. A. Pfuetzner, A. Kuo, J. M. Gulbis, S. L. Cohen, B. T. Chait and R. MacKinnon, Science, 1998, 280, 69.
27. G. Varadi, M. Strobeck, S. Koch, L. Caglioti, C. Zucchi and G. Palyi, Crit. Rev. Biochem. Mol. Biol., 1999, 34, 181.
28. B. Holland and M. A. Blight, J. Mol. Biol., 1999, 293, 381.
29. M. M. Reddy, M. J. Light and P. M. Quinton, Nature, 1999, 402, 301.
30. R. R. Crichton, Inorganic Biochemistry of Iron Metabolism, Ellis Horwood, New York, 1991..
31. W. R. Harris, A. M. Cafferty, S. Abdollahi and K. Trankler, Biochim. Biophys. Acta, 1998, 1383, 197.
32. L. van Ginneken, M. J. Chowdhury and R. Blust, Environ. Toxicol. Chem., 1999, 18, 2295.
33. H. W. van Veen, T. Abee, G. J. Kortstee, W. N. Koninge and A. J. Zehnder, Biochemistry, 1994, 33, 1766.
34. O. Errecalde, M. Seidl and P. G. C. Campbell, Water Res., 1998, 32, 419.
35. O. Wieth and J. Funder, Scand. J. Clin. Lab. Invest., 1965, 17, 399.
36. O. Wieth, J. Physiol., 1970, 207, 581.
37. B. F. Becker and J. Duhm, J. Physiol. (London), 1978, 282, 149.
38. J. Funder and O. Wieth, Scand. J. Clin. Lab. Invest., 1974, 34, 49.
39. J. O. Alda and R. Garay, Am. J. Physiol., 1990, 259, C570.
40. M. Lou, R. Garay and J. O. Alda, J. Physiol. (London), 1991, 443, 123.
41. K. Tanaka, S. Min, C. Onosaka, C. Fukuhara and M. Ueda, Toxicol. Appl. Pharmacol., 1985, 78, 63.
42. D. C. Ackley and R. A. Yorke, Toxicology, 1998, 127, 59.
43. K. Simkiss and M. G. Taylor, J. Exp. Biol., 1994, 190, 131.
44. M. G. Taylor, K. Simkiss, G. N. Greaves and J. Harries, Proc. R. Soc. London, Ser. B, 1988, 234, 463.
45. S. G. A. McLaughlin and J. P. Dilger, Physiol. Rev., 1980, 60, 825.
46. D. Randall, H. Lin and P. A. Wright, Physiol. Zool., 1991, 64, 26.
47. M. A. Anderson and F. M. M. Morel, Limnol. Oceanogr., 1982, 27, 789.
48. T. P. Murphy, D. R. S. Lean and C. Nalewajko, Science, 1996, 192, 900.
49. E. D. Wienberg, Physiol. Rev., 1984, 64, 65.
50. R. J. P. Williams, Philos. Trans. R. Soc. London, Ser. B, 1981, 294, 57.
51. K. Simkiss and K. M. Wilbur, Biomineralization, Cell Biology and Mineral Deposition, Academic Press, San Diego, CA, 1989, p. 43..
52. T. Endo, O. Kimura and M. Sakata, Pharmacol. Toxicol., 1998, 82, 230.
53. T. J. B. Simons, J. Physiol. (London), 1986, 378, 287.

---

Footnotes

† Presented at the Whistler 2000 Speciation Symposium, Whistler Resort, BC, Canada, June 25–July 1, 2000.

‡ Present address: 170 Ashwood Lane, Braselton, GA 30517, USA. E-mail: knsimkiss@aol.com

---