Monitoring cyclical air/water elemental mercury exchange†‡§
Nicholas T. Loux
Ecosystem Research Division, National Exposure Research Laboratory, U.S. Environmental
Protection Agency, 960 College Station
Road, Athens, GA 30605, USA. E-mail: loux.nick@epa.gov
First published on 13th July 2001
Abstract
Previous experimental work has demonstrated that elemental mercury evasion from natural water displays a diel cycle; evasion rates during the day can be two to three times evasion rates observed at night. A study with polychlorinated biphenyls (PCBs) found that diurnal PCB air/water exchange rates exceeded nocturnal exchange rates by 32%. Given that the exchange rates of both PCBs and elemental mercury are dominated by the resistance in the aqueous thin film at the air/water interface and that water column elemental mercury concentrations in natural water bodies also display a diel cycle (and water column PCB concentrations do not) the findings here suggest that PCBs can serve as a tracer to assess the relative contribution of diel atmospheric temperature variations on elemental mercury air/water exchange rates. Using previously published data describing water column elemental mercury concentrations and the previously published diel mercury evasion model, four evasion scenarios are examined within the context of monitoring air/water toxicant exchange: constant atmospheric temperatures and constant water column elemental mercury concentrations; variable atmospheric temperatures and constant water column elemental mercury concentrations; constant atmospheric temperatures and variable water column elemental mercury concentrations; and variable atmospheric temperatures and variable water column elemental mercury concentrations. A scenario of monthly elemental mercury air/water exchange also is examined (at constant atmospheric and water column elemental mercury concentrations). Some of the findings include: (1) atmospheric temperature variations do have a significant effect on air/water toxicant exchange; (2) diel atmospheric temperature variations become more significant to overall diel toxicant exchange rates the closer the air/water system is to equilibrium conditions; (3) for refractory toxicants, average diel exchange rates are best estimated by averaging datasets obtained over a 24 h period or, at minimum, by measuring exchange rates at average atmospheric temperature values; (4) for elemental mercury, variable diel water column concentrations are likely to be the dominant contributor to variations in diel evasion rates; (5) diel atmospheric temperature variations amplify the magnitudes of both diel mercury evasion and absorption events and can shift maximum evasion rates to later in the day; (6) variations in monthly elemental mercury air/water exchange rates may exceed diel variations; and (7) 24 h and monthly monitoring efforts will likely be required to accurately describe diel and annual elemental mercury air/water exchange in a given system.
Introduction
Many environmentally significant toxicants experience atmospheric transport as a major mechanism of environmental dispersal. This phenomenon may lead to both contamination of pristine ecosystems via deposition from the atmosphere and to transport of contaminants away from heavily polluted areas. Evidence is emerging that these contaminants display a diel cycle in observed rates of air/surface exchange. For example, the rate of elemental mercury evasion from natural waters has been observed to vary by a factor of 2–3 when day time evasion rates are compared with night time values.1–4 Thirty-two percent differences between diurnal and nocturnal air/water exchange rates for polychlorinated biphenyls (PCBs) also have been reported in the literature.5,6 Finally, studies on diel atmospheric concentrations of elemental mercury7 and five organochlorine pesticides and polychlorinated naphthalenes8 demonstrated that peak atmospheric concentrations of these compounds can be coincident with peak atmospheric temperatures. Although the origin(s) of the observed organic compounds in this last study were not necessarily definitively established, it is not unreasonable to believe that aquatic systems may have been significant sources.One can classify those contaminants exhibiting significant air/water exchange into the categories of reactive and refractory contaminants. For example, water column elemental mercury concentrations have been observed to display peak concentrations during periods of maximum sunlight intensity.9–11 Hence, given that simultaneous abiotic and biotic12 oxidation and direct (or indirect) reductive processes can yield an instantaneous steady state distribution between the elemental and ionic forms of mercury in the water column, mercury is a reactive contaminant. Persistent toxicants resistant to abiotic and biotic degradation phenomena do not exhibit dynamic species alteration in a given 24 h period and these compounds can be considered to be refractory. This distinction is being made because it will be demonstrated that diel air/water exchange rates are sensitive to diel speciation behavior.
A model has been developed13 that describes
the effects of atmospheric temperature variations on diel air/water exchange
of environmental elemental mercury. The model provides a method for extending
isothermal Henry's law constants to non-isothermal air/water temperature
conditions and accounts for the effects of diel atmospheric temperature variations
on the transport properties of the thin aqueous layer that regulates air/water
elemental mercury exchange. Using a constant water column elemental mercury
concentration scenario, previous findings from the model suggested that the
rate of elemental mercury evasion could vary by as much as 44% under
real world diel atmospheric temperature conditions (the daily atmospheric
temperature range examined in the study was 20 ± 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C).
°C).
This previous work will be extended to include the effects of variations in diel water column elemental mercury concentrations (using data published by Krabbenhoft et al.).11 An examination of the possible similarities between the expected air/water exchange behavior of elemental mercury and PCBs will be performed. Finally, an assessment of the effects of diel and monthly temperature variations and diel cycles in water column elemental mercury concentrations within the context of monitoring trace contaminant air/water exchange will be conducted.
Methods
Modeling exchange under quiescent conditions
Rates of vapor exchange between the atmosphere and underlying waters under quiescent conditions can be estimated using the two layer model:14,15 | (1) |
The concentration terms in eqn. (1)
represent analytical concentrations (ng m−3)
of the compound of interest in the aqueous and atmospheric phases. The mass
transfer coefficients (katm and kaq)
are compound specific (values for elemental mercury at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C
are 9 and 0.09 m h−1, respectively4)
and represent the molecular diffusivity in each phase divided by the thicknesses
of the thin atmospheric and aqueous films at the air/water interface.
°C
are 9 and 0.09 m h−1, respectively4)
and represent the molecular diffusivity in each phase divided by the thicknesses
of the thin atmospheric and aqueous films at the air/water interface.
The Henry's law constant defines the equilibrium partitioning of a compound between the atmospheric and aqueous phases and is defined by the expression:
 | (2) |
In a rigorous sense, the Henry's law constant is determined by extrapolation to zero concentration in both phases. Given that elemental mercury saturation concentrations in both phases under environmental temperature conditions are far less than even 1 mol% in either of the two phases, the Henry's law constant will be assumed to remain independent of concentration for the purposes of the present work.13
Diel variations in non-isothermal Henry's law constants and aqueous thin layer mass transfer coefficients
With sparingly soluble, low vapor pressure compounds (at environmental temperatures), relatively constant Henry's law constants can be calculated from experimental data by dividing the saturation atmospheric vapor pressure by the saturation aqueous solubility (at the same temperature). Although these determinations are conventionally conducted under isothermal conditions, findings from an analysis of Henry's law constants13 indicated that non-isothermal Henry's law constants also can be estimated by dividing the saturation atmospheric vapor concentration (at the atmospheric temperature) by the saturation aqueous phase concentration (at the aqueous temperature). In effect, the concept of equivalence of chemical potentials in each phase can be extended to temperature disequilibrium conditions. Secondly, it was demonstrated that non-isothermal Henry's law constants can significantly differ from isothermal values under the temperature disequilibrium conditions likely to be found in the environment.13 In the following simulations, isothermal and non-isothermal Henry's law constants for elemental mercury will be estimated using a previously published expression16 for temperature sensitive aqueous elemental mercury solubilities and a temperature sensitive atmospheric elemental mercury vapor pressure equation derived13 from experimental data.17A second effect of air/water temperature disequilibrium on estimated elemental mercury evasion rates from natural waters was the effect of temperature disequilibrium on the transport properties of the thin aqueous layer that dominates elemental mercury air/water exchange. Given that the diffusivity of heat in water can exceed molecular diffusivities by a factor of 100,18 it was suggested13 that the temperature of the thin aqueous layer at the air/water interface was more likely to equal the atmospheric value under temperature disequilibrium conditions (under conditions of very low wind speeds and/or near 100% relative humidity). It was also suggested13 that the aqueous thin layer viscosity was the most significant transport variable subject to the effects of air/water temperature disequilibrium. Finally, in accord with previously published work, it was assumed that the thickness of the thin diffusive layer did not change with interfacial temperature.13,18
Using the Othmar Thakur equation, an expression was developed13
that relates diffusivity based aqueous thin film mass transfer coefficients
at one temperature (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C) to that at another temperature
using relative aqueous viscosities. The aqueous phase mass transfer coefficient
for elemental mercury at a second temperature (T) can be
related to the aqueous phase mass transfer coefficient at 20
°C) to that at another temperature
using relative aqueous viscosities. The aqueous phase mass transfer coefficient
for elemental mercury at a second temperature (T) can be
related to the aqueous phase mass transfer coefficient at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C (T = 20)
by the following expression:
°C (T = 20)
by the following expression:
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C
and T.
°C
and T.Expressions suitable for estimating aqueous viscosity as a function of
aqueous temperature have been previously published (see ref. 17 and references cited therein) and are
given below: for 0–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C (η in cP)
°C (η in cP)
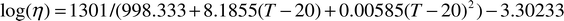 | (4a) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C:
°C: | (4b) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C; i.e., 1.002 cP).
°C; i.e., 1.002 cP).Diel variations in atmospheric temperature and water column elemental mercury concentrations
Krabbenhoft et al.11 published data on water column dissolved gaseous mercury concentrations and environmental conditions at a location in the Florida Everglades (USA). The first half of Table 1 displays an expression suitable for estimating the atmospheric temperature at the site as a function of the time of day. This expression is identical to one previously published13 except that the value of the mean daily atmospheric temperature has been increased from 20 to 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. Given the proximity
of the area sampled by Krabbenhoft et al.11
to the simulated location in the earlier work,13
the daily range in atmospheric temperatures also will be assumed to be the
mean value ± 5
°C. Given the proximity
of the area sampled by Krabbenhoft et al.11
to the simulated location in the earlier work,13
the daily range in atmospheric temperatures also will be assumed to be the
mean value ± 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C.
°C.
| a Unless otherwise noted, all data is from the March, 1996 results reported by Krabbenhoft et al.11. The fifth order polynomial fit to diel water column elemental mercury concentrations was performed using in-house software at the US EPA Laboratory in Athens. | |
|---|---|
Taq = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C °C | |
Tatm = 25 ± 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C °C | |
| Tatm,hourly = 25 + 5 × sin(h × 15 + 195) | |
| (h = 0–24; modified from ref. 13) | |
| [Hg0]atm = 1.5 ng m−3 | |
| [Hg0]aq,average = 16.8 pg L−1 | |
| [Hg0]aq,hourly = 0.00043678h5 − 0.02165706h4 + 0.3360005h3 − 1.655209h2 + 1.948715h + 7.178558 | |
| (pg L−1; h = 0–24; r = 0.943). |
To account for the effects of diel water column elemental mercury concentrations on diel mercury evasion rates, a fifth order polynomial fit to Krabbenhoft et al.'s dissolved gaseous mercury data11 from the Florida Everglades site was performed. This polynomial will be used to estimate dissolved gaseous mercury concentrations as a function of time of day in subsequent simulations. The coefficients for the fifth order polynomial are given in the second half of Table 1.
Summary of assumptions and modeling scenarios
All of the modeling scenarios in the present work include one or more of the following assumptions: (1) all aqueous dissolved gaseous mercury data developed by Krabbenhoft et al.11 represent aqueous elemental mercury concentrations; (2) the average atmospheric elemental mercury concentration is 1.5 ng m−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 and remains constant within the time period under
investigation; (3) the aqueous thin film temperature equals the atmospheric
temperature; (4) the aqueous thin film thickness remains constant; (5)
the mean atmospheric temperature in the diel simulations equals the aqueous
value of 25
11 and remains constant within the time period under
investigation; (3) the aqueous thin film temperature equals the atmospheric
temperature; (4) the aqueous thin film thickness remains constant; (5)
the mean atmospheric temperature in the diel simulations equals the aqueous
value of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C given by Krabbenhoft et al.11
and the daily atmospheric temperature range is 25 ± 5
°C given by Krabbenhoft et al.11
and the daily atmospheric temperature range is 25 ± 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C;
and (6) the aquatic temperature does not vary significantly during the
24 h modeling period.
°C;
and (6) the aquatic temperature does not vary significantly during the
24 h modeling period.Four air/water toxicant exchange scenarios will be examined in this work: (1) exchange under constant atmospheric temperature and constant water column elemental mercury concentration conditions; (2) exchange under constant atmospheric temperature and variable water column elemental mercury concentration conditions; (3) exchange under variable atmospheric temperature and constant water column elemental mercury concentration conditions; and (4) exchange under variable atmospheric temperature and variable water column elemental mercury concentration conditions.
The first scenario is perhaps what has been traditionally done with limited available data. The second scenario represents the traditional explanation for observed diel cycles in elemental mercury evasion rates. The third scenario is what can be expected for diel cycles in refractory toxicant air/water exchange. The fourth scenario best represents what can be expected with a dynamic reactive contaminant (mercury).
Results
Fig. 1 illustrates a comparison between the previously published dissolved gaseous mercury data from water samples obtained in the Florida Everglades11 and the fifth order polynomial fit to the data generated with in-house statistical software at the US EPA Laboratory in Athens (the coefficients for the polynomial are listed in Table 1). In a critique of the experimental data, it was suggested19 that any bias in these data (if a bias existed) was likely to be on the low side. The reader can see that the polynomial fit reasonably represents the data over a 24 h period. The reader should note that there was a rearrangement of the order of the data in order to start at hour 00:00 and to continue to 24:00.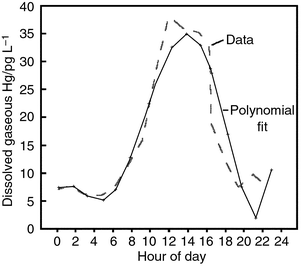 | ||
| Fig. 1 Comparison of a fifth order polynomial estimate to water column dissolved gaseous mercury data obtained by Krabbenhoft et al.11 from the Florida Everglades. | ||
Fig. 2 displays estimated atmospheric
temperatures, aqueous viscosities, non-isothermal Henry's law constants
and aqueous phase mass transfer coeffcients for the modeled system over a
24 h period. The non-isothermal Henry's law constants were generated
assuming an aqueous temperature of 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C and an atmospheric temperature
range of 20–30
°C and an atmospheric temperature
range of 20–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C.
°C.
 | ||
Fig. 2 Dependence of non-isothermal
Henry's law constants, aqueous layer mass transport coefficients and
aqueous thin layer viscosities on atmospheric temperatures over a 24 h
period (aquatic temperature remains constant at 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C in these
simulations). °C in these
simulations). | ||
The aqueous thin film mass transport terms illustrated in Fig. 2 were generated using aqueous viscosity values at the atmospheric temperatures and eqn. (3). Although not clearly discernable in the profile, the aqueous thin film mass transport terms varied by approximately 15% (with a maximum value occurring at hour 17).
Fig. 3 illustrates the estimated evasion rates under all four scenarios as a function of the time of day. For the purpose of improving reader clarity, the signs of the flux terms have been reversed in this figure (i.e., positive flux values designate evasion to the atmosphere and negative terms designate aqueous absorption). The flat horizontal line representing an evasion rate of approximately 1.24 ng m−2 h−1 is what is obtained under constant atmospheric temperature and elemental mercury concentration conditions. These findings correspond to what is commonly obtained in estimating trace toxicant air/water exchange with limited data.
 | ||
| Fig. 3 Comparison of the results from four elemental mercury air/water exchange modeling scenarios (1, constant atmospheric temperatures and water column elemental mercury concentrations; 2, constant elemental mercury concentrations and variable atmospheric temperatures; 3, constant atmospheric temperatures and variable aqueous elemental mercury concentrations; and 4, variable atmospheric temperatures and aqueous elemental mercury concentrations) for predicting elemental mercury evasion from the Florida location over a 24 h period. | ||
The mildly sinusoidal curve (with diamonds) in Fig. 3 corresponds to what would be expected for a refractory contaminant under constant water column concentration and variable atmospheric temperature conditions. This curve is comparable to that previously published.13
The curve in Fig. 3 with plus marks corresponds to simulations with variable water column elemental mercury concentrations and constant atmospheric temperature. This curve is consistent with the traditional variable water column elemental mercury concentration hypothesis that has been extended to explain previously observed diel elemental mercury evasion rate variations of a factor of two to three.
The final curve in Fig. 3, the curve
with triangles, represents the results from simulations including variable
water column elemental mercury concentrations and variable atmospheric temperatures.
In contrast to the curve including only variable water column elemental mercury
concentrations, this curve displays increases in the magnitudes of both aqueous
evasion and absorption of elemental mercury. Only when the atmospheric and
aquatic temperatures are equal (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C; at hours 11 and 23)
do this and the previously discussed curve yield identical estimates of mercury
evasion rates.
°C; at hours 11 and 23)
do this and the previously discussed curve yield identical estimates of mercury
evasion rates.
Both of the air/water exchange curves incorporating variable water column elemental mercury concentrations in Fig. 3 illustrate high to very high calculated rates of evasion at hours 23:00 and 24:00. These results illustrate what can happen when an empirical model (i.e., the fifth order polynomial fit to the water column elemental mercury concentration data published by Krabbenhoft et al.)11 is used outside of the range of the experimental data used to generate the model. Specifically, the data used to develop this polynomial had a maximum time of day of approximately 22.7 h.
Discussion
Two assumptions incorporated into the models used to develop the data displayed in Fig. 3 include constant atmospheric elemental mercury concentrations and constant water column temperatures. Published data for diel and annual atmospheric gaseous mercury concentrations suggest that atmospheric mercury concentrations are strongly dependent on meteorological phenomena. Although peak atmospheric mercury concentrations may occur at night and/or during the summer or winter seasons,20,21 the relative variation in atmospheric mercury concentrations is significantly less than what is observed in water. For example, diel water column dissolved gaseous mercury concentrations in the Florida Everglades were observed to range from 6 to 38 pg L−1,11 diel atmospheric gaseous mercury ranged from approximately 1.4 to 1.7 ng m−3 during the winter and from 1.8 to 2.2 ng m−3 in the summer in another study (in another locale).21 Specifically, at sites with near background atmospheric elemental mercury concentrations, variations in water column dissolved gaseous mercury concentrations are likely to be of a greater magnitude and hence, more significant than atmospheric elemental mercury concentration variations in modeling elemental mercury air/water exchange. Atmospheric elemental mercury concentrations at (or adjacent to) contaminated sites could conceivably display significantly greater concentration variations; therefore, empirical models (such as a fifth order polynomial similar to the one used to model aqueous concentrations) may be required to develop acceptable air/water exchange models for these systems.Given the differences in specific heat between water and solid surfaces
that heat air, air is more likely to display greater temperature variations
over a 24 h period. One study22 at
a river in Canada found that over a 3 d period, the atmospheric temperature
ranged from approximately 16.8 to 27.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C and the temperature in
the underlying river ranged from approximately 22.6 to 25.3
°C and the temperature in
the underlying river ranged from approximately 22.6 to 25.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C.
This aqueous temperature range of approximately 2.7
°C.
This aqueous temperature range of approximately 2.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C is a significant
fraction of the atmospheric temperature range of 11.1
°C is a significant
fraction of the atmospheric temperature range of 11.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C; however,
the vapor pressure of elemental mercury is much more sensitive to temperature
than the aqueous solubility. Because of these observations, non-isothermal
Henry's law constants (and air/water exchange rates) are likely
to display a greater sensitivity to diel atmospheric temperature variations
than aqueous temperature variations in the same environment.
°C; however,
the vapor pressure of elemental mercury is much more sensitive to temperature
than the aqueous solubility. Because of these observations, non-isothermal
Henry's law constants (and air/water exchange rates) are likely
to display a greater sensitivity to diel atmospheric temperature variations
than aqueous temperature variations in the same environment.
The results from the variable atmospheric temperature and water column elemental mercury concentration scenario displayed in Fig. 3 predict exchange rates ranging from approximately 3.5 to −0.3 ng m−2 h−1. Including a variable atmospheric temperature term increases the predicted duration of the nocturnal absorption event, enhances the maximum rates of evasion and absorption, and shifts the time of peak evasion to later in the day. Experimental mercury flux chamber findings from a river in Canada22 illustrated evasion during the day, absorption during the night, and magnitudes of evasion and absorption of approximately 1 and −0.5 ng m−2 h−1, respectively. Significantly, as observed in the simulations with scenario 4, the period of maximum evasion was observed to be later in the day. Given that flux chambers can yield estimated fluxes only one-third of estimates derived from presumably more accurate micro-meteorological procedures,23 and given the geographic differences between the two locales, the simulated results in Fig. 3 are at least in qualitative agreement with the experimental results obtained from the Canadian river.
The curves depicted in Fig. 3 illustrate that modeling approaches using constant atmospheric temperatures and water column elemental mercury concentrations can miss both episodes of maximum elemental mercury evasion and even brief periods of water column elemental mercury absorption (at near background sites). However, all four scenarios predict net average elemental mercury evasion; this finding supports current theories of global air/water mercury cycling mediated by aqueous elemental mercury evasion, oxidation of atmospheric elemental mercury to ionic mercury, and subsequent surface deposition of atmospheric ionic mercury.
Published evasion data for PCBs5 may be particularly suitable for considering PCBs to be a “refractory” surrogate for elemental mercury. For example, the following properties for Aroclor 1260 have been published:24kaq = 0.013 m h−1, katm = 1.02 m h−1 and a dimensionless, room-temperature Henry's law constant of 0.3. Using these values, the “resistance” to exchange can be calculated using eqn. (1) by comparing ratios of the terms in the denominator. Specifically, the ratio of 1/ katm to H/kaq is 1 ∶ 23 (with PCBs). As with a previous similar calculation for elemental mercury (the ratio of 1/katm to H/kaq for elemental mercury was estimated to be 1 ∶ 32),13 this ratio suggests that PCB air/water exchange is controlled primarily by diffusion through the aqueous diffuse layer. These observations suggest that previous nocturnal/diurnal air/water exchange findings for PCBs5 support the atmospheric temperature component of the diel mercury evasion model.
The scenario two maximum estimated evasion rate at hour 17:00 exceeds the scenario two minimum evasion rate at hour 05:00 by approximately 76%. This enhanced rate of evasion is substantially greater than a previous modeling estimate of 44%13 and an experimentally derived value of 32% for PCBs.5 However, it is not unreasonable to expect an increase in the significance of atmospheric temperature variations on air/water exchange rates when an average air/water toxicant concentration quotient begins to approach the isothermal Henry's law constant. For example, in a system where the concentration quotient is perfectly equilibrated to the Henry's law constant under isothermal conditions, one can predict net evasion if the atmospheric temperature increases above the aqueous value and net absorption if the atmospheric temperature decreases below the aqueous temperature. For refractory toxicants displaying significant air/water exchange, these simulations suggest that estimates of average exchange rates are best experimentally measured over a 24 h period, or at least measurements should be made at average atmospheric temperatures.
Although there is not sufficient data available to test the present approach on a seasonal basis, “ranging” calculations can be performed if the following assumptions are made: (1) monthly average atmospheric and aquatic temperatures are identical; (2) average water column (16.77 pg L−1) and atmospheric (1.5 ng m−3) elemental mercury concentrations can be extended over the entire year; and (3) the aquatic temperatures for a nearby location in the Kissimmee river can be applied to this system (i.e., T = 21.6 + 7.6 × sin(month × 30 − 135); where month is ascribed a value of 0–12).
Fig. 4 illustrates the estimated mean atmospheric and aquatic temperatures (divided by 10), elemental mercury evasion rates and temperature dependent isothermal Henry's law constants as a function of month of the year using the previously given assumptions. The reader can observe that all three curves peak during months 7–8. The calculated average flux for these simulations was 1.01 ng m−2 h−1; with minimum and maximum values of 0.59 and 1.47 ng m−2 h−1, respectively. Not depicted in Fig. 4 is the curve for the aqueous phase mass transport coefficient which ranged from 0.077 to 0.113 m h−1 (the peak value is coincident with peak temperatures).
![Predicted seasonal
aqueous and atmospheric temperatures, mercury evasion rates and Henry's
law constants for mercury. Model assumptions: (1) aqueous temperatures
follow a relationship for the nearby Kissimmee River [T = 21.6 + 7.6 × sin(month × 30 − 135),
months are ascribed values of 0–12]; (2)
Tatm = Taq;
(3)
[Hg]atm = 1.5 ng m−3;
and (4)
[Hg]aq = 16.77 pg L−1.](/image/article/2001/EM/b005545j/b005545j-f4.gif) | ||
| Fig. 4 Predicted seasonal aqueous and atmospheric temperatures, mercury evasion rates and Henry's law constants for mercury. Model assumptions: (1) aqueous temperatures follow a relationship for the nearby Kissimmee River [T = 21.6 + 7.6 × sin(month × 30 − 135), months are ascribed values of 0–12]; (2) Tatm = Taq; (3) [Hg]atm = 1.5 ng m−3; and (4) [Hg]aq = 16.77 pg L−1. | ||
The model simulations displayed in Figs. 3 and 4 suggest that both diel and seasonal net elemental mercury evasion will occur. This is to be expected as long as an external source of mercury is being provided to the system (probably atmospheric deposition of ionic mercury). The monthly simulations depicted in Fig. 4 illustrate the necessity of having quality representative data for all periods of the year if a reasonably accurate mass balance for the system is to be obtained. For example, with simulations under constant concentration conditions, evasion fluxes during months 7–8 are approximately 2.5 times greater than the fluxes estimated for months 2–3; hence, these findings suggest that extrapolating one seasonal average exchange estimate to an annual estimate would not be wise.
The present model simulations were conducted on a system that rarely (if ever) experiences ice cover during the year. Although ice cover on a lake is likely to isolate the atmosphere from an underlying aquatic system13 (with respect to elemental mercury air/water exchange), the decreased temperature associated with ice cover could conceivably lead to enhanced partitioning of vapor phase mercury onto ice or snow. Hence, a potential (temporary) accumulation of mercury onto frozen surfaces (i.e., lake surface ice/snow cover) is possible.25,26
Although it has been suggested that vapor phase organic compounds may experience
a global “distillation”27 effect
whereby contaminants migrate from hot (equatorial) to cold (polar
or high altitude) regions, the issue of mercury migration to cooler regions
has only been considered more recently.28–30
The present approach can lend some insight into this possibility. For example,
if one considers a maximum tropical temperature of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C and a
minimum polar temperature of −60
°C and a
minimum polar temperature of −60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C,29
the concentration ratio of an ideal gas with equal chemical potentials at
these two temperatures (where the temperatures are given in Kelvin)
can be predicted to be:
°C,29
the concentration ratio of an ideal gas with equal chemical potentials at
these two temperatures (where the temperatures are given in Kelvin)
can be predicted to be:
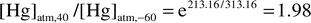 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C
rather than −60
°C
rather than −60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C; this calculation relies on the assumption
that the chemical activity of liquid mercury is approximately equal at both
temperatures):
°C; this calculation relies on the assumption
that the chemical activity of liquid mercury is approximately equal at both
temperatures): | (6) |
The simulations presented here are based on continuous distribution functions. It is not unlikely that some systems will display discontinuous anomalies resulting from the travel paths of the air masses passing over the aquatic systems; i.e., air masses that have been in contact with urban or polluted areas may display significant differences in concentration from those that have resided primarily in rural regions. Additional sources of discontinuity might include ice cover and/or water body overturn conditions (assuming hypolimnetic waters significantly differ from epilimnetic waters with respect to dissolved toxicant concentrations). Any and/or all episodic events of this nature will likely result in a requirement of increased resolution in a monitoring effort.
Future improvements to the present approach lie in four areas: conceptual improvements, computational improvements, experimental improvements, and improvements in data collection. For example, the present approach uses a two layer transport model suitable for low wind speed (quiescent)6,31 and near 100% relative humidity conditions. Semi-empirical air/water exchange models designed for higher wind speeds are within the scope of the present approach. Conceptual improvements also might include extending the model to include the effects of evaporative cooling on aqueous film mass transport properties and developing models for toxicants whose exchange behavior is dominated by the atmospheric diffusive layer. For chemical spill situations or industrial applications, an algorithm for calculating Henry's law constant composition dependences also might be useful and feasible.
Current methods for estimating air/surface toxicant exchange include mass balance approaches (i.e., when inputs exceed outputs in a pseudo steady-state system, the difference can sometimes be attributed to evasion), inferences from a comparison of a toxicant vapor phase/dissolved aqueous phase concentration quotient with a respective Henry's law constant, flux chamber measurements and micro-meteorological approaches.3,6,19,31 Unfortunately, many contaminants of concern are present in the environment at concentrations that are difficult to experimentally measure in all relevant media. Hence, improvements in both experimental detection limits and experimental methods of estimating rates of air/water contaminant exchange will lead to commensurate improvements in our ability to quantify air/water exchange of these compounds. Finally, the present diel modeling scenarios rely on the assumptions of constant atmospheric mercury concentration and constant water column temperatures; databases are not generally available to assess the significance of at least the first of these assumptions. Alternatively, the diel mercury evasion model could easily be modified to incorporate variations in either of these terms.
Conclusions
The present work has significant implications for designing monitoring programs to assess environmental air/water exchange of mercury and other toxicants. For non-reactive contaminants (i.e., non-reactive within the context of a 24 h period), average exchange rates may best be determined in the field over a 24 h period or, at a minimum, during a period of average atmospheric temperatures. For a reactive contaminant similar to mercury, 24 h field analytical19 strategies (at hourly resolution) may be required to properly understand the role of toxicant exchange in a diel mass balance assessment.Given that air/water exchange of both mercury and PCBs may be controlled by diffusion through the thin aqueous mass transport layer and that both may have similar Henry's law constants at environmental temperatures, data for PCB air/water exchange may be useful for elucidating the effects of atmospheric temperature variations on overall elemental mercury air/water exchange. Experimental data (for PCBs)5 and model predictions (for mercury see ref. 13 and the present study) suggest that air/water temperature disequilibrium has a significant effect on toxicant air/water exchange. For elemental mercury, diel variations in water column elemental mercury concentrations are likely to be a more significant contributor to diel variations in rates of air/water exchange than are diel air/water temperature disequilibria.
Acknowledgements
The author wishes to thank the US Environmental Protection Agency for providing him with the resources and opportunity to conduct this work. The author acknowledges the patience and valuable criticisms provided by the editors and reviewers for the present work and for earlier work in this area. Finally, the author acknowledges the inquiries about the effects of evaporative cooling on elemental mercury air/water exchange posed by Dr. David Amouroux and a member of the audience at the Whistler 2000 symposium; this topic will be addressed in future work. This paper has been reviewed in accordance with the US Environmental Protection Agency's peer and administrative review policies and approved for publication. Mention of trade names or commercial products does not constitute endorsement or recommendation for use by the US EPA.Note. A WindowsR or MS-DOSR compatible computer program suitable for making these computations is available free of charge from the author.§
References
- W. Schroeder, J. Munthe and O. Lindquist, Water, Air, Soil Pollut., 1989, 48, 337 CrossRef CAS.
- W. Baeyens, M. Leermakers, H. Dedeurwaerder and P. Lansens, Water, Air, Soil Pollut., 1991, 56, 731 CrossRef CAS.
- Z. F. Xiao, J. Munthe, W. H. Schroeder and O. Lindquist, Tellus Ser. B, 1991, 43B, 267 Search PubMed.
- W. Schroeder, O. Lindquist, J. Munthe and Z. Xiao, Sci. Total Environ., 1992, 125, 47 CrossRef CAS.
- P. Larson and L. Okla, Environ. Toxicol. Chem., 1987, 6, 659.
- T. F. Biddleman and L. L. McConnell, Sci. Total Environ., 1995, 159, 101 CrossRef.
- D. Amouroux, J. C. Wasserman, E. Tessier and O. F. X. Donard, Environ. Sci. Technol., 1999, 33, 3044 CrossRef CAS.
- R. G. M. Lee, V. Burnett, T. Harner and K. C. Jones, Environ. Sci. Technol., 2000, 34, 393 CrossRef CAS.
- M. Amyot, G. Mierle, D. R. S. Lean and D. J. McQueen, Environ. Sci. Technol., 1994, 28, 2366 CAS.
- J. O. Nriagu, Sci. Total Environ., 1994, 154, 1 CrossRef CAS.
- D. P. Krabbenhoft, J. P. Hurley, M. L. Olson and L. B. Cleckner, Biogeochemistry, 1998, 40, 311 CrossRef CAS.
- R. P. Mason, F. M. M. Morel and H. F. Hemond, Water, Air, Soil Pollut., 1995, 80, 775 CAS.
- N. T. Loux, Environ. Toxicol. Chem., 2000, 19, 1191 CAS.
- W. K. Lewis and W. G. Whitman, Ind. Eng. Chem., 1924, 16, 1215 Search PubMed.
- P. S. Liss and P. G. Slater, Nature, 1974, 247, 181 CAS.
- D. N. Glew and D. A. Hames, Can. J. Chem., 1971, 49, 3114 CAS.
- Handbook of Chemistry and Physics, ed. R. C. Weast, CRC, Cleveland, OH, 52nd edn., 1971–1972. Search PubMed.
- B. Jahne, K. O. Munnich, R. Bosinger, A. Dutzi, W. Huber and P. Libner, J. Geophys. Res., C, 1987, 92, 1937 Search PubMed.
- S. E. Lindberg, A. F. Vette, C. Miles and F. Schaedlich, Biogeochemistry, 2000, 48, 237 CrossRef CAS.
- M. Ames, G. Gullu and I. Olmez, Atmos. Environ., 1998, 32, 865 CrossRef CAS.
- D. S. Lee, G. J. Dollard and S. Pepler, Atmos. Environ., 1998, 32, 855 CrossRef CAS.
- L. Poissant and A. Casimir, Atmos. Environ., 1998, 32, 883 CrossRef CAS.
- M. S. Gustin, S. Lindberg, F. Marsik, A. Casimir, R. Ebinghaus, G. Edwards, C. Hubble-Fitzgerald, R. Kemp, H. Kock, T. Leonard, J. London, M. Majewski, C. Montecinos, J. Owens, M. Pilote, L. Poissant, P. Rasmussen, F. Schaedlich, D. Schneeberger, W. Schroeder, J. Sommar, R. Turner, A. Vette, D. Wallschlaeger, Z. Xiao and H. Zhang, J. Geophys. Res., D, 1999, 104D, 21831 Search PubMed.
- R. G. Thomas, in Handbook of Chemical Property Estimation Methods, ed. W. J. Lyman, W. F. Reehl and D. H. Rosenblatt, ACS, Washington, DC, 1990, ch. 15. Search PubMed.
- F. Wania, R. Semkin, J. T. Hoff and D. Mackay, Hydrol. Processes, 1999, 13, 2245 Search PubMed.
- F. Wania, D. Mackay and J. T. Hoff, Environ. Sci. Technol., 1999, 33, 195 CrossRef CAS.
- E. D. Goldberg, Proc. R. Soc. London, Ser. B, 1975, 189B, 277 Search PubMed.
- D. Mackay, F. Wania and W. H. Schroeder, Water, Air, Soil Pollut., 1995, 80, 941 CAS.
- W. H. Schroeder and J. Munthe, Atmos. Environ., 1998, 32, 809 CrossRef CAS.
- S. M. Bard, Mar. Pollut. Bull., 1999, 38, 356 CrossRef CAS.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, in Environmental Organic Chemistry, ed. R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Wiley, New York, 1993, ch. 10. Search PubMed.
Footnotes |
| † Presented at the Whistler 2000 Speciation Symposium, Whistler Resort, BC, Canada, June 25–July 1, 2000. |
| ‡ This is the work of a United States government employee engaged in his official duties. As such it is in the public domain and exempt from copyright. ©US government. |
| § Electronic Supplementary Information available. See http://www.rsc.org/suppdata/em/b0/b005545j/ |
| This journal is © The Royal Society of Chemistry 2001 |
