Apparent molar isentropic compressions and expansions of solutions†
Michael J.
Blandamer
a,
Michael I.
Davis
a,
Gérard
Douhéret
a and
João Carlos R.
Reis
a
aDepartment of Chemistry, University of Leicester, Leicester, UK LE1 7RH. E-mail: mjb@le.ac.uk
bDepartment of Chemistry, University of Texas at El Paso, El Paso, Texas 79968-0513, USA.. E-mail: mdavis@utep.edu
cLaboratoire de Thermodynamique des Solutions et des
Polymères, CNRS UPRESA 6003, Université Blaise Pascal, F-63177, Aubière Cedex, France.. E-mail: gerard.douheret@univ-bpclermont.fr
dDepartamento de Quimica e Bioquimica, Centro de Electroquimica e Cinetica, Faculdade de Ciencias, Universidade de Lisboa, P-1749-016, Lisboa, Portugal.. E-mail: jreis@fc.ul.pt
First published on 13th December 2000
Abstract
Isentropic compressibilities of solutions κS are readily calculated using the Newton–Laplace equation together with measured speeds of sound and densities. The result is an apparent molar isentropic compression for a given solute-j, ϕ(KSj; def) and a limiting property, ϕ(KSj; def)∞. This review examines the definition and calculation of ϕ(KSj; def) and ϕ(KSj; def)∞, commenting on the related isentropic expansions, ϕ(ESj; def) and ϕ(ESj; def)∞. We describe the thermodynamics which underpins the use of isentropic properties in the study of solute–solvent and solute–solute interactions.
 Michael J. Blandamer Michael J. Blandamer | Professor Mike J. Blandamer is an Emeritus Professor at the University of Leicester, having retired in September 1999. Mike graduated from the University of Southampton with BSc and PhD degrees in 1961. Following postdoctoral research at NRC in Ottawa (Canada), he joined the staff at the University of Leicester. |
 Michael I. Davis Michael I. Davis | Professor Michael I. Davis graduated from the University College London. His postgraduate studies were carried out at the University of Oslo under the mentorship of Odd Hassel. He is Professor of Chemistry at the University of Texas at El Paso. His research activities are focused on the thermodynamic properties of amphiphile + water mixtures. |
 Gérard Douhéret Gérard Douhéret | Doctor Gérard Douhéret obtained his PhD degree at the University of Clermont-Ferrand, France. He is Senior Research Scientist at the ‘Centre National de la Recherche Scientifique’. His research interests are in the thermodynamics of (water + amphiphile) mixtures in co-operation with the Chemistry Departments at the University of Texas at El Paso, USA and the ‘Kjemisk Institut’ of the University of Bergen. |
 João Carlos R. Reis João Carlos R. Reis | Professor João Carlos R. Reis graduated from the University of Lisbon. He holds a PhD (University of London), a DIC (Imperial College) and a DSc (University of Lisbon). He joined the staff at the University of Lisbon in 1973 where he is an Associate Professor and founder member of the Centre for Electrochemistry and Kinetics. His research interests centre on thermodynamics, theoretical and physical-organic chemistry. |
1 Introduction
This review explores the definition and calculation of isentropic compressibilities and, to a lesser extent, isentropic expansibilities of solutions. We direct attention to the extensive chemical literature describing these properties of aqueous solutions. We develop thermodynamic equations starting from the macroscopic properties of solutions; e.g. Gibbs energy, volume, compression and expansion. These properties are linked to partial molar properties and apparent molar properties of solutes in solution. Isentropic compressions of solutions have an interesting history. Recently published papers still refer to the classic monograph written by Harned and Owen.1 We draw particular attention to their definition of apparent molar isentropic compressions.2 Thermodynamic background
For a closed system containing n1 and n2 moles of chemical substances 1 and 2 the Gibbs energy is a dependent variable; the variables [T,p,n1,n2] are the independent variables. Temperature T is the thermal potential. Pressure p is the mechanical variable. The number of composition variables is established using the Gibbs Phase Rule. For closed systems (at defined T and p) at thermodynamic equilibrium the composition (organisation) is represented by ξeq and the affinity for spontaneous change A is zero consistent with the Gibbs energy being aminimum; eqn. (1).| Aeq = (∂G/∂ξ)eqT,p = 0 | (1) |
The Gibbs energy, volume and entropy of a solution at equilibrium are state variables. We draw a contrast with those properties which are associated with a process (pathway). Thus we contrast the state variable V with an unspecified compression K of a solution where we need to define the path followed by the system when the pressure is changed. The Gibbs energy of a system at thermodynamic equilibrium where the affinity for spontaneous change is zero and where the molecular composition/organisation is ξeq, is characterised by eqn. (2).
| G = G[T,p,n1,n2,A = 0] | (2) |
The same state is characterised by the equilibrium volume and equilibrium entropy by eqn. (3) and eqn. (4).
| V = V[T,p,n1,n2,A = 0] | (3) |
| S = S[T,p,n1,n2,A = 0] | (4) |
A common feature is the use of the two intensive variables, temperature and pressure, in the definition of extensive variables G, V and S. When pressure is increased by finite increments from p to (p + Δp) the volume changes in finite increments from V to (V + ΔV). For an important pathway, the temperature is constant. However, to satisfy the condition that the affinity for spontaneous change A is zero, the molecular organisation/composition ξ changes but continues to represent equilibrium conditions. The volume at pressure (p + Δp) is defined using eqn. (5).
| V = V[T,p + Δp,n1,n2,A = 0] | (5) |
In principle we plot volume as a function of pressure at constant temperature, n1, n2 and at ‘A =0’. The gradient of the plot at the point defined by eqn. (3) yields the equilibrium isothermal compression, KT (A = 0); eqn. (6).
| KT(A = 0) = −(∂V/∂p)T,A=0 | (6) |
| KS(A = 0) = −(∂V/∂p)S,A=0 | (7) |
The arguments outlined above are repeated with respect to both isobaric Ep(A = 0) and isentropic ES(A = 0) equilibrium expansions; eqn. (8) and eqn. (9).
| Ep(A = 0) = (∂V/∂T)p,A=0 | (8) |
| ES(A = 0) = (∂V/∂T)S,A=0 | (9) |
With reference to the set of independent variables [S,V,n1,n2] chemical equilibrium at constant S and constant V, corresponds to a minimum in thermodynamic energy, U. With reference to the set of independent variables [S,p,n1,n2] thermodynamic equilibrium at constant S and p occurs at the state where the enthalpy H is a minimum. The sets of independent variables, [S,p,n1,n2], [S,V,n1,n2] and [T,V,n1,n2] are ‘non-Gibbsian’.
3 Volume intensive variables
The (equilibrium) volume intensive compressibilities, κT and κS are defined† by eqn. (10) and eqn. (11).| κT = −(∂V/∂p)T/V = KT·V−1 | (10) |
| κS = −(∂V/∂p)S/V = KS·V−1 | (11) |
| αS = (∂V/∂T)S/V = ES·V−1 | (12) |
| αp = (∂V/∂T)p/V = Ep·V−1 | (13) |
Rowlinson and Swinton have stated that the latter property αS is ‘of little importance’.3 The isobaric heat capacity per unit volume σ is the ratio, CP/V. A quantity that is important is the difference δ between compressibilities; eqn. (14).
| δ = κT − κS = T·[αp ]2·V/Cp = T·[αp ]2/σ | (14) |
In the chemical literature the property σ is given different symbols and names; e.g. volumetric specific heat.4 We identify σ as the thermal (or, heat) capacitance. The symbol ε is the difference between isobaric and isentropic expansibilities; eqn. (15).
| ε = αp − αS = κT·σ /T·αp | (15) |
The Newton–Laplace equation5 is the starting point for the determination of isentropic compressibilities [cf. eqn. (11)] of solutions using speed of sound u and density ρ; eqn. (16).
| u2 = (κS·ρ )−1 | (16) |
In fact the speed of sound at zero frequency is a thermodynamically defined quantity.3,5 Densities and speed of sound6u (at low frequency, e.g. 1 MHz) can be precisely measured. The isentropic condition on κS means that as a sound wave passes through a liquid the pressure and temperature fluctuate within each microscopic volume but the entropy remains constant. The isentropic compressibility of water (l) at ambient T and p can be calculated using either the speed of sound κ*S (l;acoustic) or using κ*T (l), α*p (l) and σ*(l) to yield [see eqn. (14)] κ*S (l;thermodyn). The two estimates agree lending support to the practice of calculating isentropic compressibilities of solutions using the Newton–Laplace equation. We can equate the isentropic condition with adiabatic, provided that the compression and relaxation process is microscopically reversible.
4 Solutions; partial molar properties
For a solution prepared using n1 moles of solvent-1 and nj moles of solute-j, at defined T and p the extensive thermodynamic property Q [= G, H, S, V…] is related to the partial molar properties Q1 [= (∂Q/∂n1)T,p,n(j) ] and Qj [= (∂Q/∂nj)T,p,n(l) ]; eqn. (17).| Q = n1·Q1 + nj·Qj | (17) |
Equations relating partial properties with the internal energy U, its natural variables S and V, and its Legendre transforms (e.g. Helmholtz energy, enthalpy and Gibbs energy) together with T and p must have the same structure as in the general thermodynamic description of a phase. Such partial molar properties are called Lewisian.7 Lewis sought properties which play a role thermodynamically identical to molar properties such as molar volumes and molar isobaric heat capacities of pure substances and which are used in equations identical in form with those used for pure substances. Nevertheless the formalism involving partial molar properties, Qj(T,p) in general must be established in each case. Partial molar expansions Epj(T,p) and compressions KTj (T,p) are Lewisian, but partial molar isentropic compressions KSj(T,p) are not; see Section 9.
For real aqueous solutions, both V1(aq) and Vj(aq) depend on the composition of a solution. However, V1(aq) and Vj(aq) do not change independently, as the composition of the solution is changed. The Gibbs–Duhem equation leads, for systems at constant temperature and pressure, to the following condition.
| n1·dVl + nj·dVj = 0 | (18) |
A further important set of variables is called ‘apparent molar’. For a given aqueous solution, the thermodynamic property Q(aq) is related to the molar property of the solvent, water Q1*(l) and the apparent molar property of the solute ϕ(Qj); eqn. (19).
| Q(aq) = n1·Q*1 + nj·ϕ(Qj) | (19) |
Apparent ϕ(Qj) and partial molar Qj(aq) thermodynamic properties are similar and become identical in the limit of infinite dilution. In an ideal solution, each solute molecule exerts an influence on the properties of the solution independent of all other solute molecules in the solution. The solute molecules are effectively an infinite distance apart leading to the useful concept of the infinitely dilute solution.
In even a cursory investigation of the properties of solutions, a key consideration is the distance between solute molecules. For a simple solute (e.g. urea) in aqueous solutions at concentration cj the average distance apart, d, is given by (NA·cj) −1/3 where NA is the Avogadro constant. Then, if cj = 10−2 mol dm−3, d equals 5.5 nm.
Links between the macroscopic properties of a closed multi-component system, and the variables that describe properties attributed to the individual chemical components, are created through chemical potentials.8 For a system at equilibrium, chemical potentials have all the characteristics of state variables. Chemical potentials are similar in this respect to volume V, entropy S and enthalpy H; all are first derivatives of the Gibbs energy.
For a neutral solute-j in aqueous solution at fixed T and p the chemical potential, μj(aq) is related to the molality mj using eqn. (20) where γj is the activity coefficient of solute-j; m0 = 1 mol kg−1.
| μj(aq) = μ0j (aq) + R·T·ln(mj·γ j/m0) | (20) |
By definition, at all T and p, limit(mj → 0)γj = 1; μ0j (aq) is the chemical potential of solute-j in an ideal solution where mj = m0 = 1 mol kg−1. For an ideal solution, γj is unity at all molalities. A key consideration in formulating equations for the dependence of partial molar properties on composition is the limit that molality mj tends to zero; e.g. with reference to eqn. (20), limit(mj → 0)μj(aq;id) = −∞. In other words, the solute is increasingly stabilised as the solution is diluted (at fixed T and p). The Gurney model for solutions identifies cospheres of solvent around each solute molecule. Hence solute–solute interactions as described by activity coefficient γj can be understood in part in terms of cosphere–cosphere interactions. The extent to which the properties of a given neutral solute-j deviate from the state defined as thermodynamically ideal reflects to a large part the hydrophobic–hydrophilic character of solute molecules.
For an aqueous salt solution9 containing a 1∶1 salt (e.g. NaCl), the analogue of eqn. (20) takes the following form where μj(aq) is the chemical potential of salt-j in aqueous solution.
| μj(aq) = μ0j (aq) + 2·R·T·ln(mj· γ±/m0) | (21 ) |
In eqn. (21)γ± is the mean ionic activity coefficient of salt-j in solution. At all T and p, limit(mj → 0)γ± = 1; μ0j (aq) is the chemical potential of salt-j in an ideal aqueous solution having unit molality. As for simple solutes, in the limit of infinite dilution the chemical potential of a salt in solution is minus infinity. We anticipate that μ0j (aq) is given by the sum of ionic properties μ0+ (aq) and μ0− (aq) which are determined in part by cation–water and anion–water interactions respectively, i.e. ionic hydration.
The mean activity coefficient γ± describes ion–ion interactions in solution. The classic analysis in this context was given by Debye and Hückel; see, for example, reference 10. For very dilute solutions, the result is the famous Debye–Hückel Limiting Law, often simply expressed as DHLL. The algebra is simplified by defining a quantity Sγ which is characteristic of the solvent, temperature and pressure through the corresponding dependences of solvent density ρ*1 (l) and relative permittivity, εr.
Hence
| ln(γ± = −|z+·z−|· Sγ·[mj /m0]1/2 | (22) |
Therefore, limit(mj → zero)ln(γ±) = 0; γ± = 1. In other words, for very dilute solutions ln(γ±) is a linear function of (mj/m0)1/2 the gradient being defined by eqn. (22). According to the DHLL, the chemical potential of salt-j in a real solution is lower than in the corresponding ideal solution.
5 Volumes of solutions: partial and apparent molar volumes
The isothermal differential dependence of the chemical potential μj (aq) on pressure leads to the partial molar volume for solute-j, Vj(aq). From eqn. (20), for a neutral solute| Vj(aq) = V0j (aq) + R·T·[∂ln(γj)/∂ p]T | (23) |
Accordingly limit(mj → 0)Vj(aq) = V0j (aq) = V∞j (aq). Here V∞j (aq) is the limiting (infinite dilution) partial molar volume of solute-j in aqueous solution. The limiting partial molar volume of a solute in a given solution (at defined T and p) is characteristic in part of solute–solvent interactions.
The volume of an aqueous solution prepared using mj moles of solute-j and 1 kg of water is given by eqn. (24), where M1 is the molar mass of the solvent.
| V(aq; w1/kg = 1) = M1−1·V1(aq) + mj·Vj(aq) | (24 ) |
For real solutions, V1(aq) and Vj(aq) cannot be immediately calculated from the measured density, ρ(aq) of an aqueous solution because both V1(aq) and Vj(aq) depend on molality mj. An apparent molar volume of solute-j, ϕ(Vj), is defined; eqn. (25).
| V(aq;w1/kg = 1) = M−1·V*1 (l) + mj·ϕ(Vj) | (25) |
Lewis and Randall commented9 that ‘apparent molal quantities have little thermodynamic utility’, a statement repeated in the second8 but not the third10 edition of this classic monograph. A further comment concerns two plots;11 (i) V(aq; w1 = 1 kg) against mj, and (ii) [V(aq;w1 = 1 kg) − (1/M1)·V*1 (l)] against mj. Then Vj(aq) is the gradient of the tangent to the curve in plot type (i) at the specified molality mj; ϕ(Vj) is the gradient of the line in plot type (ii) joining the origin and [V(aq;w1 = 1 kg) − (1/M1)·V*1 (1)] at molality mj.
By definition, limit(mj → 0)ϕ(Vj) = ϕ(Vj)∞ = V∞j (aq); the limit of ϕ(Vj) at infinite dilution equals the limiting partial molar volume of the solute V∞j (aq). Partial and apparent molar volumes are related by eqn. (26).
| Vj(aq) = ϕ(Vj) + mj·[∂ϕ(Vj) /∂mj]T,p | (26) |
ϕ(Vj) is usually calculated using the densities of solvent ρ*j (1) and solution ρ(aq) at the same T and p together with the composition of the solution; e.g.eqn. (27) where cj is the concentration of solute-j.
| ϕ(Vj) = {[ρ*1 (1) − ρ(aq)]/cj·ρ*1 (1)} + [Mj/ρ*1 (1)] | (27) |
For dilute solutions containing simple neutral solutes, ϕ(Vj) is usually adequately described by a linear function of mj such that ϕ(Vj)∞ and V∞j are readily obtained; eqn. (28).
| ϕ(Vj) = ϕ(Vj)∞ + bv·(mj/ m0) | (28) |
The partial molar volume for a given 1∶1 salt Vj(aq) is related to the differential dependence of ln(γ±) on pressure at fixed T and molality mj; cf. eqn. (21).
| Vj(aq) = V∞j (aq) + 2·R·T·[∂ln(γ ±)/∂p]T | (29) |
From the definition of γ± limit(mj → 0)Vj(aq) = V∞j(aq) . Hence in the limit of infinite dilution the partial molar volume is a real quantity.
According to the DHLL for a 1∶1 salt,
| Vj(aq) = V∞j (aq) − 2·R·T·SV·(m j/m0)1/2 | (30 ) |
By definition, SV = (∂Sγ/∂p)T; SV is negative. According therefore to the DHLL, Vj(aq) is a linear function of (mj/m0)1/2 (at fixed T and p). According to the DHLL the dependence of apparent molar volume ϕ(Vj) on molality mj is given by eqn. (31) where V∞j equals ϕ(Vj)∞.
| ϕ(Vj) = ϕ(Vj)∞ − (4/3)·R·T·SV ·(mj/m0)1/2 | (31) |
For 1∶1 salts in aqueous solutions having molality 0.05 mol kg−1 at 298 K the difference ϕ(Vj) − ϕ(Vj)∞ does not follow the pattern required by the DHLL. Rather the deviations can be understood in terms of charge–charge interactions as described by the DHLL together with cosphere–cosphere interactions between hydration cospheres described by an additional term linear in salt concentration.12
At this point we highlight the theme being developed in this review. For a given aqueous solution at defined T and p and at equilibrium containing a single solute-j; (e.g. urea) the Gibbs energy G is a state variable; cf. eqn. (1). The solute-j in this solution can be characterised by its chemical potential, μj(aq); eqn. (20) and eqn. (21). Then μj (aq) is related to the molality mj using eqn. (20) in which μ0j (aq) is in part determined by solute–solvent interactions and γj characterises solute–solute interactions in a real solution. In the next stage the isothermal dependence of μj(aq) on pressure leads to the partial molar volume Vj(aq). Densities of solutions are used to estimate the apparent molar volume ϕ(Vj) using eqn. (27). In turn the limiting (infinite dilution) volumetric property is obtained. The next task involves identifying those properties of solute and solvent which determine V∞j (aq). One approach assumes that V∞j (aq) is given by the sum of two contributions, Vj(intrinsic) and Vj(cosphere); cf. reference 12. Thus Vj(intrinsic) reflects the ‘size’ of the solute molecule-j whereas Vj(cosphere) represents the impact of solute–solvent interactions; i.e. the hydration of solute-j in aqueous solution.
| Hence V∞j (aq) = Vj(intrinsic) + Vj(cosphere) | (32) |
Unfortunately there is no unambiguous method which allows us to calculate the two component volumes identified in eqn. (32). Nevertheless we speculate that Vj(intrinsic) is independent of temperature and pressure such that the temperature and pressure derivatives of V∞j (aq) offer a method for probing the hydration of solutes in aqueous solution viaVj(cosphere). We stress the word ‘speculate’ in this context. Therefore the isothermal compressibility κT describing the (equilibrium) dependence of volume on pressure at constant temperature might seem the property which should command most of our attention. Unfortunately isothermal compressions of solutions are not readily measured. Similarly, determination of partial molar expansions of a solute-j requires careful determination of densities of solutions as a function of both temperature and composition. Hence the amount of published information is not extensive. At first sight it is surprising that the most extensively measured property of solutions in this context is the isentropic compressibility, κS. A less commonly quoted volumetric property of aqueous solutions is the isentropic expansion, ES(aq). There is an interesting link between the isentropic compressions and expansions; section 10.
6 Thermal expansions of solutions: isobaric properties
The isobaric differential dependence of the volume, V, on temperature (at equilibrium where A = 0) is given by eqn. (8). The isobaric expansion Ep(aq) for an aqueous solution containing solute-j is related to the partial molar expansions of solute and solvent; cf.eqn. (17).| Ep(aq) = n1·Ep1(aq) + nj·Epj(aq) | (33) |
Similarly from eqn. (19) for Q
![[triple bond, length half m-dash]](https://www.rsc.org/images/entities/char_e007.gif) V,
V,
| [∂V(aq)/∂T]p = n1·[∂V*1 (l)/∂T]p + nj·[∂ϕ(Vj) /∂T]p | (34) |
Thus,
| Ep(aq) = n1·E*p1 (l) + nj·ϕ(Epj ) | (35) |
Here ϕ(Epj) = [∂ϕ(Vj)/∂T]p, the (equilibrium) apparent molar isobaric expansion for solute-j. Further, ϕ(Epj) is related to αp(aq) and α*p1 (l) using eqn. (36); cf. eqn. (27).
| ϕ(Epj) = [αp(aq)− α*p1 (l)]·(cj)−1 + α*p1 (l)·ϕ(Vj) | (36) |
Thus ϕ(Epj) is obtained for a solution having concentration cj.
7 Isentropic expansions of solutions
Generally little interest has been shown in either partial or apparent molar isentropic expansions of solutes. Complications are encountered in understanding isentropic expansions without the redeeming feature of practical accessibility via an analogue of the Newton–Laplace equation (Section 3). The isentropic expansion ES(aq) is defined by eqn. (9). The constraint on this partial differential refers to the entropy of the solution. The straightforward schemes described in eqn. (34)-(36) cannot be carried over to a consideration of ES(aq) because as we change the amount of solute nj for a fixed temperature, pressure and amount of solvent n1, so both V(aq) and S(aq) change yielding a new isentropic thermal expansion ES(aq) at a new entropy S(aq). Then for a series of solutions having different molalities, comparison of ES(aq) is not straightforward because entropy S(aq) is itself a function of solution composition. Further comparison cannot be readily drawn with the isentropic thermal expansion of the pure solvent E*Sl (l); eqn. (37).| E*Sl (1) = [∂V*1 (1)/∂T] at constant S*1 (1) | (37) |
Thus ES(aq) is a non-Gibbsian property. Consequently, familiar thermodynamic relationships involving partial molar properties are not valid in the case of partial molar isentropic (thermal) expansions which are non-Lewisian properties. We describe [∂Vj(aq)/∂T] for solute-j in aqueous solution at constant S(aq) as a semi-partial molar property.
Then for a solution having entropy S(aq), two partial molar isentropic thermal expansions are defined for the solvent and solute. Thus at S(aq) characterised by T, p, n1 and nj,
| ESl(aq;def) = [∂ES(aq)/∂n1 ] at fixed T, p and n1 | (38) |
| ESj(aq;def) = [∂ES(aq)/∂nj ] at fixed T, p and n1 | (39) |
| So that,ES(aq) = n1·ES1(aq;def) + nj·ESj(aq;def) | (40) |
Eqn. (40) relates ES(aq) to the partial molar intensive isentropic properties of both solvent and solute.
We find a similar dichotomy in defining an apparent molar isentropic expansion for solute-j, ϕ(ESj). We might assert that ϕ(ESj) is defined by the isentropic differential dependence ϕ(Vj) on temperature. Alternatively, we use an equation by analogy to those used to relate, for example, V(aq) to V*1 and ϕ(Vj).
Differentiation of eqn. (19) with
V
![[triple bond, length half m-dash]](https://www.rsc.org/images/entities/char_e007.gif) Q at constant entropy again raises the problem
that the molar entropy S(aq) does not equal the molar entropy of
the pure solvent, S*1
(l) However, by analogy with the definition of
ϕ(Epj) we define a quantity
ϕ(ESj; def) using eqn. (41); cf. eqn.
(35).
Q at constant entropy again raises the problem
that the molar entropy S(aq) does not equal the molar entropy of
the pure solvent, S*1
(l) However, by analogy with the definition of
ϕ(Epj) we define a quantity
ϕ(ESj; def) using eqn. (41); cf. eqn.
(35).
| ES(aq) = n1·E*Sl (l) + nj·ϕ(ESj ;def) | (41) |
In eqn. (41)E*Sl (l) is the molar intensive property of the solvent. Thus, the isentropic expansion of the solution at entropy S(aq) is linked with that of the pure solvent at entropy S*1 (l). Further
| ϕ(ESj;def) = [αS(aq) − α*Sl (l)]·(cj)−1 + α*Sl (l)·ϕ(Vj) | (42) |
Interesting equations link isobaric and isentropic expansions; Section 10.
8 Isothermal compressions and compressibilities of solutions
The differential dependence of V(aq) on pressure (at constant temperature) yields an equation for the isothermal (equilibrium) compression of a solution; cf. eqn. (24),| KT(aq) = n1·KTl(aq) + nj·KTj(aq) | (43) |
Partial molar compressions KTl(aq) and KTj(aq) are Lewisian properties of solute and solvent respectively. The analogue of eqn. (41) has the following form where ϕ(KTj) is the apparent molar (isothermal) compression of solute-j.
| KT(aq) = n1·KT1*(l) + nj·ϕ(KTj) | (44) |
Where
| ϕ(KTj) = −[∂ϕ(Vj)/∂p] T | (45) |
| ϕ(KTj) = [κT(aq) − κ*Tl (l)]·(cj)−1 + κ*Tl (l)·ϕ(Vj) | (46) |
The latter equation resembles the equations for ϕ(Epj) and ϕ(ESj;def) as a function of the concentration of solute cj and ϕ(Vj). Both ϕ(KTj) and KTj(aq) depend on the molality of the solute. KTj(aq) is related to the second differential of the solute activity coefficient with respect to pressure; cf. eqn. (23).
| KTj(aq) = K∞Tj (aq) − R·T·[∂2ln(γj )/∂p2]T | (47 ) |
One might have anticipated an extensive scientific literature reporting K∞Tj (aq) for a wide range of solutes. Unfortunately, direct measurement of isothermal compressibilities is difficult; at least to the precision required for determining K∞Tj (aq). Under these circumstances two procedures have been adopted, one commendable and the other perhaps less so. In both cases, the chosen route uses the isentropic compressibilities of solutions calculated from densities and speed of sound (Section 3).
The commendable route combines the measured isentropic compressibilities, densities and isobaric heat capacities Cp(aq) in order to calculate isothermal compressibilities; cf. eqn. (14) for a given solution having molality mj. An excellent example of this approach is described by Bernal and Van Hook13 who used the Desnoyers–Philip equation (see Section 10) to calculate ϕ(KTj)∞ for glucose, sucrose and fructose in aqueous solutions at 348 K. In a similar manner, Hedwig et al. used the Desnoyers–Philip equation (Section 10) to obtain estimates of limiting apparent molar isothermal compressions of glycyl dipeptides in aqueous solutions at 298 K.14
The less commendable but, under the circumstances, understandable route uses a measured κS as being effectively the same as κT. Hence ϕ(KSj;def) is often taken as a satisfactory estimate of ϕ(KTj). We return to this point in Section 9 because there are further problems which we need to address.
For neutral solutes ϕ(KTj) is satisfactorily expressed as a linear function of the concentration cj.
Thus
| ϕ(KTj) = ϕ(KTj)∞ + aK·cj | (48) |
For aqueous salt solutions the apparent molar compression, ϕ(KTj) is often a linear function of the square root of the salt concentration.15
Thus
| ϕ(KTj) = ϕ(KTj)∞ + SK·c½j | (49) |
9 Isentropic compressions and compressibilities of solutions
We turn to the definition of a property that, by analogy to ϕ(KTj), is the apparent molar isentropic compression of the solute ϕ(KSj) which, again by analogy, is related to a partial molar isentropic compression KSj of solute-j. For reasons given below, we write the apparent property ϕ(KSj;def).These isentropic properties emerge from consideration of eqn. (3) and eqn. (4). The assertion is made that an aqueous solution can be perturbed, by a small change in pressure δp, to a neighbouring state having the same entropy; cf.eqn. (4). Then the equilibrium isentropic compression is defined by eqn. (50).
| KS(aq) = −[∂V(aq)/∂p]S(aq | (50) |
The constraint on this partial differential refers to ‘at constant S(aq)’. Thus the definition of KS(aq) uses non-Gibbsian independent variables. Isentropic parameters do not arise naturally from the formalism which expresses the Gibbs energy in terms of independent variables in the case of, for example, a simple solution, [T,p,n1,nj].
The isothermal compression of a solution KT(aq) and partial molar isothermal compressions of both solvent KTl(aq) and solute KTj(aq) are defined using Gibbsian independent variables; e.g.eqn. (43)-(45). Unfortunately these equations cannot be simply carried over to the isentropic property KS(aq). Indeed the isentropic pressure dependence of the volume may be expressed as in eqn. (51). The equation emphasises that the entropy which remains constant is that of the solution.
| KS(aq) = −n1·[∂Vl(aq)/ ∂p]S(aq);A=0 − nj·[∂Vj(aq)/∂ p]S(aq);A=0 | (51) |
On the other hand, KS (aq) may also be re-expressed using Euler’s theorem.
Then,
| KS(aq) = n1·[∂KS(aq)/ ∂n1]T,p,n(j) + nj·[∂KS(aq)/ ∂nj]T,p,n(1) | (52 ) |
But KS(aq) is defined using non-Gibbsian independent variables. As a consequence two inequalities follow.
| −[∂V1(aq)/∂p ]S(aq) ≠ [∂KS(aq)/∂n1] T,p,n(j) | (53) |
| −[∂V1(aq)/∂p ]S(aq) ≠ [∂KS(aq)/∂nj] T,p,n(1) | (54) |
[∂KS(aq)/∂n1 ]T,p,n(j) and [∂KS(aq)/∂n1] T,p,n(1) are respectively the partial molar properties of the solvent and solute. Because partial molar properties should describe the effects of a change in composition on the properties of a solution, we write eqn. (52) for an aqueous solution7 in the following form.
| KS(aq) = n1·KS1(aq;def) + nj·KSj(aq;def) | (55) |
| Hence,KSj(aq;def) ≠ −[∂Vj(aq)/∂p]S( aq) | (56) |
Therefore KSj(aq;def) is a non-Lewisian partial molar property. We might define a molar isentropic compression of solute j as (minus) the isentropic differential dependence of partial molar volume on pressure. This alternative definition is consistent with eqn. (51) expressing a summation rule analogous to that used for partial molar properties. However some other thermodynamic relationships involving partial molar properties would not be valid in this case. Therefore, −[∂Vj(aq)/∂p]S( aq) is a semi-partial property. A similar problem is encountered in defining an apparent molar compression for solute-j, ϕ(KSj) in a solution having volume V(aq); cf. eqn. (56). We might assert that ϕ(KSj) is related to the isentropic differential dependence of ϕ(Vj) on pressure, −[ϕ(Vj)/∂p] S(aq). Alternatively, using as a guide the apparent molar properties ϕ(Epj) and ϕ(KTj), we could define ø(KSj;def) using eqn. (57).
| KS(aq) = n1·K*S1 (l) + nj·ϕ(KSj ;def) | (57) |
K Sj(aq;def) as given by eqn. (52) and ϕ(KSj;def) are linked; eqn. (58).
| KSj(aq;def) = ϕ(KSj;def) + nj·[∂ϕ(KS j;def)/∂nj]T,p,n(1) | (58) |
This equation is of the general form encountered for other apparent and partial molar properties; cf.eqn. (26). This form is also valid in the case of partial and apparent molar isobaric expansions, isothermal compressions and isobaric heat capacities. On the other hand, the semi-partial isentropic compression defined by −[∂Vj(aq)/∂p]S( aq) and the semi-apparent isentropic compression defined by −[∂ϕ(Vj)/∂p] S(aq) are related. Thus the isentropic pressure dependence of Vj(aq) is given by eqn. (59).
| −[∂Vj(aq)/∂p ]S(aq) = −[∂ϕ(Vj)/∂p] S(aq) −nj·{∂[∂ϕ( Vj)/∂nj]T,p,n(1 )/∂p}S(aq) | (59 ) |
| Hence, {∂[∂ϕ(Vj)/∂n j]T,p,n(1)/∂p} S(aq) ≠{∂[∂ϕ(Vj}/∂ p]S(aq)/∂nj} T,p,n(1) | (60) |
Hence, the analogue of eqn. (58) does not hold for these ‘semi’ properties. The inequalities (53) and (54) highlight the essence of non-Lewisian properties. Their origin is a combination of properties defined in terms of Gibbsian and non-Gibbsian independent variables as in eqn. (51) and eqn. (52). This combination is also the reason for the inequality (60). We stress that the isentropic condition in eqn. (51) and eqn. (52) refers to the entropy S(aq) of the solution defined as is the volume V(aq) by the Gibbsian independent variables [T,p,n1nj]. But this is not the entropy S*1 (l) of the pure solvent having volume V*1 (l). S(aq) at fixed composition is not simply related to S*1 (l) as, for example, linear functions of temperature and pressure.
The isentropic condition is involved in the definitions of isentropic compression, K*S1 (l) and isentropic compressibility κ*S1 (l) of the solvent.
| K*S1 (l) = −[∂V*1 (l)/∂p] at constant S*1 (l) | (61) |
| κ*S1 (l) = K*S1 (l)/V*1(l) = −[∂V*1(l)/ ∂p]/V*1(l) at constant S*1 (l) | (62) |
The different isentropic conditions in eqn. (50) and in eqn. (61) and eqn. (62) signal a complexity in the isentropic differentiation of eqn. (25) with respect to pressure.
Interest in the isentropic compresssibilities of solutions was stimulated by Gucker15 and, in particular, by Harned and Owen.1 The latter authors defined a (practical) property of the solute, here called ϕ(KSj;def) using eqn. (63) where the composition of a given aqueous solution is expressed using concentration cj.
ϕ(KSj;def)
![[triple bond, length half m-dash]](https://www.rsc.org/images/entities/char_e007.gif) [κS(aq) −
κ*S1
(l)]·[cj]−1 +
κ*S1
(l)·ϕ(Vj) [κS(aq) −
κ*S1
(l)]·[cj]−1 +
κ*S1
(l)·ϕ(Vj) | (63) |
ϕ(KSj;def)
![[triple bond, length half m-dash]](https://www.rsc.org/images/entities/char_e007.gif) [κS(aq)·ρ*1
(l) −
κ*S1
(l)·ρ(aq)]·[cj·
ρ*1
(l)]−1 +κ*S1
(l)·Mj·[ρ*1
(l)]−1 [κS(aq)·ρ*1
(l) −
κ*S1
(l)·ρ(aq)]·[cj·
ρ*1
(l)]−1 +κ*S1
(l)·Mj·[ρ*1
(l)]−1 | (64) |
Similar equations relate ϕ(KS;def) to the molality of the solute, mj.
ϕ(KSj;def)
![[triple bond, length half m-dash]](https://www.rsc.org/images/entities/char_e007.gif) [κS(aq) −
κ*S1
(l)]·[mj·ρ*1
(l)]−1 +
κS(aq)·ϕ(
Vj) [κS(aq) −
κ*S1
(l)]·[mj·ρ*1
(l)]−1 +
κS(aq)·ϕ(
Vj) | (65) |
ϕ(KSj;def)
![[triple bond, length half m-dash]](https://www.rsc.org/images/entities/char_e007.gif) [κS(aq)·ρ*1
(l) −
κ*S1
(l)·ρ(aq)]·[mj·
ρ(aq)·ρ*1
(l)]−1
+κS(aq)·Mj
·[ρ(aq)]−1 [κS(aq)·ρ*1
(l) −
κ*S1
(l)·ρ(aq)]·[mj·
ρ(aq)·ρ*1
(l)]−1
+κS(aq)·Mj
·[ρ(aq)]−1 | (66) |
These last four defining equations are rigorously equivalent. A crucial
feature of eqn. (63)–(66) is the equivalence symbol (i.e.
![[triple bond, length half m-dash]](https://www.rsc.org/images/entities/char_e007.gif) ). In this sense Harned and Owen1 defined an apparent isentropic compression of
solute-j in terms of the quantities on the rhs of eqn. (63). They recognised that
ϕ(KSj;def) does not have
thermodynamic basis. Unfortunately many authors refer to the proposals by
Harned and Owen1 without noting the
significance of the symbol,
). In this sense Harned and Owen1 defined an apparent isentropic compression of
solute-j in terms of the quantities on the rhs of eqn. (63). They recognised that
ϕ(KSj;def) does not have
thermodynamic basis. Unfortunately many authors refer to the proposals by
Harned and Owen1 without noting the
significance of the symbol, ![[triple bond, length half m-dash]](https://www.rsc.org/images/entities/char_e007.gif) . The target quantity is the apparent
molar isentropic compression defined by eqn.
(57) which, however, is not a description of an isentropic process
as its name might suggest. In fact
ϕ(KSj;def) is a measure of the
change in the isentropic compression of a solution when solute-j is added
under isothermal-isobaric conditions. The equivalence symbol in eqn. (63)–(66) is important.16
. The target quantity is the apparent
molar isentropic compression defined by eqn.
(57) which, however, is not a description of an isentropic process
as its name might suggest. In fact
ϕ(KSj;def) is a measure of the
change in the isentropic compression of a solution when solute-j is added
under isothermal-isobaric conditions. The equivalence symbol in eqn. (63)–(66) is important.16
The impression is often given that eqn. (63)–(66) are thermodynamic. Some authors do, however, indicate reservations especially when the estimates of ϕ(KSj;def) are discussed, particularly the dependence of ϕ(KSj;def) on solution composition. Franks and co-workers17 recognised the lack of isobaric heat capacity data which forces the adoption of the approach in which ϕ(KSj;def) is effectively assumed equal to ϕ(KTj). Owen and Simons18 estimate that overlooking the difference between κS(aq) and κT(aq) causes errors of approximately 7.5% in estimates of ϕ(KTj)∞ for NaCl(aq) and KCl(aq) at 298 K.
Interesting patterns emerge for the dependences of ϕ(KSj;def) on molality mj and on solute-j. Further, these dependences are readily extrapolated (geometrically) to infinite dilution to yield estimates of ϕ(KSj;def)∞. These comments apply to solutions of neutral solutes in both aqueous and non-aqueous solutions; e.g. solutions in propylene carbonate.19
For dilute solutions of neutral solutes ϕ(KSj;def) is often a linear function of the molality mj.
Thus
| ϕ(KSj;def) = ϕ(KSj;def)∞ + bKS·(mj/m 0) | (67) |
For aqueous solutions containing ureas, acetamides and α,ω-alkanediols, the slope bKS is positive and characteristic of the solute.20 Sakurai et al.21 report the results of a detailed investigation into the isentropic compression of alcohols in dilute solutions over the range from 5 to 45 Celsius. Interestingly ϕ(KSj;def)∞ is generally smaller than the molar property of the pure liquid-j. Galema and Høiland22 use eqn. (65) to analyse speed of sound data for several carbohydrates in aqueous solutions at 298 K. They comment on the calculation of KSj(aq;def) for solute-j using eqn. (68).
| KSj(aq;def) = ϕ(KSj;def) + mj·[∂ϕ(KS j;def)/∂mj]T,p | (68) |
This study confirmed the importance of the stereochemistry of carbohydrates on their hydration. A clear contrast is drawn between those solutes where the hydrophilic groups match and mismatch23 into the three dimensionally hydrogen-bonded structure of liquid water.
Desnoyers et al.24 used eqn. (65) to probe micelle formation by alkyldimethylamine oxides. Eqn. (65) was used to analyse the isentropic compressibilities of micellar aqueous solutions containing sodium octanoate and ethoxylated alcohols.25 Iqbal and Verrall26 use eqn. (66) in an examination of the compressibilities of glycyl peptides in aqueous solutions at 298 K. The dependence of ϕ(KSj;def) on molality mj is linear leading to estimates ϕ(KSj;def)∞. For amino acids in aqueous solution at 298 K, the calculated ϕ(KSj;def) is a linear function27 of the molality of the neutral amino acid yielding estimates of ϕ(KSj;def)∞.
For salt solutions, the dependence of ϕ(KSj;def) on the molality of the salt is generally examined in the light of equations describing the role of ion–ion interactions (see Section 4). For dilute solutions eqn. (69) forms the basis for examining the dependence of ϕ(KSj;def) on (mj)1/2 where mj is the molality of the salt-j.
Then,
| ϕ(KSj;de f) = ϕ(KSj;def)∞ + SKS·(mj/m 0)1/2 | (69) |
For a large range of 1∶1 salts, that ϕ(KSj;def)∞ is negative is attributed to electrostriction by the ionic charges. ϕ(KSj;def)∞ is more negative for solutions in D2O, than in H2O, as a consequence of more intense electrostriction in D2O.28 Further, on the basis of the Desnoyers–Philip equation (see Section 10), the difference ϕ(KSj;def) − ϕ(KTj)∞ is small but not negligible, amounting to approximately 10%. For alkylammonium ions in aqueous solutions ϕ(KSj;def)∞ decreases with increase in the hydrophobic power, matching a general increase in ϕ(Vj)∞ .29
Generally the property SKS cannot be evaluated because the isentropic dependence of the relative permittivity of the solvent is required.28 Further, the DHLL for ϕ(KSj;def) is itself a complicated function of salt molality.30 However for many dilute salt solutions ϕ(KSj;def) is approximately a linear function of (mj/m0)1/2; cf.eqn. (69). Indeed ϕ(KSj;def) is approximately a linear function of (mj/m0)1/2 for a wide range of aqueous and non-aqueous salt solutions; e.g. tetraalkylammonium salts in cyanomethane and benzonitrile.31ϕ(KSj;def) for copper(I) and sodium perchlorates in cyanobenzene, pyridine and cyanomethane show almost no dependence on salt molality.31
Determination of ϕ(KSj;def) for amino acids,32,33 proteins, nucleic acids and nucleotides34 has attracted enormous interest. Interesting patterns emerge pointing to the complexity of both solute–water and solute–solute interactions in these systems.
In terms of the development of the theory, the problem is concerned with the differential dependence of V*1 (l) on pressure at constant S(aq) describing how the volume of the solvent would depend on pressure if it were held at the same entropy as the solution.16
Thus
| −[(∂ϕ(Vj)/ ∂p]S(aq) = [κS(aq) − κ*S1 (l)]·[mj·ρ*1 (l)]−1 +κS(aq)·ϕ( Vj) + [mj·ρ*1 (l)]−1·T·α1 (l)·{[αp/σ (aq)] −[α*p1 (l)/σ*1 (l)]} | (70) |
The latter equation is thermodynamically correct. No assumptions have been made in its derivation. We adopt the procedure used by Harned and Owen.1
| −[(∂ϕ(Vj)/ ∂p]S(aq) = ϕ(KSj;def) + [mj·ρ*1 (l)]−1·T·α*p1 (l)·{[αp(aq)/σ (aq)] − [α*p1 (l)/σ*1 (l)]} | (71) |
Consequently the difference between −[∂ϕ(Vj)/∂p] S(aq) and ϕ(KSj;def) is determined by the difference Δϕ; eqn. (72).
| Δϕ = {[αp(aq)/σ(aq)] − [α*p1 (l)/σ*1 (l)]} | (72) |
However, Δϕ/mj is indeterminate at infinite dilution. But using L’Hospital’s rule,
| limit (mj → 0)Δϕ/mj =[ρ*1 (l)·α*p1 (l)/σ1(l)]{[ϕ(E pj)∞/α*p1 (l)] − [ϕ(Cpj)∞/ σ*1 (l)]} | (73) |
Nevertheless, despite the thermodynamic polish given to the analysis of isentropic compressions of solutions, there is an underlying problem. The latter again emerges in eqn. (70) which needs to refer to compressions at constant entropies for solutions and the pure solvent. In fact rarely is this feature acknowledged. Indeed one purpose of this review is to point out this feature.
10 Apparent molar isothermal and isentropic compressions and expansions: infinite dilution
Expansions and compressions of solutions under a combination of isothermal, isobaric and isentropic constraints are intimately linked.35 The most frequently quoted relationship is the Desnoyers–Philip equation4 linking ϕ(KTj) and ϕ(KSj;def). We noted that the extrapolated limiting value ϕ(KTj)∞ offers information about the hydration of a solute. Nevertheless in the face of experimental problems the favoured approach examines isentropic compressibilities. The apparent molar isothermal compression for solute-j ϕ(KTj) is related to the solute concentration cj using eqn. (46). The corresponding apparent molar isentropic compression of solute-j ϕ(KSj;def) is related to the concentration using eqn. (63). Hence ϕ(KTj) and ϕ(KSj;def) are related by the following eqn. (74).| ϕ(KTj) − ϕ(KSj;def) = (cj)−1·[δ(aq) − δ*1 (l)] + δ*1(l)·ϕ(Vj) | (74) |
The difference [ϕ(KTj) − ϕ(KSj;def)] depends on the concentration of the solute cj. Further [δ(aq) − δ*1 (l)] is not zero. Thus from eqn. (14),
| δ(aq) − δ*1 (l) = {T·[αp(aq)]2 /(aq)} − {T·[α*p1 (l)]2/σ*1 (l)} | (75) |
Using the technique of adding and subtracting the same quantity, eqn. (75) can be re-expressed as follows.
| δ(aq) − δ*1 (l) = {δ(aq)/[αp(aq)] 2}·[αp(aq) + α*p1 (l)]·αp(aq) −α*p1 (l)] − [δ*1 (l)/σ(aq)]·[σ(aq) − σ*1(l)] | (76) |
The difference, [αp(aq) − α*p1 (l)] is related to ϕ(Epj) using eqn. (36). Similarly, [σ(aq) − σ*1 (l)] is related to ϕ(Cpj) using eqn. (77).
| ϕ(Cpj) = [σ(aq) − σ*1 (l)]·(cj)−1 + σ*1 (l)·ϕ(Vj) | (77) |
Then using eqn. (76), we express eqn. (74) in the following manner.
| ϕ(KTj) − ϕ(KSj;def) = [δ(aq)/αp(aq)]· {1 +[α*p1 (l)αp(aq)]}·ϕ( Epj) −[δ*1 (l)/σ(aq)]·ϕ(Cpj ) + {δ*1 (l) −[δ(aq)·α*p1 (l)/αp(aq)]}·ϕ( Vj) | (78) |
Eqn. (78) was obtained by Desnoyers and Philip4 although a proof was not given. Desnoyers and Philip showed that if ϕ(KTj)∞ and ϕ(KSj;def)∞ are the limiting (infinite dilution) apparent molar properties, the difference is given by eqn. (79).
| ϕ(KTj) ∞ − ϕ(KSj;def)∞ = δ*1 (l)·{[2·ϕ(Epj) ∞/α*pj (l)] −[ϕ(Cpj)∞/ σ*1 (l)]} | (79) |
Using eqn. (63), ϕ(KSj;def) is plotted as a function of cj across a set of different solutions having different entropies. Then limit(cj → 0)ϕ(KSj;def) defines ϕ(KSj;def)∞. Granted two limiting quantities, ϕ(Epj)∞ and ϕ(Cpj)∞ are available for the solution at the same T and p, eqn. (79) is used to calculate ϕ(KTj)∞ using ϕ(KSj;def)∞.
An alternative form of eqn. (78 refers to a solution, molality mj.30
Thus,
| ϕ(KTj) − ϕ(KSj;def) = δ*1 (l)·{[2·ϕ(Epj) /α*p1 (l)] −[ϕ(Cpj)/σ *1 (l)] + [ρ*1 (l)·mj·[ϕ(E pj)]2/[α*p1 (l)]2]}·{1 + [ρ*1 (l)·mj·ϕ(C pj)/σ*1 (l)]}−1 | (80) |
The apparent molar expansions, ϕ(Epj) and ϕ(Epj;def) are linked by eqn. (81).
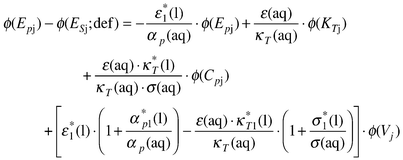 | (81) |
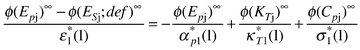 | (82) |
On the rhs of eqn. (82) each term is the ratio of a limiting apparent molar property of solute-j to the corresponding volume intensive property of the solvent. An allied set of equations incorporate terms relating to isentropic compressions. Thus
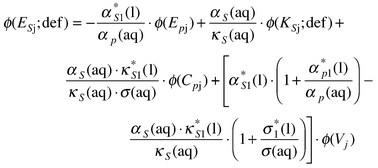 | (83) |
Then in the limit of infinite dilution,
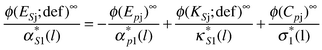 | (84) |
Finally, ‘semi’ apparent molar isentropic expansions (section 7) and compressions (Section 9) are linked; eqn. (85).
| [∂ϕ(Vj)]∂ T]S(aq)/αS (aq) = −[∂ϕ(Vj)/∂p] S(aq)/κS(aq) | (85) |
Therefore in an analogous fashion to the pattern shown by eqn. (82) and eqn. (84) an interesting pattern emerges in the form of the terms in eqn. (85).
These fascinating equations illustrate the power of thermodynamics in drawing together the properties of a given solution. Indeed this has been one of the themes of this review.
11 Acknowledgements
For their tireless efforts faced with a difficult manuscript, we acknowledge the secretarial assistance of Mrs Leonor Rodrigues (Lisbon) and Vicky Orson-Wright (Leicester). MID acknowledges support from the National Institutes of Health in the form of an institutional grant (GMO8012). JCRR thanks the Fundacao para a Ciencia e a Tecnologia (Portugal) for a research grant.12 References
-
H. S. Harned and
B. B. Owen, The
Physical Chemistry of Electrolyte Solutions,
Reinhold, New York, 3rd. edn.,
1958, section 8.7. Search PubMed
.
- M. J. Blandamer, Chem. Soc. Rev., 1998, 27, 73 RSC
.
-
J. S. Rowlinson and
F. L. Swinton,
Liquid and Liquid Mixtures, Butterworths,
London, 3rd. edn., 1982,
pp.16–17. Search PubMed
.
- J. E. Desnoyers and P. R. Philip, Can. J. Chem., 1972, 50, 1094 CAS
.
-
J. O. Hirschfelder,
C. F. Curtiss and
R. B. Bird,
Molecular Theory of Gases and Liquids,
Wiley, New York, 1954,
chapters 5 and 11. Search PubMed
.
- R. Garnsey, R. J. Boe, R. Mahoney and T. A. Litovitz, J. Chem. Phys., 1969, 50, 5222 CrossRef CAS
.
- J. C. R. Reis, J. Chem. Soc., Faraday Trans. 2, 1982, 78, 1595 RSC
.
-
G. N. Lewis and
M. Randall,
Thermodynamics, revised by K. S. Pitzer and L. Brewer,
McGraw-Hill, New York, 2nd. edn.,
1961, p. 108. Search PubMed
.
-
G. N. Lewis and
M. Randall,
Thermodynamics, McGraw-Hill, New
York, 1923. Search PubMed
.
-
K. S. Pitzer,
Thermodynamics, McGraw-Hill, New
York, 3rd. edn., 1995. Search PubMed
.
-
S. E. Wood and
R. Battino,
Thermodynamics of Chemical Systems, CUP,
Cambridge, 1990, p.
130. Search PubMed
.
- F. J. Millero, Chem. Rev., 1971, 71, 147 CrossRef CAS
.
- P. J. Bernal and W. A. van Hook, J. Chem. Thermodyn., 1986, 18, 955 CrossRef CAS
.
-
G. R. Hedwig,
J. D. Hastie and
H. Høiland,
J. Solution Chem., 1996,
25, 615 and references
therein. Search PubMed
.
- F. T. Gucker, Jr., J. Am. Chem. Soc., 1933, 55, 2709 CrossRef
.
- M. J. Blandamer, J. Chem. Soc., Faraday Trans., 1998, 94, 1057 RSC
.
- F. Franks, J. R. Ravenhill and D. S. Reid, J. Solution Chem., 1972, 1, 3 Search PubMed
.
- B. B. Owen and H. L. Simons, J. Phys. Chem., 1957, 61, 479 CrossRef CAS
.
- H. Høiland, J. Solution Chem., 1977, 6, 291 Search PubMed
.
- A. Lo Surdo, C. Shin and F. J. Millero, J. Chem. Eng. Data, 1978, 23, 197 CrossRef CAS
.
- M. Sakurai, K. Nakamura, K. Nitta and N. Takenaka, J. Chem. Eng. Data, 1995, 40, 301 CrossRef CAS
.
- S. A. Galema and H. Høiland, J. Phys. Chem., 1991, 95, 5321 CrossRef CAS
.
- F. Franks, Pure Appl. Chem., 1987, 59, 1189 CrossRef CAS
.
- J. E. Desnoyers, G. Caron, R. DeLisi, D. Roberts, A. Roux and G. Perron, J. Phys. Chem., 1983, 87, 1397 CrossRef CAS
.
- H. Huang and R. E. Verrall, J. Solution Chem., 1994, 23, 925 Search PubMed
.
- M. Iqbal and R. E. Verrall, J. Phys. Chem., 1987, 91, 967 CrossRef CAS
.
- F. J. Millero, A. Lo Surdo and C. Shin, J. Phys. Chem., 1978, 82, 784 CrossRef CAS
.
- J. G. Mathieson and B. E. Conway, J. Chem. Soc., Faraday Trans. 1, 1974, 70, 752 RSC
.
- R. Buwalda, J. B. F. N. Engberts, H. Høiland and M. J. Blandamer, J. Phys. Org. Chem., 1998, 11, 59 CrossRef CAS
.
-
J. C. R. Reis and
M. A. P. Segurado,
Phys. Chem. Chem. Phys., 1999,
1, 1501 and references
therein. Search PubMed
.
-
D. S. Gill,
P. Singh,
J. Singh,
G. Senanayake and
G. T. Hefter,
J. Chem. Soc., Faraday Trans., 1995,
91, 2789 and references
therein. Search PubMed
.
- T. V. Chalikian, A. P. Sarvazyan, T. Funck, C. A. Cain and K. J. Breslauer, J. Phys. Chem., 1994, 98, 321 CrossRef CAS
.
-
O. Likhodi and
T. V. Chalikian,
J. Am. Chem. Soc., 1999,
121, 1156 and references
therein. Search PubMed
.
- A. P. Sarvazyan, V. A. Buckin and P. Hemmes, J. Phys. Chem., 1980, 84, 692 CrossRef CAS
.
- M. I. Davis and G. Douhéret, Thermochim. Acta, 1991, 190, 267 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) is available: derivations of several key equations cited in the review. See http://www.rsc.org/suppdata/cs/a9/a908547e/ |
| This journal is © The Royal Society of Chemistry 2001 |
