3 + 1 Resonance enhanced multiphoton ionisation spectroscopy of HBr

Abstract

This paper extends the knowledge of highly excited Rydberg states of HBr by presenting detailed measurements of the 3 + 1 resonance enhanced multiphoton ionisation (REMPI) spectrum of H⁸¹Br molecules obtained following excitation in the wavelength range 366–316 nm, i.e. at energies up to the first ionisation energy. Spectra have been recorded using both linearly and circularly polarised laser light. 34 vibronic bands have been analyzed, of which 13 are identified as new Rydberg origins ([italic v]′ = 0) and 5 as new members of vibrational progressions ([italic v]′≠0) originating from the promotion of a π electron into a σ, π or δ Rydberg orbital and correlating with the ground X²Π state of the HBr⁺ ion core. Symmetry assignments in terms of either (Λ, S) or (Ω, ω) coupling schemes for the various identified excited states are offered, based on band contour simulation and quantum defect considerations. The main result of the present work is the observation of new states and bands involving vibrationally excited levels which were not accessible in previous one and two-colour spectra. In particular, the three-photon selection rules allow observation of the [italic v]′ = 0 and 1 levels of the L¹Φ₃ state arising from the dδ Rydberg manifold, as well as three other Ω = 3 states within the dπ and dδ series which are reported here for the first time.

---

1 Introduction

The electronic absorption spectra of HX (X = Cl, Br, I) molecules are of interest to the spectroscopic community because they provide particularly clear examples of the interaction of Rydberg and valence states and because of the wide variation in the strength of the spin–orbit coupling arising from the halogen atoms (882.3 cm⁻¹ for Cl; 3685.24 cm⁻¹ for Br; 7603 cm⁻¹ for I¹). There are also important practical applications of hydrogen halide spectroscopy, such as in studies of chemical reaction dynamics, for which electronic excitation of such molecules has become a common and successful means for probing product internal state distributions following inelastic or reactive scattering.² Considerable spectroscopic information has been obtained on HCl,^3–7 but fewer data are available for the heavier components in the series.

The electronic ground state of HBr is designated X1Σ0++ and the electronic configuration in molecular orbital (MO) notation is written as (1sσ)2(2sσ)2···(4sσ)2(4pσ)2(4pπ)4 or, more succinctly, ···σ2π4. The first spectroscopic study of HBr dates back to 1938 when Price recorded a low-resolution vacuum ultraviolet (VUV) absorption spectrum;8 subsequently Barrow and Stamper9 obtained a high-resolution absorption spectrum in the low energy region (between 66370 and 83570 cm−1) which was later reinvestigated and assigned by Ginter et al. in the region below 79500 cm−1.10 The latter authors extended the study to the isotopomer DBr11 and in energy to 83900 cm−1:12 they reported electronic bands due to transitions from the non-bonding π highest occupied molecular orbital (HOMO) to Rydberg states consisting of σ, π and δ Rydberg electrons associated with a ···σ2π3 core. They eschewed full nlλ type labels for the Rydberg electrons, however, arguing that such quantum number designations are overly simplistic for a complete description of the often mixed nl character of the excited states. Nee et al.13 measured the photoabsorption and fluorescence spectra of HBr in the 42500–95200 cm−1 region using synchrotron radiation with an intermediate resolution (0.05–0.1 nm): sharp absorption bands were observed which were classified into nsσ and ndπ Rydberg series, but the resolution was insufficient for rotational analysis. Subsequent high resolution single-photon vacuum UV fluorescence spectra of a room temperature sample of HBr at wavenumbers between 85900 and 90800 cm−114 resolved rotational structure in two bands assigned as the second members of the nsσ and ndπ series.

The first multiphoton absorption study of HBr¹⁵ detected HBr⁺ ions generated by 2 + 1 resonance enhanced multiphoton ionisation (REMPI): structured absorption around 79700 cm⁻¹ was observed, but no spectral assignments were offered. The use of 2 + 1 REMPI to prepare quantum state selected HBr⁺ ions for collision dynamics experiments was later demonstrated by Xie and Zare.¹⁶ More recently Callaghan and Gordon¹⁷ reported a detailed 2 + 1 REMPI study of jet-cooled HBr molecules in the wavenumber range 74000–85000 cm⁻¹: 37 bands were analyzed and assigned to transitions to valence, ion-pair and Rydberg states belonging to the sσ, pσ, dσ, pπ, dπ and dδ manifolds, and 12 new electronic states were proposed. These authors, while acknowledging the argument of Ginter et al.¹² of the inadequacies of nlλ type Rydberg electron labels, preferred to use such quantum numbers as a guide to the main Rydberg ancestry of the electronic states. They interpreted the labels used in ref. 12 and imposed principal quantum numbers such that the observed states were attributed to nlλ = 5sσ, 5pσ, 5pπ, 5dσ, 5dπ, 5dδ, 6sσ and 6pσ configurations. The particular choices of n values were apparently guided by previous assignments,^13,18 and will be discussed further later in this paper.

Kvaran and coworkers performed a series of multiphoton absorption studies of hydrogen halides at room temperature. They reported rotational constants, band origins, and isotope shift values for a number of vibrational bands of states with Ω = 0,¹⁹ observed [italic v]ia 2 + 1 REMPI, and described rotational and vibrational perturbations between the V¹Σ⁺ ion-pair state and the E¹Σ⁺ Rydberg state in HBr. Subsequent analysis of rotational structure in the spectra involving the F ¹Δ₂ Rydberg state of HBr revealed evidence of perturbation due to near resonance interaction with the V state.²⁰ Latterly, theoretical and experimental studies were undertaken of the 3 + 1 REMPI spectrum of HBr in the region 77000–86200 cm⁻¹²¹ (with assignments and analysis only as far as 83100 cm⁻¹): approximate expressions for strengths of three-photon transitions with ΔΩ = 0, 1, 2 and 3 were derived and used to simulate room temperature spectra which were compared with 2 + 1 REMPI spectra sampling the same range of intermediate state energies. One new Rydberg state, the L¹Φ₃ state, was identified in the 3 + 1 REMPI spectrum, along with the known E–X(0,0) H–X(0,0) and k–X(0,0) transitions, though the band origin reported for the latter is in poor agreement with the value in ref. 12.

Here we report a detailed 3 + 1 REMPI study of the high lying Rydberg states of HBr in the energy range 82000–95000 cm⁻¹, i.e., at energies in the vicinity of the first ionisation potential (IP). Notwithstanding the previous studies of HBr spectroscopy [italic v]ia single^{10,12–14,22} or multiphoton absorption methods,^{15–17,19–21} there are still extensive regions of the spectrum, in particular at high energies near the ionisation limit, that have not been studied or assigned in any detail. The new spectra identify numerous previously unobserved states and thus provide an extensive catalogue of the Rydberg electronic structure of HBr. The detailed characterization of these states will serve as a test of future electronic structure calculations, and maps out spectroscopic transitions for the benefit of dynamical studies involving this molecule.

The simplest picture of the excited states of interest to the current investigation is to consider Rydberg complexes built upon the ion core, either in the ground state configuration [···σ²π³]X²Π_i, or in the first excited state [···σπ⁴]A²Σ⁺. The Rydberg states in the energy range of present interest mainly correlate with the X ground state ionic core, and originate from promotion of a π electron: as in ref. 17, we will use an nlλ description of the excited orbital to categorise the primary Rydberg character of the excited state, with the caveat that such states, particularly those with Ω = 0, are often of mixed character. The states derived from ···π³nlλ electronic configurations belong to series which converge on one or other of the spin–orbit limits, ²Π_3/2 and ²Π_1/2, with respective IPs of 94 098.9 ± 1 cm⁻¹, and 96741.6 ± 3 cm⁻¹.²³

Given the Δλ = ± 3, ± 2, ± 1, 0 selection rule appropriate to a 3-photon excitation, the non-bonding π electron can be promoted to a Rydberg orbital of σ, π, δ, ϕ or γ character. Possible electronic states originating from all resultant configurations except ···π³ngλ are listed in Table 1. In the left-hand column are the molecular orbital configurations that derive from promotion of a π electron; in the middle columns the term symbols are listed for all the possible electronic states which may be observed, grouped according to the spin–orbit state of the ion to which they converge. Term symbols are given for two limiting coupling cases: (Λ, S) coupling, or Hund's case (a) and (Ω, ω) or Hund's case (c). States arising from promotion of a π electron to σ, π and δ orbitals have been described previously,¹⁷ while states originating from promotion to a ϕ type orbital have been deduced by application of the Wigner–Witner rules. As already stated in ref. 17, in the case of promotion to a π orbital, it is not possible to predict the correlation between specific 0⁺ (0⁻) and ⁻Σ⁺ (¹Σ⁻) states in the absence of ab initio calculations; thus correlations for the ···π³nfπ configuration have not been indicated in the Table. The right-hand column lists empirical values for the quantum defect δ (defined later in eqn. (1) of the present work) of each Rydberg series, based on previous assignments of observed bands.^10,12,14,17 No states belonging to the fλ series have been observed previously, but δ values ∽1.0 can be anticipated.

Table 1 Electronic states of HBr: correlation of states and ion core

(Λ,S)/(Ω, ω) term symbols^a
MO configuration	^2Π3/2	^2Π1/2	Quantum defect^bδ
a Term symbols have been grouped according to the ion core configuration (^2Πi, i = 1/2 or 3/2) to which they converge. Notation is ^2S+1ΛΩ. In some instances, just the Ω value is specified (see text). b Typical quantum defect values empirically determined from previously reported data.^10,12,14,17 Note that our choice of principal quantum numbers for the nd and nf Rydberg electrons differs from previous studies^13,17,18 and affects quantum defect values accordingly (see text for details).
(σ^2π^3)nsσ	^3Π1,2	^3Π0, ^1Π1	2.90–3.10
(σ^2π^3)npσ	^3Π1,2	^3Π0, ^1Π1	2.68–2.80
(σ^2π^3)npπ	^3Σ0^−,1^+	^1Σ0^−^−, ^3Σ1^−	2.50–2.66
^3Σ0^+^−	^1Σ0^+^+
^3Δ2,3	^3Δ1, ^1Δ2
(σ^2π^3)ndσ	^3Π1,2	^3Π0, ^1Π1	1.30–1.40
(σ^2π^3)ndπ	^3Σ0^−,1^+	^1Σ0^−^−, ^3Σ1^−	1.20–1.36
^1Σ0^+^+	^3Σ0^+^−
^3Δ2,3	^3Δ1, ^1Δ2
(σ^2π^3)ndδ	^3Π0,1	^3Π2, ^1Π1	1.10–1.25
^3Φ3,4	^3Φ2, ^1Φ3
(σ^2π^3)nfσ	^3Π1,2	^3Π0, ^1Π1
(σ^2π^3)nfπ	^3Σ1^+	^3Σ1^−
0^+, 0^−	0^+, 0^−
^3Δ2,3	^3Δ1, ^1Δ2
(σ^2π^3)nfδ	^3Π0,1	^3Π2, ^1Π1
^3Φ3,4	^3Φ2, ^1Φ3
(σ^2π^3)nfϕ	^3Δ1,2	^3Δ3, ^1Δ2
^3Γ4,5	^3Γ3, ^1Γ4

---

Multiphoton ionisation spectroscopy techniques exploit the enhanced probability of a molecule undergoing a multiphoton excitation and subsequent ionisation when there is a real excited state resonant at the energy of n absorbed photons (most commonly, n = 2 or 3).24 The REMPI spectrum obtained by measuring the ion yield as a function of laser excitation wavelength will display structure associated with the n-photon transition of the neutral molecule, and spectral congestion can be significantly reduced by preparing the molecules jet-cooled within a pulsed, supersonic molecular beam. For Hund's case (c) molecules (such as HBr), transitions from the X1Σ0++ ground electronic state involving a change of the axial projection of total electronic angular momentum Ω = 0 up to ± 3 are allowed in three-photon excitation (to be compared with ΔΩ = 0, ± 1, ± 2 and ΔΩ = 0, ± 1 for two and one-photon absorptions respectively), making accessible Ω = 3 components of Δ, Φ and Γ Rydberg states, not observed in 2 + 1 REMPI.15–17,19 Mass resolution provided by time-of-flight (TOF) detection allows separation of peaks due to isotopes and to fragments formed by dissociative ionisation, providing additional clues to aid assignment of the upper electronic states. For instance, for REMPI spectroscopy of HCl, pure Rydberg states ionise cleanly to the parent molecular ion, while perturbed states (due to coupling with valence or ion-pair states) produce both atomic and molecular ions.7

2 Experimental

REMPI spectra were recorded for formation of H⁷⁹Br⁺ and H⁸¹Br⁺ parent ions and ⁷⁹Br⁺, ⁸¹Br⁺ ion fragments over the whole three-photon wavenumber range 81971–94816 cm⁻¹ using a home-built TOF mass spectrometer (MS), described in detail in ref. 25. The excitation spectrum for forming H⁺ ions was also recorded, but only over a narrower energy range (81980–84824 cm⁻¹). A pulsed nozzle was used to produce an unskimmed molecular beam expansion of HBr (10% mixtures seeded in Ar, backing pressures ∽1 atm). Spectral analysis of band contours recorded in the REMPI spectra showed that the HBr molecules in the jet expansion were cooled to ∽40–60 K. The gas mixture and expansion conditions thus ensured a very satisfactory compromise between the need for rotational cooling to eliminate most spectral congestion, and the requirement of sufficient rotational features within each band to enable unambiguous spectral assignment and derive accurate excited state rotational constants.

The pulsed gas expansion was intersected, within the source region of the MS, by a focussed UV laser beam. The UV radiation in the range 365.8–316.3 nm was produced by frequency doubling, in a BBO crystal, the output of a pulsed Nd:YAG pumped dye laser operating on LDS698 or DCM dye solutions. The bandwidth of the dye laser fundamental output was ∽0.1 cm⁻¹. The linearly polarised second-harmonic radiation could be converted to circular polarization by passage through a Fresnel rhomb. Wavelength calibration of the visible output from the dye laser was performed, simultaneously with recording of REMPI spectra, by measurement of the optogalvanic spectrum of neon excited in a hollow cathode discharge. The standard deviation in the fitted Ne spectrum was, on average, 0.005 nm, and varied from 0.71 × 10⁻³ nm at the very best, to 0.015 nm in the worst case (in wavelength regions with very few neon lines); the average standard deviation translates into an error at the three-photon wavenumber of ± 0.7 cm⁻¹.

The unseparated visible and frequency doubled UV laser outputs were focused (using a quartz lens with f = 30 cm) into the source region of the mass spectrometer. Ions formed by the multiphoton absorption process were subjected to two stages of acceleration prior to entering the field-free drift region of the TOF MS and were detected by a pair of microchannel plates (MCPs). The output signal from the MCPs was passed to a digital oscilloscope and downloaded to a computer for subsequent analysis. To obtain mass selected REMPI spectra, the dye laser was scanned and only that part of the total ion signal that fell within a narrow time window centered on the TOF of the mass of interest was collected, averaged and stored.

In order to check for possible contributions to the measured spectra from alternative two-colour REMPI schemes involving one or more visible photons, a part of the linearly polarised spectrum, from 81981 to 84321 cm⁻¹, was recorded with a glass filter (Ealing UG-11) inserted into the laser beam path to absorb visible light. Aside from an overall decrease in signal intensity (reflecting the ∽90% transmission of the filter in the UV region) no obvious differences from previous spectra were observed, demonstrating that all spectra can safely be interpreted as arising from one-colour, UV-induced signals. Further careful checks of recorded spectra show no bands that can be assigned to alternative (2 + 1′) + 1 multiphoton absorption and ionisation schemes.

Some of the strongest lines in the observed 3 + 1 REMPI spectra have widths of as much as 2 cm⁻¹ (fwhm), most probably as a result of power broadening. Parts of the spectrum were re-recorded using decreased laser power, and smaller linewidths of ∽1 cm⁻¹ (fwhm) resulted. Such power effects will unfortunately mask any line broadening arising from weak coupling of the observed Rydberg states with dissociative states.

3 Results and discussion

3.1 Overview

Both linear and circularly polarized laser radiation were used to record spectra; differences in spectra recorded with these two laser polarizations provide an aid to spectral assignments when the effect of the selection rules is to change the relative intensities of rotational branches. A multiphoton electronic transition between two states ∣1〉 and ∣2〉 is allowed if the transition moment 〈2∣T_q^k(O)∣1〉 is non-zero, where k and q are the rank and component of the spherical tensor representation of the transition moment operator and ∣q∣⩽k: for Hund's case (c) molecules this condition is satisfied when q = ΔΩ. One-colour, three-photon excitations for ΔΩ = 0, ± 1 electronic transitions may be carried by spherical tensors T_q^k of rank k = 1 and 3.²⁴ The first rank tensor components involve transitions with rotational selection rules ΔJ = 0, ± 1 (P, Q and R branches) and third rank components give ΔJ = 0, ± 1, ± 2, ± 3 (N, O, P, Q, R, S and T) branches; the use of circularly polarized radiation suppresses first rank contributions, thus changing the relative intensity of P, Q and R branches with respect to N, O, S and T branches. Conversely, ΔΩ = ± 2, ± 3 transitions can only be driven by the third rank tensor. The accompanying rotational selection rules are ΔJ = 0, ± 1, ± 2, ± 3, and the relative intensities of the various branches will be insensitive to whether linear or circularly polarized light is used.

Most of the excited states accessible by REMPI spectroscopy are long-lived Rydberg states. Molecular Rydberg states can be viewed as a positive ion core plus a non-bonding Rydberg electron in a large, spatially diffuse orbital with specific n, l and (in the case of a linear molecule) λ quantum numbers. The energies of molecular Rydberg states can be described by the modified Rydberg equation:

where ν₀₀ is the term value (in cm⁻¹) of the [italic v]′ = 0 level of the Rydberg state, E₀ is the ionisation energy (also in cm⁻¹) for formation of the appropriate ion core (either X²Π_3/2 or X ²Π_1/2 in the [italic v]⁺ = 0 level are pertinent in the present work), R_∞ is the mass corrected value for the Rydberg constant, n is the principal quantum number of the Rydberg electron and δ is the quantum defect, whose magnitude depends on the degree of penetration of the Rydberg electron into the molecular ion core. Eqn. (1) can also be used as a guide for the energies of Rydberg levels with [italic v]′>0 (provided that E₀ is replaced by E_i, the energy for ionization to the equivalent vibrational level of the ion) because the vibrational intervals in the Rydberg states are generally very similar to those in the electronic ground state of the ion. The HOMO of HBr is essentially a pure atomic Br orbital, with the H atom providing only a minor perturbation. The Rydberg states are therefore well described as atomic like and localised on the Br atom, rather than using a united atom (Kr) model. Values for δ can then be compared with those for Rydberg orbitals of the appropriate atom to aid assignments of Rydberg orbital quantum numbers: Rydberg states can be ordered in series, each of which is characterized by a particular value of δ and converges to the ionisation limit appropriate to its ion core. For HCl Rydberg states, ns and np Rydberg series start with n = 4, but for nd-type configurations, the accepted starting point for the principal quantum number is n = 3.⁷ For HBr, there is, however, common usage of a numbering scheme for which n = 5 is the start of the Rydberg series based on ns, np, and nd Rydberg electrons.^13,17,18 Comparison of the Rydberg state energies with those of the corresponding orbitals in Br atoms,¹ however, strongly suggests that assignment of nd (and nf) Rydberg series starting at n = 4 is more appropriate (and is then more consistent with the numbering scheme employed for HCl), and we choose to adopt this labelling in the current work. This choice has consequences for the values of quantum defects deduced for nd and nf Rydberg orbitals, but the effective principal quantum number, (n–δ), is unaffected.

Spectroscopic constants (rotational constants and term values) and Ω values of 34 observed bands have been deter mined by least square fitting of all unblended rotational lines using the documented constants for ground state HBr molecules²⁶ and the spectral simulation program PGOPHER developed at Bristol.²⁷ All the spectral simulations employed an N² Hamiltonian. Given three-photon selection rules, unperturbed ΔΩ = 0, ± 1, ± 2, ± 3 transitions should exhibit the following spectral characteristics:

ΔΩ = 0 transitions: 0⁺←←←0⁺, where the triple arrow represents the three photon process, will show N, P, R and T branches (with the P and R branches showing different relative intensities to N and T when comparing spectra taken using linearly and circularly polarised laser light). 0⁻←←←0⁺ transitions are not allowed because of the parity selection rule.

ΔΩ = 1 transitions give N, O, P, Q, R, S and T branches, but, again, the intensities of the P, Q and R branches can be reduced relative to those of the N, O, S and T branches on changing from linearly to circularly polarized laser excitation.

ΔΩ = 2 and 3 transitions give N, O, P, Q, R, S and T branches and no differences in relative intensities should be observed under linear or circular polarisation.

In practice, because we are using cold molecular beams, N and O branches are rarely observed. HBr is unusual in that the vibrational spacings (≃2200–2400 cm⁻¹) of all Rydberg states correlating to the X ²Π ground state ion are very similar to the spin—orbit splitting of the ground state ion core (≃2640 cm⁻¹). This correspondence of energies serves to complicate the assignment of spectroscopic bands.

Fig. 1–9 show examples of 3 + 1 REMPI spectra of H ⁸¹Br; the bands observed in the region ∽82000–91000 cm⁻¹ for which a plausible assignment has been made are summarized in Table 2. Spectra, assignments, and derived rotational constants are all for H ⁸¹Br; equivalent spectra for H⁷⁹Br are almost identical in appearance and hence are not considered further here.

Fig. 1 A portion of the 3 + 1 REMPI spectrum of H⁸¹Br⁺ recorded with (a) circularly, and (b) linearly polarized light in the three-photon wavenumber region 83150–83650 cm⁻¹. Bands assigned to the K¹Π₁–X(0–0), r³Π₂–X(0–0), r¹Π₁–X(0–0), m³Π₀–X(0–0) and m³Π₁–X(1–0) transitions are shown and individual line assignments are indicated [italic v]ia the combs superimposed above the spectrum. Roman numerals refer to band identifiers listed in Table 2. The stick spectrum shows a spectral simulation of line positions and intensities using band origin and rotational constants from Table 2 and a rotational temperature of 50 K. Simulations for individual bands are arbitrarily weighted to mimic the relative intensities of the experimental spectra.

Fig. 2 3 + 1 REMPI spectrum of H⁸¹Br⁺ in the region 85800–86800 cm⁻¹. Other details are as in Fig. 1. Bands assigned to the r³Π_0⁺–X(0–0), R¹Π₁–X(0–0), M¹Π₁–X(1–0), band XXI (see Table 2 for assignments), [5dπ] ¹Σ⁺–X(0–0) and [5dδ] ³Π₁–X(0–0) transitions are shown. The insert in (b) provides an expanded view of the energy region 85840–86040 cm⁻¹ to identify lines belonging to the r³Π_0⁺–X(0–0) band.

Fig. 3 3 + 1 REMPI spectrum of H⁸¹Br⁺ in the region 85200–85870 cm⁻¹. Other details are as for Fig. 1. Bands assigned to the [5dδ] L¹Φ₃–X(0–0), band XVI (see Table 2 for assignments) and K¹Π₁–X(1–0) transitions are shown. Lines marked with a star belong to unfitted features in the spectra.

Fig. 4 3 + 1 REMPI spectrum of H81Br+ in the region 86760–88230 cm−1. Other details are as for Fig. 1. Bands shown are assigned to j 3Σ0+−–X(2–0), band XXV (see Table 2 for assignments), [6pπ] 3Σ0+−–X(1–0), band XXVII (for possible tentative assignments see Table 2), and [5dσ] 3Π0+–X(0–0) transitions. The band indicated by a vertical arrow in panel (a), with Q, R and T branches, belongs to a transition to an Ω = 1 or 0 state with origin at 87201 cm−1 described in Section 3.6. The broad feature near 87870 cm−1 visible in the circularly polarised spectrum is of unknown origin.

Fig. 5 3 + 1 REMPI spectrum of H⁸¹Br⁺ in the region 88910–89780 cm⁻¹. Other details are as for Fig. 1. Bands assigned to [5dδ] ¹Φ₃–X(0–0), band XXX and band XXXI of Table 2 are shown. Lines marked with a star belong to unfitted features in the spectra. The band indicated by a vertical arrow in (b), with P, Q and R branches, belongs to a transition to an Ω = 1 state with origin at 88997.8 cm⁻¹ described in Section 3.6.

Fig. 6 A portion of the 3 + 1 REMPI spectrum recorded with linearly polarised light in the region 89840–90650 cm⁻¹. (a) The ⁸¹Br⁺ fragment spectrum and (b) the parent ion H⁸¹Br⁺ spectrum. Transitions to bands XXXII, XXXIII and XXXIV of Table 2 are shown together with an unassigned band, indicated by the arrow in (a) and described in Section 3.6.

Fig. 7 3 + 1 REMPI spectrum of H81Br+ in the region 82060–83170 cm−1. Other details are as for Fig. 1. Bands assigned to j3Σ0+−–X(0–0), E1Σ+–X(2–0), k3Π1–X(1–0) and L1Φ3–X(0–0) transitions are shown. The 82060–82460 cm−1 region in (a) has been magnified by a factor of ten in order to show T branches of the j–X(0–0) and E–X(2–0) transitions.

Fig. 8 3 + 1 REMPI spectrum of H81Br+ in the region 84120–84940 cm−1. Other details are as for Fig. 1. Bands assigned to E1Σ+–X(3–0), j 3Σ0+−–X(1–0) and [6pπ] 3Σ0+−–X(0–0) transitions are shown together with an unassigned band, indicated by a vertical arrow in (a) and described in Section 3.6. Lines marked with a star belong to unfitted features in the spectra.

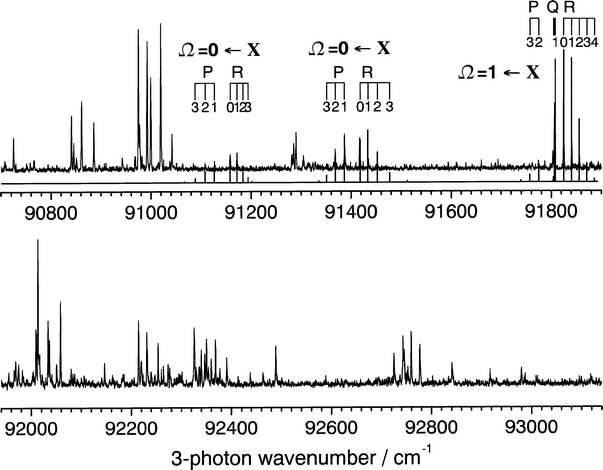Fig. 9 The high energy region of the (3 + 1) REMPI spectrum of H⁸¹Br recorded from 90700 to 93140 cm⁻¹ using linearly polarised light. The three bands for which a unique fitting to Ω values and rotational constants have been obtained are inicated [italic v]ia the combs superimposed above the spectrum, and the spectral simulations are reported in the top panel.

Table 2 Electronic bands of BHr^a observed in the region 82000–92000 cm⁻¹. Other bands not assigned are discussed in Section 3.6

#	νi 0	[italic v]′	Upper state^b	δ^c	B[italic v] ^′	D[italic v] ^′ × 10^3	I ^d	Comments^e
a Lower state rotational constants used in determining band origins and rotational constants of the upper state are B[italic v] = 0^″ = 8.34844 cm^−1 and D[italic v] = 0^″ = 3.438 × 10^−4 cm^−1.^26 Reported molecular constants are for H^81Br; all values are in cm^−1. Figures reported in brackets in νi0, B[italic v]^′ and D[italic v]^′ columns correspond to one standard deviation error in the fitted parameters, and, in the case of νi0, do not include allowance for uncertainty in the absolute wavenumber accuracy. For comparison the rotational constants of the ground electronic state of H^81Br^+ are B[italic v] = 0^+ = 7.95 cm^−1, D[italic v] = 0^+ = 3.48 × 10^−4 cm^−1. b Both (Λ, S) and (Ω, ω) labelling schemes are used in the designation of the upper state. c Quantum defect from eqn (1). Values depend on the choice of n, and thus differ from previous reports for the ndλ and nfλ configurations (see text for details). d Intensity estimates for individual bands are intended as a guide and are not quantitative. Abbreviations include: S = strong, M = medium, W = weak. e When bands have been previously reported, references to others' work are given. Br^+ in this field indicates that the band is observed mainly in the fragmen channel. f Reassigned in present work.
I	82185.53(19)	0	j^3Σ0^+^−[4dπ]	1.254	6.932(43)	5.6(22)	M	12, 17
II	82275.77(26)	2	E^1Σ0^+^+[5pπ]	2.600	6.786(33)	4.23(81)	M	12, 17, 19
III	82745.210(61)	1	k^3Π1[4dδ]	1.170	7.906(11)	1.6(36)	M	12
IV	82857.38(14)	0	L^1Φ3[4dδ]	1.189	8.390(12)	1.23(23)	S	21
V	83237.68(16)	0	K^1Π1[4dδ]	1.149	7.002(26)	−6.04(87)	S	12^f
VI	83269.84(20)	0	r^3Π2[6pσ]	2.817	8.440(24)	7.25(65)	W	12
VII	83292.92(14)	0	r^3Π1[6pσ]	2.813	8.309(35)	7.2(17)	M	12
VIII	83453.58(16)	0	m^3Π0[6sσ]	3.126	7.907(28)	−0.43(90)	W	12, 17^f
IX	83570.58(40)	1	m^3Π1[6sσ]	3.081	7.830(50)	1.1(12)	W	12
X	83848.17(20)	0	M^1Π1[6sσ]	3.083	8.230(29)	2.36(93)	S	12
XI	84041.01(23)	2	H^1Σ0^+^+[4dπ]	1.264	4.797(57)	1.9(28)	M	Br^+12, 17
XII	84251.03(38)	3	E^1Σ0^+^+[5pπ]	2.612	5.35(10)	−39.6(49)	M	17, 19
XIII	84454.03(26)	1	j^3Σ0^+^−[4dπ]	1.261	6.910(42)	1.6(13)	M
XIV	84807.21(21)	0	^3Σ0^+^−[6pπ]	2.563	7.840(26)	−1.20(64)	M	17
XV	85243.89(35)	1	L^1Φ3[4dδ]	1.184	8.137(33)	1.87(83)	M
XVI	85532.67(43)	0	^1Π1[4fσ]	0.871	7.895(74)	8.8(31)	W
		0	^3Π1[5dσ]	1.421
XVII	85621.88(22)	1	K^1Π1[4dδ]	1.145	7.369(34)	1.1(11)	S
XVIII	85901.67(26)	0	r^3Π0^+[6pσ]	2.818	7.768(48)	−3.0(16)	W	12
XIX	85944.41(30)	0	R^1Π1[6pσ]	2.812	7.858(24)	−2.60(34)	M	12
XX	86229.36(17)	1	M^1Π1[6sσ]	3.078	7.897(37)	1.1(17)	W	14
XXI	86322.60(34)	0	^3Δ3[5dπ] or	1.243	8.704(37)	0.09(55)	S
			^3Φ3[5dδ]	1.243
XXII	86510.14(45)	0	^1Σ0^+^+[5dπ]	1.197	6.604(65)	−4.0(20)	W	Br^+^14
XXIII	86585.61(12)	0	^3Π1[5dδ]	1.178	8.443(11)	4.65(20)	S
XXIV	86862.37(14)	2	j^3Σ0^+^−[4dπ]	1.246	6.970(34)	−8.4(17)	W
XXV	86976.75(35)	0	^3Δ1/^3Σ1^−[6pπ]	2.648	8.403(75)	−1.5(36)	W
			or ^3Π1[7sσ]	3.075
XXVI	87309.41(25)	1	^3Σ0^+^−[6pπ]	2.534	7.855(53)	0.7(25)	W
XXVII	87932.71(52)	0	^1Π1[5dσ] or	1.470	7.573(82)	−6.2(27)	M
		2	K^1Π1[4dδ] or	1.139
		1	^3Π1[5dσ] or	1.410
		1	^1Π1[4fσ]	0.863
XXVIII	87991.8(12)	0	^3Π0^+[5dσ]	1.459	7.558(90)	−4.3(17)	W
XXIX	88914.03(52)	0	^1Φ3[5dδ]	1.256	9.120(51)	6.5(13)	M-S
XXX	89231.4(16)	0	^3Δ3[6dπ] or	1.252	8.30(18)	−27.3(63)	W
			^3Φ3[6dδ]	1.252
XXXI	89548.15(44)	0	^1Π1[7sσ] or	3.094	7.69(11)	−7.7(51)	M-S
			^3Π1[8sσ] or	3.089
			^1Π1[5fσ]	1.094
XXXII	89948.90(39)	0	^3Π0^+[5fσ] or	0.981	6.55(15)	−8(12)	W
		0	^3Σ0^+^−[5fπ]	0.981
XXXIII	90091.67(31)	0	^1Π1[7pσ]	2.938	8.412(35)	8.12(82)	M
XXXIV	90417.33(31)	0	^3Π0^+[7pσ]	2.834	7.062(73)	9.7(34)	W	Br^+

---

Table 2 contains the band origins (ν_i0) and effective rotational constants (B_{[italic v]}′, D_{[italic v]}′) derived from spectroscopic fits, as well as deduced quantum defect (δ) values for the upper states of each analyzed band together with some brief descriptive comments and appropriate references for previously reported bands. All the observed rotational lines within the bands are listed in two tables, separated into Ω = 0⁺ and Ω>0 states, which are available as Electronic Supplementary Information.† An aid to the assignment of an observed band as belonging to a particular Rydberg state comes from the fact that, due to the non-bonding character of Rydberg orbitals, strong similarities (e.g in vibrational frequencies and rotational constants) are found between unperturbed Rydberg states and the ionic state to which they converge. The spectroscopic assignments proposed in Table 2 have been reached according to the following criteria:

1. Quantum defect value: from each best-fit term value (νi0) a quantum defect (δ) is calculated according to eqn. (1), with possible allowance for ionization to the ith vibrational level of HBr+ X2Π. The comparison of δ values for unknown states with known ones is a good guide to restrict possible assignments. Typical quantum defects from previously reported bands are summarized in Table 1. Different vibrational levels of the same Rydberg state will have similar quantum defects (when compared with the energy required to ionise to the corresponding vibrational level of the ion), but increasing (or decreasing) values can be found for Rydberg states perturbed by interaction with other Rydberg or valence states. For example, δ values for the vibrational progression of E1Σ0++ states within the 5pπ Rydberg series, as reported in ref. 17 and 19 are:

2. Consistency of rotational constants: when a δ value suggests an assignment to a vibronic band ([italic v]′≠0), the fitted first-order rotational constants (B_{[italic v]}^′) are compared with those of the band origin (B₀^′) and, if the difference is unreasonable, the assignment is rejected. It is worth noting that this criterion is strictly valid only for unperturbed Rydberg states because, as described in detail in ref. 19 and 20, interactions of Rydberg states (e.g. the E-state) with ion-pair states (e.g. the V-state) can cause a compression of the Rydberg state zero-order vibrational levels and an irregular behavior in the rotational constants with the vibrational quantum number [italic v]′.

3. Intensity: Franck–Condon considerations require that, in the case of Rydberg transitions at least, vibrational progressions should show a decrease in intensity with increasing vibrational quantum number [italic v]′.

If the aforementioned criteria are still not sufficient for a unique assignment, all the possible term symbols are reported in Table 2. In some cases, further aid to the assignments comes from the analysis of the branching between atomic (mainly Br⁺) and molecular (HBr⁺) ions. As already mentioned, the absence of signal in the fragment ion channel can be an indication of a pure Rydberg state, but the observation of signal in the Br⁺ fragment channel should be interpreted with care as, for strong signals, there can be “spill over” from the HBr⁺ time gate. Moreover, excitation to Rydberg levels with [italic v]′>0, or to states perturbed by high vibrational levels of ion-pair states should reveal an isotope shift between H⁷⁹Br and H⁸¹Br. Experimental observation of such shifts could help in the assignment of the vibrational numbering of a band system associated with an unknown electronic state; some of the observed bands have been checked for a small isotope shift, but this is rarely conclusive given the precision of the wavenumber determination (∽ ± 0.7 cm⁻¹) and the observed rotational linewidths of ∽1 cm⁻¹ or more.

We have confirmed the assignments of most of the excited states already observed in one- and two-photon studies, with the exception of two features in the low energy region, at 83237.7 cm⁻¹ and 83453.6 cm⁻¹, which have been reassigned (see Sections 3.2 and 3.4). Previous one-photon absorption^10,12 and 2 + 1 REMPI^17,19,20 studies of HBr show evidence of vibronic bands associated with transitions to the V¹Σ⁺ ion-pair state, which ionizes to the first excited state (A²Σ⁺) of the HBr⁺ ion.¹² In our MPI scheme, the resonant absorption of 3 UV photons, followed by the further absorption of another UV photon, is sufficient to overcome the I.P. for the production of HBr⁺ in the A-state (∽122519 cm⁻¹²⁶) only when using one-photon wavelengths shorter than 326.5 nm, corresponding to a three-photon wavenumber ⩾91889 cm⁻¹. As a consequence, in almost all of the energy region described here, we do not expect to observe ro-vibronic bands of the V–X transition. Some bands observed in the 3 + 1 REMPI spectra remain unfitted and unassigned, particularly at the high energy end. These bands are either too weak in the spectrum, exhibit too few lines for a definitive rotational analysis, or yield rotational constants inconsistent with plausible values.

In the following three sub-sections, 3.2–3.4, we present results for the σ manifolds, the π manifolds and the dδ manifold. Sub-section 3.5 provides a description of states with Ω = 3, while bands that defy conclusive assignment, and the densely structured and complicated high energy region, are discussed in sub-section 3.6. It is noteworthy that just one Ω = 2 state is identified in the current study. Sub-sections are, where appropriate, further sub-divided into brief discussions of the different bands, which are identified using the Roman numeric scheme employed in Table 2.

3.2 sσ, pσ and dσ manifolds

Each of the ···π³nlσ Rydberg manifolds gives rise to a ¹Π state and a ³Π multiplet (with Ω = 0, 1 and 2 components). Transitions to all are allowed under three-photon selection rules in Hund's case (c) (Ω, ω), which is appropriate in the case of strong spin–orbit coupling; transitions to triplet states are forbidden when the spin–orbit coupling is weak (Hund's case (a)). Band origins of states associated with the configurations . . .π³5sσ and . . .π³5pσ lie at energies below the region investigated here.

3.2.1 6sσ states: bands VIII, IX, X and XX. The 6sσ Π states have been labelled previously as M ¹Π and m³Π,^12,17 the latter having components with Ω = 2, 1, 0 in ascending order of energy. The appearance of transitions to some of these states in the 3 + 1 REMPI spectrum is shown in Fig. 1. All the ([italic v]′ = 0 − [italic v]″ = 0) bands plus the transition to the [italic v]′ = 1 level of the m³Π₁ state have been observed in one-photon absorption. Origin transitions involving the ³Π₂ and ³Π₁ states (i.e., those correlating with the X²Π_3/2 ion core (see Table 1)) are too low in energy to appear in our spectra, but the m³Π₁–X(1–0) transition (at 83570.6 cm⁻¹) is observed, with rotational constants and quantum defect δ value in agreement with ref. 12.

Ginter et al.¹² assigned a band observed near 83238 cm⁻¹ to the m³Π_0⁺–X(0–0) transition, though their rotational analysis was unable to confirm whether the excited state had Ω = 0⁺ or 1. In one-photon absorption, the band showed P, Q and R branches, but a one-photon 0⁺–0⁺ transition should exhibit P and R branches only. In this particularly crowded energy region, we observe a very strong band (origin at 83237.7 cm⁻¹ and rotational constants in agreement with ref. 12) with P, Q and R branches; the presence of a Q branch (with no Q(0) line) in the linearly polarised spectrum and weak S(1) and S(2) lines in the circularly polarised spectrum shows that the excited state has Ω = 1 rather than Ω = 0⁺. We thus refute the previous assignment and reassign this band to excitation to the K¹Π₁([italic v]′ = 0) state (see Section 3.4 for a detailed discussion).

A good candidate for the m3Π0+–X(0–0) transition is then the band encountered near 83453.5 cm−1 (see Fig. 1); it is weak in our linearly polarised spectrum, perhaps because of weak spin–orbit coupling in the sσ manifold, and is not apparent when using circularly polarised excitation. The definite absence of a Q branch clearly indicates that the band involves excitation to an Ω = 0+ state; it mainly shows up at the parent ion masses, with a small but detectable contribution from the H+ channel which can be an indication of some degree of perturbation, most commonly by a 1Σ0++ ion-pair state in the hydrogen halides. A corresponding band has been observed in the one-photon12 and two-photon17 absorption spectra of HBr, but in both cases was assigned to the K1Π1–X(0–0) transition. The two-photon spectrum recorded by Callaghan and Gordon17 has the appearance of an Ω = 0+–Ω = 0+ transition (with O, Q and S branches), but the authors justify their assignment in terms of an Ω = 1 excited state on the basis of absence of lines associated with transitions to a J′ = 0 level. Careful inspection of the spectrum reported in Fig. 6 of ref. 17, however, shows one unassigned line at the one-photon wavelength ∽479.47 nm (laser fundamental before frequency doubling) which closely matches the three-UV photon wavenumber (83402.9 cm−1) expected for the O(2) line. If we take the latter into account, only the definite absence of a Q(0) line, not easily resolved from the Q(1) line, would confirm the Ω = 1 assignment. Thus we believe that previous arguments for an Ω = 1 state are incorrect.

More difficult to explain is the observation of a Q branch in the region 83451–83429 cm⁻¹ of the one-photon spectrum, that Ginter et al.¹² assign to lines Q(1). . .Q(7) of the K¹Π₁–X(0–0) transition. A one-photon Ω = 0⁺–Ω = 0⁺ transition should show P and R branches only, but these are quite weak in the reported one-photon spectrum. An alternative explanation could involve overlap of Ω = 1–Ω = 0⁺ (not seen in the present three-photon spectra) and Ω = 0⁺–Ω = 0⁺ bands in the region ∽83453 cm⁻¹: the latter corresponds to m³Π_0⁺–X(0–0), while a possible assignment for the ΔΩ = 1 transition would be the i³Δ₁–X(1–0) band (on the basis of similar rotational constants and quantum defect values with the corresponding (0–0) band which is observed weakly in two-photon absorption at ∽80971 cm⁻¹).

The next origin band within the 6sσ manifold is the M¹Π₁–X(0–0) transition which appears as a strong 3 + 1 REMPI resonance under both circular and linear polarisation, with P, R, S, T branches and an unresolved Q branch around 83848 cm⁻¹. The deduced band origin and rotational constants are in good agreement with previous observation by Ginter et al.¹² Most of the intensity is in the parent ion channel, although a small amount of signal is detected at both H⁺ and Br⁺ ion masses. The different mass channels exhibit different relative intensities of the various rotational lines: for example, the P(2) line at 83814.3 cm⁻¹ (see Electronic Supplementary Information†) is the dominant feature in the H⁺ spectrum, while it is very weak in both Br⁺ and HBr⁺ mass channels. Such observation cannot be compared with previous findings as the band was not observed in two-photon absorption experiments with TOF mass resolution.¹⁷

To higher energies, a weaker transition (band XX) to an Ω = 1 state is observed ∽2381 cm⁻¹ above that to the [italic v]′ = 0 level of the M¹Π₁ state, with suitably reduced B′ rotational constant. This separation is essentially the [italic v] = 1–[italic v] = 0 vibrational spacing in HBr⁺(²Π_i) and matches well with the 2390 cm⁻¹ separation observed between [italic v]′ = 0 and [italic v]′ = 1 levels of the m³Π₁ state in ref. 12. We thus assign band XX with origin at 86229.4 cm⁻¹, shown in Fig. 2, as M¹Π₁–X(1–0). Callaghan et al. have previously attributed a strong band they observed at 86270.2 cm⁻¹ to this transition.¹⁴ Given the similarity of the deduced rotational constants (B_{[italic v]}^′ = 7.897 and 7.88 cm⁻¹ in our case and ref. 14 respectively) and the lack of any comparable feature at this higher wavenumber, the ∽40 cm⁻¹ difference in band origins can be traced to a problem with the vacuum correction of the calibration of the VUV wavelength in ref. 14.

3.2.2 6pσ states: bands VI, VII, XVIII and XIX. Ginter et al.¹² have reported the R¹Π state and the three r ³Π states which arise from the 6pσ manifold. These analogous bands have not been observed in the 2 + 1 REMPI spectrum of HBr, but the corresponding 5pσ states in HCl have been detected using the same technique.⁷ 2 + 1 REMPI transitions involving the R¹Π₁ state are very strong in HCl, while transitions to the r³Π₁ and r³Π_0⁺ states are of moderate intensity and those to the r³Π₂ state are very weak. Moreover, two-photon transitions through the r³Π_0⁺ state in HCl yield both R and S branch lines, thus leading the authors to suggest that the Ω label may not be adequate for a complete description of the sub-band symmetry and angular momentum.

Fig. 2 shows the region of the three-photon spectrum spanning the wavenumber range from 85800 to 86800 cm⁻¹. Transitions to states with Ω = 1 are readily detectable: the R ¹Π₁–X(0–0) band at 85944.4 cm⁻¹ (Fig. 2) is separated by the X²Π_i core spacing from the r³Π₁–X(0–0) band at 83292.9 cm⁻¹ (shown in Fig. 1), as expected for transitions to states in which the coupling of the electronic angular momenta closely approaches pure Hund's case (c). Band origins and rotational constants for both states are in reasonable agreement with Ginter's value (see Table I in ref. 12, which unfortunately does not give constants for the [italic v]′ = 0 level of the R¹Π₁ state).

The band at 85944.4 cm⁻¹ is strong in the circularly polarized spectrum, which was used in the fit to determine spectroscopic constants. The positions of the S(1) and S(2) lines are not well reproduced by these constants; they have thus been excluded from the fit. Even in the linearly polarised spectrum the T branch dominates over the P, Q and R branches, the position of R(0) is slightly shifted and the shape and intensity of the R(1) line do not fit with the overall intensity pattern (see Fig. 2).

Transitions through the r³Π₂ state, built on the lower spin–orbit state of the ion, and the r³Π_0⁺ state (that correlates with the X²Π_1/2 state of HBr⁺) are more difficult to identify. The band origin of the Ω = 2 component of the r multiplet has been reported in one-photon absorption as a strong band at 83271.5 cm⁻¹, despite violation of the ΔΩ = 0, ± 1 selection rule. This energy region is particularly congested in the three-photon spectrum (shown in Fig. 1), and dominated by the K ¹Π₁–X(0–0) band (see Section 3.4) and the aforementioned r³Π₁–X(0–0) band. Simulations using the spectroscopic parameters for the r³Π₂ state from ref. 12 permitted us to locate a weak band (labelled as VI) centered at ∽83270 cm⁻¹. It exhibits a blended Q branch plus a pronounced R branch and a very weak T branch in circular polarisation, while any P lines would be obscured by much stronger transitions to adjacent states. The definite absence of an R(0) line, plus the fact that no other unassigned Ω = 1 states are known to exist in this region, suggest that this could indeed be a transition to an Ω = 2 state. A best fit of the observed lines gives rotational parameters very similar to those reported previously¹² for the r³Π₂–X(0–0) band.

Simulations using constants from ref. 12 also identify a weak band in the 3 + 1 REMPI spectrum with origin at 85901.7 cm⁻¹ (see Fig. 2). The presence of an R branch and a couple of P lines support the previous assignment of excitation to the r³Π_0⁺ state, with origin at ∽85900 cm⁻¹.

3.2.3 ndσ states: bands XVI, XXVII and XXVIII. Previous studies have reported states arising from the ···π³4dσ configuration, but states associated with the 5dσ manifold have not been reported (recall that our choice of principal quantum number for nd and nf Rydberg electrons is 1 smaller than employed in previous work.^13,17,18) Ginter et al. observed the Ω = 1 components of a dσ complex (corresponding to 4dσ in our scheme) [italic v]ia the n³Π₁–X(0–0) band at 77487 cm⁻¹ and the N¹Π₁–X(0–0) band at 81311 cm⁻¹. We note that Callaghan and Gordon¹⁷ suggested that this latter band be reassigned as the I¹Δ₂–X(0—0) transition associated with the orbital promotion ···π³4dπ–···π⁴. The weak band observed with origin at 85532.7 cm⁻¹ may be assignable as the analogue of the n ³Π₁–X(0–0) transition with principal quantum number n = 5. The band, denoted as XVI and shown in Fig. 3, gives a reasonable fit, with the exception of a weak or missing Q(1) line. Such an assignment implies a quantum defect δ = 1.421. If correct, the Ω = 2 component of the ³Π multiplet should lie close in energy. Some unassigned lines appear in this region, but they fit no obvious pattern.

Higher in energy, at ∽87932.7 cm⁻¹ another medium intensity band, labelled as Band XXVII in Fig. 4, displaying a strong Q branch in the linearly polarised spectrum, indicates the presence of another Ω = 1 state. The R(1), R(2) and T(0) lines are all shifted towards higher energy than predicted from a fit to the other lines, suggesting a perturbation of the J′ = 2 and 3 rotational levels. This band is most likely to correspond to excitation to the ···π³5dσ¹Π₁ state which is the n = 5 analogue of the N¹Π₁ state. Other assignments, however, are possible. On the basis of similarities in rotational constants and quantum defects with band XVI, this could be a transition to the [italic v]′ = 1 level of the [5dσ]³Π₁ state (against such assignment is the relative intensity of the bands: the 87932.7 cm⁻¹ feature is stronger than the one at 85532.7 cm⁻¹). The bands at 85532.7 and 87932.7 cm⁻¹ could also be the [italic v]′ = 0 and 1 levels of a ¹Π₁ state associated with the ···π³4fσ configuration, although the problem of relative intensities discussed above would still apply. The magnitude of the observed quantum defect would then be δ = 0.87 and 0.86 respectively (for fσ states we have no empirical values for the quantum defect to compare with but one should expect it to be lower than the value for dδ manifold which is 1.10–1.25, see Table 1). Finally, the band could be assigned as the K¹Π₁–X(2–0) transition (to be discussed in Section 3.4).

The other feature associated with the 5dσ manifold could be band XXVIII observed in the three-photon spectrum around 87992 cm⁻¹ and reported in Fig. 4: it shows a medium-weak T branch (J″ = 0–3) and three lines corresponding to R(0), R(1) and R(2). Inclusion of the R branch lines in the rotational analysis, however, degrades the quality of the fit. Purely on the basis of similarities in quantum defect value (δ = 1.459) this feature is tentatively assigned as the [5dσ]³Π_0⁺–X(0–0) band.

3.2.4 7sσ and 8sσ states: bands XXV and XXXI. The onset of Rydberg levels arising from the ···π³7sσ configuration has been associated with an intense, sharp structure observed in VUV one-photon absorption at 115.0 nm.¹³ At the corresponding three-photon energy we see a weak band centered at 86976.7 cm⁻¹ (Band XXV in Fig. 4). The presence of a blended Q branch and R(0)–R(2) lines in the linearly polarised spectrum is consistent with an Ω = 1 state, which could be the [italic v]′ = 0 level of the [7sσ] ³Π₁ state. This would give a quantum defect δ = 3.075, comparable with the 3.085 value found for the analogous state with n = 6. Simply on the basis of quantum defect considerations, however, this band could also be assigned as either the ³Δ₁–X(0–0) or the ³Σ₁⁻–X(0–0) band within the 6pπ Rydberg manifold.

In the region around 89550 cm⁻¹ we observe a strong feature, the density of lines within which suggests contributions from more than one state (see Fig. 5). In the same energy region the VUV spectrum from ref. 13 shows an intense, localised but unresolved band (at λ = 111.6 nm) which, on quantum defect grounds, has been assigned to an overlap of n = 7 members of the sσ Rydberg series correlating with the X ²Π_1/2 ion core, and of states with configuration ···π³8sσ correlating with X²Π_3/2. If this is the case, in three-photon absorption we might observe contributions from four states: ³Π₁ and ³Π₂ components associated with ···π³8sσ plus the ³Π_0⁺ and ¹Π₁ states from the orbital promotion 7sσ–π. One Ω = 1 state is clearly apparent in the linearly polarised spectrum shown in Fig. 5(b), labelled as Band XXXI, centered at 89548 cm⁻¹ with a dominant Q branch and a much weaker R branch, but the rest of the features cannot be fitted in a unique manner. On the basis of quantum defects the Ω = 1 feature could be either the ¹Π₁–X(0–0) band (n = 8, δ = 3.094) or the ³Π₁–X(0–0) band (n = 7, δ = 3.089). A third possible assignment for this band could be the transition to the [italic v]′ = 0 level of the ¹Π₁ state within the 5fσ Rydberg manifold; this would give a quantum defect δ = 1.094, still in agreement with expectations.

3.2.5 Bands XXXII, XXXIII and XXXIV. Three further bands at high energy are plausible candidates for assignment to the ···π ³nlσ manifold of states, and are shown in Fig. 6. The first band is weak, with an origin at 89948 cm⁻¹, and exhibits just P and R branches. Accordingly, it is assigned to excitation to an Ω = 0⁺ state which is labelled as XXXII in Table 2 and may correspond to the [5fσ] ³Π_0⁺[italic v]′ = 0 state with a quantum defect of δ = 0.981. Band XXXIII at 90092 cm⁻¹ corresponds to a transition to an upper state with Ω = 1 and is assigned to excitation to the ¹Π₁ state arising from the ···π³7pσ electronic configuration. Band XXXIV, with origin at 90417 cm⁻¹ is very weak compared with others observed in the same wavenumber region. A unique fit of the rotational lines is, however, possible using the spectrum recorded from the Br⁺ mass channel, and reveals an Ω = 0⁺ excited state that is assigned as [···π ³7pσ] ³Π_0⁺.

3.3 pπ and dπ manifolds

As outlined in Table 1, the ···π3nlπ configuration gives rise to singlet and triplet Σ+, Σ− and Δ states. Excitations from the ground state to all these are allowed in the three-photon REMPI spectrum, with the exception of states having minus (−) parity (i.e. 1Σ0−− and 3Σ0−+). Previous studies have shown that the 1Σ0++ and 3Σ0+− states suffer strong perturbations because of proximity to ion-pair states. Interactions between the V1Σ+ ion-pair state and the [5pπ]E1Σ+ state are found to be particularly strong,19,20 causing a characteristic compression of rovibrational levels in the E manifold but an expansion of levels in the V state. Despite predictions from theoretical calculations28 that such perturbative effects will be irrelevant for Δ and Σ− states, at least for HCl, a recent 2 + 1 REMPI spectroscopic investigation found evidence for [5pπ]F1Δ∽V1Σ+ near-resonant interactions in both HCl and HBr.20 As is well established for both HCl6,7 and HBr,17 REMPI transitions through excited 0+ states (either 1Σ+ or 3Σ−) are distinguished by the generation of both molecular and fragment ion yield signals.

3.3.1 Bands II and XII; v′ = 2 and 3 levels of the E¹Σ⁺ state. Vibrational levels up to [italic v]′ = 4 of the E¹Σ⁺ Rydberg state have been identified in one¹² and two-photon^17,19 absorption spectra, and Kvaran and coworkers²¹ reported a 3 + 1 REMPI spectrum of the [italic v]′ = 0 level. The levels with [italic v]′ = 0 and 1 lie below the wavenumber region scanned in the current study, but transitions to [italic v]′ = 2 and 3 levels of the E¹Σ⁺ state are observed at 82275.8 cm⁻¹ (see Fig. 7) and 84251 cm⁻¹ (see Fig. 8) respectively, with ion TOF signals obtained at four masses corresponding to ⁷⁹Br⁺, H⁷⁹Br⁺, ⁸¹Br⁺ and H⁸¹Br⁺.

The band origins and rotational constants derived from our spectra agree well with previous studies of the E–X(2–0) band, while a slight discrepancy is found between our values for B′, D′ and ν₀ of the E–X(3–0) band and corresponding values determined by Callaghan and Gordon¹⁷ and Kvaran et al.¹⁹ The [italic v]′ = 4 level has been observed in 2 + 1 REMPI¹⁹ at ∽86132 cm⁻¹: in this energy region we observe transitions to two Ω = 1 states, with band origins at 85944 and 86229 cm⁻¹ (see Section 3.2 for assignments) but no transition to an Ω = 0⁺ state is observed using either circularly or linearly polarised UV radiation (see Fig. 2). The ···π³5pπ configuration also gives rise to the F¹Δ₂, f³Δ₁ and g³Σ₁⁻ states, and vibrationally excited levels of these states might be responsible for bands in our wavenumber range. No such transitions to levels with [italic v]′>1, however, are evident in the current work or in previous one and two-photon absorption experiments.

3.3.2 4dπ states: bands I, XI, XIII and XXIV. The H1Σ+ and j3Σ− states arise from the ···π34dπ electronic configuration and have been observed and analysed previously. Transitions to vibrational levels up to [italic v]′ = 2 of the former and the [italic v]′ = 0 level of the latter have been reported in ref 12, 17 and 21. We observed the H1Σ+–X(2–0) band at 84041 cm−1 (band XI) and the j3Σ0+−–X(0–0) band (band I) at 82185 cm−1 (see Fig. 7) and, in addition, report observation of the [italic v]′ = 1 and 2 levels of the j-state. The band at 84041 cm−1 is visible in the linearly polarised spectrum with medium-weak intensity: it is more evident in the Br+ channel than at the parent ion mass since the latter is dominated by overlap of the T branch of the M1Π1–X(0–0) band (see Section 3.2).

Fitted rotational constants (reported in Table 2) are in perfect agreement with those given by Callaghan and Gordon.¹⁷ These authors claim to have detected transitions to the next two vibrational levels ([italic v]′ = 3 and 4) of the H state, but do not report details in ref. 17; the H–X(3–0) band should lie in the wavenumber region 86000–86500 cm⁻¹, while the H–X(4–0) should be around 88000–88500 cm⁻¹, but our 3 + 1 REMPI spectra reveal no such bands.

Band XIII with origin at 84454 cm−1 (see Fig. 8) fits a transition with an Ω = 0+ upper state, which is assigned as the [italic v]′ = 1 level of the j3Σ0+− state on the basis of similarities in the quantum defect value (δ = 1.261) and rotational constants when compared with those derived from the j–X(0—0) band at 82185 cm−1 (δ = 1.254, see Table 2 for spectroscopic constant values).

There is a strong feature at 84440.0 cm⁻¹ in close proximity to the P(1) line; this line was thus excluded from the fit. Furthermore, several other unassigned weaker features indicate the presence of another unidentified band, with a possible blended Q branch at 84440 cm⁻¹. A weaker band centered at 86862.4 cm⁻¹ and identified as band XXIV in Table 2 shows a line pattern consistent with an Ω = 0⁺ state and rotational constants similar to the [italic v]′ level of the j-state (see Fig. 4). A T branch is present in the circularly polarised spectrum, but was disregarded in the determination of rotational constants as its inclusion in the best fit procedure increased the standard deviation significantly. A quantum defect value of δ = 1.246, together with similarities in rotational parameters, supports the assignment of this band as excitation to the [italic v]′ = 2 level of the j-state.

3.3.3 6pπ states: bands XIV, XXV and XXVI. The ···π36pπ configuration should give rise to two 0+ states around 85000 cm−1, of which only the lower in energy of the pair, corresponding to a 3Σ0+− state in (Λ, S) coupling, has been observed in two-photon absorption, with origin at 84806.5 cm−1.17 This state is evident in the 3 + 1 REMPI spectrum as a medium intensity band (XIV) (though the origin is determined to be 84807.2 cm−1); a fit to the rotational structure gives rotational constants in agreement with those derived by Callaghan and Gordon (see Fig. 8). In addition, we observe a transition which we assign to the [6pπ]3Σ0+− (1–0) band, with origin at 87309.4 cm−1 (see Fig. 4 and Band XXVI of Table 2). Band XXIV with origin at 86862.4 cm−1, assigned in Section 3.3.2 to excitation to [italic v]′ = 2 of the [4dπ]j3Σ0+− state, could alternatively correspond to a transition to the 1Σ0++ state arising from the ···π36pπ configuration; this state correlates with the X2Π1/2 spin–orbit state of the HBr+ ion. This assignment would, however, give a quantum defect δ = 2.667, and because of the difference from the δ = 2.563 value for the 3Σ0+−–X(0–0) band (XIV, with origin at 84807.2 cm−1), we prefer the earlier assignment, as listed in Table 2.

Finally in this sub-section, we note the observation of band XXV with origin at 86976.8 cm⁻¹. This band is either the 7sσ³Π₁ state (Section 3.2.4), or may be assigned as excitation to either a ³Δ₁ or ³Σ₁⁻ state arising from the ···π³6pπ configuration, with quantum defect δ = 2.648.

3.3.4 ndπ states: bands XXI, XXII and XXX. At wavenumbers around 86510 cm−1, we observe a weak band (XXII, see Fig. 2) that is most clearly discernible in the Br+ mass channel of the spectrum recorded with linearly polarised light. The band consists of a distinct R branch, with perhaps a very weak Q(1) line, which makes the assignment in terms of excitation to an Ω = 0+ or 1 state uncertain. As other Q lines are not observed, the Ω = 0+ excited state assignment seems more likely. The wavenumber of the derived origin coincides with expectations for a transition to the [italic v]′ = 3 level of the [4dπ]H1Σ0++ state, but we prefer to assign the band to the [5dπ] 1Σ0++–X(0–0) transition. This judgement is based on Franck–Condon considerations, and a previous adoption of this assignment for the corresponding band in one-photon VUV laser-induced fluorescence spectroscopy;14 an Ω = 0+ state with similar rotational constants (B′ = 6.68 cm−1) was reported with an origin value of ∽86551.3 cm−1, i.e. ∽41 cm−1 higher in energy than our fitted value for νi0 (see Table 2). As mentioned previously, comparisons drawn between one- and three-photon measurements of the origin of the M1Π1–X(1–0) transition revealed an identical shift of the former determination by ∽41 cm−1 from our three-photon value. This shift can, in both instances, be traced to an incorrect treatment of the vacuum correction in the earlier study.14

Two transitions to states with Ω = 3 (denoted as bands XXI and XXX in Table 2) are observed with origins at 86322 and 89231 cm⁻¹. The two Ω = 3 states may arise, respectively, from the ···π³5dπ and ···π³6dπ electronic configurations. As their assignments are not unique, however, further discussion is deferred to Section 3.5 which concentrates on Rydberg states with Ω = 3.

3.4 dδ manifold

The ···π³ndδ configuration results in singlet and triplet Π and Φ states. Transitions to all components are allowed from the ground state under three-photon selection rules in Hund's case (c) (Ω, ω) coupling, with the sole exception of the Ω = 4 component of the ³Φ multiplet.

3.4.1 4dδ states: bands III, IV, V, XV, XVII and XXVII. Ginter et al.¹² reported spectra of transitions to the k³Π_0,1 (both [italic v]′ = 0 and 1 levels), k³Π₂, K¹Π₁ and l³Φ₂ states of a dδ Rydberg complex; the last two states were also observed by Callaghan and Gordon.¹⁷Fig. 7 shows a 3 + 1 REMPI spectrum of the k³Π₁–X(1–0) band, which has medium intensity for linearly polarised radiation, but is weaker when circularly polarised light is employed (i.e., the transition is mainly carried by the T₁¹(O) component of the three-photon transition operator). The band origin is at 82745.2 cm⁻¹ and both quantum defect and rotational constants are in agreement with a previous report.¹²

As discussed in Section 3.2.1, the K¹Π₁–X(0–0) band was incorrectly assigned in the one-photon absorption spectrum to a band at 83453.5 cm⁻¹ and this assignment was maintained in analysis of two-photon absorption spectra. We prefer to reassign band VIII at 83453.5 cm⁻¹ as the m³Π_0⁺–X(0–0) band and instead assign the very strong band observed in the three-photon spectrum at 83237.7 cm⁻¹ to the K¹Π₁–X(0–0) transition (see Fig. 1 and Table 2 for spectroscopic constants). The spectrum shows P, Q, R and T branches together with an S(1) and a very weak S(2) line, and the T branch dominates the circularly polarised spectrum.

A transition to the [italic v]′ = 1 level of the K¹Π₁ state is evident in Fig. 3 (band XVII). The band origin is at 85621.9 cm⁻¹, i.e. [italic v]′ = 1 lies ∽2380 cm⁻¹ higher in energy than the [italic v]′ = 0 level, in good agreement with the vibrational spacing within the X²Π_1/2 state of HBr⁺, upon which ion core the K state is based. The band shows strong Q and R branches with a weaker P branch in the linearly polarised spectrum, plus a T branch that is most pronounced for circular polarisation. The best fit for determination of rotational constants excludes the weak Q(3) and Q(4), which appear slightly displaced from the corresponding simulated lines. The band assignment is based on similar quantum defect values to the [italic v]′ = 0 level (δ = 1.149 for [italic v]′ = 0 and 1.145 for [italic v]′ = 1). A further ∽2310 cm⁻¹ higher in energy than the K¹Π₁–X(1–0) band, we observe excitation to another Ω = 1 state with medium intensity in the linearly polarised spectrum and origin at 87932.7 cm⁻¹ (band XXVII, discussed previously in Section 3.2.3). The position in energy (and thus the quantum defect, δ = 1.139) and the lower relative intensity, are consistent with an assignment of the transition to the [italic v]′ = 2 level of the K state. If this assignment is correct, the first-order rotational constant (B′) for the K state shows a gradual increase with vibrational quantum numbers (B′ = 7.002, 7.369 and 7.74 cm⁻¹ for [italic v]′ = 0–2). Following the argument of ref. 19 and 20, this increase could be interpreted as being due to a decreasing downward repulsion experienced by J levels in a particular [italic v]′ level of the K¹Π₁ state, because of interactions with higher lying levels in another, unidentified, Ω = 1 state. Alternatively it could be due to heterogeneous interaction with specific [italic v]′ levels of the V¹Σ⁺ state, that lie in near-resonance with the K state vibrational levels. In particular [italic v]′ = m + 14, m + 18 and m + 23 of the V state, which have never been identified, should have energies in the regions of 83300–83400, 85620–85800 and 88000–88300 cm⁻¹, i.e. close to the [italic v]′ = 0, 1 and 2 levels of the K Rydberg state. The assignment of band XXVII with origin at 87932.7 cm⁻¹, however, remains inconclusive, and thus several possibilities are listed in Table 2.

The components associated with a Φ state arising from the ···π³4dδ configuration that have been previously reported are the Ω = 2 state of the l³Φ multiplet, and the L¹Φ₃ state. The l³Φ₂ state correlates with the upper spin–orbit state of HBr⁺ and, from 2 + 1 REMPI studies, is identified as having an origin at ∽82583 cm⁻¹.¹⁷ The Ω = 3 and 4 components, correlating with HBr⁺(X²Π_3/2), should be ∽2630 cm⁻¹ lower in energy, i.e. outside our scanned region. The other Φ component, L¹Φ₃, was observed recently using 3 + 1 REMPI spectroscopy²¹ (with an origin at 82837 cm⁻¹), and also appears strongly in the 3 + 1 REMPI spectra reported here recorded using both linearly and circularly polarised light. We observed the L–X(0–0) band (band IV) with origin at 82857.4 cm⁻¹, see Fig. 7) and the (1–0) band (band XV) at 85243.9 cm⁻¹. Further details are given in Section 3.5.

3.4.2 5dδ and 6dδ states: bands XXI, XXIII, XXIX and XXX. The corresponding 5dδ states have not been reported previously, but, on the basis of quantum defect values for n = 4, they should be grouped around 86550 and 89200 cm−1, separated by the X2Πi core spacing. At ∽86585.6 cm−1 we observe a strong band (band XXIII) within the linearly polarised spectrum (see Fig. 2), with an associated T branch evident in circular polarisation. The presence of a blended Q branch and an R(0) line indicates an Ω = 1 upper state; from purely energetic considerations, a possible assignment could be one of the two Ω = 1 states arising from the ···π36pπ configuration (either 3Δ1 or 3Σ1−). However, the 3Σ0+− state at 84807 cm−1 that also derives from this electronic configuration and which is described in Section 3.3, shows only weak intensity, and we prefer an assignment of the band with origin at 86585.6 cm−1 as the [5dδ]3Π1–X(0–0) band.

In the same energy region, at 86322.6 and 88914.0 cm⁻¹, we observe two Ω = 3 bands of considerable strength (denoted as XXI and XXIX) shown in Fig. 2 and 5 respectively. They are separated by ∽2591 cm⁻¹, close to the 2640 cm⁻¹ core spacing of HBr⁺(X²Π_i) and have similar rotational constants (B′ = 8.704 and 9.120 cm⁻¹ respectively, see Table 2). Thus, they can be assigned, respectively, as transitions to the [italic v]′ = 0 levels of the Ω = 3 components of the ³Φ and ¹Φ states derived from occupancy of the 5dδ Rydberg orbital. Further details, together with an alternative assignment for the lower energy band, are given in the next section.

There remains a band with origin at 89231.4 cm⁻¹ (band XXX) that is assigned to a transition to an upper state with Ω = 3, which is either the ³Φ₃ state from the 6dδ Rydberg complex, or alternatively may be the [6dπ]³Δ₃ state. Both options are listed in Table 2.

3.5 Ω = 3 states

The Rydberg states of hydrogen halides with Ω = 3 reported in the current study are attributed to [···π3nlπ] 3Δ and [···π3nlδ] 1,3Φ states. An advantage of the three photon selection rules is that transitions from the ground X1Σ0++ electronic state to states with Ω = 3 are fully allowed in Hund's case (c). As discussed previously, such transitions are carried by a T33(O) spherical tensor component and, as a consequence, the relative intensities of the allowed (N···T) branches are immune to the polarisation of the radiation used to excite the transition. Thus Ω = 3 states present a unique pattern of lines, which makes their assignment straightforward.

We have observed four different, previously unreported Ω′ = 3 bands, and one further such band that has been the subject of a recent, more limited 3 + 1 REMPI investigation.²¹ Bands IV and XV, at 82857.4 and 85243.9 cm⁻¹, are assigned to excitation to the [italic v]′ = 0 and [italic v]′ = 1 levels of the L¹Φ₃ state arising from the 4dδ Rydberg configuration, and the assignment of band IV is in accord with the recent work of Kvaran and coworkers.²¹ The corresponding spectra are shown in Fig. 7 and Fig. 3 respectively. These are strong bands in the 3 + 1 REMPI spectrum (although the relative intensity of the transition to [italic v]′ = 0 exceeds that for excitation to [italic v]′ = 1), with quantum defect values (∽1.19 for both [italic v]′ states) similar to the values observed for the k³Π multiplet within the same Rydberg level, seen in one-photon absorption (δ = 1.206, 1.171 and 1.207 for ground vibrational states with Ω = 0, 1 and 2). The rotational constants of the L state (see Table 2) agree very well with those derived in ref. 21 and are similar to those measured in two-photon absorption for the l³Φ₂ state.¹⁷ The Q(3), R(2) and S(1) rotational lines in the L–X(1–0) band are all shifted with respect to simulated line positions, suggesting a perturbation of the J′ = 3 rotational level.

The next observed transition to a state with Ω = 3 is band XXI at 86322.6 cm⁻¹, already mentioned in Section 3.4: it is a strong band (see Fig. 2) and two possible assignments are either the [5dπ] ³Δ₃–X(0–0) transition or the [5dδ]³Φ₃–X(0–0) transition. Both interpretations imply a quantum defect of 1.243, in reasonable agreement with analogous values for the known i³Δ₃ (4dπ, δ = 1.366) and l³Φ₂ (4dδ, δ = 1.216) states, preventing a unique assignment.

There are two further observed transitions to Ω = 3 states, bands XXIX and XXX at 88914.0 and 89231.4 cm⁻¹ respectively (see Fig. 5). They are clearly visible in the circularly polarised spectrum with medium-weak intensity, while the linearly polarised spectrum shows overlap with some unassigned structure. Band XXIX has B_{[italic v]}^′ = 9.1 cm⁻¹, different from any other observed Ω = 3 states, thus ruling out the assignment as excitation to the [italic v]′ = 1 level of the state with [italic v]′ = 0 at 86322.6 cm⁻¹. The only possible assignment, on the basis of the δ value (1.256) is to the [italic v]′ = 0 level of the [5dδ] ¹Φ₃. As with band XXI at ∽86323 cm⁻¹, two different assignments of band XXX are possible on the basis of a quantum defect value δ = 1.252: either excitation to the [6dπ] ³Δ₃ or [6dδ] ³Φ₃ state.

3.6 Other band systems and the short wavelength region

Certain features in the 3 + 1 REMPI spectrum of HBr remain unassigned but, for completeness, we report our observations of these bands and lines in this section, although they are not included in Table 2. Some previously reported bands were not observed under the conditions of our experiments: for example, the k3Π0+–X(1–0) band (with origin at 82404.8 cm−1) and the E1Σ0++–X(4–0) band (with origin at 86131.9 cm−1) do not appear in our spectrum.

A weak band with an origin at 84519 cm⁻¹ is shown in Fig. 8, and is most pronounced in the spectrum recorded with circularly polarized light. The band can be successfully simulated with Ω′ = 1, and is tentatively assigned to excitation to the [italic v]′ = 0 level of the [6pπ]³Σ₁⁺ state, although the analogous state built upon the 5pπ Rydberg orbital has not been seen in the 3 + 1 REMPI spectra. The new state will have an associated quantum defect of δ = 2.615, and a spectral fit returns rotational constants B′ = 9.92(13) cm⁻¹ and D′ = 10.9(40) × 10⁻³ cm⁻¹, the former of which is unusually large.

At 86396 cm⁻¹, a weak band is observed most clearly using circular polarization, and monitoring the Br⁺ mass channels. Analysis suggests a transition to a state with either Ω′ = 0 or 1. A moderately strong band with origin at 87201.5(8) cm⁻¹ fits most readily in terms of transition to an Ω′ = 2 state, giving B′ = 9.44(10) cm⁻¹ and D′ = 8.5(30) × 10⁻³ cm⁻¹. The band is apparent in Fig. 4 and may arise from excitation to one of the following states, [4dδ] l³Φ₂[italic v]′ = 2 (with quantum defect δ = 1.214), [6pπ]¹Δ₂ (δ = 2.609) or [7sσ]³Π₂ (δ = 3.012). The first assignment is the least likely since the analogous band with [italic v]′ = 1 has not been observed. There is another fairly strong band with origin at ∽88394 cm⁻¹ that appears to have an upper state with Ω′ = 3. The best estimate of a rotational constant for the upper state is B′ = 4.287 cm⁻¹, and this excited state is thus unlikely to correspond to a Rydberg orbital built upon an X²Π ion core.

A band in the vicinity of 88500 cm⁻¹ defied all attempts at analysis, while one with origin at 88997.8(6) cm⁻¹ fitted satisfactorily to an Ω′ = 1 − Ω = 0⁺ transition if just the R branch lines and the P(2) and Q(2) lines were included in the fit (see Fig. 5). The resultant rotational constants were B′ = 7.92(14) cm⁻¹ and D′ = − 1.0(64) × 10⁻³ cm⁻¹, and possible assignments include excitation to the [5dπ]³Δ₁, [5dπ]³Σ₁⁻, [5dδ]¹Π₁ or [6dσ]³Π₁ states. The position of the Q branch is peculiar, however, and it may be that the band is in fact an excitation to an Ω′ = 0⁺ state with an overlapping band providing a feature with the appearance of a sharp Q branch.

One band evident in Fig. 6 is unassigned, but has the appearance of an Ω = 0⁺ − Ω = 0⁺ transition, with origin at 90562.0(3) cm⁻¹. The rotational constants derived from a fit are B′ = 8.648(40) cm⁻¹ and D′ = 34.4(12) × 10⁻³ cm⁻¹. One possible assignment is excitation to the [5dσ]³Π_0⁺[italic v]′ = 1 state, with a quantum defect of 1.412 that agrees well with that for the associated [italic v]′ = 0 level.

Fig. 9 shows a spectrum spanning excitation from 90700–93140 cm−1. Numerous bands are apparent in this three-photon wavenumber range, most of which have not been interpreted in terms of an upper state value of Ω. Three bands have, however, been fitted, two to transitions involving Ω′ = 0 states, the other to an Ω′ = 1 excited state. The first of these bands, with origin at 91143.3 cm−1 yields rotational constant B′ = 7.524(85) cm−1 and is most likely to arise from excitation to the [7pπ]1Σ0++[italic v]′ = 0 level with δ = 2.573. The second band, with origin at 91402.8(8) cm−1, could arise from excitation to either the [6dπ]3Σ0+−[italic v]′ = 0 or [6dσ]3Π0+[italic v]′ = 0 level (in either case with δ = 1.466). Spectroscopic fits return B′ = 7.71(30) cm−1 and D′ = − 0.050(24) cm−1. The final characterised band has an origin at 91808.9(5) cm−1, fits to give B′ = 8.09(11) cm−1 and D′ = − 1.5(54) × 10−3 cm−1 and has several plausible assignments.

In the region beyond the IP, a number of strong, featureless bands appear, separated by ∽350 cm⁻¹, and are most clearly seen in the spectrum recorded with circular polarisation. These features have not been assigned.

4 Summary

REMPI with time-of-flight mass resolution has been used to measure the three-photon absorption spectrum of H79Br and H81Br between 81900 and 94900 cm−1 employing both linear and circularly polarised UV light. Over the energy range 82000–91000 cm−1, 34 bands have been analysed and assigned to transitions from the ground X1Σ0++ state of HBr to Rydberg states belonging to the sσ, pσ, dσ, pπ, dπ and dδ manifolds and correlating with the ground electronic state X2Π3/2,1/2 of HBr+. The analysis reveals five states with Ω = 3. The electronic energy level structure of HBr is summarised in Fig. 10 which shows the various Rydberg complexes arising from ···π3nlλ configurations.

Fig. 10 Energy level diagram including all of the assigned levels of HBr in the energy region from 80420 cm⁻¹ to the first ionisation limit. States marked ○ are those correlating with HBr⁺(X²Π_3/2), and those marked — ionize to the HBr⁺(X²Π_1/2) limit. States are grouped according to the primary lλ character of the Rydberg electron, and are labelled using ^2S+1Λ_Ω notation, together with the vibrational level, which is shown in parentheses when [italic v]≠0.

Acknowledgements

We are very grateful to Dr. C. M. Western for many valuable discussions, and to P. A. Cook and Dr. P. M. Regan for help with some of the data collection. The EPSRC is acknowledged for experimental funding and for the award of a Senior Research Fellowship to MNRA and postdoctoral financial support for SRL. DA would like to thank the EU for the award of a Marie-Curie Fellowship.

References

1. NIST Atomic Spectra Database (ASD) at http://physics.nist.gov/cgi-bin/AtData/main_asd. .
2. A. J. Orr-Ewing, W. R. Simpson, T. P. Rakitzis, S. A. Kandel and R. N. Zare, J. Chem. Phys., 1997, 106, 5961, and references therein.
3. S. G. Tilford, M. L. Ginter and J. T. Vanderslice, J. Mol. Spectrosc., 1970, 33, 505; S. G. Tilford and M. L. Ginter, J. Mol. Spectrosc., 1971, 40, 568; D. S. Ginter and M. L. Ginter, J. Mol. Spectrosc., 1981, 90, 177.
4. S. Arepalli, N. Presser, D. Robie and R. J. Gordon, Chem. Phys. Lett., 1985, 118, 88.
5. J. B. Nee, M. Suto and L. C. Lee, J. Chem. Phys., 1986, 85, 719.
6. T. A. Spiglanin, D. W. Chandler and D. H. Parker, Chem. Phys. Lett., 1987, 137, 414.
7. D. S. Green, G. A. Bickel and S. C. Wallace, J. Mol. Spectrosc., 1991, 150, 303; D. S. Green, G. A. Bickel and S. C. Wallace, J. Mol. Spectrosc., 1991, 150, 354; D. S. Green, G. A. Bickel and S. C. Wallace, J. Mol. Spectrosc., 1991, 150, 388; D. S. Green and S. C. Wallace, J. Chem. Phys., 1992, 96, 5857.
8. W. C. Price, Proc. R. Soc. London, Ser. A, 1938, 167, 216.
9. R. F. Barrow and J. G. Stamper, Proc. R. Soc. London, Ser. A, 1961, 263, 259; R. F. Barrow and J. G. Stamper, Proc. R. Soc. London, Ser. A,, 1961, 263, 277.
10. M. L. Ginter and S. G. Tilford, J. Mol. Spectrosc., 1970, 34, 206.
11. M. L. Ginter and S. G. Tilford, J. Mol. Spectrosc., 1971, 37, 159.
12. D. S. Ginter, M. L. Ginter and S. G. Tilford, J. Mol. Spectrosc., 1981, 90, 152.
13. J. B. Nee, M. Suto and L. C. Lee, J. Chem. Phys., 1986, 85, 4919.
14. R. Callaghan, Y.-L. Huang, S. Arepalli and R. J. Gordon, Chem. Phys. Lett., 1989, 158, 531.
15. S. Arepalli, N. Presser, D. Robie and R. J. Gordon, Chem. Phys. Lett., 1985, 117, 64.
16. J. Xie and R. N. Zare, Chem. Phys. Lett., 1989, 159, 399.
17. R. Callaghan and R. J. Gordon, J. Chem. Phys., 1990, 93, 4624.
18. M. A. Baig, J. Hormes, J. P. Connerade and W. R. S. Garton, J. Phys. B, 1981, 14, L147.
19. Á. Kvaran, Á. Logadóttir and H. Wang, J. Chem. Phys., 1998, 109, 5856.
20. Á. Kvaran, H. Wang and Á. Logadóttir, J. Chem. Phys., 2000, 112, 10811.
21. Á. Kvaran, B. G. Waage and H. Wang, J. Chem. Phys., 2000, 113, 1755.
22. T. Munakata, T. Muzukuki, A. Misu, M. Tsukakoshi and T. Kasuya, Laser Chem., 1987, 7, 129.
23. N. P. L. Wales, W. J. Buma, C. A. de Lange, H. Lefebvre-Brion, K. S. Wang and V. McKoy, J. Chem. Phys., 1996, 104, 4911.
24. M. N. R. Ashfold and J. D. Howe, Annu. Re[italic v]. Phys. Chem., 1994, 45, 57.
25. R. A. Morgan, A. J. Orr-Ewing, D. Ascenzi, M. N. R. Ashfold, W. J. Buma, C. R. Scheper and C. A. de Lange, J. Chem. Phys., 1996, 105, 2141.
26. K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules, Van Nostrand, New York, 1979..
27. PGOPHER spectral simulation program written by C. M. Western. A summary of the program and the Hamiltonian used is given in M. E. Green and C. M. Western, J. Chem. Phys., 1996, 104, 848..
28. M. Bettendorff, S. D. Peyerimhoff and R. J. Buenker, Chem. Phys., 1982, 66, 261.

---

Footnotes

† Electronic Supplementary Information available. See http://www.rsc.org/suppdata/cp/b0/b007425j/

‡ Current address: Dipartimento di Fisica, Universita di Trento, I-38050 Povo (TN), Italy.

---