Multivariate data analysis of quality parameters in drinking water
O.
Ortiz-Estarelles
a,
Y.
Martín-Biosca
a,
M. J.
Medina-Hernández
a,
S.
Sagrado
*a and
E.
Bonet-Domingo
b
aDepartamento de Química Analítica, Facultad de Farmacia, Universitat de Valencia, C/Vicente Andrés Estellés s/n, 46100
Burjassot, Valencia, Spain.. E-mail: salvador.sagrado@uv.es
bGeneral de Análisis Materiales y Servicios (GAMASER)
S.L., Valencia, Spain
First published on 15th December 2000
Abstract
The quality of water destined for human consumption has been treated as a multivariate property. Since most of the quality parameters are obtained by applying analytical methods, the routine analytical laboratory (responsible for the accuracy of analytical data) has been treated as a process system for water quality estimation. Multivariate tools, based on principal component analysis (PCA) and partial least squares (PLS) regression, are used in the present paper to: (i) study the main factors of the latent data structure and (ii) characterize the water samples and the analytical methods in terms of multivariate quality control (MQC). Such tools could warn of both possible health risks related to anomalous sample composition and failures in the analytical methods.
Introduction
The importance of the quality of water for human consumption with regard to health makes it necessary to establish norms to regulate it. These include limits for all the parameters that directly affect human health and can produce deterioration in quality.1 Most of these parameters are obtained by applying analytical methods. The analytical laboratory is responsible for the accuracy of analytical data2 and therefore for water quality estimation. In the case of multivariate properties, such as water quality, a vector of analytical results is generated in laboratories for each analysed sample. In such cases, monitoring univariate analytical data on individual parameters can be very misleading and difficult to interpret.3 Alternatively, it is possible to use the joint information obtained from several analytical results (multivariate statistics).Multivariate techniques, such as principal component analysis (PCA) and partial least squares (PLS) regression, are being used more and more to solve analytical problems. For example, there are numerous applications of these techniques in the water analysis field. In most cases, they centre on the characterization of environmental problems,4–8 otherwise, they centre on multivariate calibration tasks for determining chemical species.9,10 In the last few years, multivariate statistical process control (MSPC) techniques have been developed3,11–13 based on PCA and PLS models. These techniques have proven to be useful in identifying changes in the systems and sensor failures in chemical processes. However, MSPC techniques have not been widely applied in the analytical area and have centred on the control of spectral signals.14,15 As far as we know these techniques have not been used to diagnose the possible bias in analytical methods as a means of internal validation in analytical laboratories.
In the present study, several tools based on PCA and PLS models are used to characterize the water quality problem, taking into account the origin of the samples (network or well) and the sampling zone. In addition, MSPC plots are used to classify the samples into three categories: outliers, out-of-control and in-control samples. In the case of outliers and out-of-control samples, some statistical criteria have been used in combination with human expert assessment in order to decide whether the problem is due to sample contamination (with toxicity implications), or to a possible systematic error in an analytical method (which deserves to be investigated by external validation). As a case study, the quality of drinking water from the distribution network of the province of Valencia (Spain) has been approached. This is a preliminary step for further applications to the design of an internal multivariate analytical quality control programme.
Experimental
The values of 25 parameters from 136 water samples corresponding to a period of 1 year (1995) were used. The samples were taken at different points of the drinking water network and wells from the province of Valencia (Spain). The analyses were carried out in the GAMASER S.L. laboratories (specialized in the routine analysis of drinking water in this province) following standard methods of analysis.16 The 25 parameters (see Table 1), selected from a total of 60 (complete analysis), were those showing concentration levels over the quantification limits (10 × [standard deviation of the intercept/slope] from the calibration curve) of the corresponding analytical methods.| No. | Parameter | Units | Minimum value | Maximum value | Medium value | Median | Percentile 95% | Legal limit |
|---|---|---|---|---|---|---|---|---|
| 1 | Turbidity | NTU | 0.1 | 12 | 0.5 | 0.3 | 0.6 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
| 2 | pH | pH units | 7.11 | 7.97 | 7.59 | 7.60 | 7.89 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6.5–9.5 6.5–9.5 |
| 3 | Conductivity | μS/cm (20 °C) | 598 | 1558 | 1117 | 1154 | 1364 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2500 2500 |
| 4 | Chloride | mg L−1 | 30 | 193 | 109 | 117 | 150 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
| 5 | Sulfate | mg L−1 | 44 | 368 | 269 | 305 | 341 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
| 6 | Silica | mg L−1 | 2 | 16.3 | 6.2 | 5.6 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10.8 10.8 |
— |
| 7 | Calcium | mg L−1 | 86 | 194 | 140 | 141 | 169 | — |
| 8 | Magnesium | mg L−1 | 25 | 59 | 41 | 41 | 50 | (50) |
| 9 | Sodium | mg L−1 | 15 | 120 | 66 | 71 | 97 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
| 10 | Potassium | mg L−1 | 0.8 | 37.5 | 3.2 | 2.9 | 4.3 | (12) |
| 11 | Hardness | °French hardness | 32.2 | 69.7 | 51.6 | 53.3 | 63.7 | — |
| 12 | Alkalinity | mg L−1 HCO3− | 185 | 355 | 255 | 253 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 323 323 |
— |
| 13 | Total dissolved solids | mg L−1 | 396 | 1312 | 829 | 853 | 1040 | (1500) |
| 14 | Dissolved oxygen | % O2 | 77 | 115 | 98 | 98 | 108 | — |
| 15 | Nitrate | mg L−1 | 2 | 131 | 32 | 19.5 | 91 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
| 16 | Oxidation (KMnO4) | mg L−1 O2 | 0.6 | 1.8 | 1.0 | 1.0 | 1.4 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
| 17 | Total organic carbon (COT) | mg L−1 C | 0.59 | 2.98 | 1.52 | 1.49 | 2.36 | — |
| 18 | Boron | μg L−1 | 15 | 296 | 97.5 | 93.0 | 168.3 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 1000 |
| 19 | Fluoride | μg L−1 | 91 | 388 | 243 | 253 | 328 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1500 1500 |
| 20 | Trihalomethanes (THM) | μg L−1 | 10 | 137.7 | 44.5 | 36.7 | 113.7 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
| 21 | Iron | μg L−1 | 3 | 347 | 17 | 3 | 53 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
| 22 | Zinc | μg L−1 | 0.5 | 238.0 | 24.2 | 14.0 | 76.0 | (5000) |
| 23 | Chlorine residual | mg L−1 | 0.03 | 2.2 | 0.57 | 0.6 | 1.3 | — |
| 24 | Aluminium | mg L−1 | 0.001 | 0.122 | 0.016 | 0.003 | 0.074 | ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 0.2 |
| 25 | Temperature | °C | 9.0 | 28.0 | 19.3 | 19.3 | 25.0 | (25) |
All the samples are encoded, including the information relative to the zone (six zones) and the origin (network or well) of the sample. The origin refers to the specific sampling site type. Thus, ‘well’ means that the water sample was taken when coming out of an aquifer, whereas ‘network’ means that water was taken at a point in the distribution network, regardless of whether the water was from an aquifer, surface waters (the Jucar or Turia Rivers) or a mixture of the two. The frequency and distribution of analysis in the different zones was established in agreement with the legislation.1
Results and discussion
Exploratory data analysis
Table 1 shows the statistics corresponding to the univariate data analysis, as well as the limit values established by regulations1 based on the World Health Organization recommendations. Some samples have results that exceed the upper legal limit for some parameters, especially with respect to the sulfate concentration. The data were arranged in an X-matrix (136 × 25) and autoscaled. Fig. 1 shows the autoscaled data corresponding to the 25 methods. In order to ascertain the sources of variation of the data, a previous exploratory (multivariate) analysis was performed, based on PCA and PLS algorithms. The multivariate analysis of the data began with a PCA study. A critical aspect of PCA is the selection of the number of principal components (PCs). Unfortunately, there is no universal, automatic criterion for this selection,17,18 and discrepancies between different criteria are common.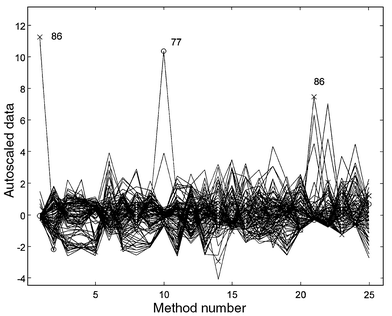 | ||
| Fig. 1 Autoscaled data corresponding to the 25 selected analytical methods for the laboratory internal quality study. | ||
Recently, Todeschini17 performed an extensive comparison of methods for establishing data correlation and the number of PCs to be used in the PCA model. Todeschini proposed a new correlation index (K) as a measure of the total quantity of correlation in the data set, as well as linear (KL) and non-linear (KP) functions for estimating the maximum and minimum number of significant PCs, respectively. The author concluded that KL and KP can be used to estimate the number of PCs giving potentially useful information, and that they are simpler than most of the traditional criteria used up to now. Applying the Todeschini criterion to the data matrix, we obtain K = 0.51, which suggests a moderate degree of correlation. The significant PC limits were KL = 13 and KP = 5. The cross-validation study indicates that for six PCs, a stabilization of the residual variance (approximately a local minimum) is produced. Thus, a model with six PCs (that accounts for 73% of the original variance) seems to be feasible. Larger values (closer to KL = 13) could also give conservative results.
However, the importance of the interpretability of the PCs should not be underestimated.18 For example, the score plot of the first two PCs [Fig. 2(a)] shows a defined structure that can be related to the zone and, in part, to the origin of the samples. PC1 discriminates between the ‘zone 2’ samples, labelled with an open circle in the plot, and the other zones. On the other hand, except for the ‘zone 2’ samples, PC2 discriminates between the ‘well’ samples, labelled with a cross, and the network samples. In contrast, Fig. 2(b) indicates that sample 86 is largely responsible for the PC3 and PC4 components. Eliminating this sample and remaking the PCA model, the PC3–PC4 score plot [Fig. 2(c)] shows scant structure and no relationship with the zone or the origin of the samples. Other aspects related to the relative importance of the PC selection will be treated at the end of the paper.
 | ||
| Fig. 2 PCA score plots: (a) PC1 vs. PC2; (b) PC3 vs. PC4; (c) PC3 vs. PC4, after eliminating sample 86; (d) u vs. t (first latent variable) plot to detect samples badly codified by zone. The u value of each group of samples corresponds to the codified zone. | ||
Knowing the structure of the analytical problem can help in solving certain aspects of sample control. The relationship between PC1 scores and the sample zone would serve to detect a codification mistake by representing the dummy variable ‘zone’ vs. the PC1 scores (not shown). However, for this purpose, it can be even more effective to employ so-called discriminant PLS (DPLS).19 This technique is based on the use of a dummy variable as the response y vector in the PLS regression, thus forcing a rotation—advantageous for our purposes—of the PLS latent variables (LV) with respect to the PCs. Until now this technique has been used to improve the discriminant capacity of a score plot19 and, more recently, to decide on the degree of influence of a categorical variable in the latent structure of a PCA model.18 In the present study, we are interested in the first LV capacity for discriminating the sample zone.
Since DPLS was applied using the original zone code (from 1 to 6) as the y vector (without autoscaling these data), the scores (u) associated with this vector coincided with the assigned zone number. Once the PLS algorithm was applied, the first LV scores associated with the X-matrix (t) were obtained. Fig. 2(d) shows the u vs. t plot. In conventional PLS analysis, the u vs. t plot usually shows the degree of linearity between the scores from the Y- and X-matrices (linear internal relations are considered indispensable at least for the first LVs when linear PLS algorithms are used). Here, since y is a non-quantitative variable, it is not necessary to look for such relationships, but objects from the same zone can be expected to form a group. In Fig. 2(d), it can be observed that sample 127 (codified in ‘zone 3’) is far from the rest of its group (u = 3). After verifying the data, an error in the codification was observed and, in fact, sample 127 belonged to ‘zone 2’ (u = 2). The use of the origin as the y variable in DPLS was less effective because this variable has less discriminating capacity.
Multivariate quality control: ‘outlier’ samples
Analysis of each water sample involves the generation of a vector with 25 analytical results, one from each method applied to the sample. In this context, each method can be considered a sensor, whereas the group of methods associated with the global performance of the laboratory can be considered a system. Finally, the totality of the analyses performed over a period can be seen as the process under study. A 136 sample data set is probably smaller than that used in most MSPC applications. However, it shows the variability of water quality over a 1 year period and therefore can be considered a representative set in this particular case. On the other hand, the main objective in this preliminary paper is to explore the possibilities of adapting the conventional MSPC control plots to the case of routine analysis data. For this purpose, the available water quality data set serves as an adequate case study.A hypothesis test to show out-of-control samples can be obtained from the Hotelling’s T2 and residual Q statistics and their confidence limits from the PCA model.12 These values depend on the number of PCs selected for the model. We select six PCs in order to prevent a ‘conservative’ result, which agrees with the previous conclusions (Exploratory data analysis section). In MSPC, the Q statistic or T2 statistic is usually plotted vs. the sample number (in many cases associated with time) as control charts. Here, we have preferred to plot Qvs.T2 for the samples, together with the control limits for both statistics.16,19Fig. 3(a) shows the Q–T2 control plot corresponding to a six PC model. As this plot shows, sample 86 presents a T2 value (distance to the multivariate mean) much higher than the corresponding control limit (T2 limit). This is interpreted as an unusual disturbance within the PCA model, which is associated with high values in several parameters simultaneously. Fig. 1 reveals that this sample presents the maximum values in parameters 1 (turbidity) and 21 (iron), widely surpassing the legal limits (see Table 1).
 | ||
| Fig. 3 Q–T 2 control plot to detect out-of-control samples and Q and T2 limits (broken lines) corresponding to the confidence limits at the 95% probability level. (a) Using all the samples and a six PC model. (b) Eliminating samples 77 and 86 and using a two PC model. | ||
At this point, the advice of a specialist could help to decide if the problem is due to contamination of the sample, or to a possible systematic error in the analytical methods that deserves to be investigated (i.e., by external method validation). Sample 86 comes from a well used seasonally (solely during the summer months), and it corresponds to the starting time after the non-utilization period. For that reason, the water sample contains substantial amounts of iron from the suction pipe. In addition, the depression generated inside the aquifer drags solid materials from the ground and increases the turbidity. Moreover, the presence of dissolved iron (FeIII coloured solution) can falsify the nephelometric measurements, which would imply a bias associated with this analytical method. This phenomenon, associated in this case with the origin and the particular circumstances of this sample, may well occur in other wells. In any case, sample 86 is non-potable water and must be rejected (until it is within the required quality levels).
As can be observed, sample 77 has a Q value well above the corresponding control limit (Q limit), which indicates that the sample data are shifted outside the normal operating PCA space. Usually, this is associated with anomalous values in only one parameter. It should be noted that sample 77 did not appear as detachable until seen on PC7–PC8 score plots (not shown). Fig. 1 indicates that sample 77 has the maximum value of parameter 10 (potassium), and Table 1 reveals that this value exceeds the legal limit. Sample 77 corresponds to a well next to a scrap meat incineration zone, which explains the presence of high concentrations of this ion in the aquifer. This fact was also confirmed when the sample’s beta radioactivity (40K is a beta and gamma emitting substance) was verified. In this case, the anomaly seems to relate not to the analytical method for potassium determination, but to the characteristics of the well location. On the other hand, the potability problems make it necessary to mix this water with low potassium content surface waters before incorporating it into the distribution network. An example of this can be seen in sample 98 (see below).
Samples 86 and 77 may exert a remarkable influence on the data structure. Since autoscaled data are used, a very high value in one parameter affects the values of that parameter for the rest of the samples (see Fig. 1). The biplot (not shown) corresponding to the PCA model associated parameters 1 and 21 (turbidity and iron) with PC1, whereas parameter 10 (potassium) is to some extent associated with PC2. Nevertheless, when samples 77 and 86 were eliminated from the matrix and the PCA model was recalculated, it was observed that the turbidity and iron parameters are in fact associated with PC2, whereas the potassium parameter is related to PC1. For this reason, we can classify those samples as outliers, which must be eliminated for subsequent studies. As shown in Fig. 3(a), there are more samples slightly exceeding Q and/or T2 limits. However, in contrast to samples 77 and 86, they do not affect the latent structure of the PCs (biplots, not shown). Therefore, they were not considered outliers, although they must be studied as an out-of-control sample category.
Multivariate quality control: ‘out-of-control’ samples
According to the conclusions of the Exploratory data analysis section [Fig. 2(a)–(c)], the interpretable data structure is concentrated in the first two PCs. Using a low factor PCA model, when an outlier-free data set is available, may present a ‘non-excessively conservative’ result. This better coincides with the new objective of detecting possible out-of-control samples in the data matrix (i.e., atypical samples that do not affect the latent structure of the PCA model). Therefore, the new PCA model was constructed with two PCs to increase the probability of revealing the maximum number of samples susceptible to investigation (this point is later extensively studied, see Fig. 6).Under these conditions, the Q–T2 plot depicted in Fig. 3(b) was obtained according to the new 134 × 25 data matrix. This plot shows some samples located outside the control limits, indicating possible sample contamination or, alternatively, errors associated with some of the analytical methods. These samples are classified as out-of-control. MSPC techniques are usually used with a data set (showing a high degree of correlation between process variables) representing a ‘clean’, ‘normal’ operation system. Therefore, the normal MSPC procedure could imply the removal of the out-of-control samples to obtain a cleaner control model in which new samples can be projected, preferably using their scores or their residuals as diagnostic values. However, we are only interested in obtaining information related to out-of-control samples [detected in Fig. 3(b)]. Therefore, since these samples did not affect the latent structure of the PCA, we decided not to eliminate them, and used their residuals directly as a source of diagnosis.
Fig. 1 was sufficient to identify the parameters responsible for the anomaly shown by the two outliers [samples 86 and 77; Fig. 3(a)]. However, this is not so simple when it is applied to the suspicious samples in Fig. 3(b)]. Examining the residual matrix of the two PC model can facilitate this task by means of the so-called residual contribution plot strategy. These plots were designed to identify the sensors (variables) responsible for a high mean residual value in periods in which a system is beyond control.20 Here, these plots may constitute an automatic tool for detecting which analytical methods contribute to the anomaly detected in a sample.
Fig. 4(a) shows the residual contribution plot associated with sample 76. In this plot, parameters 1 (turbidity) and 21 (iron) appear to be responsible for the high Q value, as occurred in the case of sample 86. In fact, sample 76 is in the same zone and origin as sample 86 and the same reasons can be given to justify these analytical results. It is remarkable that, after eliminating samples 77 and 86, sample 76 appears as an out-of-control sample [Fig. 3(b)], but it was inside the limits in Fig. 3(a). This points out the need to detect and eliminate the outliers for a definitive out-of-control sample detection study.
 | ||
| Fig. 4 Residual contribution plots for sample 76 corresponding to (a) PCA and (b) PLS approaches. | ||
As an alternative to the use of PCA residuals, a method for generating PCA-like residuals from single data blocks using PLS was developed.21 In this method, the block of data (X-matrix) is used to calibrate every variable to every other variable with PLS. The residuals in the prediction are used instead of those obtained by means of PCA. Fig. 4(b) shows the residual contribution plot corresponding to the PLS approach for sample 76. If we compare this plot with that in Fig. 4(a), it can be observed that both methods indicate that parameter 1 (turbidity) contributes greatly to the high Q value for sample 76. However, the PLS approach does not perceive the possible contribution of parameter 21 (iron), unlike the PCA approach. Sample 76 presents turbidity (2 NTV) and iron content (109 μg l−1) values above the percentile 95%. Therefore, it seems that the PLS approach centres on the parameter showing the greatest residual contribution. This behaviour was also observed for the rest of the out-of-control samples [those above the Q and/or T2 limits in Fig. 3(b), for which PCA and PLS approaches were compared].
In our opinion, the methods of generation of residuals from the PCA and PLS approaches are sufficiently distinct to consider both approaches simultaneously as complementary tools with the same objective. On the other hand, the residual contribution plot was used as a qualitative tool. At this point, we are not interested in concluding which approach is preferable (this would require a study of more cases). In contrast, we believe that, when the two plots reveal a high residual for the same method, this increases the security of the conclusion of a significant method disturbance.
Fig. 5 shows the residual contribution plots (PCA approach) for the samples showing preferentially high Q values in Fig. 3(b). Associated with sample 98, parameters 10 (potassium) and, to a lesser extent, 22 (zinc) stand out from the rest. As was indicated previously, the potassium result is logical since this network sample is obtained by diluting the well sample 77. The zinc result is related to the use of Fe–Zn galvanized pipes in this zone. In fact, the trend is to replace these old pipes with fibre pipes in those zones where the zinc concentrations tend to increase. Sample 94 displays the same problem in relation to zinc (it is the sample with the highest content of this metal) and therefore, as in the previous case, we cannot conclude that there is an error in the analytical method for zinc. The case of sample 114 is similar to those of samples 86 and 76, but, in contrast, the residual associated with parameter 21 (iron) is remarkably higher than that of parameter 1 (turbidity). This could suggest an error associated with one of these analytical methods and deserves to be investigated. Even so, it is necessary to bear in mind that samples 86 and 76 come from wells located on the coast (incorporating high sand content that contributes to the turbidity) whereas sample 114 comes from a well located inland, which may explain its lower turbidity.
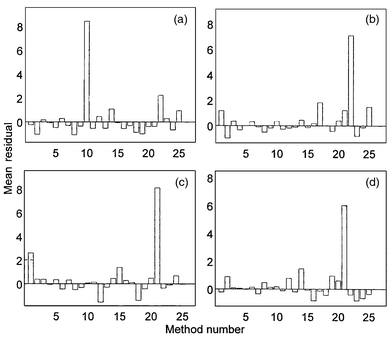 | ||
| Fig. 5 Residual contribution plots (PCA) corresponding to samples (a) 98, (b) 94, (c) 114 and (d) 131. | ||
In the plot associated with sample 131, we can see that, as in the previous cases, the parameter 21 (iron) stands out from the rest but parameter 1 (turbidity) does not. The iron content in this well (216 μg l−1) is above the percentile 95%and the legal limit, according to Table 1. This sample comes from surface water, which explains the low turbidity value. However, such a high iron level is not easily explicable, and a possible error in the iron determination deserves to be investigated. One hypothesis that would justify this result is the occasional presence of iron oxide particles large enough not to affect the turbidity measurement, but interfering in the iron determination once dissolved.
In all the cases displayed in Fig. 4 and 5, the common characteristic is that one of the methods presents a residual value (in the range 6–8) remarkably higher than the rest. This behaviour is even more noticeable when the residuals are obtained by means of the PLS approach. In such cases, coinciding with large Q/T2 values, it is reasonably probable that the detected error is due to an analytical method failure. However, as demonstrated, the participation of a specialist could justify some of these results attending to sample circumstances and, in these cases, analytical method (external) validation could be unnecessary. Nevertheless, sample contamination, in connection with its toxicity, deserves to be investigated.
The more the samples tend to be characterized by larger T2/Q values, the greater is the probability that the error is associated with the sample (different nature, storage, etc.), the analyst (non-expert analyst or staff) or changes in the laboratory environment. In such cases, several methods present a comparable and relatively low residual value. Thus, for example, the residual contribution plot for sample 84 (not shown) presents residual values lower than 4 for parameters 1 (turbidity) and 18 (boron), and a residual value of 2 for parameter 19 (fluoride). Since the sample is well water, the turbidity level is considered normal. In contrast, the boron level (296 μg l−1, the maximum value according to Table 1) could only be justified by a sampling or storage error (in a glass instead of plastic container). Something similar can be argued in the case of the fluoride level. If this kind of error did not occur, the analytical methods must be checked for bias.
Samples 54 and 135 come from wells belonging to zone 5. They have in common a high salinity and therefore present high levels of all the parameters associated with this characteristic. For example, sample 54 presents the maximum values for the parameters conductivity, calcium, hardness and total dissolved solids, and levels over the percentile 95% for the parameters turbidity, magnesium, bicarbonates and nitrates. For this reason, this sample has the largest T2 value in Fig. 3(b) and exhibits residual values around 1. A bias, therefore, can be ruled out, although from the point of view of health, the nitrate levels will have to be controlled at the water distribution sites where water from these aquifers is used.
Finally, we were interested in observing the influence of the number of PCs on the ability to detect out-of-control samples, especially with respect to the Q statistic, which may contribute to the detection of systematic errors in the analytical methods. Fig. 6 shows the Q values for samples 76, 114, 98, 94 and 131 vs. the number of PCs (between 2 and 10). It can be observed that, in all cases, the Q values of these samples are higher than the corresponding mean Q value (all the samples), and they are outside the Q limit value found for any PC number. This means that the detection of such samples was possible independent of the number of PCs chosen. This is an intrinsic valuable feature of the Q vs. T2 tool, since the number of factors is critical for most PCA applications. Logically, using two PCs, larger differences between the Q values and the Q limit are observed.
 | ||
Fig. 6
Q vs. PC number plot for samples 76 (○), 114 (+), 98 (*),
94 (×) and 131 (—). Q limit at 95% confidence level
(–![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) – –![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) –)and average Qfor all the samples (----). –)and average Qfor all the samples (----).
| ||
Conclusions
A laboratory that performs routine multiparametric analysis generates a matrix of analytical results which can be treated by multivariate data analysis techniques. In the water quality case used here, two categorical variables, the sampling zone and the origin of the samples, were the most important factors defining the latent data structure. This fact allows discriminant partial least squares (DPLS) to be used for error detection in codification (with regard to the sample zone label). On the other hand, the entire laboratory performance can be seen as a (‘particular’ case of a) process system, and therefore the data matrix can be treated by multivariate statistical process control (MSPC). Two MSPC graphical tools, the Q–T2 plot combined with the residual contribution plot, alert the user to sample/method disturbances. A high sample Q/T2 ratio combined with a relatively high method residual, a priori, suggests the presence of a systematic error in the method. Thus, this solves the first stage in the error detection process, which will allow it to be investigated by a specialist in the problem area under study and/or checked by external method validation.This preliminary work with water analysis data proves that MSPC tools can be adapted to analytical problems. However, the behaviour of MSPC tools can vary when applied to other situations. As a rule, the protocol must include previous detection and elimination of outliers. The number of PCs can help to discriminate between outliers and out-of-control samples, but it is not a crucial criterion for discriminating between out-of-control and in-control samples, at least for the water data studied. Further studies on this matter must include the possibility of an a priori determination of the parameters affecting the error detection ability and the minimum error level detectable for each of the methods under study.
These multivariate tools should be easily automated and implemented in a routine analysis laboratory with minimum effort. They could be used as an internal automatic alarm system to prevent negative consequences for health and/or at the economic level. For instance, the complete analysis cost of each water sample, 60 parameters, is approximately $1300. Therefore, in the case of drinking water quality, a cost–benefit analysis of the implementation of such tools is favourable. Finally, we suggest the inclusion of this multivariate approach in the quality assurance scheme in routine analysis laboratories (after convenient study) as a complementary way to perform data (on laboratory) quality control.
References
- EEC Directive 98/83, p. 1330, December 1998..
- Analytical Methods Committee, Analyst, 1995, 120, 29. Search PubMed.
- J. F. MacGregor, Int. Statist. Rev., 1997, 65, 309 Search PubMed.
- M. Caselli, A. De Giglio, A. Mangone and A. Traini, J. Sci. Food. Agric., 1998, 76, 533 CrossRef CAS.
- P. Barbieri, G. Adami, A. Favretto and E. Reisenhofer, Fresenius’ J. Anal. Chem., 1998, 361, 349 CrossRef CAS.
- N. Kannan, N. Yamashita, G. Petrick and J. C. Duinker, Environ. Sci. Technol., 1998, 37, 1747 CrossRef.
- G. S. Chen, K. W. Schramm, C. Klimm, Y. Xu, Y. Y. Zhang and A. Kettrup, Fresenius’ J. Anal. Chem., 1997, 359, 280 CrossRef CAS.
- J. M. Andrade, D. Prada, E. Alonso, P. López, S. Muniategui, P. de la Fuente and M. A. Quijano, Anal. Chim. Acta, 1994, 292, 253 CrossRef CAS.
- K. J. James and M. A. Stack, Fresenius’ J. Anal. Chem., 1997, 358, 833 CrossRef CAS.
- E. Engstrom and B. Karlberg, J. Chemom., 1996, 10, 509 CrossRef CAS.
- T. Kourti and J. F. MacGregor, Chemom. Intell. Lab. Syst., 1995, 28, 3 CrossRef CAS.
- B. M. Wise and B. R. Kowalski, in Process Analytical Chemistry, ed. F. McLennan and B. R. Kowalski, Chapman and Hall, London, 1995, ch. 2. Search PubMed.
- C. L. Stork, D. J. Veltkamp and B. R. Kowalski, Anal. Chem., 1997, 69, 5031 CrossRef CAS.
- A. Rius, M. P. Callao and F. X. Rius, Analyst, 1997, 122, 737 RSC.
- J. B. Marzo, M. J. Medina-Hernández, S. Sagrado, E. Bonet and R. Gimenes, J. Chemom., 1998, 12, 323 CrossRef CAS.
- APHA-AWWA-WEF Standard Methods for the Examination of Water and Wastewater, American Public Heath Association, Washington, DC, 20th edn., 1998. Search PubMed.
- R. Todeschini, Anal. Chim. Acta, 1997, 348, 419 CrossRef CAS.
- M. M. Morales, P. Martín, A. Llopis, L. Campos and S. Sagrado, Anal. Chim. Acta, 1999, 394, 109 CrossRef CAS.
- E. Jellum, M. Harboe, G. Bjune and S. Wold, J. Pharm. Biomed. Anal., 1991, 9, 663 CrossRef CAS.
- B. M. Wise, N. L. Ricker, D. J. Veltkamp and B. R. Kowalski, Process Control and Quality, 1990, 1, 41 Search PubMed.
- B. M. Wise, Process-Control-Qual., 1993, 5, 730 Search PubMed.
| This journal is © The Royal Society of Chemistry 2001 |
