Contributions of weak interactions to the inclusion complexation of 3-hydroxynaphthalene-2-carboxylic acid and its analogues with cyclodextrins

Abstract

Apparent formation constants and thermodynamic parameters of inclusion complexation of 3-hydroxynaphthalene2-carboxylic acid (3H2NA) and its analogues with cyclodextrins in aqueous solutions were determined by the steady-state fluorescence Benesi–Hildbrand method at various pH values. The pH dependence of formation constants and thermodynamic parameters for 3H2NA complexing with β-cyclodextrin (β-CD) is different from that with heptakis(2,3,6-tri-O-methyl)-β-cyclodextrin (TMβ-CD). Hydrogen bonding between 3H2NA (neutral or ionic form) and β-CD or proton-acceptors such as hydrogen ion and alkoxide ion (formed by dissociation of the secondary hydroxy group of β-CD) and its effect on the stability of the cyclodextrin complex are studied systematically and discussed in detail. It can be concluded that hydrogen bonding plays an important role in the formation of the inclusion complexes. In addition, enthalpy and entropy changes both contribute to inclusion complexation when the guest exists mainly as its molecular form. However, when the guests fully ionize, inclusion complexation is solely driven by enthalpy. The effect of host cavity size, guest diameter and position of substituents on the stability of the complexes is also observed. Linear compensatory ΔH ° vs.TΔS ° plots give slopes (α = 1.20 ± 0.10 and 1.21 ± 0.01) and intercepts (TΔS °₀ = 19.1 ± 2.5 and 20.7 ± 0.3 kJ mol⁻¹) for native CDs and modified CDs, respectively. On the basis of the enthalpy–entropy compensation effect, the big slopes of the ΔH ° vs.TΔS ° plots indicate that the structure of native and modified CDs in aqueous solution is flexible, despite the rigid skeleton of native CDs in the solid state, while the large intercepts TΔS°₀ for native and modified CDs indicate extensive desolvation of both the host and guest on host–guest complexation. These two different CDs may be considered as one kind on the basis of enthalpy–entropy compensation effect. The general validity of the enthalpy–entropy effect is supported by the present results.

---

Introduction

Cyclodextrins (CDs) are known to complex a wide variety of molecules in their hydrophobic interior.^1–6 The most likely mode of binding consists of inclusion of the less polar portion of the guest within the cavity while the polar or hydrophilic part of the guest remains solvent exposed.^6,7 It has been recognized that the binding forces involved in inclusion complexation are hydrophobic interactions, hydrogen bonding, van der Waals forces, the relief of high energy water from the CD cavity and the relief of conformational strain upon guest inclusion.^1–6 It is important to study these weak interactions, to further our understanding of the nature of the formation of supramolecules and to predict new approaches in pharmacy, analysis and material science, etc.^6,8–10

Generally, molecular association is made possible through the simultaneous cooperation of several weak interactions. The thermodynamics of inclusion complexation by CDs are a consequence of the measured contributions of these interactions.⁶ Furthermore, the observation of the linear compensatory enthalpy–entropy relationship has been extended to the cyclodextrin field.^11–16 Inoue and Liu et al. have proposed that the slope (α) and the intercept (TΔS°₀) of the compensatory ΔH° vs. TΔS° plot are characteristic of the ligand–host topology and can be used as a quantitative measure of the ligand–host’s conformational change and of the extent of cation–ligand or guest–host desolvation caused by complex formation. It is noted that only a little work has been done systematically on the contributions of hydrogen bonding to the stability of inclusion complexes.^7,17,18 Buvahi et al. studied the complex formation of β-CD with different guests and the results showed that the formation constants would relatively increase if hydrogen bonding between the hydroxy groups of β-CD and the guest is possible.¹⁷ Ross and Rekharsky determined the complexation thermodynamics of CDs with several pairs of structurally related aromatic guests, either with or without a phenolic hydroxy group and reported the increments in ΔH ° and ΔG ° that can be ascribed to hydrogen bonding interactions.¹⁸

The aim of this work is to investigate the function of noncovalent weak interactions in inclusion complexation involving cyclodextrins. We choose β-CD, TMβ-CD and γ-CD as hosts for their different hydrophobicity, abilities to form hydrogen bonds and cavity size. We select 3H2NA and some analogues of it (see Fig. 1) as guests for they all have aromatic rings, a rigid rectangular shape and two adjacent groups which may form intermolecular and intramolecular hydrogen bonds. They are suitable for the study of the effects of polarity, hydrogen bonding, position of the substituent and steric hindrance on the host–guest system. First, we determined the formation constants of the complexation of 3H2NA with β-CD and TMβ-CD at many different pH values, since the hydrophobicity and the ability of 3H2NA (pK_a = 2.6) ¹⁹ and β-CD (pK_a = 12.2) ⁵ to form hydrogen bonds are changeable in this pH range, while those of TMβ-CD are constant because it is unable to dissociate. Then we report the first measurements of thermodynamic parameters for inclusion complexation of the above host–guest systems at several pH values. Because of the low solubility ²⁰ of the guest at certain pH values and the interference of buffers on the inclusion equilibrium which has been demonstrated in our recent work,²¹ it is not by calorimetric titration ^{7,11,12,22–25} but through van’t Hoff analysis ^26–29 of the equilibrium constants that the thermodynamic parameters reported were determined, although calorimetric titration is generally thought to be more accurate. In addition, we observe that the host cavity size, the guest diameter and the position of substituent have great effect on the stability of the complexes. Finally, we discuss the host–guest inclusion caused by the weak interactions in terms of the enthalpy–entropy compensation effect.^7,11–16

Fig. 1 Guest molecules.

Results and discussion

Effect of pH values on formation constants for complexes of 3H2NA with β-CD and TMβ-CD

Typical examples of the fluorescence spectra change of 3H2NA in the presence of TMβ-CD at pH 7.0 are shown in Fig. 2. The dimerization of the guest may be ignored³⁰ due to the low concentration. We didn’t add salts to the solutions to control the pH and ionic strength since they do have an effect on the inclusion formation constants of cyclodextrin inclusion complexes.^21,31–38 A gradual increase of fluorescence intensity was observed. The formation constants are determined by the Benesi–Hildebrand method ^39–43 which can be expressed as eqn. (1), where ΔIF, α, K, [CD]_t, [3H2NA]_t are the change of fluorescence intensity after addition of CD, proportionality constant, the formation constant of the 1∶1 inclusion complex, and the total concentration of CD and 3H2NA, respectively. The linear Benesi–Hildebrand plots (see Fig. 3) indicate the formation of 1∶1 inclusion complexes. From the slope and the intercept of the Benesi–Hildebrand plot on the ΔIF⁻¹ axis, we can obtain the apparent formation constant and the proportionality constant α.⁴³ The apparent formation constants (K) of 3H2NA with β-CD and TMβ-CD in aqueous solutions at different pH values are shown in Fig. 4.

ΔIF⁻¹ = (α[CD]_t[3H2NA]_tK )⁻¹ + (α[3H2NA]_t)⁻¹

Fig. 2 Fluorescence spectra change of 3H2NA at various TMβ-CD concentrations. [3H2NA] = 9.3 × 10⁻⁶ M, [TMβ-CD]_t: (a) 0.00; (b) 0.443; (c) 0.621; (d) 0.904; (e) 1.24; (f ) 1.77; (g) 2.48; (h) 3.55 × 10⁻³ M, pH = 7.0, T = 25 °C.

Fig. 3 Double-reciprocal plots of ΔIF⁻¹vs. [β-CD]_t⁻¹. [3H2NA] = 1.8 × 10⁻⁵ M, T = 25 °C: pH = (a) 7.0; (b) 10.8; (c) 11.5; (d) 1.5; (e) 2.4.

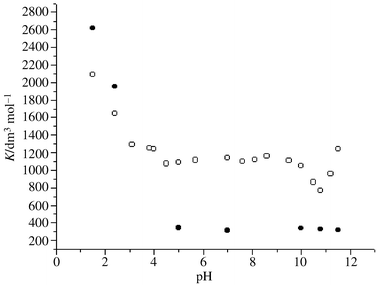Fig. 4 Plots of apparent formation constants of 3H2NA with β-CD (○) and TMβ-CD (•) in aqueous solutions at different pH values and at 25 °C.

As can be seen from Fig. 4, the apparent formation constants of 3H2NA with β-CD are different at various pH values. Owing to the large hydrophobicity of the molecular form of 3H2NA (pK_a1 = 2.6) ¹⁹ at pH 1.5 and the intermolecular hydrogen bonding which may exist between 3H2NA and β-CD, K_β-CD is large (2089 ± 211 dm³ mol⁻¹).

With increasing pH (pH < 4.5), K_β-CD decreases as expected. This may be because 3H2NA loses its hydrophobicity upon ionization. This would indicate that hydrophobic interactions are the main driving forces in the formation of the inclusion complex when the guest has large hydrophobicity.

At pH = 4.5–10.0, the carboxy group of 3H2NA (pK_a1 = 2.6) ¹⁹ ionizes totally to form 3H2NA⁻ but the hydroxy group (pK_a2 = 13.0)¹⁹ doesn’t dissociate. The hydrophobic interactions between 3H2NA⁻ and β-CD are therefore constant. Furthermore, the addition of a small amount of NaOH has little effect on the intermolecular hydrogen bond between 3H2NA⁻ and β-CD (see Scheme 1), so K_β-CD is almost constant (K_β-CD = 1075 ± 89–1047 ± 26 dm³ mol⁻¹).

Scheme 1

The most striking feature of Fig. 4 is that K_β-CD diminishes and comes to a minimum at about pH 10.8 (K_β-CD = 769 ± 64 dm³ mol⁻¹) as the pH value increases further. Then it increases with the increasing basicity (at pH 11.5, K_β-CD = 1236 ± 112 dm³ mol⁻¹). The decrease of K values could be explained by postulating that hydrogen bonding between 3H2NA⁻ and solvent hydroxide ions (see Scheme 2) may compete with β-CD for the hydroxy group of 3H2NA⁻ (see Scheme 1).

Scheme 2

It has been proposed that the more acidic or basic a proton donor or acceptor is, the more likely it is to donate or accept a proton.^44,45 Thus, hydroxide ion is a much stronger proton acceptor than the hydroxy group of β-CD (pK_a = 12.2) ⁵ and is more likely to form an intermolecular hydrogen bond with the hydroxy group of 3H2NA⁻ (see Scheme 2). The extent to which the hydroxy group of 3H2NA⁻ can form a hydrogen bond with β-CD becomes less, weakening the hydrogen bond interactions between 3H2NA⁻ and β-CD (see Scheme 1) and reducing K_β-CD. However, at pH > 11, the extent to which the alkoxide ion is ionized by the second hydroxy group of β-CD increases (pK_a = 12.2).⁵ One might expect that the K values should reduce further in view of the decrease of hydrophobicity of β-CD upon ionization. However the basicity of the β-CD alkoxide ion is much stronger than water and the carboxylate group of 3H2NA⁻, and it is more liable to form a hydrogen bond with the hydroxy group of 3H2NA⁻ (see Scheme 3). Therefore, the inclusion interactions are strengthened and K_β-CD rises. This indicates that in this pH range, hydrophobic interactions are unimportant to inclusion complexation. In addition, when a hydrogen bond forms between 3H2NA⁻ and β-CD⁻, the structure of this adduct becomes tighter and the van der Waals forces, which are related to the distance between the two molecules, may be stronger.

Scheme 3

To test the hypothesis that hydrogen bonding plays an important role in inclusion complexation, we replaced β-CD with TMβ-CD. After β-CD is permethylated into TMβ-CD, its ability to accept protons is much reduced relative to β-CD and it cannot donate a proton to form a hydrogen bond with 3H2NA. Furthermore, TMβ-CD is unable to ionize an alkoxide ion to enhance the hydrogen bonding between TMβ-CD and 3H2NA⁻.

Inspection of Fig. 4 shows that it is at pH > 10 that the pH dependence of formation constants of 3H2NA with TMβ-CD (K_TMβ-CD) is different from that with β-CD: K_TMβ-CD changes little with increasing pH values. This confirms our idea that hydrogen bonding between the dissociated β-CD alkoxide ion and the hydroxy group of 3H2NA⁻ contributes to the stability of the inclusion complex. In addition, K_TMβ-CD is almost the same at pH ⩾ 5.0, which suggests that the intermolecular hydrogen bonding between 3H2NA⁻ and TMβ-CD is very weak or even negligible. Hence, the increase of hydroxide ion has no effect on the K values.

It is interesting to note that at pH 1.5 K_TMβ-CD is considerably larger than K_β-CD (K_TMβ-CD = 2620 ± 147 dm³ mol⁻¹) while at pH ⩾ 5.0 it is much smaller than K_β-CD (K_TMβ-CD ≤ 345 ± 29 dm³ mol⁻¹). The larger K_TMβ-CD at pH 1.5 is attributable to the greater hydrophobic cavity and hydrophobicity of TMβ-CD; the smaller K_TMβ-CD at pH ⩾ 5.0 to the lower ability of TMβ-CD to form hydrogen bonds. From above, it can be concluded that hydrophobic interactions and hydrogen bonding play an important role in the stabilization of the 3H2NA–β-CD adduct.

The importance of hydrogen bonding in inclusion complexation may also be confirmed by examination of the formation constant of β-CD with naphthalene. It is an analogue of 3H2NA with greater hydrophobicity but without substituents to form intermolecular hydrogen bonds with β-CD. Consequently, the formation constant of β-CD with naphthalene (K = 630 dm³ mol⁻¹, mole ratio 1∶1) ⁴⁶ is smaller than that with 3H2NA.

Thermodynamic parameters of inclusion complexation of 3H2NA with β-CD and TMβ-CD in aqueous solutions at different pH values

In order to obtain a more comprehensive knowledge of the contributions of weak interactions to inclusion complexation, we measured the thermodynamic parameters of inclusion complexation of 3H2NA with β-CD and TMβ-CD in aqueous solutions at five pH values through van’t Hoff analysis of the equilibrium constants. Since the van’t Hoff plots are linear, the heat capacity is negligible.⁴⁷Fig. 5 shows double-reciprocal plots of ΔIF⁻¹vs. [β-CD]_t⁻¹ at five temperatures (pH = 7.0). The apparent formation constants of 3H2NA with β-CD and TMβ-CD at different pH values and five temperatures as well as enthalpy and entropy changes are listed in Tables 1 and 2, respectively. Thermodynamic parameters for 3H2NA with β-CD and TMβ-CD, as well as the contributions of enthalpy (ΔH °) and entropy (−TΔS°) changes to free energy (ΔG °) at different pH values at 25 °C, are listed in Table 3.

Table 1 Apparent formation constants (dm³ mol⁻¹) of inclusion complexation of 3H2NA with β-CD at different pH values and various temperatures as well as enthalpy (ΔH°) and entropy (ΔS°) changes

	K/dm^3 mol^−1
pH	5 °C	15 °C	25 °C	35 °C	45 °C	ΔH °/kJ mol^−1	ΔS°/J mol^−1 K^−1
1.5	2596 ± 169	2393 ± 224	2089 ± 211	2006 ± 193	1706 ± 136	−7.511 ± 0.794	38.49 ± 2.66
2.4	2398 ± 203	1924 ± 136	1647 ± 151	1515 ± 120	1205 ± 146	−11.90 ± 0.99	21.80 ± 3.30
7.0	2308 ± 150	1583 ± 71	1140 ± 44	802 ± 47	546 ± 28	−26.29 ± 0.84	−29.94 ± 2.80
10.8	1680 ± 104	1186 ± 111	769 ± 69	629 ± 45	460 ± 46	−23.71 ± 1.21	−23.62 ± 4.04
11.5	2603 ± 202	1962 ± 161	1236 ± 112	896 ± 110	584 ± 39	−27.87 ± 1.51	−34.22 ± 5.05

---

Table 2 Apparent formation constants (dm³ mol⁻¹) of inclusion complexation of 3H2NA with TMβ-CD at different pH values and various temperatures as well as enthalpy (ΔH °) and entropy (ΔS°) changes

	K/dm^3 mol^−1
pH	5 °C	15 °C	25 °C	35 °C	45 °C	ΔH °/kJ mol^−1	ΔS°/J mol^−1 K^−1
1.5	2866 ± 257	2811 ± 230	2620 ± 147	2531 ± 280	2267 ± 223	−4.269 ± 0.718	51.06 ± 2.40
2.4	2603 ± 258	2510 ± 143	1953 ± 181	1760 ± 107	1519 ± 178	−10.58 ± 1.22	27.73 ± 4.09
7.0	785 ± 47	487 ± 15	309 ± 24	256 ± 29	151 ± 21	−29.02 ± 2.11	−49.07 ± 7.07
10.8	709 ± 34	471 ± 26	328 ± 17	186 ± 16	141 ± 21	−30.67 ± 1.70	−55.37 ± 5.70
11.5	806 ± 128	536 ± 25	316 ± 11	204 ± 20	177 ± 8	−29.34 ± 2.47	−50.00 ± 8.27

---

Table 3 Thermodynamic parameters in kJ mol⁻¹ for inclusion complexation of 3H2NA with β-CD and TMβ-CD as well as the contributions of enthalpy (ΔH °) and entropy (−TΔS°) changes to free energy (ΔG °) at different pH values at 25 °C

	β-CD					TMβ-CD
pH	ΔG °	−TΔS°	ΔH °/ΔG °	−TΔS°/ΔG °	ΔG °	−TΔS°	ΔH °/ΔG °	−TΔS°/ΔG °
1.5	−18.99	−11.48	0.40	0.60	−19.50	−15.23	0.22	0.78
2.4	−18.40	−6.50	0.65	0.35	−18.85	−8.27	0.56	0.44
7.0	−17.36	8.93	1.51	−0.51	−14.39	14.63	2.02	−1.02
10.8	−16.67	7.04	1.42	−0.42	−14.16	16.51	2.17	−1.17
11.5	−17.66	10.21	1.58	−0.58	−14.43	14.91	2.04	−1.04

---

Fig. 5 Double-reciprocal plots of ΔIF⁻¹vs. [β-CD]_t⁻¹. pH = 7.0, [3H2NA] = 1.8 × 10⁻⁵ M, [β-CD]_t = 8.79 × 10⁻⁴–6.88 × 10⁻³ M: T = (a) 5, (b) 15, (c) 25, (d) 35, (e) 45 °C.

As can be seen from Table 1 and Table 2, the values of ΔH ° for all of the inclusion reactions are negative. However, values of ΔS° are positive at pH < 2.5 and are negative at pH ⩾ 7. The enthalpy gain is enhanced by entropy gain or cancelled by entropy loss. The complexation itself is enthalpy-driven at the standard temperature, but the ultimate stability of the complex is controlled by the entropy.⁶

From Table 3, we can see that at pH 1.5, the contributions of −TΔS° to ΔG ° are larger than that of ΔH °, mainly owing to the large hydrophobic interactions between neutral 3H2NA and β-CD or TMβ-CD. Thermodynamically, the entropy loss arising from the structure freezing upon the inclusion of the guest in the host cavity is compensated by the gain from the accompanying extensive desolvation of the guest and host molecules, which gives rise to the positive entropy (ΔS°) changes as high as 38.49 and 51.06 J mol⁻¹ K⁻¹ for the complexation of 3H2NA with β-CD and TMβ-CD at pH 1.5, respectively. The contribution of −TΔS° to ΔG ° for TMβ-CD is larger than that for β-CD due to the greater hydrophobicity of the former.

At pH 2.4, the enthalpic gains increase and the entropic gains decrease owing to hydrophobicity loss upon ionization of 3H2NA. However, the contribution of −TΔS° to ΔG ° for TMβ-CD is still larger than that for β-CD.

At pH ⩾ 7, the enthalpic gain is larger than that at pH < 2.5. Nevertheless, the complexes of β-CD and TMβ-CD with 3-hydroxynaphthalene-2-carboxylate (3H2NA⁻) at pH ⩾ 7 are less stable than those with the neutral 3H2NA, which may be due to the cancellation of the large enthalpy gain by the greater entropic loss. The jump in ΔS° might be due to the substantial increase in anion size upon inclusion in CDs, requiring the ordering of a much greater number of solvent molecules.

It is noted that at pH 10.8, −ΔH ° value for the reaction involving β-CD is smaller than that at pH 7.0 and K_β-CD is the smallest among all of the K_β-CD values at 25 °C. This confirms our previous proposal that the hydroxide ion forms an intermolecular hydrogen bond with the hydroxy group of 3H2NA⁻ (see Scheme 3) and the loose structure of the adduct weakens the van der Waals interactions between the guest and host, reducing the enthalpy gain. The more negative ΔS° value at pH 7.0 verifies the more rigid structure of the inclusion complex compared to that at pH 10.8.⁴⁸

It is at pH 11.5 that the enthalpy gain and entropy loss for the reaction involving β-CD are the largest, which indicates the strongest van der Waals interactions between the guest and host and the most rigid structure of the adduct. This supports our presumption that the alkoxide ion ionized by the secondary hydroxy group of β-CD forms an intermolecular hydrogen bond with 3H2NA⁻, making the adduct tighter and strenghening the inclusion complexation.

It is noted that at pH ≥ 7, the enthalpy gain and entropy loss for the reaction involving TMβ-CD are almost the same within experimental error, supporting our proposal that the intermolecular hydrogen bonding between 3H2NA and TMβ-CD is very weak. Furthermore, the similarity of the K, ΔH ° and ΔS° values indicates that the structure of the supramolecules at pH ⩾ 7 may be the same. The K, ΔH ° and ΔS ° values involving β-CD are different and those involving TMβ-CD are nearly identical at pH ⩾ 7. This is evidence for the idea that there is an intermolecular hydrogen bond between 3H2NA⁻ and either hydroxide ion or alkoxide ion dissociated by the secondary hydroxy group of β-CD, which makes the adduct looser or tighter, respectively.

Formation constants and thermodynamic parameters for inclusion complexation of CDs with some related compounds

Besides the contributions of weak interactions to inclusion complexation, the stability of supramolecules is related to the host cavity and the guest diameter as well as the position of the guest substituent, i.e. the van der Waals, hydrogen bonding and hydrophobic interactions depend on whether the size and shape of a guest fit the host cavity or not.¹¹ Formation constants for inclusion complexation of 2H1NA, 2E1NA and SAL with β-CD as well as 3H2NA with γ-CD at different temperatures at pH 7.0 (for SAL also pH 1.5) are shown in Table 4. Thermodynamic parameters as well as the contributions of enthalpy (ΔH °) and entropy (−TΔS°) changes to free energy (ΔG °) at 25 °C are listed in Table 5.

Table 4 Apparent formation constants (dm³ mol⁻¹) of 2H1NA, 2E1NA, SAL with β-CD and 3H2NA with γ-CD at different temperatures at pH 7.0

		K/dm^3 mol^−1
Host	Guest	5 °C	15 °C	25 °C	35 °C	45 °C
a  pH = 1.5.
β-CD	2H1NA	228 ± 20	177 ± 14	92 ± 8	761 ± 12	58 ± 8
β-CD	2E1NA	160 ± 15	112 ± 9	44 ± 4	23 ± 4	20 ± 3
β-CD	^a SAL	1003 ± 94	940 ± 95	720 ± 79	668 ± 34	600 ± 62
β-CD	SAL	133 ± 16	105 ± 15	83 ± 10	63 ± 8	42 ± 5
γ-CD	3H2NA	143 ± 158	95 ± 5	80 ± 9	68 ± 5	47 ± 11

---

Table 5 Thermodynamic parameters for inclusion complexation of 2H1NA, 2E1NA and SAL with β-CD and 3H2NA with γ-CD as well as the contributions of enthalpy (ΔH °) and entropy (−TΔS°) changes to free energy (ΔG °) at 25 °C and at pH 7.0

Host	Guest	ΔH °/kJ mol^−1	ΔS°/J mol^−1 K^−1	ΔG °/kJ mol^−1	−T ΔS°/kJ mol^−1	ΔH °/ΔG °	−TΔS°/ΔG °
a  pH = 1.5.
β-CD	2H1NA	−26.33 ± 2.80	−49.37 ± 9.39	−11.61	14.72	2.27	−1.27
β-CD	2E1NA	−42.18 ± 5.11	−109.0 ± 17.1	−9.68	32.50	4.36	−3.36
β-CD	SAL ^a	−10.07 ± 1.22	21.41 ± 4.1	−16.45	−6.38	0.61	0.39
β-CD	SAL	−20.87 ± 1.96	−33.81 ± 6.58	−10.79	10.08	1.93	−0.93
γ-CD	3H2NA	−18.86 ± 1.89	−26.86 ± 6.35	−10.85	8.01	1.74	−0.74

---

It is noticeable that the formation constants and thermodynamic parameters are highly sensitive to the position of the substituent of the guest molecule. K values for inclusion complexation of 2H1NA and 2E1NA with β-CD are much smaller than those for 3H2NA. Although the enthalpic gain for the reaction involving 2H1NA is the same as that for 3H2NA, the entropic loss is much larger, resulting in the low stability of the supramolecule. A possible explanation is that the hydrophobic naphthalene ring of 3H2NA is embedded into the cavity of β-CD in a longitudinal direction, leaving the carboxylate and hydroxy group in the aqueous solution. However, 2H1NA can only form a shallowly penetrating longitudinal or weakly-interacting lateral inclusion complex due to the steric hindrance of the 1-carboxylate group.

In case of 2E1NA, the large enthalpy gain is offset by a highly unfavourable entropy change, indicating the rigid structure of the supramolecule and the less extensive desolvation of the host and guest upon inclusion complexation.

Salicylic acid is also an o-arylhydroxycarboxylic acid but has only one benzene ring. At pH 1.5, β-CD forms a less stable 1∶1 inclusion complex with salicyclic acid than with 3H2NA and the contribution of −TΔS° to ΔG ° for the reaction involving SAL (0.39) is also smaller than for that involving 3H2NA (0.60), as expected in view of the lower hydrophobicity of the former. However, since hydrophobic interactions also play a major role in the formation of the supramolecule, the entropy change is still positive at pH 1.5. In addition, the K value of SAL with β-CD at pH 7.0 is substantially smaller than that at pH 1.5 due to the hydrophobicity loss upon the dissociation of SAL (pK_a = 2.97).⁴⁹ Furthermore, at pH 7.0 the entropy loss of the reaction is very large, giving a much less stable complex than that of 3H2NA with β-CD.

It has been found that the formation constant, the enthalpy gain and entropy loss of 3H2NA complexing with γ-CD are all smaller than those for β-CD at pH 7.0, which indicates a loose structure for the supramolecule. The size of the γ-CD cavity may be too large for 3H2NA with its naphthalene ring and the van der Waals forces, hydrogen bonding and hydrophobic interactions may not be effective in stabilizing the inclusion complex if the size of guest does not fit the host cavity.

Enthalpy–entropy compensation

In their study of cation binding by various acyclic and (bi)cyclic ligands and of host–guest complexation by CDs, Inoue and other workers ^7,11–16,20 have observed a good linear relationship between ΔH ° and ΔS°. Using the present data sets in Tables 1–5, ΔH ° is plotted against ΔS° (see supplementary data Fig. 4) giving good straight lines with corresponding slopes 235 ± 21 and 246 ± 2 K for native and modified cyclodextrins. The data are within the experimental error of the slope reported by Rekharsky et al. in ref. 7 and ref. 28but smaller than those reported in ref. 20 and ref. 29. The respective intercepts of the linear ΔS° vs. ΔH ° plots are −16.3 ± 1.0 and −17.1 ± 0.1 kJ mol⁻¹.

From the ΔH ° vs.TΔS° plots (see Fig. 6), we obtain slopes and intercepts which are compared with the relevant values in Table 6. Data of Inoue et al.¹¹ involving naphthalenesulfonates inclusion with native CDs (α = 1.09, TΔS°₀ = 16.5 kJ mol⁻¹) are about the same as ours (α = 1.20 ± 0.10, TΔS°₀ = 19.1 ± 2.5 kJ mol⁻¹). The present data for modified CDs (α = 1.21 ± 0.01, TΔS°₀ = 20.7 ± 0.3 kJ mol⁻¹) are in agreement with those (α = 1.07, TΔS°₀ = 20.9 kJ mol⁻¹) obtained by Inoue et al.¹²

Table 6 The slope (α) and intercept (TΔS°₀) of the ΔH ° vs. TΔS° plot for 1∶1 host–guest complexation in homogeneous solution

Host	α	TΔS°0/kJ mol^−1
a  This work. b  Naphthalenesulfonates including with native CDs in ref. 11. c  Ref. 12. d  Ref. 13.
^a Native CDs	1.20 ± 0.10	19.1 ± 2.5
^a Modified CDs	1.21 ± 0.01	20.7 ± 0.3
^a Native and modified CDs	1.21 ± 0.07	19.7 ± 1.6
^b Native CDs	1.09	16.5
^c Modified CDs	1.07	20.9
^d Glyme/podand	0.86	9.6
^d Crown ether	0.76	10.0
^c Cyclophane/calixarene	0.78	14.2
^d Cryptand	0.51	16.7
^c Quinone-receptor porphyrin	0.60	0.0
^c Metalloporphyrin	0.61	6.7

---

Fig. 6 Enthalpy–entropy compensation plots for inclusion complexation of 3H2NA and its analogues with native cyclodextrins (○) and modified cyclodextrins (•).

The slope α and intercept TΔS°₀ of the ΔH ° vs. TΔS° plot have been proposed for use as a quantitative measure of the conformational change and the extent of desolvation upon complex formation, respectively.¹¹ It has been revealed that rigid ligands, such as bicyclic cryptands, metalloporphyrin and quinone-receptor porphyrin, may undergo small conformational change, leading to the small slopes (0.51–0.61). The slopes of ΔH ° vs. TΔS° plots involving glymes/podands and crown ether, as well as cyclophane/calixarene, are large (0.76–0.86) since they have flexible skeletons and can alter their original conformations upon complexation. The large slope α (1.21) for modified CDs shows that the host suffers substantial conformational changes upon guest accommodation, owing to the greater flexibility of modified CDs upon total or partial disruption of the hydrogen-bond network by the mutable side arm.⁵⁰ It is interesting that the present slope for native CDs is quite large (1.20) in view of the rigid structure of CD itself in the solid state. However, based on the discussion above, we may safely infer that native CD in aqueous solution is not rigid but flexible, due to the hydrogen bonding between water and the hydroxy groups of CD or from the reorganization of the original hydrogen-bond network within the CD upon guest inclusion.¹¹ The large intercepts TΔS°₀ (19.1 and 20.7 kJ mol⁻¹) for native and modified CDs indicate extensive desolvation of both host and guest accompanying host–guest complexation. The large slope α and intrinsic entropic gain TΔS°₀ also show that the enthalpic gain from inclusion complexation is completely offset by entropic loss from conformational changes upon guest inclusion. Nevertheless, complexation is still possible even in the absence of enthapic stabilization if the intrinsic entropic gain from the extensive desolvation of the host and guest molecules is great enough (ΔG ° = (1 − α)ΔH ° vs. TΔS°₀). The present results also provide evidence for the proposal that the complexation phenomenon can be understood in a general context of the enthalpy–entropy effect as far as the weak interactions are involved.

Despite the different causes of their large slopes, these two different CDs may be considered as one kind on the basis of enthalpy–entropy compensation effect, since the slopes α and intercepts TΔS°₀ of the ΔH ° vs. TΔS° plots for native and modified CDs are about the same. When we integrate the present data involving TMβ-CD with those involving native CDs, the obtained slope α (1.21) and intercept TΔS°₀ (19.7 kJ mol⁻¹) of the TΔS° vs. ΔH ° plot are near the corresponding values for native and modified CDs.

Conclusion

(1) The importance of hydrogen bonding between hosts and guests in inclusion complexation is studied systematically and discussed in detail. It is found that hydrogen bonding does contribute significantly to the stability of the inclusion complex. (2) Enthalpy and entropy changes both contribute to inclusion complexation when the guest exists mainly as its molecular form, while enthalpy governs the complexation when the guests fully ionize. (3) The stability and thermodynamic parameters of the inclusion complexes are greatly affected by the host cavity size, the guest diameter and the position of substituent. (4) In terms of the enthalpy–entropy compensation effect, the skeleton of native CD in aqueous solutions is not rigid but flexible, despite its rigid skeleton in the solid state, while modified CDs have large flexibility due to their mutable side arm. Having the same large intercepts, TΔS°₀, for native and modified CDs, these two different CDs may be considered as one kind on the basis of the enthalpy–entropy compensation effect. In summary, our work gives an example of the comprehensive investigation of the function of weak interactions in inclusion complexation by cyclodextrins.

Experimental

β-CD was purchased from Nanjing Food Ferment Institute, recrystallized twice from water and dried in vacuum at 80 °C for 24 h. TMβ-CD was bought from Sigma. γ-CD was a kind gift from Professor Tabbachi (University of Neuchatel, Switzerland). 3-Hydroxy-2-naphthoic acid (3H2NA), 2-hydroxy-1-naphthoic acid (2H1NA), 2-ethoxy-1-naphthoic acid (2E1NA) and 2-hydroxy-1-benzoic acid (SAL) were recrystallized from ethanol. Other reagents used were A. R. grade. Double-distilled water was used as solvent.

Fluorescence spectra were taken on a Perkin-Elmer LS50B with 1 cm quartz cells. The temperature was maintained at 25 ± 0.1 °C by means of an external circulating water bath. Relative fluorescence intensities were measured at a constant wavelength around the emission maximum. The excitation wavelengths for 1.8 × 10⁻⁵ M 3H2NA at pH < 3 and pH > 3 were 310 and 350 nm, respectively. Those for 8.8 × 10⁻⁶ M 2H1NA and 2.6 × 10⁻⁶ M 2E1NA at pH 7.0 are 350 and 330 nm, correspondingly. Those for 1.6 × 10⁻⁵ M SAL at pH 1.5 and 7.0 are 302 and 310 nm, respectively. The solubility of the guests at pH < 3 and that of 2E1NA at pH 7.0 is poor. Since the concentration is low, the dimerization of the guests may be ignored ³⁰ and we didn’t observe the excimer fluorescence of 2∶2 inclusion complex of the guests with β-cyclodextrin. The pH values adjusted by HCl and NaOH were determined with a Leici pH meter, model 25.

Acknowledgements

This research is supported by National Science Foundation of China.

References

1. M. L. Bender and M. Komiyama , Cyclodextrin Chemistry, Springer Verlag, Berlin, 1978..
2. J. Szejtli , Cyclodextrins and their Inclusion Complexes, Academiai Kiado, Budapest, 1982..
3. S. Li and W. C. Purdy, Chem. Rev., 1992, 92, 1457.
4. G. Wenz, Angew. Chem., Int. Ed. Engl., 1994, 33, 803.
5. K. A. Connors, Chem. Rev., 1997, 97, 1325.
6. M. V. Rekharsky and Y. Inoue, Chem. Rev., 1998, 98, 1875.
7. M. V. Rekharsky, R. N. Goldberg, F. P. Schwarz, Y. B. Tewari, P. D. Ross, Y. Yamashoji and Y. Inoue, J. Am. Chem. Soc., 1995, 117, 8830.
8. H.-J. Schneider, Angew. Chem,. Int. Ed. Engl., 1991, 30, 1417.
9. J.-M. Lehn, Angew. Chem., Int. Ed. Engl., 1988, 27, 89.
10. F. Diederich, Angew. Chem., Int. Ed. Engl., 1988, 27, 362.
11. Y. Inoue, T. Hakushi, Y. Liu, L.-H. Tong, B.-J. Shen and D.-S. Jin, J. Am. Chem. Soc., 1993, 115, 475.
12. Y. Inoue, Y. Liu, L.-H. Tong, B.-J. Shen and D.-S. Jin, J. Am. Chem. Soc., 1993, 115, 10637.
13. Y. Inoue and T. Hakushi, J. Chem. Soc., Perkin Trans. 2, 1985, 935.
14. Y. Inoue, T. Hakushi, Y. Liu, L.-H. Tong, J. Hu, G.-D. Zhao, S. Huang and B.-Z. Tian, J. Phys. Chem., 1988, 92, 2371.
15. Y. Liu, L.-H. Tong, S. Huang, B.-Z. Tian, Y. Inoue and T. Hakushi, J. Phys. Chem., 1990, 94, 2666.
16. Y. Inoue, F. Amano, N. Okada, H. Inada, M. Ouchi, A. Tai, T. Hakushi, Y. Liu and L.-H. Tong, J. Chem. Soc., Perkin Trans. 2, 1990, 1239.
17. A. Buvari and L. Barcza, Acta Chim. Hung., 1989, 126, 455.
18. P. D. Ross and M. V. Rekharsky, Biophys. J., 1996, 71, 2144.
19. P. J. Kovi and S. G. Schulman, Anal. Chem., 1973, 45, 989.
20. G. L. Bertrand, J. R. Faulkner, S. M. Han and D. W. Armstrong, J. Phys. Chem., 1989, 93, 6863.
21. Z.-P. Yi, Z.-Z. Huang, J.-Y. Yu and H.-L. Chen, Chem. Lett., 1998, 1161.
22. E. E. Tucker and S. D. Christian, J. Am. Chem. Soc., 1984, 106, 1942.
23. S. Chokchainarong, O. R. Fennema and K. A. Connors, Carbohydr. Res., 1992, 232, 161.
24. K. J. Sasaki, S. D. Christian and E. E. Tucker, Fluid Phase Equilib., 1989, 49, 281.
25. R. Rymden, J. Carlfors and P. J. Stilbs, J. Inclusion Phenom., 1983, 1, 159.
26. E. A. Lewis and L. D. Hansen, J. Chem. Soc., Perkin Trans. 2, 1973, 2081.
27. G. Barone, G. Castronuovo, P. Del Vecchio, V. Elia and M. Muscetta, J. Chem. Soc., Faraday Trans., 1986, 82, 2089.
28. M. V. Rekharsky, F. P. Schwarz, Y. B. Tewari and R. N. Goldberg, J. Phys. Chem., 1994, 98, 10282.
29. M. V. Rekharsky, F. P. Schwarz, Y. B. Tewari, R. N. Goldberg, M. Tanaka and Y. Yamashoji, J. Phys. Chem., 1994, 98, 4098.
30. W. R. Ware, P. R. Shukla, P. J. Sullivan and R. V. Bremphis, J. Chem. Phys., 1971, 55, 4048.
31. Z.-P. Yi, C.-C. Zhao, Z.-Z. Huang, H.-L. Chen and J.-Y. Yu, Phys. Chem. Chem. Phys., 1999, 1, 441.
32. Y. Matsui, M. Fujie and K. Hanaoka, Bull. Chem. Soc. Jpn., 1989, 62, 1451.
33. R. I. Gelb, L. M. Schwartz, M. Radeos and D. A. Laufer, J. Phys. Chem., 1983, 87, 3349.
34. A. Buvari and L. Barcza, Inorg. Chim. Acta, 1979, 33, L179.
35. R. P. Rohrbach, L. J. Rodriguez and E. M. Eyring, J. Phys. Chem., 1977, 81, 944.
36. F. Gramer and W. Saenger and H.-Ch. Spatz, J. Am. Chem. Soc., 1967, 89, 14.
37. K. Mochida, A. Kagita, Y. Matsui and Y. Date, Bull. Chem. Soc. Jpn., 1973, 46, 3703.
38. Y. Matsui, M. Ono and S. Tokunaga, Bull. Chem. Soc. Jpn., 1997, 70, 535.
39. H. A. Benesi and J. H. Hildebrand, J. Am. Chem. Soc., 1949, 71, 2703.
40. F. G. Sanchez, M. H. Lopez and A. Heredia, Anal. Chim. Acta, 1986, 187, 147.
41. F. G. Sanchez, M. H. Lopez and J. C. Marquez Gomez, Analyst, 1987, 112, 1037.
42. S. Hamai, Bull. Chem. Soc. Jpn., 1982, 55, 2721.
43. H. Kondo, H. Nakatani and K. Hiromi, J. Biochem., 1976, 79, 393.
44. J. Hine, J. Am. Chem. Soc., 1972, 94, 5766.
45. N. Stahl and W. P. Jencks, J. Am. Chem. Soc., 1986, 108, 4196.
46. M. Fujiki, T. Deguchi and I. Sanemasa, Bull. Chem. Soc. Jpn., 1988, 61, 1163.
47. D. A. Stauffer, R. E. Barrans, Jr. and D. A. Dougherty, J. Org. Chem., 1990, 55, 2762.
48. S. Hamai and N. Satoh, Carbohydr. Res., 1997, 304, 229.
49. R. C. Weast , M. J. Astle and W. H. Beyer , CRC Handbook of Chemistry and Physics, 69th edition, CRC Press, Inc., Boca Raton, Florida, 1988–1989, D16..
50. C. D. Lavandier, M. P. Pelletier and V. C. Reinsborough, Aust. J. Chem., 1991, 44, 457.

---

Footnote

† Further figures representing experimental data are available as supplementary data. For direct electronic access see http://www. rsc.org/suppdata/p2/a9/a905463d/, otherwise available from BLDSC (SUPPL. NO. 57676, 5 pp.) or the RSC Library. See Instructions for Authors available via the RSC web page (http://www.rsc.org/authors).

---