Structural analysis and magnetic properties of the 2-D compounds [M(N3)2(bpa)]n (M = Mn, Co or Ni; bpa = 1,2-bis(4-pyridyl)ethane)![[hair space]](https://www.rsc.org/images/entities/h2_char_200a.gif) †
†
Margarita L. Hernándeza, M. Gotzone Barandikab, M. Karmele Urtiagac, Roberto Cortésb, Luis Lezamaa and M. Isabel Arriortua*c
aDepartamento de Química Inorgánica, Facultad de Ciencias, Universidad del País Vasco, Apdo. 644, Bilbao, 48080, Spain
bDepartamento de Química Inorgánica, Facultad de Farmacia, Universidad del País Vasco, Apdo. 450, Vitoria, 01080, Spain
cDepartamento de Mineralogía-Petrología, Facultad de Ciencias, Universidad del País Vasco, Apdo. 644, Bilbao, 48080, Spain. E-mail: npparmai@lg.ehu.es
First published on UnassignedUnassigned24th December 1999
Abstract
Isomorphous compounds exhibiting the general formula [M(N3)2(bpa)]n (M = MnII1, CoII2 or NiII3; bpa = 1,2-bis(4-pyridyl)ethane) have been prepared and magnetostructurally characterised. X-Ray diffraction analysis revealed a 2-D arrangement of octahedrally co-ordinated metal cations where di-μ-(1,3)-N3-bridged metallic chains are connected through bpa ligands. IR and UV-VIS spectra were consistent with this structural characterisation. Magnetic analysis carried out by means of ESR spectroscopy and susceptibility measurements indicated that the three compounds are antiferromagnetic, J values being −5.7, −14.0 and −80 cm−1 for 1, 2 and 3, respectively.
Introduction
The construction of transition-metal supramolecular arrays based on covalent interactions or hydrogen bonding is an area of great activity in inorganic chemistry. From a magnetic point of view, covalent systems are particularly interesting as they can provide high magnetic ordering. A rational design of these arrays implies the selection of appropriate bridging ligands which favour the magnetic coupling between metallic centres.A perspective on the literature about extended structures shows a large number of azide-bridged compounds from dimers to 3-D compounds depending on the relative metal to azide proportion. The M∶N3 (1∶2) stoichiometry (M being a divalent cation), in particular, has been observed to give rise to 1-D![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 1 and 2-D
1 and 2-D![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 2 systems (the dimensionality just referring to the links through azide groups). Thus, to the authors’ knowledge, just one azide-bridged 3-D compound has been reported so far.3
2 systems (the dimensionality just referring to the links through azide groups). Thus, to the authors’ knowledge, just one azide-bridged 3-D compound has been reported so far.3
The strategy for the preparation of these extended systems has been systematically examined by enhancing the linking between structural units of lower dimensionality. This can be carried out by using organic spacers acting as bridges between these smaller units. In this sense, compounds obtained by using rigid N,N′ bidentate spacers like 4,4′-bipyridine, pyrazine and other related ligands should be cited.1e,i,4 Among the N,N![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ′ bidentate ligands, 1,2-bis(4-pyridyl)ethane (bpa) represents an excellent alternative for further research as it exhibits two different conformations,5anti and gauche. Thus, isomerism and its manifestation in the structure become issues to be considered when using this ligand. Thus, a strategy was conceived leading to the preparation of MII–N3–bpa extended structures. The results presented here concern the magnetostructural characterisation of three isomorphous 2-D compounds of general formula [M(N3)2(bpa)]n (M = MnII1, CoII2 or NiII3) which exhibit intermetallic bridges through both end-to-end azide and bpa ligands.
′ bidentate ligands, 1,2-bis(4-pyridyl)ethane (bpa) represents an excellent alternative for further research as it exhibits two different conformations,5anti and gauche. Thus, isomerism and its manifestation in the structure become issues to be considered when using this ligand. Thus, a strategy was conceived leading to the preparation of MII–N3–bpa extended structures. The results presented here concern the magnetostructural characterisation of three isomorphous 2-D compounds of general formula [M(N3)2(bpa)]n (M = MnII1, CoII2 or NiII3) which exhibit intermetallic bridges through both end-to-end azide and bpa ligands.
Experimental
Synthesis
Synthesis of the three compounds was carried out from aqueous solutions of Mn(SO4)2·H2O (0.5 mmol, 20 ml) 1, Co(SO4)2·7H2O (0.5 mmol, 20 ml) 2 and Ni(SO4)2·7H2O (0.5 mmol, 20 ml) 3; 2.5 mmol of NaN3 were also dissolved in these aqueous solutions. A warm methanolic solution of bpa (0.5 mmol, 20 ml) was added to the former mixtures. The resulting solution for 1 was left to stand at room temperature after two hour stirring at 50 °C. After several days, prismatic, yellow, X-ray quality single crystals were obtained (35% yield). In the solutions containing CoII and NiII, however, pink (2) and green (3) precipitates were immediately obtained (69 and 63% yield, respectively) after the addition of bpa. Further attempts to recrystallise these precipitates in several mixtures of ethanol, methanol, acetone and water gave rise to poor quality single crystals. Elemental analysis and atomic absorption results were in good agreement with the C12H12MN8 (M = Mn, Co, Ni) stoichiometry for the three compounds. Found (calc.) (%): C, 44.92 (44.59); H, 3.96 (3.74); Mn, 17.11 (17.00); N, 34.10 (34.67), for 1: C, 44.17 (44.05); H, 3.72 (3.70); Co, 18.21 (18.01); N, 33.69 (34.24), for 2: C, 44.21 (44.08); H, 3.98 (3.70); N, 33.17 (34.27); Ni, 17.67 (17.65), for 3.Physical measurements
Microanalyses were performed with a Perkin-Elmer 2400 analyser. Analytical measurements were carried out in an ARL 3410 + ICP apparatus with Minitorch equipment. IR Spectroscopy was performed on a Nicolet 520 FTIR spectrophotometer in the 400–4000 cm−1 region, diffuse reflectance spectroscopy at room temperature on a Cary 2415 spectrometer in the range 5000–45000 cm−1 and ESR spectroscopy on powdered samples at X frequency between 4 and 300 K with a Bruker ESR 300 spectrometer, equipped with a standard Oxford low-temperature device, calibrated by the NMR probe for the magnetic field, the frequency being measured by using a Hewlett-Packard 5352B microwave frequency computer. Magnetic susceptibilities of powdered samples were measured in the temperature range 1.8–300 K (at a magnetic field of 1000 G) using a Quantum Design Squid MPM5-7 magnetometer, equipped with a helium continuous-flow cryostat. The experimental susceptibilities were corrected for the diamagnetism of the constituent atoms (Pascal tables).Crystal structure determination
Single-crystal X-ray measurements for compound 1 were made at room temperature on an Enraf-Nonius CAD-4 diffractometer with graphite-monochromated Mo-Kα radiation (λ = 0.71070 Å), operating in ω–2θ scanning mode using suitable crystals for data collection. Accurate lattice parameters were determined from least-squares refinement of 25 well centred reflections. Intensity data were collected in the θ range 1–30°. During data collection two standard reflections periodically observed showed no significant variation. Corrections for Lorentz-polarisation factors were applied to the intensity values.The structure was solved by heavy-atom Patterson methods using the program SHELXS 97![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 6 and refined by a full-matrix least-squares procedure on F
6 and refined by a full-matrix least-squares procedure on F![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 2 using SHELXL 97.7 Non-hydrogen atomic scattering factors were taken from ref. 8. Table 1 shows crystallographic data and processing parameters. As can be observed in Fig. 1, the structure for compound 1 shows remarkable disorder affecting the bpa ligand. Thus, the position of atoms C1, C2, C7 and C8 has been split into two, a and b (with multiplicities of 0.5), for a better structural resolution. Additionally, due to their slight deviation from special positions, atoms C3, C4, C5 and C6 are duplicated by symmetry.
2 using SHELXL 97.7 Non-hydrogen atomic scattering factors were taken from ref. 8. Table 1 shows crystallographic data and processing parameters. As can be observed in Fig. 1, the structure for compound 1 shows remarkable disorder affecting the bpa ligand. Thus, the position of atoms C1, C2, C7 and C8 has been split into two, a and b (with multiplicities of 0.5), for a better structural resolution. Additionally, due to their slight deviation from special positions, atoms C3, C4, C5 and C6 are duplicated by symmetry.
| Formula | C12H12MnN8 | Z | 4 |
| M | 323.24 | T/°C | 20 |
| Crystal system | Monoclinic | Dobs![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) /g cm−3 /g cm−3 | 1.55(4) |
| Space group | C2/c | Dc![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) /g cm−3 /g cm−3 | 1.52 |
| a/Å | 9.991(3) | μ/cm−1 | 9.4 |
| b/Å | 13.883(2) | Unique data | 2056 |
| c/Å | 10.482(3) | Observed data | 1516 |
| β/° | 103.15(2) | R (R′![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ) ) | 0.055 (0.1350) |
| U/Å3 | 1415.8(6) |
![An ORTEP 11 view (50% probability) of the structure for compound 1 [Mn(N3)2(bpa)]n. The position of atoms C1, C2, C7 and C8 has been split in two, a and b (with multiplicities of 0.5), for a better structural resolution. Additionally, due to their slight deviation from special positions, C3, C4, C5 and C6 are duplicated by symmetry.](/image/article/2000/DT/a906154a/a906154a-f1.gif) | ||
Fig. 1 An ORTEP![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 11 view (50% probability) of the structure for compound 1 [Mn(N3)2(bpa)]n. The position of atoms C1, C2, C7 and C8 has been split in two, a and b (with multiplicities of 0.5), for a better structural resolution. Additionally, due to their slight deviation from special positions, C3, C4, C5 and C6 are duplicated by symmetry. 11 view (50% probability) of the structure for compound 1 [Mn(N3)2(bpa)]n. The position of atoms C1, C2, C7 and C8 has been split in two, a and b (with multiplicities of 0.5), for a better structural resolution. Additionally, due to their slight deviation from special positions, C3, C4, C5 and C6 are duplicated by symmetry.
| ||
CCDC reference number 186/1722.
See http://www.rsc.org/suppdata/dt/a9/a906154a/, for crystallographic files in .cif format.
X-Ray powder diffraction data for compounds 2 and 3 were collected on a Philips X’PERT powder diffractometer with Cu-Kα radiation in steps of 0.02° over the 2θ 5–60° range and a fixed-time counting of 4 s at 25 °C. The patterns were indexed with the FULLPROF![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 9 program based on the Rietveld method
9 program based on the Rietveld method![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 10 using the Profile Matching option. Crystallographic data and processing parameters for compounds 2 and 3 are given in Table 3.
10 using the Profile Matching option. Crystallographic data and processing parameters for compounds 2 and 3 are given in Table 3.
Results and discussion
Structural analysis
The structure of compound 1 (Fig. 1) consists of a 2-D arrangement in which azide-bridged manganese(II) chains are connected through bpa ligands. The manganese(II) ions are octahedrally co-ordinated to four end-to-end azide ligands occupying the equatorial positions and two bpa ligands in the axial ones. In this way the double azide bridges give rise to the extension of the structure along the [001] direction while the bpa bridges extend along [010]. The intermetallic distances through the azide and bpa bridges are 5.329(2) and 13.883(2) Å, respectively and the interplanar distance is 8.552(1) Å. The bpa ligands crystallise in the anti conformation, the dihedral angle formed by the two pyridyl rings being 67°. The intermetallic distance through the bpa ligand is similar to those found in compounds exhibiting M(anti-bpa)M bridges![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 5c,d and slightly longer for M(
5c,d and slightly longer for M(![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) gauche-bpa)M bridges.5e
gauche-bpa)M bridges.5eTable 2 shows selected structural parameters for compound 1. As can be seen, the octahedral sphere around MnII is slightly distorted exhibiting angles very close to the ideal ones. The Mn–N distances lie among the usual ones (Mn–Nazide and Mn–Nbpa average distances are 2.219 and 2.257 Å, respectively). The azide bridge which adopts the chair conformation can be described by the Mn–N–N′ and N′–N′′–Mn angles (121.3 and 136.5°, respectively) and the τ angle (44.0°). The latter is defined as the angle between the Mn–N–N′–N′′ and N–N′–N′′–Mn′ mean planes.
| Symmetry codes: (i) −x, −y − 2, −z + 1; (ii) x, −y − 2, z − ½; (iii) −x, y, −z + ½; (iv) x, y − 1, z. | |||
|---|---|---|---|
| Mn(1)–N(5i) | 2.211(3) | Mn(1)–N(1) | 2.241(4) |
| Mn(1)–N(3) | 2.227(3) | Mn(1)–N(2iv) | 2.274(4) |
| N(4)–N(3)–Mn(1) | 121.3(2) | N(5i)–Mn(1)–N(1) | 89.9(1) |
| N(4)–N(5)–Mn(1i) | 136.5(3) | N(3iii)–Mn(1)–N(1) | 90.81(9) |
| N(5)–N(4)–N(3) | 177.4(3) | N(5i)–Mn(1)–N(2iv) | 90.1(1) |
| N(1)–Mn(1)–N(2iv) | 180.0 | N(3)–Mn(1)–N(2iv) | 89.19(9) |
| N(5i)–Mn(1)–N(3) | 90.7(1) | ||
X-Ray diffraction patterns for compounds 2 and 3 are very similar to the theoretical pattern generated for 1. Therefore, the values corresponding to the cell parameters and space group of compound 1 were used as initial data for the refinement of the experimental patterns for 2 and 3. The experimental, calculated (according to the best fit parameters shown in Table 3) and difference patterns are shown in Fig. 2 for 2 and 3. As can be seen, the crystallinity of the powdered sample for compound 3 is remarkably poor. These results clearly indicate that compounds 1, 2 and 3 are isomorphous.
| 2 | 3 | |
|---|---|---|
a Rb = 100[Σ|Io − Ic![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) |]/Σ|Io |]/Σ|Io![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) |.b Rp = 100[Σ| |.b Rp = 100[Σ|![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) yo−yc yo−yc![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) |]/Σ| |]/Σ|![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) yo yo![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) |.c Rwp = [Σ[w| |.c Rwp = [Σ[w|![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) yo − yc yo − yc![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) |2]/Σ[w| |2]/Σ[w|![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) yo yo![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) |2]]½. |2]]½. | ||
| Formula | C12H12CoN8 | C12H12N8Ni |
| M | 327.21 | 327.97 |
| Crystal system | Monoclinic | Monoclinic |
| Space group | C![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 2/c 2/c | C![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 2/c 2/c |
| a/Å | 10.037(3) | 10.019(3) |
| b/Å | 14.622(5) | 14.541(4) |
| c/Å | 10.360(4) | 10.262(2) |
| β/° | 102.92(1) | 102.49(2) |
| U/Å3 | 1482.0 | 1459.4 |
| Z | 4 | 4 |
| T/°C | 25 | 25 |
| λ/Å | 1.5418 | 1.5418 |
Rb![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) a a | 3.82 | 0.291 |
Rp![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) b b | 14.5 | 6.58 |
Rwp![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) c c | 20.0 | 8.50 |
![Experimental, calculated and difference powder X-ray diffraction patterns for (top) [Co(N3)2(bpa)]n2 and (bottom) [Ni(N3)2(bpa)]n3.](/image/article/2000/DT/a906154a/a906154a-f2.gif) | ||
| Fig. 2 Experimental, calculated and difference powder X-ray diffraction patterns for (top) [Co(N3)2(bpa)]n2 and (bottom) [Ni(N3)2(bpa)]n3. | ||
IR and UV-VIS spectroscopies
A summary of the most important IR bands corresponding to compounds 1, 2 and 3 together with their tentative assignment![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 12 is given in Table 4. As can be seen, the three spectra exhibit an intense absorption at about 2068 cm−1 which is associated with the asymmetric stretching mode of the azide ligand. The splitting of this band is indicative of the bridging mode of the azide in the three compounds.
12 is given in Table 4. As can be seen, the three spectra exhibit an intense absorption at about 2068 cm−1 which is associated with the asymmetric stretching mode of the azide ligand. The splitting of this band is indicative of the bridging mode of the azide in the three compounds.
| bpa | 1 | 2 | 3 | |
|---|---|---|---|---|
| i = Intense, m = medium, sp = split. | ||||
| Azide, νa | 2071i,sp | 2063i,sp | 2065i,sp | |
Pyridyl ring stretching, ν(C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) C) C) | 1594i | 1609m | 1611m | 1612m |
ν(aromatic C–C, C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) N) N) | 1413i | 1424m | 1425m | 1427m |
| Pyridyl ring breathing, δ(aromatic C–H) | 982m | 1012m | 1018m | 1022m |
| Pyridyl out of plane bending, ν(aromatic C–H) | 817i | 822m | 825m | 825m |
| Pyridyl ring in plane vibration | 539i,sp | 532m,sp | 534m,sp | 536m,sp |
On the other hand, the frequencies of the bands related to the bpa ligand in the three compounds are very close to their positions for the “free” ligand (which are also displayed in Table 4) indicating that the pyridyl rings are nearly planar in the complexes. These results are indicative of a similar co-ordination of the ligands to the metal ions, as expected for isomorphous compounds.
The diffuse reflectance spectrum for compound 2 is typical of octahedral high spin cobalt(II) complexes. Thus, the UV-VIS spectrum shows three spin-allowed transitions from 4T1g to 4T2g (ν1 8698 cm−1), 4A2g (ν2 18886 cm−1) and 4T1g(P) (ν3 20585 cm−1), respectively, the ν2 transition appearing as a shoulder of ν3 (ν2/ν1 = 2.17). The values of Dq = 683 cm−1 and B = 668 cm−1 which have been calculated from these transitions are typical for high spin cobalt(II) complexes.13 The value of B is indicative of a 70% covalency of the Co–N bonds in 2. The spectrum also shows a charge-transfer band above 30000 cm−1.
Compound 3 exhibits four UV-VIS bands which have been assigned to the spin allowed transitions from 3A2g to 3T2g (ν1 9622 cm−1), 3T1g (ν3 15867 cm−1) and 3T1g(P) (ν4 28800 cm−1) and the spin forbidden transition to 1Eg (ν2 15415 cm−1). According to these bands, values of Dq = 962 cm−1, B = 954 cm−1 and C = 4175 cm−1 have been calculated (indicating an 88% covalency of the Ni–N bonds). These values are typical for octahedral nickel(II) compounds.13 The spectrum also shows a charge-transfer band above 35000 cm−1.
In summary, UV-VIS data for compounds 2 and 3 are consistent with the presence of slightly distorted octahedral co-ordination spheres around the metal ions as expected from the structural characterisation carried out for the isomorphous compound 1.
ESR spectroscopy and magnetic properties
X-Band powdered ESR spectra recorded for compound 1 exhibit isotropic signals (![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) g ;= 2.000) over the whole range of temperature (4–300 K) studied. This
is consistent with the presence of octahedral MnN6 chromophores in which manganese(II) ions are very slightly distorted. In order to study the thermal variation of the area under the ESR signal (which is directly proportional to the magnetic susceptibility), the ΔH (linewidth in Gauss) and I (intensity in arbitrary units) of the signals at each temperature were estimated by fitting the spectra by Lorentzian curves (R > 0.999 for T ≥ 50 K, >0.99 for T ≥ 15 K, >0.96 for T ≥ 4 K). The variations of the gain, attenuation and modulation amplitude during measurements were considered for the fitting.
g ;= 2.000) over the whole range of temperature (4–300 K) studied. This
is consistent with the presence of octahedral MnN6 chromophores in which manganese(II) ions are very slightly distorted. In order to study the thermal variation of the area under the ESR signal (which is directly proportional to the magnetic susceptibility), the ΔH (linewidth in Gauss) and I (intensity in arbitrary units) of the signals at each temperature were estimated by fitting the spectra by Lorentzian curves (R > 0.999 for T ≥ 50 K, >0.99 for T ≥ 15 K, >0.96 for T ≥ 4 K). The variations of the gain, attenuation and modulation amplitude during measurements were considered for the fitting.Plotting ΔHvs. T (Fig. 3) reveals that the linewidth remains practically constant down to 50 K, at which a broadening can be observed. The great increase of the linewidth is indicative of 1-D magnetic coupling taking place at low temperatures. This can also be deduced from the analysis of the thermal variation of the signal area (I·ΔH product which is also shown in Fig. 3). Thus, I·ΔH values continuously increase upon cooling to a broad maximum (ca. 65 K) below which the curve rapidly decreases. The 1-D ordering temperature has been estimated to be 36 K, at which a tangent plotted on the increasing region of ΔH reaches the zero value (Fig. 3). The nature and extension of the 1-D magnetic coupling deduced from ESR spectroscopy will be discussed below after analysing the magnetic susceptibility data.
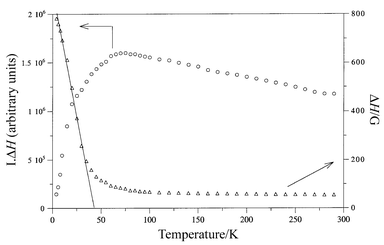 | ||
| Fig. 3 Thermal variation of ΔH (linewidth of the ESR signal) and the ΔH·I product (I = intensity of the ESR signal) for compound 1. | ||
Fig. 4 shows the thermal variation of the magnetic susceptibility, χm, and the χmT product for compound 1. As can be seen, χm values increase for decreasing temperatures (from 11.31 × 10−3 cm3 mol−1 at RT) reaching a broad maximum at 62 K (18.18 × 10−3 cm3 mol−1). The curve drops to a minimum at 12 K (15.35 × 10−3 cm3 mol−1), at which χm values exponentially increase upon further cooling. The χmT magnitude continuously decreases with decreasing temperature. On the other hand, χm−1 has been observed not to follow the Curie–Weiss law over the measured temperature range.
![Thermal evolution of χm and χmT for compound 1, [Mn(N3)2(bpa)]n, and their corresponding theoretical curves. Discontinuous and continuous lines correspond to the fittings through eqns. (1) and (2), respectively.](/image/article/2000/DT/a906154a/a906154a-f4.gif) | ||
| Fig. 4 Thermal evolution of χm and χmT for compound 1, [Mn(N3)2(bpa)]n, and their corresponding theoretical curves. Discontinuous and continuous lines correspond to the fittings through eqns. (1) and (2), respectively. | ||
Taking into account that the magnetic interactions through bpa ligands must be very weak, just the coupling through azide-bridged chains should be considered to be responsible for the bulk magnetic behaviour. Therefore, magnetic data can be interpreted in terms of an infinite-spin, linear chain model, eqn. (1),14 scaled for S = 5/2, where N and k are the Avogadro and Boltzmann constants, respectively, and β is the Bohr magneton. According to eqn. (1), the best fit parameters for compound 1 have been determined to be g = 2.003 (in good agreement with the experimental data) and J = −5.7 cm−1. As can be seen in Fig. 4, this theoretical curve quite well reproduces the thermal variation of χm, with the exception of the region below 12 K. These data indicate the occurrence of antiferromagnetic coupling along the di-μ-(1,3)-N3 chains, which accounts for the bulk magnetic behaviour down to the minimum. The further increase of χm can be explained by considering the presence of a paramagnetic impurity of the same molar mass as 1 whose contribution (δ) can be evaluated by means of eqn. (2). The best fitting obtained by using eqn. (2) corresponds to δ = 0.002 and the same values of J and g (−5.7 cm−1 and 2.003, respectively). As can be seen in Fig. 4, the corresponding theoretical curve does reproduce a minimum at 12 K but exhibits noticeable discrepancy with the experimental χm around it. Therefore, although present in small amount, the contribution of the impurity clearly obscures the antiferromagnetic coupling at very low temperatures.
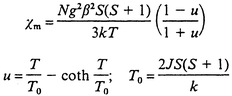 | (1) |
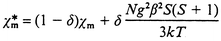 | (2) |
It is worth mentioning the excellent correspondence between ESR and magnetic data for compound 1. Thus, the thermal variation of the I·ΔH product shows a similar trend to that observed for χm (with the exception of the contribution of the impurity to the magnetic susceptibility at low temperatures). Additionally, an excellent correlation has been found between the 1-D ordering temperature (calculated from ESR analysis) and the temperature at which χm is maximum. Thus, according to de Jongh and Miedema,15 both temperatures should be related by a factor of 1.8. For compound 1 this factor has been calculated to be 1.72, confirming the validity of this approach.
The magnetic data recorded for compound 2 are displayed in Fig. 5 as the thermal variation of χm and χmT. As can be observed, the curves are qualitatively similar to those for 1. Thus, χm values increase (from 8.58 × 10−3 cm3 mol−1 at RT) upon cooling reaching a maximum (ca. 62 K, 14.02 × 10−3 cm3 mol−1), followed by a drop to 26 K (1.30 × 10−3 cm3 mol−1) and a further increase. Additionally, the χmvs. T curve shows another small maximum at 54 K (14.59 × 10−3 cm3 mol−1) which will be discussed below. The χmT values, on the other hand, continuously decrease upon cooling. As for 1, χm−1 does not follow the Curie–Weiss law. The bulk magnetic behaviour of compound 2 should also be expected to be the result of the antiferromagnetic coupling along the azide-bridged chains. Therefore, χm* in eqn. (2) has been calculated by using χm in eqn. (1) scaled for S = 3/2. The best fit parameters were J = −14.0 cm−1, g = 2.69 and δ = 0.015 (the molar mass of the impurity being the same as that of 2). As can be seen in Fig. 5, the theoretical data quite well reproduce both χm and χmT experimental values, with the exception of the region close to the minimum in χm. This discrepancy can be attributed to the fact that S = 1/2 can be expected to be the most populated state at low temperatures. It should also be pointed out that, on the JS(S + 1) criterion (S(S + 1) being the scaling parameter for eqn. (1), the values of J for 1 and 2 are comparable in magnitude.
![Thermal evolution of χm and χmT for compound 2, [Co(N3)2(bpa)]n , and their corresponding theoretical curves.](/image/article/2000/DT/a906154a/a906154a-f5.gif) | ||
Fig. 5 Thermal evolution of χm and χmT for compound 2, [Co(N3)2(bpa)]n![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) , and their corresponding theoretical curves. , and their corresponding theoretical curves.
| ||
In Fig. 6 the magnetic data for compound 3 are shown as the thermal variation of χm−1 and χmT. The χmTvs. T curve is similar to those for 1 and 2, with the curvature increasing from 3 to 1. The χm values continuously increase upon cooling (from 2.40 × 10−3 cm3 mol−1 at RT), the increase becoming exponential for temperatures below 45 K. On the other hand, the variation of χm−1 obeys the Curie–Weiss law down to 150 K, with values of Cm and θ of 1.128 cm3 K mol−1 and −228.7 K, respectively. The calculated value of g = 2.123 lies among the usual ones for octahedral NiII, while the high value of θ may be indicative of strong antiferromagnetic coupling. The magnetic data for compound 3 have been treated on the basis of the Weng equation![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 16(3) for the calculation of χm in χm* (eqn. (2)). This equation is applicable to linear chains with S = 1 being based upon the spin Hamiltonian H = −ΣSi
16(3) for the calculation of χm in χm* (eqn. (2)). This equation is applicable to linear chains with S = 1 being based upon the spin Hamiltonian H = −ΣSi![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) Si + 1
Si + 1![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) , where A = 0.019, B = 0.777, C = 4.346, D = 3.232, E = 5.834 and α = J/kT. The best fit (shown in Fig. 6) has been carried out by using J = 80 cm−1, g = 2.05 and δ = 0.11. As for 1 and 2, the paramagnetic impurity in this case has also been supposed to exhibit the same molar mass as 3. Thus, since the amount of paramagnetic impurity cannot be disregarded in this case, the value of J for 3 is not presumed to be very accurate. In fact, it implies stronger antiferromagnetic coupling than that predicted from the JS(S + 1) criterion in comparison to 1 and 2. In this sense, it should also be mentioned that several unfruitful attempts were made to fit the magnetic data for 3 by using lower values of J.
, where A = 0.019, B = 0.777, C = 4.346, D = 3.232, E = 5.834 and α = J/kT. The best fit (shown in Fig. 6) has been carried out by using J = 80 cm−1, g = 2.05 and δ = 0.11. As for 1 and 2, the paramagnetic impurity in this case has also been supposed to exhibit the same molar mass as 3. Thus, since the amount of paramagnetic impurity cannot be disregarded in this case, the value of J for 3 is not presumed to be very accurate. In fact, it implies stronger antiferromagnetic coupling than that predicted from the JS(S + 1) criterion in comparison to 1 and 2. In this sense, it should also be mentioned that several unfruitful attempts were made to fit the magnetic data for 3 by using lower values of J.
![Thermal evolution of χm and χmT for compound 3, [Ni(N3)2(bpa)]n, and their corresponding theoretical curves.](/image/article/2000/DT/a906154a/a906154a-f6.gif) | ||
| Fig. 6 Thermal evolution of χm and χmT for compound 3, [Ni(N3)2(bpa)]n, and their corresponding theoretical curves. | ||
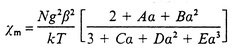 | (3) |
As mentioned above, the χmvs. T curve for compound 2 exhibits a small maximum at 54 K. However, the cause of this peak has not been positively confirmed. Thus, a 2-D magnetic ordering through the bpa ligands does not seem to be very probable. On the other hand, the possibility of a canting phenomenon should also be dismissed as the metallic centres are magnetically equivalent. Thus, the occurrence of certain structural modifications could be thought to be responsible for this small peak. It is worth mentioning that there is also a small anomaly on the χm curve for 1 which could correspond to the same effect but is obscured by the broad maximum close to it. For compound 3, on the other hand, the contribution of the paramagnetic impurity is clearly hiding any signal attributed to 1-D ordering or to any other effect.
Magneto-structural correlations
The theoretical approaches to the magnetostructural correlations in end-to-end azide-bridged systems reported so far![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 1f,m,2b,17 indicate that both the M–N–N and the τ angles are the key structural parameters for octahedral systems. Thus, MO analysis for systems based on d5–9 cations has demonstrated that an increase of the M–N–N angle causes a decrease of the antiferromagnetic contribution to the exchange constant J. Additionally, for the same value of M–N–N, the torsion angle is also expected to provide a decreasing antiferromagnetic term. Experimental evidence of these conclusions has been found for some azide-bridged systems of NiII
1f,m,2b,17 indicate that both the M–N–N and the τ angles are the key structural parameters for octahedral systems. Thus, MO analysis for systems based on d5–9 cations has demonstrated that an increase of the M–N–N angle causes a decrease of the antiferromagnetic contribution to the exchange constant J. Additionally, for the same value of M–N–N, the torsion angle is also expected to provide a decreasing antiferromagnetic term. Experimental evidence of these conclusions has been found for some azide-bridged systems of NiII![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 17 and MnII.1f,2b
17 and MnII.1f,2bIt is worth mentioning that homogeneous doubly end-to-end metal(II) (M = Mn, Ni or Co) azide-bridged chains are not very common in the literature. In fact, to our knowledge, just one manganese(II) compound![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) 1m with these characteristics has been reported so far. For this reason, in order to compare the results concerning the present compounds with others found in the literature, magnetostructural parameters corresponding to non-uniform 1-D compounds exhibiting double azide links have been summarised in Tables 5 and 6 for manganese(II) and nickel(II) systems, respectively. Unfortunately, no information has been found for comparison among cobalt(II) compounds. As can be seen, compounds 1 and 3 exhibit representative values of the M–N–N angle and the J constant but no further conclusions can be drawn from this set of data.
1m with these characteristics has been reported so far. For this reason, in order to compare the results concerning the present compounds with others found in the literature, magnetostructural parameters corresponding to non-uniform 1-D compounds exhibiting double azide links have been summarised in Tables 5 and 6 for manganese(II) and nickel(II) systems, respectively. Unfortunately, no information has been found for comparison among cobalt(II) compounds. As can be seen, compounds 1 and 3 exhibit representative values of the M–N–N angle and the J constant but no further conclusions can be drawn from this set of data.
| Compound | JdEE | M–N–N | τ | Characteristics | Ref. |
|---|---|---|---|---|---|
| JdEE = J corresponding to the double end-to-end azide bridge; dEE = double end-to-end azide bridge; dEO = double end-on azide bridge; pyOH = 2-hydroxypyridine; 3-Etpy = 3-ethylpyridine; bipy = 2,2′-bipyridine. | |||||
| [Mn(pyOH)2(N3)2]n | −7 | 123.8/122.4 | 63.1 | Uniform dEE | 1(m) |
| [Mn(3-Etpy)2(N3)2]n | −11.7 | 134.7/131.7 | 13.5 | Alternating dEE | 1(m) |
| −13.8 | 134.8/129.7 | 23.2 | |||
| [Mn(bipy)(N3)2]n | −11.9 | 131.1/127.3 | 41.1 | dEE–dEO | 1(b),(![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) f f![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ),( ),(![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) g) g) |
| [Mn(N3)2(bpa)]n | −5.7 | 136.5/121.3 | 44 | Uniform dEE | This work |
![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) J in cm−1, Ni–N–N and τ angles in °; the dimensionality refers just to the azide links)
J in cm−1, Ni–N–N and τ angles in °; the dimensionality refers just to the azide links)
| Compound | JdEE | Ni–N–N | τ | Characteristics | Ref. |
|---|---|---|---|---|---|
JdEE = J corresponding to the double end-to-end azide bridge; dEE = double end-to-end azide bridge; dEO = double end-on azide bridge; NN-dmen = N,N-dimethylethylenediamine; aep = 2-aminoethylpyridine; NN′-dmen = N,N![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ′-dimethylethylenediamine.
a Fully asymmetric. ′-dimethylethylenediamine.
a Fully asymmetric. | |||||
| [Ni(bipy)(N3)2]n | −2.6 | 118.2/129.9 | 35.2 | dEE–dEO | 1(b),(![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) g),(h) g),(h) |
| [Ni(NN-dmen)(N3)2]n | −156 | 121.1/139.4 | 0 | dEE–dEO | 1(c),(![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) j j![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ) ) |
| [Ni(aep)(N3)2]n | −28 | 125.6/124.4 | a | dEE–dEO | 1(c),(![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) j j![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ) ) |
| 121.6/117.9 | |||||
| [Ni(NN′-dmen)(N3)2]n | −120 | 130.9/132.9 | 0 | dEE–(dEO)3 | 1(d![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) ) ) |
| [Ni(N3)2(bpa)]n | −80 | 136.5/121.3 | 44 | Uniform dEE | This work |
Concluding remarks
Three compounds of general formula [M(N3)2(bpa)] (M = Mn![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) II, Co
II, Co![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) II or Ni
II or Ni![[hair space]](https://www.rsc.org/images/entities/char_200a.gif) II) were synthesized and magnetostructurally characterised. X-Ray diffraction analysis revealed that their structure consists of linear chains extending through di-μ-(1,3)-N3 bridges which are connected by bpa ligands in anti conformation giving rise to a 2-D arrangement. The thermal variation of the magnetic susceptibility for the three compounds has been interpreted in terms of the occurrence of antiferromagnetic coupling between metal ions along the azide-bridged chains.
II) were synthesized and magnetostructurally characterised. X-Ray diffraction analysis revealed that their structure consists of linear chains extending through di-μ-(1,3)-N3 bridges which are connected by bpa ligands in anti conformation giving rise to a 2-D arrangement. The thermal variation of the magnetic susceptibility for the three compounds has been interpreted in terms of the occurrence of antiferromagnetic coupling between metal ions along the azide-bridged chains.Acknowledgements
This work has been carried out with the financial support of the Universidad del País Vasco/Euskal Herriko Unibertsitatea (Grant UPV 130310-EB201/1998), the Gobierno Vasco/Eusko Jaurlaritza (Project PI96/39) and the Ministerio de Educación y Cultura (Project PB97-0637). M. L. H. also thanks the Universidad del País Vasco/Euskal Herriko Unibertsitatea for grant UPV 130.310.EB234/95.References
- (a) J. Ribas, M. Monfort, C. Díaz, C. Bastos and X. Solans, Inorg. Chem., 1994, 33, 484 CrossRef CAS; (b) R. Cortés, L. Lezama, J. L. Pizarro, M. I. Arriortua, X. Solans and T. Rojo, Angew. Chem., Int. Ed. Engl., 1994, 33, 2488 CrossRef; (c) J. Ribas, M. Monfort, B. Kumar-Gosh, X. Solans and M. Font-Bardía, J. Chem. Soc., Chem. Commun., 1995, 2375 RSC; (d) J. Ribas, M. Monfort, I. Resino, X. Solans, P. Rabu, F. Maingot and M. Drillon, Angew. Chem., Int. Ed. Engl., 1996, 35, 2520 CrossRef CAS; (e) G. De Munno, T. Poerio, G. Viau, M. Julve, F. Lloret, Y. Journaux and E. Riviere, Chem. Commun., 1996, 2587 RSC; (f) R. Cortés, M. Drillon, X. Solans, L. Lezama and T. Rojo, Inorg. Chem., 1997, 36, 677 CrossRef CAS; (g) G. Viau, M. G. Lombardi, G. De Munno, M. Julve, F. Lloret, J. Faus, A. Caneschi and J. M. Clemente-Juan, Chem. Commun., 1997, 1195 RSC; (h) J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and F. Lloret, Chem. Phys. Lett., 1997, 275, 79 CrossRef CAS; (i) R. Cortés, M. K. Urtiaga, L. Lezama, J. L. Pizarro, M. I. Arriortua and T. Rojo, Inorg. Chem., 1997, 36, 5016 CrossRef CAS; (j) F. Esposito and G. Kamieniarz, Phys. Rev. B, 1998, 57, 7431 CrossRef CAS; (k) A. Escuer, R. Vicente, M. S. El Fallah, M. A. S. Goher and F. A. Mautner, Inorg. Chem., 1998, 37, 4466 CrossRef CAS; (l) A. Escuer, M. Font-Bardía, E. Peñalba, X. Solans and R. Vicente, Polyhedron, 1998, 18, 211 CrossRef; (m) A. Escuer, R. Vicente, M. A. S. Goher and F. A. Mautner, Inorg. Chem., 1998, 37, 782 CrossRef CAS; (n) M. A. S. Goher and F. A. Mautner, Polyhedron, 1998, 17, 1561 CrossRef CAS.
- (a) A. Escuer, R. Vicente, M. A. S. Goher and F. A. Mautner, Inorg. Chem., 1995, 34, 5707 CrossRef CAS; (b) 1996, 35, 6386; ; (c) J. Chem. Soc., Dalton Trans., 1997, 4431; ; (d) Inorg. Chem., 1997, 36, 3440. .
- M. A. S. Goher and F. A. Mautner, Croat. Chim. Acta, 1990, 63, 559 Search PubMed.
- M. L. Tong, X. M. Chen, X. L. Yu and T. C. W. Mak, J. Chem. Soc., Dalton Trans., 1998, 5 RSC; A. J. Blake, S. J. Hill, P. Hubberstey and W. S. Li, J. Chem. Soc., Dalton Trans., 1998, 909 RSC; T. O. S. Jung, S. H. Park, D. C. Kim and K. M. Lim, Inorg. Chem., 1998, 37, 610 CrossRef; L. Carlucci, G. Ciani, D. M. Proserpio and A. J. Sironi, J. Chem. Soc., Dalton Trans., 1997, 1801 RSC; M. Kondo, T. Yoshitomi, K. Seki, H. Matzusaka and S. Kitagawa, Angew. Chem., Int. Ed. Engl., 1997, 36, 1725 CrossRef CAS; A. J. Blake, N. R. Champness, A. Khlobystov, D. A. Lemenovskii, W. S. Li and M. Schöder, Chem. Commun., 1997, 2027 RSC.
- (a) T. L. Hennigar, D. C. MacQuarrie, P. Losier, R. D. Rogers and M. J. Zaworotko, Angew. Chem., Int. Ed. Engl., 1997, 36, 972 CrossRef CAS; (b) K. N. Power, T. L. Hennigar and M. J. Zaworotko, Chem. Commun., 1998, 595 RSC; (c) M. Ferbinteanu, G. Marinescu, H. W. Roesky, M. Noltemeyer, H.-G. Schmidt and M. Andruh, Polyhedron, 1998, 18, 243 CrossRef; (d) C. S. Hong and Y. Do, Inorg. Chem., 1998, 37, 4470 CrossRef CAS; (e) M. L. Hernández, M. G. Barandika, M. K. Urtiaga, R. Cortés, L. Lezama, M. I. Arriortua and T. Rojo, J. Chem. Soc., Dalton Trans., 1999, 1401 RSC.
- G. M. Sheldrick , SHELXS 97, Program for the Solution of Crystal Structures, University of Göttingen, 1997. Search PubMed.
- G. M. Sheldrick , SHELXL 97, Program for the Refinement of Crystal Structures, University of Göttingen, 1997. Search PubMed.
- International Tables for X-Ray Crystallography, Kynoch Press, Birmingham, 1974, vol. IV. Search PubMed.
- J. R. Carvajal, FULLPROF, Program Rietveld Pattern Matching Analysis of Powder Patterns, 1997 Search PubMed(see www-11b.cea.fr/fullweb/ winplotr/winplotr.htm/)..
- H. M. Rietveld, Acta Crystallogr., 1967, 12, 151 CrossRef CAS; J. Appl. Crystallogr., 1969, 6, 65. Search PubMed.
- C. K. Johnson , ORTEP II, Report ORNL-5138, Oak Ridge National Laboratory, Oak Ridge, TN, 1976. Search PubMed.
- K. Nakamoto , Infrared Spectra of Inorganic and Coordination Compounds, Wiley, New York, 1997. Search PubMed.
- A. B. P. Lever , Inorganic Electronic Spectroscopy, Elsevier, Amsterdam, 1984. Search PubMed.
- M. E. Fisher, Am. J. Phys., 1964, 32, 343.
- L. J. de Jongh and A. R. Miedema, Adv. Phys., 1974, 23, 1 CAS.
- C. Y. Weng , Ph.D. Thesis, Carnegie Institute of Technology, 1968. Search PubMed.
- A. Escuer, R. Vicente, J. Ribas, M. S. El Fallah, X. Solans and M. Font-Bardía, Inorg. Chem., 1993, 32, 3727 CrossRef CAS; Inorg. Chem, 1994, 33, 1842; Search PubMed; J. Chem. Soc., Dalton Trans., 1996, 1013; Search PubMed; R. Vicente and A. Escuer, Polyhedron, 1995, 14, 2133 Search PubMed.
Footnote |
| † Supplementary data available: rotatable 3-D crystal structure diagram in CHIME format. See http://www.rsc.org/suppdata/dt/a9/a906154a/ |
| This journal is © The Royal Society of Chemistry 2000 |

