The rotational spectrum of dichlorocarbene, C35Cl2, observed by molecular beam-Fourier transform microwave spectroscopy†
N.
Hansen
,
H.
Mäder
and
F.
Temps
*
Institut für Physikalische Chemie, Christian-Albrechts-Uni![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ersität Kiel, Olshausenstr. 40-60, D-24098, Kiel, Germany. E-mail: temps@phc.uni-kiel.de
ersität Kiel, Olshausenstr. 40-60, D-24098, Kiel, Germany. E-mail: temps@phc.uni-kiel.de
First published on 6th December 2000
Abstract
The rotational spectrum of the most abundant isotopomer of dichlorocarbene, C35Cl2, in its ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 ground
electronic state has been recorded using a molecular beam—Fourier transform microwave spectrometer. The CCl2 was generated by flash pyrolysis in a pulsed free jet expansion using CBr2Cl2 or CHCl2COCl as precursors. 43 hyperfine structure lines of 6 rotational transitions were recorded in the frequency range 8–40 GHz. The analysis of the observed spectrum yielded the rotational constants, the complete 35Cl nuclear quadrupole coupling tensor, and the nuclear
spin-rotation interaction constants. In addition, a refined r0 structure of CCl2 was derived.
1A1 ground
electronic state has been recorded using a molecular beam—Fourier transform microwave spectrometer. The CCl2 was generated by flash pyrolysis in a pulsed free jet expansion using CBr2Cl2 or CHCl2COCl as precursors. 43 hyperfine structure lines of 6 rotational transitions were recorded in the frequency range 8–40 GHz. The analysis of the observed spectrum yielded the rotational constants, the complete 35Cl nuclear quadrupole coupling tensor, and the nuclear
spin-rotation interaction constants. In addition, a refined r0 structure of CCl2 was derived.
1. Introduction
Carbenes are highly reactive intermediates whose physical properties and chemical reactions have been extensively studied for quite some time.1 Depending on the nature of the substituents, the carbenes may have either singlet or triplet electronic ground states. In many cases, these states are very close in energy. Singlet and triplet carbenes exhibit very different chemical properties.1–4
Dichlorocarbene, CCl2, is a prototypical halogen-containing carbene. Its electronic structure is particularly
important for understanding the unique chemical behavior of
carbenes. Over the years, CCl2 has therefore been the subject
of numerous spectroscopic5–22 and theoretical23–36 investigations. Most of the theoretical studies focused on the energy
gap between the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 and the ã3B1 electronic states. A consensus seemed to have emerged that the ã3B1 electronic state should be at about T0(ã) = (7000 ± 1000) cm−1 above the X1A1 ground state. A more sensitive and higher resolution investigation of the photoelectron spectrum of the CCl2−
anion has recently been published, however, by the Lineberger
group,22 in which a value for the singlet–triplet splitting of
T0(ã) = (1000 ± 1000) cm−1 was derived, much lower than the
theoretical estimates. Barden and Schaefer36 have argued, on
the other hand, that this low experimental value should be
outside the error limits of the theoretical calculations. In this
situation, further experimental work on the spectroscopy of
CCl2 clearly seems desirable.
1A1 and the ã3B1 electronic states. A consensus seemed to have emerged that the ã3B1 electronic state should be at about T0(ã) = (7000 ± 1000) cm−1 above the X1A1 ground state. A more sensitive and higher resolution investigation of the photoelectron spectrum of the CCl2−
anion has recently been published, however, by the Lineberger
group,22 in which a value for the singlet–triplet splitting of
T0(ã) = (1000 ± 1000) cm−1 was derived, much lower than the
theoretical estimates. Barden and Schaefer36 have argued, on
the other hand, that this low experimental value should be
outside the error limits of the theoretical calculations. In this
situation, further experimental work on the spectroscopy of
CCl2 clearly seems desirable.
The present paper is part of our continuing studies of the
rotational spectra of halogen-containing carbenes. Previously,
we investigated the rotational spectrum of CF2 (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1).37 In the observed CF2
spectra, we detected unusually large nuclear spin–rotation interaction parameters for the two identical 19F nuclei. This also motivated us to analyze the rotational spectrum of the corresponding CCl2 carbene.
1A1).37 In the observed CF2
spectra, we detected unusually large nuclear spin–rotation interaction parameters for the two identical 19F nuclei. This also motivated us to analyze the rotational spectrum of the corresponding CCl2 carbene.
In this work, high resolution molecular beam-Fourier transform microwave (MB-FTMW) spectroscopy has been used to
observe a series of low lying rotational transitions of C
35Cl2
(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1) in its ground vibrational state in the frequency range
from 8 to 40 GHz. This investigation complements an earlier study by Fujitake and Hirota, who reported a weak pure rotational spectrum of CCl2 in the millimeter and submillimeter wave region.21 Because of the high resolution of the
MB-FTMW spectrometer, even very small perturbations could be detected. All of the observed lines were split into several components due to the nuclear quadrupole hyperfine interaction of the two identical 35Cl nuclei. Furthermore, additional perturbations were observed caused by the 35Cl nuclear spin–rotation interaction and by the influence of the
off-diagonal element in the nuclear quadrupole coupling
tensor. The results of the measurements were used to determine
precise rotational and 35Cl nuclear spin–rotation interaction constants as well as the complete nuclear quadrupole
coupling tensor. Diagonalization of this tensor revealed a small deviation of the principal axes of the χ tensor from the
C–Cl internuclear axis. In addition, an r0
structure of CCl2 in the singlet ground state was derived by using the effective moments of inertia obtained from the rotational constants.
1A1) in its ground vibrational state in the frequency range
from 8 to 40 GHz. This investigation complements an earlier study by Fujitake and Hirota, who reported a weak pure rotational spectrum of CCl2 in the millimeter and submillimeter wave region.21 Because of the high resolution of the
MB-FTMW spectrometer, even very small perturbations could be detected. All of the observed lines were split into several components due to the nuclear quadrupole hyperfine interaction of the two identical 35Cl nuclei. Furthermore, additional perturbations were observed caused by the 35Cl nuclear spin–rotation interaction and by the influence of the
off-diagonal element in the nuclear quadrupole coupling
tensor. The results of the measurements were used to determine
precise rotational and 35Cl nuclear spin–rotation interaction constants as well as the complete nuclear quadrupole
coupling tensor. Diagonalization of this tensor revealed a small deviation of the principal axes of the χ tensor from the
C–Cl internuclear axis. In addition, an r0
structure of CCl2 in the singlet ground state was derived by using the effective moments of inertia obtained from the rotational constants.
2. Experimental
The rotational spectra were recorded with a pulsed MB-FTMW spectrometer described in some detail previously.38 Some modifications have been made in order to increase its sensitivity and, in addition, the accessible frequency range has been extended from the previous 7–26 GHz up to 40 GHz. These changes are described in the following.2.1 Microwave circuits
The electronic set-up of the spectrometer in its extended version for the frequency range from 26.5 to 40 GHz is shown in Fig. 1. The detection cavity is formed by a flat and a concave aluminium mirror (1 and 2) with diameters of 45 cm at a distance of ≈70 cm. Since in the region from 26.5 to 40 GHz some MW components are not available or very expensive, the polarizing frequency is produced by frequency doubling. The primary MW signal at frequency ν is generated with a synthesizer (3). A single pole double throw (SPDT) PIN diode switch (4) guides the signal alternately into the polarization or detection sections. In the former, the MW pulses are prepared for excitation of the molecules; in the latter, a superheterodyne detection of the response signal of the molecular ensemble is carried out. For polarization, the MW power can be adjusted with the variable attenuators (5) and (6). The single side-band modulator (7) generates a MW signal at a frequency ν + 80 MHz. The SPDT switch (8) modulates the 80 MHz signal synchronously to the MW pulse creation. The power amplifier (9) compensates for the conversion loss of (7). The polarization frequency is then generated by doubling this primary MW frequency. The frequency doubler (10) provides sufficient MW power for the excitation of weakly polarized molecules. The power level can be monitored![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ia the directional coupler (11) and the power meter (12). The MW pulses
are reshaped by the SPDT PIN diode switch (13). The MW
signal is then coupled into the spectrometer cavity
ia the directional coupler (11) and the power meter (12). The MW pulses
are reshaped by the SPDT PIN diode switch (13). The MW
signal is then coupled into the spectrometer cavity ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ia an L-shaped antenna.
ia an L-shaped antenna.
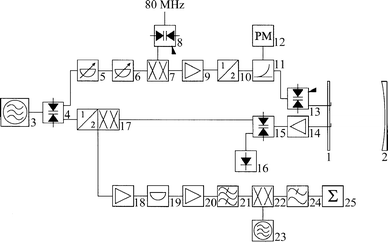 | ||
| Fig. 1 Microwave circuit of the MB-FTMW spectrometer for the frequency range from 26.5–40 GHz. (1) Flat aluminium mirror; (2) concave aluminium error; (3) MW synthesizer; (4) SPDT switch; (5 and 6) variable attenuators; (7) single side-band modulator; (8) SPDT switch; (9) power amplifier; (10) MW frequency doubler; (11) directional coupler; (12) power meter; (13) SPDT switch; (14) MW low-noise amplifier; (15) SPDT switch; (16) detector diode; (17) second harmonic mixer; (18) RF amplifier; (19) RF attenuator; (20) RF amplifier; (21) band pass filter; (22) RF mixer; (23) RF synthesizer; (24) low pass filter; (25) digitizer. See the text for a detailed explanation. | ||
During the detection period, the molecular response is received by a second antenna and passed to the low-noise MW amplifier (14). The MW antennas are mounted near the center of the flat mirror. To avoid any degradation of the molecular signal, the amplifier is directly mounted to the back-side of the mirror, with no protection switch installed. The recovery time of the unprotected MW amplifier after the microwave pulse is fast enough to enable the detection of the free induction decay (FID) of the molecular sample without additional delay. The SPDT switch (15) passes the excitation power to the diode (16) to protect the subsequent detection electronics from saturation. Following a short delay after the MW pulse, the signal path is set by (15) to the second harmonic mixer (17) which down-converts the molecular MW signal to an intermediate frequency band around 160 MHz. This signal is amplified (18–20) and band-pass filtered (21). An RF mixer (22) uses a 157.5 MHz frequency signal (23) to convert the molecular signal down to a frequency around 2.5 MHz. This signal is low-pass filtered (24), digitized (25) and sent to a PC microcomputer for data averaging, storage and analysis. For frequency tuning of the resonator, the switches (4), (8) and (13) are set for cw power, while switch (15) passes the transmitted MW signal to the detector diode (16). The diode output is A/D converted to provide the required tuning feedback.
With slight modifications, the spectrometer can also be operated in the 7 to 26.5 GHz frequency range. The frequency doubler (10) has to be removed and the components (11–15) have to be replaced by similar ones specified for the lower frequencies. Furthermore, instead of using the second harmonic mixer, an image rejection mixer is used. The RF components (18–24) are the same for both set-ups. For the single sideband generation (7), an RF signal at 160 MHz (instead of 80 MHz) is used.
2.2 Generation of CCl2 and measurement of the FTMW spectra
The spectrometer offers two options for generating free radicals.37 Using the first source, transient species can be produced by laser photolysis in the expanding molecular beam. In the second source, radicals are produced by high-temperature flash pyrolysis in a SiC extension tube attached to the face plate of the pulsed molecular beam valve (General Valves Series 9).39 The nozzle is located in the center of the spherical mirror so that the expanding gas forms a free jet along the cavity axis.In the present study, CCl2 was produced by the flash pyrolysis method using dibromodichloromethane (CBr2Cl2) or
dichloroacetylchloride (CHCl2COCl) as precursors. The latter
was found to give somewhat stronger signals. Using
CHCl2COCl, the pyrolysis initially leads to dichloroketene
(Cl2C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) C
C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) O) by elimination of HCl. At higher temperatures, the Cl2C
O) by elimination of HCl. At higher temperatures, the Cl2C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) C
C![[double bond, length half m-dash]](https://www.rsc.org/images/entities/char_e006.gif) O loses CO to yield the CCl2 carbene. The gas flow was maintained by bubbling Ar at a backing pressure of 5 bar through liquid CHCl2COCl or CBr2Cl2
contained in a stainless-steel
reservoir at room temperature. The radicals in the jet were excited with microwave pulses of 0.2 μs duration at an optimal power
of ≈5 mW. After the decay of the polarization pulse in the cavity (7–10 μs), the molecular emission signal was amplified and down-converted to the frequency band around 2.5 MHz, as
described above. This signal was sampled at a rate of 50
(or 100) MHz using a transient digitizer. Free induction decay signals were averaged over 1024 cycles for the strongest rotational transitions and over 8192 cycles for the weakest ones, transferred to the PC microcomputer, and Fourier transformed to obtain power or amplitude spectra. Linewidths of ca. 4 kHz (HWHM) were obtained. The precision
of the measurements for strong, well resolved lines is ca. 2
kHz. The precise transition frequencies were determined from fits to the time-domain signals.40
O loses CO to yield the CCl2 carbene. The gas flow was maintained by bubbling Ar at a backing pressure of 5 bar through liquid CHCl2COCl or CBr2Cl2
contained in a stainless-steel
reservoir at room temperature. The radicals in the jet were excited with microwave pulses of 0.2 μs duration at an optimal power
of ≈5 mW. After the decay of the polarization pulse in the cavity (7–10 μs), the molecular emission signal was amplified and down-converted to the frequency band around 2.5 MHz, as
described above. This signal was sampled at a rate of 50
(or 100) MHz using a transient digitizer. Free induction decay signals were averaged over 1024 cycles for the strongest rotational transitions and over 8192 cycles for the weakest ones, transferred to the PC microcomputer, and Fourier transformed to obtain power or amplitude spectra. Linewidths of ca. 4 kHz (HWHM) were obtained. The precision
of the measurements for strong, well resolved lines is ca. 2
kHz. The precise transition frequencies were determined from fits to the time-domain signals.40
3. Results
3.1 Observed spectra
The measurements of the CCl2 FTMW spectra were initiated using the spectroscopic constants of Fujitake and Hirota21 to predict approximate transition frequencies in the frequency range of our spectrometer. After adjusting all pulse lengths and delay times, signals which were due to CCl2 were readily detected. Fig. 2 shows as an example the power spectrum of the JKa,Kc = 31,3 − 40,4 transition with different hyperfine structure components. All observed frequencies are listed in Table 1. A total of 43 hyperfine structure components were resolved and assigned to 6 different rotational transitions.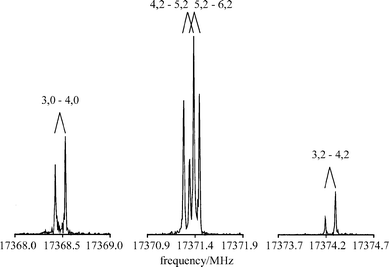 | ||
| Fig. 2 Different hyperfine components of the JKa,Kc = 31,3–40,4 transition of C35Cl2. Shown are the Doppler doublets. The components are denoted by F′–F. Recording conditions: molecular pulse width: 990 μs; molecular pulse–MW pulse delay: 500 μs; polarization frequencies: 17368.36, 17371.28, 17374.20 MHz, respectively; MW pulse width: 0.2 μs; MW power: 5 mW; MW FID delay: 9 μs; sample interval: 10 ns, 8 k = 8192 data points; number of cycles averaged: 3164, 4214, 8192, respectively. | ||
| J′ | Ka ′ | Kc ′ | J | Ka | Kc | F′ | I′ | F | I | ν obs/MHz | Δν/kHz |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 0 | 2 | 1 | 0 | 2 | 2 | 32277.8185 | −0.5 |
| 3 | 2 | 4 | 2 | 32266.3445 | −1.4 | ||||||
| 2 | 2 | 3 | 2 | 32266.2685 | −0.2 | ||||||
| 2 | 1 | 2 | 0 | 32254.6628 | −0.8 | ||||||
| 2 | 1 | 2 | 3 | 0 | 3 | 4 | 3 | 4 | 3 | 24885.8464 | 4.3 |
| 3 | 3 | 4 | 3 | 24885.4179 | 1.0 | ||||||
| 5 | 3 | 5 | 3 | 24884.7243 | −1.5 | ||||||
| 1 | 1 | 2 | 1 | 24883.0832 | −0.4 | ||||||
| 2 | 3 | 3 | 3 | 24882.9971 | −1.9 | ||||||
| 4 | 3 | 5 | 3 | 24882.7135 | −0.3 | ||||||
| 3 | 1 | 4 | 1 | 24879.6759 | 1.5 | ||||||
| 5 | 3 | 6 | 3 | 24877.1207 | −0.8 | ||||||
| 2 | 1 | 3 | 1 | 24875.7305 | 3.6 | ||||||
| 3 | 1 | 3 | 4 | 0 | 4 | 4 | 2 | 4 | 2 | 17377.1627 | −0.4 |
| 3 | 2 | 4 | 2 | 17374.2478 | 0.9 | ||||||
| 5 | 2 | 6 | 2 | 17371.3947 | 0.5 | ||||||
| 4 | 2 | 5 | 2 | 17371.3348 | −2.2 | ||||||
| 3 | 0 | 4 | 0 | 17368.4787 | 0.2 | ||||||
| 4 | 1 | 4 | 5 | 0 | 5 | 5 | 3 | 6 | 3 | 9746.2240 | −1.2 |
| 4 | 3 | 5 | 3 | 9745.7052 | −0.1 | ||||||
| 3 | 1 | 4 | 1 | 9745.3181 | 0.4 | ||||||
| 6 | 3 | 7 | 3 | 9744.3190 | 0.3 | ||||||
| 3 | 3 | 4 | 3 | 9743.5268 | −4.0 | ||||||
| 5 | 1 | 6 | 1 | 9743.4949 | 2.2 | ||||||
| 2 | 3 | 3 | 3 | 9742.6413 | 0.0 | ||||||
| 7 | 3 | 8 | 3 | 9741.6703 | 1.0 | ||||||
| 4 | 1 | 5 | 1 | 9741.2656 | −0.6 | ||||||
| 8 | 0 | 8 | 7 | 1 | 7 | 8 | 2 | 7 | 0 | 13809.2160 | 0.8 |
| 6 | 2 | 5 | 2 | 13807.5659 | −0.4 | ||||||
| 7 | 2 | 6 | 2 | 13807.5659 | 1.5 | ||||||
| 10 | 2 | 9 | 2 | 13807.5474 | −0.9 | ||||||
| 9 | 2 | 8 | 2 | 13807.5354 | 0.8 | ||||||
| 8 | 0 | 7 | 2 | 13805.8884 | −0.9 | ||||||
| 9 | 0 | 9 | 8 | 1 | 8 | 6 | 3 | 5 | 3 | 21862.6046 | 0.1 |
| 9 | 1 | 8 | 1 | 21862.4057 | −1.5 | ||||||
| 12 | 3 | 11 | 3 | 21862.2254 | 0.2 | ||||||
| 7 | 3 | 6 | 3 | 21861.2014 | −1.7 | ||||||
| 8 | 3 | 7 | 3 | 21860.8600 | 0.4 | ||||||
| 10 | 1 | 9 | 1 | 21860.8432 | −1.9 | ||||||
| 11 | 3 | 10 | 3 | 21860.5039 | 3.8 | ||||||
| 8 | 1 | 7 | 1 | 21859.4576 | 1.8 | ||||||
| 9 | 3 | 8 | 3 | 21859.3088 | −2.2 | ||||||
| 10 | 3 | 9 | 3 | 21859.1228 | 1.5 | ||||||
The observed characteristic quadrupole hyperfine patterns are caused by the coupling of the nuclear spin angular momenta I1 and I2 of the Cl nuclei with the rotational angular momentum J. For molecules with two identical nuclei, like C35Cl2, it is most convenient to analyze the spectra using the symmetric coupling scheme
which means that the nuclear spins I1 and I2 of the two 35Cl atoms couple to form a total nuclear spin I which then couples with the rotational angular momentum J to form the resultant total angular momentum F. Since CCl2 has a plane of symmetry which contains the a and b inertial axes, the quadrupole coupling tensors of the chlorine nuclei have only one nonzero off-diagonal element, χab. Moreover, since the χ tensors are traceless, only two of the three diagonal elements of each tensor are independent. In the present work, χbb and χcc were treated as the two adjustable diagonal elements and χaa was fixed accordingly. The first-order quadrupole splittings are completely determined by the diagonal elements χgg. Measurements of higher-order effects are necessary to determine the χab element.
For the symmetric molecule C35Cl2, the hyperfine patterns consist of a symmetric triplet of strong lines (with the central line being much more intense than the others) or a more complex pattern. The former occurs for transitions between states in which Ka and Kc are both odd (oo) or both even (ee), whereas the more complex pattern occurs when Ka and Kc are of different parity (eo; oe). In a totally symmetric vibronic state, only antisymmetric nuclear spin states (I = 0, 2) exist for the symmetric rotational levels A(ee) and Bb(oo), while only symmetric nuclear spin states (I = 1, 3) exist for the antisymmetric rotational levels Ba(eo), and Bc(oe).
3.2 Theory
The effective Hamiltonian employed for analyzing the spectra is:

| (1) |
The asymmetric rotor Hamiltonian Hrot contains the rotational constants A, B and C of the molecule:

| (2) |
The components of the total angular momentum are denoted by Pg, referring to the principal inertia axes g = a, b, c. The centrifugal distortion term Hcd in the Hamiltonian (1) contains the fourth-order terms of the standard Hamiltonian of Watson in the A reduced form:41
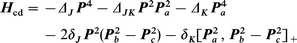
| (3) |
[,]+ denotes an anticommutator.
The quadrupole Hamiltonian Hnqhfs(35Cl) represents the interaction between the nuclear quadrupole moments and the electric field gradients at two identical 35Cl nuclei. It can be expressed as the scalar product of two spherical tensor operators of rank 2 as follows:

| (4) |
V i (2) denotes the electric field gradient tensors and Qi(2) the nuclear quadrupole moment tensors of the ith nuclei. Due to the symmetry of dichlorocarbene, only three of the five components of V(2) are different from zero. Instead of these spherical components, we used the Cartesian components of the “negative” field gradient tensor, defined in the principal axes inertial system of the molecule, qgg′ = (∂2V/∂g∂g′) (g = a, b, c). The interpretation of the quadrupole hyperfine structure is then made in terms of the quadrupole coupling tensors χ(1) and χ(2), χgg′ = eQqgg′ , where e is the elementary charge and Q the quadrupole moment of the 35Cl nuclei. In the case of C35Cl2, for the two equivalent nuclei, χgg(1) = χgg(2) and χab(1) = − χab(2).
In addition, the end-over-end rotation of the molecule generates a weak magnetic field with which the 35Cl nuclear magnetic moments interact. Therefore, an extra term due to the nuclear spin–rotation interaction was included. The Hamiltonian Hnsr(35Cl) can be written in the form

| (5) |
where Ci is the nuclear spin–rotation coupling tensor of the ith nuclei. Due to the small g-factor for the 35Cl nucleus, this magnetic perturbation is very small and only the diagonal elements of the C tensor were taken into consideration.
3.3 Analysis—Determination of hyperfine constants
Using the Hamiltonian as defined by eqn. (1), all observed rotational transitions were assigned and fitted to the spectroscopic constants using the program SPFIT.42 The present MB-FTMW spectra were taken into account in the least squares analysis with an uncertainty of 2 kHz. In addition, the rotational transitions reported by Fujitake and Hirota21 in the millimeter and submillimeter wave region were taken into consideration with uncertainties of 500 kHz. A compilation of the millimeter and submillimeter frequencies (Table S1) can be found as Electronic Supplementary Information.† The total data base consists of 169 transition frequencies.The molecular constants from the final fit are given in Table 2. We fitted simultaneously the rotational constants, the fourth-order centrifugal distortion constants, the χ tensor components (including the off-diagonal element χab), and the nuclear spin–rotation interaction parameters. As seen from the standard errors, all constants are well determined. Diagonalization of the complete χ tensor gave the principal 35Cl quadrupole coupling constants which are also included in Table 2. The small residual deviations between observed and calculated transition frequencies for the molecular beam spectra (Table 1) indicates that all relevant effects have been accounted for. Effects of nuclear spin–nuclear spin coupling and centrifugal distortion contributions to the quadrupole coupling constants were found to be negligible.
| C35Cl2 | ||
|---|---|---|
| Ref. 21 | This work | |
| Rotational constants: | ||
| A/MHz | 50229.524(65) | 50229.503(3) |
| B/MHz | 3695.3440(31) | 3695.3459(5) |
| C/MHz | 3438.3633(32) | 3438.364(1) |
| Centrifugal distortion constants: | ||
| ΔJ/kHz | 1.5048(17) | 1.505(1) |
| ΔJK/kHz | −33.324(50) | −33.2(1) |
| ΔK/MHz | 1.5633(56) | 1.557(1) |
| δJ/kHz | 0.15602(18) | 0.1558(3) |
| δK/kHz | 8.8517(516) | 9.3(3) |
| ΦJ/Hz | 0.00057(30) | — |
| ΦJK/Hz | −0.0027(99) | — |
| ΦKJ/Hz | −6.8(24) | — |
| ΦK/kHz | 0.25(17) | — |
| ϕJ/Hz | 0.000198(37) | — |
| Quadrupole coupling constants: | ||
| χbb/MHz | 17.40(85) | 17.319(1) |
| χcc/MHz | 5.21(85) | 5.540(2) |
| ∣χab∣/MHz | 46.2(5) | |
| χzz/MHz | −63.37 | −53.1(4) |
| χxx/MHz | 58.16 | 47.6(4) |
| χyy/MHz | 5.21 | 5.540(2) |
| Nuclear spin–rotation interaction parameters: | ||
| Caa/kHz | 58.2(9) | |
| Cbb/kHz | 2.8(2) | |
| Ccc/kHz | 1.4(3) | |
| Fit properties: | ||
| number of lines | 169 | |
| σ/kHz | 116.3 | |
3.4 Structure determination
For CCl2 as a planar C2v molecule, the geometry is determined by two parameters, the C–Cl bond lengths and the Cl–C–Cl angle. Since the molecule is vibrating, and only ground vibrational state rotational constants were obtained, any structure obtained is an effective structure. The ground state or r0 structure of CCl2 was determined using the program MWSTR.43 The C–Cl bond length and the Cl–C–Cl angle were determined to be r0(C–Cl) = 1.714(1) Å and Θ0(Cl–C–Cl) = 109.35(4)°, where the values in parentheses denote the 3σ standard deviations.4. Discussion
The derived rotational constants are in good agreement with the published results of Fujitake and Hirota.21 However, due to the higher resolution and sensitivity of the present study, the rotational constants are now much better defined. Compared to ref. 21, the better defined rotational constants lead to refined structural parameters. In the most recent theoretical investigation, Barden and Schaefer36 predicted the equilibrium geometry at different levels of theory. Their calculated equilibrium values of re(C–Cl) = 1.720 Å and Θe(Cl–C–Cl) = 109.1° are in close agreement with our experimental values for the ground vibrational state.Fujitake and Hirota21 used only first-order perturbation theory to determine the diagonal elements of the nuclear quadrupole coupling tensor. They could not detect higher-order contributions from the off-diagonal element. In this work, we found it necessary to include the nuclear spin–rotation interaction and higher-order nuclear quadrupole interaction effects in the Hamiltonian to describe the rotational spectrum to within the experimental error. Only with these additional terms did the standard error of the fit become comparable with the estimated errors of the measurements.
Knowledge of χab allowed us to diagonalize the χ tensor for C35Cl2 and to determine the principal values and the angle θza between the z principal axis of the coupling tensor and the a principal axis of the inertia tensor. The coupling constants χgg (g = x, y, z) in the principal axes system of the coupling tensor are given in Table 2. The z axis of the χ tensor makes an angle of 56.76(3)° with the b inertial axis that bisects the Cl–C–Cl angle. According to the r0 structure, the C–Cl internuclear axis makes an angle of 54.68° with the b inertial axis. This indicates a small deviation of the z axis of the χ tensor from the C–Cl internuclear axis of 2.16° in a direction away from the bisector of the Cl–C–Cl angle. Although this deviation is derived from r0 structural data, it is considered to be significant since the equilibrium bond angles are only slightly different (<0.5°) as seen from data for other triatomic molecules.44 In general, it is common to assume coincidence between the principal axes of the χ tensor and the internuclear axes for terminally bonded atoms. On the other hand, the conclusion that there is a deviation of the principal axes of the χ tensor from the C–Cl internuclear axis in CCl2 and that that deviation is in the direction away from the bisector of the Cl–C–Cl angle is supported by work on related molecules. By analyzing the microwave spectrum of phosgene (COCl2), Ferguson and Flygare45 determined a deviation of the z axis of the χ tensor from the C–Cl axis of 2.0(4)° in a direction away from the bisector of the Cl–C–Cl angle. Merke and Dreizler46 showed that the z axis of the coupling tensor in SCl2 is tilted by 1.3° with respect to the S–Cl bond direction. Again, the angle between both z tensor axes is larger than the bond angle.
Considering the magnetic interaction between the nuclear magnetic moment of the Cl nuclei and the molecular rotation, due to the weakness of this interaction, only a few molecules are known so far, where this effect has to be taken into consideration (see, for example, ref. 47–57). Normally the nuclear spin–rotation coupling constants are very small. Noticeable in the present results is the relatively large Caa constant. For comparison, the Caa constant in CCl2 is significantly (about one order of magnitude) larger than in SOCl2.52 Due to the lack of nuclear spin–rotation interaction parameters in similar molecules, we reanalyzed the SCl2 spectra of Merke and Dreizler46 and found nuclear spin–rotation coupling constants similar to those derived for the SOCl2.52 However, considering our results of CF237 in comparison to those for CCl2, this is the second time that large nuclear spin–rotation interaction constants were determined for an unstable carbene. This may be further evidence that low lying excited electronic states of CCl2 and CF2 play an important role for this magnetic hyperfine interaction.
5. Conclusion
High resolution molecular beam-Fourier transform microwave (MB-FTMW) spectroscopy has been used to observe rotational transitions of C35Cl2 in its ground vibrational state. The measured lines were split into several components due to the nuclear quadrupole hyperfine interaction of the two identical 35Cl nuclei. Because of the high resolution of the MB-FTMW spectrometer, even small perturbations were detected so that the off-diagonal quadrupole coupling constant could be determined. The results were used to derive the complete nuclear quadrupole coupling tensor, which upon diagonalization revealed a slight deviation of the z axis of the χ tensor from the C–Cl internuclear axis. In the process, a set of refined and more precise rotational constants, and the 35Cl nuclear spin–rotation constants have been determined. As in CF2, the large coupling constants may hint at an influence of low lying electronic states in these unstable carbenes. In addition, an accurate r0 structure of CCl2 for the singlet ground state was determined. This success is a result of the high resolution and precision obtainable with the MB-FTMW technique.Acknowledgements
The authors thank Dr. H. S. P. Müller (Universität Köln) for helpful information regarding the SPFIT program. Financial support of this work by the Deutsche Forschungsgemeinschaft is gratefully acknowledged.References
- P. P. Gaspar and G. S. Hammond, in Carbenes, ed. R. A. Moss and M. Jones, Jr., Wiley, New York, 1975, vol. 2, p. 207. Search PubMed.
- T. Böhland, S. Dóbé, F. Temps and H. Gg. Wagner, Ber. Bunsen-Ges. Phys. Chem., 1985, 89, 1110 Search PubMed.
- T. Böhland, F. Temps and H. Gg. Wagner, Ber. Bunsen-Ges. Phys. Chem., 1986, 90, 468 Search PubMed.
- M. Koch, F. Temps, R. Wagener and H. Gg. Wagner, Z. Naturforsch. A, 1989, 44, 195 Search PubMed.
- D. E. Milligan and M. E. Jacox, J. Chem. Phys., 1967, 47, 703 CrossRef CAS.
- L. Andrews, J. Chem. Phys., 1968, 48, 979 CrossRef CAS.
- M. E. Jacox and D. E. Milligan, J. Chem. Phys., 1970, 53, 2688 CrossRef CAS.
- J. S. Shirk, J. Chem. Phys., 1971, 55, 3608 CrossRef CAS.
- A. K. Maltsev, O. M. Nefedov, R. H. Hauge, J. L. Margrave and D. Seyferth, J. Phys. Chem., 1971, 75, 3984 CrossRef CAS.
- L. Andrews, J. M. Grzybowski and R. O. Allen, J. Phys. Chem., 1975, 79, 904 CrossRef CAS.
- D. E. Tevault and L. Andrews, J. Mol. Spectrosc., 1975, 54, 110 CrossRef CAS.
- V. E. Bondybey, J. Mol. Spectrosc., 1977, 64, 180 CrossRef.
- R. E. Huie, N. J. T. Long and B. A. Thrush, Chem. Phys. Lett., 1977, 51, 197 CrossRef CAS.
- J. J. Tiee, F. B. Wampler and W. W. Rice, Chem. Phys. Lett., 1979, 65, 425 CrossRef CAS.
- D. A. Predmore, A. M. Murray and M. D. Harmony, Chem. Phys. Lett., 1984, 110, 173 CrossRef CAS.
- K. K. Murray, D. G. Leopold, T. M. Miller and W. C. Lineberger, J. Chem. Phys., 1988, 89, 5442 CrossRef CAS.
- D. J. Clouthier and J. Karolczak, J. Phys. Chem., 1989, 93, 7542 CrossRef CAS.
- D. J. Clouthier and J. Karolczak, J. Chem. Phys., 1991, 94, 1 CrossRef CAS.
- J. Choe, S. R. Tanner and M. D. Harmony, J. Mol. Spectrosc., 1989, 138, 319 CrossRef CAS.
- J. Choe, S. R. Tanner and M. D. Harmony, J. Mol. Spectrosc., 1990, 140, 193 CrossRef.
- M. Fujitake and E. Hirota, J. Chem. Phys., 1989, 91, 3426 CrossRef CAS.
- R. L. Schwartz, G. E. Davico, T. M. Ramond and W. C. Lineberger, J. Phys. Chem. A, 1999, 103, 8213 CrossRef CAS.
- C. W. Bauschlicher, Jr., H. F. Schaefer III and P. S. Bagus, J. Am. Chem. Soc., 1977, 99, 7106 CrossRef.
- T. Ha, H.-U. Gremlich and R. E. Bühler, Chem. Phys. Lett., 1979, 65, 16 CrossRef CAS.
- M. T. Nguyen, M. C. Kerins, A. F. Hegarty and N. J. Fitzpatrick, Chem. Phys. Lett., 1985, 117, 295 CrossRef.
- E. A. Carter and W. A. Goddard III, J. Phys. Chem., 1986, 90, 998 CrossRef CAS.
- E. A. Carter and W. A. Goddard III, J. Phys. Chem., 1987, 91, 4651 CrossRef CAS.
- E. A. Carter and W. A. Goddard III, J. Chem. Phys., 1988, 88, 1752 CrossRef CAS.
- G. L. Gutsev and T. Ziegler, J. Phys. Chem., 1991, 95, 7220 CrossRef CAS.
- N. Russo, E. Sicilia and M. Toscano, J. Chem. Phys., 1992, 97, 5031 CrossRef CAS.
- Z.-L. Cai, X.-G. Zhang and X.-Y. Wang, Chem. Phys. Lett., 1993, 210, 481 CrossRef CAS.
- A. Gobbi and G. Frenking, J. Chem. Soc., Chem. Commun., 1993, 14, 1162 RSC.
- V. M. Garcia, O. Castell, M. Reguero and R. Caballol, Mol. Phys., 1996, 87, 1395 CrossRef CAS.
- M. Schwartz and P. Marshall, J. Phys. Chem. A, 1999, 103, 7900 CrossRef CAS.
- K. Sendt and G. B. Bacskay, J. Chem. Phys., 2000, 112, 2227 CrossRef CAS.
- C. J. Barden and H. F. Schaefer III, J. Chem. Phys., 2000, 112, 6515 CrossRef CAS.
- N. Hansen, H. Mäder and F. Temps, Chem. Phys. Lett., 2000, 327, 97 CrossRef CAS.
- N. Hansen, U. Andresen, H. Dreizler, J.-U. Grabow, H. Mäder and F. Temps, Chem. Phys. Lett., 1998, 289, 311 CrossRef CAS.
- D. W. Kohn, H. Clauberg and P. Chen, Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) . Sci. Instrum., 1992, 63, 4003 Search PubMed.
. Sci. Instrum., 1992, 63, 4003 Search PubMed. - J. Haekel and H. Mäder, Z. Naturforsch. A, 1988, 43, 203 Search PubMed.
- J. K. G. Watson, in Vibrational Spectra and Structure, ed. J. Durig, Elsevier, Amsterdam, 1977, vol. 6, p. 1. Search PubMed.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371 CrossRef CAS.
- V. Typke, MWSTR program for the determination of r0 structures using experimentally derived rotational constants..
-
W. Gordy and R. L. Cook,
Microwa
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) e Molecular Spectra, Wiley, New York, 1984, ch. XIII, p. 678. Search PubMed.
e Molecular Spectra, Wiley, New York, 1984, ch. XIII, p. 678. Search PubMed. - A. C. Ferguson and W. H. Flygare, J. Phys. Chem., 1979, 83, 3161 CrossRef CAS.
- I. Merke and H. Dreizler, Z. Naturforsch. A, 1992, 47, 1141 Search PubMed.
- A. Dubrulle, D. Boucher, J. Burie and J. Demaison, Chem. Phys. Lett., 1977, 45, 559 CrossRef CAS.
- H. E. Gillis Singbeil, W. D. Anderson, R. Wellington Davis, M. C. L. Gerry, E. A. Cohen, H. M. Pickett, F. J. Lovas and R. D. Suenram, J. Mol. Spectrosc., 1984, 103, 466 CrossRef.
- G. Wlodarczak, N. Heineking and H. Dreizler, J. Mol. Spectrosc., 1991, 147, 252 CrossRef CAS.
- N. Heineking, W. Jäger and M. C. L. Gerry, J. Mol. Spectrosc., 1993, 158, 69 CrossRef CAS.
- H. S. P. Müller and M. C. L. Gerry, J. Chem. Soc., Faraday Trans., 1994, 90, 2601 RSC.
- H. S. P. Müller and M. C. L. Gerry, J. Chem. Soc., Faraday Trans., 1994, 90, 3473 RSC.
- B. Gatehouse, H. S. P. Müller, N. Heineking and M. C. L. Gerry, J. Chem. Soc., Faraday Trans., 1995, 91, 3347 RSC.
- H. S. P. Müller and M. C. L. Gerry, J. Mol. Spectrosc., 1996, 175, 120 CrossRef CAS.
- J. Preusser and M. C. L. Gerry, J. Chem. Phys., 1997, 106, 10037 CrossRef CAS.
- H. S. P. Müller, G. O. Sørensen, M. Birk and R. R. Friedl, J. Mol. Spectrosc., 1997, 186, 177 CrossRef CAS.
- B. Gatehouse, H. S. P. Müller and M. C. L. Gerry, J. Mol. Spectrosc., 1998, 190, 157 CrossRef CAS.
Footnote |
| † Electronic Supplementary Information available. See http://www.rsc.org/suppdata/cp/b0/b007492f |
| This journal is © the Owner Societies 2001 |

