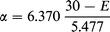Reaction of nitrogen dioxide with hydrocarbons and its influence on spontaneous ignition. A computational study†
Wai-To
Chan
,
Simone M.
Heck
and
Huw O.
Pritchard
*
Department of Chemistry, York Uni![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ersity, Toronto, Canada M3J 1P3. E-mail: huw@yorku.ca
ersity, Toronto, Canada M3J 1P3. E-mail: huw@yorku.ca
First published on 11th December 2000
Abstract
Estimates are made, by using BHandHLYP/6-311G** density functional molecular orbital theory, of the activation energies and frequency factors for the reaction of NO2 with methane, ethane, propane, isobutane, and benzene. For the aliphatic hydrocarbons, over the temperature range 600–1100 K, the rate of formation of a new isomer of nitrous acid, HNO2, is very similar to that for the formation of the common isomer, HONO. This complicates our description of the acceleration of spontaneous ignition of diesel fuels by organic nitrates. These rate data are used in a reduced kinetic model to examine the effect of NO2 upon the spontaneous ignition of some linear- and branched-chain aliphatic hydrocarbons. It is concluded that, under typical diesel engine operating conditions, the spontaneous ignition of linear-chain paraffins is accelerated by the presence of NO2, but may be retarded for heavily branched-chain isomers. An Appendix discusses the relative importance of tunnelling in hydrogen-transfer reactions.
Introduction
Organic nitrates, principally 2-ethylhexyl nitrate, are commonly used as accelerants to improve the ignition quality of hydrocarbon fuels in diesel engines. The basic mechanism by which these work was, until now, thought to be quite simple: viz.1,2

| (1) |

| (2) |
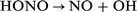
| (3) |

| (4) |
The OH radicals are responsible for initiating the destruction of the hydrocarbon, and the NO is converted back to NO2 to begin another cycle. Because reactions (2)–(4) constitute a chain, the the alkoxyl radical formed in reaction (1) makes only a minor contribution, principally through dissociation to form formaldehyde and a smaller (Alk−1) radical.2–4 Hence, at this exploratory stage, we need only concentrate on the reactions of NO2 itself; this simplification is supported by the experimental observation that NO2 or an equivalent amount of organic nitrate are about equally effective in promoting ignition in a real engine.1
The simplicity of the reaction scheme is compromised by recent theoretical predictions,5 described more extensively below, that in the reaction of NO2 with aliphatic hydrocarbons the formation of a new isomer isonitrous acid, HNO2, can be competitive with the formation of ordinary nitrous acid, HONO. In contrast with HONO, HNO2 cannot dissociate to give OH radicals, nor can it isomerise to HONO at the temperatures of interest, but it still provides a vehicle for ignition acceleration through the reaction

| (5) |
which is important because O2 is present in large excess before ignition occurs.
Fuels from different sources respond differently to the addition of 2-ethylhexyl nitrate,6,7 but the reasons for this remain only speculation at the present time. Understanding is hampered by the lack of kinetic data on the hydrogen abstraction reactions between NO2 and hydrocarbons, of which there seem to be only two examples, namely methane and propane.
In this paper, we report the results of molecular orbital structure calculations on the reactions of NO2 with methane (for calibration), at the primary, secondary and tertiary positions, respectively, in ethane, propane and isobutane, and (for future use) with benzene. Rate constants for these reactions are calculated by standard transition state theory, and these are then used in a reduced kinetic model8 to simulate the effect of NO2 on the spontaneous ignition of four isomeric dodecanes and two isomeric hexadecanes.
Molecular orbital calculations
Ab initio calculations were performed by using the GAUSSIAN 98 molecular orbital program package,9 at the BHandHLYP/6-311G** density functional level (DFT) of approximation. The computational procedures were identical with those described previously;10 however, the justification given for their use needs, perhaps, some minor amplification.DFT methods are known to be problematic for the simple hydrogen-transfer reaction11 H + H2 → H2 + H and for addition of H atoms to radicals and to radical cations.12 Nonetheless, they have gained acceptance as a tool for computation of a variety of H-abstraction reactions, as exemplified by several recent surveys13–15 of DFT and ab initio calculations for reactions of the form X − H + Y → X + H − Y, where DFT methods were shown to provide generally reasonable results for transition state properties. In particular the study of Susnow et al. reported that DFT in combination with transition state theory is capable of providing accurate predictions of pre-exponential factors as well as the curvature of the Arrhenius plots.15 Our choice of the BHandHLYP/6-311G** DFT method for calculation of self-abstraction in alkyl peroxyl radicals and cyclisation of alkyl hydroperoxyl radicals was originally based10 on the recommendation of Truong and coworkers,16 performance comparisons by Durant,17 and reasonable agreement with high-level calculations where known.10 In addition, we have observed that the BHandHLYP/6-311G** method transition state properties for the reaction18 H2 + NO2 → H + cis-HONO are in better agreement with QCISD/6-311G** results reported by Lin and coworkers than their (U)MP2 results;19 they attributed a spurious MP2 frequency for the transition state to spin-contamination, to which DFT is known to be less susceptible.20 The BHandHLYP/6-311G** method also provides minimum energy paths for hydrogen abstraction reactions with a series of fluoromethanes (CHnF4−n, n = 1–4) that closely mimic those obtained from a higher level MP4 method.21 Hence, our contention that the DFT-BHandHLYP method provides a viable alternative to the more costly ab initio methods.
The principal results are listed in Table 1, confirming the observation of Yamaguchi et al.5 that the unknown isomer HNO2 is formed in preference to the trans-HONO ground state. We also confirm18 their result that the isomerisation barrier between HNO2 and trans-HONO is in excess of 50 kcal mol−1. However, they overlooked the possible formation of a third product, cis-HONO, having the lowest activation energy of all. Hence, rather than it being necessary to reformulate completely our ideas on how nitrate ignition improvers function, the existence of this new pathway only adds a little complication.
| trans-HONO | cis-HONO | HNO2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Product RH | ΔE | ΔE‡ | ΔH | ΔH‡ | ΔE | ΔE‡ | ΔH | ΔH‡ | ΔE | ΔE‡ | ΔH | ΔH‡ |
| a Zero point energies calculated by using unscaled frequencies. b CCSD(T)/6-311G(2d,p)//DFT calculation. c CCSD(T)/6-311 + + G(2d,p)//DFT calculation. d Secondary C–H bond. e Tertiary C–H bond. | ||||||||||||
| CH4 | 27.0 | 39.4 | 25.0 | 36.2 | 26.3 | 33.7 | 24.3 | 31.0 | 35.1 | 36.3 | 34.2 | 34.3 |
| 28.8b | 41.3b | 28.2b | 35.1b | 37.3b | 38.3b | |||||||
| 27.5c | 40.7c | 28.0c | 35.5c | 35.3c | 36.8c | |||||||
| C2H6 | 23.0 | 35.4 | 20.8 | 31.9 | 22.3 | 29.7 | 20.1 | 26.5 | 31.2 | 31.8 | 30.0 | 29.3 |
| C3H8d | 19.8 | 32.4 | 17.6 | 28.8 | 19.1 | 26.6 | 16.9 | 23.2 | 27.9 | 28.3 | 26.8 | 25.6 |
| C4H10e | 17.2 | 30.4 | 15.3 | 26.7 | 16.5 | 24.2 | 14.6 | 20.8 | 25.3 | 25.4 | 24.5 | 22.6 |
| C6H6 | 34.5 | 41.8 | 33.8 | 37.6 | 33.8 | 36.8 | 33.1 | 33.1 | 42.6 | 39.9 | 43.0 | 37.5 |
Confidence in the results of Table 1 is justified by the close coincidence between the DFT predictions for the reaction with methane and those of two higher-level sets of calculations, also listed there. Moreover, the agreement between experiment and theory for the ΔH values of these reactions lies between + 1.2 and + 1.6 kcal mol−1 for four of them, and is + 3.2 kcal mol−1 for the propane case. Somewhat disappointing, however, is the fact that several high-level approximations place cis-HONO below trans-HONO, for example: CCSD(T)/6-311G(2d,p) by 220 cm−1, CCSD(T)/6-311 + + G(2df,2p) by 150 cm−1, whereas it should be 180 cm−1 above;22 our BHandHLYP/6-311G** DFT calculation puts it 250 cm−1 below, but the CCSD(T)/6-311 + + G(2d,p) approximation in Table 1 actually puts it near the correct position, about 195 cm−1 above.
Throughout Table 1, the activation energies follow the
somewhat unexpected pattern of being lowest for the formation of cis-HONO and highest for the formation of trans-HONO, with that for the production of HNO2 being in
between. The lower energy path ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ia the cis-configuration
arises because the transition state comprises a 5-membered
ring, with its attendant stabilisation; similar effects have been
noted elsewhere.23 The formation of the trans-tautomer is by
far the slowest reaction, but the other two reactions are of
comparable rates because the transition state for the formation of cis-HONO is much tighter than that for the formation
of HNO2. The transition state structures are very similar for
all five hydrocarbons in each reaction type, and only one set
of transition configurations, for methane, is shown in Fig. 1;
additional structural parameters are listed in Table A1 of
Appendix 1. The three diagrams illustrate the more constrained nature of that for the cis-reaction product, where it is
evident that the cis-conformation is already nascent at the
saddle point. Notice also the very small values for the lowest
frequency ω1 in the transition state for the formation of
HNO2, found in Table A3.
ia the cis-configuration
arises because the transition state comprises a 5-membered
ring, with its attendant stabilisation; similar effects have been
noted elsewhere.23 The formation of the trans-tautomer is by
far the slowest reaction, but the other two reactions are of
comparable rates because the transition state for the formation of cis-HONO is much tighter than that for the formation
of HNO2. The transition state structures are very similar for
all five hydrocarbons in each reaction type, and only one set
of transition configurations, for methane, is shown in Fig. 1;
additional structural parameters are listed in Table A1 of
Appendix 1. The three diagrams illustrate the more constrained nature of that for the cis-reaction product, where it is
evident that the cis-conformation is already nascent at the
saddle point. Notice also the very small values for the lowest
frequency ω1 in the transition state for the formation of
HNO2, found in Table A3.
 | ||
| Fig. 1 Structures of the three possible transition states for the reaction of NO2 with CH4; distances are in Å and angles in degrees. For NO2 itself, the bond lengths are 1.173 Å and the bond angle is 135.1°. | ||
Finally, we remark in passing that the computational study of the reactions of NO2 is much more intricate than might be assumed: not only are there multiple pathways, but when reactions with, for example, alcohols are examined, potential minima are sometimes to be found between reactants and the transition state, and between the transition state and the products.24
Rate constants
Rate constants were calculated by standard transition state theory methods25 for a series of temperatures 600⩽T/K⩽1100, and then fitted to a strict Arrhenius equation by least squares, with results as listed in Table 2. It is seen that the derived activation energies are consistently some 1–2 kcal mol−1 higher than the 0 K values shown in Table 1.| trans-HONO | cis-HONO | HNO2 | ||||
|---|---|---|---|---|---|---|
| Product RH | E | A | E | A | E | A |
| a Secondary C–H bond. b Tertiary C–H bond. | ||||||
| CH4 | 40.7 | 2.1 × 1014 | 35.2 | 8.7 × 1013 | 38.4 | 9.5 × 1014 |
| C2H6 | 36.7 | 5.7 × 1013 | 31.1 | 2.2 × 1013 | 33.8 | 1.6 × 1014 |
| C3H8a | 33.8 | 1.4 × 1013 | 28.1 | 5.8 × 1012 | 30.3 | 3.0 × 1013 |
| C4H10b | 31.9 | 2.1 × 1013 | 25.8 | 9.3 × 1012 | 27.6 | 2.8 × 1014 |
| C6H6 | 43.0 | 4.3 × 1014 | 38.2 | 7.4 × 1013 | 42.2 | 2.5 × 1014 |
For the aliphatic hydrocarbons, the rates of formation of cis-HONO and of HNO2 are similar throughout the temperature range of interest, but for benzene, the formation of cis-HONO is faster than the other two below about 1400 K.
There is a severe lack of experimental kinetic data for these reactions: Slack and Grillo26 give an activation energy for the reaction with methane as 30.0 kcal mol−1, originally with an A-factor of 7.0 × 1011 but later revised to 1.2 × 1013 mol−1 cm−3 s−1; and for propane, Titarchuk et al.27 give an activa tion energy of 22.6 kcal mol−1, with an A-factor of 2.4 × 1011 mol−1 cm−3 s−1.
It has been our experience with this DFT method that although the reaction energies are in good agreement with experiment, the fitted Arrhenius activation energies are often too high.10 In fact, inclusion of NO2 in the modelling calculations with these activation parameters gives rise to an insignificant acceleration in the ignition rate. Since the computed frequency factors should be fairly reliable, we standardised the computed activation energies by subtracting 5 kcal mol−1 from each of them. Thus, for the two cases where experimental measurements exist, the selected (experimental) values for the activation energies are: CH4, 30.2 (30.0) kcal mol−1; C3H8, 23.1 (22.6) kcal mol−1. Note, the implication that the initial pathway in these experiments leads to cis-HONO and not to the slightly more stable tautomer,22 but no distinction between the two forms of HONO was made in the modelling.
Consequently, for the modelling calculations, we have used the A-factors listed in Table 2, but have reduced the activation energies for attack of NO2 at the primary, secondary, and tertiary C–H sites to 26.1, 23.1, and 20.8 kcal mol−1, respectively, for the formation of HONO, and to 28.8, 25.3, and 22.6 kcal mol−1, respectively, for the formation of HNO2.
Modelling calculations
(a) Refinement of the model
The original reduced kinetic model of Griffiths et al.8 was stated to be slightly defective in that it treated all (1,nt) self-abstraction reactions RO2 →![[Q with combining dot above]](https://www.rsc.org/images/entities/char_0051_0307.gif) ;OOH as having the same rate constant. Since we wish to examine a series of isomeric dodecanes containing tertiary C–H bonds in different environments, this could now be important. We have therefore extended the model slightly by treating the (1,4t) and (1,5t)
reactions separately.
;OOH as having the same rate constant. Since we wish to examine a series of isomeric dodecanes containing tertiary C–H bonds in different environments, this could now be important. We have therefore extended the model slightly by treating the (1,4t) and (1,5t)
reactions separately.
Previous calculations had shown that the second of these two reactions should have both a lower activation energy and a lower A-factor.10a We adopted an arbitrary procedure, starting with the estimated Arrhenius parameters for these two classes of reaction,10a and iterating until the ignition delay for heptamethylnonane–air mixtures was the same as we had found previously by using the original model.28 Consistency was then checked by calculating the ignition delays for the normal C8, C10, C12 and C14 paraffins and comparing the values with those for artificial mixtures of n-hexadecane and heptamethylnonane having the same Cetane numbers. Whereas before, the latter values always exceeded the former (see Fig. 2 of ref. 28) by between 0.02 and 0.06 ms, now the corresponding differences do not exceed 0.01 ms, as shown in Table 3. The rate constant values used were 5 × 1012 exp(−17000/T) s−1 for the (1,4t) reaction and 2.5 × 1012 exp(−16000/T) s−1 for the (1,5t) reaction, per H atom; these two values are not unique but, as shown, they provide consistent results.
| Without (1,5t) | With (1,5t) | ||||||
|---|---|---|---|---|---|---|---|
| RH | CN | Molecule | Mixture | Difference | Molecule | Mixture | Difference |
| C8H18 | 64 | 2.11 | 2.13 | 0.02 | 2.05 | 2.05 | 0.00 |
| C10H22 | 77 | 2.00 | 2.06 | 0.06 | 1.98 | 1.99 | 0.01 |
| C12H26 | 88 | 1.97 | 2.00 | 0.03 | 1.95 | 1.96 | 0.01 |
| C14H30 | 96 | 1.94 | 1.96 | 0.02 | 1.92 | 1.93 | 0.01 |
(b) The inclusion of NO2 reactions
Before the modelling can proceed, it is necessary to establish the fate of HNO2 in the system. Several possibilities were explored, but the only viable one was found to be:18

| (6) |
For completeness, the analogous reaction between O2 and HONO was also considered. Here too, there are two possible transition states with two quite different rate expressions:18
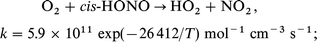
| (7) |

| (8) |
Of these two, the latter is always the faster, but its inclusion in the reaction set did not affect any of the computed ignition delays.
Another new reaction which must be considered is that of NO2 with formaldehyde, to form HNO2, since the parallel reaction to form HONO is a crucial part of the modelling.1 However, unlike the hydrocarbon cases, the reaction with formaldehyde to form HNO2 has an activation energy about 5 kcal mol−1 higher than that to form HONO,5b,18 and was therefore excluded.
In our previous work,28 we had examined the ignition behaviour of four isomeric dodecanes, n-dodecane, 3-ethyldecane, 4,5-diethyloctane, and 2,2,4,6,6-pentamethylheptane, since ignition quality measurements by Petrov et al. were available for these hydrocarbons.29 We now also include calculations on n-hexadecane and heptamethylnonane, which are used to define fixed points on the Cetane number scale. The effect of NO2 on the spontaneous ignition of stoichiometric mixtures in air was estimated by use of the reduced kinetic model of Griffiths et al.,8 augmented by a minimal set of reactions involving nitrogen-containing species. Rate constants for these reactions were the same as we had used previously in the modelling of the original Bone and Gardner30 ignition measurements on CH4–O2–NO2 mixtures,1 as follows:
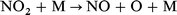
| (9) |
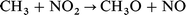
| (10) |
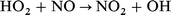
| (11) |
were taken from Burcat;31 those for

| (12) |

| (13) |

| (14) |

| (15) |
from Slack and Grillo;26b and

| (16) |

| (17) |
from Lin et al.32 Where appropriate, the reverse reactions were also included.
Likewise, the compression–ignition simulation model remained unchanged from the previous one: air, initially at 358 K and 1 atm, was compressed to 1/12th of its volume in a time of 22 ms; fuel and the NO2 (when present) were injected homogeneously 2 ms before the end of the compression stroke, at about 745 K and 10 atm. The results of this modelling are given in Table 4, where ignition delay is defined as the time taken to reach 1000 K on a trajectory leading to complete combustion.
| Mechanism(s) included | |||||
|---|---|---|---|---|---|
| Hydrocarbon | CN | [NO2] = zero | HONO | HNO2 | both |
| a Cetene number, approximately commensurate with Cetane number.29 | |||||
| n-Dodecane | 82a | 1.95 | 1.89 | 1.92 | 1.89 |
| 3-Ethyldecane | 55a | 1.99 | 1.95 | 1.96 | 1.95 |
| 4,5-Diethyloctane | 23a | 2.14 | 2.00 | 2.02 | 2.00 |
| 2,2,4,6,6-Pentamethylheptane | 10a | 2.77 | 2.46 | 2.53 | 2.51 |
| n-Hexadecane | 100 | 1.92 | 1.85 | 1.87 | 1.85 |
| Heptamethylnonane | 15 | 2.60 | 2.96 | — | — |
It is clear throughout Table 4 that the HONO mechanism is somewhat more efficient than the HNO2 mechanism with the chosen rate parameters. The only significant difference appears when there is multiple methyl group substitution and a paucity of secondary C–H bonds, whence there is also a slight interference between the two mechanisms. Moreover, it is only for such cases that the inclusion of the (1,5t) reactions makes any significant difference. For 4,5-diethyloctane, their inclusion only changes the computed ignition delays by 0.02–0.03 ms in the presence of NO2, but for 2,2,4,6,6-pentamethylheptane, NO2 has no effect when only (1,4t) reactions are considered, but causes a significant acceleration when the (1,5t) reactions are added to the reaction set.
In the special case of heptamethylnonane, one has to raise the pre-compression temperature from 358 to 373 K for ignition to occur in the presence of 0.1% of NO2 when the (1,5t) reactions are missing (corresponding to an increase of injection temperature from 745 to 776 K). On the other hand, when these reactions are included, the HONO mechanism is retarded somewhat but the HNO2 mechanism still extinguishes the combustion.
Given the complexity of the reaction set, it is often not easy to assign changes in ignition behaviour definitively to distinct sub-sets of reactions within the mechanism. However, some trends are fairly obvious. Among the dodecanes, the HONO mechanism is essentially as shown in reactions (1)–(4), with the OH concentration elevated by a factor of 3–4 in the period before ignition. Acceleration of ignition by the second mechanism can only occur through the reaction of O2 with HNO2 to give NO2 and HO2, and the pre-ignition concentrations of HO2, H2O2, and of OH are all elevated by factors of 2–5 or more. However, the two mechanisms do not reinforce each other because rather over half of the NO2 is trapped as HNO2, so that the rates of formation of HONO by reactions (3), (16) and (17) are lowered, with a corresponding reduction in the rate of formation of OH radicals.‡ Of course, the magnitude of this effect is sensitive to the choice of the rate parameters for reaction (6) between O2 and HNO2, for which we have used the virgin computed result, without any manipulation.
The reason for the retardation in heptamethylnonane with
the HONO mechanism is less clear. Comparison of the population
distributions between n-hexadecane and heptamethylnonane
reveals that the presence of NO2 increases the OH radical concentration in the former case, but reduces it in the latter. This traces back to a much greater difference in activation energy between abstraction at the primary sites to give R1 radicals and at the tertiary sites to give R3 radicals for NO2
than there is for O2, thereby altering the balance between the peroxyl radical concentrations in favour of R3O2. In the Griffiths model,8 this radical isomerises less readily into the chain-generating ![[Q with combining dot above]](https://www.rsc.org/images/entities/char_0051_0307.gif) ;OOH radical than does R1O2, and the resulting loss of OH radicals is not compensated by the additional formation
;OOH radical than does R1O2, and the resulting loss of OH radicals is not compensated by the additional formation ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ia HONO dissociation.
ia HONO dissociation.
Extinction of the heptamethylnonane combustion by the inclusion of the HNO2 mechanism stems from a similar cause. The activation energy for its formation by reaction at the tertiary site is much less than it is from the primary site. Not only does this accentuate the R3O2/R1O2 disparity, but it increases the fraction of the NO2 trapped as HNO2, thus reducing the rates of formation of HONO by reaction with RH and with other minor constituents such as CHO and CH2O.
The possibility that NO2 may actually retard the spontaneous ignition of heptamethylnonane can only be considered as tentative, depending as it does on the theoretical prediction that there is a greater difference in activation energy between primary and tertiary C–H bonds for attack by NO2 than the model assumes8 that there is for O2 . Despite recent advances in computational methods, the estimation of activation energies still remains a difficult challenge. For this reason too, refinements to transition state theory such as allowance for restricted rotation or tunnelling were ignored: both types of correction are minuscule relative to that due to the mismatch between the computed and the observed activation energies, noted above.§
Comments
The general perception in the petroleum industry is that the better the diesel fuel, i.e. the higher the Cetane number (CN), the more strongly it responds to the addition of nitrate; such a correlation can be seen in a study of 13 different fuels by Nandi and Jacobs.7 In practice, it is usual to express the effect as the change in CN for a given concentration of nitrate, but since the relationship between CN and ignition delay is non-linear, quantitative comparison with the results shown in Table 4 is difficult. However, for the poorest fuel, CN = 13, that they studied,7 there was no improvement in ignition delay upon addition of 2-ethylhexyl nitrate, which is qualitatively consistent with the behaviour that we have found for heptamethylnonane. It is obvious that one can construct suitable mixtures with other hydrocarbons that will give a null response to NO2.An attempt to do just this led to a rather unexpected result: NO2 retarded the ignition of n-hexadecane–heptamethylnonane mixtures until the mol fractions were almost equal, with CN = 55. Contrast this with the behaviour of 3-ethyldecane in Table 4, for which CN is raised from ∽55 to the mid-80s by the addition of 0.1% of NO2. Thus, not only may the absence of secondary hydrogen atoms in a hydrocarbon result in its ignition being retarded by nitrates, but also it can lead to different responses from mixtures of hydrocarbons of the same CN. Here again examples of such behaviour are known: in Nandi and Jacobs' study,7 three fuels of CN = 44 (samples 6, 7 and 8) were improved to CN = 50, 46, and 47 respectively by the addition of 0.1% of 2-ethylhexyl nitrate.
Comparison of the results in Table 4 with those of Nandi and Jacobs7 suggests that the calculated reductions in ignition delay are somewhat too large. A mole fraction of 0.1% of NO2 in dodecane corresponds approximately to the inclusion of 0.1 wt.% of 2-ethylhexyl nitrate in the fuel. This would raise the CN of a relatively non-aromatic fuel from ∽55 to ∽65, whereas in our calculation, the CN of 3-ethyldecane is raised from ∽55 to ∽88 (the same delay as for n-dodecane itself).
It would, of course, be possible to manipulate the model so as to achieve weaker increments in CN, but that would not improve our understanding of the phenomenon. To that end, the measurement of the rates of reaction of NO2 with a series of hydrocarbons (with a definitive discrimination between the relative rates of formation of HONO and of HNO2) and the establishment of the fate(s) of HNO2 in combustion systems are fundamental. In addition, the determination of the CN improvement for a selection of pure hydrocarbons by 2-ethylhexyl nitrate in a test engine (or in a static bomb) are prerequisites. Aromatic hydrocarbons must be included in these studies since most fuels contain considerable amounts of aromatic components,7 and the aromatic centres themselves, as our calculations suggest, are rather inert to NO2 attack.
This could then be followed by a more extensive modelling calculation in which the reactions of NO2 with important reaction intermediates, such as aldehydes, would be included. But it has to be remembered that CN improvement may not be a function only of the hydrocarbon content of the fuel, but that trace hetero-impurities can have a pivotal effect, as we have found recently when di-tert-butyl peroxide is used as an ignition improver.34
This Appendix contains three tables of auxiliary data from the DFT calculations on reactions used in the modelling calculations. Further details can be obtained by electronic mail from 〈wtchan@yorku.ca〉; also, all 15 sets of transition state co-ordinates are available in XMOL-xyz form as Electronic Supplementary Information.† These data are provided so as to enable others either to verify or to reproduce the results of these molecular orbital calculations.| trans-HONO | cis-HONO | HNO2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Product RH | C–H | H–O | ∠CHO | C–H | H–O | C–O | ∠CHO | C–H | H–N | ∠CHN |
| a Secondary C–H bond. b Tertiary C–H bond. | ||||||||||
| CH4 | 1.252 | 1.252 | 176.5 | 1.345 | 1.191 | 3.042 | 177.7 | 1.471 | 1.182 | 180.0 |
| C2H6 | 1.229 | 1.296 | 174.7 | 1.317 | 1.226 | 3.064 | 177.0 | 1.437 | 1.206 | 175.1 |
| C3H8a | 1.212 | 1.339 | 172.9 | 1.298 | 1.258 | 3.117 | 175.0 | 1.411 | 1.225 | 177.7 |
| C4H10b | 1.196 | 1.379 | 175.6 | 1.283 | 1.284 | 3.165 | 172.5 | 1.390 | 1.242 | 177.7 |
| C6H6 | 1.272 | 1.208 | 178.4 | 1.372 | 1.157 | 3.142 | 172.3 | 1.548 | 1.132 | 179.9 |
| Reactant | State | E | ZPE | Product | State | E | ZPE |
|---|---|---|---|---|---|---|---|
| CH4 | T d | −40.4973 | 0.0459 | CH3 | D 3h 2A2″ | −39.8241 | 0.0304 |
| CH3CH3 | D 3d | −79.7927 | 0.0767 | CH3CH2 | C s 2A′ | −79.1257 | 0.0608 |
| (CH3)2CH2 | C 2v | −119.0901 | 0.1063 | (CH3)2CH | C s 2A′ | −118.4283 | 0.0905 |
| (CH3)3CH | C 3v | −158.3885 | 0.1351 | (CH3)3C | C 3v 2A1 | −157.7309 | 0.1199 |
| C6H6 | D 6h | −232.1563 | 0.1037 | C6H5 | C 2v 2A1 | −231.4711 | 0.0902 |
| NO2 | C 2v 2A1 | −205.0119 | 0.0094 | trans-HONO | C s | −205.6422 | 0.0218 |
| cis-HONO | C s | −205.6433 | 0.0218 | ||||
| HNO2 | C 2v | −205.6292 | 0.0234 | ||||
| trans-HONO | cis-HONO | HNO2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Product RH | E | ZPE | ω i | ω 1 | E | ZPE | ω i | ω 1 | E | ZPE | ω i | ω 1 |
| a State designation C1, 2A. b State designation C2v , 2A1. | ||||||||||||
| CH4 | −245.4465 | 0.0503 | 1974i | 39 | −245.4554 | 0.0510 | 2010i | 73 | −245.4513 | 0.0521 | 1710i | 6 |
| CH3CH3 | −284.7482a | 0.0806 | 1722i | 37 | −284.7574a | 0.0812 | 1943i | 54 | −284.7540a | 0.0822 | 1801i | 9 |
| (CH3)2CH2 | −324.0503 | 0.1100 | 1438i | 36 | −324.0596 | 0.1105 | 1852i | 50 | −324.0570 | 0.1114 | 1820i | 18 |
| (CH3)3CH | −363.3520 | 0.1388 | 1120i | 36 | −363.3619 | 0.1392 | 1737i | 49 | −363.3599 | 0.1400 | 1815i | 4 |
| C6H6 | −437.1016 | 0.1065 | 2051i | 11 | −437.1096 | 0.1073 | 1919i | 25 | −437.1046b | 0.1093 | 820i | 13 |
Allowance for tunnelling is often made in these types of calculation by the use of an implied partition function QT in the rate constant expression.14,15 This is estimated (in the limit of small barrier width and height) by using Wigner's approximation35
Since the temperature range over which we integrate the set of kinetic equations is from 745 and 1000 K, we display in Table A4 the estimated corrections for this method at 750 and at 1000 K. The correction is seen to lie generally between 30 and 60% for the reactions of interest in this study.
However Wigner's formula tends to overestimate tunnelling effect36 and it is desirable to use more sophisticated methods such as the zero-curvature tunnelling (ZCT) or the small-curvature tunnelling (SCT) approximations.37 Such methods, however, entail use of variational transition-state theory and are beyond the scope of this paper. As an example of the degree of overestimation, we cite the hydrogen transfer reaction between OH and fluoroethane
where the value of the imaginary frequency is ωi = 1920i cm−1 and the barrier height is 1.95 kcal mol−1.38 At room temperature, Wigner's method yields a value of QT = 4.58, instead of a value of 2.04 obtained from the SCT method;39 at 1000 K, the effect was reported to be negligible while Wigner's method gives a value of 1.32.
We present here an alternative method for judging the relative importance of tunnelling in our series of reactions. Since most molecular orbital computational methods characterise the transition state by an imaginary harmonic oscillator frequency, ωi, a useful procedure is to match the curvature of this hypothetical harmonic oscillator to that of a symmetric Eckart potential. Defining these two potential functions as
and
the condition for equal curvature at the saddle point is40
where μ is the reduced mass of the tunnelling particle, i.e. μ∽1 u, and ωi is in cm−1.
The transmission coefficient for a symmetric Eckart barrier at energy E is40
where
Extension to unsymmetric barriers (if needed) is logically straightforward, but cumbersome.
If we take E0 = 30 kcal mol−1 and ωi = 1800i cm−1, then the characteristic Eckart length L = 1.468 Å, and
Transmission coefficients for this example are listed in Table A5.
Clearly, for barriers of this kind, it is not necessary to go more than 1 kcal mol−1 below the saddle point. The contribu tion to the rate is then found by integrating over the fraction of collisions lying in the 1 kcal mol−1 band below the barrier, i.e.
| E | απ | exp(−απ) | κT(E) |
|---|---|---|---|
| 28.0 | 7.72 | 4.44 × 10−4 | 4.44 × 10−4 |
| 29.0 | 2.86 | 2.10 × 10−2 | 2.06 × 10−2 |
| 29.5 | 1.93 | 0.145 | 0.127 |
| 29.6 | 1.54 | 0.214 | 0.176 |
| 29.7 | 1.16 | 0.314 | 0.239 |
| 29.8 | 0.77 | 0.462 | 0.316 |
| 29.9 | 0.39 | 0.680 | 0.405 |
Considering the two temperatures that span our range of integration: at 750 K, the number of collisions with energy along the line of centres lying between E = 29 and 30 kcal mol−1 is 95% of the number between E = 30 kcal mol−1 and ∞; for 1000 K, it is 54%. The first point to note is that the correction therefore reduces the activation energy slightly, but not by enough to eliminate the discrepancies already discussed above. Taking a mean value of κT(E) over this range of about 0.2, then the tunnelling correction is about 20% at 750 K, 10% at 1000 K—perhaps only a third of those shown in Table A4 for the formation of cis-HONO or of HNO2; these are trivial in comparison with the uncertainties presently existing in the computational methods.
Acknowledgements
Work supported by the Natural Sciences and Engineering Research Council of Canada and, in part, by Esso Petroleum Canada.References
- P. Q. E. Clothier, B. D. Aguda, A. Moise and H. O. Pritchard, Chem. Soc. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1993, 22, 101 Search PubMed.
., 1993, 22, 101 Search PubMed. -
M. A. R. Al-Rubaie, J. F. Griffiths and C. G. W. Sheppard, Some Obser
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ations on the Effecti
ations on the Effecti![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) eness of Additi
eness of Additi![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) es for Reducing the Ignition Delay Period of Diesel Fuels, SAE Technical Paper Series, 1991, 912333. Search PubMed.
es for Reducing the Ignition Delay Period of Diesel Fuels, SAE Technical Paper Series, 1991, 912333. Search PubMed. - H. O. Pritchard, Combust. Flame, 1989, 75, 415 CrossRef CAS.
- P. Q. E. Clothier, H. O. Pritchard and M.-A. Poirier, Combust. Flame, 1993, 95, 427 CrossRef CAS.
- (a) Y. Yamaguchi, Y. Teng, S. Shimomura, K. Tabata and E. Suzuki, J. Phys. Chem. A, 1999, 103, 8272 CrossRef CAS; (b) K. Tabata, Y. Teng, Y. Yamaguchi, H. Sakurai and E. Suzuki, J. Phys. Chem. A, 2000, 104, 2648 CrossRef CAS.
- R. Galiasso and E. Rodriguez, A Low Emission Diesel Fuel, SAE Technical Paper Series, 1993, 932731. Search PubMed.
- M. K. Nandi and D. C. Jacobs, Cetane Response of di-tertiary-Butyl Peroxide in Different Diesel Fuels, SAE Technical Paper Series, 1995, 952368. Search PubMed.
- J. F. Griffiths, K. J. Hughes, M. Schreiber and C. Poppe, Combust. Flame, 1994, 99, 533 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, J. L. Andres, C. Gonzalez, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98, Revision A.6, Gaussian, Inc., Pittsburgh, PA, 1998. Search PubMed.
- (a) W.-T. Chan, I. P. Hamilton and H. O. Pritchard, J. Chem. Soc., Faraday Trans., 1998, 94, 2303 RSC; (b) W.-T. Chan, H. O. Pritchard and I. P. Hamilton, Phys. Chem. Chem. Phys., 1999, 1, 3715 RSC.
- B. G. Johnson, C. A. Gonzales, P. M. W. Gill and J. A. Pople, Chem. Phys. Lett., 1994, 221, 100 CrossRef CAS.
- M. T. Nguyen, S. Creve and L. G. Vanquickenborne, J. Phys. Chem., 1996, 100, 18422 CrossRef CAS.
- H. Basch and S. Hoz, J. Phys. Chem., 1997, 101, 4416 CrossRef CAS.
- S. Skokov and R. A. Wheeler, Chem. Phys. Lett., 1997, 271, 251 CrossRef CAS.
- R. G. Susnow, A. M. Dean and W. H. Green, Chem. Phys. Lett., 1999, 312, 262 CrossRef CAS.
- Q. Zhang, R. Bell and T. N. Truong, J. Phys. Chem., 1995, 99, 592 CrossRef CAS.
- J. L. Durant, Chem. Phys. Lett., 1996, 256, 595 CrossRef CAS.
- W.-T. Chan and H. O. Pritchard, to be published..
- C.-C. Hsu, M. C. Lin, A. M. Mebel and C. F. Melius, J. Phys. Chem., 1997, 101, 60 CrossRef CAS.
- J. Baker, A. Scheiner and J. Andzelm, Chem. Phys. Lett., 1993, 216, 380 CrossRef CAS.
- D. K. Maity, W. T. Duncan and T. N. Truong, J. Phys. Chem., 1999, 103, 2152 CrossRef CAS.
- G. Herzberg, Molecular Spectra and Molecular Structure, III, Electronic Spectra and Electronic Structure of Polyatomic Molecules, Van Nostrand, New York, 1966, p. 614. Search PubMed.
- J. M. Bofill, S. Olivella, A. Solé and J. M. Anglada, J. Am. Chem. Soc., 1999, 121, 1337 CrossRef CAS.
- D. Shen and H. O. Pritchard, unpublished results..
- S. Glasstone, K. J. Laidler and H. Eyring, The Theory of Rate Processes, McGraw-Hill, New York, 1941, pp. 191–195. Search PubMed.
-
(a)
M. W. Slack
and A. R. Grillo, Ele
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) enth International Shock Tube Symposium, University of Washington Press, Seattle, WA, 1977, p. 408 Search PubMed;
(b) M. W. Slack and A. R. Grillo, Combust. Flame, 1981, 40, 155 CrossRef CAS.
enth International Shock Tube Symposium, University of Washington Press, Seattle, WA, 1977, p. 408 Search PubMed;
(b) M. W. Slack and A. R. Grillo, Combust. Flame, 1981, 40, 155 CrossRef CAS. - T. A. Titarchuk, A. P. Ballod and V. Ya. Shtern, Kinet. Katal. (Engl. Transl.), 1976, 17, 932 Search PubMed.
- S. M. Heck, H. O. Pritchard and J. F. Griffiths, J. Chem. Soc., Faraday Trans., 1998, 94, 1725 RSC.
- A. D. Puckett and B. H. Caudle, Ignition Qualities of Hydrocarbons in the Diesel-fuel Boiling Range, United States Department of the Interior, Bureau of Mines, 1948, I.C. 7474. Search PubMed.
- W. A. Bone and J. B. Gardner, Proc. R. Soc. London, Ser. A, 1936, 154, 297 Search PubMed.
- A. Burcat, Combust. Flame, 1977, 28, 319 CrossRef CAS.
- C.-Y. Lin, H.-T. Wang, M. C. Lin and C. F. Melius, Int. J. Chem. Kinet., 1990, 22, 455 CrossRef CAS.
- K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions, Wiley, Chichester, 1996, pp. 108–110. Search PubMed.
- P. Q. E. Clothier, S. M. Heck and H. O. Pritchard, Combust. Flame, 2000, 121, 689 CrossRef CAS.
- J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical Kinetics and Dynamics, Prentice Hall, Englewood Cliffs, NJ, 1989, p. 320. Search PubMed.
- I. Shavitt, J. Chem. Phys., 1959, 31, 1359 CrossRef CAS.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, in Theory of Chemical Reaction Dynamics, ed. M. Baer, CRC Press, Boca Raton, FL, 1985, vol 4. Search PubMed.
- S. Sekusak, H. Gusten and A. Sabljic, J. Phys. Chem., 1996, 100, 6212 CrossRef CAS; S. Sekusak, H. Gusten and A. Sabljic, J. Phys. Chem., 1997, 101, 967 CrossRef.
- S. Sekusak, K. R. Liedl, B. Rode and A. Sabljic, J. Phys. Chem., 1997, 101, 4245 CrossRef CAS.
- D. Rapp, Quantum Mechanics, Holt, Rinehart and Winston, New York, 1971, pp. 168–170. Search PubMed.
Footnotes |
| † Electronic Supplementary Information available. See http://www.rsc.org/suppdata/cp/b0/b006088g/ |
| ‡ Incidentally, this sequestering of the NO2 further helps to justify the exclusion of the reaction between NO2 and formaldehyde to form HNO2. |
| § For the reactions to form HNO2, where the problem is most acute (see Table A3), the difference between restricted rotor and simple harmonic partition functions amounts to less than 20% for the tabulated cases; for larger R, the effect declines because of the appearance of an effective reduced mass in the restricted rotor formulae.33 The neglect of tunnelling is addressed in Appendix 2. |
| This journal is © the Owner Societies 2001 |