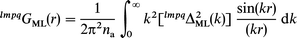Microscopic structure of nickel(II) co-ordination shell in NiCl₂–methanol solution: neutron diffraction and ab initio studies

Abstract

Neutron diffraction measurements were carried out on ∽1.4 molal solutions of NiCl₂ in methanol under ambient conditions. First-, second- and high-order difference methods with isotopic substitution on nickel, chlorine and hydroxy hydrogen (H_O) were applied in conjunction with ab initio calculations of Ni²⁺–methanol complex to derive Ni–O, Ni–H_O, Ni–Cl, Ni–C and Ni–H(methyl) pair radial distribution functions, RDFs. Analyses of these RDFs demonstrates that Ni²⁺ is co-ordinated octahedrally by five methanol molecules and one chloride anion with the nearest-neighbour Ni–O, Ni–Cl and Ni–H_O distances of 2.057(1), 2.348(2) and 2.619(6) Å, respectively. The results also reveal a preferential triangular orientation of the methanol molecules surrounding Ni²⁺ in its co-ordination shell.

---

I. Introduction

In spite of wide technical applications of non-aqueous electrolyte solutions (NAES),¹ our ability to predict their thermodynamic and kinetic properties is still restricted by the simple ion–ion and ion–dipole electrostatic models. One reason for this is the absence of detailed information about solvation structure of ions, especially multicharged and transition metal cations. Such information essentially means a deeper understanding of these systems at a microscopic level.

Among the various direct experimental methods (i.e., those methods for which the space and time dimensions are comparable to the molecular dimensions and characteristic time of molecular processes, respectively), neutron diffraction with isotopic substitution (NDIS) offers the most powerful technique for analysing the microscopic structure of ion–molecular systems.^2,3 This method allows us to derive structural information of nearest-neighbour ion environment in terms of pair radial distribution functions (RDFs), interatomic distances and co-ordination numbers.

Solutions of NiCl₂ in methanol are ideally suited for applying the NDIS technique due to (i) the availability of suitable nickel, chlorine and, hydrogen isotopes, and (ii) the high solubility of nickel chloride in this solvent. Among the non-aqueous solvents, methanol possesses interesting characteristics due to the presence of both hydrophobic (CH₃) and hydrophilic (OH) groups. It forms a well established hydrogen bonding network which is responsible for many of the macroscopic properties of this solvent and its electrolyte solutions.⁴

Although solutions of NiCl₂ in methanol have been investigated earlier by using the NDIS method,⁵ the results of this work have caused some controversy. Powell and Neilson⁵ reported that Ni²⁺ is co-ordinated to 3.7 methanol molecules and they estimated at least 0.8 chloride ions to be in contact with the nickel. The total co-ordination number, 3.7+0.8=4.5 is apparently inconsistent not only with the well established 6-coordinated octahedral structure of 3d- ransition metal(II) ions in aqueous solutions,⁶ but also with the results of nickel(II) co-ordination in non-aqueous oxygen-donating solvents^7,8 without chloride as a counter ion. It made us wonder whether this behavioural change of Ni²⁺-coordination is caused with a change of the counter ion to Cl⁻. To answer this question, the pair RDF g_NiCl(r) should be obtained experimentally and, as far as we know, this has not been reported so far in any non-aqueous solvent.

Further motivation for the present study has been provided by a necessity to elucidate spatial correlations of nickel with carbon and hydrogens of methanol's methyl group since this will allow us to obtain information about the orientation of methanol molecules around the cation in its co-ordination shell.

In this paper we present the results of a comprehensive structural study of Ni²⁺ co-ordination shell in a 1.4 molal solution of NiCl₂ in deuterated methanol by using nickel, chlorine and hydroxy hydrogen isotopic substitution technique of neutron diffraction (ND). To further facilitate interpretation of experimental results at the pair RDF level, ab initio calculations on methanol molecule and [Ni(CH₃OH)]²⁺ complex were also performed. The paper has the following structure. Section II describes the essential theory behind the NDIS method. The experimental method is given in Section III. The ND data analyses are described in Section IV with special attention being paid to the normalisation of scattering patterns. In Section V the results of NDIS experiments and ab initio calculations are presented and discussed in terms of Ni²⁺ pair RDFs, mean interatomic distances, co-ordination numbers and orientation of the methanol molecules around the nickel(II).

II. Theoretical background

The isotopic substitution technique of neutron diffraction, as applied to ionic solutions, has been described elsewhere.² Only those relations necessary for understanding this article are described below.

From a single neutron diffraction experiment on a multicomponent solution one obtains, after correction and normal isation, a differential cross-section (DCS), F₀(k), which is given by the expression⁹

where k=4π/λsin(θ) is the scattering vector defined by the scattering angle, 2θ , and the incident wavelength, λ; x_i and σ_i^s are the atomic fraction and total bound (coherent and incoherent) scattering cross-section (TSCS) of species i, respectively, n is the total number of chemical species in the solution. The ε(k) is a term that arises from inelasticity effects owing to a departure from the static approximation.^10,11 The total structure factor, F(k), is a linear combination of the partial structure factors

where b_i is mean coherent scattering length of species i. The partial structure factor, S_ij(k), is related to the pair RDF, g_ij(r), by the Fourier transformation

where n_a is the total atomic number density of the solution, averaged over all the species. It is worth noting that when i and j indices belong to the solvent atoms, both S_ij(k) and g_ij(r) consist of two parts, intra- and intermolecular, often with overlapping contributions. The difference method of isotopic substitution enables cancellation of the intramolecular parts from the S_ij(k) and g_ij(r) functions.

The Fourier transformation of the F(k) yields the total RDF, G(r), which is a linear combination of the pair RDFs, g_ij(r)

where W_ij=∑_ij(2−δ_ij)x_ix_jb_ib_j and δ_ij is the Kronecker delta-function. For the solution of NiCl₂ in methanol there are six (n=6) atomic species [Ni, Cl, O, H_O(D_O), C and H(D)], taking into account the different spatial positions of the hydrogens, H and H_O of the methyl and hydroxy groups, respectively. Consequently, the number of different partial functions S_ij(k) is equal to n(n+1)/2=21. However, hydrogen atoms of the methyl group are not all equal. While two methyl hydrogen atoms are closer to the hydroxy hydrogen and lie out of the symmetry plane of the methanol molecule, the third methyl hydrogen together with C, O and H_O(D_O) define this symmetry plane (see Fig. 1). The F(k) will then comprise of 28 partial structure factors, making it extremely difficult to interpret the total RDF, G(r) in terms of individual pair contributions.

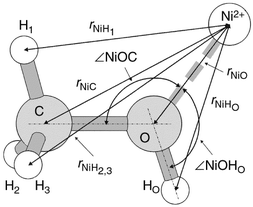Fig. 1 Sketch of the Ni(CH₃OH)²⁺ complex optimised by MP2/TZV** ab initio calculations.

In the first-order difference method, DCS is measured for two solutions denoted as m and l, identical except for the isotopic composition of one of the atomic species, ^αM and ^βM, which are characterised by different coherent scattering lengths, b_αM and b_βM, respectively. Difference in the two scattering functions, ^lF₀(k) and ^mF₀(k), gives

^lmΔF₀(k)=^lF₀(k)−^mF₀(k)

=^lmΔ_M¹(k)+^lmE′(k), (5)

where ^lmΔ_M¹(k)=∑_i=1^nlmW_Mi[S_Mi(k)−1], with weighting factors

The real-space first-order difference function, ^lmG_M(r), is obtained from

An important property of the difference function ^lmΔ_M¹(k) is that the ε(k) term in eqn. (1) will, to a first-order approximation, be identical for both the solutions.¹² It cancels to give negligible contribution from the ε′(k) term in eqn. (5). The validity of this approximation can be checked on several accounts. Firstly, since g_Mi(r)=0 at r-values below the distance of closest approach of the M and i species (i.e., r_min), ^lmG_M(r) should be equal to the calculated limit, ^lmG_M(0)=−σ^lmW_Mi at low r. In practice, ^lmG_M(r) will oscillate about this value owing to statistical noise on the k-space data, truncation of the data at a finite k-value and systematic errors. However, if these effects are small, setting ^lmG_M(r) equal to the ^lmG_M(0) limit for r⩽r_min and back Fourier transformation will yield the k-space first-order difference function in close agreement at all k-values with ^lmΔ_M¹(k). Secondly, since S_ij(k)→1 in the limit k→∞, ^lmΔF₀(k) should oscillate about the calculated self-scattering difference, x_M(σ_αM^s−σ_βM^s)/(4π).¹³ Thirdly, the k-space difference function should satisfy the sum-rule relation¹⁴

In reality, it is difficult to apply the second and third criteria due to relatively short range of the scattering vector (k⩽20 Å⁻¹) and significant inelasticity effects while using a reactor-based neutron source.

Additional isotopic substitution can be used to further separate the partial structure factors.¹⁵ The neutron second-order difference technique may be used to isolate the ion–ion and ion–hydrogen partial RDFs.^2,3,15 Consider two first-order difference experiments identical except that apart from M, atom species ^γL is replaced by another isotope, ^δL. Assuming as usual that the structure of the solutions are not altered by the isotopic substitution, one obtains for the k- and r-spaces

[^lF₀(k)−^mF₀(k)]−[^pF₀(k)−^qF₀(k)]=^lmΔF₀(k)

=W_ML[g_ML(r)−1], (9)

where W_ML=2x_Mx_L(b_αM−b_βM)(b_γL−b_δL).

For further consideration it is useful to introduce a co-ordination number, n̄_Mⁱ,

which defines the mean number of particles of type i contained in a volume restricted by two concentric spheres of radii r₁ and r₂, and centred on a particle of type M. If a peak in a real space difference function, g_Mi(r) or G_M(r) may be associated with an individual pair, a co-ordination number can be calculated by integration of the corresponding function over the range of the relevant peak

The superscript ‘eff’ indicates the possibility of multiple contributions to the peak.

III. Experimental

Sample solutions were prepared as follows. The solid mixtures of Zn³⁷Cl₂+K³⁷Cl, used by Badyal and Howe¹⁶ in their previous experiments on molten salts and kindly sent to us, were converted into aqueous solution of H³⁷Cl by using an Amberlit IR-120 (H) ion-exchange resin. To avoid any loss of expensive isotopes, the ion-exchange column was connected to a specially designed and calibrated conductometric sensor and a conductance bridge. The solid mixture of ⁶²NiCl₂+KCl also obtained from Howe,¹⁶ was converted into ⁶²NiCO₃·xH₂O by reaction with an aqueous solution of Na₂CO₃ (Ultrapure, Alfa, Puratronic®, 99.995%) at ∽90°C. The light-green gelatinous precipitate of ⁶²NiCO₃·xH₂O was thoroughly rinsed with deionised water by a combination of centrifuging and decantation processes, repeated until the centrifugate showed negative reaction of Cl⁻, Na⁺ and CO₃²⁻ ions. Aqueous solutions of ⁶²Ni^NCl₂ , ^NNi³⁷Cl₂ and ⁶²Ni³⁷Cl₂ were further prepared by mixing H*Cl and *NiCO₃, where the asterisks refer to the isotopes. An aqueous solution of H^NCl (BDH, Aristar®) was used for preparing ⁶²Ni ^NCl₂ salt. Powder of ^NNiCO₃·2Ni(OH)₂·4H₂O (Alfa, Puratronic®, 99.996%) was used for preparing ^NNi³⁷Cl₂ salt. An aqueous solution of ^NNi^NCl₂ was obtained by dissolving crystalline ^NNi^NCl₂ (Alfa, Puratronic®, 99.995%) in a very dilute H^NCl solution to avoid any hydrolysis. The solutions of *Ni*Cl₂ were then evaporated to a solid form of *Ni*Cl₂·6H₂O and further dried on a vacuum line under 1–100 Pa by gradually increasing the temperature from 25 to 70°C during one week. Such a procedure reduced the water content to less then 0.01%, and this was estimated by frequent and accurate weighting of the samples. Anhydrous salts so obtained were yellow or yellow–brownish, as expected.¹⁷

The solutions of ^NNi^NCl₂ and ⁶²Ni^NCl₂ in methanol-d₃, CD₃OH, (Cambridge Isotope Laboratories, 99.5% deuterated) and ^NNi^NCl₂, ⁶²Ni^NCl₂, ^NNi³⁷Cl₂ and ⁶²Ni³⁷Cl₂ in methanol-d₄, CD₃OD (Cambridge Isotope Laboratories, 99.8% deuterated) were made by weight in a dried, nitrogen filled glove box. The solvents were preliminary dried under 4 Å molecular sieves during one week.

The sample densities were measured by using Anton Paar DMA 58 densimeter at 25.2°C, the average temperature during neutron diffraction experiments.

The neutron diffraction (ND) experiments were performed using the D4B instrument at the Institute Laue-Langevin, Grenoble, France. The incident wavelength was 0.7046 Å giving an available k-range of 0.2<k<17 Å⁻¹. The scattered neutrons were detected with two 64-channel multidetectors, which were calibrated by using the scattering from a vanadium bar. Diffraction patterns were obtained for (i) the solutions in their containers, (ii) the empty containers, (iii) the instrumental background with the sample absent, (iv) a cadmium bar of 7 mm diameter in order to estimate the background correction at low scattering angles¹⁸ and, (v) a vanadium standard rod of diameter 6.08 mm. The two containers used were hollow vanadium cylinders of inner diameters 6.8 and 6.67 mm and outer diameters 7.02 and 7.053 mm, respectively. The cylinder's axis was oriented perpendicular to the incident beam of height 5.0 cm.

The details of the solutions used in the diffraction experiments are given in Table 1. The coherent scattering lengths of the ⁶²Ni and ³⁷Cl isotopes, as defined by mass spectrometry,¹⁶ were respectively, −6.75 and 3.68 fm (1 fm=10⁻¹⁵ m). The scattering lengths of the natural isotopes [C, 6.6460(12); O, 5.803(4); H, −3.7390(11); ^NNi, 10.3(1); ^NCl, 9.5770(8) fm] and deuterium [D, 6.671(4) fm] were taken from Sears.¹⁹ The scattering lengths, total bound and absorption cross-sections for deuterium in each solvent, CD₃OH and CD₃OD, were calculated by taking into account its enrichment in each one of them.

Table 1 Experimental details of the sample solutions

							Total scattering cross-section, σs/b
Solute	Solvent	Designation of scattering pattern	Molality, m/mol kg^−1	Molar ratio, solvent to solute	Total atomic number density, na/atom Å^−3	Density, ρ/g cm^−3 (at 25.2°C)	Bound^a	Free atom^b	Total absorption cross-section^cσa/b
a Calculated using the bound scattering cross-sections for all the atoms.b Calculated using the free atom scattering cross-sections for methanol.c At a wavelength of 1.798 Å.
^NNi^NCl2	CD3OH	^1F0(k)	1.395	20.5	0.0929	1.03864	19.26	3.05	0.624
^NNi^NCl2	CD3OD	^2F0(k)	1.371	20.2	0.0924	1.05948	7.07	3.40	0.576
^62Ni^NCl2	CD3OH	^3F0(k)	1.313	21.7	0.0927	1.03220	19.20	—	0.659
^62Ni^NCl2	CD3OD	^4F0(k)	1.364	20.3	0.0924	1.06250	7.01	—	0.645
^NNi^37Cl2	CD3OD	^5F0(k)	1.374	20.2	0.0924	1.06352	6.85	—	0.094
^62Ni^37Cl2	CD3OD	^6F0(k)	1.324	20.9	0.0922	1.06089	6.79	—	0.160

---

IV. Data analyses

The total differential cross-section, F₀(k) can be obtained from the measured intensity, I(k), after applying various corrections in the form¹⁰

F₀(k)=α(k)×[I(k)+δ(k)]/(4π), (12)

where α(k) accounts for normalisation, absorption and self-shielding and, δ(k) is the contribution from multiple scattering. Both the functions, α(k) and δ(k) depend on the total scattering and absorption cross-sections, σ_s and σ_a of the sample.

A major problem with normalisation of the DCS for NAES, unlike the case for aqueous solutions,²⁰ is that the σ_s values are not known exactly and these must be estimated from some assumptions. There are two common practices to calculate TSCS by using either bound atom or free atom approaches,^5,7 and there is no straightforward rule to choose either one of them. The consequence is that firstly, the σ_s values calculated by using the two approaches differ several times from each other and secondly, this leads to a significant difference not only in the differential cross-sections, but also in the RDFs, G(r) and the co-ordination numbers. In order to establish how and to what extent the variation in TSCS alters the experimental DCS, initial analyses of the data were made on the total scattering patterns of only two samples, ‘1’ and ‘2’ (see Table 1). The raw data for these solutions were corrected for scattering and absorption by the container, for self-absorption²¹ and for multiple scattering,²² and put on an absolute scale of b sr⁻¹‡ by using scattering from the vanadium rod.²³ All these corrections were performed by using three different values of the TSCS for each sample: 19.26, 6.0 and 2.0 b for ^NNi^NCl₂ in CD₃OH and 7.08, 3.5 and 2.0 b for ^NNi^NCl₂ in CD₃OD. These values cover the changes in σ_s from the bound to the free-atom TSCS values (see Table 1). The calculated F₀(k) functions are shown in Fig. 2.

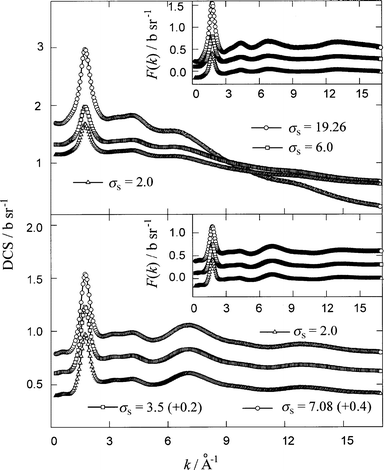Fig. 2 Experimental differential cross-sections, F₀(k), for the solutions of ^NNi ^NCl₂ in CD₃OH (sample ‘ 1’, upper panel) and in CD₃OD (sample ‘2’, lower panel) obtained by using different value, in b, of the total scattering cross-section (TSCS), σ_s, as indicated in the figure. Insets show the total structure factors, F(k), for the samples ‘1’ (upper panel) and ‘2’ (lower panel) after applying inelasticity correction to the F₀(k) functions. For the inset in the upper panel, TSCS, σ_s=19.26 (+0.6) (circles), σ_s=6.0 (+0.3) (squares), σ_s=2.0 (triangles) and for that in the lower panel, σ_s=7.08 (+0.6) (circles); σ_s=3.5 (+0.3) (squares); σ_s=2.0 (triangles).

Another problem with the evaluation of the total structure factor, F(k), is the inelasticity correction.^24,25 The main effect of the inelasticity on hydrogenated and deuterated samples can be clearly seen in the droop of the DCS data at high k-values (see Fig. 2). In this work we have adopted an empirical approach based on the knowledge that the falloff is proportional to k² in the low k-region,²⁵ and at higher k-values there are additional terms which contribute to the Placzek droop. The total structure factors, F(k) were thus extracted from the F₀(k) by subtraction of the polynomials, E(k) in the form of eqns. (13a) and (13b) for the samples ‘1’ and ‘2’, respectively.

E₃(k)=a+bk²+ck³+dk⁴, (13a)

E₄(k)=a+bk²+dk⁴. (13b)

The coefficients a, b, c and d of eqn. (13) were found by least-square fitting of E(k) to the experimental F₀(k) functions. The F(k) functions, and the total RDFs, G(r) obtained by their Fourier transformation are shown in Figs. 2 (insets) and 3, respectively. For Fourier transformation we used our own program based on Numerical Recipes Fortran package.²⁶ A comparison of the F(k) and G(r) functions for both the samples revealed that the use of different TSCS values for normalisation of the F₀(k), followed by appropriate inelasticity correction, affects only the amplitude of these functions without any influence on their functional form. As an additional confirmation of this conclusion, one can see in Fig. 4 that the ratios G_3.5(r)/G_7.08(r), G_2.0(r)/G_7.08(r) and G_2.0(r)/G_3.5(r) for ^NNi^NCl₂ in CD₃OD (sample ‘2’) are almost flat over the entire r-range.

Fig. 3 Total radial distribution functions, G(r), for the samples ‘1’ (upper panel) and ‘2’ (lower panel) obtained by Fourier transformation of the F(k) functions shown in Fig. 2 (insets).

Fig. 4 The ratios of the total RDFs shown in Fig. 3 obtained by using different values of the total scattering cross-section for the sample ‘2’: G_2.0(r)/G_7.08(r) (circles), G_3.5(r)/G_7.08(r) (squares) and G_2.0(r)/G_3.5(r) (triangles). Full curves are the linear regressions over the data.

It may be concluded from the above initial analyses that both the functions, F(k) and/or G(r) for a given sample can be easily renormalised by simply multiplying the corresponding functions calculated by using bound TSCS with an appropriate normalisation factor, nf, which is independent of the scattering vector, k, and/or interatomic distance, r.

As a most reliable criterion for the choice of the normalisation factor, the effective co-ordination number over the first peak in the total RDF, G(r) of NiCl₂–methanol solutions can be used.⁵ This peak located at ∽1 Å in the total G(r) (see Fig. 3) is a weighted sum of the O–H_O(D_O) and C–D intramolecular correlations in accordance with the geometry of the methanol molecule (see Fig. 1 and Table 6 later). Thus, by integration of the total RDF one can obtain

where X_O denotes either hydrogen or deuterium of the hydroxy group, n̄_C^D=3 and n̄_O^X_O=1 are the theoretical values of the co-ordination numbers for the D-atom around carbon of the methyl group and X_O-atom around oxygen of the hydroxy group, respectively. Eqn. (14) yields the theoretical value of ^effn̄_C^D equal to 2.507 for CD₃OH and 3.873 for CD₃OD, respectively.

On the basis of the above discussion, the following scheme of initial data analyses was adopted. (i) In the first stage, the experimental scattering patterns for all the six solutions were corrected for scattering and absorption by the container, for self-absorption and for multiple scattering, and put on an absolute scale by using scattering from the vanadium rod. At this stage, only total bound (coherent plus incoherent) scattering cross-sections listed in Table 1 were used. (ii) The total structure factor, F(k), for each solution was then extracted from the observed DCS function, F₀(k). For applying the inelasticity corrections, polynomials in the form of eqn. (13), E₃(k) for the solutions in methanol-d₃ and E₄(k) for the solutions in methanol-d₄, were used. For each sample, the coefficients a, b, c and d were treated as adjustable parameters in the least squares refinement. It should be noted (see eqn. (1)) that the polynomials E₃(k) and E₄(k) incorporate not only the inelasticity effects, but also the self scattering term, σx_iσ_i^s/(4π) of the measured DCSs. (iii) In the final step of the initial analysis procedure, the normalisation factors, nf₃ and nf₄, for the solutions in CD₃OH and CD₃OD, respectively, were found by scaling (see eqn. (14)) the total RDFs, G(r), obtained by Fourier transformation of the corresponding F(k) functions. This operation was continued until the effective co-ordination numbers, ^effn̄_C^D, calculated by integration of the scaled total RDFs, G^†(r)=nf_i×G(r) (see Fig. 5) over the first peak yielded their theoretically expected values. It was found (see Table 2) that the normalisation factors should be nf₃=0.466 and nf₄=0.747 to satisfy the above described criterion. Using these values of nf₃ and nf₄, the experimental DCS functions were renormalised according to the relations

Fig. 5 Renormalised total RDFs (scaled for intramolecular C–D and O–X_O (X=H or D) correlations) for the solutions of nickel chloride in methanol-d₃ (upper panel) and methanol-d₄ (lower panel): 1,2—^NNi^NCl₂, 3,4—⁶²Ni^NCl₂, 5—^NNi³⁷Cl₂ and 6—⁶²Ni³⁷Cl₂.

Table 2 The effective co-ordination number, ^effn̄_C^D calculated by integration of the renormalised total RDFs, G^†(r)=nf_i×G(r) (Fig. 5) over the first peak, for 1.4 molal solutions of NiCl₂ in methanol

Sample	^effn̄C^D	Integration range/Å
a The theoretical value is 2.507 for solutions of *Ni*Cl2 in CD3OH.b The theoretical value is 3.873 for solutions of *Ni*Cl2 in CD3OD.
CD3OH (nf3=0.466)
1	2.52	0.9–1.3
3	2.48	0.9–1.3
Mean value	2.50^a
CD3OD (nf4=0.747)
2	3.85	0.825–1.325
4	3.93	0.825–1.325
5	3.84	0.825–1.325
6	3.89	0.825–1.325
Mean value	3.88^b

---

F₀^†(k)=nf₃×F₀(k) (15a)

and

F₀^†(k)=nf₄×F₀(k) (15b)

for the solutions of *Ni*Cl₂ in CD₃OH and CD₃OD, respectively. The renormalised F₀^†(k) functions, shown in Fig. 6, were used for further analyses as described in Section V. In the sub sequent discussion we omit the ‘†’ sign as a superscript in the DCS functions bearing in mind that these functions have already been renormalised.

Fig. 6 Renormalised experimental differential cross-sections for the ∽1.4 molal solutions of nickel chloride in methanol-d₃ (upper panel) and methanol-d₄ (lower panel): 1,2—^NNi^NCl₂, 3,4—⁶²Ni^NCl₂, 5—^NNi³⁷Cl₂ and 6—⁶²Ni³⁷Cl₂.

V. Results and discussion

A. First-order differences

The three first-order difference functions, ¹³Δ_Ni¹(k), ²⁴Δ_Ni¹(k) and ⁵⁶Δ_Ni¹(k), describing the co-ordination structure around the nickel cation are illustrated in Fig. 7. These were obtained from the renormalised DCSs, F₀(k)s, (see Section IV) for the pairs of samples 1 and 3, 2 and 4, and 5 and 6 (for designation of the samples, see Table 1), respectively. To account for the residual self-scattering and inelasticity effects (eqn. (5)), polynomials of the form

Fig. 7 First-order difference functions, ^lmΔ_Ni¹(k), where l and m are the designations (Table 1) of the two scattering patterns used for their evaluation. Symbols are the data points and curves are the back Fourier transforms of the real-space ^lmG_Ni(r) functions after setting them to their low r-value limits, ^lmG_Ni(0) (full curves in Fig. 8).

Fig. 8 First-order real-space difference functions, ^lmG_Ni(r) vs. r. The dotted curves are the Fourier transforms of the measured ^lmΔ_Ni¹(k) functions of Fig. 7 and full curves are ^lmG_Ni(r) after the unphysical oscillations at r⩽1.85 Å have been set to their low r-value limits, ^lmG_Ni(0) (see Table 3).

^lmE′(k)=a+bk²+ck⁴ (16)

were subtracted from each difference function ^lmF₀(k). The coefficients a, b and c for each of the difference functions were obtained by least-square fitting procedure.

The three real-space difference functions, ¹³G_Ni(r), ²⁴G_Ni(r) and ⁵⁶G_Ni(r), obtained by Fourier transformation of ^lmΔ_Ni¹(k), are shown in Fig. 8. The unphysical features at r⩽1.85 Å oscillate about the correct ^lmG_Ni(0) values (see Table 3). Also, the back Fourier transforms of ^lmG_Ni(r) obtained after setting ^lmG_Ni(r)=^lmG_Ni(0) at r⩽1.85 Å (see Fig. 7) are in good agreement with the corresponding ^lmΔ_Ni¹(k) functions from which they are obtained. This demonstrates that the residual inelasticity corrections incorporated by the ^lmE′(k) polynomials (eqn. (16)) are small, that the cross-sections used in data analyses are reasonable, and that the obtained real-space first-order difference functions are correctly behaved.

The RDFs shown in Fig. 8 are linear combinations of the weighted nickel(II) pair distribution functions

Table 3 The weighting factors, ^lmW_NiX, and low r-value limits ^lmG_Ni(0) and ^lmG_NiX^*(0) (in mb) for the first- and high-order differences

Difference (lm)
Correlation	1–3	2–4	5–6
Ni–Ni	0.042	0.040	0.041
Ni–Cl	0.395	0.421	0.158
Ni–O	2.503	2.583	2.557
Ni–HO(DO)	−1.613	2.960	2.931
Ni–C	2.867	2.959	2.930
Ni–D	8.565	8.881	8.792
^lmGNi(0)	12.759	17.845	17.409
^lmGNiX^*(0)	13.977	14.462	14.320

---

As the values of the weighting factors, ^lmW_NiX (Table 3) suggest, the difference functions ^lmG_Ni(r) are mainly dominated by contributions from the correlations of Ni²⁺ with methanol atoms, but the influence of Ni–Cl correlation cannot be ignored. It should be noted (eqn. (17)), that the two kinds of methyl hydrogens, D₁(H₁) and D_2,3(H_2,3) are made distinguishable according to their different spacial orientation with respect to the hydroxy group and symmetry plane of the methanol molecule (Fig. 1).

All the three first-order difference functions, ¹³G_Ni(r), ²⁴G_Ni(r) and ⁵⁶G_Ni(r) reveal four sharp and well-separated peaks (see Fig. 8). To obtain reliable quantitative characteristics of these peaks, each ^lmG_Ni(r)−^lmG_Ni(0) function was fitted by a sum of four Gaussians given by the expression

where A, σ and r_max are, respectively, the area, half-width at half-maximum and mean position of the peak. The results of the fitting are shown in Fig. 9, and the fitted parameters are listed in Table 4. The first peak occurring at 2.065–2.097 Å can obviously be assigned to Ni–O nearest-neighbour correlations on the basis that the methanol molecule acts as an oxygen-donating ligand. The second peak at 2.582–2.729 Å is negative for the NiCl₂ solutions in CD₃OH and positive for those in CD₃OD. This peak, thus, corresponds to Ni–H_O (hydroxy hydrogen) correlations since the coherent scattering length of hydrogen is negative. The third and fourth peaks are then readily associated with the correlations of the nickel cation with the carbon and hydrogen (deuterium) of the methyl group, although exact assignment of these peaks to individual correlations can not be made from the present NDIS experiments. To clarify the spatial disposition of the methanol molecule with respect to Ni²⁺, ab initio calculations were performed (see Section V.C).

Fig. 9 [^lmG_Ni(r)−^lmG_Ni(0)] functions fitted by a sum of four Gaussians represented by the functions f_i(r) of eqn. (18). The symbols represent the data, the dotted curves give the individual fitted Gaussians and the full curve gives their sum.

Table 4 Structural parameters for the Ni²⁺ co-ordination shell obtained by fitting the first-order difference functions, ^lmG_Ni(r)−^lmG_Ni(0) shown in Fig. 9 with Gaussian peak shapes^a

Difference (lm)
Peak and its parameters	1–3	2–4	5–6
a rmax, σ and A are the mean position, half-width at half-maximum and area of a peak. ^effn̄Ni^O and ^effn̄Ni^HO are the effective co-ordination numbers of the oxygen and hydroxy hydrogen around the Ni^2+ obtained by integration of the corresponding Gaussians over the ranges ΔrNiO and ΔrNiHO, respectively.
1st peak
rmax/Å	2.065(1)	2.097(1)	2.082(1)
σ/Å	0.115	0.117	0.109
A/b	0.0162	0.0170	0.0162
^effn̄Ni^O	5.3(3)	5.5(3)	5.2(3)
ΔrNiO/Å	1.65–2.45	1.7–2.5	1.7–2.5
2nd peak
rmax/Å	2.729(9)	2.581(2)	2.600(3)
σ/Å	0.127	0.147	0.151
A/b	−0.0043	0.0137	0.0135
^effn̄Ni^HO	3.8(5)	5.9(4)	5.9(4)
ΔrNiHo/Å	2.2–3.2	2.1–3.1	2.1–3.1
3rd peak
rmax/Å	3.163(4)	3.158(2)	3.160(3)
σ/Å	0.179	0.182	0.167
A/b	0.0167	0.0196	0.0181
4th peak
rmax/Å	4.007(7)	4.012(6)	4.002(9)
σ/Å	0.189	0.173	0.191
A/b	0.0098	0.0104	0.0107

---

Table 4 reveals that there are certain discrepancies in the positions of the first and second peaks obtained from the three first-order difference functions. Although the positions of the first peaks are in good agreement with those reported by Powell and Neilson,⁵ the three values of 2.065, 2.097 and 2.082 Å are slightly greater than the Ni–O distance of 2.05 Å derived by Inada et al.⁸ from a recent EXAFS experiment on 0.3 molal solution of NiCl₂ in methanol. Moreover, the position of the second peak in the case of ¹³G_Ni(r) RDF is shifted by ∽0.1 Å towards high r as compared to those for ²⁴G_Ni(r) and ⁵⁶G_Ni(r) RDFs (see Table 4).

The effective co-ordination numbers of the oxygen and hydrogen of the hydroxy group around the nickel, obtained by integration of the first two normalised Gaussians

are also reported in Table 4. As it follows from the molecular structure of the methanol molecule, the co-ordination numbers ^effn̄_Ni^O and ^effn̄_Ni^H_O, for a given ^lmG_Ni(r) RDF, should be equal to each other. Table 4, however, shows that these values are different, the difference being −1.5, 0.4 and 0.7 for 1–3, 2–4 and 5–6 difference, respectively.

The above discrepancies in both the peak positions and the co-ordination numbers, as will be shown in the following sections, can be easily explained by considering the penetration of the first solvation shell of Ni²⁺ by chloride ion.

B. The pair RDFs, g_NiHO(r) and g_NiCl(r)

On the assumption that co-ordination structure around Ni²⁺ is unaffected by any isotopic substitution, e.g., ^NNi by ⁶²Ni, H_O by D_O, and ^NCl by ³⁷Cl, the two second-order difference functions, ²⁴¹³Δ_NiHO²(k) and ²⁴⁵⁶Δ_NiCl²(k) were evaluated (Fig. 10) from the corresponding first-order difference functions

Fig. 10 Second-order difference functions, ^lmpqΔ_NiX²(k) for the Ni–Cl (upper panel) and Ni–H_O (hydroxy hydrogen) (lower panel) correlations. Symbols are the data points and curves are the back Fourier transforms of the real-space ^lmpqG_NiX(r) functions after setting them to their low r-value limits, ^lmpqG_NiX(0) (full curves in Fig. 11). The statistical noise (errors) cannot be seen for ²⁴¹³Δ_NiHO²(k) on the given scale.

²⁴¹³Δ_NiHO²(k)=²⁴Δ_Ni¹(k)−¹³Δ_Ni¹(k)

=²⁴¹³W_NiHO[S_NiHO(k)−1], (21)

²⁴⁵⁶Δ_NiCl²(k)=²⁴Δ_Ni¹(k)−⁵⁶Δ_Ni¹(k)

=²⁴⁵⁶W_NiCl[S_NiCl(k)−1] (22)

without applying any additional inelasticity correction. Their Fourier transformations yielded the real-space functions, ²⁴¹³G_NiHO(r) and ²⁴⁵⁶G_NiCl(r), which are shown in Fig. 11. The back Fourier transforms of these functions, after the unphysical oscillations at r⩽r_min have been set to the calculated values of ^lmpqG_NiX(0)=−^lmpqW_NiX (X=H_O, Cl) (Table 5), are found to be in good agreement with the original k-space functions (see Fig. 10). This validates the correctness of the procedure used for determination of the second-order difference functions. The pair RDFs, g_NiHO(r) and g_NiCl(r) as given by

Fig. 11 Second-order real-space difference functions, ²⁴⁵⁶G_NiCl(r) (upper panel) and ²⁴¹³G_NiHO(r) (lower panel) vs. r. The dotted curves are the Fourier transforms of the measured ^lmpqΔ_NiX²(k) functions of Fig. 10 and full curves are ^lmpqG_NiX(r) after the unphysical oscillations at r⩽r_min have been set to their low r-value limits, ^lmpqG_NiX(0).

Table 5 The weighting factors, ^lmpqW_NiX=−^lmpqG_NiX^*(0), and the structural parameters for the Ni²⁺ co-ordination shell obtained by fitting the pair RDFs, g_NiCl(r) and g_NiHo(r) shown in Fig. 12 with Gaussian peak shape^a

Correlation
Parameter	Ni–Cl	Ni–HO
a rmax, σ and A are the mean position, half-width at half-maximum and area of a Gaussian. n̄Ni^X and ΔrNiX are the corresponding co-ordination numbers and their integration ranges.
^lmpqWNiX/mb	0.262	4.573
rmax/Å	2.348(2)	2.619(6)
σ/Å	0.104	0.189
A/G	7.1	4.4
n̄Ni^X	0.72(5)	5.4(5)
ΔrNiX/Å	2.0–2.7	2.0–3.2

---

Fig. 12 The pair RDFs, g_NiCl(r) (upper panel) and g_NiHO(r) (lower panel). The symbols correspond to the data and the full curves give the fitted Gaussians represented by the function f_i(r) of eqn. (18).

g_NiHO(r)=²⁴¹³G_NiHO(r)/²⁴¹³W_NiHO+1, (23)

g_NiCl(r)=²⁴⁵⁶G_NiCl(r)/²⁴⁵⁶W_NiCl+1 (24)

along with the fitted individual Gaussian functions in the form of eqn. (18) are shown in Fig. 12. The object of the Gaussian fitting of individual RDFs is to increase the accuracy in peak positions and co-ordination numbers, especially in the case of g_NiHO(r) where small artificial shoulders apart from the main peak are also observed (Fig. 12). The fitted and other important parameters of the second-order difference functions are summarised in Table 5. It can be seen that in 1.4 molal solution of NiCl₂ in methanol, the mean Ni–H_O distance at 2.619(6) Å is comparable to that in aqueous²⁰ (2.67–2.80(2) Å) and ethylene glycol⁷ (2.82–2.86(2) Å) solutions with the same concentration of Ni²⁺. The Ni–Cl nearest-neighbour distance of 2.348(2) Å is very close to the sum of the Pauling ionic radii,²⁷ 2.41=0.6+1.81 Å. This is an obvious evidence of direct cation–anion complexation (‘contact ion pair’¹) in contrast to the results for aqueous NiCl₂ solutions.²⁸ A compari son of the positions of the first and second peaks in the real-space first-order difference functions (Table 4, Fig. 9) with the average Ni–Cl distance (Table 6) indicates that nickel–chlorine correlation contributes significantly to the first and second peaks in ^lmG_Ni(r), and also to the ^effn̄_Ni^O and ^effn̄_Ni^H_O co-ordination numbers.

Table 6 Total molecular energy, E (in E_h^a) and geometry (in Å and degrees) of a methanol molecule and Ni²⁺–methanol complex from theory and experiment

Methanol molecule
	Ab initio calculations			Experiment			Ni^2+–methanol complex Ab initio calculations
Parameter	MP2/3-21G	MP2/TZV**	Gas phase^b	Liquid phase^c	MP2/3-21G	MP2/TZV**
a 1 Eh=627.51 kcal mol^−1.b Ref. 30.c Ref. 31.
rOHO	0.992	0.960	0.9451	0.961	0.997	0.978
rCO	1.471	1.421	1.4246	1.415	1.577	1.541
rCH1	1.090	1.085	1.0936	1.096	1.090	1.086
rCH2,3	1.098	1.091	1.0936	1.096	1.088	1.083
∠COHO	107.0	107.9	108.53	111.0	108.3	113.1
∠OCH1	105.5	106.6	—	—	105.8	105.6
∠OCH2,3	111.2	112.1	—	—	106.1	105.4
rNiO	—	—	—	—	1.775	1.752
rNiHO	—	—	—	—	2.479	2.407
rNiC	—	—	—	—	3.004	2.936
rNiH1	—	—	—	—	2.971	2.887
rNiH23	—	—	—	—	3.642	3.565
∠NiOC	—	—	—	—	127.2	125.9
∠NiOHO	—	—	—	—	124.4	121.0
E	−114.6093	−115.5188	—	—	−1613.5240	−1621.7095

---

Integration of the fitted g_NiHO(r) and g_NiCl(r) RDFs over the ranges 2.0⩽r⩽3.2 Å and 2.0⩽r⩽2.7 Å, respectively, gives n̄_Ni^Cl=0.72(5) and n̄_Ni^H_O=5.4(5) (Table 5). This finding is consistent with the 6-site octahedral co-ordination of Ni²⁺ that corresponds to the sp³d² hybridisation of its atomic orbitals.⁶ This type of co-ordination is typical for nickel cation in its aqueous⁶ and non-aqueous^7,8 solutions. From this point of view, the value of 3.7(3) for the n̄_Ni^H_O co-ordination number obtained by Powell and Neilson⁵ for 1 molal NiCl₂–methanol solution seems to be underestimated.

C. Ab initio calculations

Ab initio calculations were performed by using the GAMESS program²⁹ on Digital Alpha Workstation at the University of Abertay Dundee, Dundee, Scotland, UK. The two basis sets, 3-21G and TZV** (triple zeta with polarisation functions) of different quality were used for a full geometry optimisation of the methanol molecule and Ni²⁺–methanol complex. The structures optimised at the restricted Hartree-Fock (RHF) level were further optimised at the second-order Møller–Plesset perturbation (MP2) level. The optimised structural parameters of the methanol molecule and Ni(CH₃OH)²⁺ complex along with total molecular energies are presented in Table 6. The equilibrium geometry of the Ni(CH₃OH)²⁺ complex is shown diagrammatically in Fig. 1. The intramolecular geometrical parameters of the methanol molecule obtained experimentally in gas³⁰ and liquid phases³¹ are also included in Table 6.

The results of our calculations can be summarised as follows. Despite the fact that the total molecular energy of CH₃OH obtained at the MP2/TZV** level of theory differs significantly from the corresponding 3-21G value, the struc tural parameters of an isolated methanol molecule calculated by using both the basis sets are in reasonable agreement with the experimental results.

The co-ordination of methanol molecule with Ni²⁺ alters significantly the C–O bond length and the ∠OCH₂₍₃₎ for both the basis sets (see Table 6). The ∠COH_O , calculated at the MP2/TZV** level, is also changed upon co-ordination. The C–O bond length increases by ∽0.11 Å and the ∠OCH₂₍₃₎ decreases by 5–6° whereas the ∠COH_O obtained at MP2/TZV** level increases by ∽5°. As shown in Table 6, the O–H_O and C–H bond lengths are almost insensitive to the co-ordination of methanol with Ni²⁺.

The most interesting result in Table 6 is that the interatomic Ni–C and Ni–H₁ distances obtained at the same level of theory coincide with each other within 0.03–0.06 Å. However, they differ significantly from the Ni–H₂₍₃₎ distance. Upon the basis of the results given in Table 6, the third and fourth peaks in the RDFs, ^lmG_Ni(r) obtained by using the first-order difference method of ND (see Fig. 8 and 9) can be safely assigned. Thus, the third peak corresponds to a combination of the Ni–C and Ni–H₁(D₁) interatomic correlations seen at ∽3.16 Å, whereas the fourth one occurring at ∽4 Å results from overlapping Ni–H₂(D₂) and Ni–H₃(D₃) correlations. The difference of 0.2–0.4 Å in the positions of the fourth peak in ^lmG_Ni(r) (Table 4) and Ni–H₂₍₃₎ interatomic distances as calculated by ab initio method (Table 6) can be associated with the absence of other co-ordinating species, such as Cl⁻ and four additional methanol molecules in the modelled Ni²⁺–methanol complex.

D. High-order differences

Using the partial structure factors S_NiHO(k) and S_NiCl(k), obtained by using the second-order difference technique of ND (see Section V.B), the high-order k-space difference functions

where X=(Ni, O, C, D₁–D₃) and lm=(13, 24, 56), were also extracted (Fig. 13) at the level of accuracy relevant to this work. The corresponding RDFs, ^lmG_NiX^*(r) obtained by Fourier transformation of the k-space data, are shown in Fig. 14. The back Fourier transforms of these RDFs, after setting ^lmG_NiX^*(r) equal to ^lmG_NiX^*(0) (Table 3) at r⩽r_min, are found to be in good agreement with the original scattering functions (see Fig. 13) from which they were obtained. The calculated real-space functions (Fig. 14) show three well pronounced peaks, which correspond to the first, third and fourth peaks, respectively, in the first-order difference functions, ^lmG_Ni(r) (see Fig. 8).

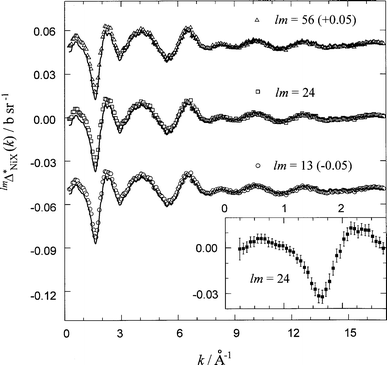Fig. 13 High-order difference functions, ^lmΔ_NiX^*(k). Symbols are the data points and curves are the back Fourier transforms of the real-space ^lmG_NiX^*(r) functions after setting them to their low r-value limits, ^lmG_NiX^*(0) (full curves in Fig. 14). The inset shows the level of statistical noise (errors) in the experimental data at the high-order difference level.

Fig. 14 High-order real-space difference functions, ^lmG_NiX^*(r) vs. r. The dotted curves are the Fourier transforms of the measured ^lmΔ_NiX^*(k) functions of Fig. 13 and full curves are ^lmG_NiX^*(r) after the unphysical oscillations at r⩽1.85 Å have been set to their low r-value limits, ^lmG_NiX^*(0) (see Table 3).

Next, the functions

were fitted by the sum of three Gaussians, f₁(r)+f₂(r)+f₃(r), each in the form of eqn. (18). The results of the fit are illustrated in Fig. 15, and the fitted parameters of the Gaussians are summarised in Table 7. Firstly, the Ni–Ni contribution is negligible due to low concentration of Ni²⁺ as compared to methanol atoms (see Tables 1 and 3). Secondly, since it is impossible for two nickel ions to be at such short distances where the first solvation shell of Ni²⁺ is observed, only the correlations of Ni²⁺ with O, C and D₁–D₃ atoms should be taken into account for further consideration.

Fig. 15 [^lmG_NiX^*(r)−^lmG_NiX^*(0)] functions fitted by a sum of three Gaussians represented by the functions, f_i(r) of eqn. (18). The symbols correspond to the data, the dotted curves give the individual fitted Gaussians and the full curve gives their sum.

Table 7 Structural parameters for the Ni²⁺ co-ordination shell obtained by fitting the high-order difference functions, ^lmG_NiX^*(r)−^lmG_NiX^*(0) shown in Fig. 15 with Gaussian peak shapes^a

Difference (lm)
Peak and its parameters	1–3	2–4	5–6
a rmax, σ and A are the mean position, half-width at half-maximum and area of a peak. n̄Ni^O, n̄Ni^C+n̄Ni^D1 and n̄Ni^D2,3 are the co-ordination numbers of the methanol atoms around the Ni^2+ obtained by integration of the corresponding Gaussians over the ranges Δr1, Δr2 and Δr3, respectively.
1st peak
rmax/Å	2.057(1)	2.056(1)	2.057(1)
σ/Å	0.103	0.103	0.103
A/b	0.0157	0.0150	0.0159
n̄Ni^O	5.0(3)	4.9(3)	4.9(3)
Δr1/Å	1.7–2.4	1.7–2.4	1.7–2.4
2nd peak
rmax/Å	3.163(2)	3.163(2)	3.163(2)
σ/Å	0.154	0.153	0.153
A/b	0.0154	0.0157	0.0157
n̄Ni^C+n̄Ni^D1	10.2(6)	10.1(6)	10.1(6)
Δr2/Å	2.6–3.7	2.6–3.7	2.6–3.7
3rd peak
rmax/Å	4.000(7)	3.999(8)	3.999(7)
σ/Å	0.213	0.218	0.218
A/b	0.0105	0.0109	0.0109
n̄Ni^D2,3	11(1)	11(1)	11(1)
Δr3/Å	3.5–4.5	3.5–4.5	3.5–4.5

---

The first peak in ^lmG*_NiX(r) functions is undoubtedly due to the Ni–O correlation. It is interesting to note that the position of this peak at 2.057 Å coincides for all the three RDFs within an accuracy of 0.001 Å (Table 7), thus resolving the discrepancy observed for this distance at the first-order difference level (see Table 4 and Section V.A). This distance is also in excellent agreement with the mean Ni–O distance of 2.05 Å in Ni(CF₃SO₃)₂–methanol solution obtained from the recent EXAFS experiment.⁸

On the basis of the ab initio calculations performed (see Table 6 and Section V.C), one expects that the correlation of Ni²⁺ with hydrogens of the methyl group can be split into two types, Ni–D₁ and Ni–D_2,3, in accordance with Fig. 1. So, the second peak occurring at 3.163(2) Å (Table 7, Fig. 15) arises from a combination of Ni–C and Ni–D₁ correlations, which can not be separated into individual contributions. The third peak at 4.000(8) Å, according to the spatial orientation of the methanol molecule with respect to the nickel cation (see Fig. 1), arises purely from the Ni–D_2,3 correlations.

Following the above assignment of peaks and distances, the pair RDFs, g_NiO(r), g_NiC(r)+g_NiD1(r) and g_NiD2,3(r) calculated by using the fitted parameters from Table 7 are shown in Fig. 16. The pair RDFs, g_NiHO(r) and g_NiCl(r) obtained by using the second-order difference technique (see Section V.B) are also included in this figure. Fig. 16 clearly shows a high degree of overlap of the g_NiCl(r) with both g_NiO(r) and g_NiHO(r). This is the reason why the positions of the first peaks (Table 4) in the first-order difference functions ^lmG_Ni(r) (Fig. 8) are shifted by 0.01–0.04 Å towards high r-values as compared to those obtained from high-order RDFs (Table 7). On the basis of similar arguments, the positions of the second peaks in the ^lmG_Ni(r) that reflect Ni–H_O correlation are shifted towards the low r-values for CD₃OD samples and, to the high r side for CD₃OH samples, as compared to the r_max at 2.619 Å of g_NiHO(r) (see Tables 4 and 5).

Fig. 16 The pair RDFs, g_NiX(r) (full curves) describing the nearest-neighbour environment of Ni²⁺ in NiCl₂–methanol solutions as obtained by using the second- and high-order difference techniques of neutron diffraction. The dotted curve is the g_NiCl(r) pair RDF scaled as it contributes into the g_NiO(r) and g_NiHO(r) pair RDFs in the first-order difference functions, ^lmG_Ni(r) shown in Figs. 8 and 9.

The co-ordination numbers obtained by integration of the fitted Gaussians, f₁(r), f₂(r) and f₃(r), are listed in Table 7. Since the weighting factors ^lmW_NiC and ^lmW_NiD/3 are the same within 0.5% (Table 3), the integration of the f₂(r) as an individual pair correlation function yields

Similarly, on the basis of the methanol molecule structure and its spatial disposition in the Ni²⁺ solvation shell (Fig. 1), one can expect the value for the n̄_Ni^D_2,3 co-ordination number to be twice that for the n̄_Ni^O. Our results of 4.9–5.0(3), 10.1–10.2(6), and 11(1) (Table 7) for the co-ordination numbers, n̄_Ni^O, n̄_Ni^C+n̄_Ni^D₁ and n̄_Ni^D_2,3, respectively, confirm the conclusion (see Section V.B) that the first co-ordination shell of Ni²⁺ is comprised of five methanol molecules and one chloride anion disposed in an octahedral arrangement around the central cation.

E. The orientation of the methanol molecule in the cation solvation shell

The sketch of Ni²⁺–methanol conformation optimised by ab initio calculations (Fig. 1) and the mean interatomic distances derived by using the second- and high-order difference techniques of ND, allow us to calculate the two angles, viz. ∠NiOC and ∠NiOH_O,

cos(∠NiOC)=(r_NiC²−r_NiO²−r_CO²)/(−2r_NiOr_CO), (28)

cos(∠NiOH_O)=(r_NiHO²−r_NiO²−r_OHO²)/(−2r_NiOr_OHO). (29)

These angles, in fact, determine the orientation of the methanol molecule with respect to the co-ordinating ion. The distances r_NiO=2.057 Å, r_NiHO=2.619 Å and r_NiC=3.163 Å were taken from Tables 5 and 7, whereas for r_CO and r_OHO, three different data sets were used: from (i) ab initio MP2/TZV** calculations, (ii) microwave gas-phase experiment³⁰ and, (iii) ND liquid-phase experiments³¹ (Table 6). Calculated values of ∠NiOC and ∠NiOH_O are summarised in Table 8 along with the values of ∠COH_O derived by assuming that the Ni²⁺ lies within the symmetry plane of the methanol molecule. On the basis of a joint analysis of the structural parameters presented in Tables 6 and 8, two conclusions can be drawn.

Table 8 The orientation of methanol molecule with respect to the Ni²⁺ ion derived by using the experimental values of r_NiO, r_NiHO and r_NiC and three data sets for r_CO and r_OHO distances: (a) from ab initio MP2/TZV** calculations (b) from microwave gas-phase experiment³⁰ and, (c) from ND liquid-phase experiment³¹

Angle/degrees	(a)	(b)	(c)
∠NiOC	122.4	129.7	130.38
∠NiOHO	114.6	116.5	115.54
∠COHO	123.0	113.8	114.08

---

First, the ∠NiOC of 122.4°, obtained by using the Ni–C and Ni–O distances from our NDIS experiments and intramolecular C–O distance from the MP2/TZV** ab initio calculations, is in good agreement with the one calculated theoretically, 125.9°. Worse agreement is, however, observed for the ∠NiOH_O. This is, perhaps, because the ab initio calculations were performed only with one methanol molecule in the Ni²⁺–methanol complex. The presence of additional ligands around Ni²⁺ in the real solution will bring a change in the position of hydroxy hydrogen, and consequently, in the ∠NiOH_O.

The second point to note is that all the three angles, i.e., ∠NiOC, ∠NiOH_O and ∠COH_O lie close to a value of 120°, which corresponds to sp² hybridisation of the oxygen of methanol molecule with a plane-triangular geometry of the surrounding atoms, Ni, H_O and C. In this case one can expect that residual lone-pair of the oxygen atom should occupy its 2p_x (2p_y) orbital situated perpendicular to the symmetry plane of the methanol molecule and the triangle formed by Ni, C and H_O atoms. A strong preference for a triangular orientation of the methanol molecules surrounding Mg²⁺ in its octahedral solvation shell was also established by Tamura et al.³² from a molecular dynamics simulation of MgCl₂ solution in methanol.

VI. Conclusions

A detailed investigation of the Ni²⁺ co-ordination shell at an atomic level in NiCl₂–methanol solution has been carried out by combining neutron diffraction experimental results with ab initio calculations of Ni²⁺–methanol complex. The first-, second- and high-order difference methods with isotopic substitution on nickel, chlorine and hydroxy hydrogen were applied to obtain pair radial distribution functions of Ni²⁺. Special attention was paid to properly normalise the various scattering patterns, which is crucial to obtain accurate values of the structural parameters such as inter-atomic distances and co-ordination numbers. The main results of the present work can be summarised as follows.

For the first time in non-aqueous media, it has been shown that chloride ion penetrates the nickel(II) solvation shell, forming contact Ni–Cl complex (‘ contact ion pair’) with a mean separation distance of 2.348(2) Å and co-ordination number of 0.72(5) in NiCl₂–methanol solution. We also established that because of this inner sphere complexation, it is not possible to derive exact values of mean Ni–O distance and n̄_Ni^O co-ordination number purely from the first-order difference functions. By applying the second and high-order difference methods of ND we found, with high accuracy, the mean Ni–O distance of 2.057(1) Å and n̄_Ni^O value of 5.0(3). The integration of g_NiHO(r) pair RDF with a maximum at 2.619(6) Å gave a co-ordination number of 5.4(5) for the n̄_Ni^H_O.

On the basis of the ab initio analysis of the interatomic distances in Ni²⁺–methanol complex, the peaks occurring ca. 3.16 and 4.00 Å in the first- and high-order real-space difference functions have been assigned to Ni–C+Ni–D₁ and Ni–D_2,3 correlations, where D_1,2,3 are the three methyl hydrogens split spatially into two different environments (D₁ and D_2,3) around Ni²⁺. The integrations of these peaks confirm that the Ni²⁺ is co-ordinated to five methanol molecules. By taking into account the electronic structure of the nickel(II) ion, it was concluded that the Ni²⁺ has a 6-coordinated octahedral structure of its nearest-neighbour environment.

The theoretically calculated and experimental interatomic distances have been used to derive ∠NiOC and ∠NiOH_O. These angles are found to be consistent with sp²-hybridisation of the hydroxy oxygen and triangular-planar orientation of the methanol molecules surrounding Ni²⁺ in its solvation shell.

The above results have unequivocally demonstrated the power of using complementary techniques in resolving structural details of non-aqueous electrolyte solutions at a microscopic level. In a forthcoming paper, we shall present the results of a similar neutron diffraction study of Cl⁻ co-ordination shell in NiCl₂–methanol solutions.

Acknowledgements

We are grateful to Dr R. A. Howe for providing us with the isotopes, Dr H. E. Fischer (ILL) for help with the NDIS experiments, Dr V. V. Ivanov for helpful discussions regarding ab initio calculations and, the EPSRC, UK for support. One of us (O.N.K.) wishes to thank the Royal Society/NATO for the award of a post-doctoral fellowship and the University of Abertay Dundee for hosting his visit.

References

1. H.-J. Gores and J. Barthel, Pure Appl. Chem., 1995, 67, 919.
2. G. W. Neilson and J. E. Enderby, J. Phys. Chem., 1996, 100, 1317.
3. G. W. Neilson and A. K. Adya, Annu. Rep.–R. Soc. Chem. Sect. C, 1997, 93, 101.
4. G. Sesê and J. A. Padro, J. Chem. Phys., 1998, 108, 6347.
5. D. H. Powell and G. W. Neilson, J. Phys. Condens. Matter, 1990, 2, 5867.
6. R. Ripan and I. Ceteanu, Chimia Metalelor, Editura Didactica Si Pedagogica, Bucharest, Romania, 1969, vol. II..
7. P. B. Lond, P. S. Salmon and D. C. Champeney, J. Am. Chem. Soc., 1991, 113, 6420.
8. Y. Inada, H. Hayashi, K. Sugimoto and S. Funahashi, J. Phys. Chem. A, 1999, 103, 1401.
9. D. G. Montague, I. P. Gibson and J. C. Dore, Mol. Phys., 1981, 44, 1355.
10. G. L. Squires, Introduction to the Theory of Thermal Neutron Scattering, Cambridge University Press, Cambridge, 1978..
11. P. A. Egelstaff, An Introduction to the Liquid State, Oxford University Press, Oxford, 1992..
12. A. K. Soper, G. W. Neilson, J. E. Enderby and R. A. Howe, J. Phys. C: Solid State Phys., 1977, 10, 1793.
13. C. Cossy, A. C. Barnes, J. E. Enderby and A. E. Merbach, J. Chem. Phys., 1989, 90, 3254.
14. J. E. Enderby, D. M. North and P. A. Egelstaff, Philos. Mag., 1966, 14, 961.
15. G. W. Neilson and J. E. Enderby, Proc. R. Soc. London, Ser. A, 1983, 390, 353.
16. Y. S. Badyal and R. A. Howe, J. Phys. Condens. Matter, 1996, 8, 3733.
17. Yu. V. Karyakin and I. U. Angelov, Pure Chemical Substances, ‘‘Khimiya’’ Publishers, Moscow, 1974, p. 292..
18. M. Bertagnolli, P. Chieux and M. D. Zeidler, Mol. Phys., 1976, 32, 759.
19. V. F. Sears, Neutron News, 1992, 3, 26.
20. D. H. Powell and G. W. Neilson, J. Phys. Condens. Matter, 1990, 2, 3871.
21. H. H. Paalman and C. J. Pings, J. Appl. Phys., 1962, 33, 2635.
22. I. A. Blech and B. L. Averbach, Phys. Rev., 1965, 137, 1113.
23. J. E. Enderby and G. W. Neilson, in Water, A Comprehensive Treatise, ed. F. Franks, Plenum Press, New York, 1979, vol. 6, ch. 1..
24. G. Placzek, Phys. Rev., 1952, 86, 377.
25. J. G. Powles, Adv. Phys., 1973, 22, 1.
26. W. H. Press, S. A. Teukolsky, W. T. Veterling and B. P. Flannery, Numerical Recipes in Fortran: The art of Scientific Computing, Cambridge University Press, Cambridge, 1992..
27. R. A. Robinson and R. H. Stokes, Electrolyte Solutions, Butterworths Scientific Publishers, London, 1959..
28. G. W. Neilson, in Water and Aqueous Solutions, ed. G. W. Neilson and J. E. Enderby, Adam Hilger, Bristol, 1986, p. 169..
29. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347.
30. R. M. Lees and J. G. Baker, J. Chem. Phys., 1968, 48, 5299.
31. A. K. Adya, L. Bianchi and C. J. Wormald , J. Chem. Phys., in the press..
32. Y. Tamura, E. Spohr, K. Heinzinger, G. Pálinkás and I Báko, Ber. Bunsen-Ges. Phys. Chem., 1992, 96, 147.

---

Footnotes

† Permanent address: Department of Inorganic Chemistry, Kharkov State University, Kharkov, Svobody Square 4, 61077, Ukraine. E-mail: Oleg.N.Kalugin@univer.kharkov.ua

‡ 1 b (barn)=10⁻²⁸ m²

---