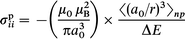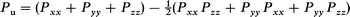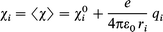Empirical calculations of 29Si NMR chemical shielding tensors: A partial charge model investigation of hydrolysis in organically modified alkoxy silanes
Todd M. Alam*a and Marc Henryb
aDepartment of Aging and Reliability, Sandia National Laboratories, MS-1407, Albuquerque, NM 87185-1407, USA. E-mail: tmalam@sandia.gov
bLaboratoire de Chimie Moleculaire de l'Etat Solide, Universite Louis Pasteur , 67070, Strasbourg Cedex, France
First published on UnassignedUnassigned22nd December 1999
Abstract
The 29Si NMR chemical shifts for a series of organically modified silane compounds, MexSi(OR)y(OH)4 − x − y (OR = OMe, OEt), were evaluated using a partial charge model (PCM) approach to describe the chemical bonding. These PCM results allow the relative contributions of the diamagnetic and paramagnetic terms in the 29Si NMR chemical shielding constant to be discussed. An explanation for the unique variations in the 29Si chemical shifts during for hydrolyzed organically modified silanes is presented.
1 Introduction
Organically modified alkoxy silanes play an important role in tailoring different properties of silica produced by the sol–gel method. Changes in the size and functionality of the organic group allows control of both physical and chemical properties of the resulting gel, with the kinetics of the polymerization process playing an important role in the design of new siloxane materials. High resolution 29Si NMR has proven to be a valuable tool for monitoring the polymerization reaction, and has been used to investigate a variety of organically modified alkoxy silane systems.1–4 The initial steps of acid-catalyzed sol–gel polymerization are the hydrolysis and esterification (reverse of hydrolysis) reactions described by| Rx′ Si(OR)4 − x + nH2O↔Rx′ Si(OR)4 − n − x(OH)n + nROH | (1) |
The identification and quantification of the different hydrolysis species (Rx′Si(OR)4 − x − n(OH)n) produced in eqn. (1) is important to understanding the initial steps of the sol–gel polymerization process. Recently it has been noted that the assignment of the high-resolution 29Si NMR spectra for the resulting hydrolysis species in organically modified alkoxy silanes is complicated by upfield and/or downfield variations in the chemical shifts with hydroxy addition.2,4–6 More complicated NMR experiments, including INEPT (insensitive nuclei enhanced by polarization transfer) and DEPT (distortionless enhancements by polarization transfer) based experiments have been used to correctly assign these different 29Si NMR chemical shifts in simple organically modified alkoxy silanes.2,4,6–9 A basic understanding of what factors control the magnitude and sign of these chemical shift variations with hydroxy addition remains unclear. The development of theoretical methods that would allow the assignment of 29Si chemical shifts for the hydrolysis products for a wide range of organically modified silanes based on some easily predicted property would prove valuable in future investigations. There have been a limited number of ab initio 29Si chemical shift tensor calculations for simple silanes.10–13 Increases in computational speed and efficiency suggest that ab initio calculations for silicon containing compounds will become more routine in the near future. Empirical methods have also been used to calculated 29Si chemical shifts,14,15 including the use of partial charge models (PCM).16 The advantage of PCM methods is that it allows chemical shift calculations for large molecular systems with limited computational expense. In this manuscript, we report the empirical PCM evaluation of the 29Si chemical shifts in methyl substituted methoxy and ethoxy alkoxy silanes, MexSi(OR)y(OH)4 − x − y (OR = OMe, OEt). Using a structurally dependent PCM the variations in the 29Si chemical shift are directly related to changes in the partial charge, q(Si), on the silicon atom and the average excitation energy (ΔE) of the silane.
2 Experimental and computational methods
The silanes tetraethoxysilane TEOS (Kodak), methyltriethoxysilane MTES (Aldrich), dimethyldiethoxysilane DMDES (Gelest), trimethylethoxysilane TMES (Gelest), tetramethoxysilane TMOS (Aldrich), methyltrimethoxysilane MTMS (Petrarch Systems), dimethyldimethoxysilane DMDMS (Gelest) and trimethylmethoxysilane TMMS (Aldrich) were used as received without further purification. For each silane investigated a 2.24 M solution was prepared in the parent alcohol (MeOH or EtOH). The stock solution was analyzed for condensation and hydrolysis contaminants prior to use by 29Si NMR. Hydrolysis species were generated by the addition of 3 molar equivalents of doubly distilled H2O (Rw = 3.0). No acid or base catalysts were employed in these investigations to reduce condensation reactions during investigations.All 29Si NMR experiments were performed at 79.49 MHz on a Bruker AMX400 spectrometer, using a 5 mm broadband probe at 298±0.2 K. A DEPT pulse sequence was used to assign the hydrolysis species in these investigations.17 The interpulse delay τ and the variable pulse angle θ in the DEPT experiment were optimized for the multiple heteronuclear Si–H couplings present in these silanes, as previously described.6 Chemical shifts were referenced to 0.1% internal TMS (δ = 0.0 ppm), with positive δ values corresponding to increased frequency.
Empirical 29Si chemical shift calculations were obtained using a C++ program running on a 166 MHz PC. Starting 3D-geometries were approximated using standard sets of bond lengths, assuming tetrahedral symmetry around silicon, carbon and oxygen atoms and imported as Z-matrices in MOPAC format. The charge distributions reported were computed assuming that the s-orbital participation to a chemical bond of an element having Nv valence electrons was 1/Nv18 except for chlorine where a value of 25% seems to be more appropriate than the standard 14.3%. For the chemical hardnesses η, the Bragg–Slater set of radii which provide a good measure of the spatial extent of the outer valence orbitals of the elements have been used.19
3 Theoretical background
The NMR resonance frequency ω of a nucleus with gyromagnetic ratio γ placed in a static magnetic field B0 is given by ω = γB0(1 − σ). The nuclear magnetic shielding tensor σ measures the influence of the molecular environment and shifts the observed NMR resonance from the frequency of a bare nucleus. It is often convenient to express the perturbation theory expansion of the chemical shielding tensor as a sum of a first-order (diamagnetic) term σd and a second-order (paramagnetic) term σp, both resulting from electronic currents localized on the atom containing the nucleus of interest.20–22| σ = σd + σp | (2) |
The diamagnetic term contains only matrix elements involving the ground state wavefunctions, and can be expressed as (in ppm):23
 | (3) |
where μ0 is the vacuum permeability, e is the electron charge, me is the electron mass (μ0e2/12πm = 9.39 ppm Å). Pγγ is the charge density in the atomic orbital γ which is at an average distance of rγ from the nucleus of interest.
The paramagnetic contribution to the shielding tensor component σp is opposite in sign to σd, and involves unperturbed excited wavefunctions surrounding the nucleus. If a mean excitation energy ΔE is introduced,24 then the individual shielding tensor elements (σxxp, σyyp and σzzp) are defined by
 | (4) |
where Pij is the charge distribution and bond order matrix, 〈r − 3〉np the average electron–nucleus distance r over p-orbitals, μB the Bohr magneton and a0 the Bohr radius (μ0μB2/πa03=1449 ppm eV). For the isotropic 29Si NMR chemical shieldings reported in the Results section only the rotational average of the individual tensor elements in eqn. (4) are observed, producing an isotropic shielding defined by
 | (5) |
where Pu is the population asymmetry and measures the deviation from spherical symmetry of the electronic cloud and is defined by
 | (6) |
The changes in the observed 29Si chemical shielding result from the fine balance between four terms σd, 〈r − 3〉np, ΔE and Pu. The first two terms, σd and 〈r − 3〉np, are functions of the gross atomic population N = Ps + Pxx + Pyy + Pzz and can be related to the partial atomic charge on silicon q(Si) = Z − N. The last two terms ΔE and Pu are generally obtained from molecular orbital theory, but have also been shown to be dependent on the silicon partial atomic charge q(Si).16 A reliable way of estimating these atomic charges should then be of a considerable help in analysis of chemical shift trends.
3.1 The partial charge model (PCM) approach of chemical bonding
The identification of the electronegativity χ as the opposite of the electronic chemical potential μe(χ = −μe),25 and of the chemical hardness η to the HOMO–LUMO energy gap,26 allows a straightforward and reliable evaluation of partial atomic charges q independently of any molecular orbital calculations. From a practical point of view, given any system resulting from the association of n atoms with a total electrical charge Z, it is possible to write the system electronegativity as:27 | (7) |
where ε0 is the vacuum permittivity, χi0 are Mulliken electronegativities of the valence orbitals used for chemical bonding,18ri the atomic radii modelling the spatial extent of these orbitals and Rij is the distance between atoms i and j in the compound with partial charge qi. Eqn. (7) allows a set of chemical parameters (electronegativities, sizes and atomic spatial positions) and the associated partial charge distribution qi to be easily related, and thereby allow relationships between chemical shielding and partial charge to be established.
Using the PCM, the diamagnetic shielding described by eqn. (3) can be easily calculated taking into account the partial charge distribution using the polynomial approximation of Saxena and Narasimhan for a 29Si nucleus bearing a partial charges q(Si).28 The shielding is given by23,29
 | (8) |
where σd (free atom) is the free atom diamagnetic susceptibility, ZN is the atomic number of atom N, rN is the distance from the nucleus of interest and atom N, and the summation runs over all atoms directly attached to the atom of interest.
For the evaluation of the paramagnetic shielding in eqn. (5) the radial term 〈a0/r3〉np is known to vary with the partial charge q(Si) as24
| 〈(a0/r)3〉np = 〈(a0/r)3〉np0 + f×q(Si) = R0 + f×q(Si) | (9) |
where f is an adjustable parameter close to unity. Fortunately, PCM gives us not only the partial charge at the silicon q(Si), but also the partial charges on all of the surrounding nuclei allowing the anisotropy of the charge to be determined. The charge deviation (Δq) from the average isotropic charge and the deviation from axial symmetry (δq) are defined by
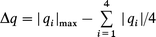 | (10a) |
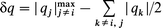 | (10b) |
Assuming that the silicon atom form four molecular orbitals using one s- and three p-orbitals, charge conservation requires
| Ps + Pxx + Pyy + Pzz = 4 − q(Si) | (11) |
The charge and charge deviation can be related to the orbital populations by
| Pxx = 1 − [q(Si) + qs(Si) + Δq + δq]/3 (12a) | (12) |
| Pyy = 1 − [q(Si) + qs(Si) + Δq]/3 (12b) | (13) |
| Pzz = 1 − [q(Si) + qs(Si) − 2Δq − δq]/3 (12c) | (14) |
where qs(Si) = 1 − Ps.
From these relationships Pu and 〈a0/r3〉np are directly related to the silicon partial charge q(Si). The main obstacle remaining is the evaluation of the ΔE parameter, whose values can have a substantial influence on the paramagnetic contribution. The approach outlined in this manuscript entails the initial optimization of the parameters R0, f and ΔE for a standard set of reference molecules for which structures and absolute 29Si chemical shielding values are known. The remaining parameters in eqns. (2)–(12) (σd, q(Si) and qs(Si)) are fixed by molecular geometry and the assumptions about the electronegativity and hardness of the atoms. Fixing these parameters obtained for the reference compounds allows the 29Si chemical shifts for the remaining alkoxysilane species investigated to be directly evaluated.
4 Results and discussion
The 29Si NMR chemical shifts for the organically modified silane compounds, MexSi(OR)4 − x (OR = OMe, OEt) under different solution conditions were evaluated and are provided in Table 1S in the supplementary material.† Chemical shifts (with respect to internal TMS) increase from approximately +0.2 to +2 ppm on going from a neat alkoxy solution to a 2.24 M solution in the parent alcohol. The symmetric TEOS and TMOS compounds show the smallest variation with only a +0.2 to +0.25 ppm increase. After the addition of three equivalents of water (Rw = 3.0) to the stock solution (and prior to extensive condensation) an additional increase in the 29Si chemical shift of approximately +1 ppm was observed for the entire series, except TEOS and TMOS where only a ∽+0.2 ppm variation was observed. These changes in the 29Si NMR chemical shifts clearly justify the importance of defining the solution conditions during investigations where the magnitude of chemical shift variations due to solvent composition are comparable to the differences produced by hydrolysis. In the work described here this is the situation encountered, where the observed chemical shift dispersion due to hydrolysis of methyl modified alkoxy silanes in very small and could be easily masked by changes in the composition of the solution. Due to the influence of the solvent, the chemical shifts for the methyl alkoxy silane series discussed in this paper were all obtained under identical conditions of 2.24 M and Rw = 3.0. This strong solvent dependence also precludes the direct comparison of 29Si NMR chemical shifts previously reported in the literature. The 29Si NMR chemical shifts for the MexSi(OR)y(OH)4 − x − y (OR = OMe, OEt) series are listed in Table 1. The use of consistent solution conditions allows the variation of the chemical shift (Δδ) with each OH functional group incorporated into the alkoxysilane during hydrolysis to be directly compared, and are given in Table 1.| Silane | δ(ppm)b | σ(ppm)c | Δδd |
|---|---|---|---|
| a 2.24 M solutions, Rw = 3.0, 298 K.b All chemical shifts internally referenced to TMS (0.1%), with higher frequencies corresponding to positive δ values.c Chemical shielding values assuming σ = 386.5 ppm for TMS.30d Δδ is the relative chemical shift with respect to the unhydrolyzed monomer species. | |||
| Si(OEt)4 | −81.82 | 450.32 | — |
| Si(OEt)3(OH) | −78.88 | 447.38 | +2.94 |
| Si(OEt)2(OH)2 | −76.45 | 444.95 | +5.37 |
| Si(OEt)(OH)3 | −74.34 | 442.84 | +7.48 |
| Si(OH)4 | −72.43 | 440.93 | +9.39 |
| MeSi(OEt)3 | −42.14 | 410.64 | — |
| MeSi(OEt)2(OH) | −40.43 | 408.93 | +1.71 |
| MeSi(OEt)(OH)2 | −39.03 | 407.53 | +3.11 |
| MeSi(OH)3 | −37.85 | 406.35 | +4.29 |
| (Me)2Si(OEt)2 | −3.85 | 372.35 | — |
| (Me)2Si(OEt)(OH) | −3.41 | 371.91 | +0.44 |
| (Me)2Si(OH)2 | −4.17 | 372.67 | −0.32 |
| (Me)3Si(OEt) | 17.78 | 386.28 | — |
| (Me)3Si(OH) | 14.60 | 383.10 | −3.18 |
| Si(OMe)4 | −78.29 | 446.79 | — |
| Si(OMe)3(OH) | −76.03 | 444.53 | +2.26 |
| Si(OMe)2(OH)2 | −74.46 | 442.96 | +3.83 |
| Si(OMe)(OH)3 | −73.22 | 441.72 | +5.07 |
| Si(OH)4 | −72.21 | 440.71 | +6.08 |
| MeSi(OMe)3 | −38.24 | 406.74 | — |
| MeSi(OMe)2(OH) | −38.11 | 406.61 | +0.13 |
| MeSi(OMe)(OH)2 | −38.13 | 406.63 | +0.11 |
| MeSi(OH)3 | −38.43 | 406.93 | −0.19 |
| (Me)2Si(OMe)2 | 1.25 | 367.25 | — |
| (Me)2Si(OMe)OH | −1.46 | 369.96 | −2.71 |
| (Me)2Si(OH)2 | −4.05 | 372.55 | −5.30 |
| (Me)3Si(OMe) | 20.72 | 389.22 | — |
| (Me)3Si(OH) | 14.84 | 383.34 | −5.88 |
Fig. 1 shows the correlation between Δδ and the number of attached hydroxy groups for compounds with differing number of attached methyl groups in both the methoxy and ethoxy silanes. For the unmodified alkoxy silanes, Si(OR)y(OH)4 − y (OR = OMe, OEt), a positive increase in the chemical shift was observed for each OH group added during hydrolysis. For the ethoxy series an increase of ∽+2 to +3 ppm was observed for each hydroxy group, while for the methoxy series a slightly smaller shift of ∽+1 to +2 ppm per hydroxy group was observed. For the single methyl modified ethoxy series, (x = 1) MexSi(OEt)y(OH)4 − x − y, a variation of approximately +1.2 to +1.7 ppm shift per hydroxy group was observed, while for the methyl modified methoxy series (x = 1) MexSi(OMe)y(OH)4 − x − y both positive and negative shifts on the order of ±0.1 to ±0.2 ppm per hydroxy group was observed. Both positive and negative chemical shift variations with hydroxy substitution was also observed for the dimethyl substituted series, (x = 2) MexSi(OEt)y(OH)4 − x − y. For the trimethyl substituted ethoxy silanes, (x = 3) MexSi(OEt)y(OH)4 − x − y, and the di- and trimethyl substituted methoxy silanes, (x = 2 or 3) MexSi(OMe)y(OH)4 − x − y, negative chemical shift variations of approximately −3 to −6 ppm per hydroxy group were observed. As seen in Fig. 1 the addition of hydroxy groups can produce both negative and positive variations in the chemical shifts depending on the number of methyl substituents attached to the silicon, as well as the identity of the alkoxy group. An explanation of these trends based on semi-empirical predictions of the 29Si chemical shift are detailed below.
 | ||
| Fig. 1 Changes of the chemical shift variation (Δδ) with number of attached hydroxy groups (nH2O = 4 − x − y) in the alkoxy silane series (a) MexSi(OEt)y(OH)4 − x − y and (b) MexSi(OMe)y(OH)4 − x − y. Note that the addition of hydroxy groups produces both positive and negative variations in the chemical shift vs. the non-hydrolyzed alkoxy silanes. | ||
4.1 PCM model and calibration
The Theory section detailed the semi-empirical PCM procedure to predict the diamagnetic shielding [eqn. (3)] and the paramagnetic shielding [eqn. (6)]. To calibrate and validate eqns. (2)–(12), the 29Si NMR chemical shielding constants for a set of reference molecules, for which shielding constants and molecular structure are known, were evaluated. Previously the absolute 29Si chemical shielding for SiH4 (σ0 = 475.3±10 ppm), SiF4 (σ0 = 482±10 ppm), SiCl4 (σ0 = 384.15±10 ppm), SiMe4 (σ0 = 368.5±10 ppm) and SiO2 (quartz) (σ0 = 475.90±10 ppm) have been reported.30 In addition the chemical shielding for the symmetric compounds Si(OH)4, Si(OMe)4 and Si(OEt)4 reported in this study (Table 1S) were included in the original parameterization of the PCM model.Based on the molecular geometries of these reference compounds, the partial charge on silicon q(Si) was easily calculated using PCM. As a first approximation the mean excitation energy ΔE used in eqn. (6) is confined between the lowest UV absorption band and the ionization potential of the investigated compounds. If eqns. (2)–(12) are correct the absolute shielding constants of these reference compounds should be reproduced with just three adjustable parameters: ΔE, R0 and f, while the remaining parameters, σd, q(Si) and qs(Si) are directly determined by the geometry and the assumptions about the electronegativities and hardness of the atoms. In fact once R0 and f are known or fixed, eqn. (6) can be easily inverted to obtain the ΔE values from the experimental shielding constants.
Table 2S† shows the populations of silicon outer-valence orbitals deduced from PCM for the reference compounds. As expected, the s-orbital population (Ps) was found to be higher with good electron-donor ligands such as H−, CH3−, O22−, MeO− and EtO− and significantly lower with more electronegative ligands such as P−, Cl− and OH−. Using these PCM populations and a simplex optimization a minimum in the average error between theory and experiment for the 29Si chemical shielding of 0.2 ppm was obtained for R0 = 3.277, f = 3.155 and corresponding ΔE as presented in Table 3S.†
Fig. 2 shows that the average excitation energies, ΔE, vary smoothly with partial charge q(Si). The typical U-shaped curve obtained is not unexpected from a theoretical point of view and has been noted before.16Fig. 2 also provides an explanation for the quite surprising experimental observation that SiH4 and SiF4, which have very different electronic structures, nevertheless have very similar shielding constants. The basis for the similar ΔE values in these two compounds arises from the fact that for SiH4, ΔE approximates the HOMO–LUMO gap, whereas for SiF4, ΔE is more accurately described by the energy difference in atomic orbitals.
 | ||
| Fig. 2 Correlation between the average excitation energy (ΔE) and the partial charge on the silicon atom q(Si) for the eight reference compounds (see also Table 3S†). The fourth order polynomial ΔE = ∑n = 03anqn(Si) where a0 = 10.43, a1 = −27.95, a2 = 66.67 and a3 = −45.54, is shown for visual reference. | ||
The strong deshielding experimentally observed for TMS relative to SiH4 or SiCl4 relative to SiF4 (Table 3S) is also a direct consequence of the U-shaped dependence of ΔE on q(Si). From Fig. 2, these two pairs of molecules are located on opposite branches of the ΔE − q(Si) correlation with the reduced ΔE value observed for TMS reflecting a more polar covalent bond, and for SiCl4 a more covalent polar bond. For Si–O bonds the polarities are intermediate between SiCl4 and SiF4. This results in compounds containing SiO4 units being shielded relative to TMS or SiCl4, and deshielded relative to SiF4. The regular increase in ΔE observed in the series Si(OEt)4→Si(OMe)4→Si(OH)4→SiO2 is easily understandable in terms of the mean electronegativities 〈χ〉 of the ligands attached to silicon: OEt = 8.10<OMe = 8.35<OH = 9.23<O = 12.56, as this parameter is a direct measure of the Fermi level of the electrons in the compounds.
4.2 PCM analysis of 29Si chemical shielding
A similar analysis of 29Si shielding tensors can be performed for the series, MexSi(OR)y(OH)4 − x − y (OR = OMe, OEt). From PCM analysis the gross populations of the outer valence orbitals were determined and are given in Table 4S.† Fixing the radial parameters to the values obtained for the reference compounds, R0 = 3.277 and f = 3.155, the experimentally observed 29Si shielding constants can be reproduced by variation of a single adjustable parameter ΔE. The resulting parameters following optimization are shown in Table 2. As a check of the quality of these optimized values, Fig. 3 shows the variation of ΔE vs. the partial charge on silicon q(Si). The smooth variation between ΔE and q(Si) observed suggests that the approximations utilized are relatively good. This relationship between ΔE and q(Si) can be used to predict 29Si chemical shifts for other organically modified alkoxysilanes based on the determination of q(Si). PCM also allows an estimate of the chemical shielding anisotropy (CSA). As shown in Table 2, predicted CSA values range between 0 and 60 ppm, with a mean value of 39 ppm computed for the unsymmetrical silanes. Fortunately, 29Si chemical shielding parameters have been reported in the literature for the three compounds Me3Si(OMe) (Δσ = 40 ppm, η = 0.08), Me2Si(OMe)2 (Δσ = 47 ppm, η = 0) and MeSi(OMe)3 (Δσ = 39 ppm, η = 0.46).31 While the agreement is not perfect, the right order of magnitude and experimental trends are correctly predicted for Δσ (Δσ[SiX3Y]∽Δσ[SiY3X]<Δσ[SiX2Y2]). This observation also supports the PCM semi-empirical method.| Compound | σexp (ppm) | σiso (ppm)a | σd (ppm) | q(Si) | ΔE | Δσ (ppm) | η |
|---|---|---|---|---|---|---|---|
| a Error between experiment and theoretical shielding given in parenthesis. | |||||||
| Si(OEt)4 | 450.72 | 450.97(+0.25) | 1068.28 | 0.808 | 11.87 | 1.17 | 0.25 |
| Si(OEt)3(OH) | 447.38 | 447.96(+0.58) | 1068.12 | 0.814 | 11.90 | 3.60 | 0.26 |
| Si(OEt)2(OH)2 | 444.95 | 445.43(+0.48) | 1067.74 | 0.830 | 12.00 | 2.35 | 0.31 |
| Si(OEt)(OH)3 | 443.24 | 443.08(−0.16) | 1067.01 | 0.862 | 12.22 | 1.14 | 0.37 |
| Si(OH)4 | 440.82 | 440.79(−0.03) | 1066.87 | 0.917 | 12.60 | 0.10 | 0.00 |
| MeSi(OEt)3 | 412.56 | 412.75(+0.19) | 1053.19 | 0.640 | 10.85 | 29.05 | 0.33 |
| MeSi(OEt)2(OH) | 408.93 | 408.93(−0.00) | 1053.04 | 0.642 | 10.86 | 29.76 | 0.32 |
| MeSi(OEt)(OH)2 | 407.53 | 406.90(−0.63) | 1052.60 | 0.664 | 11.01 | 29.45 | 0.32 |
| MeSi(OH)3 | 406.93 | 406.80(−0.13) | 1052.63 | 0.716 | 11.31 | 31.36 | 0.32 |
| Me2Si(OEt)2 | 374.07 | 374.10(+0.03) | 1038.28 | 0.456 | 9.71 | 53.35 | 0.14 |
| Me2Si(OEt)(OH) | 371.91 | 372.27(+0.36) | 1038.08 | 0.467 | 9.78 | 55.69 | 0.13 |
| Me2Si(OH)2 | 372.44 | 372.05(−0.39) | 1038.09 | 0.504 | 10.02 | 58.39 | 0.12 |
| Me3Si(OEt) | 353.84 | 353.39(−0.45) | 1023.21 | 0.287 | 8.73 | 31.36 | 0.00 |
| Me3Si(OH) | 353.43 | 352.32(−1.11) | 1024.04 | 0.319 | 8.91 | 35.95 | 0.00 |
| Si(OMe)4 | 447.31 | 446.55(−0.76) | 1067.98 | 0.817 | 11.94 | 0.00 | 0.00 |
| Si(OMe)3(OH) | 444.53 | 444.81(+0.28) | 1067.69 | 0.831 | 12.01 | 1.52 | 0.33 |
| Si(OMe)2(OH)2 | 442.96 | 442.57(−0.39) | 1067.25 | 0.849 | 12.14 | 0.37 | 0.47 |
| Si(OMe)(OH)3 | 441.72 | 441.71(−0.01) | 1066.66 | 0.876 | 12.32 | 1.17 | 0.41 |
| MeSi(OMe)3 | 408.61 | 407.98(−0.63) | 1053.06 | 0.637 | 10.84 | 30.27 | 0.30 |
| MeSi(OMe)2(OH) | 406.61 | 406.34(−0.27) | 1052.83 | 0.649 | 10.91 | 30.62 | 0.31 |
| MeSi(OMe)(OH)2 | 406.63 | 407.46(+0.83) | 1052.41 | 0.682 | 11.09 | 32.96 | 0.31 |
| Me2Si(OMe)2 | 370.48 | 371.33(+0.85) | 1038.25 | 0.450 | 9.66 | 52.96 | 0.13 |
| Me2Si(OMe)(OH) | 369.96 | 370.07(+0.11) | 1038.02 | 0.464 | 9.76 | 55.48 | 0.11 |
| Me3Si(OMe) | 351.18 | 352.10(+0.92) | 1022.84 | 0.289 | 8.72 | 29.96 | 0.00 |
| Me4Si | 368.50 | 368.55(+0.05) | 1008.13 | 0.121 | 8.10 | 0.00 | 0.00 |
 | ||
| Fig. 3 Correlation between the average excitation energy (ΔE) and the partial charge on the silicon atom q(Si) for the alkoxy silane series MexSi(OR)y(OH)4 − x − y (R = Me, Et). A fourth order polynomial curve ΔE = ∑n = 03anqn(Si) where a0 = 8.155, a1 = −3.03, a2 = 24.64 and a3 = −28.48 is shown for visual reference. | ||
The goodness of the fit between experimental and theoretical 29Si chemical shielding is shown in Fig. 4, where the correlation of fit was r2 = 0.9998 and an average error of 0.5 ppm for the isotropic shielding constants. This excellent agreement again supports the parameterization and allows insight into balance between σd, 〈(a0/r)3〉np, ΔE and Pu in these compounds. From these results, it is clear that the deshielding observed during TEOS or TMOS hydrolysis results from the interplay between shielding action of the ΔE term and its ability to cancel the conjugate deshielding action of σd and 〈(a0/r)3〉3p. This leaves the deshielding contribution from the increase in Pu as an important factor for the observed chemical shift variations in the Si(OEt)4 − x(OH)x and Si(OMe)4 − x(OH)x series. When electronegative OH groups replace less electronegative ethoxy groups, the silicon s-orbital populations are more affected than the orbitals (see Table 4S). It is this preferential overlap of OH groups with the silicon s-orbital which is responsible for the increased population asymmetry (Pu) in the p-orbital, thus producing the deshielding of the 29Si nucleus with hydrolysis of TEOS or TMOS. The methoxy group is more electronegative than the ethoxy substituent, with the Pu variation being accordingly reduced. This increase in electronegativity explains the reduced chemical shift range observed for TMOS hydrolysis species relative to TEOS hydrolysis species. A similar argument is observed for the MeSi(OEt)3 − x(OH)x series, with the reduced variation in Pu producing smaller deshielding effects that in TEOS.
 | ||
| Fig. 4 The correlation between the observed chemical shielding (σexp) and the theoretically predicted chemical shielding (σtheory) using the PCM model. The correlation of linear fit r2 = 0.9998 was obtained. | ||
In the MeSi(OMe)3 − x(OH)x and Me2Si(OEt)2 − x(OH)x series, there is nearly an equal compensation between the deshielding action of the 〈(a0/r)3〉3p term and the shielding action of the ΔE. In these compounds the changes in the Pu term can now produce either relative shielding or deshielding of the 29Si nucleus. The almost exact balance of terms leads to the very small chemical shift variations observed. For the limited Me3Si(OEt)1 − x(OH)x, Me2Si(OMe)2 − x(OH)x and Me3Si(OMe)1 − x(OH)x series there is either a very small change or an increase in the diamagnetic shielding with hydroxy addition, plus a shielding effect of the decreasing Pu term. These decreases in the orbital asymmetry suggest that with substitution of the electronegative OH group for ethoxy or methoxy, the effect on the population of p- and s-orbitals are very similar in silanes with a higher number of methyl substitutions. In general the chemical shifts observed for the hydrolysis of these modified silanes is dominated by the population asymmetry Pu, with the effects of the 〈(a0/r)3〉3p and ΔE nearly balancing the negligible changes in σd.
A different picture emerges from the analysis of the MexSi(OR)4 − x series. In this series the 〈(a0/r)3〉3p and ΔE terms still produce opposite effects, but the radial term produces a shielding trend as the partial charge on silicon q(Si) decreases with increasing x, while ΔE produces a deshielding effect as it decreases with increasing x. The diamagnetic contribution σd is no longer negligible and has a constant deshielding effect. In addition, the Pu contribution is high for oxygen-rich compounds and tends to be low for carbon-rich ones. With the combination of these effects, the result is a deshielding trend with increasing x, except for the end of the series Me3SiOR and TMS. In that case the high shielding effect results from the large decrease in q(Si) produced by removing the last oxygen, and cannot be compensated by the very modest ΔE and Pu variations. This same effect gives rise to the well-known ‘‘sagging pattern ’’ of 29Si NMR shielding in RxSiX4 − x series where R is an alkyl group and X an electronegative substituent.
An important conclusion from this study is that the 〈(a0/r)3〉3p and ΔE terms tend to cancel each other, leaving the domination of the paramagnetic shielding to the orbital unbalance Pu term. It was also demonstrated that it is not the absolute values of the R0, f or ΔE parameters which are important, but rather the correlation in the p-orbitals expansion to increases or decreases in ΔE. These two parameters, 〈(a0/r)3〉3p and ΔE, cannot be varied in an independent way, but instead are strongly related. In previous work performed on 29Si NMR shielding constants, the so-called ‘‘average excitation energy’’ approximation is surely a very good one but the concept of a ‘‘constant average excitation energy ’’ is not sufficient. Instead the 29Si chemical shielding can be better approximated by maintaining a constant 〈(a0/r)3〉3p/ΔE ratio.
Acknowledgements
This work was partially supported (TMA) by the Basic Energy Science (BES) program at Sandia National Laboratories. Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the US Department of Energy under Contract No. DE-AC04-94AL8500.References
- R. J. Hook, J. Non-Cryst. Solids, 1996, 195, 1 Search PubMed.
- T. M. Alam, R. A. Assink and D. A. Loy, Chem. Mater., 1996, 8, 2366 CrossRef CAS.
- Y. Sugahara, T. Inoue and K. Kuroda, J. Mater. Chem., 1997, 7, 53 RSC.
- F. Brunet, J. Non-Cryst. Solids, 1998, 231, 58 Search PubMed.
- T. M. Alam, R. A. Assink, S. Prabakar and D. A. Loy, Magn. Reson. Chem., 1996, 34, 603 CrossRef CAS.
- T. M. Alam, Spectrochim. Acta Part A, 1997, 53, 545 CrossRef.
- P. Lux, F. Brunet, H. Desvaux and J. Virlet, J. Chim. Phys., 1994, 91, 409 Search PubMed.
- P. Lux, F. Brunet, J. Virlet and B. Cabane, Magn. Reson. Chem., 1996, 34, 100 CrossRef CAS.
- P. Lux, F. Brunet, J. Virlet and B. Cabane, Magn. Reson. Chem., 1996, 34, 173 CrossRef CAS.
- J. F. Hinton, P. L. Guthrie, P. Pulay and K. Wolinski, J. Magn. Reson., 1993, 103, 188 CrossRef CAS.
- D. Cremer, L. Olsson and H. Ottosson, J. Mol. Struct. (THEOCHEM.), 1994, 313, 91 CrossRef.
- H. Nakatsuji, T. Nakajima, M. Hada, H. Takashima and S. Tanaka, Chem. Phys. Lett., 1995, 247, 418 CrossRef CAS.
- R. Wolff and R. Radeglia, J. Mol. Struct. (THEOCHEM.), 1994, 313, 111 CrossRef.
- D. Kovacek, Z. B. Maksic, S. Elbel and J. Kudnig, J. Mol. Struct. (THEOCHEM.), 1994, 304, 247 CrossRef.
- G. Englehardt, R. Radeglia, H. Jancke, E. Lippmaa and M. Mägi, Org. Magn. Reson., 1973, 5, 561 Search PubMed.
- M. Henry, C. Gerardin and F. Taulelle, Electronegativity-Based Computation of 29Si Chemical Shifts, ed. M. Henry, C. Gerardin and F. Taulelle, Materials Research Society, San Francisco, CA, 1992, vol. 271, p. 243. Search PubMed.
- D. T. Pegg, D. M. Doddrell and M. R. Bendall, J. Chem. Phys., 1982, 77, 2745 CrossRef CAS.
- S. G. Bratsch, J. Chem. Educ., 1988, 65, 34 Search PubMed.
- J. C. Slater, J. Chem. Phys., 1964, 41, 3199 CrossRef CAS.
- M. Karplus and T. P. Das, J. Chem. Phys., 1961, 34, 1683 CrossRef CAS.
- A. Abragam, in Principles of Nuclear Magnetism, ed. R. K. Adair, R. J. Elliot, W. C. Marshall and D. H. Wilkinson, Clarendon Press, Oxford, 1961, p. 599. Search PubMed.
- A. Carrington and A. D. McLachlan, in Introduction to Magnetic Resonance, ed. S. A. Rice, Harper & Row, New York, 1967, p. 266. Search PubMed.
- W. H. Flygare and J. Goodisman, J. Chem. Phys., 1968, 49, 3122 CrossRef CAS.
- A. Velenik and R. M. Lynden-Bell, Mol. Phys., 1970, 19, 371 CAS.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801 CrossRef CAS.
- R. G. Pearson, Coord. Chem. Rev., 1990, 100, 403 CrossRef CAS.
- M. Henry, Coord. Chem. Rev., 1998, 170–180, 1109 CrossRef.
- K. M. S. Saxena and P. T. Narasimhan, Int. J. Quantum Chem., 1967, 1, 731 CAS.
- W. B. Moniz and C. F. Poranski, J. Magn. Reson., 1973, 11, 62 CAS.
- C. J. Jameson and A. K. Jameson, Chem. Phys. Lett., 1988, 149, 300 CrossRef CAS.
- M. G. Gibby, A. Pines and J. S. Waugh, J. Am. Chem. Soc., 1972, 94, 6231 CrossRef CAS.
Footnote |
| † Available as supplementary material (SUP 57681; 5 pp.) deposited with the British Library. Details are available from the Editorial Office. For direct electronic access see http://www.rsc.org/suppdata/cp/a9/a906445a. |
| This journal is © the Owner Societies 2000 |